Low dose CBCT reconstruction via prior contour based total variation regularization (PCTV): a feasibility study

Abstract

Purpose

Compressed sensing reconstruction using total variation (TV) tends to over-smooth the edge information by uniformly penalizing the image gradient. The goal of this study is to develop a novel prior contour based TV (PCTV) method to enhance the edge information in compressed sensing reconstruction for CBCT.

Methods

The edge information is extracted from prior planning-CT via edge detection. Prior CT is first registered with on-board CBCT reconstructed with TV method through rigid or deformable registration. The edge contours in prior-CT is then mapped to CBCT and used as the weight map for TV regularization to enhance edge information in CBCT reconstruction. The PCTV method was evaluated using extended-cardiac-torso (XCAT) phantom, physical CatPhan phantom and brain patient data. Results were compared with both TV and edge preserving TV (EPTV) methods which are commonly used for limited projection CBCT reconstruction. Relative error was used to calculate pixel value difference and edge cross correlation was defined as the similarity of edge information between reconstructed images and ground truth in the quantitative evaluation.

Results

Compared to TV and EPTV, PCTV enhanced the edge information of bone, lung vessels and tumor in XCAT reconstruction and complex bony structures in brain patient CBCT. In XCAT study using 45 half-fan CBCT projections, compared with ground truth, relative errors were 1.5%, 0.7% and 0.3% and edge cross correlations were 0.66, 0.72 and 0.78 for TV, EPTV and PCTV, respectively. PCTV is more robust to the projection number reduction. Edge enhancement was reduced slightly with noisy projections but PCTV was still superior to other methods. PCTV can maintain resolution while reducing the noise in the low mAs CatPhan reconstruction. Low contrast edges were preserved better with PCTV compared with TV and EPTV.

Conclusion

PCTV preserved edge information as well as reduced streak artifacts and noise in low dose CBCT reconstruction. PCTV is superior to TV and EPTV methods in edge enhancement, which can potentially improve the localization accuracy in radiation therapy.

I. Introduction

Cone-beam computed tomography (CBCT) has been widely used in radiation therapy (RT) for on board target localization. 3D CBCT has been developed to localize targets with minimal motion, such as brain tumor; while 4D CBCT has been developed to localize targets affected by respiratory motion, such as lung and liver tumors in the image guided RT [1–6]. CBCT delivers imaging dose to patients through a large volume of the body. Accumulated imaging dose from repeated 3D/4D CBCT scans to the normal tissue may be clinically significant, which requires re-planning in order to satisfy the dose constrains [7–9]. In addition, high imaging dose increases the risk of secondary cancer induction. Therefore, low dose CBCT with adequate image quality for accurate target localization is highly demanded in radiation therapy.

CBCT imaging dose is positively correlated with the acquired projection number and exposure level (mAs) per projection. Reducing one of these two acquisition parameters or both will reduce the CBCT imaging dose. However, the CBCT image quality will suffer from the low dose acquisition when using the conventional Feldkamp, Davis, and Kress (FDK) algorithm[10] for image reconstruction. Reducing the projection number will violate the Nyquist-Shannon sampling theorem leading to serious streak artifacts, while reducing the exposure will reduce the number of photons detected leading to increased noise level in the reconstructed images.

To solve these issues, compressed sensing methods based on total variation (TV) or total generalized variation (TGV) regularization have been developed to improve the image quality of low dose CT/CBCT [11–15]. Although these methods successfully reduce the streak artifacts and noise, they also tend to over-smooth the edge information by uniformly penalizing the image gradient throughout the entire images in the TV regularization. This blurriness of edges can potentially affect the diagnosis in radiology and target localization in radiation oncology. To overcome this limitation of TV based methods, edge guided total variation methods were developed for both MR and CT reconstruction [16–20]. In CT reconstruction, edge preserving TV (EPTV) [16] and adaptive-weighted TV (awTV) [18] were developed to enhance the edge information in the TV based method by deriving the isotropic and anisotropic edges expressed as the exponential function of image gradient from intermediate images on generated during the iterative reconstruction. Reweighted TV optimization can also enhance edge sharpness by normalizing the TV weighting term by the image gradient in the in adaptively reweighted TV[20] and few-view reweighted sparsity hunting (FRESH) method[19]. In these reweighted based optimization methods, TV weight will be reduced in the edge regions with high image gradient to reduce the smoothing of edges. Reweighted anisotropic TV, which combined reweighted technology with anisotropic TV was then proposed to further improve reconstruction performance[21]. Although improvements were achieved over TV based method, the capability of deriving and enhancing the edges in these methods was limited by the quality of the intermediate images, which was dependent on the projection number and the exposure level per projection. As a result, the edges were still blurred when reconstructing CBCT using these adaptive weighted TV methods from relatively low number of projections or low mAs [16].

Alternatively, other compressed sensing based methods used prior images for low dose 4D-CT/CBCT reconstruction[22]. In the prior image constrained compressed sensing (PICCS)[23] method, prior images was used as an additional constraint to minimize image total variation. Thus, the image quality of PICCS may be affected by quality of the prior images, which is susceptible to motion artifacts[23]. Adaptive prior image constrained compressed sensing (APICCS) and penalized weighted least-square using normal-dose image induced total variation prior (PWLS-ndiTV) were then proposed to enhance the image quality of PICCS by adaptive weighted constraint considering mismatch regions between prior image and on-board CBCT[24, 25]. Other method such as prior image based anisotropic edge guided TV (PIEGTV) was developed to improve previous awTV methods using edge information of prior image as initial weights and updated based on intermediate edge images[26]. Compensation of mismatch between prior image and reconstructed volume was then considered via registration (rigid or deformable) of prior image and combined with reconstruction model to improve image quality and accuracy.[27–29] Moreover, another approach using prior images and limited angle projections, the limited-angle intrafraction verification (LIVE) method, has been proposed for 4D CBCT reconstruction using a motion model from prior knowledge and a free-form deformation (MM-FD) technique [30–33]. Adaptive prior knowledge guided LIVE system was then developed to further reduce the scan angle needed for 4D-CBCT reconstruction[34]. In principle, low dose CBCT reconstruction accuracy can be improved with the information from prior images.

In this study, we proposed a prior contour based TV (PCTV) method, which uses the existing edge contour information from high quality prior planning CT images for edge enhancement in on-board CBCT reconstruction. Since the edge information is derived from CT instead of the low dose CBCT, the method is more robust against projection number and mAs reduction in CBCT acquisition compared with previous methods. To our knowledge, this is the first-time prior edge information is used for edge enhancements in compressed sensing reconstruction. With the addition of high-quality edge information, PCTV can substantially improve the CBCT image quality by removing noise and streak artifact while preserving edge sharpness. The reconstructed images of TV, EPTV and new PCTV were evaluated using digital 4D lung phantom, physical phantom and clinical head patient data both qualitatively and quantitatively. The results indicated that the new PCTV method is superior to previous EPTV and conventional TV methods in preserving edge information while minimizing the streak artifacts and noise in the images.

II. Methods and Materials

II.A. Prior contour based TV reconstruction

In traditional TV based CT/CBCT reconstruction, TV is defined as the integration of the gradient of an image f in the following formula:

$${\Vert f\Vert }_{TV}=\int {\Vert \nabla f\left(x\right)\Vert }_{2}dx$$ (1)

The goal of TV based reconstruction is to minimize the TV of the image being reconstructed:

$$f\ast =\mathit{argmin}{\Vert f\Vert }_{TV}$$ (2)

Subject to the data fidelity constraint:

$${\Vert \mathit{DRR}\left(f\right)-\mathit{Proj}\Vert }_2^2\le \epsilon$$ (3)

where f is the image to be reconstructed, and DRR(f) is forward projection of image f. Proj represents the on-board CBCT projections acquired.

TV regularization has shown to be effective in reducing the streak artifacts and noise in low dose CT/CBCT reconstruction. However, as defined in Eq. (1), TV minimization uniformly penalizes the image gradient throughout the entire image, which can lead to over-smoothing of edges. The PCTV method aims to solve this problem by extracting the edge information from the prior CT images as prior information to guide the TV minimization for the edge enhancement.

The general flowchart of the PCTV is shown in Figure 1. First, prior contour was generated from the prior CT using a Sobel based edge detection filter. Second, an initial on-board CBCT is reconstructed from the low dose projections (limited projection number and/or low mAs projections) using the TV method. Then, CT is registered with the initial on-board CBCT using either rigid or deformable registration depending on the imaging site to generate a transformation map which was in turn used to transform the prior contour to the on-board contour for new CBCT reconstruction. The on-board contour was finally converted into a weight map, w(x) in Equation (4), as a TV regularization term to reduce the TV minimization enforcement at the edges in PCTV reconstruction.

Figure 1.

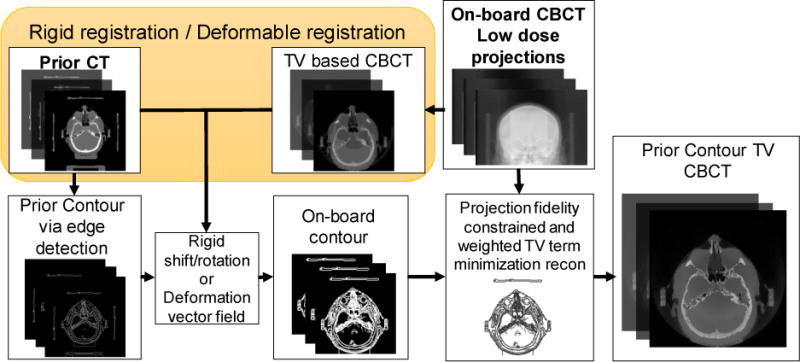
Flowchart of the PCTV method.

$$\text{PCTV}\left(f\right)=\int w\left(x\right){\Vert \nabla f\left(x\right)\Vert }_{2}dx$$ (4)

The ASD-POCS[12] algorithm was used in the PCTV iterative reconstruction to balance the minimization of PCTV defined in Equation (4) and the data fidelity constraints in Equation (3).

II.B. Prior contour based weight map generation

In this study, planning CT was used as prior CT and prior contour information was extracted automatically from prior CT via edge detection. Prior contour based weight map generation was implemented in the following steps as shown in Figure 2:

1. Prior edge information was extracted from the prior CT by MATLAB (The MathWorks, Inc., Natick, MA) using Sobel edge detection to generate initial contour map. The edge region was assigned to 1 and non-edge region was assigned to 0;

2. The edge width was increased from 1 pixel to 3 pixels in this project with two steps. 2D Gaussian smoothing filter (3 × 3 kernel size, standard deviation σ = 0.65) was used in the first step to smooth the edge. Then, all pixels with value above zero were assigned to 1;

3. 3D Gaussian smoothing (5 × 5 × 5 kernel size and standard deviation σ = 0.65) was applied to avoid abrupt change in the edge map from slice to slice;

4. Registration vectors were then applied to form the on-board contour map;

5. TV weight map w(x) was converted from the contour map, map_contour (x), with a global

Figure 2.

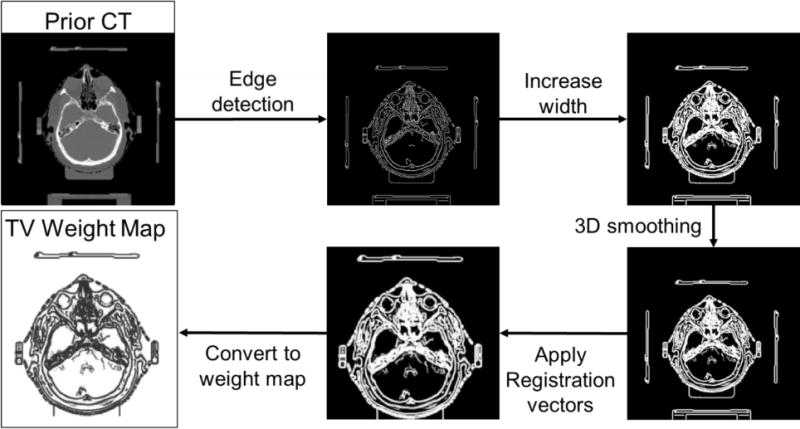
Flowchart of weight map generation.

weighting factor as described in Equation (5). If the global weighting factor is zero, then PCTV will become the conventional TV method.

$$w\left(x\right)=1-\mathit{weighting}\ast ma{p}_{\mathit{contour}}\left(x\right)$$ (5)

II.C. PCTV implementation

The PCTV reconstruction algorithm is implemented by using the weight map from the prior CT to adaptively penalize the image gradient while preserving the edge sharpness. The detailed algorithm was shown in Figure 3 with the pseudo code and corresponding parameters. The orange section is the work flow for the weight map generation while the blue section is the main reconstruction algorithm applying the generated weight map w. The optimization algorithm was implemented using similar workflow with ASD-POCS described in [12]. In the workflow, PROJ is on-board CBCT projection as input for reconstruction in following steps: 1) initial image f was reconstructed via FDK. 2) Estimated projection DRR was calculated by forward projecting previous iteration image f and estimated update image df was reconstructed from the difference between PROJ and DRR. dDRR was then calculated from forward projection. 3) Line search with backtracking was used to find the optimal step size t in the gradient descent optimization algorithm. 4) After that update projection and image, weighted total variation minimization was applied. Parameters of reconstruction and weight edge map generation were optimized empirically.

Figure 3.

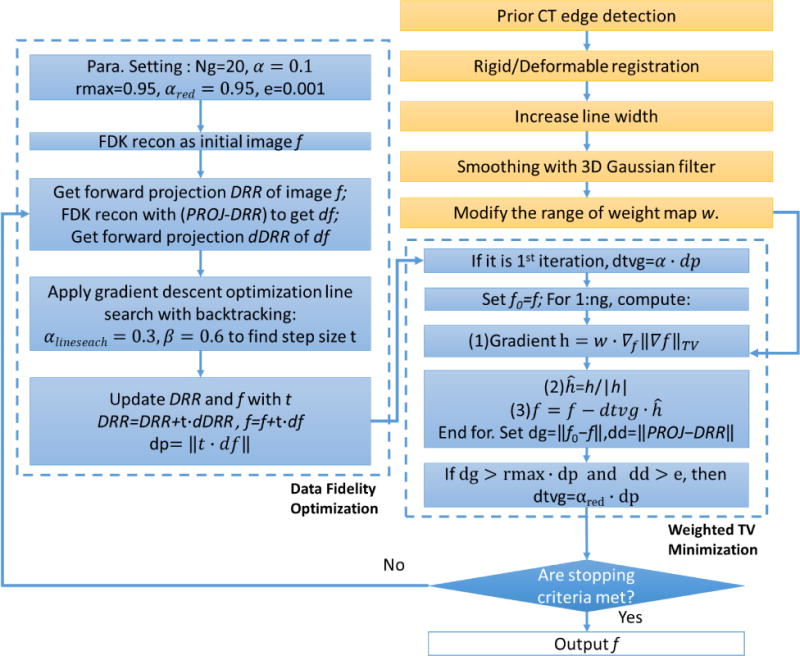
Detailed PCTV reconstruction algorithm.

II.D. Evaluation studies

The PCTV method was evaluated using digital Extended-cardiac-torso (XCAT) phantom[35], physical Catphan phantom and brain patient data.

II.D.1 XCAT simulation study

XCAT is a digital anthropomorphic phantom developed based on National Library of Medicine and patient datasets to model detailed human anatomy[35]. In this XCAT study, prior 4D-CT set and onboard ground truth CBCT and CBCT projections were simulated using XCAT. Lesion volume can be defined and inserted in the XCAT phantom. 4D images were generated by using specific anatomical parameters and respiratory profiles for a total of 10 phases. Respiratory profiles have two main curves (diaphragm curve and chest wall curve) to determine the motion in the superior-inferior (SI) direction and in the anterior-posterior (AP) direction respectively.

II.D.1.a Prior 4D CT, on-board volume and cone-beam simulation

Ten-phase 4D CT was first simulated by using XCAT with a 30mm diameter spherical lesion inserted in the right lung region as the prior 4D CT. The breathing peak-to-peak respiratory motion amplitudes used for both the body and the lesion were 3cm in SI direction and 2cm in AP direction, respectively. On-board volume was then simulated with the same anatomy but different respiratory motion amplitudes from the prior 4D CT. The breathing peak-to-peak amplitude of on-board volume was changed to 2cm in the SI direction and 1.2 cm in the AP direction. Half-fan on-board projections were simulated by the Siddon’s ray-tracing techniques based on on-board volume covering 360° for CBCT reconstruction in cone-beam geometry, which is based on the TrueBeam machine (Varian Medical Systems, Inc., Palo Alto, CA). The distance between source and detector was set to 150cm and the distance between source and isocenter was 100cm. The detector was shifted 16cm for half-fan mode acquisition. The matrix size for each projection was 512 × 384 pixels and each pixel size was 0.78 × 0.78 mm². Deformable registration was performed between the corresponding phases of the prior 4D CT and TV reconstructed 4D-CBCT using Velocity (Varian Medical Systems, Inc., Palo Alto, CA). After registration, deformation vector field was generated to transform the prior contour map to the on-board contour map. Finally, the TV weight map was calculated from the on-board contour map and used in the PCTV reconstruction using simulated limited on-board CBCT projections. Both CBCT and CT volumes at each phase were composed of 256 × 256 × 150 voxels with voxel size of 1.67 × 1.67 × 1.67 mm³.

II.D.1.b Effects of projection number

To investigate the effectiveness of edge enhancement with various sparseness of the projection sampling, 36 (10° per projection), 45 (8° per projection) and 60 (6° per projection) half fan projections were simulated and reconstructed with TV, EPTV and PCTV for evaluation and comparison.

II.D.1.c Effects of noise

Noise with both Poisson and normal distributions was also added directly to the projections to evaluate the robustness of the method using the following equation[31]:

$$P_{\mathit{noise}}\left(i,j\right)=-{\log }_{\mathrm{e}}\left(\frac{\mathit{Possion}\left(I_0{e}^{-P\left(i,j\right)}+\mathit{Normal}\left(0,{\sigma }^2\right)\right)}{I_0}\right)$$ (6)

Noise was added pixel by pixel in each projection. I₀ was set to 10⁵ as initial intensity of photons.

Different noise levels were simulated with specific a sigma value of normal distribution. Poisson and normal distributions simulated the nature of the x-ray quantum noise and the background electronic noise in the CBCT projections.

II.D.2. CatPhan Phantom study

In the physical phantom study, a CatPhan phantom (The Phantom Laboratory, Inc., Salem, NY) was centered in the prior CT scan and shifted in the CBCT scan to simulate patient set up deviations. Prior CT was acquired and reconstructed on Siemens CT simulator (Siemens Medical Solutions USA, Inc., Malvern, PA) and CBCT projections with low and high dose protocols were acquired on a Varian True-beam machine. The low dose full-fan protocol (10 mA/10 ms per projection, 100 kVp, and total 250 projections) was used for the PCTV study. The high dose full-fan protocol (53mA/15 ms per projection, 100 kVp, and total 250 projections) was used to acquire data to reconstruct reference images via FDK for the evaluation of the PCTV method. In the PCTV study, CBCT images was initially reconstructed with the TV method at low dose. Prior CT was then rigidly registered to low dose TV CBCT images via Velocity. Prior contour was generated from prior CT images and propagated using CT-CBCT rigid registration results to form the weight map for PCTV reconstruction. Reconstructed CBCT volume was 400 × 400 × 200 with the voxel size of 0.5 × 0.5 × 1mm³.

II.D.3 Patient study

In the patient study, clinical images of a brain patient, including planning CT (acquired on Philips CT simulator (Philips Medical Equipment, Inc., Andover, MA)) and CBCT projections (acquired by a Varian TrueBeam machine) were acquired under an IRB-approved protocol. Planning CT was acquired and reconstructed with 512 × 512 × 199 volume and the voxel size of 0.7422 × 0.7422 × 0.9933mm³ and used as prior CT. On-board full-fan projections with a clinical protocol (33 mA/15 ms per projection, 100kVp) were acquired over 200° angle. A total of 500 CBCT full-fan projections was used to reconstruct the reference images via off-line FDK reconstruction algorithm. Prior contour was generated via edge detection. Prior CT was rigidly registered to TV based CBCT via Velocity, and the registered shifts/rotations were used for on-board contour map generation for PCTV reconstruction. To investigate edge enhancement effect with various sparseness of the projection sampling, 41, 50 and 62 (the projection number reduction factors are 8, 10 and 12 respectively) full-fan projections were extracted and used to reconstruct CBCT based on TV, EPTV and PCTV methods for evaluation. Reconstructed CBCT volume was 256 × 256 × 150 with the voxel size of 1.0224 × 1.0224 × 2mm³.

II.E Evaluation methods

The results from TV, EPTV and PCTV were compared both qualitatively and quantitatively. Qualitative evaluation was used in all studies: digital XCAT, physical phantom and clinical patient data. In XCAT study, edge sharpness of bone and detectability of tiny structures such as lung vessels were evaluated visually as well as via image profile comparison. In the CatPhan study, resolution and low contrast edge sharpness were tested with the images from the line-pair slice and the contrast slice respectively. In the clinical head scan cases, we focused on the bone edge sharpness and small bone structure recovery. In addition to qualitative evaluation, as we have ground truth in the digital XCAT study, TV, EPTV and PCTV were also evaluated quantitatively by calculating the relative error and edge cross correlation coefficient[16] between the reconstructed images and ground truth images. Relative error is defined in Equation (7) to evaluate reconstruction accuracy.

$${\mathit{E}}_{\mathit{relative}\mathit{e}\mathit{r}\mathit{r}\mathit{o}\mathit{r}}=\frac{{\Vert \mathit{f}\mathit{-}{\mathit{f}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}\Vert }_{\mathit{2}}^{\mathit{2}}}{{\Vert {\mathit{f}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}\Vert }_{\mathit{2}}^{\mathit{2}}}$$ (7)

f is the reconstructed 3D volume images and f_truth is the ground truth of XCAT. Since edge information is important for tumor localization in radiation therapy, edge cross correlation coefficient was introduced as another matrix to evaluate edge enhancement effect[16].

$${\mathit{E}}_{\mathit{e}\mathit{d}\mathit{g}\mathit{e}\mathit{C}\mathit{C}}=\frac{\sum \left(\mathit{e}\left(\mathit{i}\mathit{,}\mathit{j}\right)-\overline{e}\right)\left({\mathit{e}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}\left(\mathit{i}\mathit{,}\mathit{j}\right)-\overline{{\mathit{e}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}}\right)}{\sqrt{\sum {\left(\mathit{e}\left(\mathit{i}\mathit{,}\mathit{j}\right)-\overline{e}\right)}^{\mathit{2}}\sum {\left({\mathit{e}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}\left(\mathit{i}\mathit{,}\mathit{j}\right)-\overline{{\mathit{e}}_{\mathit{t}\mathit{r}\mathit{u}\mathit{t}\mathit{h}}}\right)}^{\mathit{2}}}}$$ (8)

e is the binary edge map detected from the corresponding image for each slice while e_truth is the binary edge map detected from the ground truth.

In this study, both relative error and edge cross correlation coefficient were calculated within a region of interest (ROI) defined to contain the entire lung region of XCAT phantom. $\overline{{\mathit{E}}_{\mathit{e}\mathit{d}\mathit{g}\mathit{e}\mathit{C}\mathit{C}}}$ is the mean value of edge cross correlation of each slice in the ROI volume.

III. RESULTS

III.A. XCAT simulation

III.A.1 Edge enhancement with PCTV

CBCT images were reconstructed from 45 noise-free XCAT projections with TV, EPTV and our PCTV methods, compared with ground truth as shown in Figure 4. All methods were capable of removing the streak artifact even with limited projections. However, conventional TV and EPTV methods were not able to reconstruct some small structures and over-smoothed edges of anatomical structures. Compared to TV and EPTV method, the PCTV method is capable of capturing small structures such as lung vessels and further enhancing the edge information of both bone and tumor in XCAT reconstruction as shown in Figure 4(a)–(c). The horizontal intensity profile as pointed in the orange dot line in Figure 4(a) were plot in Figure 4(e) to illustrate better edge enhancement using the PCTV method. In addition, Table 1 shows the relative error and the edge cross correlation coefficient of TV, EPTV and PCTV images.

Figure 4.

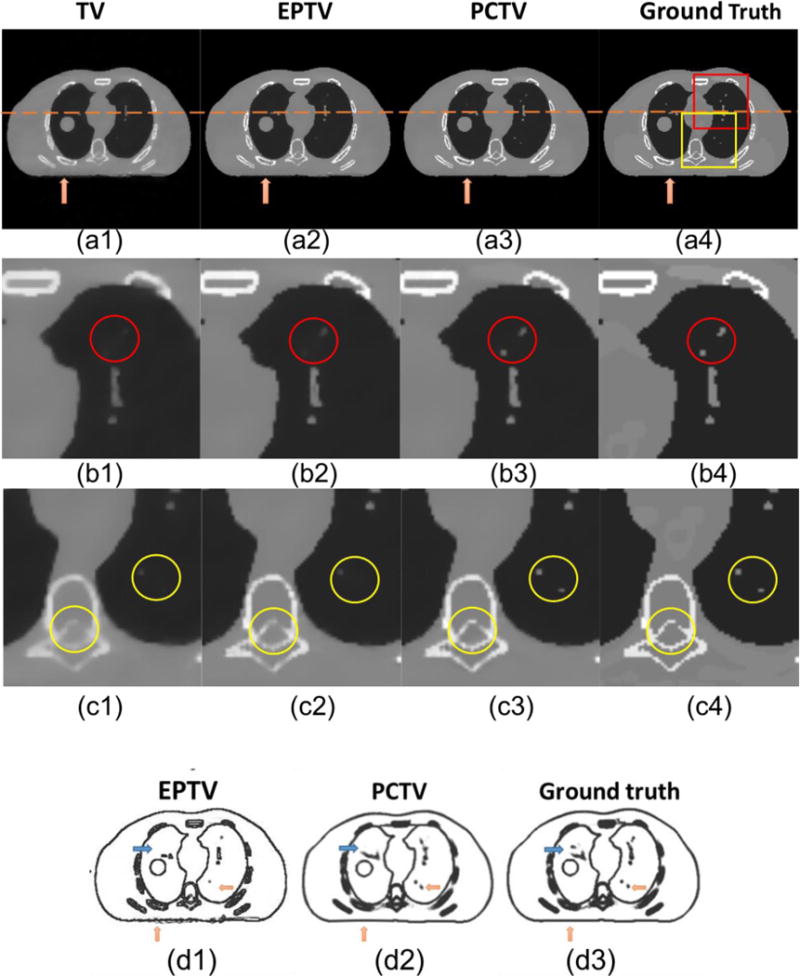
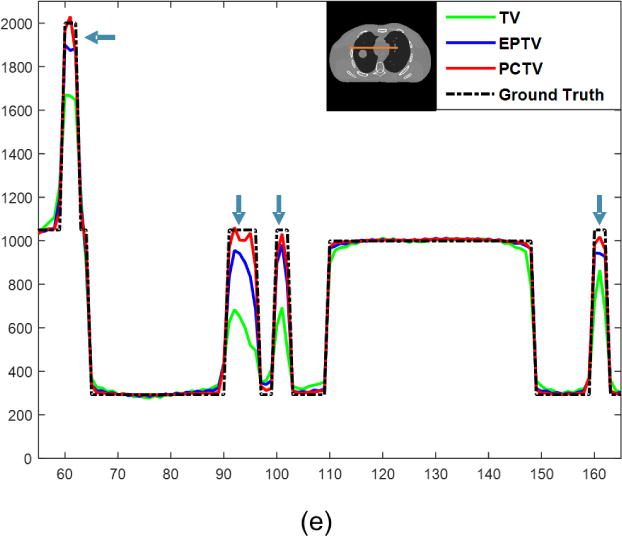
(a1)–(a4) show reconstructed 45 noise-free projections of XCAT with different breath amplitudes between prior images and on-board CBCT. (b1)–(b4) are the zoomed in images of red square in (a4) and (c1)–(c4) show the zooming in images of yellow square. Both red and yellow circles point that PCTV is superior to other methods in edge enhancement and small structures recovery. From left to right columns: TV, EPTV, PCTV and ground truth. In the fourth row, edge map were compared using 45 half-fan projections as shown in: (d1) weight map of last reconstruction iteration in EPTV, (d2) weight map used in PCTV and (d3) weight map extracted by edge detection on the ground truth images. (e) shows the profiles along the orange line of ground true image shown in (e).

Table 1.

Relative error and edge cross correlation of reconstructed TV, EPTV and PCTV images using 45 half-fan projections.

	TV	EPTV	PCTV
Relative error	1.5%	0.7%	0.3%
Edge cross correlation coefficient	0.66	0.72	0.78

Figure 4(d) shows the edge map of EPTV and PCTV compared with the ground truth edge map. As pointed by the orange arrows, weight map used in PCTV is much closer to the ground truth than the EPTV weight map. In the EPTV method, weight map was derived from the intermediate results, which may miss some small structures with very few projections. These small structures can be detected in the prior CT image and used to reduce TV minimization at edges in the PCTV method, as indicated by the orange arrows. In addition, EPTV will enhance the streak artifacts because EPTV treats the high gradient artifact as edge, which will be removed in the PCTV method. Moreover, blue arrows show that structure may also be missed in the PCTV edge map due to deformable registration error, which will be further discussed in IV. Discussion section.

III.A.2 Effects of projection number

Figure 5(a)–(c) shows the axial, coronal and sagittal reconstructed images of the noise-free XCAT study with different projection numbers. As expected, image quality was improved with more projections. The PCTV method provided superior results than the TV and EPTV methods in terms of enhancing edge sharpness and reconstructing small structures using limited projections, as indicated by red arrows. Furthermore, in 36 half-fan projections reconstruction, EPTV enhanced the streak artifacts as indicated by yellow arrows. The high gradient artifacts were treated as edges in the EPTV method, but will be removed in the PCTV method. To better evaluate the reconstruction performance, quantitative evaluation methods were included and the results were plotted in Figure 5 (d) and (e). PCTV was robust to the projection number reduction with low relative error and high edge correlation.

Figure 5.

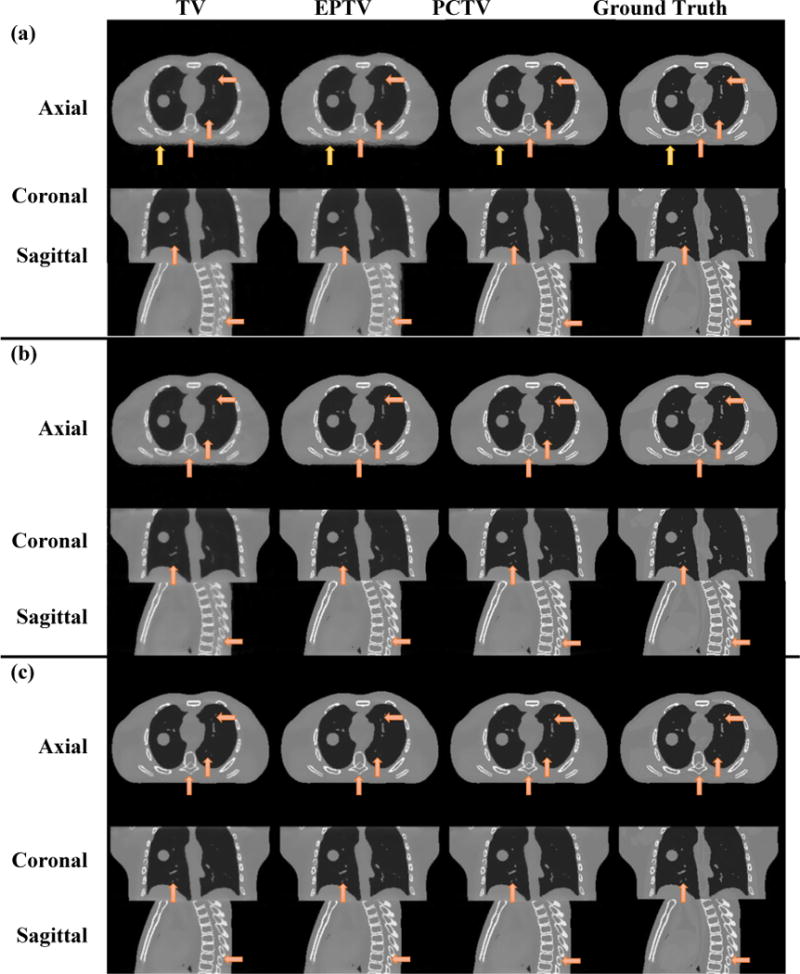
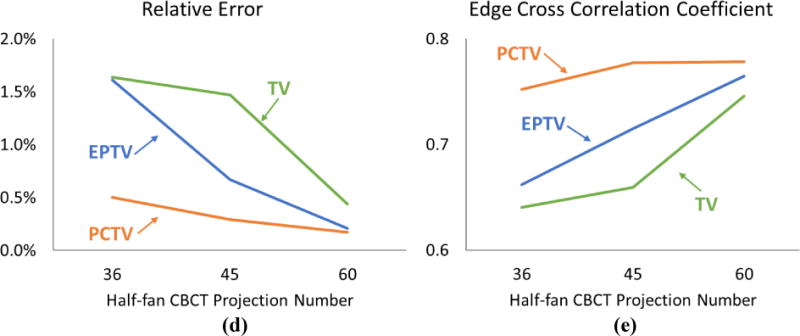
Comparisons of XCAT CBCT reconstructed via TV, EPTV and PCTV using a) 36projections, b) 45 projections and c) 60 projections. Ground truth are listed at the right column as the reference. In the quantitative evaluation, relative error and edge cross correlation for TV, EPTV and PCTV as functions of the number of CBCT projection number were plotted in (d) and (e), respectively.

III.A.3 Noise study

Figure 6 shows relative error and edge cross correlation of reconstructed images using 45 half-fan projections with increasing noise level. Image quality was decreased with increasing noise level for all reconstruction methods. The PCTV method is superior to the TV and EPTV methods for all noise level scenarios.

Figure 6.

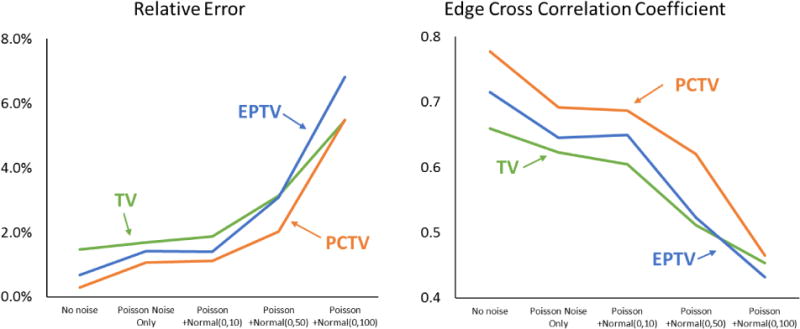
Relative error (left) and edge cross correlation (right) for TV, EPTV and PCTV as functions of noise level of 45 half-fan CBCT projections.

III.B. Physical phantom study

Figure 7 shows the reconstruction results of Catphan phantom. Figure 7(a)–(c) show the results of the multi-contrast slice. Some streak artifacts in FDK reconstructed images are caused by asymmetric projection among 200° acquisition and will be removed if using 360° projections. Low contrast visibility degrades with the low-dose protocol because of increasing noise. PCTV reduced the noise and maintained edge sharpness for all contrast, especially for the low contrasts as indicated by the arrows. Moreover, only one of four small white point structures were recovered in EPTV as shown in Figure 7(a3), but these four small structures were all reconstructed in PCTV. Besides, Figure 7(d)–(e) show the reconstruction results of Catphan resolution slice. Compared with high-dose FDK reconstructed images, low-dose FDK image still maintains the resolution about 6 lp/cm with increased noise. TV based method can reduce image noise, but the resolution is degraded. PCTV and EPTV can both maintain spatial resolution (6 lp/cm) while reducing image noise. Besides, some shading artifacts in the FDK, caused by 200° scan, can be removed by all three TV methods.

Figure 7.

Reconstructed images of Catphan Phantom. (1)–(4) show the images reconstruction by FDK, TV, EPTV, PCTV, respectively at 25mAs (250 projections, 10 mA/10ms per projections). (5) shows high dose FDK at 200mAs((250 projections, 53 mA/15 ms per projections). (a)–(c) show the reconstructed images of Catphan multi-contrast slice.(b1)–(b5) Zoom in the right block shown in (a5). (c1)–(c5) Zoom in the left block shown in (a5). Arrows in (b) and (c) show that PCTV is superior to EPTV and TV in the low contrast edge enhancement. (d)–(e) show the reconstructed images of Catphan resolution slice. (e1)–(e5) Zoom in the corresponding part in the first-row images. Arrows in (e) show that PCTV and EPTV can achieve 6 lp/cm while reduce noise, which is superior to TV.

III.C. Clinical data study

Figure 8(a) and (b) show the results of the head patient data study. The full-fan projection number was reduced from 500 to 50 for the low dose reconstruction. TV based method can remove streak artifacts and reduce noise for under-sampled projections. Most complex bone structures were missing in TV and partially recovered with EPTV. With the new PCTV method, bone structures especially in nasal and inner ear regions were reconstructed, which is comparable to full-sampling FDK images.

Figure 8.

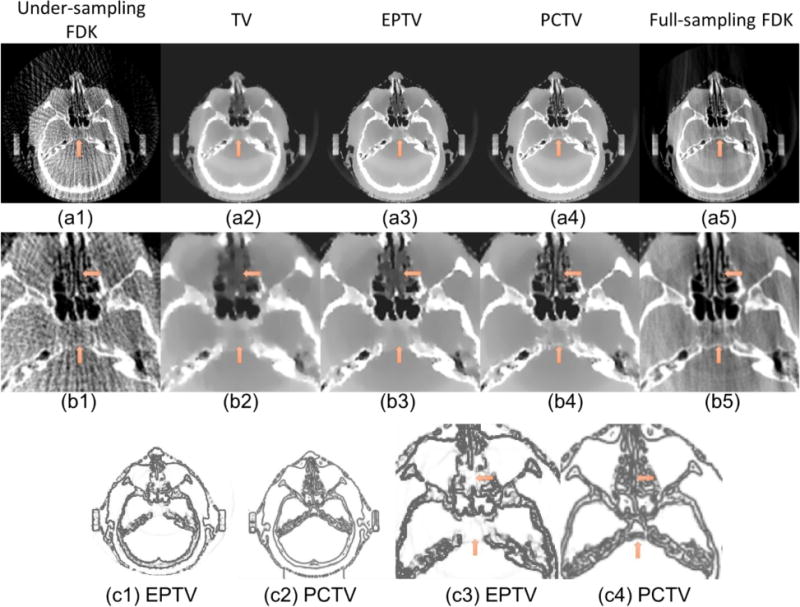
(a1)–(a5) Reconstructed images of patient head. From left to right: FDK (50proj.), TV, EPTV, PCTV and full sampling FDK (500proj.). (b1)–(b5) Zoom in reconstruction images of clinical patient head on the first row. Edge map comparisons: (c1) is the weight map of last reconstruction iteration in EPTV while (c2) is the weight map used in PCTV. (c3) and (c4) are the zooming in of (c1) and (c2) respectively. Arrows point out the differences between weight map in EPTV and PCTV.

Figure 8(c) shows the comparison of the weight map in the EPTV and PCTV methods, which demonstrates PCTV is superior to EPTV because more structures were detected in the prior contour based weight map.

Figure 9 shows results for reconstruction using different projection numbers. Similar to the XCAT study, the image quality was improved with increasing projections. PCTV is the most robust to projection number reduction and is also superior to TV and EPTV in all under-sampling projections.

Figure 9.

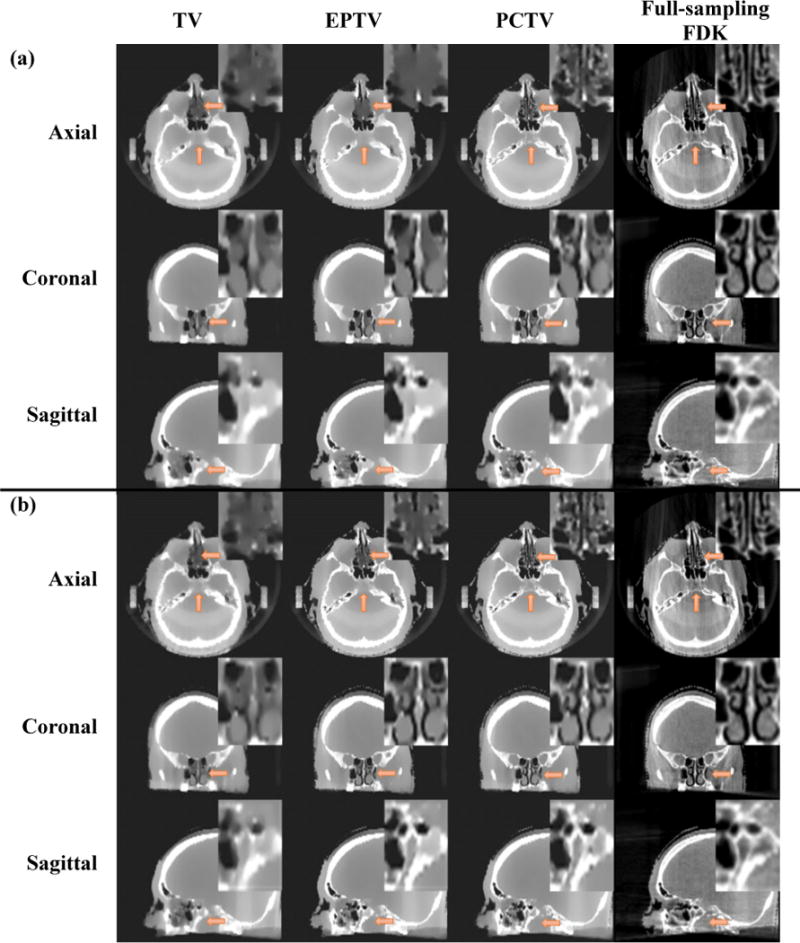
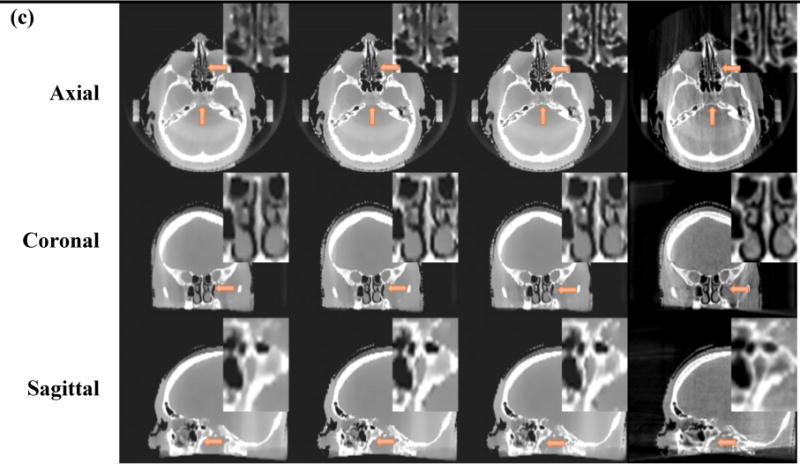
Comparisons of brain CBCT reconstructed via TV, EPTV and PCTV using a) 41 projections, b) 50 projection and c) 62 projections. Full sampling FDK using 500 projections are listed at the right column as the reference. Zooming in images are listed in the right and upper corner.

IV. Discussion

The prior contour based TV (PCTV) method uses the existing edge contour information from high quality prior CT images for edge enhancement in on-board CBCT reconstruction. Since the method doesn’t rely on the quality of on-board CBCT to derive edge information, it is robust against projection number and mAs reduction in CBCT acquisition. In addition, PCTV converges much faster than other methods (TV and EPTV) with smaller relative error and higher edge correlation as shown in Figure 10. In the practice, data fidelity constraint was applied in the first two iterations and then TV minimization was combined with adjustment toward data consistency after the third iteration to reconstruct images effectively[12]. Thus, the coverage speeds are the same in the first two iterations and diverge after the third iteration with various TV terms. With the high-quality edge information available, PCTV can substantially improve the CBCT image quality by removing noise and streak artifacts while preserving edge sharpness.

Figure 10.

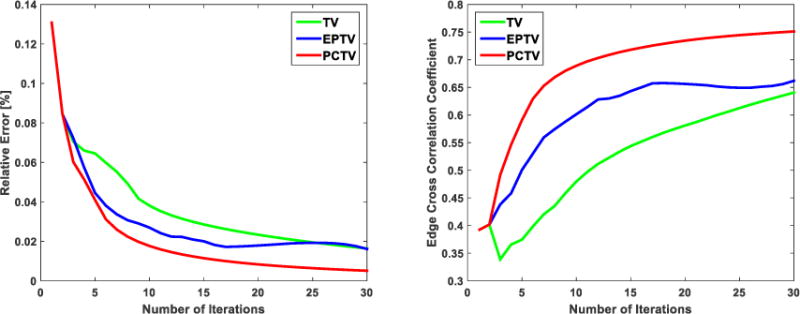
Left and right figures show the revolution curve of the relative error and edge cross correlation during 30 iteration using 36 half-fan XCAT projections

Both EPTV and PCTV are weighted total variation regularization and can enhance edge sharpness. However, for EPTV, the weight map was automatically generated and updated in each reconstruction iteration, which may miss some small structures due to loss of edge information during the iterations. In the PCTV, the edge weight map was extracted from high quality prior CT and can be verified and modified manually before reconstruction, which is much more accurate. Thus, PCTV achieves better edge enhancement than EPTV due to more accurate edge derivation during the reconstruction, as demonstrated in Figure 4.

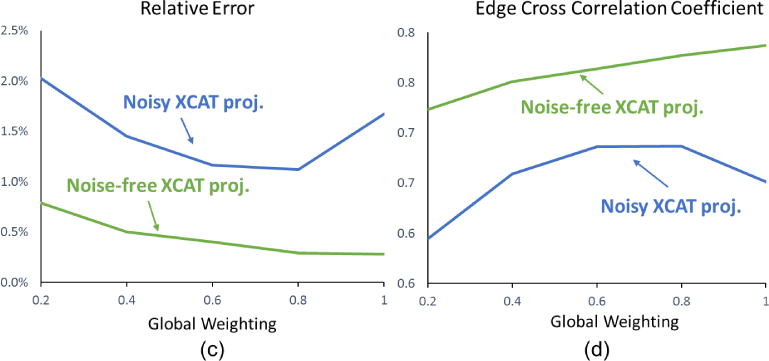
Note that edge enhancement can be affected by the parameters in the edge weight map generation. In this study, three edge weight map generation parameters (edge width, smoothing and global weighting factor) can be specified in PCTV. After optimization, edge width was selected as 3 pixels and MATLAB 3D smoothing Gaussian kernel with 5×5×5 kernel size and default standard deviation (σ = 0.65) was used. To further investigate the weighting effects on the reconstructed images, global weighting factor from 0.2, 0.4, 0.6, 0.8 and 1.0 were investigated in both noise-free and noisy XCAT cases as shown in Figure 11. Relative error and edge cross correlation coefficient were calculated as shown in Figure 11(c) and (d). In the noise-free XCAT study, the relative error monotonically decreased and edge correlation monotonically increased with increasing global weighting factor, which indicates that the edge enhancement effect is positively correlated with the weighting factor. Nevertheless, the noisy XCAT study shows an optimal value for the global weighting factor to balance edge enhancement and noise level in the edge boundary region.

Figure 11.

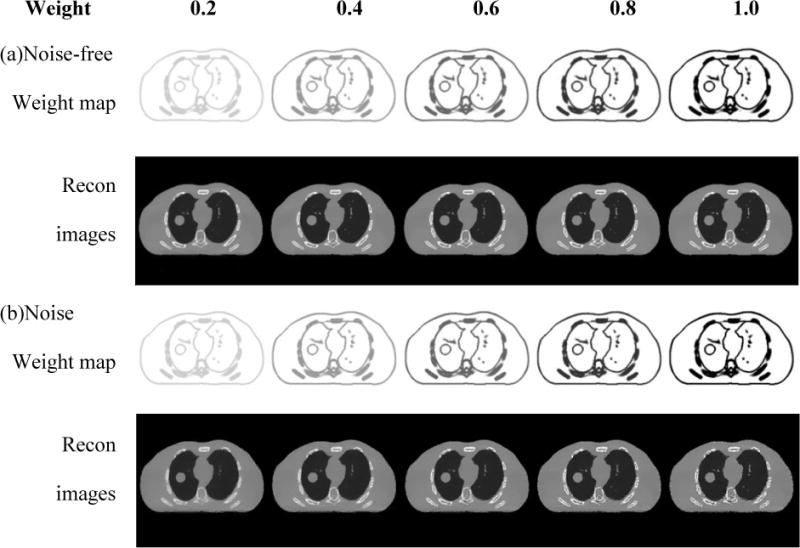
Comparisons of XCAT CBCT reconstructed via PCTV using different weighting factors and 45 projections. Weighting factors are increased from 0.2 to 1.0 from left to right columns in the (a) and (b). (a) shows weight map and reconstructed images using noise-free CBCT projections while (b) shows weight map and reconstructed images using CBCT projections with Poisson noise and normal noise (mean is 0 and standard deviation is 10). Relative error and edge cross correlation for TV, EPTV and PCTV as the function of the weighting factor for 45 half-fan CBCT projections with/without noise reconstruction were shown in the (c) and (d), respectively.

Furthermore, three weighting factors of 1.0, 0.6 and 0.2 were investigated for the clinical data study as shown in Figure 12. Similar to the noisy XCAT study, clinical study demonstrates that global weighting factor should be tuned to achieve high image quality with edge enhanced.

Figure 12.

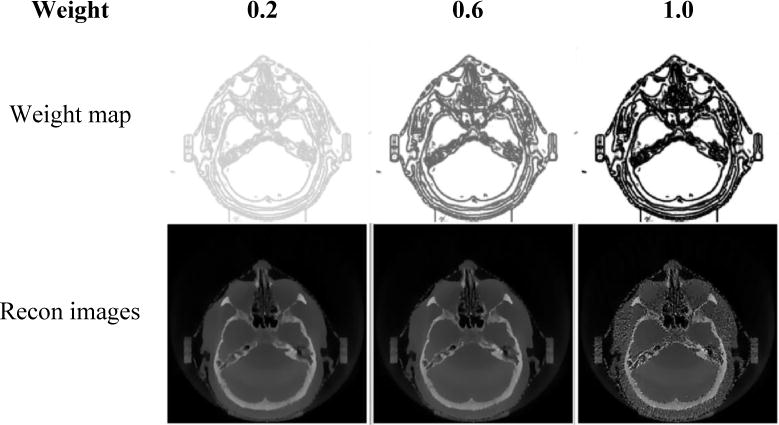
Comparisons of clinical head images reconstructed via PCTV using different weighting factors using 50 half-fan projections. Weighting factors are increased from 0.2, 0.6 to 1.0 from left to right columns. First row is weight map while the second row is reconstructed images with corresponding upper map.

The accuracy of weight map is critical for the reconstructed image quality with the new PCTV method. Two main processes will affect weight map accuracy: prior contour generation and registration. In this study, we generated prior contour automatically by edge detection in prior CT and visually verify the edge information afterwards to examine the accuracy of edge extraction. The threshold is the key parameter for Sobel edge detection and was selected empirically to find edge information for reconstruction. In digital XCAT phantom study, simple threshold was applied as the edge information is easily extracted with simple object geometry. In contrast, in the phantom and patient data, image noise and complex anatomical structures made it hard to find a single optimal threshold for edge detection. Thus, multiple edge detection process with different threshold was implemented and edge information from each process was combined as the edge map for reconstruction. Moreover, artifacts in CT images may affect the accuracy of the edge extraction, especially for large patients or patients with metal implant. In the future, more robust edge detection or auto-segmentation methods such as machine learning can be used in our proposed method. On the other side, clinical contours of organs close to the treatment area are usually drawn manually by the physician, and can be used directly as the edge information. For the structures not typically contoured by clinicians, automatic edge detection can be used first, followed by manual verification and modifications. Area of interest can also be defined for edge enhancement based on the clinical application. Currently prior CT is used to extract edge information. Since CBCT has higher resolution than CT images, it may be beneficial to use patients’ prior CBCT images to extract edges with higher resolution to achieve finer modulation of the edge enhancement effects. One possibility is to acquire fully sampled CBCT images on the first day of radiation therapy treatment to extract edge information, which is then used for edge enhancement in under sampled CBCT reconstruction on the rest of the days in the treatment course.

Regarding registration, edge enhancement in final images may be affected by the edge map accuracy, which will be influenced by the accuracy of registration. Based on registration, the applications of the PCTV method can be classified into two categories: rigid and deformable registrations. Rigid registration is used for brain, head-neck, and spine patients, which represent a significant amount of patient cohort in radiation therapy. On-board contours were propagated from the prior contours via rigid registration to achieve accurate edge enhancement, as shown in Figures 8–9. This represents the first major clinical application of the PCTV method. Deformable registration is used for sites prone to deformation (such as lung, abdomen and pelvis). The potential deformable registration errors with low-contrast organ boundaries like abdominal or pelvic regions may limit the performance of PCTV reconstruction. Besides image contrast, the quality of TV image might also affect the accuracy of deformable registration. When small structures are missing in the TV reconstructed CBCT images, the deformation fields for the small structures might be recovered based on deformation fields registered at other structures surrounding the small structures using deformation field regularization (such as energy constraint) or basis functions (such as B-spline) to propagate weight map, such as pointed by orange arrows in Figure 4 (d2) and (d3). In our study, a smoothing window was applied to the weight map to account for the uncertainties in the deformable registration. As shown in the XCAT study, although some mismatch existed in the edges in the lung, most edges were still correctly enhanced after using the smoothed weighting map in PCTV. Another potential solution to address the uncertainties in deformable registration is to develop a hybrid method to combine PCTV with other adaptive edge guided weighted TV method such as EPTV. Basically, after the deformation registration, image similarity can be calculated region by region to estimate registration accuracy. PCTV will be applied in the regions with high similarity (i.e. high registration accuracy), while adaptive edge guided weighted TV can be applied in the regions with low similarity (i.e. low registration accuracy).

After edge detection and registration, 3D smoothing was implemented in the weight map to avoid sudden change and account for registration uncertainty. Although edges of small structures may be blurred by 3D smoothing in the weight map, the regions surrounding the edges still received lower TV weighting values to enhance the edges in the reconstructed images as shown in Figure 4(b3)(c3) and Fig. 8. In practice, 3D smoothing kernel can be optimized for different anatomical sites.

For further clinical application, the reconstruction time of the PCTV method can be accelerated substantially using parallel computing and GPU. For the 4D CBCT reconstruction, the process for each phase can be implemented in parallel so that the 4D CBCT reconstruction time will be equivalent to a 3D CBCT reconstruction time. For 3D CBCT reconstruction, the main computational time cost is twice TV based reconstruction: initial TV image for registration and weighted TV reconstruction with edge map. Several studied have shown that the iterative reconstruction time can be speed up with GPU [11, 36, 37], which can be incorporated with our method to implement on-line image reconstruction for image-guide RT. The total calculation time of the compressed sensing based iterative reconstruction for a typical clinical case can be reduced to about 30s as reported by Yan et al[38]. Based on this reference, the time for two TV reconstructions in our algorithm can be potentially reduced to 1 minute, which is clinically acceptable for image guidance in radiation therapy.

V. CONCLUSION

A new PCTV method was developed to preserve edge information and to reduce the streak artifacts and noise in low dose CBCT reconstruction. Compared to TV and EPTV methods, PCTV provided better edge enhancement especially for complex or small anatomical structures. The improvement of CBCT quality in the low dose mode by PCTV has a great potential for improving the accuracy for on-board target localization, post treatment dosimetric assessment or adaptive therapy using CBCT. It also paves the way for further reducing the CBCT radiation dose so it can be used on a daily basis for fractionated treatments.