Diffusion kurtosis imaging with free water elimination: A bayesian estimation approach

Abstract

Purpose

Diffusion kurtosis imaging (DKI) is an advanced magnetic resonance imaging modality that is known to be sensitive to changes in the underlying microstructure of the brain. Image voxels in diffusion weighted images, however, are typically relatively large making them susceptible to partial volume effects, especially when part of the voxel contains cerebrospinal fluid. In this work, we introduce the “Diffusion Kurtosis Imaging with Free Water Elimination” (DKI‐FWE) model that separates the signal contributions of free water and tissue, where the latter is modeled using DKI.

Theory and Methods

A theoretical study of the DKI‐FWE model, including an optimal experiment design and an evaluation of the relative goodness of fit, is carried out. To stabilize the ill‐conditioned estimation process, a Bayesian approach with a shrinkage prior (BSP) is proposed. In subsequent steps, the DKI‐FWE model and the BSP estimation approach are evaluated in terms of estimation error, both in simulation and real data experiments.

Results

Although it is shown that the DKI‐FWE model parameter estimation problem is ill‐conditioned, DKI‐FWE was found to describe the data significantly better compared to the standard DKI model for a large range of free water fractions. The acquisition protocol was optimized in terms of the maximally attainable precision of the DKI‐FWE model parameters. The BSP estimator is shown to provide reliable DKI‐FWE model parameter estimates.

Conclusion

The combination of the DKI‐FWE model with BSP is shown to be a feasible approach to estimate DKI parameters, while simultaneously eliminating free water partial volume effects. Magn Reson Med 80:802–813, 2018. © 2018 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine. This is an open access article under the terms of the Creative Commons Attribution NonCommercial License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.

INTRODUCTION

Diffusion kurtosis imaging (DKI) 1, 2 is a magnetic resonance imaging technique to probe the diffusion of water molecules. The DKI model is a mathematical extension of the commonly used diffusion tensor imaging (DTI) model 3, 4. Whereas DTI only quantifies the Gaussian component of the diffusion of the water molecules, DKI also allows to quantify the degree of non‐Gaussianity. In many biological tissues, including the brain, the DKI model is generally considered to be a more accurate representation of the signal compared to DTI since it is known that tissue heterogeneity and biological restrictions in the tissue microstructure, such as cell membranes and myelin sheets, cause the distribution of the water diffusion to be non‐Gaussian 1, 5, 6. Moreover, DKI has been shown to be sensitive to certain pathological microstructural changes that are not revealed using DTI 7. These include, but are not limited to, changes due to cancer 8, 9, Alzheimer's disease 10, Parkinson's disease 11, 12, Huntington's disease 13, epilepsy 14, attention deficit hyperactivity disorder 15, traumatic brain injury 16, 17, 18 and cerebral infarction 19, 20, 21, 22, 23. Besides the diffusion metrics produced by DTI, for example, fractional anisotropy (FA) and mean diffusivity (MD), DKI also produces kurtosis related metrics like the radial‐ ( $K_{\parallel }$), axial‐ ( $K_{\perp }$) and mean kurtosis (MK).

In many DTI and DKI brain studies, the model parameters are derived from voxels presumably containing one underlying tissue type, usually white matter. In reality however, besides potentially containing multiple tissue types, many voxels will also contain a fraction of free water, often in the form of cerebrospinal fluid (CSF). Although in most cases this free water volume is relatively small, it may still have a large impact on the diffusion signal because of its high diffusivity 24, 3 $\mu {\mathrm{m}}^2/\text{ms}$ compared to a typical MD ∼ 1 $\mu {\mathrm{m}}^2/\text{ms}$ for brain parenchyma. Moreover, the long T ₂ relaxation time of free water in comparison of white matter will inflate the free water signal fraction, further increasing its impact 25. Among other effects, neglecting to account for free water will lead to underestimation of FA and to an overestimation of MD and MK. For example, in a voxel with FA = 0.7 and MD = 0.8 $\mu {\mathrm{m}}^2/\text{ms}$, a free water signal fraction of 0.1 will already reduce FA with more than 7% and increase MD with more than 10%.

Free water contamination can generally be dealt with in two ways, either during data acquisition or with post‐acquisition correction strategies. During acquisition, the free water signal can be suppressed with the fluid‐attenuated inversion recovery technique (FLAIR) 26, 27, 28 or similar diffusion weighted inversion recovery sequences 29. Although these acquisition techniques succeed in suppressing the free water signal to a large extent, they also have several drawbacks. First, the scan time is significantly longer compared to a ‘regular’ diffusion acquisition while the signal‐to‐noise ratio (SNR) is typically lower. Furthermore, the use of cardiac gating is precluded, the specific absorption rate (SAR) increases and the data is sensitive to artifacts specific to inversion recovery sequences 24. These drawbacks explain the interest in employing voxel based post‐acquisition correction strategies.

For DTI, multiple strategies have already been proposed 30, 31 of which the free water elimination (FWE) model is probably most widely used 32. FWE models the diffusion signal by combining a free water compartment with a tissue compartment described by the DTI model, effectively making FWE a bi‐tensor model. A downside of this model is that the inverse problem of estimating its parameters is ill‐conditioned, causing conventional estimation techniques like non‐linear least squares (NLS) model fitting or maximum likelihood (ML) estimation to produce diffusion parameter estimates that may differ several orders of magnitude from their true underlying values 33. To deal with the ill‐conditionedness of this model fitting problem, prior knowledge can be included, for example in the form of a set of constraints, a regularization term 32 or a statistical prior 31.

In this work, we extend the DKI model to also include a free water compartment. The model is referred to as the “Diffusion Kurtosis Imaging with Free Water Elimination” (DKI‐FWE) model. To address the ill‐conditionedness of the model fitting problem, we propose to use a Bayesian estimation technique with a shrinkage prior (BSP). First, the optimal b‐values for the acquisition of the diffusion weighted data are determined using a Cramér‐Rao lower bound (CRLB) optimization procedure 34. The goodness of fit of DKI‐FWE is subsequently compared to that of the standard DKI model using the generalized likelihood ratio test. Finally, simulation and real data experiments are performed to evaluate the performance of the proposed combination of the DKI‐FWE model with a BSP estimator in terms of estimation error. This performance is compared to that of two other combinations of model and estimator, namely (i) the DKI‐FWE model combined with a constrained ML estimator, and (ii) the DKI model combined with a BSP estimator.

THEORY

Diffusion Kurtosis Imaging Model

The diffusion of water molecules in tissue can be detected as an attenuation of the measured magnetic resonance signal intensity. The DKI model approximates the natural logarithm of the magnitude of the noise‐free diffusion weighted signal $S(b,\mathbf{g})$ by a second‐order Maclaurin series expansion in powers of the diffusion weighting strength b 35, 36:

$$\ln \left(S\left(b,\mathit{g};{\mathit{\theta }}_{DKI}\right)\right)=\ln \left(S_0\right)-b{\displaystyle \sum _{i,j=1}^3{g}_i}{g}_j{D}_{ij}+\frac{b^2}{6}{\left({\displaystyle \sum _{i=1}^3\frac{D_{ii}}{3}}\right)}^2{\displaystyle \sum _{i,j,k,l=1}^3{g}_i}{g}_j{g}_k{g}_l{W}_{ijkl}+\mathcal{O}(b^3).$$ (1)

Here, S ₀ denotes the non‐diffusion weighted signal and g_i the $i$th component of the normalized diffusion weighting gradient direction vector $\mathit{g}$. D_ij represents the $ij$th element of the fully symmetric second order diffusion tensor $\mathit{D}$, which can be characterized by 6 independent elements: ${\mathit{\theta }}_D={\left\{D_{ij}\right\}}_{i\le j\le 3}$. Furthermore, W_ijkl represents the $ijkl$th element of the fully symmetric fourth order diffusion kurtosis tensor $\mathit{W}$, which can be characterized by 15 independent elements: ${\mathit{\theta }}_W={\left\{W_{ijkl}\right\}}_{i\le j\le k\le l\le 3}$. In summary, the DKI model is parameterized by 22 independent parameters: ${\mathit{\theta }}_{DKI}=[S_0,{\mathit{\theta }}_D,{\mathit{\theta }}_W]$.

Diffusion Kurtosis Imaging with Free Water Elimination Model

We propose a two‐compartment model:

$$S(b,\mathit{g};{\mathit{\theta }}_{DKI},f)=(1-f)S_{\text{tissue}}+f{S}_{\text{csf}},$$ (2)

where the signal contribution of the tissue, $S_{\text{tissue}}$, is non‐specifically represented by the DKI model (1), f is the fraction of the diffusion signal that corresponds to the free water compartment (also known as the free water fraction) and $S_{\text{csf}}$ denotes the signal contribution of the free water compartment, which can be modeled as:

$$S_{csf}=S_0{e}^{-bd},$$ (3)

with the assumption of $d=3\hspace{0.17em}\mu {\mathrm{m}}^2/\text{ms}$, the diffusivity of free water at body temperature. The DKI‐FWE model (2) is parameterized by 23 independent parameters $\mathit{\theta }=\{{\mathit{\theta }}_{DKI},f\}$. A disadvantage of the DKI‐FWE model, is that the corresponding model fitting problem is ill‐conditioned or, if the diffusion in the tissue is isotropic, even ill‐posed.

Bayesian Shrinkage Prior Estimation

To deal with the inherent ill‐conditionedness of the inverse problem of fitting the DKI‐FWE model to data, we propose to use a Bayesian estimation approach with a shrinkage prior (BSP). BSP has already shown promising results when applied to the Intravoxel Incoherent Motion (IVIM) model 37, 38, 39, 40, which is also a bi‐exponential diffusion model that gives rise to an ill‐conditioned parameter estimation problem. The BSP method is based on Bayes’ theorem which states that the posterior distribution of the parameters $\mathit{\theta }$ given the data $\mathit{y},\hspace{0.17em}p(\mathit{\theta }|\mathit{y})$, can be expressed as:

$$p(\mathit{\theta }|\mathit{y})=\hspace{0.17em}\frac{p(\mathit{y}|\mathit{\theta })}{p(\mathit{\theta })}p(\mathit{y}),$$ (4)

where $p(\mathit{y}|\mathit{\theta })$ denotes the conditional distribution of $\mathit{y}$ given $\mathit{\theta }$. When viewed as a function of the parameter $\mathit{\theta }$ for a given outcome $\mathit{y},\hspace{0.17em}p(\mathit{y}|\mathit{\theta })$ is called the likelihood function, which is denoted as $L(\mathit{\theta };\mathit{y})$. The functions $p(\mathit{\theta })$ and $p(\mathit{y})$ denote the prior distributions of $\mathit{\theta }$ and $\mathit{y}$, respectively. Each factor in Equation (4) will be discussed shortly in the sections below. For a more extensive description of the BSP estimator and its implementation, we refer the reader to the work by Orton et al. 38.

Likelihood Function

The probability density function (PDF) for voxel i, $p(y_i|{\mathit{\theta }}_i)$, describes the probability of measuring a certain value y_i given the parameter vector ${\mathit{\theta }}_i$. Under general conditions 41, 42, an MR magnitude signal is Rician distributed 43, 44:

$$p(y_i|{\mathit{\theta }}_i)=\frac{y_i}{\sigma }exp(-\frac{y_i^2+S{({\mathit{\theta }}_i)}^2}{2{\sigma }^2})I_0\left(\frac{y_{i}S({\mathit{\theta }}_i)}{{\sigma }^2}\right).$$ (5)

Here, I ₀ denotes the zeroth order modified Bessel function of the first kind and σ is the standard deviation of the Gaussian noise disturbing the underlying complex data. If the PDF (5) is viewed as a function of the unknown parameter vector ${\mathit{\theta }}_i$ for a given observation y_i, it is called the likelihood function, which is denoted as $L({\mathit{\theta }}_i;y_i)$.

Prior Distributions

The components of the parameter vector $\mathit{\theta }$ are assumed to be Gaussian distributed across the region of interest (ROI). For this work, the ROI will include the entire brain. The distribution of the parameter f however, will deviate significantly from a Gaussian distribution because it is constrained between 0 and 1, with around $2/3\text{th}$ of the voxels having a free water fraction in the $0\le f\le 0.25$ range 45. Therefore, during the estimation procedure, a transformation $f\to F$ is introduced: $F=\log (f)-\log (1-f)$. Besides the fact that the distribution of F now much more resembles a Gaussian distribution, the implicit constraints on f: $0\le f\le 1$ are now also respected for all possible values of F. To support the assumption of Gaussian distributed DKI‐FWE model parameters, https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27075&attachmentId=2171641237 shows the distributions of all parameter estimates. The prior distribution of the parameters can be written as a multivariate Gaussian distribution:

$$p({\mathit{\theta }}_i|\mathit{\mu },{\mathrm{\Sigma }}_{\mu })=|2\pi {\mathrm{\Sigma }}_{\mu }{|}^{-1/2}\exp \left(-\frac{1}{2}{({\mathit{\theta }}_i-\mathit{\mu })}^T{\mathrm{\Sigma }}_{\mu }^{-1}({\mathit{\theta }}_i-\mathit{\mu })\right),$$ (6)

where $\mathit{\mu }$ is a 23 × 1 vector containing the mean of every DKI‐FWE parameter across the ROI and ${\mathrm{\Sigma }}_{\mu }$ denotes the 23 × 23 ROI covariance matrix that models the variance of, and correlations between parameters. In the BSP approach, $\mathit{\mu }$ and ${\mathrm{\Sigma }}_{\mu }$ are jointly inferred from the data. Only the Gaussian shape is imposed on the prior distribution. Jeffreys’ prior is used as a non‐informative hyper‐prior to express uncertainty on the hyper‐parameters $\mathit{\mu }$ and ${\mathrm{\Sigma }}_{\mu }$: $p(\mathit{\mu },{\mathrm{\Sigma }}_{\mu })=|{\mathrm{\Sigma }}_{\mu }{|}^{-1/2}$ 46, 47, 48. Finally, the prior distribution is multiplied with a uniform distribution $p_u({\mathit{\theta }}_i)$ to confine the parameter estimates to a biologically plausible range and to deal with extreme outliers in the parameter distributions after the initialization step:

$$p_u({\mathit{\theta }}_i)=\{\begin{array}{ll}1\hfill & \hspace{1em}\text{for} \text{lb}\le {\mathit{\theta }}_i\le \text{ub}\hfill \\ 0\hfill & \hspace{1em}\text{for} {\mathit{\theta }}_i<\text{lb} \text{or} {\mathit{\theta }}_i>\text{ub}\hfill \end{array}.$$ (7)

Here lb and ub, denote the lower and upper bounds on ${\mathit{\theta }}_i$, respectively, and are set as to confine ${\mathit{\theta }}_i$ to this range. The imposed constraints can be found in Table 1. The term 'shrinkage’ in BSP describes the effect of this prior on the final estimates. In voxels where the estimation problem is severely ill‐conditioned and parameter uncertainties are high, estimates can significantly diverge from the true value when no prior information is taken into account. The BSP prior will shrink these estimates toward the center of the distribution, thereby better conditioning the problem.

Table 1.

Lower and Upper Bounds Imposed on Parameter Estimates. Bounds of the DTI Model Parameters Are in μm²/ms.

Parameter(s)	lb	ub
$\ln ({\mathrm{S}}_0)$	0	$\text{inf}$
${\mathrm{D}}_{\text{xx}},{\mathrm{D}}_{\text{yy}},{\mathrm{D}}_{\text{zz}},{\mathrm{W}}_{\text{xxxx}},{\mathrm{W}}_{\text{xxyy}},{\mathrm{W}}_{\text{xxzz}},{\mathrm{W}}_{\text{yyyy}},{\mathrm{W}}_{\text{yyzz}},{\mathrm{W}}_{\text{zzzz}}$	0	2.5
${\mathrm{D}}_{\text{xy}},{\mathrm{D}}_{\text{xz}},{\mathrm{D}}_{\text{yz}},{\mathrm{W}}_{\text{xxxy}},{\mathrm{W}}_{\text{xxxz}},{\mathrm{W}}_{\text{xxyz}},{\mathrm{W}}_{\text{xyyy}},{\mathrm{W}}_{\text{xyyz}},{\mathrm{W}}_{\text{xyzz}},{\mathrm{W}}_{\text{xzzz}},{\mathrm{W}}_{\text{yyyz}},{\mathrm{W}}_{\text{yzzz}}$	−2.5	2.5
F	−7.6	7.6

Posterior Distribution

When the prior distributions $p({\mathit{\theta }}_i|\mathit{\mu },{\mathrm{\Sigma }}_{\mu }),\hspace{0.17em}{p}_u({\mathit{\theta }}_i)$ and likelihood function $L({\mathit{\theta }}_i;{\mathit{y}}_i)$ are known for each voxel, one can determine the posterior distribution $p(\mathit{\theta },\mathit{\mu },{\mathrm{\Sigma }}_{\mu }|\mathit{y})$ over both the voxel‐wise parameters ${\mathit{\theta }}_i$ and the ROI mean and covariance parameters $\mathit{\mu }$ and ${\mathrm{\Sigma }}_{\mu }$, using Bayes’ theorem (4):

$$p(\mathit{\theta },\mathit{\mu },{\mathrm{\Sigma }}_{\mu }|\mathit{y})=\frac{p_u(\mathit{\theta })p(\mathit{\mu },{\mathrm{\Sigma }}_{\mu }){\displaystyle \prod _{i=1}^{N_v}L({\mathit{\theta }}_i;{\mathit{y}}_i)p({\mathit{\theta }}_i|\mathit{\mu },{\mathrm{\Sigma }}_{\mu })}}{p(\mathit{y})},$$ (8)

where N_v denotes the number of voxels. The prior distribution $p(\mathit{y})$ only serves as a normalizing constant that does not depend on the model parameters. Therefore it does not need to be evaluated during the estimation procedure. The posterior PDF summarizes the state of knowledge about the parameters after the data $\mathit{y}$ are observed. Estimators of the parameters are given by the expected values with respect to this posterior PDF. These estimators minimize the Bayesian mean squared error (MSE), where the mean is taken over all realizations of the parameters and the data 49. Unfortunately, the high dimensional integrals needed to determine the expectation values cannot be calculated analytically. Markov Chain Monte Carlo (MCMC) approaches, however, are an established solution to solve these integrals numerically 50. After disregarding a sufficient number of initialization samples (N_i = 1500) and subsequently taking sufficient samples (N_s = 15,000), the estimates of the parameters of interest are approximated by the average over all N_s samples. The MCMC procedure was initialized using a voxel‐wise constrained NLS (cNLS) fit of the DKI‐FWE model. For the cNLS fit, the lsqnonlin MATLAB function 51 was used with the trust‐region‐reflective algorithm 52, 53 and the constraints from Table 1.

Maximum Likelihood Estimator and Cramér‐Rao Lower Bound

The ML estimator ${\widehat{\mathit{\theta }}}_{ML}$ is defined as the value of $\mathit{\theta }$ that maximizes the likelihood function $L(\mathit{\theta };\mathit{y})$, that is,

$${\widehat{\mathit{\theta }}}_{ML}=\arg \underset{{}_{\mathit{\theta }}}{\max }L(\mathit{\theta };\mathit{y}).$$ (9)

The ML estimator is asymptotically both unbiased and efficient 54. Indeed, for an increasing number of observations, the PDF of the ML estimator tends to a normal PDF with the true values of the parameters as expectations and the CRLB as covariance matrix, where the CRLB is defined as the inverse of the Fisher information matrix $\mathit{I}(\mathit{\theta })$, which in turn is defined as 54

$$\mathit{I}(\mathit{\theta })=\mathbb{E}\left\{\frac{\partial \ln p(\mathit{y}|\mathit{\theta })}{\partial \mathit{\theta }}\frac{\partial \ln p(\mathit{y}|\mathit{\theta })}{\partial {\mathit{\theta }}^T}\right\}.$$ (10)

The so‐called Cramér‐Rao inequality states that for any unbiased estimator $\widehat{\mathit{\theta }}$:

$$\text{cov}(\widehat{\mathit{\theta }})\ge {\mathit{I}}^{-1}(\mathit{\theta })\equiv \text{CRLB}(\mathit{\theta }).$$ (11)

In other words, the CRLB provides a theoretical lower bound on the variance of any unbiased estimator of $\mathit{\theta }$ 49, 55. In this work, often hard constraints are imposed on the ML estimator. These constraints are needed to deal with the ill‐conditionedness of the parameter estimation problem and are chosen the same as described in Table 1.

METHODS

Real Data Acquisition and Post‐Processing

For the real data experiments in the subsections below, a diffusion weighted MRI data set of a healthy, 27‐year‐old male volunteer was acquired using a 3T Siemens MAGNETOM PrismaFit system. An EPI/spin echo (SE) diffusion weighted pulse sequence was used with a 96 × 96 acquisition matrix which resulted in an image with an isotropic voxel size of 2.5 mm. We acquired 36 slices with an inter slice gap of 30%, an echo time (TE) of $73\hspace{0.17em}\text{ms}$ and pulse repetition time (TR) of 4000 ms. The diffusion weighted gradient settings that were used consisted of six b = 0 images and three b‐values shells (b = 0.25, 1.15, 2.00 $\text{ms}/\mu {\mathrm{m}}^2$) with 60 non‐collinear magnetic field gradient directions for each of the non‐zero b‐value shells. The gradient directions were generated using electrostatic repulsion resulting in a unique set of 60 directions for each shell 56, 57. Reversed phase encoded b = 0 images were acquired to allow for correction of susceptibility distortions. The total acquisition time was 12:56 min.

The first step in the post processing pipe‐line was the denoising of the dMRI data by exploiting its inherent redundancy using random matrix theory 58. Next, Gibbs ringing correction based on local interpolation in k‐space was applied 59. Finally, the data was corrected for susceptibility, eddy current distortions, and subject motion using the “Topup” 60 and “Eddy” 61 tools in FSL.

Ill‐Conditionedness of the DKI‐FWE Model Fitting Problem

To illustrate the ill‐conditionedness of the DKI‐FWE model fitting problem, the condition number of the relevant Fisher information matrix $\mathit{I}(\mathit{\theta })$ is determined, where a high condition number indicates ill‐conditioning. An ill‐conditioned Fisher information matrix is known to be a major symptom of problems of (approximate) nonidentifiability, highly correlated estimates, and poor precision 62, 63, 64. In the extreme case of a singular Fisher information matrix, the condition number of that matrix is infinite, the model parameters are unidentifiable, and the CRLB does not exist 54. For reasons of comparison, the condition number κ of the Fisher information matrix $\mathit{I}(\mathit{\theta })$ is determined for both the DKI‐FWE and DKI model. It is calculated in a real data slice as 65:

$$\kappa (\mathit{I}(\mathit{\theta }))=\left|\right|\mathit{I}{(\mathit{\theta })}^{-1}|{|}_2||\mathit{I}(\mathit{\theta })|{|}_2.$$ (12)

where $\left|\right|·|{|}_2$ denotes the 2‐norm operator and $\kappa (\mathit{I}(\mathit{\theta }))$ is evaluated at the parameter estimates obtained from a voxel‐wise constrained ML estimator fit.

DKI‐FWE Optimal Experiment Design

In this experiment, the b‐values in the acquisition protocol are optimized in terms of the CRLB 34. During the optimization procedure, for simplicity, the number of shells in the acquisition is assumed to be fixed to 4 or 5. Acquisition protocols with less than four shells are not considered because of the associated increase in ill‐conditionedness of the DKI‐FWE model parameter estimation problem (see https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27075&attachmentId=2171641237). We do not explicitly incorporate non‐diffusion weighted images in the optimization protocol, but instead give the diffusion weighted shells the freedom to have a diffusion weighting of 0. The number of measurements in each shell is chosen in correspondence with the acquired real data: 6 measurements in the lowest shell and 60 in the other shells. Gradient directions were obtained using a electrostatic repulsion algorithm 66.

Since the optimal b‐values will depend on the unknown parameters to be estimated, 10 sets of 100 voxels were simulated containing DKI‐FWE model parameter values that are representative for white matter containing a possible partial CSF volume. To achieve this, white matter voxels were randomly selected from a real data set, after which the DKI model was voxel‐wise fitted using an unconstrained weighted linear least squares (WLLS) fit 67. Selection of white matter voxels was done from a white matter mask composed of voxels with FA $\ge$ 0.5, after which voxels containing potential partial volume effects, based on MD $\ge 1.5\mu {\mathrm{m}}^2/\text{ms}$, were removed. Subsequently, a uniformly distributed random CSF partial volume fraction was added to the voxel. The optimization algorithm was set to minimize the following function:

$$f(\mathit{b})={\displaystyle \sum _{i=1}^{N_v}{\displaystyle \sum _{j=1}^{N_p}{\text{CRLB}}_{jj}}}(\mathit{b};\mathit{g},{\mathit{\theta }}_i)$$ (13)

with N_v = 100, N_p = 23 the number of model parameters and ${\text{CRLB}}_{jj}(\mathit{b};\mathit{g},{\mathit{\theta }}_i)$ the jth diagonal CRLB element in function of the b‐values $\mathit{b}$ given a set of gradient directions $\mathit{g}$ and underlying DKI‐FWE model parameters ${\mathit{\theta }}_i$. Minimizing this function corresponds to minimizing the sum of CRLB variances of the DKI‐FWE model parameters, averaged over a set of representative model parameter values.

The accuracy of the DKI model is b‐value dependent (see Equation (1)). Although the precision of DKI estimators would benefit from a large b‐range, simulations indicate that limiting the b‐range is necessary to provide a reasonable trade‐off between precision and accuracy 68. Since optimization based on the CRLB relies on unbiased estimators and hence focuses on precision only, we need to enforce an upper bound on b to avoid severe loss in accuracy. In this study, we choose $b_{\text{max}}=2$ $\text{ms}/\mu {\mathrm{m}}^2$.

Generalized Likelihood Ratio Test: DKI‐FWE vs DKI Model

In the next experiment, the statistical significance of introducing the extra free water volume fraction parameter f in the DKI‐FWE model is studied. That is, we test the null hypothesis H ₀: f = 0 (corresponding with the standard DKI model) against the alternative hypothesis H ₁: $f\ne 0$ (corresponding with the DKI‐FWE model). For this purpose, we use the generalized likelihood ratio test (GLRT) 49, 69. The generalized likelihood ratio, denoted by Λ, is defined as:

$$\mathrm{\Lambda }(\mathit{y})=\frac{\underset{{\mathit{\theta }}_{\text{DKI}}}{\sup }\left\{L({\mathit{\theta }}_{\text{DKI}},f=0;\mathit{y})\right\}}{\underset{{\mathit{\theta }}_{\text{DKI}},f}{\sup }\left\{L({\mathit{\theta }}_{\text{DKI}},f;\mathit{y})\right\}},$$ (14)

where the numerator of Λ is the likelihood function $L({\mathit{\theta }}_{\text{DKI}},f;\mathit{y})$ evaluated at the unconstrained ML estimates of the unknown parameters under H ₀, whereas the denominator is the likelihood function evaluated at the unconstrained ML estimates of the unknown parameters under H ₁. In this work, we assume the MRI data to be Rician distributed 42. For nested models, such as the ones compared in the current hypothesis test, the modified test statistic $D(\mathit{y})=-2\ln \left(\mathrm{\Lambda }(\mathit{y})\right)$ is known to be asymptotically ${\chi }^2$ distributed with 1 degree of freedom when H ₀ is true 70. Employing the GLRT principle, H ₀ is rejected if and only if $D(\mathit{y})>\gamma$, with γ a fixed constant that is specified by fixing the significance level of the test. In this work, the significance level of the GLRT was set to 0.05 for all experiments.

The GLRT was applied on both simulated and real data. For the simulations, DKI parameters were taken from a conservative white matter mask from the real data set in the same way as described in the “DKI‐FWE optimal experiment design” section. A free water volume fraction, uniformly distributed between 0 and 1, was subsequently added. Rician distributed data was generated with an SNR ranging from 10 to 40, where the SNR was defined as $\mu /\sigma$, with μ the average noiseless non‐diffusion weighted signal. For each f‐value and SNR level, data from 2000 voxels was simulated using the same acquisition protocol as described in the real data acquisition section.

DKI‐FWE Model with BSP Estimator: Estimation Error Study

This section describes two experiments that study the proposed combination of the DKI‐FWE model with the BSP estimation technique in terms of the error distributions and robustness. In the first experiment, the BSP estimator was compared to the more common constrained ML estimation technique for the estimation of the DKI‐FWE model parameters. The choice to use constrained ML estimation as a comparison was motivated by the fact that both estimators take the Rician distribution of the MRI data into account. Furthermore, note that constrained ML estimator is equivalent to using a Bayesian estimation approach with a uniform prior distribution over the constraining region 38. The constrained ML estimator was implemented in MATLAB 51 using the fmincon function with the interior‐point algorithm 71, 72, 73. The applied constraints were taken from Table 1. In the second experiment, the BSP estimates of the DKI‐FWE and standard DKI model parameters were compared. This gives insight in the effect of incorporating a free water compartment on the estimates of DKI parameters.

In summary, three different combinations of diffusion model and estimation technique were tested: DKI‐FWE with BSP, DKI‐FWE with constrained ML estimation and DKI with BSP estimation. As in the GLRT experiment, these combinations were evaluated in both simulations and real data. For the simulations, 2500 voxels with the same white matter DKI parameter set as in the “optimal experiment design” section were combined with realistic free water fractions sampled from a representative distribution taken from literature 45. The simulation data was Rician distributed with SNR = 17.5. The acquisition protocol is identical to the one described in the real data acquisition section.

RESULTS

Ill‐conditionedness of the DKI‐FWE model

The condition numbers of the DKI‐FWE and DKI parameter estimation problems are shown in Figure 1. It is clear that in general, DKI‐FWE yields larger condition numbers, indicating a more ill‐conditioned problem. The histogram in Figure 1c also shows that even though for most voxels the condition number stays within a reasonable range, the DKI‐FWE model fit produces a considerable amount of condition numbers that become so large that they even exceed the upper bound of this plot (i.e., ${\kappa }_{\text{DKI}-\text{FWE}}>15\mathrm{e}4$). This indicates the need for more advanced estimators that are able to handle these ill‐conditioned problems.

Figure 1.

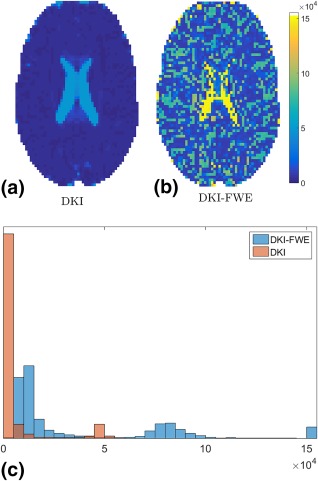
Condition numbers in a real data slice for (a) the Diffusion Kurtosis Imaging (DKI) model and (b) the “Diffusion Kurtosis Imaging with Free Water Elimination” (DKI‐FWE) model. Panel (c) shows the histograms of the condition numbers of both the DKI and DKI‐FWE fit. Condition numbers larger than 15e4 have been set to 15e4 for visual clarity.

DKI‐FWE Optimal Experiment Design

Averaged over 10 sets of 100 voxels, the optimization procedure yields four b‐values with a mean and standard deviation of $0.000\pm 0.000,0.363\pm 0.001,1.187\pm 0.004,2.000\pm 0.000$ $\text{ms}/\mu {\mathrm{m}}^2$. The optimization procedure is also repeated with 5 shells. The results for the 5 shells optimization procedure always reduce to the results of the 4 shell optimization, that is, one of the aforementioned b‐values appears twice.

Generalized Likelihood Ratio Test: DKI‐FWE vs DKI Model

Simulation Experiments

The results of the GLRT simulation experiments are shown in Figure 2a. Here, the ML estimate of the probability of success P_s in a given binomial trial based on the number of times the DKI‐FWE was found to successfully describe the data significantly better compared to the DKI model, is plotted against the free water fraction f. The 95% confidence interval is visualized by colored bands around the plots. It is clear that for both f = 0 and f = 1, the DKI‐FWE model is reduced to the standard DKI model or an isotropic diffusion model, respectively, and DKI‐FWE offers no advantage over DKI. For free water volume fractions in the approximate range of $0.2<f<0.8$, however, DKI‐FWE succeeds in describing the data significantly better than the standard DKI model for a large number of voxels, even for low SNR values.

Figure 2.

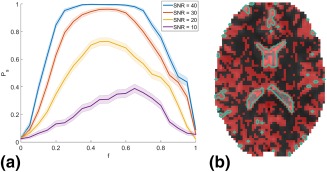
a: The maximum likelihood estimate of the probability of success P_s where the DKI‐FWE model is significantly better at describing the data compared to the standard DKI model for simulated data in function of the true free water signal fraction f. Colored bands indicate the 95% confidence interval (b) B ₀ image overlayed with the voxels where the DKI‐FWE model describes the data significantly better compared to the standard DKI model (red). Cerebrospinal fluid (CSF) regions are indicated with a green contour plot.

Real Data Experiments

Next, a slice from a b ₀ image from the real data set is shown for anatomical reference in Figure 2b. In this image, the voxels in which the extended DKI model describes the data significantly better than the standard DKI model are indicated in red. Note that these significant voxels are found throughout the entire brain, but mostly on the border of CSF regions and brain tissue (indicated by the green contour plots).

Bayesian Shrinkage Prior and DKI‐FWE Study

The BSP estimator was first compared to the ML estimator for the estimation of the DKI‐FWE model parameters. Next, the DKI‐FWE model was in its turn compared to the standard DKI model, where the model parameters for both models were estimated using the BSP estimator. The error of a metric x was defined as: $\text{error}(x)=x_{\text{estimated}}-x_{\text{true}}$.

Simulation Experiments

Figure 3 shows the error distributions of f, FA, MD, and MK from the simulation experiments. The BSP estimator with the DKI‐FWE model shows relatively narrow and symmetric peaks, indicating a high precision. Moreover, the BSP estimator also has a high accuracy as indicated by the associated error distributions that are centered around zero. The ML estimators of the same DKI‐FWE model, however, exhibit lower precision compared to BSP. Finally, the BSP estimator using the DKI model underestimates FA and overestimates MD and MK. Table 2 summarizes the respective error distributions in terms of the root MSE (RMSE).

Figure 3.

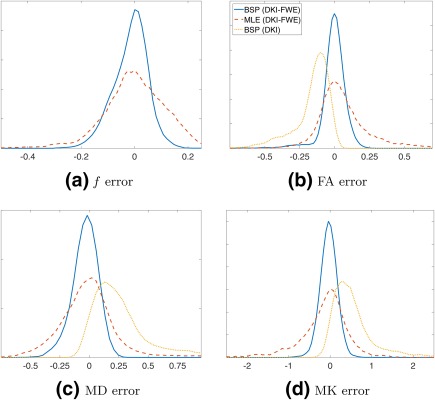
Error distributions of f (a), fractional anisotropy (FA) (b), mean diffusivity (MD) (c), and mean kurtosis (MK) (d), for 3 different diffusion model and estimation technique combinations: BSP with the DKI‐FWE model (solid blue), ML with the DKI‐FWE model (dashed red) and BSP with the standard DKI model (dotted yellow).

Table 2.

RMSE of Estimates of f, FA, MD and MK for 3 Different Diffusion Model and Estimator Combinations: BSP with the DKI‐FWE Model, ML with the DKI‐FWE Model and BSP with the Standard DKI Model

	f	FA	MD	MK
BSP (DKI‐FWE)	0.070	0.049	0.073	0.180
ML (DKI‐FWE)	0.101	0.095	0.158	0.380
BSP (DKI)	/	0.143	0.338	0.647

Real Data Experiments

Next, the same combinations of models and estimators as in the simulation experiments were applied on the real data set. Figure 4 shows the BSP estimates of various DKI‐FWE model metrics. The associated ML estimates of the DKI‐FWE model metrics are shown in https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27075&attachmentId=2171641237. Figure 5 shows the difference maps of each DKI‐FWE metric determined using both estimators (= BSP ‐ ML). Here, one should note that even though both estimators produce very similar results in most voxels, in all maps multiple spurious voxels appear where the ML estimator is unable to deal with the ill‐conditionedness of the DKI‐FWE model. The difference between BSP and ML is, however, best visualized when looking at the distributions of their respective parameter estimates, shown in Figure 6. Here, it is clear that the ML estimator often produces estimates on the upper and lower boundaries of the imposed constraints, as opposed to the BSP estimator. Figure 6 also shows that, although a Gaussian prior is imposed on the parameter distributions during the BSP estimation, the BSP parameter distributions can still differ to a large extent from the Gaussian shape and maintain their original distribution.

Figure 4.

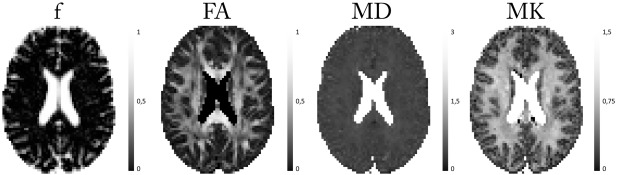
Real data maps of DKI‐FWE model metrics (f, FA, MD, and MK) using the BSP estimator.

Figure 5.

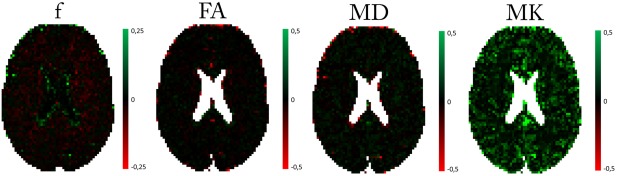
Real data difference maps of DKI‐FWE model metrics (f, FA, MD, and MK) between the BSP estimator and the ML estimator.

Figure 6.

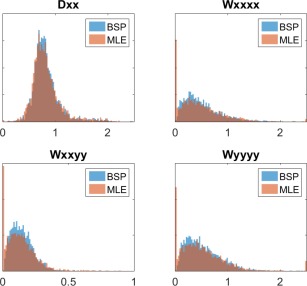
Distribution of BSP estimator (blue) and ML estimator (orange) parameter estimates of a selection of four parameters from the DKI‐FWE model in a real human data set. CSF was masked out to make parameters representative of brain tissue.

Figures 7 and 8 show the BSP estimates of various DKI model metrics and their difference with the associated DKI‐FWE model metrics, respectively. Notice the FA estimated with the standard DKI model to be substantially lower than that of the DKI‐FWE model, especially in regions around the CSF where large free water volume fractions can be expected. In the same regions, MD and MK tend to be substantially higher for the standard DKI model. These findings are all in agreement with the simulation experiments. For the real data figures, a mask of f > 0.85 was used to represent CSF regions. Inside this mask, FA, MD, and MK values were removed because these diffusion properties have no meaning as they are tissue specific and require a minimal amount of signal to reliably represent the tissue compartment.

Figure 7.

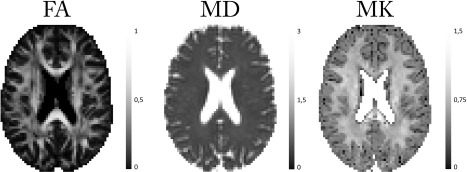
Real data maps of DKI model metrics (FA, MD, and MK) using the BSP estimator.

Figure 8.

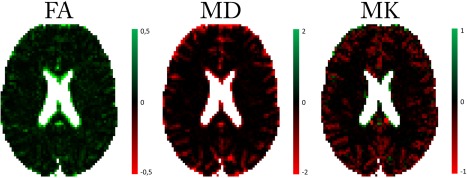
Real data difference maps between the DKI‐FWE model and the DKI model in terms of their common model metrics (FA, MD, and MK). Both model parameters are estimated using the BSP estimator.

DISCUSSION

To address the problem of CSF partial volume effects in DKI, the DKI‐FWE diffusion model was introduced in this work. The DKI‐FWE parameter estimation problem is, however, shown to be ill‐conditioned, demonstrating the need for parameter estimation techniques that can deal with this ill‐conditioned nature. A Bayesian approach with a shrinkage prior was therefore proposed to estimate the DKI‐FWE model parameters.

Optimal b‐values for Precise DKI‐FWE Model Parameter Estimation

First, using the CRLB, an acquisition protocol with four distinct b‐values: b = 0, 0.36, 1.19, and 2 $\text{ms}/\mu {\mathrm{m}}^2$, was found to be optimal in terms of the maximally theoretical attainable precision of the parameter estimators. The acquisition protocol that was used to acquire the real human data approximates this optimal protocol. Using the CRLB, we were able to quantify the loss in precision as a result of using a slightly different acquisition protocol compared to the optimized one. The precision $ϵ$ of an acquisition protocol is defined here as the root of the average of the diagonal CRLB elements (except for S ₀):

$$ϵ=\sqrt{\frac{1}{22}{\displaystyle \sum _{i=1}^{22}{\text{CRLB}}_{ii}}}$$ (15)

The average relative difference in precision of the parameter estimates between the optimal acquisition protocol and the one used to acquire the data was found to be around 4%. To remain sensitive to the free water signal, the lowest nonzero b‐value should not be chosen too high. At b = 0.36 $\text{ms}/\mu {\mathrm{m}}^2$, the free water signal intensity is just 34% of that of the non‐diffusion weighted signal. Choosing the lowest b‐value to be b = 0.75 for example, would lead to a 41% drop in precision. https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27075&attachmentId=2171641237 gives a visual representation of these results.

Statistical Significance of Introducing a Free Water Compartment in DKI

Extending mathematical models by introducing extra parameters, as done in this work, can introduce the risk of overfitting the data. A statistical study based on the GLRT, however, indicates that this is not the case for the DKI‐FWE model compared to DKI. Both simulation and real data experiments support that for a substantial amount of voxels, DKI‐FWE is significantly better at describing the data compared to DKI, especially in regions where free water partial volumes in the approximate range of $0.2<f<0.8$ are expected. When the f‐fraction is very close to either 0 or 1, the DKI‐FWE model essentially reduces to the DKI model or an isotropic diffusion model, respectively, and offers no improvement over DKI.

Effect of the DKI‐FWE Model on Diffusion Metrics Compared to DKI

We showed that ignoring free water compartments in DKI studies can have a considerable effect when relating DKI metrics solely to tissue. The change in FA and MD can be understood most intuitively by considering separating an isotropic signal compartment with high diffusivity from a normal tissue compartment. Removing an isotropic compartment will evidently raise the FA while removing a compartment with high diffusivity will lower MD. The decreased MK in FWE‐DKI compared to DKI can be explained analytically because it is known that diffusional heterogeneity increases the kurtosis 6. Separating a high diffusivity compartment from the signal, will thus reduce the diffusional heterogeneity and subsequently reduce the kurtosis. This effect can also be seen in Table 2 where the RMSE of DKI is 3 to 7 times larger than that of the DKI‐FWE model. In Figure 8 the effects on the DKI metrics can be seen as either red or green regions in the respective FA and MD or MK difference maps. Note that these differences are most distinct around CSF regions.

Bayesian Estimation for DKI‐FWE Model Parameters

A downside of the DKI‐FWE model is that it leads to an ill‐conditioned parameter estimation problem. The BSP approach is shown to be able to estimate the DKI‐FWE model parameters in a robust way. A constrained ML estimation approach will result in a loss in precision, as is indicated by the broader error distributions in Figure 3, and produce a considerable number of parameter estimates that lie on the upper or lower bounds of the applied constraints, as shown in Figure 6. BSP on the other hand, produces accurate and precise parameter estimates, while still respecting the underlying parameter distributions. These findings are also quantified in Table 2 and confirm that BSP substantially outperforms ML estimation in terms of the RMSE.

A limitation of the BSP estimator is its computational expense. Although our current implementation is very slow, around 10 s per voxel implemented in MATLAB 51 running on a 2.80GHz Intel(R) Core(TM) i7 desktop PC, it is relevant as proof‐of‐concept. Nonetheless, further developments and optimization to speed up the algorithm are required to enable more routine use of the technique. One such approach could be to employ supervised machine learning 74.

Another important consideration to make is that the proposed BSP method uses a global prior, inferred from all voxels of the brain. In future work, we will investigate the effect of ROI size on the accuracy of the estimator, especially in case of the diseased brain. Indeed, large lesions in the brain will interfere with the prior distribution, potentially biasing the parameter estimates in healthy voxels and thereby introducing a confounding factor in any subsequent statistical analysis. Vice versa, parameter estimates in lesion voxels might also be affected by using a global prior 39.

TE‐Dependency of the DKI‐FWE Model

Note that the reported free water fractions are basically T ₂‐weighted signal fractions instead of the biophysically more relevant volume fractions. Since the T ₂ relaxation time of free water is an order of magnitude longer than the T ₂ relaxation time of white matter, the free water signal decays slower. As a consequence, for any given TE, the estimated free water signal fraction exceeds the actual volume fraction. This can be quantified with the following expression for the free water signal fraction f in function of the free water volume fraction f_v 75:

$$f=\frac{f_v{e}^{-\text{TE}/T_{2,\text{CSF}}}}{f_v{e}^{-\text{TE}/T_{2,\text{CSF}}}+(1-f_v)e^{-\text{TE}/T_{2,\text{WM}}}}.$$ (16)

Literature reports free water volume fractions in deep white matter of 1–2% 76. Assuming $T_{2,\text{WM}}=69\text{ms}$ 77, $T_{2,\text{CSF}}=1250\text{ms}$ 78, 79 and $\text{TE}=73\text{ms}$, this would lead to free water signal fractions of 2.7–5.3%. This is in line with the free water signal fractions of (3.9 ± 5.5)% that we find in the deep white matter in our study.

The TE dependency of the free water signal fraction can be exploited to estimate the actual volume fraction. We recently showed that including the T ₂ signal decay of both compartments, the (DKI‐)FWE model fitting problem gets better conditioned without the need for regularization 80. However, such an approach requires the acquisition of diffusion‐weighted images at different TEs, which makes it inapplicable to most available data sets.

CONCLUSION

In conclusion, the DKI‐FWE model, an extension to the DKI model that incorporates a free water compartment, is introduced. To deal with the ill‐conditioned nature of the associated parameter estimation problem, a Bayesian approach with shrinkage prior is proposed. Both simulation and real data experiments indicate that the combination of the DKI‐FWE model with BSP is a feasible approach to estimate DKI parameters, while simultaneously eliminating free water partial volume effects.

Supporting information

Fig. S1. Real data maps of DKI‐FWE model metrics (f, FA, MD and MK) using the BSP estimator for the 4 shell acquisition protocol with $b=0,0.25,1.15,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (top row), a 3 shell acquisition protocol with $b=0.25,1.15,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (middle row) and a 3 shell acquisition protocol with $b=0,0.25,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (bottom row). Model parameters were estimated using the BSP estimator as described in the manuscript. The data set that was used is the same one as the data set described in the manuscript. Note the difference in f, MD and MK maps of the 3 shell protocols compared to the 4 shell protocol.

Fig. S2. Condition number of the Fisher information matrix for the 4 shell acquisition protocol with $b=0,0.25,1.15,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (left), a 3 shell acquisition protocol with $b=0.25,1.15,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (middle) and a 3 shell acquisition protocol with $b=0,0.25,2.00$ $\text{ms}/\mu {\mathrm{m}}^2$ (right). Condition numbers were attained as described in the manuscript. The underlying parameter values used for determining the FIM are the same for all acquisition protocols and where determined based on the 4 shells protocol as described in the paper. The data set that was used is the same one as the data set described in the manuscript.

Fig. S3. Histograms (blue) and associated Gaussian distribution fits (red) of all 23 parameters of the DKI‐FWE model. The DKI model is fitted in an unconstrained and weighted least squares sense to whole brain real data without CSF. The F parameter distribution is determined using simulations based on a realistic distribution of f 45.

Fig. S4. Real data maps of DKI‐FWE model metrics (f, FA, MD and MK) using the ML estimator.

Fig. S5. The average precision over all DKI‐FWE model parameters (except S ₀), calculated using the diagonal CRLB elements, in terms of the value of the lowest (a) or middle (b) non‐zero b‐value shell of the DKI‐FWE model acquisition protocol. All other b‐values are kept equal to the associated optimized acquisition protocol b‐values.