Solvation of Carbon Nanoparticles in Water/Alcohol Mixtures: Using Molecular Simulation To Probe Energetics, Structure, and Dynamics

Abstract

Molecular dynamics simulations were used to examine the solvation behavior of buckminsterfullerene and single-walled carbon nanotubes (SWCNT) in a range of water/alcohol solvent compositions at 1 atm and 300 K. Results indicate that the alcohols assume the role of pseudosurfactants by shielding the nanotube from the more unfavorable interactions with polar water molecules. This is evident in both the free energies of transfer (ΔΔG_water→xOH = −68.1 kJ/mol and −86.5 kJ/mol for C₆₀ in methanol and ethanol; ΔΔG_water→xOH = −345.6 kJ/mol and −421.2 kJ/mol for the (6,5)-SWCNT in methanol and ethanol) and the composition of the solvation shell at intermediate alcohol concentrations. Additionally, we have observed the retardation of both the translational and rotational dynamics of molecules near the nanoparticle surface through use of time correlation functions. A 3-fold increase in the residence times of the alcohol molecules within the solvation shells at low concentrations further reveals their surfactant-like behavior. Such interactions are important when considering the complex molecular environment present in many schemes used for nanoparticle purification techniques.

Graphical abstract

INTRODUCTION

Since their discovery in 1991,¹ single-walled carbon nanotubes (SWCNTs) have been extensively studied due to their interesting mechanical and electrical properties. They have been used in many applications including molecular,² electrochemical,³ and optical sensors,⁴ nanocomposite materials,⁵ drug delivery agents,⁶ and DNA sequencing.^7,8 The main barrier inhibiting the widespread use of this material is the nonuniformity of the nanotube fabrication process that produces polydisperse mixtures of different size (diameter and length), thickness (single- and multiwalled), chirality, and handedness. This wide range of species means that significant postsynthesis purification steps must be performed before specific topologies can be isolated for metrology or industrial use. Various separation methodologies address this problem through the use of surfactants to disperse the tubes in aqueous media before using techniques such as ultracentrifugation,⁹ ion-exchange chromatography (IEX),¹⁰ and aqueous two-phase extraction (ATPE)¹¹ to separate the SWCNTs based on their physiochemical properties. Many surfactants have shown promise in these separation protocols, including anionic surfactants such as sodium dodecyl sulfate (SDS),¹² sodium deoxycholate (DOC) among other bile salts,^9,11,12 and perhaps most interestingly, single-stranded DNA (ssDNA).^10,13 This sequence-specific ssDNA-based approach has not only shown success in separating particular SWCNT chiralities^14,15 but also has demonstrated the ability to separate individual enantiomers within populations of the same chirality.¹⁶ Other techniques involve first dispersing the SWCNTs in one surfactant and then using alcohol to replace with another¹⁷ as certain alcohols have demonstrated a stabilizing effect on the surfactant-dispersed systems.¹⁸ The solution environment around these nanoparticles is complex, as multicomponent solvents are often used to tune the colloidal solvation and improve the separation. It is with this motivation that we examine the interaction between aqueous solutions of methanol/ethanol and bare carbon nanoparticles.

The energy of solvation of carbon nanoparticles is an extremely important quantity because many of their applications are as sensors in aqueous environments. Much work has been done to examine fullerene particles such as C₆₀^19–24 in water, but relatively few studies have examined SWCNTs in the same detail.²⁵ Similarly, the behavior of the solvent surrounding the nanoparticle has been extensively examined for water–C₆₀ systems^23,26,27 and occasionally for other solvents,^28,29 but to our knowledge, work with nanotubes is nonexistent as is that with mixed solvents. The purpose of this study is to understand the energetics, structure, and dynamics of the solvation of bare carbon nanoparticles in multicomponent water/alcohol systems. It is a precursor to an ongoing larger study examining the effects of such multicomponent solvent systems on surfactant adsorption of ssDNA and the effect on the dispersion and separation characteristics of SWCNTs.

METHODS

System Description and Simulation Details

This study examines a variety of carbon nanoparticles (see Table 1) in water/alcohol mixtures. The SWCNTs were treated as infinitely long tubes that cross the periodic boundaries of the simulation box. Bucky ball systems were built containing 2134 total solvent molecules while SWCNT systems contained 3857 total solvent molecules. The composition of these solvent molecules was varied in increments of 10 mol % in order to examine the effects of water/alcohol mixtures (see Table S1 for details of individual simulations).

Table 1.

Properties of Fullerene Nanoparticles Studied

nanoparticle	abbreviated name	diameter (Å)	length (Å) (one unit cell)	no. of carbon atoms
buckminsterfullerene	C60	7.1		60
(6,5)-SWCNT	T65	7.47	40.64	364
(8,3)-SWCNT	T83	7.71	41.96	388
(7,6)-SWCNT	T76	8.82	48.01	508
(8,6)-SWCNT	T86	9.53	25.91	296
(9,7)-SWCNT	T97	10.88	59.18	772

Simulations were performed using the open source software package GROMACS (ver. 5.1.2)^30–32 applying the SPC/E model for water³³ and the CHARMM36 force field³⁴ for treatment of the alcohols. All carbon atoms in the nanoparticles were treated identically and given the force field parameters of aromatic sp2 carbon and carried no partial charge. The LINCS constraint algorithm³⁵ was used to maintain the correct bond lengths of all hydrogen-containing bonds, thereby allowing a time step of 2 fs. Equilibration was carried out first for 200 ps in the NVT ensemble using a velocity rescaling thermostat³⁶ to maintain the temperature at 300 K, followed by 200 ps in the NPT ensemble making use of the Parrinello–Rahman barostat³⁷ to maintain a pressure of 1 atm. In the case of the bucky ball system, this barostat was applied in an isotropic manner, allowing all box dimensions to vary; however, in the systems containing SWCNTs it was applied in a semi-isotropic fashion in order to maintain the correct box size in the axial dimension corresponding to the length of the periodic SWCNT unit cell. Following these equilibration steps, data was collected over production runs of 1 ns.

Free Energy Calculation Details

The change in Gibbs free energies of solvation, ΔG_solv, of the carbon nanoparticles was calculated using free energy perturbation (FEP) by applying a coupling parameter, λ, to insert/remove the solute from the surrounding solution.³⁸ By gradually changing this parameter between 0 and 1, the nanoparticle can be “grown into” or “faded out of” the solution. Here λ = 0 corresponds to a state in which the nanoparticle does not see the solvent and effectively behaves as if in vacuum and λ = 1 corresponds to the state of normal nanoparticle/solvent interaction. Values of 0 < λ < 1 correspond to intermediate “ghost states” in which a soft-core Lennard-Jones-type potential is used to avoid singularities. A separate simulation is run for each value of λ, and the average derivative of the parametrized Hamiltonian, 〈∂H/∂λ〉, is calculated. The simulated free energy can then be obtained via thermodynamic integration as in eq 1.

$$\mathrm{\Delta }{G}_{\text{sim}}={\int }_0^1\langle \frac{\partial H}{\partial \lambda }\rangle \mathrm{d}\lambda$$ (1)

Shirts et al.³⁸ have developed a relationship between the simulated solvation free energy, ΔG_sim, and the actual solvation free energy, ΔG_solv, that corrects for the change in the system volume upon the insertion/deletion of the solute (eq 2).

$$\mathrm{\Delta }{G}_{\text{solv}}=\mathrm{\Delta }{G}_{\text{sim}}-kT\text{ ln}\left(\frac{V^{\ast }}{V_1}\right)$$ (2)

Here, V* denotes the system volume at with full solute/solvent interaction and V₁ is the volume of a box of pure solvent with the same number of molecules. In our simulations, the largest volume change observed was roughly 3%, which results in a correction factor on the order of ~80 J/mol (see Table S2 for details). This correction value is much lower than the statistical uncertainty of our simulations and can therefore be neglected in all cases.

Another method to calculate free energy differences is the Bennet acceptance ratio (BAR),^39–42 which is expressed in eq 3 for the free energy difference between two adjacent λ-states, n and n+1 (see Bennet,³⁹ Pohorille et al.,⁴⁰ or Kim and Allen⁴² for detailed equation development).

$${\langle f(-u+\mathrm{\Delta }{G}_{n\to n+1})\rangle }_{n+1}={\langle f(u-\mathrm{\Delta }{G}_{n\to n+1})\rangle }_n$$ (3)

Here, u = U_n+1 − U_n is the energy difference between the two states, and f(x) = (1 + exp(x/kT))⁻¹ is the Fermi function. Recursively solving eq 2 yields the free energy difference. This technique is attractive as it allows for better estimation of the statistical error (eq 4) by comparing the histograms of the energy difference between the two adjacent λ states:

$$\langle {\delta }^2(\mathrm{\Delta }{G}_{n\to n+1})\rangle =\frac{2k^2{T}^2}{N_{\mathrm{s}}}(\frac{1}{2S}-1)$$ (4)

Here, 〈δ²(ΔG_n→n+1)〉 is the mean square error in the free energy estimation, N_s is the number of times each energy state is sampled, and S is a measure of the overlap between the two densities of u and equals zero for no overlap and 0.5 for two identical distributions (eq 5).

$$S=\int \frac{{\rho }_n(u){\rho }_{n+1}(u)}{{\rho }_n(u)+{\rho }_{n+1}(u)}\mathrm{d}u$$ (5)

This acceptance ratio technique was used in the current work via the g_bar module within GROMACS. All ΔG_solv values were found using 50 evenly spaced λ states and were performed in a decoupling manner to avoid particle overlap and to prevent the encapsulation of solvent molecules within the nanoparticle.

Entropic and Enthalpic Contribution to Solvation

Given the definition of Gibbs free energy, it is possible to calculate the change in entropy for the solvation process by finding the solvation free energy at several temperatures and using a finite difference approximation⁴³ as in eq 6.

$$\mathrm{\Delta }{S}_{\text{solv}}(T)=-\frac{\partial \mathrm{\Delta }{G}_{\text{solv}}}{\partial T}\approx -\frac{\mathrm{\Delta }{G}_{\text{solv}}(T+\mathrm{\Delta }T)-\mathrm{\Delta }{G}_{\text{solv}}(T-\mathrm{\Delta }T)}{2\mathrm{\Delta }T}$$ (6)

This approach assumes that the heat capacity remains constant over the temperature range, which is valid for small ΔT (here we use ΔT = 20 K). Once this quantity is known, the calculation of the enthalpic contribution to solvation is trivial (eq 7).

$$\mathrm{\Delta }H=\mathrm{\Delta }G+T\mathrm{\Delta }S$$ (7)

Radial and Angular Distribution Functions

To better understand the solution behavior in the vicinity of the nanoparticle, the radial distribution functions (RDFs) are calculated from the center of the respective fullerenes. In the case of C60, this is done in the traditional, spherical manner. However, for SWCNTs, it is done using cylindrical shells taking the tube axis as the center. In the case of water, the RDF is taken with respect to the oxygen atom (OW), and when considering the various alcohol molecules, multiple RDFs are found, one with respect to the oxygen atom (OA) and the others using each carbon atom (C1 for methanol; C1 and C2 for ethanol). The first peak in the RDF is representative of the first solvation shell nearest to the particle. The location of the first minimum is taken as a cutoff and only the solvent molecules within this cutoff are used in all subsequent analyses of the solvation layer.

Angular distributions of these solvating waters and alcohols are constructed so that any favorable molecular orientations relative to the nanoparticle may be observed. In the case of both C60 and the SWCNTs, the reference vectors from which these angles are measured are drawn such that they are normal to the nanoparticle surface and pointing directly at the solvent molecule of interest. Two different distributions (θ and ω) are found between these surface normal reference vectors and various intramolecular vectors to orient the solvent molecule in 3-dimensional space with respect to the nanoparticle. In water molecules, these correspond to the angles of the dipole vector, n_μ, and the O → H vector, n_WOH. For methanol, the vectors are the O → C vector, n_OC, and the O → H vector, n_MOH; for ethanol, which is slightly more complicated due to extra degrees of freedom, the C1 → C2 vector, n_CC, and again, the O → H vector, n_EOH (Note that these definitions for ethanol require that two reference vectors be drawn). These vectors and angles are visualized in Figure 1.

Figure 1.

Schematic cartoon of angles used to construct angular histograms (not to scale).

Dynamics of the First Solvation Layer

While RDFs and angular distributions yield some idea of the structure/arrangement of solvent molecules surrounding the carbon nanoparticles, also relevant are the dynamics of this first layer. We use correlation functions of the form shown in eq 8 to this end so that diffusion coefficients of solvent molecules near the surface can be estimated as well as their average residence times within the solvation shell:

$$C^{\alpha }(t)=\frac{{\sum }_{i=1}^N[{\mathit{\alpha }}_{\mathit{i}}(t+t_0){\mathit{\alpha }}_{\mathit{i}}(t_0)]}{{\sum }_{i=1}^N{|{\mathit{\alpha }}_{\mathit{i}}(t_0)|}^2}$$ (8)

Here, α_i is the vector of interest for solvent molecule i, and N is defined as the population of solvent molecules that remain within the solvation layer for a minimum of 2 ps. This method is similar to previous studies²³ and is applied to eliminate from consideration those molecules that cross between the bulk solution and the region of interest and vice versa. Translational dynamics (i.e., self-diffusion) are studied using velocity autocorrelation functions (α = ν) (VACF) and Green–Kubo relationships as in eq 9 where M is the molar mass of the molecule of interest.

$$D=\frac{\mathit{\text{RT}}}{M}{\int }_0^{\infty }{C}^{\nu }(t)\mathrm{d}t$$ (9)

Reorientational dynamics apply eq 7 to the orientational vectors defined previously (α = n_μ, n_WOH, n_OC, n_MOH, n_CC, and n_EOH). These reorientational correlation functions (ROCF) often display stretched exponential decay, a characteristic of the Kohlrausch–Williams–Watts (KWW)^44–46 law that is used to describe the relaxation of various phenomena in complex condensed matter systems.^47,48 This technique has not only been applied to the study of the hydration shells of proteins,^49,50 but also to water confined near inorganic surfaces and other fullerene-containing systems.^{23,26–28,51} The KWW equation

$$C_{\beta }(t)={\mathit{\text{Ae}}}^{-{(t/\tau )}^{\beta }}$$ (10)

where A is a prefactor, β is the stretched exponential constant, and τ is the central relaxation time can be fit to the ROCF to extract information about the dynamics. Specifically, τ, which gives a measure for the relaxation time of solvent molecules within the region of interest. Furthermore, the average relaxation time can be estimated through use of the Gamma function as in eq 11.

$$\langle \tau \rangle =\frac{A\tau }{\beta }\mathrm{\Gamma }\left(\frac{1}{\beta }\right)$$ (11)

This same KWW analysis can be used to estimate the residence time of solvent molecules in the hydration shell. This is done by defining the “cage correlation function” (CCF) by letting α_i = Z_i(t), where Z_i(t) = 1 when the ith solute molecule is in the solvation shell at time t and zero otherwise.

Further information about the solvent behavior and its local environment can be extracted by examining the low-frequency vibrational modes of the molecules. This is accomplished via the power density spectra

$$P(\nu )=|ℱ\{C^{\nu }(t)\}|$$ (12)

where ℱ{C^ν(t)} is the Fourier transform of the VACF:

$$F\{C^{\nu }(t)\}={\int }_0^{\infty }{C}^{\nu }(t)e^{-2\pi i\nu t}\mathrm{d}t$$ (13)

RESULTS AND DISCUSSION

Solvation Energy and Entropy of Nanoparticles in Water

The free energies of solvation found for the various carbon nanoparticles in water are reported in Table 2. Our value of −50.9 kJ/mol measured for C₆₀ agrees well with previous studies on a similar system by Varanasi et al. (−55.27 kJ/mol)²³ and Garde et al. (−54.1 kJ/mol)²² and shows similar favorable solvation behavior to the works of Muthukrishnan et al. (−36.10 kJ/mol),²¹ Graziano (−18.4 kJ/mol),²⁰ and Stukalin et al. (−2.9 kJ/mol).¹⁹ Furthermore, a solvation free energy of −17.4 kJ/mol is calculated by Marcus²⁴ based on the solubility of C₆₀ in water and using the sublimation free energy using data obtained from Heymann.⁵² Density functional theory has also shown a net negative energy for the formation of fullerene–water clusters⁵³ and SWCNT–water interactions.⁵⁴ These negative estimates for solvation energies are in line with that of benzene (−3.6 kJ/mol) which can be thought of as a one-dimensional analogue to fullerene particles.

Table 2.

Breakdown of Solvation Free Energies into Enthalpic and Entropic Contributions for Carbon Nanoparticles in Water at 300 K^a

nanoparticle	ΔGsolv (kJ/mol)	ΔHsolv (kJ/mol)	−TΔSsolv (kJ/mol)
C60	−50.9 ± 0.8	−150.1 ± 11.2	99.2 ± 11.2
T65	−325.0 ± 1.6	−747.2 ± 14.8	422.2 ± 14.7
T83	−364.8 ± 1.5	−845.9 ± 12.0	481.1 ± 12.0
T76	−502.1 ± 4.0	−1051.0 ± 19.1	548.9 ± 18.7
T86	−315.0 ± 8.7	−984.0 ± 16.2	669.0 ± 13.7
T97	−769.4 ± 25.2	−1560.4 ± 40.0	791.0 ± 31.1

^aUncertainty values determined using g_bar module within GROMACS and represent the sum of variance in free energy between each successive λ state.

The values for the SWCNTs in water are similarly negative in sign, suggesting a favorable solubility which clashes with our intuition of how hydrophobic solutes should behave in aqueous environments. Further examination of the solvation process via decomposition into its enthalpic and entropic contributions (via eqs 6 and 7) reveals that there is a significant entropic penalty due to the rearrangement of the water molecules surrounding the nanoparticle. The solvation of C₆₀ yields an entropic change of −0.33 kJ/mol·K which agrees with the result obtained by Muthukrishnan (−0.33 kJ/mol·K).²¹ The same method results in entropy changes of −1.41, −1.60, −1.83, −2.23, −2.64 kJ/mol·K for the nanotubes T65, T83, T76, T86, and T97, respectively. This effect is often referred to as “caging” and comes about because the water molecules attempt to avoid interaction with the hydrophobic solute thereby increasing the interactions with their neighbors. These entropic penalties are overcome by the strong van der Waals interactions between the carbon atoms and the water molecules, in part due to the high surface density of carbon atoms (~0.2 atoms/Ų for all particles in this study).

While the solvation energies and entropies for the SWCNTs may appear to span a large range, this is an artifact of the size of the unit cell for each nanotube. It can be seen in Figure 2 that ΔG_solv scales with the surface area of the nanoparticle and ΔS_solv scales with its diameter. This is not surprising as the water interacts with the carbon atoms which only exist on the surface of the nanoparticle, and more rearrangement of the solvent is necessary when inserting a particle with larger diameter (i.e., larger volume). Due to the similar values for the free energies and entropies of solvation of the nanotubes upon scaling, only the C60 bucky ball and the T65 SWCNT were considered in all further simulations to examine any effect of nanoparticle shape on the behavior of the solvating molecules.

Figure 2.

(a) Scaling of ΔG_solv with particle surface area and (b) ΔS_solv with particle diameter. The entropy of the spherical C60 nanoparticle scales differently than that of the cylindrical nanotubes due to the different surface area to volume relationship.

Solvation Energy of Nanoparticles in Methanol and Ethanol

The solubility of fullerenes in these two solvents has been shown to be marginally higher than in water²⁴ and to extend within the limits of experimental measurements (>1 parts per billion). This allows for a direct comparison with the values obtained in our simulations for C60. When considering the dissolution of a solute, solvation is only a portion of the process. The dissociation of a single molecule from the larger bulk material must also be considered. The free energy of sublimation is used as a measure of this additional aspect and the total free energy change of dissolution can be written as in eq 14

$$\mathrm{\Delta }{G}_{\text{dis}}=\mathrm{\Delta }{G}_{\text{solv}}+\mathrm{\Delta }{G}_{\text{sub}}$$ (14)

where ΔG_dis, ΔG_solv, and ΔG_sub are standard Gibbs free energies of dissolution, solvation, and sublimation, respectively. Using existing solubility data for C60 presented by Marcus et al.,²⁴ ΔG_dis can be estimated as in eq 15

$$\mathrm{\Delta }{G}_{\text{dis}}=-RT\text{ ln}(x_{C60})$$ (15)

where x_C60 represents the molar fraction of C60 in solution. Applying a value of 180 kJ/mol for the free energy change of sublimation²⁴ allows for the prediction of ΔG_solv based on experimental measurements (see Table 3)

Table 3.

Experimentally Predicted and Simulated Solvation Free Energies and Relative Energies with Respect to Water for Buckminsterfullerene (C60) and a Periodic (6,5) SWCNT (T65) in Methanol and Ethanol at 300 K^a

nanoparticle	solvent	ΔGsolv (kJ/mol) (EXP)24	ΔGsolv (kJ/mol) (FEP)	ΔΔGwater→i (kJ/mol)
C60	methanol	−130.0	−119.0 ± 0.7	−68.1 ± 1.3
C60	ethanol	−139.3	−137.4 ± 0.8	−86.5 ± 1.3
T65	methanol		−670.6 ± 2.7	−345.6 ± 3.2
T65	ethanol		−746.2 ± 3.3	−421.2 ± 3.7

^aUncertainty values determined using g_bar module within GROMACS.

The solvation free energies of C60 and T65 in methanol and ethanol were found using the same FEP technique described previously and are presented in Table 3. From this data, the relative free energies from water (sometimes termed transfer energies) can also be calculated. As expected, the solvation of the carbon nanoparticles becomes more favorable as additional alkyl groups are added to the solvent molecule because it is known that their solubility increases in less polar compounds.²⁴

Our simulated results agree well with the predictions for C60 in methanol and ethanol based on experimental measurements (within 10%). This further verifies the results obtained as we extend the method to different carbon nanostructures (SWCNTs) and solvents.

Solvation in Water/Alcohol Mixtures

All previous simulations were performed in pure solvents; however, during experimental processes such as the separation of SWCNTs into populations of uniform size or chirality, the use of more complex, multicomponent solvents is common, especially when exchanging from one dispersant to another. The properties of such heterogeneous solvents enable the manipulation of nanoparticle solvation energies leading to their eventual separation. The solvation energies of the carbon nanoparticles in these mixed solvents are again found via FEP and presented in Figure 3 (and tabulated in Table S4). These curves again indicate that the carbon nanoparticles prefer to be solvated by solvent molecules containing more nonpolar alkyl groups. Particularly drastic is the large change in ΔG_solv upon addition of small amounts of ethanol which appears to suggest that the alcohol is approximating the behavior of a surfactant in these systems and reducing the amount of unfavorable interactions between the carbon nanoparticle and the polar water molecules.

Figure 3.

Solvation free energies of (a) C60 and (b) T65 in water/alcohol mixtures. Error bars are within the bounds of the data point. Values are tabulated in Tables 2, 3, and S2.

In addition to this surfactant-like behavior, it is likely the dielectric constant of the solvents play an important role in solvation. The values for methanol and ethanol are ~33 and ~25 respectively,⁵⁵ much lower than that of water (~80). Additional discussion of this aspect can be seen in the Supporting Information, and a comprehensive investigation of this phenomena is worthy of further research.

Composition and Structure of the Solvation Layer

To further examine how this pseudosurfactant behavior presents itself in mixed solvents, the radial distribution functions (RDFs) for the various solvent molecules are calculated from the center of the carbon nanoparticles. Using the first minimum of the RDF as a cutoff, the average number of each solvent molecule in the solvation shell can be quantified. In the case of pure water, the C60 and T65 nanoparticles are solvated by ~63 and ~192 water molecules, respectively. This coordination number for the bucky ball agrees well with results from previous simulations.^56,57 As the concentration of alcohols is increased, these waters are quickly replaced by alcohol molecules (Figure 4). This is easily visualized as the drastic decrease in the size of the first RDF peak for water upon addition of 10 mol % alcohol (Figure 4, inset) which is further indicative of the pseudosurfactant behavior of the alcohol molecules in these systems. Again, this effect is more pronounced in the case of ethanol mixtures.

Figure 4.

Average number of molecules in the first solvation shell of T65 as a function of alcohol concentration. (Inset) Change in RDF of water oxygen sites from 0 mol % alcohol (dashed line) to 10 mol % alcohol (solid line) indicating exclusion of water from solvation layer: (a) methanol; (b) ethanol. Error bars represent one standard deviation.

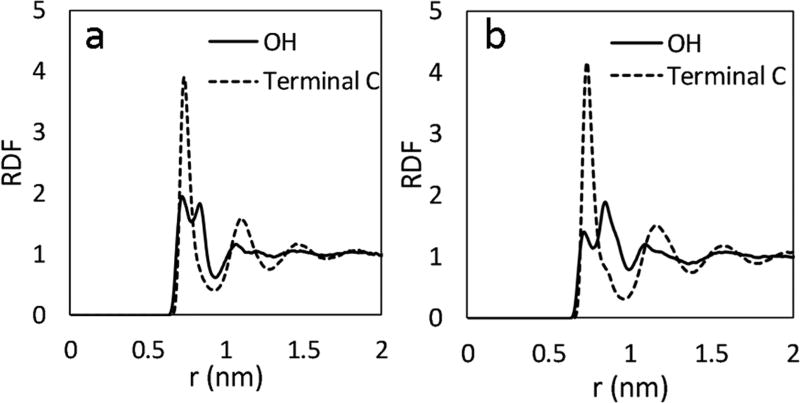
In pure alcohol solvents, the C60 coordination number is ~37 for methanol and ~31 for ethanol, agreeing with previous findings of Malaspina²⁹ and Cao.²⁸ In the case of T65, the coordination numbers are ~107 for methanol and ~100 for ethanol. Further examination of the RDFs of the alcohol molecules (Figure 5) suggest that the terminal methyl groups prefer to be nearest to the carbon surface (single peak) while the hydroxyl group assumes multiple configurations (double peak) depending on the orientation of the molecule. Also of note are the well-defined peaks in the RDF for the alcohols beyond the first solvation shell. This increased structure is likely due to hydrophilic/hydrophobic “head-to-tail” interactions from one solvation shell into another and has been observed previously.²⁸

Figure 5.

RDFs for 100 mol % methanol (a) and 100 mol % ethanol (b) around the T65 nanoparticle.

In order to better quantify these molecular orientations and their location within the solvation shell, angular histograms are constructed from the angles previously defined in Figure 1. Because each set of molecular coordinates defines an orientation and a distance from the carbon surface (θ, ω, r), multiple two-dimensional free energy surfaces (FES) can be constructed relative to the most probable placement/orientation, e.g.

$$\frac{\mathrm{\Delta }G({\theta }_i,{\omega }_i)}{\mathit{\text{kT}}}=-\text{ln}\left(\frac{N({\theta }_i,{\omega }_i)}{N_{\text{max}}}\right)$$ (16)

Here, N(θ_i, ω_j) is the count of orientations that appear in the bin with indices (i, j) and N_max is the count of the bin with the highest population. Both the (θ, ω) and (θ, r) free energy surfaces are presented in Figure 6 for each of the three pure solvents (water, methanol, and ethanol) around the T65 nanoparticle. The one-dimensional histograms of each value have also been projected onto the corresponding axis for visualization. Representative orientations of the molecules (labeled “a”–“i”) have been taken from separate simulation snapshots and displayed in the right column of Figure 6 with respect to the SWCNT surface as well as overlaid on their location within the FES.

Figure 6.

Free energy surfaces and histograms of molecular orientation for solvation shells of water (row A), methanol (row B), and ethanol (row C) around T65. Column I: (θ, ω) distributions. Column II: (θ, r) distributions. Column III: Representative molecular orientations from separate simulation snapshots. See Figure 1 for angle definitions. Here, r represents the normal distance of the solvent oxygen atom from the center of the carbon atoms forming the SWCNT. The dashed red line is the tube axis.

These free energy surfaces reveal that there are molecular orientations/positions that are preferred (in green). The white regions in the free energy maps represent configurations that are geometrically impossible (e.g., the dipole vector and OH vector of water cannot both point in the same direction simultaneously). Favorable orientations for water molecules are labeled “a” through “c”: Regions labeled “a” are both representative of an orientation where one of the n_WOH vectors is pointing directly away from the carbon surface (molecular symmetry therefore requires that the second n_WOH must be at an angle of ~105° and the dipole must be at an angle of ~52°). Region “b” indicates an orientation in which θ_w and ω_w are equal and the molecule is nearly “flat” on the nanotube surface. Region “c” is small compared to the others and is a configuration where the molecular dipole points straight at the carbon surface (θ_w = 180°). This only occurs when the water molecule is on the outer reaches of the solvation shell (r_w ≈ 0.45 nm). Taking all of this together, the water molecules prefer to assume configurations that maximize their ability to form hydrogen bonds by avoiding regions where n_WOH points toward the nanoparticle surface.

In the case of methanol, preferred molecular orientations exist when the n_OC vector points at the surface allowing for interactions between the alkyl group and the carbon atoms of the nanoparticle (regions labeled “d”). This region is relatively spread in the (θ, ω) map due to rotation around the n_OC axis. Region “e” indicates both the n_OC and n_MOH vectors are at 90° angles with the surface normal and the molecule lays “flat” on the surface. Similar to the water molecule, there is a third, smaller region of favorability (labeled “f”) in which the n_OC vector points away from the surface in such a way that the n_MOH vector can be nearly tangent to the nanoparticle. Additionally, note the relative positions of the oxygen atom within the solvation layer in the (θ, r) map: near the surface when n_OC points out and when the molecule lays “flat” (θ = 0–90°), and moving further from the surface as n_OC begins to point toward the nanoparticle (θ > 90°). This phenomenon accounts for the double peak in the oxygen RDF shown in Figure 5. Again, this indicates that preferred arrangements avoid having n_MOH point toward the nanoparticle to maximize the hydrogen bonding within the solvation shell.

Finally, the ethanol molecules exhibit similar behavior, avoiding regions where n_EOH point toward the surface and preferring orientations where n_CC either points toward (region “g”) or along (region “h”) the surface and again with a smaller region of favorability pointing away from the surface (region “i”). As alcohol is added to the system and the solvating water molecules are replaced, their orientational distributions remain roughly the same with a few subtle changes (see Figure 7). While the OH vectors still avoid pointing toward the carbon surface (relatively few at 180°), the fraction of them that point away is reduced (decreasing value at 0°). This indicates that the hydrogen bonds formed by the water molecules at higher alcohol concentrations remain within the solvation layer rather than bridging between the first and second shells. Not shown are the free energy surfaces for C60, which reveals that the solvent molecules behave similarly whether solvating C60 or the SWCNT.

Figure 7.

Relative histograms of the molecular orientation of water OH vectors within the T65 solvation shell at increasing methanol concentrations.

Dynamics of Solvation Layer

The dynamics of the solvation layer are examined via several time correlation functions (VACF, ROCF, and CCF) as discussed in the Methods. Figure 8 (left column) displays velocity autocorrelation functions of each pure solvent for both those molecules that reside in the bulk and those in the solvation shell. This analysis reveals the effect of the nanoparticle surface on the translational motion of the solvating molecules.

Figure 8.

Velocity autocorrelation functions and reorientational correlation functions for water (a, b), methanol (c, d), and ethanol (e, f) in the bulk and while solvating T65 SWCNT. For the VACF, the larger area below the axis for the solvating molecules is indicative of the inhibited diffusion, as is the slower decay in the ROCF.

A similar analysis is performed for the solvation layers at increasing alcohol concentration. Self-diffusion constants are calculated by numerically integrating these VACFs (as in eq 9) and are presented in Figure 9 and tabulated in Table S5. As seen in previous work,^23,26–28 the presence of the carbon surface inhibits the diffusion of the solvating molecules. This is due to both the interactions between the surface and the solvation shell and the decrease in local entropy invoked by the surface. We also observe that relative concentration plays an effect on the diffusion as the motion is slower at intermediate alcohol compositions. This is a phenomenon that has been seen for bulk water/alcohol mixtures without the additional surface effects⁵⁸ and has been ascribed to an increase in the stability of the hydrogen bonding network upon addition of the alcohols.

Figure 9.

Diffusion coefficients (a, b) and characteristic reorientation times of n_OH (c, d) for water/methanol and water/ethanol mixtures in the bulk and the solvation shell of T65 SWCNT. At concentrations above 50 mol % ethanol the low number of water molecules present in the solvation shell (recall Figure 4) prevents calculation of statistically meaningful results.

The reorientational dynamics of the solvating molecules are examined by estimating an average “relaxation time” by fitting the reorientational correlation function to a stretched exponential function (eqs 10 and 11). Figure 8 (right column) presents the ROCFs of the O → H vector for both bulk and solvating water, methanol, and ethanol molecules. Following a short-time liberational relaxation due to intramolecular constraints, the orientation of the O → H vector decorrelates monotonically with time. The KWW law is used to fit the curves starting at 0.2 ps in order to capture the long-time behavior and neglect this initial relaxation. Characteristic reorientational times were also found for solvation shells of varying alcohol concentration and are shown in Figure 9 (tabulated in Table S6 along with the KWW fitting parameters). Again, the effect of the nanoparticle is evident in that the reorientation times are longer. This is further verification of the presence of preferred molecular orientations at the carbon surface due to geometric constraints and the hydrogen bonding network surrounding the solvated particle. Also of note is the effect of concentration. The reorientation time for the water molecules greatly increases at higher alcohol concentrations. Due to the relatively few number of water molecules in the solvation shell at these alcohol concentrations (Figure 4), the local environment of solvating alcohol molecules prevents them from behaving as they would in bulk conditions. In the case of the water/ethanol mixtures, this low number of solvating water molecules at ethanol concentrations greater than 50 mol % prevents the estimation of statistically meaningful reorientation times. Methanol and ethanol reorientation times follow the opposite trend as the relaxation times at low concentrations approach those of the bulk other than a maximum at 50 mol %. This effect is similar to the translational diffusion in that the hybridized water/alcohol hydrogen bonding network exhibits some restriction of the molecular motions.

Residence times of solvent molecules within the solvation shell can be estimated in a similar manner. By extracting the characteristic decorrelation time from the cage correlation function (CCF) via the same KWW law as in the case of the ROCF, we can obtain a measurement of how long, on average, the molecules spend directly solvating the nanoparticle. Characteristic residence times, 〈τ〉_res, are shown in Figure 10 for both water/methanol and water/ethanol mixtures around the T65 SWCNT.

Figure 10.

Average residence times of solvent molecules in the solvation shell of the T65 SWCNT.

This analysis reveals an interesting trend in that as the number of water molecules near the nanoparticle decreases so does its residence time near the surface; this is in contrast with the alcohol molecules whose residence time increases as their number decreases. This is again further validation of the carbon nanoparticle’s preference to be solvated by the molecules containing alkyl groups. At low alcohol concentrations (10 mol %) there are fewer alcohol molecules near the surface, requiring that they spend a longer period of time solvating the nanoparticle before they exchange with a water molecule. At high alcohol concentrations (90–100 mol %) this residence time decreases as they are able to exchange with an excess of equally attractive alcohol molecules rather than less attractive water molecules. Also of note is that the residence time of the ethanol molecules (~300–700 ps) is two to three times that of the methanol molecules (~100–300 ps).

Low-Frequency Vibrational Spectra of Solvating Molecules

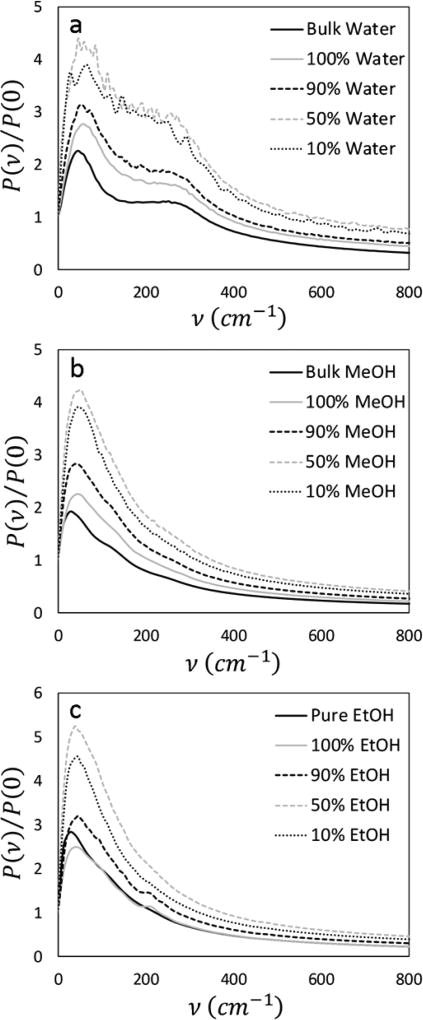
Power spectra have previously been used to examine the properties of water in the hydration shells of biomolecules⁵⁹ as well as in the context of bulk water/methanol and water/ethanol mixtures.⁵⁸ The analysis of these computational spectra for water and other hydrogen bonding liquids is still somewhat ambiguous. The water spectrum is characterized by two bands at ~50 and ~250 cm⁻¹. The 250 cm⁻¹ band has been interpreted as vibrations in the O⋯O direction between two hydrogen-bonded molecules^60–62 and has been shown to diminish as the amount of hydrogen bonding decreases.⁶³ The peak at 50 cm⁻¹ represents the bending mode of the angle formed by O⋯O⋯O triplets⁶⁰ which can again be indicative of hydrogen bonding. However, as this peak also exists in non-hydrogen bonding liquids, it may instead represent the restricted transverse vibrations of a molecule against the cage of its nearest neighbors,^63,64 which would, in any case, be stronger if the molecules were stabilized by hydrogen bonds. In total, this interpretation regards the high frequency (~50 cm⁻¹) peak to be a measure of the rigidity of the surrounding molecular cage (which increases with increasing hydrogen bonding) and the low frequency peak (~250 cm⁻¹) to be more directly indicative of the hydrogen bonding strength. The spectra obtained by transforming the VACFs of the water molecules surrounding the T65 SWCNT in its methanol mixtures are normalized and presented in Figure 11 (top). While some noise exists in the 50 and 10 mol % traces (a sampling issue due to the relatively low number of water molecules surrounding the nanoparticle at these concentrations; recall Figure 4), a number of interesting trends are observed. As more alcohol is included in the solvation layer, the first peak is blue-shifted by approximately 15 cm⁻¹ to 20 cm⁻¹ while the position of the high frequency peak remains unchanged. This phenomenon has been seen previously in the solvation layers of biomolecules⁵⁹ and indicates that the degrees of freedom of the water motion are changed nonuniformly as they assume their position in the solvation layer of carbon nanoparticles. The increase in the magnitude of the spectra through 50 mol % represents a higher degree of rigidity, or stabilization, of the hydrogen bonding network. This enhanced structure has been seen experimentally^65,66 and agrees with our observation of inhibited diffusion and molecular rotation within the solvation layer at intermediate alcohol concentrations. Additionally, the smearing together of the two peaks is likely due to the growing presence of water–alcohol hydrogen bonds. The water spectra with its ethanol mixtures (not presented here) show generally similar trends, however more noise exists even at lower alcohol concentrations due to the relatively low number of water molecules present in the water/ethanol solvation shell.

Figure 11.

Normalized power spectra for bulk and solvating molecules: water in its mixture with methanol (a), methanol (b), and ethanol (c).

The power spectra for the alcohol molecules exhibit similar characteristics to that of water. For methanol (cf. Figure 11, center), a high frequency band (~30 cm⁻¹) corresponding to vibration against the surrounding molecular cage and a much less pronounced shoulder at lower frequencies (~130 cm⁻¹). As increasing amounts of water are added, this shoulder disappears, suggesting the breakdown of methanol–methanol hydrogen-bonded chains, which has been seen both experimentally⁶⁷ and in other MD studies.⁶⁸ At the same time, the ~30 cm⁻¹ peak broadens and blue-shifts as the surrounding molecular environment contains more water molecules. The ethanol spectra are very similar (Figure 11, bottom), with the addition of the appearance of a peak at ~200 cm⁻¹ that is present for the solvation shell at high concentrations and not the bulk. This could be ascribed to hydrogen bonds within the ordered structure that arises as the ethanol molecules arrange themselves on the carbon surface. As more water molecules are present in the shell, this structure becomes less ordered leading to the disappearance of this small peak.

CONCLUSIONS

We have used molecular simulations to extensively study the solvation characteristics of carbon nanoparticles in various solvents and their mixtures. The use of free energy perturbation techniques demonstrates that the energetics of solvation is highly dependent on the size of the nanoparticle. This solvation is enthalpically driven and the strong van der Waals interactions between the solvent and surface overcome large entropic penalties that arise during the caging of the hydrophobic nanoparticle. As alcohol is added to the water, it behaves in a manner that is analogous to that of a surfactant by partitioning the water away from the carbon surface and thereby decreasing the free energy of solvation. While both alcohols display this behavior, it is more clear in the case of ethanol as it has a higher number of hydrophobic molecular interaction sites. Examination of the solvation shell structure and composition reveal that the nanoparticle surface is quickly saturated with ordered alcohol molecules even at relatively low bulk concentrations. The dynamics of the solvating molecules agree with previous findings in that their translational and rotational motion is slowed by the presence of the nanoparticle. There is additional retardation at intermediate water/alcohol compositions as the hydrogen bonding network increases in stability (further shown in the vibrational spectra). This phenomenon has been observed in bulk solvent mixtures and the presence of the carbon surface does not seem to eliminate this concentration dependence. The molecular residence times within the solvent shell also indicate the pseudosurfactant behavior of the alcohols. At low alcohol concentrations, this quantity increases for the methanol and ethanol molecules as exchanging with a water molecule is energetically unfavorable.

This study yields insight into the solvation behavior of carbon nanoparticles in complex, multicomponent solvent environments. Many SWCNT purification schemes utilize such complex solvents to help tune surfactant quality leading to improved separation. In such schemes, the nanoparticles are coated with surfactants and then dispersed, and future work will focus on the solvation of such coated nanoparticles. Many questions remain to be answered in terms of how the packing of the surfactant affects solvation energies and how the solvent molecules might behave in the proximity of a hydrophobic nanoparticle and the amphiphilic surfactant. The present work serves as a baseline to which the surfactant-coated SWCNTs can be compared and should be of interest to those studying hydrophobic hydration and multicomponent solvation.