Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors

We demonstrate the artificial construction of magnetic atom chains on a conventional superconductor as a Majorana platform.

Abstract

Realizing Majorana bound states (MBS) in condensed matter systems is a key challenge on the way toward topological quantum computing. As a promising platform, one-dimensional magnetic chains on conventional superconductors were theoretically predicted to host MBS at the chain ends. We demonstrate a novel approach to design of model-type atomic-scale systems for studying MBS using single-atom manipulation techniques. Our artificially constructed atomic Fe chains on a Re surface exhibit spin spiral states and a remarkable enhancement of the local density of states at zero energy being strongly localized at the chain ends. Moreover, the zero-energy modes at the chain ends are shown to emerge and become stabilized with increasing chain length. Tight-binding model calculations based on parameters obtained from ab initio calculations corroborate that the system resides in the topological phase. Our work opens new pathways to design MBS in atomic-scale hybrid structures as a basis for fault-tolerant topological quantum computing.

INTRODUCTION

Majorana fermions (1)—particles being their own antiparticles—have recently attracted renewed interest in various fields of physics. In condensed matter systems, Majorana bound states (MBS) with a non-Abelian quantum exchange statistics have been proposed as a key element for topological quantum computing (2–4). One of the most promising platforms to realize MBS are one-dimensional (1D) helical spin systems being proximity-coupled to a conventional s-wave superconductor (5–9). In such a surface-confined system, the MBS can directly be investigated by local probe techniques such as scanning tunneling microscopy/spectroscopy (STM/STS). Previously reported experiments aiming at the direct visualization and probing of the MBS have focused on self-assembled magnetic chains on superconducting Pb substrates (10–15). However, such self-assembled nanowires have unavoidable limitations, for example, a lack of control over chain structure and length, as well as problems with atomic intermixing between the magnetic adsorbates and the Pb substrate during the annealing process, which is required to form the 1D chains. The unclear geometric and electronic structure of the magnetic nanowires can lead to ambiguous interpretations and make them inadequate to serve as true model systems for MBS (16–18).

Here, we demonstrate the atomically controlled fabrication of 1D Fe chains on a superconducting Re(0001) substrate using STM-based single-atom manipulation methods (19). The precise positioning of individual Fe atoms, together with the local probing of the local density of states (LDOS) around the Fermi energy by STS, makes it possible to build up atomic chains of controlled length without any ambiguities concerning the geometric and electronic structure of the chains.

RESULTS

As a building block for the atomic chains, we first explored the electronic structure of individual Fe atoms. Figure 1 shows STM/STS data of single Fe atoms (Fig. 1A) and an Fe dimer (Fig. 1B), which were positioned to specific sites by STM-based single-atom manipulations (Materials and Methods). The Fe atoms with localized magnetic moments can be distinguished from nonmagnetic adsorbates by identifying the so-called Yu-Shiba-Rusinov (YSR) bound states (20–22), which are reflecting the quasi-particle excitations of the broken Cooper pair on the superconducting surface. The YSR states of the magnetic Fe atoms show up as a pair of characteristic resonances inside the superconducting gap of Re (Δ_Re = 0.28 meV) around the Fermi energy in differential tunneling conductance (dI/dV) spectra (23–25) displayed in Fig. 1C, which are a direct probe of the system’s LDOS. The pair of resonances lie very close to the Fermi level (~±0.020 meV), so at the experimental temperature (350 mK or 0.030 meV), they could only be resolved by a superconducting Nb tip (Fig. 1C), but not with the nonsuperconducting PtIr tip because of the thermal broadening (red curves in Fig. 1, D and E).

Fig. 1. YSR states of individual magnetic Fe atoms and their interactions on Re(0001).

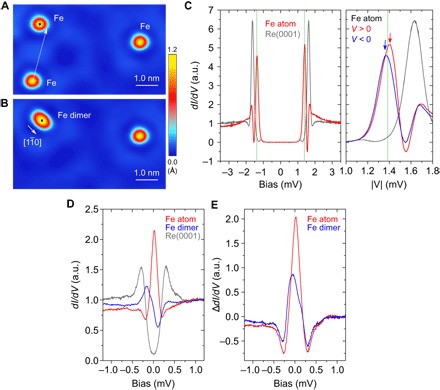
(A and B) STM topographic images of isolated Fe atoms (A) and an Fe dimer (B) on Re(0001). Tunneling current, I_T = 5.0 nA; sample bias voltage, V_S = 3.0 mV; scan area, 7.0 × 4.0 nm². The Fe dimer in (B) was created by placing an Fe atom next to another [white dotted arrow in (A)] at a distance of a_Re = 0.274 nm. (C) Left: dI/dV spectra on a single Fe atom (red) and on the bare Re substrate (gray) measured with a superconducting Nb tip (I_T = 1.0 nA, V_S = 3.0 mV). Right: Same spectra plotted as a function of |V|. The green dotted line indicates the energy position of the superconducting gap edge of the Nb tip (Materials and Methods). A pair of YSR resonances are indicated by red and blue arrows at |Δ_Nb ± E_B|, with Δ_Nb = 1.38 meV and E_B = 0.020 meV, providing a signature for the localized magnetic moment of the Fe atom. (D) dI/dV spectra obtained at the positions marked by black dots in (A) and (B) for a single Fe atom (red), an Fe dimer (blue), and the bare Re(0001) (gray) measured with a nonsuperconducting tip (I_T=5.0 nA, V_S=1.5 mV). (E) Difference spectra for an Fe atom and a dimer after subtracting the spectrum obtained on the bare Re(0001) surface. Except for (C), a PtIr tip was used for taking topography images and spectra. All STM images and tunneling spectra were measured at T = 350 mK. a.u., arbitrary units.

When a dimer is formed from two Fe atoms at neighboring hexagonal close-packed (hcp) hollow sites on the Re(0001) substrate at a distance of a_Re = 0.274 nm (Fig. 1B), they become strongly coupled and form hybridized YSR states. In Fig. 1 (D and E), these hybridized states appear as broad resonances with peaks or shoulders located at ~±0.110 meV and pronounced asymmetric spectral weights compared to the ones for single Fe adatoms (see also fig. S1 for spatial distributions) (26). This hybridization of the YSR states between the magnetic adatoms is a requirement for the formation of MBS in the chains discussed below.

Subsequently, we fabricated 1D atomic chains by placing Fe atoms in hcp hollow sites along one of the close-packed directions ([$1\overline{1}0$]) of the Re crystal, as schematically depicted in Fig. 2A, making use of STM-based atom-by-atom manipulations (Materials and Methods). Figure 2B shows intermediate steps of creating the chain starting from a dimer and ending with a length of 40 atoms (see also movie S1). Before attaching them to the chain, each individual Fe atom was identified by confirming the characteristic YSR bound state energies in the dI/dV spectra shown in Fig. 1. The smooth and uniform STM topography images in Fig. 2 (B and C) indicate the well-defined atomic structure of the constructed chains.

Fig. 2. Artificially constructed atomic Fe chains on Re(0001) and SP-STM measurements for the magnetic structure.

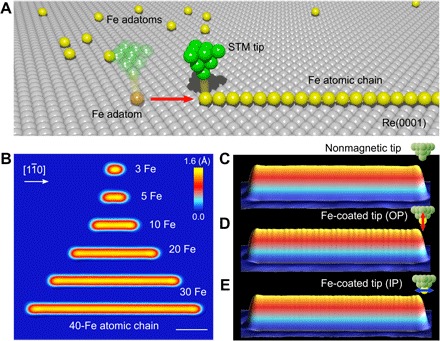
(A) Schematic view of the atom manipulation procedure applied to form a 1D atomic chain with an STM tip. (B) Stacked STM images for the artificially constructed Fe chains of various lengths along the close-packed [$1\overline{1}0$] direction (I_T = 5.0 nA, V_S = 3.0 mV; scale bar, 2.0 nm). (C) 3D-rendered STM image of a 40-atom-long Fe chain measured with a nonmagnetic PtIr tip. (D and E) SP-STM images recorded with Fe-coated PtIr tips sensitive to the (D) OP and the (E) IP component of the spins in the chain, with the magnetization directions schematically depicted in the inset. The same tunneling conditions of I_T = 5.0 nA and V_S = 3.0 mV were used for the measurements in (C) to (E). The magnetization directions of the Fe-coated tips were determined in situ directly before the SP-STM measurements on the atomic Fe chains (Materials and Methods) (28).

To understand the magnetic structure of atomic Fe chains on Re(0001), we performed spin-polarized STM (SP-STM) measurements with Fe-coated PtIr tips (27, 28), which are sensitive to the direction of the localized magnetic moments on the surface with respect to the tip magnetization direction (Materials and Methods) (28). The SP-STM images obtained with different magnetic tips being sensitive to either the out-of-plane (OP) or in-plane (IP) spin components (Fig. 2, D and E, respectively) show clear spatial modulations along the chain with periods of ~0.36 nm (4/3a_Re) and ~1.1 nm (4a_Re) (see also the bottom part of Fig. 3A and fig. S2 for the real-space profile and the fast Fourier transform analysis). Because the STM image in Fig. 2C obtained with a nonmagnetic probe tip shows a featureless surface profile, these modulations can be attributed to the magnetic structure. Furthermore, the shifted phase of the spatial oscillations between SP-STM images recorded with differently oriented magnetic tips proves the presence of a spin spiral ground state (29) for the Fe chain on Re(0001), which was theoretically assumed for the prediction of MBS at chain ends (5–9). The spin spiral ground state originates from interfacial Dzyaloshinsky-Moriya interaction, which is strong for Fe chains on 5d transition metal substrates (29). This is in stark contrast to the cases of self-assembled Fe and Co chains on Pb(110), which were reported to be ferromagnetic (10, 14).

Fig. 3. Spatial and energy dependence of the LDOS in the 40-atom-long chain.

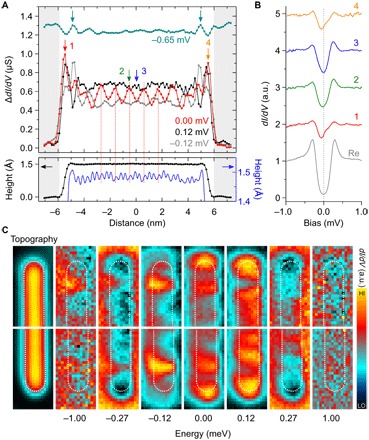
(A) Top: Differential tunneling conductance (dI/dV) profiles at V_S = 0.00 mV, +0.12 mV, −0.12 mV, and −0.65 mV along the 40-atom-long Fe chain, reflecting the spatial variation of the LDOS. All profiles were extracted from the spatially resolved dI/dV spectra after subtracting the spectrum on the bare Re substrate. The profile for V = −0.65 mV is vertically shifted for clarity (offset, 1.3 μS). Dark cyan arrows in the profile at −0.65 mV denote spatial locations for the confined states; the other colors show the spatial positions where the energy-resolved spectra in (B) were measured. Bottom: Constant-current STM profile (black, left vertical axis), which was recorded simultaneously with the dI/dV spectra and corresponding magnetic profile (blue, right vertical axis) obtained from the SP-STM image measured with the OP spin-sensitive tip. The gray shaded regions correspond to the Re substrate. The dotted lines in red are guides to the eye for the comparison of the spatial variation of the LDOS with the SP-STM profile. (B) dI/dV spectra obtained at the positions indicated by the arrows in (A) and the gray one for the Re substrate. The dotted vertical line shows the zero energy. (C) Spatial distribution of the LDOS at various energies for the two different ends of the 40-atom-long Fe chain. The white dotted lines indicate the boundary of the chain. The scan size of all images is 1.1 nm × 2.2 nm. The intensity scale at the right side is adjusted for each figure separately. Both ends show an identical and symmetric distribution of LDOS with respect to the center of the chain. The localized end states are visible in the LDOS maps at zero energy for both ends. The tunnel junctions were stabilized at I_T = 5.0 nA and V_S = 3.0 mV for all spectroscopic measurements.

A typical characteristic of MBS is an enhancement of the LDOS spatially localized at the ends of the chain and at zero energy (10–13, 15). To explore this property for the 40-atom-long Fe chain, we measured spatially resolved dI/dV spectra along the chain. Figure 3A displays the spatial variation of the LDOS by plotting the difference between the dI/dV values measured on the chain and on the substrate at four different bias voltages: V = 0.00 mV (zero energy), ±0.12 mV (inside the gap), and −0.65 mV (outside the gap). Note that the LDOS profiles at ±0.12 mV have been chosen to reveal the spatial modulation of the hybridized YSR states in the chain. We find that the measured dI/dV profiles at zero energy indicate an enhancement of the LDOS with the highest peaks at both ends of the chain (red and orange arrows in Fig. 3A). Although the profiles at +0.12 mV also display enhancements at the ends of the chain, the enhancement of the zero-energy LDOS is localized half a lattice constant of Re(0001) away from the one at +0.12 mV (Fig. 3, A and C).

The dI/dV spectra obtained on the chain in Fig. 3B display an enhanced and considerably asymmetric LDOS inside the gap, which can be attributed to the hybridized YSR states. At the chain ends (red and orange curves), we observe shoulders in the spectra around zero energy, contributing to the highest peaks in the spatially resolved profile (Fig. 3A), whereas these shoulders are absent in the spectra at the middle of the chain (green and blue curves). However, it is difficult to unambiguously separate the contributions to these shoulders from the YSR states and from a possible MBS inside a topological superconducting gap in the dI/dV spectra because of the limited energy resolution at the current experimental temperature (~350 mK).

Note that electron confinement effects not connected to superconductivity are also observed in the 1D chain, however, at energies outside the gap (−0.65 meV, dark cyan curve in Fig. 3A). Moreover, the spatial positions of the peaks (dark cyan arrows) outside the gap are significantly different from the ones at zero energy. On the other hand, all subgap features disappear above the superconducting transition temperature (T_C ~ 1.6 K) of the Re substrate (see fig. S3 and movie S3). This proves that the observed in-gap features of the 1D magnetic chain are strongly linked to the superconductivity of the Re substrate.

Most remarkably, the overall dI/dV profiles in Fig. 3A exhibit a symmetric distribution of the LDOS with respect to the center of the chain, as it should be for an ideal chain composed of regularly arranged Fe atoms without any geometric or chemical defects. In addition, the periodic modulations of the zero-energy LDOS show a clear correlation with the periodicity in the SP-STM profile, which are significantly different from the previously studied self-assembled Fe chains on the Pb substrate with inhomogeneous LDOS (10–13, 15). The enhanced LDOS at zero energy at the ends of the chain is visualized in the spatially and energy-resolved tunneling conductance maps in Fig. 3C (see also movie S2), also displaying the symmetry between the two ends.

To gain more insight into the nature of the observed enhanced LDOS at zero energy at the chain ends, we explored the spatial distribution of the LDOS for atomic chains of various lengths. Figure 4A shows dI/dV profiles at zero energy along close-packed chains consisting of 3 to 12, 20, 30, and 40 Fe atoms. The measured profiles for most chains show a symmetric distribution with respect to the center and exhibit strong spatial modulations within the chains because of the formation of the hybridized YSR states. For shorter chains, the values of zero-energy conductance measured both at the ends and in the middle oscillate as the number of atoms in the chain is increased. However, for longer chains, a considerable difference develops between the LDOS values measured at the ends and in the middle, also shown in Fig. 4B. Both the conductance values (Fig. 4B) and the shape of the LDOS profiles (Figs. 3A and 4A) at the ends of the chains gradually become stabilized with increasing chain lengths at around 12 atoms. These observations indicate that a minimum number of Fe atoms are necessary to fully develop a spatially localized electronic state at the chain ends around the Fermi energy.

Fig. 4. Development and stabilization of enhanced zero-energy LDOS at the ends with increasing chain length and the calculated topological phase diagram for the Fe chain.

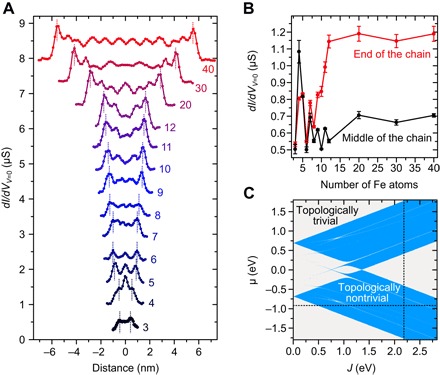
(A) Measured zero-energy dI/dV profiles along the chains for (from bottom to the top) 3 to 12, 20, 30, and 40 Fe atoms. For clarity, the profiles are shifted vertically. (B) Comparison of the variation of zero-energy tunneling conductance between the middle and the ends of the chains with increasing number of atoms. The conductance values at the end are averaged over the positions indicated by the two dotted lines in the profiles, whereas the ones for the middle are averaged values from the regions around the center of the chains. The tunneling junctions were stabilized at I_T = 5.0 nA and V_S = 3.0 mV for all spectroscopic measurements. (C) Calculated topological phase diagram for a straight monoatomic Fe chain with noncollinear magnetization as a function of the on-site energy μ and spin splitting parameter J (section S3 and Supplementary Materials). Blue and gray shaded regions correspond to the topologically nontrivial superconducting phase and the trivial phase, respectively. The two dotted lines represent the parameters determined from ab initio calculations for Fe on the Re(0001) surface, μ = −0.92 eV and J = 2.18 eV.

To further elucidate the nature of the experimentally observed localization of the enhanced zero-energy LDOS at the chain ends, we examined a realistic nearest-neighbor tight-binding model describing the atomic Fe chain in the experimentally determined spin spiral state (Fig. 2, D and E). As shown in Fig. 4C, we found that the chain with noncollinear spin structure resides in a topologically nontrivial phase in a wide parameter range, where MBS are expected to be formed. By using material-specific parameters for the Fe chain on Re(0001) derived from first-principles calculations (sections S1 and S2, and Supplementary Materials), the theoretical model suggests that the current system is in the topologically nontrivial superconducting phase.

Finally, it is worth mentioning that our detailed studies on artificially constructed atomic Fe chains on Re(0001) have shown that local structural or chemical defects can significantly modify the LDOS at the ends of the chains, for example, zero-bias peaks at the chain end can be generated by single-atom defects. In Fig. 5, we constructed an 8-atom-long Fe chain with a single structural defect at one end of the chain, which shows an asymmetric apparent height in the surface profile (Fig. 5F). The defect-free 8-atom-long chain displays a quite flat spatial modulation of the zero-energy LDOS in the bottom part of Fig. 5G, which cannot be interpreted as an indication for the presence of an MBS (see also Fig. 4, A and B). Surprisingly, although it is expected not to observe an enhancement of the zero-energy LDOS at the ends of the perfect 8-atom-long Fe chain (Fig. 4, A and B), such a structural defect creates a localized defect state at the Fermi energy in the spectroscopic maps, as shown in Fig. 5G, which is absent at the other end and for the defect-free 8-atom-long chain. This implies that single-atom control, as demonstrated by our experiments, is required to safely rule out defect-induced zero-energy modes mimicking MBS at the chain ends.

Fig. 5. Defect-induced zero-energy in-gap state for an Fe chain with a structural defect.

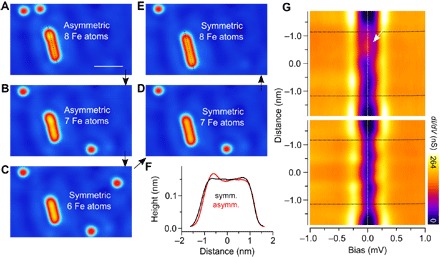
(A to E) Sequential STM images for the demonstration of disassembling (A to C) and reassembling (C to E) the 8-atom-long Fe chain by continuous atom manipulations (scale bar, 2.0 nm). (F) Surface profiles along the dotted lines in (A) and (E) for the asymmetric and symmetric 8-atom-long chain, respectively. The 8- and 7-atom-long Fe chains in (A) and (B) show an asymmetric apparent height and are slightly bent from the chain axis because of the mislocated Fe atoms in the chains. After reassembling the 8-atom-long Fe chain, it becomes symmetric and straight. (G) Spatially resolved dI/dV spectra and the color-encoded spectroscopic maps for the asymmetric (top) and symmetric (bottom) 8-atom-long Fe chains. The black dotted lines indicate the boundary between the chains and the substrate. The white arrow indicates the defect-induced zero-energy bound state, which is absent at the other end and at the ends of the symmetric chain. We stabilized the tunneling junction at I_T = 5.0 nA and V_S = 3.0 mV for all STM images and the tunneling spectra.

DISCUSSION

In conclusion, we have demonstrated that single-atom manipulation techniques offer a reliable and unique pathway to design and realize model-type platforms with well-defined atomic, electronic, and magnetic structures. We investigated signatures of MBS by performing STS measurements and found an enhancement in the zero-energy LDOS localized at the chain ends. Theoretical calculations confirm that the Fe chain on the Re substrate is in the topological superconducting phase. From the experimental point of view, improving the energy resolution at lower temperature or investigating the spin-polarized nature of in-gap states in future experimental studies will allow a more direct access to the topological character of the chains (15, 30). However, most importantly, the methodology introduced in this study can straightforwardly be extended to more complex magnetic adatom structures on various superconducting substrates, going far beyond linear adatom arrangements. This new approach will pave the way not only for a deeper fundamental insight into the underlying physics of MBS but also for their future applications in topological quantum computing (2–4, 31).

MATERIALS AND METHODS

Preparation of the sample and the tip

The rhenium single crystal was prepared by repeated cycles of O₂ annealing at 1400 K followed by flashing at 1800 K to obtain an atomically flat Re(0001) surface (28, 32). Fe was deposited with a 0.6 to 0.7 monolayer (ML) coverage onto the clean Re(0001) surface in situ at room temperature from a pure Fe rod (99.99+%) using an electron beam evaporator. The surface cleanliness was checked by STM after transferring the sample into the cryostat. For most measurements, we used a mechanically polished Pt/Ir alloy wire as the STM tip. The tip was conditioned by applying voltage pulses (about a few volts for 50 ms), and its quality was judged to be suitable if it showed a flat LDOS outside the superconducting gap of rhenium. A mechanically cut Nb wire was used as a superconducting tip to improve the energy resolution in the tunneling spectra for the Fe adatom on Re.

STM/STS and SP-STM measurements

All the experiments were carried out in a ³He-cooled low-temperature STM system (USM-1300S, Unisoku, Japan) operating at T = 350 mK under ultrahigh vacuum conditions. Tunneling spectra were obtained by measuring the differential tunneling conductance (dI/dV) using a standard lock-in technique with a modulation bias voltage of 20 μV and a frequency of 971 Hz with opened feedback loop. The bias voltage was applied to the sample, and the tunneling current was measured through the tip using a commercially available controller (Nanonis, SPECS, Swiss). For STS measurements with the Nb tip, we estimated the energy position of the superconducting gap edge of the tip (green dotted lines in Fig. 1C) from the tunneling spectrum on the Re substrate. Note that the two pairs of peaks in the spectrum on Re correspond to ±|Δ_Re − Δ_Nb| and ±|Δ_Re + Δ_Nb|, respectively (Δ_Re = 0.28 meV, Δ_Nb = 1.38 meV) (33–35). For SP-STM measurements, we coated several Fe atoms in situ at the apex of PtIr tips by picking them up from an Fe island. The magnetization directions of the Fe-coated tip were determined by revealing the magnetic contrast of spin spirals in ML-thick Fe islands on Re(0001), as discussed in detail by Palacio-Morales et al. (28).

Vertical and lateral STM tip–induced atom manipulation

Single Fe atoms were introduced by a vertical manipulation method from ML-thick Fe islands on the Re(0001) surface (36). The STM tip was softly indented into the Fe islands to pick up several Fe atoms and release them onto the clean Re(0001) surface by adjusting the tip-sample distance. Fe atoms were identified after vertical transfer by observing the characteristic YSR states of single Fe atoms on Re(0001) in the tunneling spectra. Nonmagnetic atoms, which are mostly from the tip materials and sometimes also transferred to the surface during the vertical atom manipulation process, do not exhibit YSR states. We applied the lateral atom manipulation method to form Fe atomic chains. We switched the tunneling parameters from imaging condition (2.0 to 5.0 nA, 3.0 mV) to manipulation condition (90 to 120 nA, 3.0 mV) after placing the tip next to a single Fe atom. We picked up an atom by moving the tip across it and manipulated the Fe atom precisely to the aimed atomic site of the Re(0001) surface with closed feedback loop while monitoring the profile of the tip movement. STM images after sequential atom manipulations were collected during the formation of the Fe chains (see movie S1).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaar5251/DC1

section S1. Ab initio calculations

section S2. Model parameters

section S3. Tight-binding model

fig. S1. Spatial distribution of the YSR states for a single Fe atom and an Fe dimer on the Re(0001) surface.

fig. S2. The fast Fourier transformation analysis for the magnetic structure of the 40-atom-long Fe chain.

fig. S3. Absence of the in-gap states on the 40-atom-long Fe chain above the superconducting critical temperature of Re.

movie S1. Demonstration of subsequent atom manipulations to construct the close-packed chains of various lengths.

movie S2. Spatially resolved 2D spectroscopic maps for two different ends of the 40-atom-long Fe chain below T_C.

movie S3. Spatially resolved 2D spectroscopic maps for the 40-atom-long Fe chain above T_C.

References (37–46)