Technical Note: Single time point dose estimate for exponential clearance

Abstract

Objective

Although personalized dosimetry may be desirable for radionuclide therapy treatments, the multiple time samples required to determine the total integrated activity puts a burden on patients and clinic resources. The aim of this paper is to demonstrate that when some prior knowledge is known about the tracer kinetic parameters, the total integrated activity (and thus radiation dose) can be estimated from a single time sample.

Methods

Mathematical derivations have been performed to generate equations for the total integrated activity in terms of a single time sample of activity for monoexponential and biexponential clearance. Simulations were performed using both exponential models where the rate constants and associated parameters were randomly sampled from distributions with a known mean. The actual total integrated activity for each random sample was compared with the estimated total integrated activity using the mean value of the parameters. Retrospective analysis of ⁹⁰Y DOTATOC data from a clinical trial provided a comparison of actual kidney dose with the estimated kidney dose using the single time point approach.

Results

The optimal sampling time for the single point approach was found to be equal to the mean time of the rate constant. The simulation results for the monoexponential and biexpoential models were similar. Regressions comparing the actual and estimated total integrated activity had very high correlations (r ² > 0.95) along with acceptable standard errors of estimate, especially at the optimal sampling point. The retrospective analysis of the ⁹⁰Y DOTATOC data also yielded similar results with an r ² = 0.95 and a standard error of estimate of 61 cGy.

Conclusions

In situations where there is prior knowledge about the population averages of kinetic parameters, these results suggest that the single time point approach can be used to estimate the total integrated activity and dose with sufficient accuracy to manage radionuclide therapy. This will make personalized dosimetry much easier to perform and more available to the community.

1. Introduction

Personalized dosimetry is highly desirable for many radionuclide therapy protocols in order to deliver the maximum tumor dose while sparing critical organs.^{1, 2, 3, 4, 5} The determination of the total integrated activity ($\tilde{\mathrm{A}}$) for radiation dose estimates when the tracer kinetics are described by exponential equations generally requires measurements of tissue activity at multiple time points with a minimum of at least two time samples for each exponential component. Since the long component associated with many radiotherapeutic agents is often more than 24 h, this adds additional days to the procedure creating a burden for both the patient and the clinic. The aim of this paper is to demonstrate that in certain situations where the clearance of the radiotracer is described by a monoexponential or biexponential model and quantitative information about the long component parameters is approximately known, it may be possible to obtain a useful estimate of $\tilde{\mathbf{A}}$ from a single time point measurement. This single time point estimate of the time‐integrated activity will be indicated by ${\tilde{\mathbf{A}}}^{\ast }$. This approach may prove to be accurate and simple enough to allow routine personalized dosimetry in the management of radionuclide cancer treatments.

2. Materials and methods

2.A. Monoexponential derivation

We first derive the single point estimation approach for a single component exponential. The equation for monoexponential clearance is given by

$$\mathbf{A}(\mathbf{t})={\mathbf{A}}_{\mathbf{0}}{\mathbf{e}}^{-\mathit{k}\mathbf{t}}$$ (1)

where ${\mathbf{A}}_{\mathbf{0}}$ is the activity at t = 0 and $\mathit{k}$ is the effective clearance rate constant for a specific individual sample. The total number of decays associated with (1) is given by:

$$\tilde{\mathbf{A}}={\mathbf{A}}_{\mathbf{0}}/\mathit{k}=\mathbf{A}(\mathbf{T}){\mathbf{e}}^{\mathit{k}\mathbf{T}}/\mathit{k}$$ (2)

where A(T) is a quantitative activity measurement made at time T. Suppose that A(T) is known from a direct measurement for an individual sample, but only a population mean value is known for k (indicated by $\widehat{\mathit{k}}$.). We hypothesize that the estimate of à (denoted by Ã*) can be determined from:

$${\tilde{\mathbf{A}}}^{\ast }=\mathbf{A}(\mathbf{T}){\mathbf{e}}^{\widehat{\mathit{k}}\mathbf{T}}/\widehat{\mathit{k}}$$ (3)

In Eq. (3), A(T) is measured at a known time T and $\widehat{\mathit{k}}$ is known from either previous population measurements or from theoretical pharmacokinetic considerations. The optimal sampling time for T for any individual case can be determined from the recognition that there exists a sample time T for any k where ${\tilde{\mathbf{A}}}^{\ast }=\tilde{\mathbf{A}}$:

$${\mathbf{A}}_{\mathbf{0}}/\mathit{k}=\mathbf{A}(\mathbf{T}){\mathbf{e}}^{\widehat{\mathit{k}}\mathbf{T}}/\widehat{\mathit{k}}={\mathbf{A}}_{\mathbf{0}}{\mathbf{e}}^{-\mathit{k}\mathbf{T}}{\mathbf{e}}^{\widehat{\mathit{k}}\mathbf{T}}/\widehat{\mathit{k}}$$ (4)

If Eq. (4) is solved for T, we obtain

$$\mathbf{T}=\frac{\mathit{l}n(\widehat{\mathit{k}}/\mathit{k})}{(\widehat{\mathit{k}}-k)}=\frac{\mathbf{1}/\widehat{\mathit{k}}\mathit{l}n(\widehat{\mathit{k}}/\mathit{k})}{(\mathbf{1}-\mathit{k}/\widehat{\mathit{k}})}=\frac{\widehat{\tau }\mathit{l}n(\widehat{\mathit{k}}/\mathit{k})}{(\mathbf{1}-\mathit{k}/\widehat{\mathit{k}})}$$ (5)

where $\widehat{\mathit{\tau }}$ is the mean time associated with the estimated clearance rate, $\widehat{\mathit{\tau }}=\mathbf{1}/\widehat{\mathit{k}}$. Fig. 1(a) shows a plot of Eq. (5) which gives the sample time T for which Ã* = Ã for different values of $\widehat{\mathit{k}}/\mathit{k}$. There is a singularity in Eq. (5) when $\mathit{k}=\widehat{\mathit{k}}$ which is due to the fact that all sampling times are equally valid for that condition. However, Eq. (5) smoothly converges to T = $\widehat{\mathit{\tau }}$ as $\mathit{k}$ approaches $\widehat{\mathit{k}}$ for both $\mathit{k}<\widehat{\mathit{k}}$ and $\mathit{k}>\widehat{\mathit{k}}$.

Figure 1.

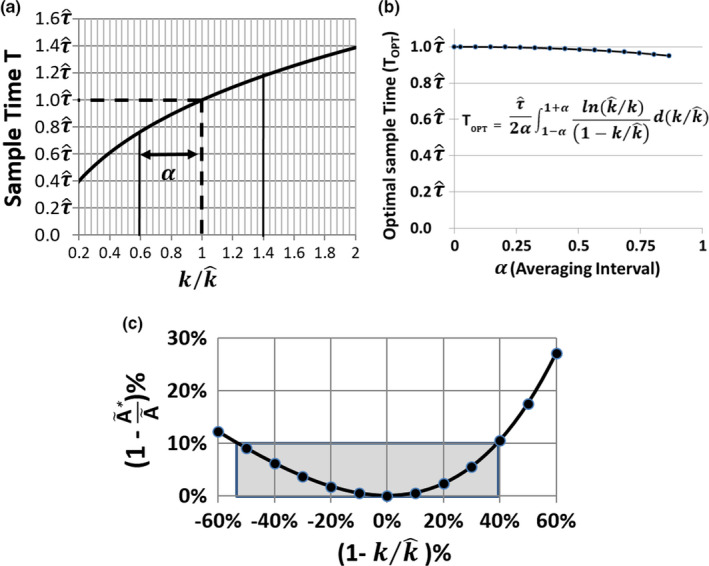
Monoexponential support data. (a) Plot of the sampling time T for accurately determining $\tilde{\mathbf{A}}$ when k varies from $\widehat{\mathit{k}}$. (b) Plot of the optimal sampling time T _OPT as a function of the averaging interval. T _OPT is determined by integrating Eq. (5) over the interval 1 − α to 1 + α. The plot indicates that over a relatively large range, T _OPT  ≈ $\widehat{\tau }$. (c) Plot of the error in the estimated total integrated activity as a function of the error in the estimated rate constant. Large variations in k from $\widehat{\mathit{k}}$ have a relatively small effect on the accuracy of ${\tilde{\mathbf{A}}}^{\ast }$ over a wide range. [Color figure can be viewed at wileyonlinelibrary.com]

When the value k is not precisely known, but it is distributed more or less normally about $\widehat{\mathit{k}}$, then a reasonable choice for the optimal sample time, T _OPT , can be determined by finding the average of Eq. (5) over the range from 1 − α to 1 + α which defines an interval equally distributed about the point where $\mathit{k}=\widehat{\mathit{k}}$ as shown in Fig. 1(a). Fig. 1(b) shows a plot of T _OPT as a function of α demonstrating that over a relatively wide interval that the best sample time for T is $\approx \widehat{\mathit{\tau }}$. This result can be used to explore the accuracy of the approach. If Eq. (3) is divided by Eq. (2), we obtain: $\frac{{\tilde{\mathbf{A}}}^{\ast }}{\tilde{\mathbf{A}}}=\frac{A(\mathbf{T}){\mathit{e}}^{\widehat{\mathit{k}}\mathbf{T}}/\widehat{\mathit{k}}}{\mathbf{A}(\mathbf{T}){\mathbf{e}}^{\mathit{k}\mathbf{T}}/\mathit{k}}=\frac{\mathit{k}}{\widehat{\mathit{k}}}{\mathit{e}}^{(\widehat{\mathit{k}}-\mathit{k})\mathbf{T}}.$

The ratio at the optimal sampling time T = $\widehat{\mathit{\tau }}=\mathbf{1}/\widehat{\mathit{k}}$ becomes

$$\frac{{\tilde{\mathbf{A}}}^{\ast }}{\tilde{\mathbf{A}}}=\frac{\mathit{k}}{\widehat{\mathit{k}}}{\mathit{e}}^{(\mathbf{1}-k/\widehat{\mathit{k}})}$$ (6)

Fig. 1(c) shows a plot derived from Eq. (6) which demonstrates that even rather substantial variations of $\mathit{k}$ with respect to $\widehat{\mathit{k}}$ yield only modest inaccuracies in Ã* as an estimate of Ã. It should be noted that Eq. (6) indicates that ${\tilde{\mathbf{A}}}^{\ast }$ is always less than or equal to $\tilde{\mathbf{A}}$ at the optimal sampling time. If the sample is made at T = 0 where A(T) = A ₀ , then the error in ${\tilde{\mathbf{A}}}^{\ast }$ is directly proportional to just the ratio of $\mathit{k}/\widehat{\mathit{k}}$. However, as T increases, the difference between ${\mathbf{A}}_{\mathbf{0}}$ and $\mathbf{A}(\mathbf{T})\mathbf{e}\widehat{\mathit{k}}\mathbf{T}$ becomes greater and in the opposite direction of $\mathit{k}/\widehat{\mathit{k}}$. When $\mathbf{T}=\widehat{\mathit{\tau }}$, then the exponential extrapolation term has the magnitude to ensure that ${\tilde{\mathbf{A}}}^{\ast }\le \tilde{\mathbf{A}}$.

2.B. Biexponential derivation

The derivation of an estimator for the total number of decays for biexponential clearance is similar to the monoexponential derivation. The equation for biexponential decay is given by:

$$\mathbf{A}(\mathbf{t})={\mathbf{A}}_{\mathbf{1}}{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{1}}\mathrm{t}}+{\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{t}}$$ (7)

where A₁ and k ₁ are associated with the fast components and A₂ and k ₂ the slow components.

The total integrated activity is equal to:

$$\tilde{\mathbf{A}}={\mathbf{A}}_{\mathbf{1}}/{\mathit{k}}_{\mathbf{1}}+{\mathbf{A}}_{\mathbf{2}}/{\mathit{k}}_{\mathbf{2}}$$ (8)

In many radionuclide therapy treatments, the major portion of the radiation dose comes from the longer component (${\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{t}}$). Hence, Eqs. (7) and (8) are rewritten in terms of A ₂ and k ₂ by making the following assignments: A ₁ /A ₂  =  c ; k ₁ / k ₂  =  a . Thus,

$$\mathbf{A}(\mathbf{t})=\mathit{c}{\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-\mathit{a}{\mathit{k}}_{\mathbf{2}}\mathbf{t}}+{\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{t}}$$ (9)

and

$$\tilde{\mathbf{A}}={\mathbf{A}}_{\mathbf{2}}/{\mathit{k}}_{\mathbf{2}}(\mathit{c}/\mathit{a}+\mathbf{1})$$ (10)

If an activity measurement is made at time T, it is easy to show from Eq. (9) that

$${\mathbf{A}}_{\mathbf{2}}=\frac{\mathbf{A}(\mathbf{T})}{\mathit{c}{\mathbf{e}}^{-\mathit{a}{\mathit{k}}_{\mathbf{2}}\mathbf{T}}+{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{T}}}$$ (11)

It follows from Eqs. (10) and (11) that:

$$\tilde{\mathbf{A}}=\frac{\mathbf{A}(\mathbf{T})\left(\mathit{c}/\mathit{a}+\mathbf{1}\right)/{\mathit{k}}_{\mathbf{2}}}{\mathit{c}{\mathbf{e}}^{-\mathit{a}{\mathit{k}}_{\mathbf{2}}\mathbf{T}}+{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{T}}}$$ (12)

Equation (12) gives the exact total integrated activity for an individual activity sample at time T when c , a , and k ₂ are exactly known. Using a similar approach as with the single exponential case, we consider the case for a population where the exact values of c , a , and k ₂ are unknown, but there is information about the associated population means, $\widehat{\mathit{c}}$, $\widehat{\mathit{a}}$, and ${\widehat{\mathit{k}}}_{\mathbf{2}}$ The equation for the estimated total integrated activity is then written as:

$${\tilde{\mathbf{A}}}^{\ast }=\frac{\mathbf{A}(\mathbf{T})\left(\widehat{\mathit{c}}/\widehat{\mathit{a}}+\mathbf{1}\right)/{\widehat{\mathit{k}}}_{\mathbf{2}}}{\widehat{\mathit{c}}{\mathbf{e}}^{-\widehat{\mathit{a}}{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}+{\mathbf{e}}^{-{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}}$$ (13)

As with Eq. (3), A(T) is measured at a known time T for each subject individually while $\widehat{\mathit{c}},\widehat{\mathit{a}},$ and ${\widehat{\mathit{k}}}_{\mathbf{2}}$ have been predetermined from previous population measurements or derived from theoretical considerations.

2.C. Monoexponential simulation

We hypothesize that Eq. (3) can be used to estimate the actual total integrated activity for a population of subjects without precisely knowing the actual individual clearance rates k if we know the expectation value $\widehat{\mathit{k}}$ for the population. As noted above, $\widehat{\mathit{k}}$ may have been determined from previous studies where sufficient samples were acquired to accurately determine individual k values or in some cases from prior knowledge about the tracer pharmacokinetics. To evaluate this hypothesis, a simulation using Excel was performed where the actual total integrated activity for a specified activity level A ₀ and rate constant k were compared against the estimated integrated activity using Eq. (3). In the simulation, the total integrated activity was expressed in units of activity multiplied by time. Because of that, the numerical results are independent of the activity units which could be Bq, kBq, MBq, etc., and are also independent of the time units which could be seconds, minutes, hours, days, etc. As a result, the simulation yields general results that are true at all scales. For the same reason, one could select any value of $\widehat{k}$ for the simulation by simply changing the time scale, but we chose $\widehat{k}$ = 1 (day)⁻¹ to be on the same order as what one might find for a radiotherapeutic agent.

For the simulation, A ₀ was selected to range from 50 to 2500 in steps of 50 (arbitrary activity units) and there were ten random samples of k for each value of A₀ yielding a total of 500 samples. The values of k were selected from a random number generator with a Gaussian distribution that was obtained by adding ten random numbers together and dividing by 5. This resulted in mean of 1 (day)⁻¹ and a standard deviation of 0.18 (day)⁻¹. In the 500 samples that were taken, k ranged from 0.42 (day)⁻¹ to 1.58 (day)⁻¹. The actual total integrated activity à for each of the 500 samples determined from Eq. (2) was compared against the estimated total number of decays Ã* determined from Eq. (3): ${\tilde{\mathbf{A}}}^{\ast }=\mathbf{A}(\mathbf{T}){\mathbf{e}}^{\widehat{\mathit{k}}\mathbf{T}}/\widehat{\mathit{k}}$ at five different time points: T = 0.2$\widehat{\mathit{\tau }}$, 0.6$\widehat{\mathit{\tau }}$, $\widehat{\mathit{\tau }}$, 1.4$\widehat{\mathit{\tau }}$, 1.8$\widehat{\mathit{\tau }}$ ($\widehat{\mathit{\tau }}$ = 1/$\widehat{\mathit{k}}$ = 1 day for the simulation). These time points were chosen to bracket the expected optimal sampling time point (T _OPT  = $\widehat{\mathit{\tau }}$). Linear regressions were performed on the plots of à as a function of Ã* to determine the slope, intercept, correlation coefficient, and the standard error of estimate (SEE) at each sampling time.

2.D. Biexponential simulation

Using a similar approach as with the single exponential case, we hypothesize that Eq. (13) can be used to estimate the actual total integrated activity in a population of subjects without precisely knowing the actual biexponential parameters c , a , and k ₂ as long as we know their expectation values ($\widehat{\mathit{c}}$, $\widehat{\mathit{a}}$, and ${\widehat{\mathit{k}}}_{\mathbf{2}}$). An Excel simulation was performed where the total integrated activity for specified values of A _2, c , a , and k ₂ was compared against the estimated total integrated activity using a single time point and the parameter expectation values. For the simulation, A ₂ ranged from 50 to 2500 in steps of 50 (arbitrary activity units) and for each A ₂ value, ten random samples of c , a , and k ₂ were obtained so that there was a total of 500 samples. For each sample, the actual total integrated activity was calculated using Eq. (12) and this was compared against the estimated total integrated activity using Eq. (13) at five time different points. Similar to the monoexponential simulation, the activity sample time points T ranged from 0.2 ${\widehat{\mathit{\tau }}}_{\mathbf{2}}$ to 1.8 ${\widehat{\mathit{\tau }}}_{\mathbf{2}}$ $({\widehat{\mathit{\tau }}}_{\mathbf{2}}=\mathbf{1}/{\mathit{k}}_{\mathbf{2}})$ to potentially bracket the optimal sampling point which cannot be analytically derived as it was for the monoexponential case, but we believed that T _OPT would likely be close to ${\widehat{\mathit{\tau }}}_{\mathbf{2}}$.

The parameters used in the simulation are given in Table 1. The values of $\widehat{\mathit{c}}$, $\widehat{\mathit{a}}$, and ${\widehat{\mathit{k}}}_{\mathbf{2}}$ in Table 1 along with their histogram distributions were approximated from an actual clinical protocol that focused on the radiation dose to kidneys from ⁹⁰Y DOTATOC treatments (see Table 2). Note that while the standard deviation associated with the k ₂ samples is relatively small, the standard deviations associated with c and a are large. The maximum and minimum values for each of the parameters in the 500 samples that were generated show the large range over which c and a varied.

Table 1.

Biexponential simulation parameters

Parameter	$\widehat{c}$	$\widehat{a}$	${\widehat{k}}_2$
Mean	1.6	12.1	0.020 h−1
Standard deviation	1.04	3.90	0.0036 h−1
Maximum value	4.2	19.0	0.034 h−1
Minimum value	0.03	5.4	0.009 h−1

Table 2.

Mean values of $\widehat{c}$, $\widehat{a}$, and ${\widehat{k}}_2$ obtained from clinical ⁹⁰Y DOTATOC data (n = 47)

Parameter	$\widehat{c}$	$\widehat{a}$	${\widehat{k}}_2$
Mean	1.11	12.3	0.020 h−1
Standard deviation	1.06	7.3	0.005 h−1
Maximum value	4.0	31.3	0.028 h−1
Minimum value	0	2.9	0.009 h−1

The individual values of k ₂ were selected from a random number generator with a Gaussian distribution while the probability distribution for c was triangular and the probability distribution for a was uniform. As stated above, this was based on our observation from the clinical protocol described in the next section (see Fig. 2). Linear regressions were performed on the plots of $\tilde{\mathbf{A}}$ as a function of ${\tilde{\mathbf{A}}}^{\ast }$ to determine the slope, intercept, correlation coefficient, and the standard error of estimate as a function of the sampling time.

Figure 2.

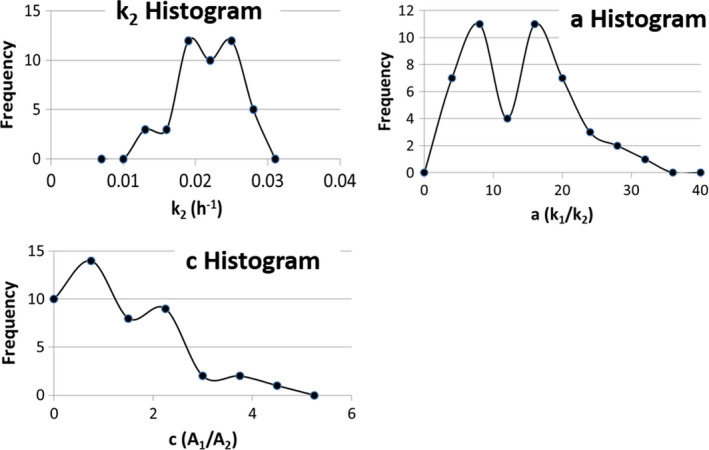
Histograms of the biexponential parameters ( c , a , and k ₂) obtained from the 47 dosimetry studies of the kidneys. [Color figure can be viewed at wileyonlinelibrary.com]

2.E. Retrospective of clinical ⁹⁰Y DOTATOC kidney dose data

There has been an ongoing clinical trial at the University of Iowa in which three cycles of ⁹⁰Y DOTATOC have been used to treat patients with neuroendocrine cancer.⁶ The radiation dose to the kidneys (the critical organ) was determined using conventional sampling methods and was used to manage the amount of administered activity given to the patients in the final two cycles of treatment. The radiation dose to the kidneys from the first two cycles was determined using the following procedure. After the administration of ⁹⁰Y DOTATOC (nominally 4.4 GBq) and treatment with amino acids (T ~ 5 h), subjects were imaged with time‐of‐flight PET/CT to quantify kidney activity. The PET/CT system was a Siemens mCT Flow and a single bed position with the kidneys in the field of view was acquired for 30 min. Immediately following the PET/CT scan, a 30 min bremsstrahlung SPECT/CT scan was performed. Additional bremsstrahlung SPECT/CT scans were acquired at 24, 48, and 72 h.

The PET images were reconstructed with an OSEM iterative algorithm that incorporated the time‐of‐flight information. The vendor calibration for quantifying Y‐90 activity was used and was verified with a calibrated Y‐90 standard. The activity in each kidney was determined by integrating the PET activity concentration in manually drawn regions for each kidney over the slices that encompassed the kidneys. The mass of the kidneys was determined by integrating the manually drawn regions over the kidneys on the CT study.

The SPECT/CT imaging of the kidneys was performed on a dual detector Siemens Symbia T2 system equipped with medium energy collimators. A single energy window centered at 170 keV with a 100% energy window was used to acquire the bremsstrahlung emission data. The calibrated Y‐90 standard was located on the subject's abdomen. The SPECT images for each time point were reconstructed with the same OSEM iterative algorithm both with and without attenuation correction. The relative activity at each time point was assessed by summing over all the counts in manually drawn regions for each kidney over the slices that encompassed the kidneys.

The kidney clearance curve from the bremsstrahlung SPECT/CT was fit to a biexponential clearance model using the Excel Solver tool and was calibrated to activity from the results of the PET/CT scan and the total integrated activity was generated using Eq. (8). The kidney dose was determined by multiplying the total integrated activity of the kidneys by the kidney S factor for ⁹⁰Y scaled for the actual mass of the kidney.

The single time point approach was applied retrospectively to this data as follows. The results from 47 dosimetry studies as described above were used to calculate the population means for $\widehat{\mathit{c}}$, $\widehat{\mathit{a}}$, and ${\widehat{\mathit{k}}}_{\mathbf{2}}$. These results are given in Table 2 and the histograms associated with parameters are shown in Fig. 2.

The actual measured kidney activity (A(T)) was available for T = 5, 24, 48, and 72 h. Equation (13) was used to calculate the estimated total integrated activity at each of these time points and the estimated kidney was determined by multiplying the estimated total integrated activity by the ⁹⁰Y kidney S factor adjusted for the kidney mass. Comparisons were made for kidney dose calculated using the conventional 4‐point sampling with the kidney dose estimates obtained from the single time point approach for each of the 47 dosimetry studies.

3. Results

3.A. Monoexponential simulation results

The results for the monoexponential simulation are given in Table 3 and Fig. 3(a). The results from the linear regression show acceptable correlations at all the sample times, but are clearly the best when the sample time is equal to the mean time as determined by the inverse of the mean rate constant. More importantly, the standard error of estimate is minimized as well as substantially reduced at the expected optimal sampling time ($\mathbf{T}=\widehat{\mathit{\tau }}$). The slope of the regression line is approximately 1 and the intercept is near 0 which is consistent with there being a direct linear relationship between à and Ã*.

Table 3.

Single‐exponential linear regression results for comparing à to Ã*as a function of sample time

Sample time T	Slope	Intercept	r 2	SEE
0.2 ${\widehat{\tau }}_2$	1.07	−43.7	0.89	266.8
0.6${\widehat{\tau }}_2$	1.08	−60.7	0.96	160.1
${\widehat{\tau }}_2$	1.04	−23.3	0.99	67.1
1.4${\widehat{\tau }}_2$	0.96	57.2	0.99	80.2
1.8 ${\widehat{\tau }}_2$	0.86	165.3	0.96	163.8

Figure 3.

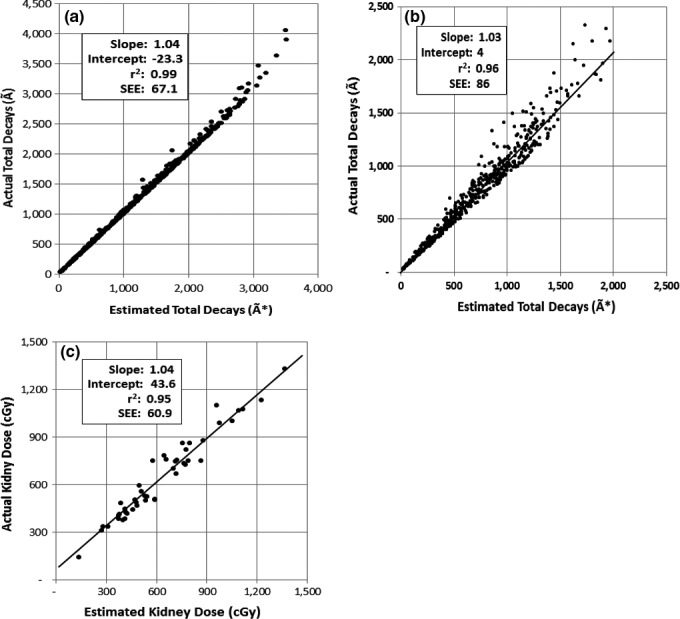
Plots showing the performance of the single time point method. (a) Monoexponential simulation results comparing the actual and estimated total integrated activity for $\mathbf{T}=\widehat{\tau }$. (b) Biexponential simulation results comparing the actual and estimated total integrated activity for $\mathbf{T}={\widehat{\mathit{\tau }}}_2$. (C) Retroscpective clinical results comparing the kidney radiation dose obtained from conventional mulitple time samples with the single time sample approximation at T = 48 h.

3.B. Biexponential simulation results

The biexponential simulation results are given in Table 4 and Fig. 3(b). Although the correlation coefficient and standard error of estimate associated with the biexponential simulation are not as good as those obtained for the single exponential experiment, there still is a very strong correlation between the estimated and actual total integrated activity. In addition, a similar result is obtained as with the monoexponential case where the best regression results (especially the standard error of estimate) are obtained when the sample time T is equal to ${\widehat{\mathit{\tau }}}_{\mathbf{2}}$.

Table 4.

Biexponential simulation linear regression results for comparing à to Ã*as a function of sample time T

Sample time T	Slope	Intercept	r 2	SEE
0.2${\widehat{\tau }}_2$	0.93	41	0.91	134
0.6${\widehat{\tau }}_2$	1.05	−21	0.96	90
${\widehat{\tau }}_2$	1.03	4	0.96	86
1.4${\widehat{\tau }}_2$	0.96	46	0.95	102
1.8${\widehat{\tau }}_2$	0.88	99	0.92	132

3.C. Retrospective clinical results

The results for the retrospective analysis of the radiation dose to the kidneys from ⁹⁰Y DOTATOC treatments are given in Table 5 and Fig. 3(c). As with the simulation results, there is a strong correlation between the estimated kidney dose using the single time point approach and the actual kidney dose from the multiple sample times along with a very good standard error of estimate. The best linear regression result with the minimum standard error of estimate occurred at the 48 h sample time which is very close to the predicted optimal sampling time of 50 h (${\widehat{\mathit{\tau }}}_{\mathbf{2}}$ = 1/0.02 h⁻¹). The average magnitude of the error associated with the single time point approach was 7.2% with a maximum dose overestimate of 17.5% and a minimum dose underestimate of 22.3%. Thirty‐three of the 47 dose estimates were within 10% of the actual dose.

Table 5.

Retrospective analysis of clinical ⁹⁰Y DOTATOC data comparing the actual and estimated kidney dose as a function of sample time

Sample time T (h)	Slope	Intercept	r 2	SEE
5 (0.10 ${\widehat{\mathit{\tau }}}_2$)	0.83	115.4	0.83	108.1
24 (0.48 ${\widehat{\mathit{\tau }}}_2$)	0.86	63.8	0.94	66.8
48 (0.96 ${\widehat{\mathit{\tau }}}_2$)	0.94	43.6	0.95	60.9
72(1.44 ${\widehat{\mathit{\tau }}}_2$)	0.94	62.3	0.92	75.4

${\widehat{\mathit{\tau }}}_2$ = 1/${\widehat{\mathbf{k}}}_2$ = 1/0.020 h⁻¹ = 50 h.

4. Discussion

In this paper, we have demonstrated that under conditions where there is exponential clearance of a radiotracer along with prior knowledge about the tracer kinetics, it is potentially possible to accurately estimate the total integrated activity (and thereby radiation dose) from a single time point measurement of activity if the range over which the rate constant varies among individuals is not too extreme. Equation (6) shows for the monoexponential case that as long as the actual rate constant k is within the range from 0.6 $\widehat{\mathit{k}}$ to 1.53 $\widehat{\mathit{k}}$, the error in estimating the total integrated activity from the single point approach will be less than 10%. Equations (3) and (13) show how the integrated activity can be estimated from the single point activity measurement and the expected population means of the exponential parameters. Once the integrated activity is known, the radiation dose is calculated by multiplying this quantity by the appropriate S factor. The simulations from both the single exponential and biexponential cases show excellent results for the estimation of total integrated activity when the optimal sample time is used even when the exponential parameters are allowed to vary substantially from the population means.

It has been demonstrated that the best sample time is equal to the mean time associated with the rate constant $\widehat{\mathit{k}}$ for single exponential clearance and is equal to the mean time associated with the rate constant ${\widehat{\mathit{k}}}_{\mathbf{2}}$ for the biexponential case. The simulations support this result since the minimum standard error of estimate is found when T is equal to the associated mean times. The actual clinical results obtained by retrospectively applying the single time dose approach shows the same behavior. However, it should be noted that although the average error for the clinical results was less than 10% for the retrospective clinical results, there were some outliers where the dose error was as high as 22%. This occurred in subjects whose exponential parameters had the largest deviation from the population means.

In the biexponential simulation, the ratio of the rate constants, a, was approximately 12 and that was also the case for the clinical data. The ratio has that magnitude because the fast component ( k ₁ ) is associated with the initial blood clearance which typically has a half time on the order of several hours while the slow component ( k ₂ ) is associated with the portion of the tracer that targets the particular binding sites that the radiopharmaceutical was designed for. It certainly is desirable that the biologic half time associated with that binding be much longer than the blood clearance in order to deliver a therapeutic radiation dose. For the DOTATOC peptide, that biologic half time is on the order of 70 h leading to an effective half time of about 35 h when labeled with ⁹⁰Y. Although there will be exceptions (and perhaps even many exceptions), it can be expected that there will be other radionuclide situations where $\widehat{\mathit{a}}$ is larger than 10. When that occurs, Eq. (13) becomes similar to Eq. (3) since $\left(\widehat{\mathit{c}}/\widehat{\mathit{a}}+\mathbf{1}\right)\approx \mathbf{1}$ and $\widehat{\mathit{c}}{\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-\widehat{\mathit{a}}{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}+{\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}\approx {\mathbf{A}}_{\mathbf{2}}{\mathbf{e}}^{-{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}$, thus ${\tilde{\mathbf{A}}}^{\ast }\approx \mathbf{A}(\mathbf{T}){\mathbf{e}}^{{\widehat{\mathit{k}}}_{\mathbf{2}}\mathbf{T}}/{\widehat{\mathit{k}}}_{\mathbf{2}}$ which is the monoexponential result given in Eq. (3). We are not suggesting that this approximation be used instead of Eq. (13), but it does explain why the biexponential case has similar behavior to the monoexponential case with respect to the optimal sampling time and the magnitude of the estimation errors.

A recent paper by Hanscheid et al.⁷ proposes a similar single time point estimate for the specific case of ¹⁷⁷Lu dosimetry. Their method is also based on the recognition that there is a relationship between the activity at a specific time point, A(T), and the total integrated activity as we show in Eqs. (2) and (12). They make the argument for a single exponential that the errors are small if the sampling time is selected to be within the range of 0.75 Teff to 2.5 Teff, where Teff is the effective half‐life associated with the kinetics of the radiopharmaceutical agent for a given population. This range brackets the optimal sampling time derived in our paper which would be equal to 1.44 Teff. Although they do not specifically address it in their derivation, their approach also requires that the population mean Teff (or equivalently the rate constant) not only be known, but that the variation in the individual rate constants in the population is not too large. The approach derived in our work comes to the same conclusions as Hanscheid et al.⁷ about the potential for a single time point dose estimate, but our derivation is more fundamental and more general for both the monoexponential and biexponential cases. In particular, one can judge from Eqs. (3) and (13) what the important parameters are that affect the errors in the approximation due to the single time point approach. In addition, the derivation of the optimal sampling time and the magnitude of expected errors are more rigorous.

We note that there is a straightforward way that follows from Eqs. (2) and (12) to predict whether this approach will work for a specific radiotherapeutic agent where conventional dosimetry was performed on a population of subjects and the information about the total integrated activity is available. These equations define the relationship between the total integrated activity and a single activity sample. For example, if we look at Eq. (12), $\tilde{\mathbf{A}}=\frac{\mathbf{A}(\mathbf{T})(\mathit{c}/\mathit{a}+\mathbf{1})/{\mathit{k}}_{\mathbf{2}}}{\mathit{c}{\mathbf{e}}^{-\mathit{a}{\mathit{k}}_{\mathbf{2}}\mathbf{T}}+{\mathbf{e}}^{-{\mathit{k}}_{\mathbf{2}}\mathbf{T}}}$, this can be written as $\tilde{\mathbf{A}}=\mathbf{A}(\mathbf{T})/{\mathit{k}}_{\mathbf{2}}\mathbf{g}(\mathbf{c},\mathbf{a},{\mathit{k}}_{\mathbf{2}},\mathbf{T})$. The single point technique will only work if the function g(c, a, k ₂ , T) is approximately constant within the population for a specific radiotherapeutic agent. Thus, if the dosimetry data exists from a previous study with the radiotherapeutic agent, one only needs to plot the total integrated activity for each of the subjects against one of the corresponding activity samples that were used to calculate the integrated activity. If there is a strong linear relationship, that implies that the variations in the parameters (e.g., c , a , and k ₂ for the biexponential case) among subjects in the population are small enough that Eq. (13) is applicable and that subsequent future treatments using the that radiopharmaceutical on different groups of patients may be able to rely on the single time point method given in this paper. In these situations, the application of this approach will substantially reduce the burden of both patients and the clinic through the reduction in imaging procedures over many days while still providing sufficient radiation dose information to guide the treatment of these patients.

5. Conclusion

A method for accurately estimating the total number of decays for internally distributed radionuclide therapy agents from a single time point measurement has been described. This method requires prior knowledge about population averages for tracer kinetic parameters. Simulations and data from one clinical study support the feasibility of this approach when the variation in the exponential parameters (particularly the rate constant) among individuals is not too extreme. We conclude that if the appropriate information is available, the single time point method has the potential in applicable cases to provide substantial reductions in the time and resources required for patient specific dosimetry.