Acuros CTS: A fast, linear Boltzmann transport equation solver for computed tomography scatter – Part I: Core algorithms and validation

Abstract

Purpose

To describe Acuros^® CTS, a new software tool for rapidly and accurately estimating scatter in x‐ray projection images by deterministically solving the linear Boltzmann transport equation (LBTE).

Methods

The LBTE describes the behavior of particles as they interact with an object across spatial, energy, and directional (propagation) domains. Acuros CTS deterministically solves the LBTE by modeling photon transport associated with an x‐ray projection in three main steps: (a) Ray tracing photons from the x‐ray source into the object where they experience their first scattering event and form scattering sources. (b) Propagating photons from their first scattering sources across the object in all directions to form second scattering sources, then repeating this process until all high‐order scattering sources are computed using the source iteration method. (c) Ray‐tracing photons from scattering sources within the object to the detector, accounting for the detector's energy and anti‐scatter grid responses.

To make this process computationally tractable, a combination of analytical and discrete methods is applied. The three domains are discretized using the Linear Discontinuous Finite Elements, Multigroup, and Discrete Ordinates methods, respectively, which confer the ability to maintain the accuracy of a continuous solution. Furthermore, through the implementation in CUDA, we sought to exploit the parallel computing capabilities of graphics processing units (GPUs) to achieve the speeds required for clinical utilization.

Acuros CTS was validated against Geant4 Monte Carlo simulations using two digital phantoms: (a) a water phantom containing lung, air, and bone inserts (WLAB phantom) and (b) a pelvis phantom derived from a clinical CT dataset. For these studies, we modeled the TrueBeam^® (Varian Medical Systems, Palo Alto, CA) kV imaging system with a source energy of 125 kVp. The imager comprised a 600 μm‐thick Cesium Iodide (CsI) scintillator and a 10:1 one‐dimensional anti‐scatter grid. For the WLAB studies, the full‐fan geometry without a bowtie filter was used (with and without the anti‐scatter grid). For the pelvis phantom studies, a half‐fan geometry with bowtie was used (with the anti‐scatter grid). Scattered and primary photon fluences and energies deposited in the detector were recorded.

Results

The Acuros CTS and Monte Carlo results demonstrated excellent agreement. For the WLAB studies, the average percent difference between the Monte Carlo‐ and Acuros‐generated scattered photon fluences at the face of the detector was −0.7%. After including the detector response, the average percent differences between the Monte Carlo‐ and Acuros‐generated scatter fractions (SF) were −0.1% without the grid and 0.6% with the grid. For the digital pelvis simulation, the Monte Carlo‐ and Acuros‐generated SFs agreed to within 0.1% on average, despite the scatter‐to‐primary ratios (SPRs) being as high as 5.5. The Acuros CTS computation time for each scatter image was ~1 s using a single GPU.

Conclusions

Acuros CTS enables a fast and accurate calculation of scatter images by deterministically solving the LBTE thus offering a computationally attractive alternative to Monte Carlo methods. Part II describes the application of Acuros CTS to scatter correction of CBCT scans on the TrueBeam system.

1. Introduction

Cone‐beam CT (CBCT) has proven to be an invaluable clinical tool in the areas of radiotherapy, interventional procedures, and dentistry.^{1, 2, 3} The acquisition of extensive volumetric data in a single rotation is made possible by a wide‐area detector such as an amorphous silicon flat‐panel imager. However, the wide‐area beam generates a large amount of scatter in the projection images, which remains one of the main challenges to achieving high‐quality CBCT images.^{4, 5} If scatter is not accounted for, reconstructed images can suffer from cupping, shading, streaks, inhomogeneities, and quantification inaccuracies.^{6, 7}

Standard approaches to reducing scatter include use of a bowtie filter to reduce the peripheral dose^{8, 9} and an anti‐scatter grid mounted to the flat‐panel detector.^{10, 11} However, scatter still contributes a substantial amount of signal to each projection. Numerous hardware‐ and/or software‐based approaches have been proposed to estimate and correct for the remaining scatter signal. While there are too many of these techniques to enumerate, they can broadly be classified as belonging to one of several categories including: (a) source intensity modulation^{12, 13} or blocking,^{14, 15, 16, 17, 18, 19, 20, 21, 22} (b) scatter deconvolution,^{23, 24, 25, 26, 27} (c) utilizing a priori knowledge of the object,^{28, 29, 30} (d) Monte Carlo modeling,^{31, 32, 33, 34, 35, 36, 37, 38, 39} or (e) other empirical approaches.^{40, 41, 42}

Our motivation was to find a fast and accurate scatter correction method that would not require sophisticated hardware and could be used on existing platforms. Scatter deconvolution, also known as scatter kernel superposition (SKS), is the technique most widely applied commercially. The x‐ray cone beam is modeled as an array of pencil beams that interact with the object. The scatter produced by each pencil beam is approximated by predetermined point‐spread functions or kernels. SKS methods have the advantage of being computationally efficient (i.e., regarding real‐time processing of projections) while not requiring additional hardware. We previously developed a variant of SKS — fast adaptive scatter kernel method (fASKS) — that uses object‐dependent asymmetric scatter kernels to estimate and subtract scatter from projection images.^{25, 26} The method has been used in the TrueBeam^® product (Varian Medical Systems, Palo Alto, CA) and proven to be remarkably effective given the limitations of this class of corrections. However, SKS methods only approximate the interaction of x‐ray photons with a heterogeneous object, which fundamentally limits their accuracy. Residual artifacts are often seen that limit CT number accuracy and can be clinically adverse (Fig. 1).

Figure 1.

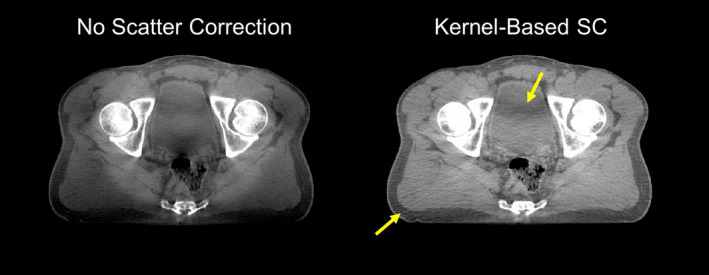
Reconstructed cone‐beam CT images of a clinical pelvis scan. Severe shading is seen when no scatter correction is applied. Even after kernel‐based (fASKS) scatter correction, some residual scatter artifact remains, including shading in the bladder (arrows). Display window [−300, 300] HU. [Color figure can be viewed at wileyonlinelibrary.com]

More accurate software‐based scatter estimation and correction methods have been proposed, primarily based on Monte Carlo methods. In principle, Monte Carlo methods can model quite accurately how x‐rays propagate through components of the imaging system and the imaged object. However, in practice, Monte Carlo calculations are typically slow and resource intensive, with there being a tradeoff between run times and the amount of stochastic noise present. While it is possible to improve performance by utilizing graphics processing units (GPUs), implementing variance reduction techniques, and simplifying the approximations of the underlying physics, it remains to be seen whether a sufficiently fast and accurate calculation can be achieved to meet clinical demands.

Under standard imaging conditions, the behavior of photons as they interact with an object is described by the linear Boltzmann transport equation (LBTE).⁴³ There are two classes of methods for solving the LBTE — stochastic (i.e., Monte Carlo) and deterministic. Both Monte Carlo and deterministic methods inherently model the LBTE, but take fundamentally different approaches to solving it. The former repeatedly samples the behavior of individual particles to stochastically buildup a solution, while the latter directly computes a discretized solution for the entire object. Stochastic and deterministic methods both converge to the same solution given enough simulated particles for the former or sufficiently fine discretization for the latter.

Recent advances in deterministic methods have shown great promise as an alternative to Monte Carlo techniques in applications such as dose calculation for radiotherapy treatment planning and, more generally, modeling particle transport.^{44, 45, 46, 47, 48} In particular, Varian recently introduced Acuros^® XB, a deterministic program providing computation speeds approaching those of kernel‐based methods and accuracies equivalent to those of Monte Carlo methods.^{49, 50, 51, 52} Inspired by the success of Acuros XB, we sought to apply a similar deterministic approach to rapidly and accurately estimate scatter in kV projections to improve CBCT image quality. As a result, a new deterministic method called Acuros CTS was born.^{53, 54} To our knowledge, this paper describes the first complete implementation and validation of a deterministic LBTE solver for estimating scatter in kV projection images.

The description of Acuros CTS and its use for scatter correction is organized as a two‐part paper. In Part I, we first present the steps that form the LBTE solver in Acuros CTS. Then, we highlight the numeric methods used to produce a fast and accurate implementation. Finally, we demonstrate the ability of Acuros CTS to produce scatter estimates equivalent to Monte Carlo simulations while benchmarking computation times. In Part II,⁵⁵ we describe how the imaging system is modeled and how Acuros CTS is used to correct for scatter in projection images with results demonstrated on phantom and clinical data on a commercial system. For brevity, we will henceforth refer to Acuros CTS simply as Acuros.

2. Materials and methods

The flow of photons during a CBCT projection can be organized overall into three steps: (a) photons travel from the x‐ray source to the object, where they (b) interact and scatter, possibly multiple times, before (c) continuing their path into the detector panel. These steps, depicted in Fig. 2, are also natural steps in our computational effort. We have, therefore, organized the Acuros calculation accordingly.

Figure 2.

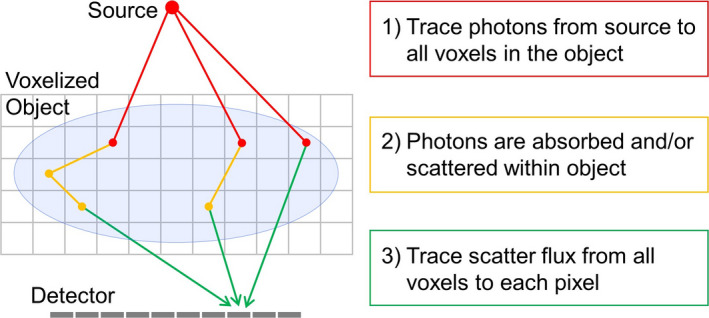
Overview of the computational algorithm in Acuros CTS. Photons depart the source and arrive into the object in step 1 (red), where they scatter one or multiple times in step 2 (orange) to finally arrive at the detector panel in step 3 (green). [Color figure can be viewed at wileyonlinelibrary.com]

1. Ray trace photons from the x‐ray source to the object.

2. Compute the interaction of photons with the object.

3. Ray trace scattered photons from the object to the detector.

Thus, the result from an Acuros calculation is the detector's scatter signal.

In each step of the algorithm, the steady‐state linear Boltzmann transport equation (LBTE) governs how photons behave:

$$\begin{array}{cc}& \widehat{\mathrm{\Omega }}·\overrightarrow{\mathrm{\nabla }}{\varphi }_{\mathrm{\Omega }E}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})+{\mu }_t(\overrightarrow{r},E){\varphi }_{\mathrm{\Omega }E}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=\hfill \\ & S(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})+{\int }_0^{E_0}d{E}^{\prime }{\int }_{4\pi }d{\mathrm{\Omega }}^{\prime }\left[{\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }})\right.\hfill \\ & \left.{\varphi }_{\mathrm{\Omega }E}(\overrightarrow{r},E^{\prime },{\widehat{\mathrm{\Omega }}}^{\prime })\right],\hfill \end{array}$$ (1)

where

• ☐ ϕ _ΩE is the angular fluence (sometimes referred to as angular flux) which quantifies the tracks of particles in a differential volume dV about position $\overrightarrow{r}$ with energy E traveling along the direction $\widehat{\mathrm{\Omega }}$. Using the ICRU Report 85 convention for notation and units,⁵⁶ the units to the angular fluence are m⁻² sr⁻¹ J⁻¹.
• ☐ S is a source of photons to the LBTE. The photon source describes the number of photons inserted into position $\overrightarrow{r}$ with energy E traveling along direction $\widehat{\mathrm{\Omega }}$. The unit of the photon source term is m⁻³ sr⁻¹ J⁻¹. The maximum energy of all sources in the system is E ₀.
• ☐ ${\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }})$ is a linear directional scatter coefficient (sometimes referred to as the directional scattering macroscopic cross section) that describes the fraction of photons having energy E ^′ travelling along direction ${\widehat{\mathrm{\Omega }}}^{\prime }$ that scatter into a new direction $\widehat{\mathrm{\Omega }}$ with a new energy E. μ _s is an intrinsic property of the material(s) being modeled and can be thought of as a total cross section that encompasses all Compton and Rayleigh scattering events (photoelectric events that produce characteristic x‐rays may also be included in the “scatter” model). The values for μ _s used in Acuros were obtained from theoretical Klein–Nishina and Thompson scatter coefficients for Compton and Rayleigh scattering, respectively.⁵⁷ We then adjusted these theoretical coefficients by the incoherent scattering and atomic form factor functions, which adjust the theoretical coefficient to the effects of the electron‐bounding energies.⁵⁸ The units of this directional coefficient are m⁻¹ sr⁻¹ J⁻¹.
• ☐ μ _t is the linear attenuation coefficient (sometimes referred to as the macroscopic total interaction cross section) of the material(s) being modeled and accounts for all scattering and absorption events. The units of the linear attenuation coefficient are m ⁻¹. The total attenuation coefficient equals the scattering coefficient plus the photoelectric absorption coefficient. We derived photoelectric coefficients from the Biggs–Lighthill analytic model.⁵⁹

To better understand the LBTE, we describe each one of its terms physically:

1. The first term in Eq. (1) is a projection of the gradient of the angular fluence distribution ${\varphi }_{\mathrm{\Omega }E}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})$. $\widehat{\mathrm{\Omega }}·\overrightarrow{\mathrm{\nabla }}{\varphi }_{\mathrm{\Omega }E}$ accounts for how x‐rays stream across a differential volume.

2. The second term represents the angular fluence along the direction $\widehat{\mathrm{\Omega }}$ that collide with the object. This term includes all photoelectric absorption and Rayleigh and Compton scattering events.

3. The third term provides a mechanism for introducing photons into the system, for example, from an x‐ray source either internal or external to the object.

4. The fourth term describes scattering interactions that can increase the angular fluence along the direction $\widehat{\mathrm{\Omega }}$.

The LBTE states that for a given position $\overrightarrow{r}$ and direction $\widehat{\mathrm{\Omega }}$, the amount of streaming photons (first term) plus that which collide (second term) is equal to the angular fluence generated by external sources (third term) plus that which scatters into $\overrightarrow{r}$ with direction $\widehat{\mathrm{\Omega }}$ (fourth term). The spatially dependent object material and density maps, which form both ${\mu }_t(\overrightarrow{r},E)$ and ${\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }})$, are assumed to be known a priori, for example, as from a reconstructed CT scan. Finally, for kV imaging, the photon energies are too low to merit the explicit modeling of secondary electrons. Instead, where an interaction occurs that produces Compton or Auger electrons, the electrons are assumed to travel a negligible distance and deposit their energies locally.

The angular fluence distribution ϕ _ΩE in the LBTE can be solved analytically for a limited subset of problems, for example, when radiation travels through a purely absorbing material (or scatter is ignored) or in problems where there is scatter, but the geometry is one dimensional.⁶⁰ More commonly, a generalized LBTE solution is numerically computed either through Monte Carlo or deterministic methods whose solutions will converge to each other given enough time and resources.⁴³ While Monte Carlo methods arrive at their answer by statistically sampling the underlying (absorption and scattering) probability density functions (PDFs) that govern x‐ray transport and then propagating particles stochastically according to those PDFs, deterministic methods iteratively solve the LBTE by propagating a current iteration of the angular fluence estimate across the object and updating the estimate for the next iteration, based on the predicted effects of the local values of μ _s and μ _t , until convergence is reached. The advantages of deterministic methods are that they produce a solution over the entire LBTE domain (cf. Monte Carlo tallies) and, with efficient implementation, can be fast relative to the stochastic Monte Carlo approach.⁴³

We implemented a combination of analytic and deterministic techniques in Acuros to solve the LBTE. Specifically, the ray tracing operations in Steps 1 and 3 were performed analytically. For Step 2, a deterministic approach was chosen based on the well‐known linear discontinuous finite element, multigroup, and discrete ordinates methods for discretization along the spatial, energy, and angular domains, respectively. Although these methods are partly described in the literature,⁴³ we include a brief description here for completeness since our implementation forms a unique combination of methods for kV imaging.

2.A. Continuous domains $(\overrightarrow{\mathit{r}},\mathit{E},\widehat{\mathbf{\Omega }})$

This section describes Acuros’ three steps with a continuous representation of the spatial, energy, and angular domains. It best illustrates the methodology employed to solve the LBTE. However, we do not solve the LBTE in the continuous domain. In Section 2.B, we show how the problem is discretized and the Acuros solver implemented.

2.A.1. Source‐to‐object ray trace

In Acuros’ first step, we trace photons as they depart from the x‐ray source S ⁽⁰⁾, arrive to the object, and first interact. Our goal is to compute a distribution of uncollided (UC) angular fluence (i.e., photons that have not been absorbed or scattered) inside the object, then assemble a first‐collision source to drive the next step of the algorithm. We begin by tracing the angular fluence from the source position to the object, and remove photons as they are absorbed or scattered:

$$\widehat{\mathrm{\Omega }}·\overrightarrow{\mathrm{\nabla }}{\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=S^{(0)}(E\widehat{\mathrm{\Omega }})·\delta (\overrightarrow{r}-{\overrightarrow{r}}_0)-{\mu }_t(\overrightarrow{r},E){\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }}),$$ (2)

where S ⁽⁰⁾ is the source that drives the uncollided problem (in units of sr⁻¹ J⁻¹) and is defined on a singular point in space — that is, the focal point of our beam ${\overrightarrow{r}}_0$ from which x‐rays emanate. We can analytically solve for the uncollided ${\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}$ since all uncollided photons arrive to any point $\overrightarrow{r}$ from a single position ${\overrightarrow{r}}_0$:

$$\begin{array}{cc}\hfill {\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}(\overrightarrow{r},E)=& \frac{S^{(0)}\left(E,{\widehat{\mathrm{\Omega }}}^{\mathit{UC}}\right)}{\Vert \overrightarrow{r}-{\overrightarrow{r}}_0{\Vert }^2}\hfill \\ & exp\left[-{\int }_0^{\Vert \overrightarrow{r}-{\overrightarrow{r}}_0\Vert }dl{\mu }_t\left({\overrightarrow{r}}_0+l{\widehat{\mathrm{\Omega }}}^{\mathit{UC}},E\right)\right].\hfill \end{array}$$ (3)

Here $\overrightarrow{r}$ is an evaluation point inside the object, ${\widehat{\mathrm{\Omega }}}^{\mathit{UC}}$ is a unit vector pointing in the streaming direction from the x‐ray source located at ${\overrightarrow{r}}_0$ to this evaluation point and l is a variable of integration along the streaming direction. Variations in angular intensity due to the heel effect, collimation, and/or a bowtie filter are assumed to be known a priori and can be incorporated into the point source distribution $S^{(0)}\left(E,{\widehat{\mathrm{\Omega }}}^{\mathit{UC}}\right)$. Note that Eq. (3), which shows that the uncollided angular fluence arriving at a given location $\overrightarrow{r}$ is simply the exponentially attenuated source fluence S⁽⁰⁾ divided by $\Vert \overrightarrow{r}-{\overrightarrow{r}}_0{\Vert }^2$ thus confirming Beer's law and the inverse‐square law.

Once the uncollided fluence entering each location in the object is computed, we calculate the magnitude and distribution of, what is termed, the first‐scattered or first‐collision (FC) scattering source:

$$\begin{array}{cc}& S^{\mathit{FC}}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})={\int }_E^{E_0}d{E}^{\prime }{\int }_{4\pi }d{\widehat{\mathrm{\Omega }}}^{\prime }\hfill \\ & \left[{\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }}){\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}(\overrightarrow{r},E^{\prime })·\delta ({\widehat{\mathrm{\Omega }}}^{\prime }-{\widehat{\mathrm{\Omega }}}^{\mathit{UC}})\right].\hfill \end{array}$$ (4)

We note that since E ^′ ≥ E, this energy integral assumes that photons cannot gain energy from scattering events. Particles arrive to $\overrightarrow{r}$ from the uncollided direction ${\widehat{\mathrm{\Omega }}}^{\mathit{UC}}$ only. We, therefore, do not need to integrate the scattering kernel in angle to evaluate the first‐collided source. The nature of the uncollided fluence automatically simplifies this integral.

2.A.2. Scattering source calculation

In this second step, we transport photons as they travel and collide multiple times with the object to produce higher order scattering sources. While the first‐collision scattering source computed in Eq. (4) is, by nature (e.g., as described by Thompson and Klein–Nishina scattering equations⁵⁷), forward peaked along the direction ${\widehat{\mathrm{\Omega }}}^{\mathit{UC}}$, the higher order scattering sources are more isotropic and as shall be shown, can be efficiently modeled using spherical harmonic functions. The combined scattering sources of all orders produce a total scattering source for each position in the object, which then drives the final step of computing the scatter signal measured at the detector.

The LBTE describing this second step is more complex than for the first step since the scattering term now couples the angular fluence ϕ _ΩE from all streaming directions, Ω′:

$$\begin{array}{cc}\hfill \widehat{\mathrm{\Omega }}& ·\overrightarrow{\mathrm{\nabla }}{\varphi }_{\mathrm{\Omega }E}^C(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=S^{\mathit{FC}}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})+\hfill \\ & {\int }_0^{E_0}d{E}^{\prime }{\int }_{4\pi }d{\mathrm{\Omega }}^{\prime }[{\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }})\hfill \\ & {\varphi }_{\mathrm{\Omega }E}^C(\overrightarrow{r},E^{\prime },{\widehat{\mathrm{\Omega }}}^{\prime })]-{\mu }_t(\overrightarrow{r},E){\varphi }_{\mathrm{\Omega }E}^C(\overrightarrow{r},E,\widehat{\mathrm{\Omega }}).\hfill \end{array}$$ (5)

Here, the superscript C indicates that this solution is the collided component of the angular fluence (i.e., photons that have scattered at least once within the object). Unlike for the first step, there is no generalized analytic solution to compute the angular fluence distribution, as the LBTE is now an integro‐differential equation. Thus, we rely instead on numerical techniques.

We choose the source iteration (SI) method to solve the problem.⁶¹ To understand SI, consider expanding the collided angular fluence into a series:

$${\varphi }_{\mathrm{\Omega }E}^C=\sum _{n=1}^{\infty }{\varphi }_{\mathrm{\Omega }E}^{(n)},$$ (6)

where n is the number of collisions that each generation of the angular fluence has encountered. That is, ${\varphi }_{\mathrm{\Omega }E}^{(1)}$ is the angular fluence of particles that has scattered only once with the object, ${\varphi }_{\mathrm{\Omega }E}^{(2)}$ is the twice‐scattered fluence, etc. We ignore ${\varphi }_{\mathrm{\Omega }E}^{(0)}$ because this is the angular fluence of uncollided particles ${\varphi }_{\mathrm{\Omega }E}^{\mathit{UC}}$, which we have already addressed (step 1).

SI solves each generation n of the angular fluence distribution sequentially. First, we solve ${\varphi }_{\mathrm{\Omega }E}^{(1)}$, then ${\varphi }_{\mathrm{\Omega }E}^{(2)}$, and so forth. The LBTE for each generation n has only three terms, the particle streaming and interaction terms plus the scattering source from the higher order fluence:

$$\widehat{\mathrm{\Omega }}·\overrightarrow{\mathrm{\nabla }}{\varphi }_{\mathrm{\Omega }E}^{(n)}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=S^{(n)}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})-{\mu }_t(\overrightarrow{r},E){\varphi }_{\mathrm{\Omega }E}^{(n)}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }}),$$ (7)

where ${\varphi }_{\mathrm{\Omega }E}^{(n)}$ is the unknown angular fluence and S ⁽ⁿ⁾ is the amount of (scattered) particles emerging from their nth collision:

$$\begin{array}{cc}\hfill S^{(n)}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=& {\int }_0^{E_0}d{E}^{\prime }{\int }_{4\pi }d{\mathrm{\Omega }}^{\prime }\hfill \\ & \left[{\mu }_s(\overrightarrow{r},E^{\prime }\to E,{\widehat{\mathrm{\Omega }}}^{\prime }\to \widehat{\mathrm{\Omega }}){\varphi }_{\mathrm{\Omega }E}^{(n-1)}(\overrightarrow{r},E^{\prime },{\widehat{\mathrm{\Omega }}}^{\prime })\right].\hfill \end{array}$$ (8)

Here, ${\varphi }_{\mathrm{\Omega }E}^{(n-1)}$ is known; we obtained it in the previous iteration of our process. Note that, on average, each generation has a smaller fluence magnitude than the previous one since not all photons will scatter into the next generation — some photons will instead escape from the object while others will be absorbed. Therefore, after a finite number N iterations, the calculation converges and contributions from further iterations are negligible (i.e., our collided fluence expansion is truncated after N terms):

$${\varphi }_{\mathrm{\Omega }E}^C=\sum _{n=1}^{\infty }{\varphi }_{\mathrm{\Omega }E}^{(n)}\approx \sum _{n=1}^N{\varphi }_{\mathrm{\Omega }E}^{(n)}.$$ (9)

We apply a convergence criteria <0.1% change between iterations, which in our experience, requires only a modest number of iterations (typically 10 < N < 15) for keV photons compared to the dozens of iterations required for optical photons or the hundreds needed to model low absorption environments like thermal neutrons in water.⁴³

The complete multiple‐collision source is the number of particles that have scattered at least twice:

$$S^{\mathit{MC}}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }})=\sum _{n=2}^N{S}^{(n)}(\overrightarrow{r},E,\widehat{\mathrm{\Omega }}).$$ (10)

2.A.3. Scatter image

In the remaining step of the algorithm, the scattered photons are ray traced to the detector. The solution to the LBTE for the angular fluence ${\varphi }_{\mathrm{\Omega }E}^D({\overrightarrow{r}}_D,E,\widehat{\mathrm{\Omega }})$ at detector point ${\overrightarrow{r}}_D$ for those particles arriving with direction $\widehat{\mathrm{\Omega }}$ along the line l is:

$$\begin{array}{cc}\hfill {\varphi }_{\mathrm{\Omega }E}^D({\overrightarrow{r}}_D,E,\widehat{\mathrm{\Omega }})=& {\int }_0^{\infty }dl[S^{\mathit{FC}}+S^{\mathit{MC}}]({\overrightarrow{r}}_D-l\widehat{\mathrm{\Omega }},E,\widehat{\mathrm{\Omega }})\hfill \\ & \frac{exp\left[-{\int }_0^{l}d{l}^{\prime }{\mu }_t({\overrightarrow{r}}_D-l^{\prime }\widehat{\mathrm{\Omega }},E)\right]}{l^2}.\hfill \end{array}$$ (11)

This calculation is analogous to the first step of the algorithm, except that now a distributed source is being ray traced to locations on the detector panel. The exponential attenuation in Eq. (12) deserves special attention. While it may be intuitive to remove x‐rays that are absorbed in the object, it may be somewhat counterintuitive to also remove those x‐rays that scatter since we, after all, seek to compute the scatter image. However, these x‐rays have already been accounted for in the source iteration process and must not be double counted.

The detected scatter signal $S({\overrightarrow{r}}_D)$ is then the integral of the fluence ${\varphi }_{\mathrm{\Omega }E}^D$ over all energies and angles, weighted by the grid and detector responses:

$$\begin{array}{cc}\hfill S({\overrightarrow{r}}_D)=& {\int }_0^{E_0}dE{\int }_{4\pi }d\mathrm{\Omega }{\varphi }_{\mathrm{\Omega }E}^D({\overrightarrow{r}}_D,E,\widehat{\mathrm{\Omega }})G({\overrightarrow{r}}_D,E,\widehat{\mathrm{\Omega }})\hfill \\ & D({\overrightarrow{r}}_D,E,\widehat{\mathrm{\Omega }}),\hfill \end{array}$$ (12)

where G is the generalized grid response (e.g., transmission fraction) and D is the generalized detector response (e.g., energy deposited). By integrating ${\varphi }_{\mathrm{\Omega }E}^D$ over all angles, we ensure that the contributions from the entire object volume is collected.

2.A.4. Primary image

The primary image P is a weighted response to the uncollided photons that travel from the source through the object to the detector. As in Step 1 above, we analytically trace rays, this time from the beam origin to the detector while removing those photons that interact with the object. The analytic LBTE solution for this ray trace is the familiar Beer's and inverse‐square laws, combined with the grid and detector responses:

$$\begin{array}{cc}\hfill P({\overrightarrow{r}}_D)=& {\int }_0^{E_0}dE\frac{S^{(0)}(E,{\widehat{\mathrm{\Omega }}}^P)}{\Vert {\overrightarrow{r}}_D-{\overrightarrow{r}}_0{\Vert }^2}\text{exp}\left[-{\int }_0^{\Vert {\overrightarrow{r}}_D-{\overrightarrow{r}}_0\Vert }dl{\mu }_t({\overrightarrow{r}}_0+\right.\hfill \\ & \left.l{\widehat{\mathrm{\Omega }}}^P,E)\right]G({\overrightarrow{r}}_D,E,{\widehat{\mathrm{\Omega }}}^P)D({\overrightarrow{r}}_D,E,{\widehat{\mathrm{\Omega }}}^P),\hfill \end{array}$$ (13)

where ${\widehat{\mathrm{\Omega }}}^P=({\overrightarrow{r}}_D-{\overrightarrow{r}}_0)/\Vert {\overrightarrow{r}}_D-{\overrightarrow{r}}_0\Vert$ is the direction of a primary ray from the point source position ${\overrightarrow{r}}_0$ to detector position ${\overrightarrow{r}}_D$.

2.B. Discrete domains $({\overrightarrow{\mathit{r}}}_{\mathit{i}},{\mathit{E}}_{\mathit{g}},{\widehat{\mathbf{\Omega }}}_m)$

The expressions in Section 2.A describe the LBTE in continuous space, energy, and directional domains. In practice, we discretize the transport problem to make it computationally tractable. These numerical methods are designed to be very close approximations to the continuous problem while providing for clinically acceptable run times utilizing readily available computer architectures. Furthermore, these discretizations offer the advantage of being convergent. That is, as the computational mesh becomes finer, the discretized solution approaches the continuous solution.

At the core of the calculation is a spatial grid that describes the object's material properties, providing a framework for evaluating the angular fluence distribution. The Acuros voxels were chosen to be rectangular cuboid shaped. The Acuros computational mesh is therefore uniform (all voxels have equal size) and orthogonal (built on voxels). Moreover, each step in the Acuros calculations uses the same computational grid, simplifying the coupling of the three steps. Given the computational mesh, we reserve the index i to indicate voxel i.

The next domain is energy, where the spectrum is organized into a set of energy bins or groups indexed by g:

$${\varphi }_{\mathrm{\Omega },i,g}(\widehat{\mathrm{\Omega }})\approx {\int }_{E_{g+1/2}}^{E_{g-1/2}}dE{\varphi }_{\mathrm{\Omega }E,i}(E,\widehat{\mathrm{\Omega }}),$$ (14)

Traditionally, energy groups are organized from the most energetic to the least (i.e., group 1 is the highest energy group and group G the least energetic one), where each group is bound by energies E _g  ∈ [E _g + 1/2, E _g − 1/2]. The energy group structure is used throughout the LBTE for discretizing the x‐ray source spectrum, total attenuation, and scatter coefficients. In our work, we used six energy groups separated by predetermined energy thresholds. While this was felt to be sufficient, the number of groups and their thresholds could be further explored in future work.

2.B.1. Source‐to‐object ray trace

In this step, we describe the uncollided fluence inside voxel i for group g. Then, we define the first‐collided source belonging to this group and voxel. The discretized uncollided fluence closely resembles its continuous counterpart:

$${\varphi }_{\mathrm{\Omega },i,g}^{\mathit{UC}}({\widehat{\mathrm{\Omega }}}^{\mathit{UC}})=\frac{S_g^{(0)}({\overrightarrow{r}}_0,{\widehat{\mathrm{\Omega }}}^{\mathit{UC}})}{\Vert {\overrightarrow{r}}_i-{\overrightarrow{r}}_0{\Vert }^2}exp\left[-\sum _{i^{\prime }}{\mu }_{t;i^{\prime },g}·l_{i^{\prime }}\right].$$ (15)

Here, the source spectrum has now been collapsed into G energy groups. The total interaction coefficient has also been collapsed into its group equivalent form μ _t;g in a way that conserves the group's attenuation.⁴³ Finally, we apply Siddon's algorithm to ray trace through the object.⁶² The attenuation of each intersected voxel is weighted by the path length $(l_{i^{\prime }})$ of the ray inside that voxel. With this description, Acuros accumulates the ray's line integral of the attenuation coefficient through the object and exponentially attenuates the uncollided rays.

Given the uncollided fluence, the first‐collided distributed source inside voxel i for energy group g is:

$$S_{i,g}^{\mathit{FC}}(\widehat{\mathrm{\Omega }})=\sum _{g^{\prime }=1}^g{\mu }_{s;i,g^{\prime }\to g}({\widehat{\mathrm{\Omega }}}^{\mathit{UC}}\to \widehat{\mathrm{\Omega }}){\varphi }_{\mathrm{\Omega },i,g^{\prime }}^{\mathit{UC}}({\widehat{\mathrm{\Omega }}}^{\mathit{UC}}).$$ (16)

Here, $S_{i,g}^{\mathit{FC}}$ is the first‐collided scatter source, ${\mu }_{s;i,g^{\prime }\to g}$ is the group‐collapsed linear scatter coefficient from group g′ into group g inside voxel i, and ${\varphi }_{\mathrm{\Omega },i,g^{\prime }}^{\mathit{UC}}$ is the uncollided angular fluence. Note that the downscatter energy integral has been replaced by a summation of down‐scattering groups.

2.B.2. Scattering source calculation

We now define how to compute the multiple‐collision source, step 2 in the Acuros algorithm. The multiple‐collision source, Eq. (9), integrates the contribution from a continuum (in angle) of angular fluences. Evaluating this integral is challenging. We must evaluate the entire angular fluence continuum or somehow approximate the angular integral. We avoided this challenge in the previous step since the uncollided fluence is defined only in one direction: from the beam's focal point to the coordinate $\overrightarrow{r}$ of interest.

To evaluate the multiple‐collision source integral, we implemented the Discrete Ordinates (DO) method to discretize the streaming direction $\widehat{\mathrm{\Omega }}$ into a set of M angles ${\widehat{\mathrm{\Omega }}}_m$ that span 4π.^{43, 63} The multiple‐collision integral for the nth Source Iteration becomes:

$$S_{i,g}^{(n)}({\widehat{\mathrm{\Omega }}}_m)=\sum _{g^{\prime }=1}^g\sum _{m^{\prime }=1}^M{w}_{m^{\prime }}{\mu }_{s;i,g^{\prime }\to g}({\widehat{\mathrm{\Omega }}}_{m^{\prime }}\to {\widehat{\mathrm{\Omega }}}_m){\varphi }_{\mathrm{\Omega },i,g^{\prime },m^{\prime }}^{(n-1)}.$$ (17)

Here, ${\varphi }_{\mathrm{\Omega },i,g,m}^{(n-1)}$ is the collided angular fluence along direction ${\widehat{\mathrm{\Omega }}}_m$. The multiple‐collision source angular integral is now approximated by a quadrature integral, where each direction ${\widehat{\mathrm{\Omega }}}_m$ is assigned a quadrature weight w _m for its evaluation. In addition, ${\mu }_{s;i,g^{\prime }\to g}$ is the scattering coefficient from energy group g′ to group g and from direction ${\widehat{\mathrm{\Omega }}}_{m^{\prime }}$ into direction ${\widehat{\mathrm{\Omega }}}_m$. Consequently, we collapsed the multiple‐collision source integral into a summation of energy groups and directions.

The DO approach avoids the need to map the scatter contribution from each point in the object to all its neighbors — a O(I ²) algorithm for a problem with I voxels. By solving the angular fluence only along M directions for each voxel, we reduce this effort to an O(MI) algorithm (with M ≪ I). The set of streaming directions ${\widehat{\mathrm{\Omega }}}_m$ and their corresponding weights w _m are preselected to maximize the accuracy of the angular integral. Problems with low anisotropy such as the MC source require a small M to capture this integral accurately. Problems with high anisotropy such as the FC source would require a large M if using DO, but we avoid this by evaluating the FC source analytically.

The scatter coefficients ${\mu }_{s;i,g^{\prime }\to g}$ can be simplified by condensing the discrete directions ${\widehat{\mathrm{\Omega }}}_{m^{\prime }}\to {\widehat{\mathrm{\Omega }}}_m$ into a single variable ${\eta }_{m^{\prime },m}={\widehat{\mathrm{\Omega }}}_{m^{\prime }}·{\mathrm{\Omega }}_m,$ the inner product of the two vectors. This simplification stems from the physics of scattering interactions; the probability of a scattering event depends on the outgoing direction ${\widehat{\mathrm{\Omega }}}_m$ relative to the incoming one, ${\widehat{\mathrm{\Omega }}}_{m^{\prime }}$. We exploit this simplification to represent scattering coefficient sections with a Legendre series P ^l :

$$\begin{array}{cc}\hfill {\mu }_{s;i,g^{\prime }\to g}({\widehat{\mathrm{\Omega }}}_{m^{\prime }}\to {\widehat{\mathrm{\Omega }}}_m)=& \frac{{\mu }_{s;i,g^{\prime }\to g}({\eta }_{m^{\prime },m})}{2\pi }\hfill \\ & \approx \sum _{l=0}^L\frac{2l+1}{4\pi }{\mu }_{s;i,g^{\prime }\to g}^l{P}^l({\eta }_{m^{\prime },m}).\hfill \end{array}$$ (18)

Here ${\mu }_{s;i,g^{\prime }\to g}^l$ is the l‐th Legendre moment of the linear scattering coefficient (computed a priori), with the series being truncated after L terms.

To continue reducing the cost of evaluating the multiple‐collision source, we expand the angular fluence distribution for each voxel and energy group into its own Spherical Harmonics series:

$${\varphi }_{\mathrm{\Omega },i,g,m}\approx \sum _{l=0}^L\sum _{k=-l}^l{\zeta }_{i,g}^{l,k}{Y}^{l,k}({\widehat{\mathrm{\Omega }}}_m),$$ (19)

where Y ^l,k are Spherical Harmonics functions of degree l and order k, and ${\zeta }_{i,g}^{l,k}$ are known as the spherical harmonics fluence moments. Due to the orthogonality of the Spherical Harmonic functions, the moments can be determined from the angular fluence using quadrature weighting:

$${\zeta }_{i,g}^{l,k}={\int }_{4\pi }d\mathrm{\Omega }{Y}^{l,k*}(\widehat{\mathrm{\Omega }}){\varphi }_{\mathrm{\Omega },i,g}(\widehat{\mathrm{\Omega }})\approx \sum _{m=1}^M{w}_m{Y}^{l,k*}({\widehat{\mathrm{\Omega }}}_m){\varphi }_{\mathrm{\Omega },i,g,m},$$ (20)

where * is the complex conjugate.

To calculate the scattering source from the angular fluence, we insert the Legendre expansion of the scattering coefficient, Eq. (19), and the Spherical Harmonics expansion of the fluence, Eq. (20), into the scatter source, Eq. (18). The result is:

$$S_{i,g}^{(n)}(\widehat{\mathrm{\Omega }})=\sum _{g^{\prime }=1}^g\sum _{l=0}^L{\mu }_{s;i,g^{\prime }\to g}^l\sum _{k=-l}^l{\zeta }_{i,g^{\prime }}^{(n-1);l,k}{Y}^{l,k}(\widehat{\mathrm{\Omega }}),$$ (21)

which, like the angular fluence, is also represented by spherical harmonic functions. The derivation can be found in the Appendix A and reference.⁴³

Next, we apply the Linear Discontinuous (LD) finite element method^{64, 65} to discretize the LBTE in space. We seek a method to evaluate the angular fluence inside voxel i, energy group g, and streaming direction m. The LD method approximates the spatial in the angular fluence within a voxel with a set of first‐order polynomials and provides a framework to evaluate its unknowns:

$${\varphi }_{\mathrm{\Omega },i,g,m}(\overrightarrow{r})\approx {\varphi }_{\mathrm{\Omega },i,g,m}^0+{\varphi }_{\mathrm{\Omega },i,g,m}^x·P^1(x_i)+{\varphi }_{\mathrm{\Omega },i,g,m}^y·P^1(y_i)+{\varphi }_{\mathrm{\Omega },i,g,m}^z·P^1(z_i).$$ (22)

Here, P ¹ is a linear Legendre polynomial, x _i , y _i , and z _i are spatial coordinates of point $\overrightarrow{r}$ in a coordinate system local to voxel i, and ${\varphi }_{\mathrm{\Omega },i}^0,{\varphi }_{\mathrm{\Omega },i}^x,{\varphi }_{\mathrm{\Omega },i}^y$ and ${\varphi }_{\mathrm{\Omega },i}^z$ are the LD unknowns also for voxel i. Note that, these amplitudes are only defined within this voxel, and it is the union of the ϕ _Ωi across all voxels that define the complete LD solution to the LBTE.

To compute the LD angular fluence amplitudes, we project the LBTE into the LD solution space {1, P ¹(·)}, the details of which are in the Appendix B. As a result, this spatial discretization produces a system of four equations (one for each weighted moment of the LBTE) and four unknowns (the angular fluence amplitudes) for each voxel, energy group, and streaming direction.

An important aspect to stress is that the LD method implicitly communicates to each voxel its boundary conditions. This choice is important, as it implies that the LD method does not require the angular fluence be continuous across the faces of a voxel. Although discontinuities across voxel faces are nonphysical, the LD method is said to superconverge since volume integrals of its solution exhibit quadratic convergence (or a cubic error) of a solution built on linear polynomials. Armed with a superconvergent method, Acuros can compute sharp variations in the angular fluence accurately and with relatively few (and large) voxels. We refer to the LD literature for further review on its mechanics and properties.^{64, 65}

In step 2 of the Acuros algorithm, the multiple‐collision source is computed. We presented three methods to discretize the LBTE in space (Linear Discontinuous), energy (Multigroup), and angle (Discrete Ordinates). The product of these discretizations is 4 × I × G × M angular fluence unknowns and the matching number of moments of the LBTE. We solve these amplitudes iteratively by assembling the latest scattering source, transporting (along M discrete directions) the x‐rays it emits across the object (I voxels), and updating the angular fluence (four unknowns per voxel). This Source Iteration process is performed until the angular fluence converges for all G energy groups. We then collect the moments of the collided angular fluence:

$${\zeta }_{i,g}^{C;l,k}=\sum _{m=1}^M{w}_m{Y}^{l,k*}({\widehat{\mathrm{\Omega }}}_m)\sum _{n=1}^N{\varphi }_{\mathrm{\Omega },i,g,m}^{(n)}(\overrightarrow{r}),$$ (23)

and compute the multiple‐collision source in the direction $\widehat{\mathrm{\Omega }}$:

$$S_{i,g}^{\mathit{MC}}(\overrightarrow{r},\widehat{\mathrm{\Omega }})=\sum _{g^{\prime }=1}^g\sum _{l=0}^L{\mu }_{s;i,g^{\prime }\to g}^l\sum _{k=-l}^l{\zeta }_{i,g^{\prime }}^{C;l,k}(\overrightarrow{r})Y^{l,k}(\widehat{\mathrm{\Omega }}).$$ (24)

2.B.3. Scattering source to detector

In step 3 of Acuros, we evaluate the FC and MC sources in the direction of the detector panel, transport the combined x‐ray emissions in the panel's direction, and accumulate the energy deposited in the detector. The scatter signal is the accumulation of these emissions from scatter sources in all voxels. To organize this calculation, the angular fluence arriving to our detector from a position inside voxel i is defined:

$${\varphi }_{\mathrm{\Omega },i,g}^D(\overrightarrow{r},{\overrightarrow{r}}_d)=\left[S_g^{\mathit{FC}}+S_g^{\mathit{MC}}\right](\overrightarrow{r},{\widehat{\mathrm{\Omega }}}_d)\frac{exp\left[-{\sum }_{i^{\prime }}{\mu }_{t;i^{\prime },g}·l_{i^{\prime }}\right]}{\Vert {\overrightarrow{r}}_d-\overrightarrow{r}{\Vert }^2}.$$ (25)

Here, ${\varphi }_{\mathrm{\Omega },i,g}^D$ is the angular fluence of group g arriving at point ${\overrightarrow{r}}_d$ in the detector pixel. ${\widehat{\mathrm{\Omega }}}_d$ is the streaming direction pointing from $\overrightarrow{r}$ to ${\overrightarrow{r}}_d$, and $\overrightarrow{r}$ is a point inside voxel i. Similar to step 1 in our algorithm, a ray trace is performed to determine the ray's line integral of the attenuation coefficient and attenuate the ray accordingly. We again use Siddon's algorithm to determine which voxels (i′) each ray intersects and the length of each voxel intersection $(l_{i^{\prime }})$.

The contribution of ${\varphi }_{\mathrm{\Omega },i,g}^D$ to the scatter signal is:

$$S_{i,g}(\overrightarrow{r},{\overrightarrow{r}}_d)={\varphi }_{\mathrm{\Omega },i,g}^D(\overrightarrow{r},{\overrightarrow{r}}_d)·G_g({\widehat{\mathrm{\Omega }}}_d)·D_g({\widehat{\mathrm{\Omega }}}_d),$$ (26)

where $S_{i,g}(\overrightarrow{r},{\overrightarrow{r}}_d)$ is the contribution to the scatter signal from point $\overrightarrow{r}$ in voxel i to point ${\overrightarrow{r}}_d$ in the panel. The grid and detector responses have been simplified, as described below in Section 2.C. To numerically integrate the total contribution from voxel i to this point in the detector, we subsample each voxel by applying a spatial quadrature, where ${\overrightarrow{r}}_{i,j}$ are quadrature points (j) inside voxel i, and w _j are quadrature weights. To determine the total scatter signal in a pixel (u), we also subsample each pixel with a spatial quadrature and sum over all voxels and energy groups:

$$\begin{array}{cc}\hfill S_u=& \sum _d{w}_d·\sum _{g=1}^G\sum _{i=1}^I\sum _j{w}_j·{\varphi }_{\mathrm{\Omega },i,g}^D({\overrightarrow{r}}_{i,j},{\overrightarrow{r}}_d)·G_g({\widehat{\mathrm{\Omega }}}_{i,j\to d})·\hfill \\ & D_g({\widehat{\mathrm{\Omega }}}_{i,j\to d}),\hfill \end{array}$$ (27)

where w _d and ${\overrightarrow{r}}_d$ are the quadrature weights and points, respectively, that numerically integrate the area of the pixel.

2.B.4. Computation of primary

The computation of the primary signal in a pixel (P _u ) closely mimics its analytic counterpart. We apply pixel subsampling, our group structure, and simplified anti‐scatter grid and detector models:

$$\begin{array}{cc}\hfill P_u=& \sum _d{w}_d·\sum _{g=1}^G{S}_g^{(0)}({\widehat{\mathrm{\Omega }}}_p)\frac{exp\left[-{\sum }_{i^{\prime }}{\mu }_{t;i^{\prime },g}·l_{i^{\prime }}\right]}{\Vert {\overrightarrow{r}}_d-{\overrightarrow{r}}_0{\Vert }^2}\hfill \\ & G_g({\widehat{\mathrm{\Omega }}}_p)·D_g({\widehat{\mathrm{\Omega }}}_p).\hfill \end{array}$$ (28)

Here, $S_g^{(0)}({\widehat{\mathrm{\Omega }}}_p)$ is beam strength of group g along the primary direction ${\widehat{\mathrm{\Omega }}}_p$. Each primary ray is traced from the beam's focal point to ${\overrightarrow{r}}_d$ in the panel. The ray's line integral of the attenuation coefficient is evaluated with Siddon's algorithm, as exemplified in step 1 and 3 of the scatter signal calculation. Finally, pixel subsampling is used to find the total primary signal in pixel u, where w _d and ${\overrightarrow{r}}_d$ form the spatial quadrature that integrates the area of pixel u.

2.C. Generating the grid and detector responses

The generalized grid and detector responses can be difficult to model if they are dependent on all three variables (location, energy, and angle). Fortunately, the response functions can be simplified by making reasonable assumptions. For example, our models include a 1D anti‐scatter grid that is assumed to be spatially invariant and is dependent on two angles (θ ₁, θ ₂), where θ ₁ is with respect to the focusing direction in the v‐source plane and θ ₂ is with respect to the normal direction in the u‐source plane (Fig. 3). The grid response is then simplified to:

$$G_g(\widehat{\mathrm{\Omega }})=G_g({\theta }_1,{\theta }_2).$$ (29)

Figure 3.

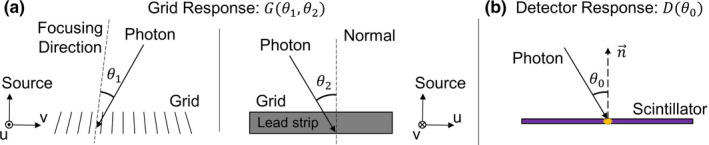
(a) Simplified grid response for focused 1D grid and (b) simplified detector response. [Color figure can be viewed at wileyonlinelibrary.com]

Therefore, a 2D lookup table (LUT) in (θ ₁, θ ₂) for each energy group g is sufficient to characterize G. The response was precomputed using a Geant4 (v9.6)⁶⁶ simulation of transmission fractions through the grid. TrueBeam's 10:1 grid was modeled as a series of lead strips focused at the source, using the manufacturer's specifications: 60 line pairs/cm, 36 μm lamellae thickness, 1.5 mm lamellae height, and 150 cm focal distance (Smit Roentgen, Philips, Best, Netherlands). A line beam of length 1/60 cm in the v‐direction was directed at the modeled grid at various angles (θ ₁, θ ₂) to determine the average transmission of each energy group, which was then stored as a LUT in Acuros.

The detector response was simplified further by assuming it is spatially invariant, but dependent on the angle between the incident direction and the normal vector of the detector plane, accounting for the effectively thicker scintillator encountered by nonperpendicular rays:

$$D_g(\widehat{\mathrm{\Omega }})=D_g({\theta }_0).$$ (30)

Accordingly, D can be represented as a 1D LUT in θ ₀ for each energy group g. The detector response was modeled using a Geant4 simulation of energy deposited in the Cesium Iodide (CsI) scintillator (600 μm thick, ρ = 4.51 g/cm³) in TrueBeam's flat‐panel imager. For each energy group, a pencil beam was directed at the scintillator at varying angles θ ₀ to determine D _g . It was then assumed the detected signal (analog–digital units, ADU) is proportional to the energy deposited.

2.D. Monte Carlo validation

Validation was performed by comparing Geant4 Monte Carlo results with Acuros results for projections of two digital phantoms. A simple geometric phantom composed of water, lung, air, and bone materials (WLAB) was used to test various components (fluence, energy deposited in detector, grid model) of the Acuros calculation. The WLAB phantom [Fig. 4(a)] is composed of a right rectangular prism of water (20 × 30 × 40 cm³, ρ = 1.0 g/cm³), with lung (6 × 6 × 40 cm³, ρ = 0.26 g/cm³), air (2 × 2 × 40 cm³, ρ = 1.205 × 10⁻³ g/cm³), and bone (2 × 2 × 40 cm³, ρ = 1.85 g/cm³) inserts. The phantom extends ±20 cm in/out of the page, while the detector extends ±15 cm in/out of the page. The phantom was defined using geometrical primitives in Geant4, while Acuros modeled the phantom using isotropic 1 cm voxels. The geometry of the imaging system is illustrated in Fig. 4(a) and was similar to that of TrueBeam in full‐fan position — 100 cm source–axis distance, 150 cm source–detector distance, and a centered 40 × 30 cm² detector. The isotropic x‐ray point source was collimated to the detector. For the Geant4 simulations, photon energies were sampled from a 125 kVp Bremsstrahlung spectrum while Acuros binned the same spectrum into six energy groups. The spectrum was validated to match the half‐value layer attenuation properties of the TrueBeam system (no bowtie filter) including its standard 0.89 mm Ti filter. The 10:1 grid and 600 μm CsI scintillators described above were physically modeled in the Geant4 simulations, while their precomputed response functions were used in Acuros. Both Acuros and Geant4 discretized the detector into 100 × 75 pixels of size 4 × 4 mm². The primary and scatter images were recorded for fluence (photons/mm²) at the detector (without grid) as well as energy deposited in the detector (without, with grid). The Geant4 Livermore physics model was used with a range cutoff 0.1 mm (with similar results obtained from Geant4 Penelope physics, not shown).^{67, 68} The Geant4 spectrum, material definitions, and results have been included as supplemental material with the manuscript.

Figure 4.

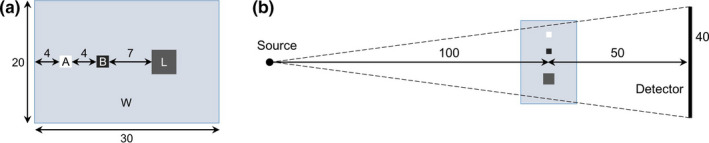
(a) Digital WLAB phantom showing dimensions of water (W) and lung (L), air (A), and bone (B) inserts. (b) Imaging geometry, as viewed from above. All dimensions are in centimeters. The phantom extends ±20 cm in/out of the page, while the detector extends ±15 cm in/out of the page. [Color figure can be viewed at wileyonlinelibrary.com]

A second digital phantom with more realistic anatomy and density variations was also tested. A pelvis CT volume was converted from CT numbers into water and bone of variable density (Fig. 5). The patient volume was placed on top of a digital model of Varian's standard IGRT patient couch, as the patient couch is known to be a substantial source of scatter in certain views.²⁶ Details of the CT number conversion into material density process and of the patient couch model are presented in Part II. The patient was fairly large, with ~40 cm lateral width. The Geant4 simulation utilized the high‐spatial resolution of the CT volume with isotropic 1.25 mm voxels. The volume was downsampled for Acuros by a factor of 10 × in each direction, enabling each of Acuros’ isotropic 12.5 mm voxels to represent 10 × 10 × 10 of the original voxels by taking the average water and bone densities of each subvolume. As downsampling was performed by an integer factor, the downsampled grid boundaries were aligned with the original grid boundaries. The simulated imaging system was identical to that of the WLAB phantom, with the exception of the beam being collimated to the detector in half‐fan position (lateral shift of 16 cm) and the addition of an analytic model of TrueBeam's half‐fan bowtie filter.

Figure 5.

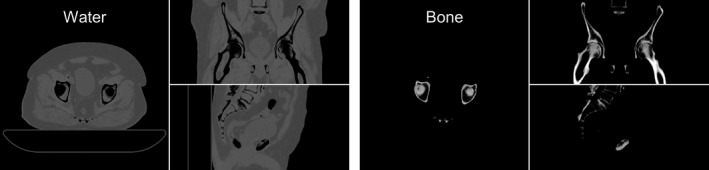
Multiplanar reformat of a digital pelvis phantom on an IGRT table, showing water and bone densities. Display window [0, 2] g/cm³.

Geant4 simulations were conducted with an in‐house distributed network of computers (HTCondor, University of Wisconsin, Madison, WI) without any acceleration or variance reduction. Acuros was run on a standard workstation, with the core algorithms written in the CUDA programming language (CUDA 8.0, Nvidia, Santa Clara, CA) and run on a GPU (GeForce GTX 1080, Nvidia, Santa Clara, CA).

3. Results

3.A. Digital WLAB phantom

WLAB results are shown in Fig. 6 comparing primary and scatter images of fluence at the detector (without grid) that were generated by Acuros and Geant4. The primary images show variable attenuation due to the air, bone, and lung inserts. The scatter images are smooth, and the effect of the inserts is not immediately apparent. Horizontal line profiles across the center of the image show excellent agreement between Geant4 and Acuros for both primary and scatter fluence, with an average relative difference of −0.2% and −0.7%, respectively. As the results are normalized to one photon/steradian at the source, the fluence at the detector is on the order of 10⁻⁸ photons/mm².

Figure 6.

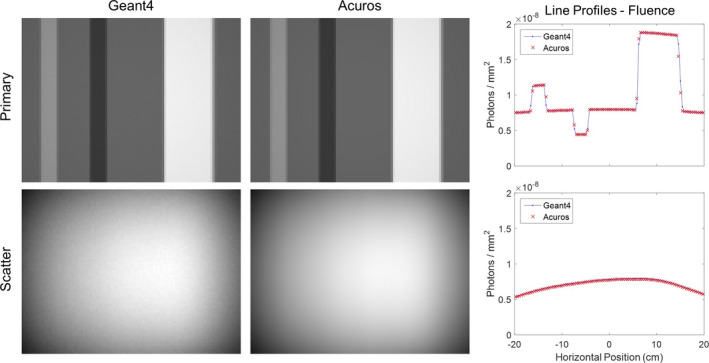
WLAB phantom primary and scatter images of fluence at the detector, comparing Geant4 and Acuros. Primary images shown on [0, 2 × 10⁻⁸] photons/mm², scatter images shown on [4 × 10⁻⁹, 8 × 10⁻⁹] photons/mm² window. Horizontal line profiles are taken across the central row. [Color figure can be viewed at wileyonlinelibrary.com]

The scatter fraction (SF) is a useful metric for quantifying the joint accuracy of primary and scatter images and is defined as the scatter signal divided by the total (primary plus scatter) signal:

$$SF=S/(P+S).$$ (31)

The SF for energy deposited in the detector without and with the grid is shown in Fig. 7, again demonstrating the excellent agreement between Geant4 and Acuros. The average relative SF difference was −0.1% without the grid and 0.6% with the grid, respectively. The results with the detector but without a grid support the simplified detector response model, and the results with the addition of a grid support the simplified grid response model.

Figure 7.

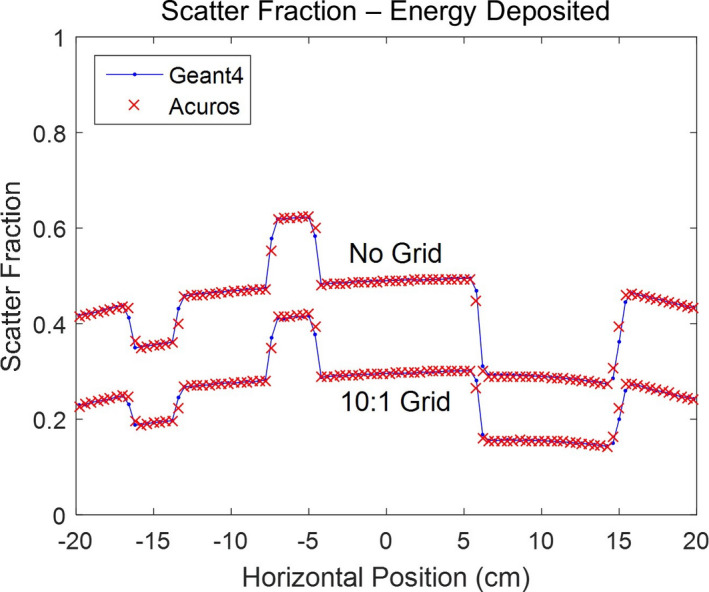
Scatter fraction line profiles for WLAB phantom, using energy deposited in the CsI scintillator, for cases without and with a 10:1 grid. [Color figure can be viewed at wileyonlinelibrary.com]

For these experiments, Acuros had a major computation time advantage. The WLAB scatter image with 7,500 detector pixels was computed in only 1.1 s using a single GPU for an object comprising 24,000 voxels. For the Geant4 simulation, 4 × 10¹⁰ source photons were launched, with the computation taking ~1,200 CPU‐h on our distributed computing system. Note, some noise (0.4% relative to the mean) is still visible in the Geant4 scatter image, while the Acuros result is free of stochastic errors.

3.B. Digital pelvis phantom

Results from the digital pelvis phantom simulation are shown in Fig. 8. Two (half‐fan) projection angles (0° and 270°) were compared. Primary and scatter images of energy deposited in the detector for the 0° anterior–posterior (AP) projection show good visual agreement. Although the same 4 × 10¹⁰ source photons were used in Geant4, noise in the scatter image is much more apparent than with the WLAB phantom due to the higher attenuation of the pelvis. Horizontal line profiles of SF across the central row show the strong agreement between Geant4 and Acuros. The 270° lateral projection experiences a higher SF behind the object due to greater attenuation and scatter coming from the patient couch. Despite the presence of the bowtie filter and anti‐scatter grid, the SF goes as high as 0.85 [or equivalently, a scatter‐to‐primary ratio (SPR) of 5.5]. Nevertheless, the average relative difference in SF between Acuros and Geant4 is only 0.1%.

Figure 8.

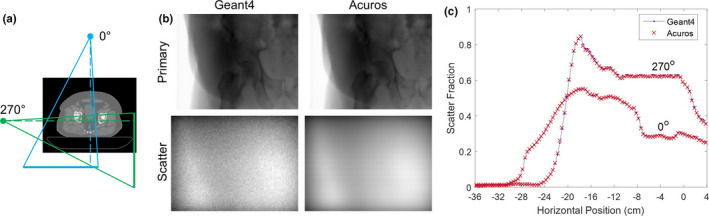
(a) Orientation of 0° (AP) and 270° (lateral) projections relative to patient. Geometry not to scale. (b) Primary and scatter images of energy deposited in the detector for Geant4 and Acuros for the 0° projection. Primary images are shown on the same log scale, while the scatter images are shown on the same linear scale. (c) Horizontal line profiles of scatter fraction across central row. [Color figure can be viewed at wileyonlinelibrary.com]

4. Discussion

Our results show excellent agreement between Monte Carlo‐ and Acuros‐generated scatter estimates, first for a simple geometric object and then for a more realistic example of a spatially varying x‐ray beam projecting through a heterogeneous object. The CBCT system that was modeled consisted of a polychromatic kV x‐ray source, bowtie filter, and an energy‐integrating indirect detector with an anti‐scatter grid. Despite discretizing the problem using coarse voxels, limited energy groups, and a finite number of streaming directions, Acuros’ accuracy was equivalent to that provided by the Monte Carlo methods, which used finer voxels (or geometrical primitives), a continuous energy spectrum, and continuous directions. The ability to achieve such a good correspondence is not only due in part to the low‐frequency nature of the projected scatter image but also due to carefully constructed discretization methods.

We measured Acuros run times of ~1 s/projection for fairly representative problems using a single GPU. Conversely, the (CPU) Monte Carlo implementations were not optimized for speed. Rather, they were intended to produce a high‐quality solution with minimal noise as required to benchmark Acuros’ accuracy. Consequently, a direct comparison between Geant4 and Acuros run times is difficult due to the lack of implementing run‐time optimization techniques for Monte Carlo, including variance reduction methods and GPU implementation. As such, the purpose of this study was not to determine which method is inherently faster for this application, but rather to determine if Acuros’ accuracies and run times are well suited for our clinical applications. This was found to be the case as reported in Part II, where we explore the trade‐offs between scatter estimation accuracy and run times.

Although many of the underlying algorithms are shared between Acuros CTS and Acuros XB, key differences exist. First, Acuros CTS was designed and optimized for estimating primary and scatter images, whereas Acuros XB (external beam) and BV (brachytherapy) were designed to compute dose delivered to a patient. Acuros CTS incorporates the last‐collided technique and anti‐scatter grid and detector models to form the scatter image from scattering sources that lie within the object. This computationally expensive step requires ray tracing from every object voxel to every detector pixel but can be performed efficiently on a GPU. Additionally, Acuros CTS does not model electron transport (which is negligible at kV energies), does not utilize adaptive mesh refinement (a uniform spatial grid is sufficient for estimating scatter), and does not require secondary source modeling (a point source is sufficient).

Acuros was designed to provide a flexible framework for estimating scatter and primary images at diagnostic energies. To match actual imaging conditions, the user can specify the x‐ray beam's spectrum and distribution, system geometry, object's material and density distribution, grid response, and detector size and response. Although designed with cone‐beam CT in mind, Acuros may be able to extend to other medical imaging modalities such as radiography, PET, or SPECT or other applications such as security or industrial imaging. We have also begun investigation of Acuros CTS for calculating radiation dose delivered by a kV imaging system, similar to how the original Acuros XB code calculates MV treatment dose. This is a natural fit for Acuros CTS since the calculation required (angular fluence within the object) is already performed in the second step. Hence, essentially, we stop before ray tracing the fluence from the volume to the detector. Once the angular fluence distribution is calculated, we can convert to dose delivered by using the mass density and mass energy‐absorption coefficient of each voxel, which is simply a property of its materials. While the full details of our preliminary dose study are beyond the scope of this paper, the Acuros CTS results showed excellent agreement with Geant4 simulations.⁶⁹ We anticipate being able to use Acuros CTS to compute dose from a cone‐beam CT scan or for diagnostic CT scans, where there is great interest in better dose reporting.^{70, 71}

5. Conclusion

We have described Acuros CTS, a new software tool for fast and accurate scatter estimation in kV imaging applications that can be used as an alternative to Monte Carlo methods. We have demonstrated that the LBTE can be deterministically solved using a combination of efficient discretization methods implemented on parallel‐computing platforms, with validation against Monte Carlo simulations. In Part II, we will discuss modeling a clinical CBCT system with Acuros CTS and using the output to remove the scatter signal from the projection data before reconstruction.

Conflict of Interest

All authors were employees of Varian Medical Systems.

Supporting information

Table S1. Source spectrum.

Table S2. Geant4 line profiles for WLAB phantom.

Table S3. WLAB phantom material definitions.

 

Appendix A.

Legendre polynomial and spherical harmonics expanions

Substituting the Legendre polynomial and Spherical Harmonic expansions, into Eq. (18), we find:

$$\begin{array}{cc}\hfill S_{i,g}({\widehat{\mathrm{\Omega }}}_m)=& \sum _{g^{\prime }=1}^g\sum _{m^{\prime }=1}^M{w}_{m^{\prime }}\left[\sum _{l=0}^L\frac{2l+1}{4\pi }{\mu }_{s;i,g^{\prime }\to g}^l{P}^l({\eta }_{m^{\prime },m})\right]\hfill \\ & \left[\sum _{l^{\prime }=0}^L\sum _{k^{\prime }=-l^{\prime }}^{l^{\prime }}{\zeta }_{i,g^{\prime }}^{l^{\prime },k^{\prime }}{Y}^{l^{\prime },k^{\prime }}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})\right].\hfill \end{array}$$ (A1)

Therefore, to evaluate the scattering source in direction ${\widehat{\mathrm{\Omega }}}_m$, we must evaluate two polynomial expansions. This is an expensive proposition. To combine and simplify this expansion, we refer to the Addition Theorem for Legendre Polynomials:

$$P^l({\widehat{\mathrm{\Omega }}}_m·{\widehat{\mathrm{\Omega }}}_{m^{\prime }})=\frac{4\pi }{2l+1}\sum _{k=-1}^l{Y}^{l,k}({\widehat{\mathrm{\Omega }}}_m)Y^{l,k*}({\widehat{\mathrm{\Omega }}}_{m^{\prime }}),$$ (A2)

Furthermore, we reorganize the scattering source terms to take advantage of the orthogonality of Spherical Harmonics functions:

$$\begin{array}{cc}\hfill S_{i,g}({\widehat{\mathrm{\Omega }}}_m)=& \sum _{g^{\prime }=1}^g\sum _{l=0}^L{\mu }_{s;i,g^{\prime }\to g}^l\sum _{k=-1}^l{Y}^{l,k}({\widehat{\mathrm{\Omega }}}_m)\sum _{l^{\prime }=0}^L\hfill \\ & \sum _{k^{\prime }=-l^{\prime }}^{l^{\prime }}{\zeta }_{i,g^{\prime }}^{l^{\prime },k^{\prime }}\sum _{m^{\prime }=1}^M{w}_{m^{\prime }}{Y}^{l,k*}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})Y^{l^{\prime },k^{\prime }}({\widehat{\mathrm{\Omega }}}_{m^{\prime }}),\hfill \end{array}$$ (A3)

where $Y^{l,k*}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})$ and $Y^{l^{\prime },k^{\prime }}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})$ are orthogonal functions:

$$\sum _{m^{\prime }=1}^M{w}_{m^{\prime }}{Y}^{l,k*}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})Y^{l^{\prime },k^{\prime }}({\widehat{\mathrm{\Omega }}}_{m^{\prime }})={\delta }_{k,k^{\prime }}{\delta }_{l,l^{\prime }}.$$ (A4)

Here, M is large enough, so that it exactly integrates spherical harmonic functions of degree l, l′, and order k, k′ thus reducing the scatter source expression to Eq. (22).

Appendix B.

Linear discontinuous solution space

To project the LBTE into the LD solution space, we integrate the LBTE over the volume of the voxel, weigh this integral by each function in the solution space, and replace the angular fluence by its LD definition. For example, the P ¹(x _i ) projection is:

$$\begin{array}{cc}& {\oint }_{\partial V_i}dS·(\widehat{N}·{\widehat{\mathrm{\Omega }}}_m)·P^1(x_i)·{\varphi }_{\mathrm{\Omega },i,g,m}^{(n)}(\overrightarrow{r})\hfill \\ & -{\int }_{V_i}dV·[\widehat{\mathrm{\Omega }}·\overrightarrow{\mathrm{\nabla }}{P}^1(x_i)]·{\varphi }_{\mathrm{\Omega },i,g,m}^{(n)}(\overrightarrow{r})\hfill \\ & ={\int }_{V_i}dV·S_{g,m}^{(n)}(\overrightarrow{r})·P^1(x_i)-{\mu }_{t;i,g}·{\varphi }_{\mathrm{\Omega },i,g,m}^{(n);x}{\int }_{V_i}dV·{[P^1(x_i)]}^2.\hfill \end{array}$$ (B1)

Here, we have integrated the LBTE of the nth source iterate of the collided fluence, ${\varphi }_{\mathrm{\Omega },i,g,m}^{(n)}$. The integral was weighted by the P ¹(x _i ) function and is defined over the volume of voxel i. We applied the Divergence Theorem to cast the integral of the first term into a surface integral form. This surface integral evaluates the angular fluence on the voxel surface and communicates to each the voxel boundary conditions from its upstream neighbors. $\widehat{\mathrm{N}}$ is a vector normal to the voxel's surfaces that points outward. The integral of the interaction term (second term on the right‐hand side) was simplified. Here, we exploited the orthogonality properties of Legendre polynomials to ignore those integrals that are equal to zero. Finally, the integral of the source term equals:

$$\begin{array}{cc}& {\int }_{V_i}dV·S_{g,m}^{(n)}(\overrightarrow{r})·P^1(x_i)\hfill \\ & =\left\{\begin{array}{c}\begin{array}{cc}\sum _{g^{\prime }=1}^g{\mu }_{s;i,g^{\prime }\to g}({\widehat{\mathrm{\Omega }}}^{\mathit{UC}}\to {\widehat{\mathrm{\Omega }}}_m)& \\ & n=0,\\ \sum _{j=1}^J{w}_j·{\varphi }_{\mathrm{\Omega },g^{\prime }}^{\mathit{UC}}({\overrightarrow{r}}_j,{\widehat{\mathrm{\Omega }}}^{\mathit{UC}})·P^1(x_{\mathit{ij}});& \\ \sum _{g^{\prime }=1}^g\sum _{l=0}^L{\mu }_{s;i,g^{\prime }\to g}^l\sum _{k=-l}^l{\zeta }_{i,g^{\prime }}(n-1);l,k,x·Y^{l,k}({\widehat{\mathrm{\Omega }}}_m)·& \\ & n>0\\ {\int }_{V_i}dV·{[P^1(x_i)]}^2;\end{array}\hfill \end{array}\right.\hfill \end{array}$$ (B2)

where we have integrated the P ¹(x _i ) moment of $S_{g,m}^{(n)}$, the source of the nth iteration of group g and streaming direction m. We have two formulations for this integrand. The first belongs to the initial step in the Source Iteration process (n = 0). Here, the driving source is the first‐collision source. We numerically evaluate this integral over the volume of the voxel using a quadrature set of J points $\overrightarrow{r_j}$ and weights w _j . The second integrand evaluates the P ¹ moments of the multiple‐collision source, where we use the properties of Legendre Polynomials to evaluate the volume integral.