Modeling and simulation of bone mineral density in Japanese osteoporosis patients treated with zoledronic acid using tartrate-resistant acid phosphatase 5b, a bone resorption marker

Abstract

Summary

Annual intravenous administration of zoledronic acid is used in the treatment of osteoporosis. A mathematical model was developed to predict bone mineral density up to 2 years after two annual doses of zoledronic acid from the early values of a bone resorption marker in osteoporosis patients.

Introduction

The measurement of bone mineral density (BMD) has been used as a surrogate marker instead of the observation of incident fractures to detect the efficacy of treatment. However, this method requires a long time to obtain significant changes. On the other hand, bone resorption markers respond to bone resorption inhibitors within a few weeks. Therefore, the aim of this study was to develop a mathematical model predicting long-term BMD after two annual doses of zoledronic acid (ZOL) using the early response of a bone resorption marker in osteoporosis patients.

Methods

The model was constructed using 3410 tartrate-resistant acid phosphatase 5b (TRACP-5b) serum concentrations and 1146 lumbar spine (L2-L4) BMD values from 306 patients with primary osteoporosis. A mathematical model was developed to describe the time-dependent profiles of TRACP-5b and BMD.

Results

The percentage changes from baseline of the BMD (%BMD) at up to 2 years were predicted from patients’ baseline BMD and baseline and 12-week TRACP-5b values by the model obtained. The simulated 90% prediction interval almost covered the observed %BMD distribution at each time point, and the predictions were comparable to the observed %BMD.

Conclusions

This is the first model to predict BMD for up to 2 years following two annual doses of ZOL using patients’ background characteristics and the early response of TRACP-5b. This model allows us to inform patients at the initial stage of ZOL treatment of their predicted response to treatment.

Electronic supplementary material

The online version of this article (10.1007/s00198-018-4376-1) contains supplementary material, which is available to authorized users.

Introduction

Osteoporosis, characterized by decreased bone strength [1], is a serious health problem in an aging society, because of its associated high fracture susceptibility. Bone mineral density (BMD) accounts for 70% of bone strength [1] and is thought to be the standard measure for the diagnosis of osteoporosis and the assessment of fracture risk [2]. BMD is used in the diagnostic criteria for osteoporosis defined by the World Health Organization (WHO); a BMD that lies − 2.5 standard deviations or less below the average value for young healthy adults (T-score < − 2.5 SD) is considered to indicate osteoporosis [3]. Furthermore, it is known that a T-score > − 2.5 is important for reducing the future fracture risk and would be the goal of osteoporosis treatment [4, 5]. Therefore, BMD measurement has been considered a good surrogate marker for the occurrence of new osteoporotic fractures. However, the detection of changes in BMD after treatment to the level of the least significant increase requires a long time [6]. On the other hand, changes in bone turnover markers are observed within a few weeks after the start of treatment with bisphosphonates, and the early changes in bone markers predict the long-term response of BMD [7–9]. Diez-Perez et al. proposed that the amino-terminal extension peptide of procollagen type 1 (PINP) and C-telopeptide of type I collagen (CTx) after 3 months of therapy could be used to screen for the treatment effect of oral bisphosphonate therapy [8].

Since a high susceptibility to bone fractures is caused by increased bone resorption, bone resorption inhibitors, especially bisphosphonates, have been used as first-line drugs for preventing osteoporotic fractures. Annual intravenous administration of zoledronic acid (ZOL), a third-generation nitrogen-containing bisphosphonate, has been approved in Japan for the treatment of osteoporosis. In a 2-year, randomized, placebo-controlled study of 665 Japanese patients with primary osteoporosis (ZONE study), the 2-year cumulative incidence of new morphometric vertebral fractures was 3.3% in the ZOL group versus 9.7% in the placebo group [10]. In addition, the ZONE study showed that ZOL increased lumbar spine BMD [10].

Over the past decade, many efforts have been made to develop mathematical models to describe the time-dependent lumbar spine BMD response to anti-osteoporosis agents [11–16]. Two mathematical models to predict the profiles of percentage change from baseline BMD (%BMD) after denosumab treatment have been developed. One is a bone homeostasis model that integrates denosumab pharmacokinetics with binding to receptor activator of nuclear factor–κB ligand and ibandronate inhibition of osteoclast precursor differentiation to active osteoclasts and, furthermore, incorporates the activity of bone resorption markers such as CTx and N-telopeptide of type I collagen (NTx) [14, 16]. Another model is a multiscale systems pharmacology model that incorporates calcium and bone homeostasis and osteoclastic activity (measured by CTx) and osteoblastic activity (measured by bone-specific alkaline phosphatase) [13, 15]. Other than denosumab, Hasegawa et al. constructed an exposure-response model to describe the BMD response to ONO-5334, a selective inhibitor of cathepsin K [12]. In addition, Nakai et al. developed a population pharmacodynamic model to relate urinary CTx to the BMD response after treatment with ibandronate, adequately predicting %BMD at 3 years after treatment [11]. These reports have shown the successful training of mathematical models to describe the BMD response at 1 to 4 years after drug treatment. However, these efforts did not focus on the use of bone turnover markers at the initial stage of drug treatment to predict individual BMD responses years later.

Taken together, the aim of the present study was to develop a mathematical model that would adequately predict BMD for up to 2 years following two annual doses of ZOL using the early values of a bone resorption marker.

Methods

This study was conducted in compliance with the World Medical Association Declaration of Helsinki–Ethical Principles for Medical Research Involving Human Subjects and Good Clinical Practice. The protocol was approved by the institutional review board at each study site. Written, informed consent was obtained from all subjects before enrollment in the study.

Clinical study data

All data used in this analysis were obtained from a previously reported study [10]. In summary, this was a multicenter, randomized, placebo-controlled, double-blind, parallel-group, comparative, 2-year study conducted in Japan. All patients with primary osteoporosis were randomly allocated to either ZOL 5 mg or the placebo group in a 1:1 ratio. Randomized patients were administered the study drug once yearly by intravenous infusion (over 15 min). Data from both groups were used in this analysis. Although 665 patients (333 for ZOL; 332 for placebo) were randomized in the study, data from 306 patients (145 for ZOL; 161 for placebo) who had values for at least one serum bone resorption marker value and BMD were analyzed in this study.

The following bone resorption markers were collected under overnight-fasted conditions and measured at baseline and at 1, 2, 4, and 12 weeks and 6, 12, 18, and 24 months after the first infusion and at 1, 2, and 4 weeks after the second infusion. Serum tartrate-resistant acid phosphatase 5b (TRACP-5b) was measured with an Osteolinks™ TRACP-5b kit (DS Pharma Biomedical Co., Ltd. Osaka, Japan), which was a fragment absorbed immunocapture enzymatic assay. This method employs two monoclonal antibodies (anti-active TRACP-5b antibody and anti-inactive TRACP-5b antibody) and enables highly specific measurement of TRACP-5b without cross-reaction with TRACP-5a derived from macrophages with interassay coefficients of variation of 1.8–7.5% (unpublished data). CTx was determined using an Elecsys® β-CrossLaps/serum assay (Roche Diagnostics K.K., Tokyo, Japan) with interassay coefficients of variation of 1.8–6.0% [10]. Urinary NTx (u-NTx) was measured using Osteomark® (Alere Medical Co., Ltd. Tokyo, Japan) with interassay coefficients of variation of 4.7–10.8% (unpublished data). All samples were measured by LSI Medience Corporation (Tokyo, Japan). Lumbar spine (L2-L4) BMD was measured using dual-energy X-ray absorptiometry (DXA) at baseline and at 6, 12, and 24 months, as previously described [10]. All study sites used the same DXA brand (Hologic Co., Bedford, MA).

Base model for bone resorption markers

Bone resorption maker models were developed using TRACP-5b, CTx, or u-NTx, respectively, as follows.

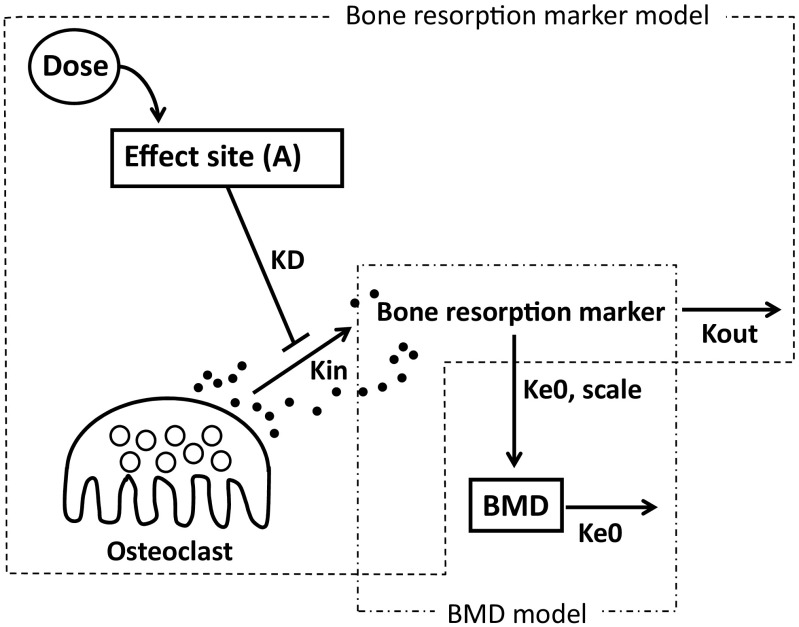
In the first step, the drug effects on the profiles of bone resorption markers were directly modeled with the same model as that used by Nakai et al. [11] (Fig. 1), because no drug concentration data were obtained in this study. In this mathematical model, ZOL dosage was linked to the hypothetical “Effect Site” drug amounts (A), which, in turn, affected bone resorption markers. It was postulated that the bone resorption markers were synthesized in a zero-order manner with a constant Kin and eliminated with the first-order rate constant Kout. The drugs in the “Effect Site” were assumed to inhibit the synthesis of bone resorption markers. The mathematical equations for the model are shown below.

Fig. 1.

Schematic description of the mathematical model of ZOL to describe the time-dependent profiles of bone resorption markers and BMD. Effect site hypothetical site where ZOL is stored until the onset of the inhibitory effect, KD first-order equilibrium rate constant, Kin bone resorption marker production rate constant, Kout bone resorption marker elimination rate constant, Ke0 effect-compartment equilibrium rate constant, Scale ratio of change in bone resorption marker values to change in BMD, BMD bone mineral density

$$\begin{array}{l}\frac{\mathit{dA}}{\mathit{dt}}=-\mathit{KD}\times A\\ \mathit{EFF}=\frac{{\left(\mathit{KD}\times A\right)}^{\gamma }}{{\mathit{EKD}}_{50}^{\gamma }+{\left(\mathit{KD}\times A\right)}^{\gamma }}\\ \frac{\mathit{\text{dMarker}}}{\mathit{dt}}=\mathit{Kin}\times \left(1-\mathit{EFF}\right)-\mathit{\text{Kout}}\times \mathit{\text{Marker}}\end{array}$$

KD is the first-order equilibrium rate constant, and EKD₅₀ corresponds to the value of KD × A that leads to 50% inhibition of Kin. γ is the Hill’s coefficient.

Next, the effect of daily oral supplements (calcium 610 mg, vitamin D 400 IU, and magnesium 30 mg) and the natural disease progression effect were added to the above calculated marker levels. These two effects could not be independently estimated because all patients received the daily oral supplements; therefore, these effects were simultaneously modeled with the equation shown below.

$$\mathit{\text{Marker}}\left(t\right)=\mathit{\text{Marker}}\times \left(1+\mathit{\text{Slope}}\times t+\frac{\mathit{\text{Emax}}\times t}{T_{50}+t}\right)$$

where Marker(t) is the bone resorption marker at time t (day), whereas Marker is calculated as above. Slope was a linear time effect, and the last term of the equation showed a time-saturating effect on disease progression, in which Emax was the relative maximal effect, and T₅₀ was the time at which the effect reached half of the maximal effect.

Base model for BMD

BMD models were developed using TRACP-5b, CTx, or u-NTx, respectively.

The mathematical model used in the BMD model is also depicted in Fig. 1. In this model, the time profiles for BMD were assumed to be linearly affected by the bone resorption marker values with a first-order equilibrium constant Ke0, and they decreased with the same constant. The scale was used to adjust the change in bone resorption marker values to the change in BMD. The mathematical equation for this model is as follows:

$$\frac{\mathit{\text{dBMD}}}{\mathit{dt}}=\mathit{Ke}0\times \left[\mathit{\text{Scale}}\times \left(\mathit{\text{Marker}}-\mathit{\text{Marker}}\mathit{0}\right)-\left(\mathit{BMD}-\mathit{BMD}0\right)\right]$$

where Marker0 and BMD0 are the baseline values for the bone resorption markers and BMD, respectively. The bone resorption marker for this model development was selected from among TRACP-5b, CTx, and u-NTx based on statistical significance testing.

Statistical models

The inter-individual variabilities for the model parameters both for the bone resorption markers and the BMD models were assumed to be normally or log-normally distributed with mean 0 and variances ω², in which parameters with positive values were modeled by a log-normal distribution, and those with positive and negative values were modeled with a normal distribution. Correlations between variabilities of two random effect parameters were also assumed. Intra-individual variability for the bone resorption markers was assumed to follow a relative error model with a standard deviation σ. Intra-individual variability for the BMD was modeled with absolute error.

Covariate models for each model were also tested using the following patient characteristics: sex, age, body weight, prior usage of some bisphosphonates, and baseline bone resorption markers and BMD. Continuous covariates were modeled by the power model with standardization to their median values, and the power coefficients were estimated. Categorical covariates such as sex and prior bisphosphonate usage were modeled in a relative effect manner.

The likelihood ratio test using a forward inclusion or a backward elimination process was used to compare nested models and select the final model. The full model was developed by incorporating the statistically significant candidates after the forward inclusion process. Each candidate was then tested in turn by removing them one by one to confirm their statistical significance. A minus twice log-likelihood difference was used to judge the statistical significance of the candidate covariates. The p values for the forward inclusion process and the backward elimination process were < 0.05 and < 0.01, respectively. The final model was reached using the remaining significant covariates.

Model evaluation

The final model was evaluated by goodness-of-fit plots, as follows: (1) observed values versus population- or individual-predicted values were plotted and (2) conditional weighted residuals [17] versus time after the first dose and population-predicted values were plotted.

Bootstrap validation [18, 19] was used to estimate the standard errors for the estimates and to evaluate the validity and robustness of the final model. Two hundred bootstrap replicates were generated by randomly non-parametric resampling the original dataset with replacement. The final model was fitted repeatedly to the 200 datasets. Successful estimation was defined as the normal completion of the Phoenix software. The means of parameter estimates calculated from the successful estimations were compared with the final parameter estimates obtained from the original dataset.

Simulation based on the final model

Two-year BMD was simulated following two annual doses of ZOL using baseline (bone resorption marker and BMD) and 12-week (bone resorption marker) values as follows. To evaluate the prospective predictability of the model based on TRACP-5b, a visual predictive check [20] was performed. Ten thousand virtual patients were randomly simulated, and the time-dependent profiles of TRACP-5b and BMD were predicted using the final model. To compare predictability with other bone resorption markers, the same models were also developed with CTx or u-NTx instead of TRACP-5b, and empirical Bayes estimation was performed.

The relationships between the change from baseline in TRACP-5b at 12 weeks and the changes in T-scores and BMD at 2 years following two annual doses of ZOL were evaluated using simulation. Ten thousand virtual patients were randomly simulated, and the time-dependent profiles of TRACP-5b and BMD were predicted using the final model. A visual predictive check was performed to evaluate the predictability of the simulation. The percentages of patients whose BMD improved by more than 2.4% or a T-score greater than − 2.5 were estimated against three categories of TRACP-5b decreases (100, 200, and 300 mU/dL).

Model development and simulation

All modeling and simulation in this study were performed using a nonlinear mixed-effects modeling in Phoenix NLME 1.3 software (Pharsight Corporation, Certara, LP, Princeton, NJ) with the FOCE-ELS algorithm.

Results

Patients and measured data

Data from a total of 306 patients who had values for at least one bone resorption marker and BMD were used in this analysis, with 145 patients in the ZOL group and 161 in the placebo group. Patients’ demographics are shown in Table 1. No significant differences between the ZOL and placebo groups were seen for any factors.

Table 1.

Summary of subject data used in the modeling and simulation

	Zoledronic acid (N = 145)	Placebo (N = 161)	Total (N = 306)
Sex
Male	11 (7.6%)	6 (3.7%)	17 (5.6%)
Female	134 (92.4%)	155 (96.3%)	289 (94.4%)
Age (years)	72.9 ± 5.2 [65–86]	72.9 ± 5.3 [65–87]	72.9 ± 5.2 [65–87]
Weight (kg)	51.4 ± 7.4 [36.0–76.4]	53.1 ± 8.4 [34.1–83.6]	52.3 ± 8.0 [34.1–83.6]
Prior usage of bisphosphonate
Never used	132 (91.0%)	145 (90.0%)	277 (90.5%)
Used with sufficient washout	13 (9.0%)	16 (10.0%)	29 (9.5%)
TRACP-5b (mU/dL)	398.0 ± 143.6 [183–1240]	403.9 ± 152.0 [157–1030]	401.1 ± 147.9 [157–1240]
CTx (ng/mL)	0.406 ± 0.175 [0.08–1.00]	0.404 ± 0.190 [0.10–0.99]	0.405 ± 0.183 [0.08–1.00]
u-NTx (nMBCE/mMCr.)	54.52 ± 21.43 [16.4–119.0]	54.97 ± 25.69 [14.0–150.0]	54.76 ± 23.73 [14.0–150.0]
Lumbar spine T-score (L2-L4)	− 2.769 ± 0.800 [− 5.51 to − 0.68]	− 2.829 ± 0.791 [− 5.25 to − 0.25]	− 2.801 ± 0.795 [− 5.51 to − 0.25]
Lumbar spine BMD (L2-L4) (g/cm2)	0.680 ± 0.095 [0.36–0.93]	0.674 ± 0.094 [0.39–0.98]	0.677 ± 0.094 [0.36–0.98]

Values are expressed as means ± SD [range]

TRACP-5b tartrate-resistant acid phosphatase 5b, CTx C-telopeptide of type I collagen, u-NTx urinary N-telopeptide of type I collagen, BMD bone mineral density

Bone resorption markers (TRACP-5b, CTx, and u-NTx, 3410 points), BMD (1146 points), and %BMD were plotted against time since first administration (Fig. 2). In the ZOL group, bone resorption markers showed clear decreases from baseline even only a few weeks after the first administration. On the other hand, BMD and %BMD showed improvements in the ZOL group, although there were no clear trends in the placebo group.

Fig. 2.

Time profiles of bone resorption markers and the percentage change from baseline of the BMD following two annual doses of placebo (a) or ZOL (b). The expanded scale is shown in the inset plot. TRACP-5b tartrate-resistant acid phosphatase 5b, CTx C-telopeptide of type I collagen, u-NTx urinary N-telopeptide of type I collagen, BMD bone mineral density

Base model

The model depicted in Fig. 1 gave an adequate prediction. Inter-individual random effects were estimated for EKD₅₀, Emax, Slope, T₅₀, Ke0, and Scale. Among the three bone resorption markers, TRACP-5b was selected as the best one to predict the BMD profile.

Covariate exploration

Statistically significant covariates were detected for the baseline TRACP-5b effect on EKD₅₀, Slope, T₅₀, and Scale. As far as Scale, baseline TRACP-5b was significant only in the ZOL group. No covariates were statistically significant for Slope and Ke0.

Goodness-of-fit

Goodness-of-fit plots are shown in Supplemental Fig. 1. The plots of the observed vs. prediction values were almost evenly distributed centering on the 1:1 line. Most conditional weighted residuals were evenly distributed around 0 independently of the population-predicted values and time after the first dose. The final parameter estimates are shown in Table 2.

Table 2.

Parameter values estimated by the mathematical model (TRACP-5b)

Parameter (unit)	Estimate	SEa
Bone resorption marker model
KD (1/day)	3.719 × 10−3	2.941 × 10−5
Gamma	4.583 × 10−1	2.626 × 10−3
EKD50 (mg/day)	5.776 × 10−3	3.800 × 10−5
Kout (1/day)	4.584 × 10−1	3.592 × 10−3
Slope (1/day)	2.688 × 10−4	2.877 × 10−6
Emax	− 8.266 × 10−2	2.053 × 10−3
T50 (day)	1.166 × 102	3.091
TRACP-5b baseline effect on EKD50	− 1.534	1.699 × 10−2
TRACP-5b baseline effect on Slope	− 1.350	2.093 × 10−2
TRACP-5b baseline effect on T50	− 1.319	2.974 × 10−2
σ	3.551 × 10	1.204 × 10−1
Inter-individual variability
ωEKD502	2.255 × 10−1	4.892 × 10−3
ωslope2	1.573 × 10−1	3.136 × 10−3
ωEmax2	8.584 × 10−2	2.655 × 10−3
ωT502	2.095	3.662 × 10−2
ωEmax, slope	− 7.576 × 10−2	2.806 × 10−3
ωEmax, T50	− 8.732 × 10−2	3.911 × 10−3
ωslope, T50	8.697 × 10−2	4.525 × 10−3
BMD model
Ke0 (1/day)	3.802 × 10−3	6.429 × 10−4
Scale ((g/cm2)/(mU/dL))	− 2.521 × 10−4	3.709 × 10−5
TRACP-5b baseline effect on Scale	− 1.112	2.635 × 10−1
σ	2.447 × 10−2	1.215 × 10−3
Inter-individual variability
ωKe02	1.406 × 10−3	2.964 × 10−1
ωScale2	2.361 × 10−8	1.028 × 10−8

^aSE was obtained from Bootstrap validation

SE standard error, EKD₅₀ the value of KD × A that led to 50% inhibition of bone resorption marker production rate constant, E_max the relative maximal effect, Gamma Hill coefficient, KD first-order equilibrium rate constant, Kout bone resorption marker elimination rate constant, slope a linear time effect, T₅₀ the time at which the effect reached half of the maximal effect, Ke0 effect-compartment equilibrium rate constant, Scale ratio of change in bone resorption marker values to change in BMD

Simulation

Using the final model, BMD up to 2 years was predicted using only the background values (baseline of TRACP-5b and BMD) and the early values (TRACP-5b at 12 weeks). %BMD was calculated using predicted BMD. A visual predictive check showed that the simulated 90% prediction interval almost covered the observed %BMD distribution, though it was simulated with only three values (Fig. 3). To compare predictability with other bone resorption markers, the same models with CTx or u-NTx (Supplemental Table 1) instead of TRACP-5b were also developed, and empirical Bayes estimation was performed using the baseline and 12-week values of each bone resorption marker. TRACP-5b model showed the best predictive performance among the three kinds of bone resorption markers statistically, whereas they showed almost the same predictability by visual inspection (Supplemental Fig. 2).

Fig. 3.

Predicted percentage change from baseline of the BMD (%BMD) simulated from the data at baseline and 12 weeks. Ten thousand virtual BMDs following two annual doses of ZOL were simulated from background data (baseline of TRACP-5b and BMD) and early values (TRACP-5b values at 12 weeks). %BMD was calculated from simulated BMD. The solid lines indicate the medians of simulated %BMD. The upper and lower chain lines indicate the 95th and 5th percentiles of simulated %BMD, respectively

The relationships between the change from baseline in TRACP-5b at 12 weeks and the changes in T-scores and BMD at 2 years following two annual doses of ZOL were examined. A visual predictive check was performed to evaluate the predictability of the simulation. Virtual %BMD to 2 years following two annual doses of 10,000 patients with baseline T-scores less than − 2.5 were simulated and plotted against the TRACP-5b change from baseline to 12 weeks. The simulated 90% prediction interval showed good coverage for the observed %BMD distribution with some points falling outside the interval (Supplemental Fig. 3). The percentages of the patients whose T-score greater than − 2.5 or BMD improved by more than 2.4% against three categories of TRACP-5b decrease (100, 200, and 300 mU/dL) were estimated by this simulation (Table 3).

Table 3.

The relationship between the change in TRACP-5b from baseline to 12 weeks and the predicted percentage T-score or BMD improvement at 2 years

Predicted value at 2 years	Change in TRACP-5b from baseline to 12 weeks
	100 mU/dL	200 mU/dL	300 mU/dL
T-score > − 2.5	19.6%	26.6%	34.2%
%BMD > 2.4%	68.5%	76.9%	82.7%

BMD of 10,000 patients at 2 years following two annual doses were randomly simulated using the baseline BMD and TRACP-5b values of patients with baseline T-scores less than − 2.5. T-scores and %BMD were calculated from the predicted BMD

%BMD percentage change from baseline of the BMD

Discussion

In this analysis, mathematical models were constructed using TRACP-5b serum concentrations and lumbar spine BMD data from 306 patients with primary osteoporosis treated with ZOL to predict BMD at up to 2 years. The constructed models showed that good predictability, in particular, BMD up to 2 years could be predicted from background data (baseline TRACP-5b and BMD) and early values (TRACP-5b values at 12 weeks) (Fig. 3 and Supplemental Fig. 2).

For the BMD prediction, Hasegawa et al. constructed an exposure-response model after administration of ONO-5334, a selective inhibitor of cathepsin K [12]. In addition, Nakai et al. developed a population pharmacodynamic model to relate urinary CTx to BMD response after treatment with ibandronate, adequately predicting %BMD at 3 years after treatment [11]. The present model showed almost the same predictability for BMD. However, these previous efforts did not focus on the use of bone turnover markers at the initial stage of drug treatment to predict the BMD response years later. In the present analysis, BMD at up to 2 years could be predicted using only background (baseline TRACP-5b and BMD) and early (TRACP-5b at 12 weeks) values, which supports the prediction of long-term BMD profiles using only very early stage data after first dosing. Diez-Perez et al. suggested that PINP and CTx after 3 months of therapy could be used to screen for the treatment effect of oral bisphosphonates [8]. These findings, in which the changes in bone turnover markers in the early phase of bisphosphonate treatment predict future changes in BMD, have also been observed in cases receiving a bone formation agent. Namely, Chen et al. reported that early changes in bone turnover markers, PICP at 1 month and PINP at 3 months, correlated with the 18-month BMD response to daily teriparatide therapy in women with postmenopausal osteoporosis [7]. In addition to this study, Tsujimoto et al. proposed an algorithm using PINP to monitor patients, since there was a strong relationship between early changes in PINP and later changes in lumbar spine %BMD during teriparatide therapy [9]. These three reports suggested that the long-term BMD profiles might be predictable using values of bone turnover markers in the early stage, regardless of the mode of therapy, and they thus support the present findings.

In the present analysis, three base models were constructed using each of the bone resorption markers, TRACP-5b, CTx, and u-NTx. Though the simulation of 2-year BMD from early values of CTx or u-NTx gave almost the same predictability as that of TRACP-5b by visual inspection (Supplemental Fig. 2), the TRACP-5b model was superior based on statistical significance. The statistical superiority of TRACP-5b could be due to the possibility that the biological variability of TRACP-5b is smaller than that of CTx, as has been previously reported [21]. Our established models also supported this possibility as the intra-individual variability of the TRACP-5b model was smaller than that of the CTx model (8.9 vs. 13.3%; Supplemental Table 2). It is therefore suggested that the TRACP-5b model is the best indicator to describe the BMD profile after treatment with ZOL.

In addition, TRACP-5b has been shown to be a good marker for serum bone resorption, since it is not affected by renal dysfunction [22]. Furthermore, its intra-individual variability is low because it is not affected by food intake [21]. Therefore, the present model may be useful to predict BMD in patients with normal renal function or in patients with renal dysfunction, which should be confirmed in a further study.

The relationship between the change from baseline in TRACP-5b at 12 weeks and the changes in T-scores and %BMD at 2 years following two annual doses of ZOL were estimated. The percentages of patients whose BMD improved by more than 2.4% as a short-term treatment goal [6, 23] or achieved T-score greater than − 2.5 as a long-term treatment goal [4, 5] against three categories of TRACP-5b decrease (100, 200, and 300 mU/dL) have been shown to be predictable by this simulation (Table 3).

In the present model, there are two limitations. Firstly, the present study population was patients who met the selection criteria and were given supplemental calcium and vitamin D. Thus, the generalizability of the present results must be clarified in the real world. Another is that the model could not be applied to patients who were switched from other bisphosphonates, because the model was developed from the ZONE study in which all patients never used bisphosphonates or used bisphosphonates with sufficient washout. This should also be tested in a further study.

In this study, the focus was on future values of BMD as the expected benefit of ZOL treatment, because BMD is generally accepted as the standard measure of fracture risk, which is the clinical outcome of osteoporosis [2]; however, it still does not entirely assess fracture risk [1]. Bell et al. demonstrated that early changes of hip BMD and serum NTx after ZOL treatment were ranked highly for prediction of clinical fractures [24]. It was thought that further study was needed to predict fracture risk quantitatively from the early response to ZOL treatment.

In conclusion, this is the first model to predict BMD at 2 years following two annual doses of ZOL using patients’ baseline data and the early response of TRACP-5b. This model allows us to inform patients of their predicted response at the initial stage of ZOL treatment.

Compliance with ethical standards

This study was conducted in compliance with the World Medical Association Declaration of Helsinki–Ethical Principles for Medical Research Involving Human Subjects and Good Clinical Practice. The protocol was approved by the institutional review board at each study site. Written, informed consent was obtained from all subjects before enrollment in the study.

Conflicts of interest

Yoko Mori, Atsushi Ose, Masashi Serada, and Masashi Ishiguro are employees of Asahi Kasei Pharma. Hidefumi Kasai and Masataka Shiraki received consulting fees from Asahi Kasei Pharma. Yusuke Tanigawara received research funds from Asahi Kasei Pharma.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Informed consent

Informed consent was obtained from all individual participants included in the study.