Direct Measurement of Xylem Pressure in Leaves of Intact Maize Plants. A Test of the Cohesion-Tension Theory Taking Hydraulic Architecture into Consideration

Abstract

The water relations of maize (Zea mays L. cv Helix) were documented in terms of hydraulic architecture and xylem pressure. A high-pressure flowmeter was used to characterize the hydraulic resistances of the root, stalk, and leaves. Xylem pressure measurements were made with a Scholander-Hammel pressure bomb and with a cell pressure probe. Evaporation rates were measured by gas exchange and by gravimetric measurements. Xylem pressure was altered by changing the light intensity, by controlling irrigation, or by gas pressure applied to the soil mass (using a root pressure bomb). Xylem pressure measured by the cell pressure probe and by the pressure bomb agreed over the entire measured range of 0 to −0.7 MPa. Experiments were consistent with the cohesion-tension theory. Xylem pressure changed rapidly and reversibly with changes in light intensity and root-bomb pressure. Increasing the root-bomb pressure increased the evaporation rate slightly when xylem pressure was negative and increased water flow rate through the shoots dramatically when xylem pressure was positive and guttation was observed. The hydraulic architecture model could predict all observed changes in water flow rate and xylem. We measured the cavitation threshold for oil- and water-filled pressure probes and provide some suggestions for improvement.

In recent years, the cohesion-tension (CT) theory of the ascent of sap in plants has been questioned (Balling and Zimmermann, 1990; Benkert et el., 1991; Zimmermann et al., 1993). According to direct measurements with cell pressure probes, the pressures measured in xylem vessels (P_x) were usually not more negative than −0.5 MPa (reference zero pressure = atmospheric pressure). Indirect measurements of P_x using a Scholander-Hammel pressure bomb (Scholander et al., 1965) suggest that P_x might be as low as −10 MPa in some plants (Kolb and Davis, 1994; Kramer and Boyer, 1995; Steudle, 1995; Sperry et al., 1996; Tyree, 1997). Early pressure probe results have failed to corroborate the pressure bomb (Balling and Zimmermann, 1990) although better agreement has been reported more recently (Melcher et al., 1998). Nevertheless, prior reports have failed to emphasize that the validity of the CT theory is independent of the correctness of pressure-bomb estimates of P_x (Tyree, 1997). Failure of the pressure probe to detect rapid changes in P_x following rapid changes in transpiration (Benkert et al., 1991) has provided a more troubling conflict with the CT theory.

The CT theory, as originally proposed (Dixon and Joly, 1894), makes few quantitative predictions of how negative P_x must be in plants; it only suggests that the pressure is negative (below atmospheric). The CT theory predicts a hydrostatic-pressure gradient, dP_s/dx ≈ −0.01 MPa/m change in height, when there is no transpiration, i.e.:

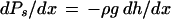1

where ρ is the density of water, g is the acceleration due to gravity, and dh/dx is the change in height per unit change in distance along a stem. The CT theory must be augmented by the Ohm's law analog of water flow in plants (van den Honert, 1948) to predict dP/dx values in stem segments with water flow rate > 0. The hydrostatic pressure gradient in a stem segment will be augmented by a hydrodynamic pressure gradient (dP_h/dx) when the water flow rate (f, in kilograms per second) in a stem is >0, i.e.:

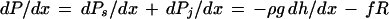2

where R is the hydraulic resistivity of the stem segment in megapascals per second per meter per kilogram.

Long-term measurements of P_x in lianas using the pressure probe have also been cited as evidence against the CT theory. Benkert et al. (1995) and Thürmer (1999) report pressure gradients of about −0.01 MPa m⁻¹ at night when f ≅ 0, but the CT theory appeared to be challenged because dP/dx seemed to decline as f increased. But this report must be discounted because the authors committed two logical errors in their analysis of the data: (a) a simple sign convention error and (b) the failure to integrate Equation 2 over x to predict how P_x should change between two measuring points at different heights.

The sign convention error occurred because their liana stem segments were upside down, i.e. height decreased from physiological base to the apex in the vines. The sign convention comes into Equation 2 when we define the direction of increasing x to be from base to apex and positive f to be for flow from base to apex. With this sign convention it is obvious that dh/dx must be negative. So the pressure gradient should start out as a positive quantity at f = 0 then decline to 0 and then advance to negative values as f increases. This is exactly what is found in Figure 5 (Benkert et al., 1995), so their experiments actually provide strong qualitative support to the CT theory. However, their experiments fail to provide strong quantitative support for the CT theory because they did not measure the hydraulic architecture of the lianas. Hydraulic architecture measurements would provide information on hydraulic resistances within stems, petioles, and leaves. Such information is needed to provide quantitative predictions of how much P_x should change between any two given points in a shoot and how P_x differences should change with the transpiration rate. Even in vertically oriented shoots, P_x can increase with height in some transpiring plants (Tyree, 1988, 1997) if R decreases rapidly from large to small diameter branches.

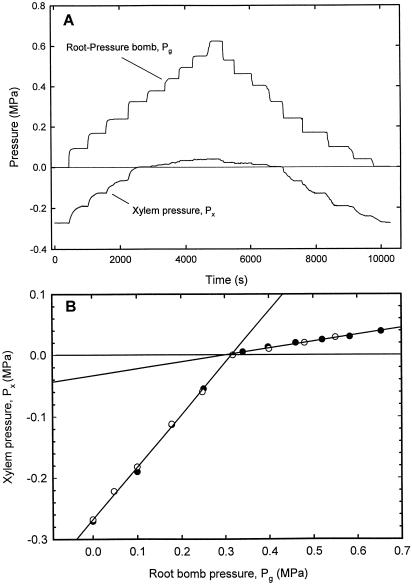
Figure 5.

Effect of P_g applied to the root on xylem pressure, P_x. A, At 0 (atmospheric) pressure, xylem pressure was P_x = −0.28 MPa. As the bomb pressure was raised in steps, xylem pressure increased in steps, too. Responses to bomb pressure were on the order of seconds (see Fig. 3). In the range of xylem pressures of below atmospheric, there was a substantial response of xylem pressure. This was strongly reduced when P_x was larger than atmospheric pressure and guttation occurred. B, Effect of P_g applied to a maize root on steady P_x: plot of data from an experiment such as that shown in A. White and black circles represent the step-up and step-down of P_g, respectively. Responses were linear in both the ranges of low and high pressures. Guttation occurred when P_x attained a certain threshold (P_x ≥ atmospheric pressure which was the reference). There was a nearly 1:1 response of P_x:P_g at low pressures (ΔP_x slightly smaller than ΔP_g; slope = 0.852; r² = 0.998). At pressures where guttation occurred, the slope was only 0.112. This indicated a substantial reduction of the hydraulic resistance across the plant when hydaothodes allowed the passage of water.

Although the pressure bomb must be used with due consideration of what it can and cannot measure, more recent evidence obtained with other indirect methods supported the results obtained with the Scholander-Hammel bomb and the CT theory (Holbrook et al., 1995; Pockman et al., 1995). The discussion is still ongoing and alternative mechanisms have been proposed, some of which are somewhat exotic (Canny, 1995) and argued to be erroneous (Tyree et al., 1999).

The CT theory has been criticized occasionally over the past 100 years, and there has been a search for alternative mechanisms. Criticism arose from the striking fact that water under tension is in a metastable state and should cavitate immediately when gas seeds are around. Therefore, the xylem would be a quite vulnerable pipe (Milburn, 1979). The recent criticism does not completely exclude the CT mechanism. However, it does claim that there have to be other mechanisms besides CT in tall trees. P_x values of only −0.5 MPa would be sufficient to lift a static water column only to a height of 50 m, whereas the tallest trees can exceed 100 m. P_x would have to be more negative than −0.5 MPa in many common situations, e.g. when plants are in dry soils or when dP/dx values must be very negative because of large hydrodynamic gradients caused by high f or R values (Eq. 2). Although the pressure probe has been used to measure P_x values down to −0.7 MPa in extreme cases, little consideration has been given to theoretical limitations of the pressure probe to measure negative pressures. How vulnerable is the pressure probe to cavitation within the instrument? How can the insertion of the pressure probe into vessels induce cavitation in the vessel being measured?

From the above considerations it is clear that future tests of the CT theory need to take into account quantitative aspects of the hydraulic architecture of the plants being studied. In the present paper, we have used 1- to 1.5-m-tall maize plants to test the validity of the CT theory and the reliability of the pressure-bomb technique. We have also examined the limitations of cell (xylem) pressure probes to measure negative pressure.

MATERIALS AND METHODS

Plants

Maize plants (Zea mays L. cv Helix) were grown from seeds in soil (sand:loam:peat, 1:2:1, v/v) in plastic pots (1.9 L; diameter: 150 mm; depth: 105 mm) in the greenhouse of the University of Bayreuth (Germany). Plants were watered daily, and once a week were supplied with nutrient solution containing 150 mm K₂HPO₄, 150 mm Ca(NO₃)₂, 200 mm Mg(NO₃)₂, 100 mm NH₄NO₃, 150 mm (NH₄)₂SO₄, and micronutrients. Experiments were conducted on 4- to 5-week-old plants that were 1 to 1.5 m tall. Plants were replaced after each experiment involving destructive sampling of a leaf tip.

Experimental Setup

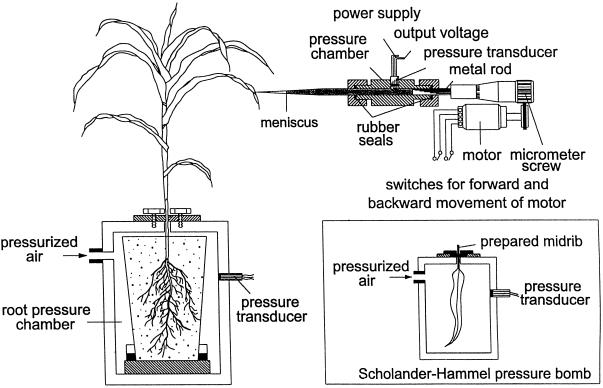
A maize plant was brought from the greenhouse and set up for an experiment as shown in Figure 1. The pot containing the root was sealed in a metal pressure chamber, or “root-bomb” (i.d. 185 mm, depth 305 mm), using rubber seals. Plants were usually watered before placing them in the root-bomb, but in cases where more negative P_x values were desired, the plants were not irrigated for 1 or more days prior to the start of the experiment. P_x was adjusted by changing the air pressure in the root-bomb. A pressure transducer (resolution ± 0.001 MPa) was mounted in the root-bomb to measure gas pressure.

Figure 1.

Experimental setup for measuring P_x using a cell pressure probe (schematical). P_x could be changed by P_g to the root (“root-bomb”) or by changing light intensity, which affected transpiration. A cell pressure probe was used to directly measure P_x. When a stable xylem pressure was observed, P_g was increased in steps and then decreased again. Leaf tips were harvested to measure water potential (balance pressure, P_b) using a conventional pressure chamber (shown in right corner). In some cases, leaf tips were covered with aluminum foil (not shown), in other cases the leaf tip was allowed to transpire. For further explanation, see text.

The direct measurement of xylem pressure using a cell pressure probe was very sensitive to vibrations, which tended to cause cavitation and failure of the experiment (presumably by air seeding where the tip punctured the vessel). The cell pressure probe was mounted on a manipulator (Leitz, Midland, Ontario, Canada) that was screwed on a thick iron plate and placed on a heavy stone table. The iron plate was also used as a magnetic stand for fixing a metal frame used to secure the leaf while inserting the microcapillary into the vessel.

Measurement of Xylem Pressure

Xylem pressure was measured with an oil-filled cell pressure probe rather than the water-filled xylem pressure probe used in many earlier experiments (see “Results” for justification). The function of cell pressure probes has been described in many earlier papers (e.g. Steudle, 1993; Henzler and Steudle, 1995). The resolution of the pressure transducer in the probe chamber was ±0.001 MPa. Microcapillaries were made by pulling borosilicate glass capillaries (i.d. approximately 0.5 mm; o.d. = 1 mm) on a microcapillary puller. Tips were polished with a grinding machine (Bachhofer, Reutlingen, Germany). Tip diameters (o.d. approximately 5 μm) and tip sharpness (approximately 45° angle) were achieved during grinding. Smaller-diameter tips cause less damage and are less likely to cause cavitation during insertion into vessels, but hydraulic conductivity of the tips declines with the fourth power of the tip diameter.

The half-time for pressure relaxation (pressure stability) of the pressure probes was 3 to 10 s when the 5 μm were not plugged with cellular debris. The half-time for pressure relaxation measures the time for a pressure change beyond the tip of the pressure probe to be registered in the body of the probe and requires the flow of sufficient water across the tip to swell the volume of fluid in the body of the probe. Microcapillaries were filled with low-viscosity silicone oil (type CQ 240 D, Kulite, Leonia, NJ), but the tip was filled with 3 to 4 μL of degassed water. During probing, no silicone oil entered the xylem vessel probed. This was known because the meniscus between silicone oil and water remained in the microcapillary. The insertion of the probe was followed with a stereomicroscope. A computer and a chart recorder were simultaneously used to record both probe and root-bomb pressure.

The microcapillary was inserted about 0.2 m behind the leaf tip. In some cases, the leaf tip was covered with aluminum foil to reduce transpiration and to promote equilibration of water potential between leaf tissue and xylem at the site of probe insertion. In other cases, the leaf tip was allowed to transpire. Xylem vessels probed usually were in ribs 2 or 3 counted from the midrib. The insertion of the microcapillary into vessels was performed manually at an angle of 75° to 90° between leaf blade and microcapillary. When the tip of the microcapillary touched the rigid xylem wall, the tip bent, “struggling” against the wall. The position of the microcapillary was then adjusted (manipulator) to make it straight before puncturing the vessel. The probe pressure was usually kept at an overpressure during insertion in a vessel (0.02–0.05 MPa above atmospheric) by slowly advancing the metal rod of the pressure probe. This helped to prevent the formation of air bubbles in the tip and ensured that the tip was not blocked during puncturing. When a negative pressure was read with the probe, it was only possible to push the metal rod into the probe and increase pressure. It was not possible to pull the rod and decrease pressure without causing cavitation.

Criteria for Proper Measurement of Xylem Pressure

When the tip was blocked, a positive pressure pulse applied to the probe (by means of the metal rod mounted into the probe chamber) did not relax. When the tip broke during insertion, the probe pressure rapidly returned to atmospheric pressure. The probe pressure returned to subatmospheric (approximately −0.1 MPa) in less then 0.1 s following cavitation, and then to atmospheric pressure in 10 to 100 s. Successful insertion of the tip in a vessel depended on keeping it straight while pushing it forward. Several criteria for successful insertion of the microcapillary into a vessel were used: (a) the tip experienced bending against the vessel wall that was followed immediately by a drop of probe pressure below atmospheric; (b) the xylem pressure rapidly responded to changes in air pressure applied to the root and to changes in light intensity; (c) water from the tip, labeled with a dye, entered a single vessel following insertion.

Vulnerability to Cavitation (Tensile Strength) of Pressure Probes

Direct measurement of negative pressure with probes requires that there are no cavitation problems caused by the cell pressure probe itself. In other words, when pressures down to −10 MPa are going to be measured (Kolb and Davis, 1994; Steudle, 1995; Tyree, 1997), probes should not cavitate at pressures >−10 MPa. Usually, liquids withstand high tensile stresses of up to several-hundred megapascals (Oertli, 1971; Pickard, 1981). However, in the presence of hydrophobic surfaces, impurities, or fissures in the walls, cavitations may occur sooner (Fisher, 1948; Zimmermann, 1983).

Seven different pressure probes were evaluated for vulnerability to cavitation: five were fabricated in Würzburg (three water-filled and two oil-filled) and two were oil-filled probes fabricated in Bayreuth. The pressure of the probe could be raised or lowered by raising or lowering, respectively, the temperature of a sealed microcapillary. Sealed microcapillaries, about 80 mm long, were immersed in a water bath and the pressure changed about 0.1 MPa/1°C change in bath temperature for oil-filled capillaries. Water-filled capillaries changed pressure less with temperature because of the lower thermal expansion of water versus silicone oil. Slow changes in pressure (<2 kPa s⁻¹) were achieved by adjusting the temperature of the bath at the maximum cooling rate of the refrigeration system while the microcapillary was totally immersed. Rapid changes in pressure (>50 kPa s⁻¹) were achieved by lowering the microcapillary into a bath at 0.5°C over a period of 10 to 30 s. In some cases the microcapillaries were drawn on the puller and the tips ground, filled with water/oil, and then sealed with glue. In most cases blunt capillaries were just flame-sealed and filled with water and/or oil. The oil-filled capillaries still had water in the tip (10 mm); they were first completely filled with water using a 0.4-mm-o.d. syringe needle, then back-filled with oil while holding the needle 10 mm back from the tip. All solutions were partly degassed by vacuum before use.

Pressures at which a fracture of the liquid phase occurred were recorded. Cavitations were evidenced by a rapid increase of pressure to about −0.1 MPa (depending on the vapor pressure of the fluid), followed by a gradual increase of pressure to 0 MPa as air came out of solution to fill the cavity. In many cases the location of the resulting embolism was observed at ×10 to ×30 magnification using the stereoscope. Embolisms were removed by raising the temperature of the fluid in the microcapillary until the pressures were above atmospheric, which forced the gases back into solution. Probes could be put repeatedly through cycles of positive pressure to remove embolisms and negative pressure to induce cavitation.

Responses of Xylem Pressure to Root-Bomb Pressure and to Light

Most of the probing of leaf xylem was performed when root-bomb pressure was atmospheric. When a stable xylem pressure was attained, root-bomb pressure was increased in steps of 0.05 to 0.075 MPa and kept constant at each level until a new constant xylem pressure was established. Usually, steady pressures were attained after 8 to 12 min following a step change. The whole range of root-bomb pressure included sufficient pressure for guttation to occur. The root-bomb pressure was then decreased in steps to atmospheric.

Without root-bomb pressure, leaves were probed under a photosynthetic flux density (PFD) of 150 μmol m⁻² s⁻¹ (measured at the leaf area probed with the same orientation as the leaf blade). When a stable P_x was observed, light intensity was increased by adding a second light, making the light intensity 200 μmol m⁻² s⁻¹. Data were collected until a steady P_x, and then a third light was added (260 μmol m⁻² s⁻¹). The light sources used were two 400-W lamps (Multi-Hi-Ace, Iwasaki, Japan) and one 400-W floodlight lamp (Siemens AG, Frankfurt, Germany). Except for the study of how light intensity affected xylem pressure and transpiration rate, the other experiments were performed at 200 μmol m⁻² s⁻¹ PFD. RH in the lab was 60% to 75% and the air temperature was 20°C to 24°C.

Measurement of Balancing Pressure (P_b) and Comparison with Xylem Pressure P_x

When a stable xylem pressure was observed with the pressure probe, the leaf was harvested above the point of the insertion of the probe and immediately wrapped in thin plastic wrap. An artificial petiole was made by excising leaf-blade tissue from the midrib, while the leaf was still wrapped in plastic. Then the balance pressure was measured in the usual way with a pressure bomb. Gas pressure (P_g) was increased in steps at a rate <0.075 MPa min⁻¹ between steps of 0.1 MPa or less. When water appeared at the cut end of the midrib, the balance pressure could be confirmed by lowering the bomb pressure by a <0.04 MPa until the water was sucked back into the xylem and then the balance point was reconfirmed. Balance points were usually repeatable to ±0.005 MPa. The resolution of the pressure transducer used in the pressure chamber was ±0.001 MPa.

Estimation of Transpiration under Different Conditions

In some experiments, the transpiration of plants was measured by weighing the plant, including the pot and root pressure bomb. Transpiration was measured as a function of light (PFD) and the pressure applied to the roots. The weight of the plants and the root-bomb was measured on a balance scale with a resolution of ±0.01 g at a maximum weight of 60 kg. The transpiration rate (W, kilograms per second) was computed from the weight change in 180-s intervals. During weighing, the tubing of the pressure bomb was arranged in a way so that it did not affect the measurement of small weight changes (as confirmed by adding small known weights to the system). Pressure steps of 0.075 MPa were applied to the roots within 50 s and kept for about 10 min until the transpiration rate became stable. The highest applied P_g was 0.6 MPa, which was then was decreased in steps. Similarly, light intensity was changed (150, 200, and 260 μmol m⁻² s⁻¹) and the corresponding changes in the rate of transpiration were measured. Transpiration became stable within 15 min after changing light intensity.

Hydraulic Architecture Measurements

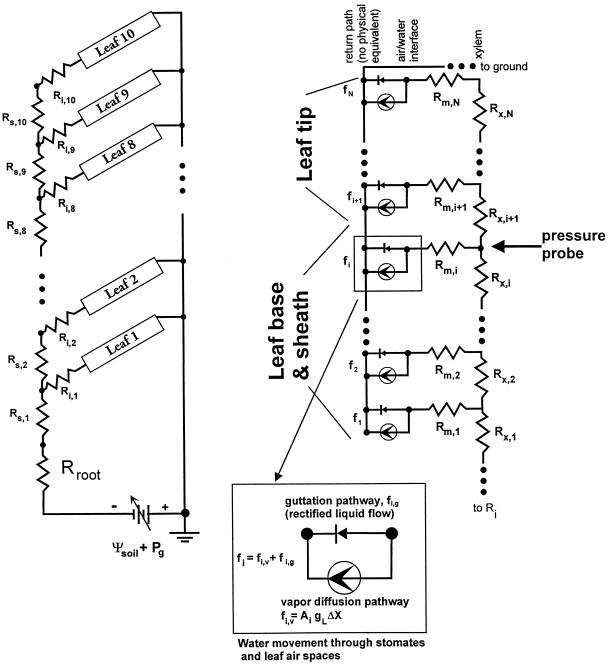
The model used is shown in Figure 2. The root was described by a single hydraulic resistance, R_root. The stem was divided into 10 segments divided at each node (segment resistance, R_s). Stem resistances could be measured only between midpoints of the internodes (R_si) because water-tight seals could not be established at the nodes, hence the values used in the model for any given stem segment was computed from half the basal internodal resistance plus half the apical internodal resistance. The hydraulic connection between the stem and base of the leaf sheath was described by a leaf insertion resistance, R_i. The leaf sheath and leaf blade were divided into segments 10 mm long and each segment had two resistances: a xylem resistance, R_x, and a mesophyll resistance, R_m. The xylem resistance is the resistance of all the leaf vessels in parallel in the segment, and the mesophyll resistance is the radial resistance for water flow from the xylem vessels to the evaporative surface in the mesophyll air spaces of the leaf. Component resistances in the model have been measured as follows.

Figure 2.

Electrical analog used for the hydraulic architecture of maize. The root is represented by a single resistance R_root and the stem is divided into 10 segments, the divisions being at the middle of the nodes, each with a resistance R_s,1 to R_s,10. A leaf insertion resistance is assumed, R_I,1 to R_I,10, is assigned to the resistance of the complex vascular structure of the node. Each of the 10 leaves are divided into 10-mm segments (up to 130 segments for the longest leaves). Each leaf segment (for both leaf sheath and leaf blade) has an axial resistance, R_x,i, for the resistance of all the vessels in parallel and R_m,i, the resistance of water movement from the vessels to the internal mesophyll air spaces where water evaporates. The rate of evaporation from each leaf segment is represented by a constant current source (circle with arrow). This is justified because the normal range of leaf water potential has little impact on the magnitude of the driving force for water vapor diffusion (ΔX). The rate of evaporation is given by A_i g_L ΔX, where A_i is the surface area of the ith leaf segment and g_L is the vapor diffusion conductance (stomates, cuticle plus boundary layer). The guttation pathway is represented by a diode. The diode permits liquid water flow (advance of the meniscus) through leaf air spaces when the fluid pressure is >0. The diode prohibits the movement of the meniscus (liquid flow) into the cell wall (because of surface tension) when the fluid pressure in the wall is <0 but still in a physiological range. These two electrical components are best interpreted as a visualization of the boundary conditions at the evaporative surface. Finally, a variable battery represents the water potential of the soil plus the gas pressure applied in the root pressure bomb (Ψ_soil + P_g).

Root Resistance

Transient measurements of root conductance, K_root = 1/R_root, were made with a high-pressure flowmeter (HPFM) (Dynamax, Houston). The theory of operation of the HPFM when attached to roots is discussed in more detail in Tyree et al. (1994, 1995). Tyree et al. (1995) also showed a linear relationship between F and P_i and good agreement with the K_root measured by the pressure chamber method. The HPFM measures K_root by pushing water from the base of an excised root to the tips (opposite to the normal direction of flow during transpiration). The shoot was excised from the root about 0.05 m above the soil at the first internode, hence the R_root values included the resistance of the first node plus half of the first internode. The HPFM was attached to internodes (5–8 mm in diameter) with the root system still in the pot. A water-tight seal between the internode and the HPFM was achieved using the compression fittings manufactured by Dynamax. Water pressure at the base was rapidly increased from 0 to 0.5 MPa at a constant rate of 3 to 7 kPa s⁻¹ while measuring flow, F, and applied pressure, P_i, every few seconds. The slope of the relationship between F and P_i was taken as K_root, and R_root was calculated form the inverse of K_root.

Stem Resistances

The HPFM was first developed for measurement of shoot and leaf resistances (for details, see Tyree et al., 1993; Yang and Tyree, 1994). Stem and leaf resistances were measured in the quasi-steady-state mode with a constant applied pressure (P) of 0.3 to 0.4 MPa. Stem segments cut at the midpoint of nodes could not be sealed in the compression fittings without leaks, so resistances were measured from stem segments cut at the midpoint of internodes with one node in the center of the segment. The leaf sheath was removed from the node. Constant pressure, P, was applied until a stable flow rate, F, was recorded and the resistance calculated from R = P/F. During these measurements, water flow followed two pathways: from the base of the segment to the apex and from the base to the point of leaf insertion.

The flow through leaf insertion was measured by sealing the apical end of the stem segment with cyanoacrylic glue, and the flow rate through the leaf insertion, F′, was measured at a constant pressure, P′. The resistance of the leaf insertion was computed from R_i = P′/F′. It is not clear whether R_i should be viewed as being in parallel with R or as a separate resistance in series with R but emerging from the middle or R. Values of R_i, measured when the apical internode was sealed with glue tended to be 11 to 14 times R (the resistance with both pathways open). The stem resistance, R_si, was assumed to equal to R − R_I, which probably underestimated R_si slightly. On the other hand, R_i included a small portion of the stem resistance below the node and was probably overestimated.

At the other extreme, we could view R_si and R_i as independent parallel resistors, in which case R_si should be equated to R R_i/(R + R_i). Hydraulic models were computed with both views of the resistance pattern with little difference in the results, so we choose to use the former case to compute R_si and R_i. The resistance values used in the model equaled the resistance from the midpoint of the one node to the midpoint of the adjacent node, and were computed from R_s = (R_bsi + R_asi)/2, where R_bsi and R_asi are the stem resistance of adjacent basal and apical stem segments, respectively. These measurements were repeated for seven to eight segments from the base to the apex of the plant. The two nodes at the top of the plant could not be measured since the internodes were too soft to seal in the compression fittings without crushing them.

Leaf Resistances

Leaf resistance could only be measured while attached to a node because the HPFM could not be sealed to isolated leaf blades or leaf sheaths. Most nodes were surrounded by the sheath of the leaf immediately below. To isolate a single leaf we had to remove all leaves to the apex without damaging the sheath so this could be done only on leaves near the middle of the maize plants where the nodes were above the sheath of the isolated leaf. The internode above the isolated leaf was sealed with cyanoacrylic glue and the HPFM was connected to the internode below the node to which the leaf was attached. The leaves were between 0.9 and 1.2 m long (length of the sheath plus the blade). The resistance of the entire leaf was computed from the applied pressure, P, divided by the quasi-steady-state flow. Then 0.10 to 0.15 m of the leaf apex was excised. This increased the flow and hence decreased the resistance of the remaining leaf. The resistance was recorded and then the process of removal of 0.10 to 0.15 m of leaf apex followed by measurement of the residual resistance was repeated until only the sheath remained. Then the sheath was removed and the resistance of the remaining internode plus node was recorded. The resistance was plotted against the length of leaf remaining, and a computer program was written to fit the curve. Curve fitting using the leaky cable model provided estimates of R_m and R_x per meter length of leaf.

Curve filling in the leaky cable model involved trial and error selection of values of R_m and R_x until a single pair of values provided estimates of leaf resistance that fit the entire curve of resistance versus length of leaf remaining. The basic method of solution is described in the discussion. A non-steady-state simulation program was written to solve for the pressure and flow at each resistance element. The simulation was iterated computationally until the flow (f) into the base of the leaf equaled the sum of the flows out with a constant applied pressure (P) at the base at which point the condition of steady-state flow has been met. The leaf resistance was then computed as P/f and compared with experimental values. We found that a single pair of R_m and R_x values could predict the changes in leaf resistance (P/f) as the leaf was trimmed back from the apex. For a discussion of how the measurement of R_m might differ from the effective R_m during normal transpiration, see Yang and Tyree (1994).

During HPFM measurements, the leaf air spaces filled with water and water emerged both from stomates and through hydaothodes at the leaf margins. A porometer (model 1600, Li-Cor, Lincoln, NE) was used to estimate the rate of evaporation from the upper and lower leaf surfaces during measurement of leaf resistance in the HPFM. This provided information on the percentage of guttation that occurred through stomates.

RESULTS

Tensile Strength and Response Time of Pressure Probe

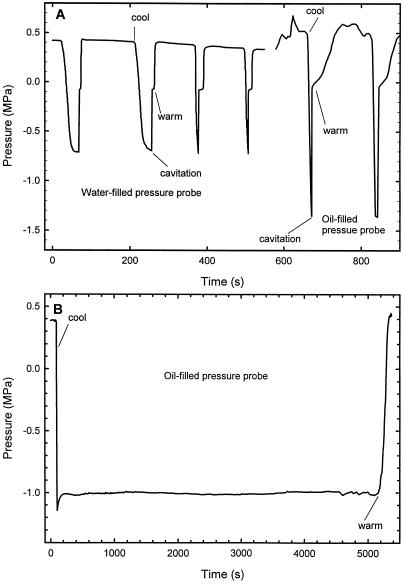
All pressure probes were cavitated 25 to 50 times. Usually, the first few cavitations occurred at less negative pressures than subsequent cavitations, but cavitation thresholds became repeatable when probes were repeatedly cavitated with little time between. Typical test runs for measuring the tensile strength are shown in Figure 3. Water-filled probes tended to cavitate at −0.6 to −0.7 MPa and oil-filled probes at −1.3 to −1.4 MPa. Embolisms were found to be near the metal rod (90% of the cases), suggesting that the most vulnerable air seeds were at the metal surface of both water- and oil-filled probes. In 10% of the cases embolisms were found at a plastic surface. Embolisms were never observed inside the glass microcapillary and never at the oil/water interface (in the microcapillary) of the oil-filled probes. In one instance, a sealed, water-filled probe was taken down to −1.05 MPa (Thürmer et al., 1999), and in a few instances an oil-filled probe was taken to −1.6 MPa (B. Stumpf, personal communication), but these observations are not representative of a “typical” pressure probe. Stable negative pressures could not be held for more than a few minutes when the pressure was within 90% of the cavitation threshold, but negative pressures could be sustained for >1 h within 70% of the cavitation threshold, i.e. about −0.5 and −1.0 MPa in water-filled and oil-filled probes, respectively.

Figure 3.

Measurement of the vulnerability to cavitation of cell pressure probes. Seven different pressure probes were cavitated 25 to 50 times each and these data are typical of many experiments performed. Pressure was a function of the temperature of the sealed microcapillary. In the case of oil-filled probes there was a linear relation between pressure and temperature whereas for water-filled probes the relations were non-linear (data not shown). A, Water-filled pressure probes cavitated at less negative pressure than oil-filled probes. Attempts to hold the pressure very near the threshold of cavitation generally failed within seconds (first two attempts in water-filled probe) and last attempt in oil-filled probe. B, Long-term stability of an oil-filled probe that could hold −1.0 MPa for more than 1.5 h without cavitation; water-filled probes could hold −0.5 MPa for the same period of time (data not shown).

Contrary to earlier suggestions, these data indicate that oil-filled probes are more stable than water-filled probes. This means that measurements with the cell pressure probe should be safe to −1 MPa. This was the range measured in this paper. However, it should be noted that the situation during an experiment (when the tip of the probe is located in a vessel) was somewhat different from that during tests, when the tip is closed, tending to reduce the useful range (see “Discussion”). The tests also showed that cavitation in probes could be reversed by the application of some overpressure for a short period of time (Fig. 3). In the xylem, this is usually thought to be the major mechanism by which repair of embolism takes place (by root pressure or stem pressure in spring).

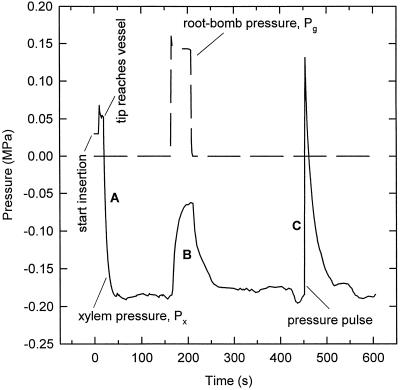
Figure 4 demonstrates how P_x measured with the pressure probe responds to insertion into a vessel, to a rapid change in air pressure in the root-bomb, and to a pressure pulse induced by rapid movement of the metal rod into the pressure probe. When the probe was introduced into a vessel, xylem pressure attained a stationary value after about 30 s (Fig. 4A). A pressure change in the roots was registered rapidly in the P_x of leaf vessels with a response time of 5 to 20 s (Fig. 4B). Response times are related to hydraulic resistances and capacities in the system, including the pressure probe. Reduction of tip diameter increased its hydraulic resistance and the half-time. By measuring the relation between rod position and pressure when the microcapillary is sealed, we found that about 100 nL of water must move into or out of the pressure probe per megapascal change in pressure. (The 100-nL volume displacement is due to the elasticity of the rubber seals in the pressure probe and not due to the compressibility of water.) This volume displacement corresponds to a water column 80 mm long in a vessel 30 μm wide, so a considerable volume of water must flow through the leaf and into the probe before a pressure change in the roots is registered in the probe. In Figure 4C, a positive pressure pulse was produced by rapidly moving the metal rod into the cell pressure probe. It can be seen that in this case, the half-time was about the same as in Figure 4B.

Figure 4.

Test for proper location and functioning of cell pressure probes in the leaf xylem of intact maize plants. In A, the insertion of the cell pressure probe is shown followed by an adjustment to a steady value of P_x. In B, a pulse of pneumatic pressure was applied to the root which was rapidly reflected into a change of xylem pressure (half time: ≈8 s; see also Fig. 4). In C, a typical pressure relaxation is shown following a pressure pulse produced by the probe. Pressure relaxations exhibited short half-times as well (half time of approximately 10 s in the experiment given in the figure). Test B) indicates that the probe was able to rapidly detect changes in xylem pressure. Test C indicates that the tip of the probe was open and that its response time (half-time) for measuring changes was short. It should be noted that the half-time measured in C would represent an upper limit for the resolution in time of changes of P_x that could be detected.

Xylem Pressure versus Root-Bomb Pressure

A typical response of P_x (measured with the cell pressure probe) to P_g is shown in Figure 5A. P_x responded differently to P_g depending on the sign of P_x. P_x changed almost as much as P_g when P_x was < 0 and much less when P_x > 0. This was more clearly visualized when stationary values of P_x were plotted versus P_g (Fig. 5B). Responses were linear in both ranges of pressure. This experiment was repeated on 14 different plants. When P_x was < 0 (below atmospheric pressure), the mean slope of the response was 0.846 (n = 14 plants; sd ± 0.086). Although this slope was close to unity, it was significantly different from unity and may be explained by a slight increase in the transpiration rate of 15% as P_x increased from the initial value to 0 (see below). When P_x > 0 (above atmospheric pressure), the slope was only 0.113 (sd ± 0.040). The air pressure (P_g) required for guttation to occur depended on factors such as soil water potential, hydraulic resistance of the plant, temperature, and relative humidity. Guttation started to occur at a certain threshold pressure P_x that decreased the hydraulic resistance of the guttation pathway (hydaothodes and stomates). The threshold pressure at which the slope changed was equal to or somewhat higher than atmospheric pressure.

Leaf blades became translucent during guttation. When leaves were examined under the microscope at ×200 with surface illumination, water could be seen emerging from the stomates. When water emerged it tended to spread out and form small pools on the leaf surface rather than droplets. This guttation phenomenon could be reproduced using the HPFM. Single leaves were perfused with the HPFM while simultaneously measuring flow rate into the leaf, and the porometer was used to measure the rate of evaporation of water from the surface pools on the upper and lower surface of the leaves. Guttation through the stomates accounted for 90% (sd ± 8%; n = 20) of the flow into the base of the leaf; therefore, flow through hydaothodes was about 10% of the total flow into the leaves.

Effects of Light Intensity on Xylem Pressure

Light intensity may affect transpiration in two different ways. First, at a given stomatal opening, an increase in light intensity increases leaf temperature and the water vapor pressure at the evaporative surface. This, in turn, increases the force driving for the diffusion of water vapor across the stomatal pore. The other way in which light intensity affect transpiration is that an increase of light intensity will usually increase transpiration by increasing stomatal width. Our results (Fig. 6) are in agreement with the conventional idea of a continuous water pipe that rapidly transmits changes in water potential across the plant (CT theory). Light effects were reversible with similar time constants (data not shown). Contrary to other findings (Benkert et al., 1991), responses were substantial even at the relatively low light intensities used in the experiments presented in this paper (150–260 μmol m⁻² s⁻¹).

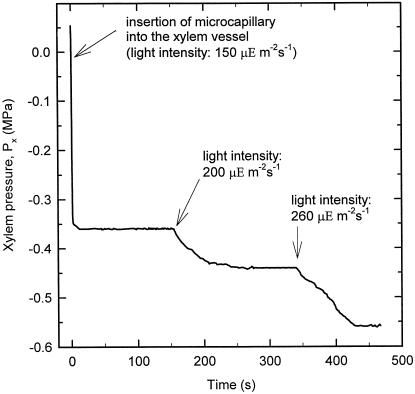
Figure 6.

Effect of light intensity on leaf xylem pressure. In the typical experiment shown, light intensity was 150 μmol m⁻² s⁻¹, when a xylem vessel of the leaf was probed (arrow). It was then increased in steps to 200 and 260 μmol m⁻² s⁻¹ (arrows). It can be seen that there was a substantial and rapid response of P_x to light intensity that correlated with a higher transpiration rate as measured by weighing the plant (data not shown). Note that the half-time for attaining a steady P_x after puncturing was about 5 s and about 20 to 50 s following a change in light intensity.

Comparison between P_x and P_b

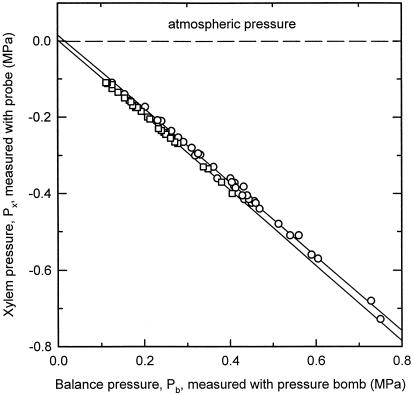
A total of 65 leaves was used for the comparison of P_x with P_b, with stable P_x ranging between −0.11 and −0.73 MPa. Comparison showed a good agreement between P_x and −P_b (Fig. 7). For transpiring leaves, the slope was 0.967 (r² = 0.9964; n = 36 leaves); for non-transpiring leaves, the slope was 0.984 (r² = 0.9988; n = 29 leaves). Both slopes were not significantly different from unity (t test; P = 0.05). These statistics were based only on the P_x values that were stable during the measurements. Forty-two other experiments were performed in which cavitations occurred before stable P_x values could be observed, including P_x values down to −1 MPa. These values were not included in Figure 7 because P_b is an equilibrium measure, whereas the pressure probe is capable of both dynamic and equilibrium measures of P_x.

Figure 7.

Comparison between P_x and P_b measured in the same leaf (Fig. 1). Each symbol represents measurements of P_x and P_b for a different leaf (total: 65 leaves measurement on 65 plants). □, Leaf tip was covered with aluminum foil to prevent transpiration (slope = −0.984); ○, uncovered leaf that was allowed to transpire (slope = −0.967). The results indicate that the pressure probe and the Scholander-Hammel bomb measure similar values.

The dynamic situation is characterized by water flow through the leaf and gradients of water potential and P_x. These gradients disappear when leaves are harvested for P_b measurement. A stable P_x value indicates that the leaf had approached steady-state evaporation with pressure gradients that are time independent. We would expect the offset between P_x and P_b to be proportional to the steady-state transpiration rate. In our experiments transpiration was approximately constant and P_x was changed by adjusting P_g; therefore, we expect and in fact found a constant offset between P_x and P_b. This is in contrast to less-controlled experiments in which P_x varied because of changing transpiration in leaves (Fig. 1; Melcher et al., 1998). Melcher et al. (1998) found better agreement between P_x and P_b in non-transpiring leaves than when the leaves were transpiring, which is fully consistent with the CT theory.

Effect of Root-Bomb Pressure on Transpiration Rate

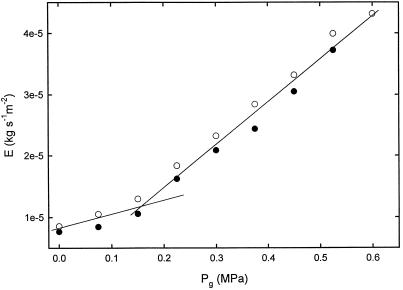
Transpiration rate very much depends on environmental conditions (air temperature, relative humidity, wind speed, etc.) and the plant itself (water status, leaf temperature, stomatal opening, leaf area, etc.). The transpiration rate should increase with increasing root-bomb pressure, because increasing P_g increases the water potential of the shoot and improves its water status. This was observed in the experiments, and a representative plot is shown in Figure 8. Average evaporative flux density (E) measured by weighing ranged from 0.5 to 6 × 10⁻⁶ kg s⁻¹ m⁻² in five replicate experiments. Higher P_g resulted in higher transpiration rates. Effects were reversible, i.e. when P_g was decreased, transpiration also decreased. P_g was changed in steps of ±0.075 MPa within 50 s. After a step change in P_g, 1 to 2 min were required to attain a new stable P_x. Thus, a time period of 9 min was sufficient to attain a stable transpiration rate.

Figure 8.

Effect of increased P_g on E. ●, Increasing pressure; ○, decreasing pressure. Each point is the mean of three 3-min readings and pressure was changed every 10 min. The light intensity for these experiments were less than for Figure 5 because, to get accurate weights, the plant had to be moved so that it did not touch nearby objects; the lights were not moved with the plant. Consequently the initial E values were lower than for most other experiments.

When E was plotted against P_g, the relationship was linear when P_g > 0.2 MPa, which corresponded to the pressure at which guttation began near the base of the maize shoot. The slope with guttation (P_g from 0.2–0.6 MPa) was 7.5 to 9.4 × 10⁻⁵ kg s⁻¹ m⁻² MPa⁻¹ in five replicate experiments. The slope was significantly less, 5 to 8 × 10⁻⁶, for P_g < 0.2. Our findings are in agreement with other reports of an increase in E with increasing root-bomb pressure (Saliendra et al., 1995; Fuchs and Livingston, 1996).

Hydraulic Resistance

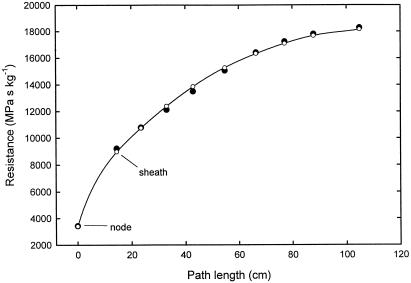
The hydraulic resistance of leaves was maximal in whole leaves and decreased as progressively more tissue was removed from the apex. A typical plot of leaf resistance versus the length of leaf remaining is shown in Fig. 9. These data were fitted to a leaky-cable model of water flow through leaves producing a good fit in all six leaves measured. The R_x of a 1-m length of leaf blade was 6 × 10⁴ ± 1 × 10⁴ (sd) MPa s⁻¹ kg⁻¹. The R_m of a 1-m length of leaf was 4.5 × 10⁴ ± 0.8 × 10⁴ (sd) MPa s⁻¹ kg⁻¹. To simulate the change in resistance after removal of the leaf sheath we had to assume that the xylem and radial resistances were about 1.8 times that of the leaf blade. A summary of root and stem resistances is shown in Table I. The leaf insertion resistances were about 10 times the resistance between adjacent nodes.

Figure 9.

Theoretical (○) and measured (●) hydraulic resistance of a single maize leaf as a function of the leaf length (including the sheath). The leaf was progressively cut back from the tip and the resistance was recorded after each cut. The leaf parameters for the theoretical curve were: R_x = 6.0 × 10⁴ MPa s⁻¹ kg⁻¹ m⁻¹ and R_m = 4.5 × 10⁴ MPa s⁻¹ kg⁻¹ m⁻¹ and a stalk plus node resistance of 1.68 × 10⁴ MPa s⁻¹ kg⁻¹. The R_x and R_m values of the leaf sheath had to be set to 1.8 times the values for the leaf blade to fit the last two points.

Table I.

Summary of R_root, R_si, and R_i

Root or Node No.	Rsi	Ri
	× 10−3 MPa s−1 kg−1
Root + node 1	29 ± 9
Node 2	1.67 ± 0.15	5.94 ± 1.4
Node 3	2.06 ± 0.26	8.36 ± 2.1
Node 4	2.92 ± 0.42	4.9 ± 2.0
Node 5	5.4 ± 1.9	5.5 ± 1.5
Node 6	6.7 ± 1.6	7.1 ± 2.2
Node 7	6.7 ± 1.6	4.0 ± 2.2
Node 8	6.56 ± 0.72	13.8 ± 7.2
Node 9	[7.5]	[15]
Node 10	[8.5]	[20]

Maize plants had 10 nodes numbered from 1 (base) to 10 (apex). R_root includes node 1 because the HPFM could not be sealed to the root below node 1. Resistances for nodes 9 and 10 could not be measured because the tissue was too soft to mount on the HPFM connector, but the values used for modeling purposes are given in square brackets. All values are given as means ± se; n = 6.

DISCUSSION

Pressure probes as they stand have a fairly limited tensile strength. They may cavitate at a pressure that is considerably less negative than that proposed to exist in the xylem of some transpiring plants (−10 MPa according to indirect measurements with the pressure bomb; Kolb and Davis, 1994). To our knowledge, there have been no attempts to measure the vulnerability to cavitation in oil-filled versus water-filled probes nor any suggestions on how to improve probes based on these measurements reported in the literature. Oil-filled probes seem to be superior to water-filled probes, which cavitate at −0.7 versus −1.4 MPa, respectively. Therefore, each type can be used only in its respective range. Immediate improvements in technique would result by switching to oil-filled probes. Another useful improvement would be to replace the metal rod with a rod made out of a material with better adhesive property with the surrounding oil. But as materials are changed in probe design, both water- and oil-filled versions should be tested. With some material, the higher surface tension of water may prove advantageous because of the role of surface tension in air seeding.

With the pressure probe technique as it stands it is not possible to test predictions about the existence of very negative values of P_x as predicted from experiments with the pressure bomb and other techniques. The minimum P_x measured in punctured vessels were somewhat smaller than those found with sealed probes, probably because of probability of air seeding through the seal in the annulus between the outer surface of the micropipette and the wall of the punctured vessel.

From the minimum value of pressure, which could be obtained in sealed pressure probes, we may estimate the maximum diameter (2r) of the air (gas) seeds causing cavitation. This would be given by ΔP = 2τ/r, where ΔP represents the pressure difference of the fluid minus the vapor pressure of the fluid and τ is the surface tension of the fluid (τ = 0.025 Newtons m⁻¹ in an oil-filled probe and 0.073 in a water-filled probe at 20°C). In an oil-filled probe the critical diameter is 76 nm when ΔP = 1.3 MPa and for a water-filled probe the critical diameter is 420 nm when ΔP = 0.7 MPa, i.e. diameters of gas seeds were less than or equal to the wavelength of visible light (400–800 nm). Cavitations are not thought to arise in the bulk liquid phase (water, oil). Cavitations are thought to arise at air seeds harbored in solid/liquid interfaces. Surfaces have to be clean enough to prevent gas-seeding (Fisher, 1948; Briggs, 1950; Zimmermann, 1983; Steudle, 1995). Once the probe is inserted into a vessel another locus of air seeding is the annulus of space between the cell wall of the vessel and the outer surface of the probe.

A thin layer of water with a meniscus may exist at this annulus. The thickness of this annulus, δ, may prove to be the ultimate limitation to the pressure probe techniques. Air seeding through the annulus would occur whenever ΔP > 2τ/δ (assuming δ is much less than the diameter of the hole in the vessel created by the probe). Assuming this annulus harbors an air/water meniscus, the thickness of the annulus must be less than 296 nm when P_x = −1 MPa, which is the most negative pressure measured in this study. Therefore, future experiments designed to measure pressure down to −10 MPa would succeed only if the pressure probe is improved and the annulus is <30 nm thick, i.e. about one-third the thickness of a cell membrane.

Contrary to earlier reports, we find many results immediately consistent with the CT theory, e.g. the quick response of pressure measured in vessels of maize leaves to changes in root-bomb pressure (Fig. 4) and to changes in light (Fig. 6). We also found good agreement between the pressure bomb and the pressure probe (Fig. 7). Our results more than double the range of agreement between the pressure probe and the pressure bomb, i.e. 0 to −0.7 MPa (Fig. 7) versus 0 to −0.3 MPa in Melcher et al. (1998). Other results, such as Figure 5 and the disagreement between P_x and P_b in transpiring leaves reported by Melcher et al. (1998), requires a more detailed analysis of the hydraulic architecture to explain.

A computer model was written to solve for the pressure drop across the network of resistors shown in the hydraulic architecture model of a maize plant (Fig. 2). The method of computation was identical to that used previously (Tyree, 1988) for the dynamic solution of water flow through large trees. The capacitance associated with each resistance element was not measured, so realistic non-steady-state solutions could not be computed, but steady-state solutions are independent of capacitance. Each resistance element (R) was assigned an arbitrary capacitance value (C) such that RC = 1 s. The dynamic solutions were iterated with time steps of dt = 0.5 s until the rate of water flow into the root resistance equaled the sum of water flow out of all leaf segments, which is the condition that defines steady state. The flows at the root and leaf boundaries were determined by the boundary conditions.

The boundary condition used for the root was a pressure equal to the soil water potential plus P_g. The boundary condition at the surface of the leaf segments depended on the pressure at the surface. When the surface pressure was negative, the boundary condition was a constant evaporation rate: A_i g_L ΔX, where A_i is the surface area of the ith leaf segment, g_L is the vapor diffusion conductance (stomates, cuticle plus boundary layer), and ΔX is the driving force on vapor diffusion. The value of A_i g_L ΔX was set at E* + dE*/dP_g where dE*/dP_g was the rate of increase of evaporative flux density with P_g observed in this study before guttation. Guttation starts when the pressure at the surface equals or slightly exceeds 0 (atmospheric pressure). Therefore, the boundary condition at the evaporative surface was changed from E* + dE*/dP_g to pressure = 0 when guttation occurred.

The program listing was originally written in Turbo Pascal and later updated to a Windows 95/98 version of Pascal (Delphi 4.0). Space does not permit printing the full program in this paper but a copy of the program will be provided upon written request to the corresponding author.

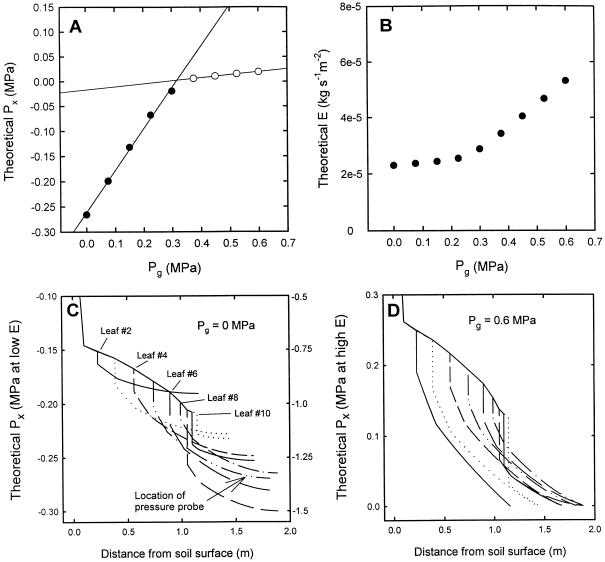
The model successfully predicted the observed dependence of xylem pressure at the pressure probe (P_x) on whole plant evaporative flux density (E) and the dependence on changes in root-bomb pressure (P_g), Figure 10, A and B. The model also made realistic predictions of the gradients of P_x throughout the entire shoot. Figure 10C (left and right axis) shows the predicted gradients of P_x that occur at the PFD of 200 μmol s⁻¹ m⁻² (our experimental conditions) and at 1,200 μmol s⁻¹ m⁻² (typical greenhouse conditions on a sunny day), respectively.

Figure 10.

Theoretical output of the hydraulic architecture model. A, Computed P_x in leaf 5 (0.25 m from the tip) versus P_g (= root-bomb pressure); compare to data in Figure 5B. B, Computed water flow rate put unit leaf area of maize shoot versus P_g; compare to data in Figure 8. C, Computed profile of P_x versus distance in maize stalk and leaves when P_g = 0 and all leaves have an evaporative flux density of E = 2.6 × 10⁻⁵ kg s⁻¹ m⁻² (= 1.44 mmol s⁻¹ m⁻²) on left axis and for E = 13 × 10⁻⁵ (7.2 mmol s⁻¹ m⁻²) on right axis, which corresponds to the probable value in a greenhouse. D, Computed profile of P_x versus distance in a maize stalk and leaves when P_g = 0.6 and guttation occurred from all leaves. Guttation rate at each point along the leaves is in proportion to P_x, so most guttation occurred near the base of the leaves and mostly from the lowest leaves.

The hydraulic architecture model was able to simulate the change of slope as well as the approximate value of the slopes between positive and negative values of P_x (Fig. 10A). The evaporative flux, E*(leaf area), and liquid flow rate should be equal under steady-state conditions. The slope for P_x < 0 would have been 1.0 had the steady-state E remained constant, because then the liquid flow rate from the root to the evaporative surfaces would have been constant and the difference in pressure would have therefore been constant as well. Therefore, an increase in root pressure would necessarily have caused an equal increase in P_x. Direct measurements of E*(leaf area) demonstrated an increase in evaporative flux. An increase in E*(leaf area) should cause a decrease in P_x in the leaf, and an increase in P_g should cause a 1:1 increase in P_x; when both effects are superimposed, a slope < 1 between P_x and P_g would result. Model results confirmed that an increase of E*(leaf area) of about 15% explained a slope of 0.85, while P_g changed from 0 to 0.3 MPa.

This 15% increase in evaporative flux was input into the model as the boundary condition at the leaf surface, but doing so does not explain the increase in evaporation rate. Since the evaporation rate = A g_L ΔX, the increase must be caused either by an increase in g_L or an increase in ΔX. The increase in ΔX can be estimated from the environmental conditions. Air temperature and humidity were about 22°C and 65%, respectively, so the water vapor pressure in the air must have been 1.719 kPa (computed from vapor pressure tables). During the experiment the leaf water potential changed from −0.3 to 0 MPa, which will affect RH and hence vapor pressure at the evaporative surface (equation 2.21 of Nobel, 1991). Given a leaf temperature of 22°C, the vapor pressure at the evaporative surface must have been 2.639 and 2.645 kPa at −0.3 and 0 MPa, respectively, and the increase in ΔX would have been 100*(2.645 − 2.639)/(2.639 − 1.719) = 1.4%. Consequently, the increase in evaporative flux must have been caused by an additional 13.6% increase in g_L and this would explain the slope of 0.85.

The dramatic fall in slope from 0.85 to 0.11 (see “Results”) was somewhat overestimated by the model, which gave a change in slope from 0.832 to 0.06 (Fig. 10A). This dramatic change in slope is caused in part by the dramatic rate of increase in water flow across the root and basal portion of the shoot due to guttation (Fig. 10B). The model predicted that most of the guttation was confined to the base of the shoot (Fig. 10D) and that the guttation started while P_x was still negative (where the pressure probe was located) and P_g = 0.2 MPa (Fig. 10B and other data not shown). Therefore, the water flow was “short-circuited” by the guttation pathway at the base of the shoots (lower diodes in Fig. 2). The pressure probe measured only the much reduced pressure required to drive the reduced water flow rate from the probed vessel at P_x > 0 across the mesophyll resistors (R_m) adjacent to the probe in Figure 2. The model could be fine-tuned to exactly simulate the observed change in slope by making the values of R_x and R_m larger in the lower leaves than in the upper leaves, but we could not confirm this experimentally. The morphology of the shoot permitted measurement of leaf resistance (Fig. 9) only in the largest leaves (leaf 5 or 6) near the middle of the shoot.

The steady-state gradients of P_x are shown in Figure 10C for low and high evaporation rates (read from left and right axis, respectively). These curves provide useful insights into the reason for the deviation between P_x and P_b in transpiring leaves. The relationship (in this paper) between P_x and P_b was very linear with little dispersion of data points about the lines in both transpiring and non-transpiring leaves; the offset between the two lines was also small (about 0.01 MPa in Fig. 7). In contrast, the dispersion of data and the offset was much more in similar work reported by Melcher et al. (1998). The differences can be explained by the hydraulic architecture model and by differences in experimental design. In our experiments the transpiration rate was lower than in Melcher (1998); and in our experiments the leaf tip (0.2 m) just above the probed vessel was harvested for comparison of P_x and P_b; conversely, Melcher et al. (1998) harvested adjacent leaves in the plant.

The model predicted rather minor gradients of P_x in the leaf tip when E = 2.6 × 10⁻⁵ kg s⁻¹ m⁻² (Fig. 10C, read from left axis), and much bigger gradients (Fig. 10C, read from right axis) when E was 5 times more. The model also predicted large differences in P_x between leaves even when E was the same in every leaf; therefore, the experiment of Melcher et al. (1998) was not well designed to compare P_x and P_b because the presumption that adjacent leaves should have nearly identical pressures is clearly wrong. The amount of variation in P_x between adjacent leaves is likely to be even more than shown in Figure 10C (right axis), because this model was computed assuming the same E value for every leaf. In reality, E will be approximately proportional to the adsorbed light energy and the amount of light absorbed by each leaf will vary widely between leaves. Light interception will be equal to the incident radiation times the sine of the angle between the incident rays and the surface of the leaf plane. In addition to this, some leaves will be shaded by other objects (equipment, stalks, leaves, etc.). We recommend that all future comparisons of P_x to P_b be done on the same leaves and that care be taken to document the light intensity on the measured leaf.

Recently, Thürmer et al. (1999) report an extended study of P_x and simultaneous cell turgor pressure (P_t) measurements in mesophyll cells of the leaves of a liana, Tetrastigma voinierianum. Everything presented in that paper is qualitatively consistent with the CT theory, even though the authors failed to draw this conclusion. The authors drew a rather startling and incorrect inference that the minimum attainable P_x value is determined by P_t, i.e. when P_t reaches 0 there is no longer a stable equilibrium between P_t and P_x. Thürmer et al. (1999) write “Considering that the xylem pressure is determined by the turgor pressure (and vice versa), the xylem pressure of the liana could not drop to… less than −0.4 MPa because this pressure corresponds to zero turgor pressure.” The water potential of a vessel should be nearly equilibrated with the water potential of an adjacent living cell. Changes in cell water potential are driven mostly by changes in P_t with little change in osmotic pressure (π) (see fig. 1 in Tyree, 1999). Therefore, P_t and P_x, should increase and decrease together in nearly a 1:1 relationship when the cell osmotic pressure (π) is nearly constant; this has been confirmed quite conclusively in Thürmer et al. (1999).

The minimum P_x is limited only by vulnerability to air seeding and not by the nature of the equilibrium (or lack of equilibrium) between water potential in the xylem (determined mostly by P_x) and water potential in living cells (determined by P_t − π). Clearly, the water potential of living cells can drop below the turgor loss point (Tyree and Jarvis, 1982) and P_x will be approximately in equilibrium with cell water potential until the limit of pressure by air seeding is reached. In woody living cells, P_t could swing to negative values as water loss progresses past the turgor loss point, because the lignified wall prevents cell collapse. Even if these rigid living cells cavitate, equilibrium will continue to exist between the cavitated living cells and the xylem vessels. In soft mesophyll cells, P_t will fall to and remain near zero with water loss beyond the turgor loss point. Mesophyll cells will collapse and decrease in volume because the cellulose is not lignified, and water potential will equal π beyond the turgor loss point, as is easily confirmed by pressure-volume curves (Tyree and Jarvis, 1982). Cavitations generally begin in some vessels near the turgor loss point in many species, but many vessels remain functional to much more negative values of P_x; however, there is no cause-and-effect relationship between loss of turgor in living cells and the start of cavitations.

In conclusion, there is strong evidence in favor of the CT theory of water movement in plants. The CT theory combined with the Ohm's law of quantification of the transport process provides a very robust model capable of explaining all of the observations in this paper. There is also good agreement between the pressure bomb and the pressure probe under well-defined conditions. Large gradients in P_x in transpiring leaves have been known for a long time (Begg and Turner, 1970; Turner and Long, 1980; Turner, 1981). The existence of such gradients does not invalidate the pressure bomb technique. The pressure bomb can measure only the equilibrium P_x of a leaf in a non-transpiring state, which necessarily follows after a leaf is enclosed in a dark and humid chamber. However, most people use the pressure bomb to estimate the average leaf water potential of transpiring leaves. The pressure bomb is ideally suited to do this because, once a transpiring leaf is harvested and mounted in the pressure bomb, the gradients dissipate in the leaf and equilibrium P_x that results is an “average” of the gradients of water potential that existed in the leaf prior to excision. The only exception to this generalization would be expected in leaves with high solute concentrations in the xylem fluid. In general P_x = “average” water potential of the living cells plus the “average” osmotic pressure in the xylem fluid. Some of the theory on how water potentials average has already been worked out (Tyree and Hammel, 1972; Tyree, 1981). The xylem pressure probe is ideally suited to measure P_x at any given point in a leaf and thus could be used to directly measure the gradients within the leaf and to quantify how the water potential gradients within the leaf “average out” to achieve the balance pressure.

ACKNOWLEDGMENTS

M.T.T. thanks the Humboldt Foundation (Bonn) for a research award (Humboldt-Forschungspreis) and Prof. U. Zimmermann for use of several water-filled and oil-filled pressure probes during tests of cavitation thresholds. We acknowledge the expert technical assistance of Burkhard Stumpf (Lehrstuhl für Pflanzenökologie, Universität Bayreuth).