Sporadic sampling, not climatic forcing, drives observed early hominin diversity

Significance

Paleoanthropologists have long been intrigued by the observed patterns of human evolution, including species diversity, and often invoked climatic change as the principal driver of evolutionary change. Here, we investigate whether the early hominin fossil record is of suitable quality to test these climate-forcing hypotheses. Specifically, we compare early hominin diversity to sampling metrics that quantify changes in fossil preservation and sampling intensity between 7 and 1 million years ago. We find that observed diversity patterns are governed by sporadic sampling and do not yield a genuine evolutionary signal. Many more fossil discoveries are required before existing hypotheses linking climate and evolution can be meaningfully tested.

Abstract

The role of climate change in the origin and diversification of early hominins is hotly debated. Most accounts of early hominin evolution link observed fluctuations in species diversity to directional shifts in climate or periods of intense climatic instability. None of these hypotheses, however, have tested whether observed diversity patterns are distorted by variation in the quality of the hominin fossil record. Here, we present a detailed examination of early hominin diversity dynamics, including both taxic and phylogenetically corrected diversity estimates. Unlike past studies, we compare these estimates to sampling metrics for rock availability (hominin-, primate-, and mammal-bearing formations) and collection effort, to assess the geological and anthropogenic controls on the sampling of the early hominin fossil record. Taxic diversity, primate-bearing formations, and collection effort show strong positive correlations, demonstrating that observed patterns of early hominin taxic diversity can be explained by temporal heterogeneity in fossil sampling rather than genuine evolutionary processes. Peak taxic diversity at 1.9 million years ago (Ma) is a sampling artifact, reflecting merely maximal rock availability and collection effort. In contrast, phylogenetic diversity estimates imply peak diversity at 2.4 Ma and show little relation to sampling metrics. We find that apparent relationships between early hominin diversity and indicators of climatic instability are, in fact, driven largely by variation in suitable rock exposure and collection effort. Our results suggest that significant improvements in the quality of the fossil record are required before the role of climate in hominin evolution can be reliably determined.

The factors that shaped diversification in the hominin lineage have long intrigued paleoanthropologists (1). Much of the debate on the underlying drivers of early hominin diversification has centered on whether change in the hominin fossil record is gradual or pulsed (e.g., refs. 2 and 3), and whether diversification is causally linked to discrete shifts in climate or periods of intense climatic instability (e.g., refs. 4–8). The majority of studies report a direct link between climate and either a taxic diversity estimate (TDE) or the frequency of first appearances (a proxy for speciation) (refs. 9–11, but see ref. 12). In all of these studies, however, fluctuations in TDE are routinely accepted as genuine changes in species richness. This is at odds with a large and growing body of evidence indicating that TDE often largely reflects fluctuations in sampling metrics such as rock outcrop area, fossiliferous formation counts (FFCs), collections counts, and locality counts or their total area, more so than a genuine evolutionary signal (13–22).

The covariation between sampling metrics and paleodiversity can be explained by three hypotheses: (i) the rock record bias hypothesis, that human sampling effort and its underlying driver, rock availability, control observed paleodiversity (13, 15, 23); (ii) the common-cause hypothesis, that both genuine diversity and the rock/fossil records are driven by a third, often environmental, factor (24, 25); or (iii) the redundancy hypothesis, that supposed sampling metrics and the fossil record are redundant with respect to each other (i.e., greater collection effort might result in higher diversity, but higher genuine diversity might also result in more collecting) (26, 27).

Here, we test climatic-forcing hypotheses of early hominin diversity alongside the rock record bias, common-cause, and redundancy hypotheses. To do this, we compared TDE and four phylogenetically corrected diversity estimates (PDEs) (28, 29) to: (i) a strict FFC consisting of only those formations that have yielded a hominin fossil; (ii) a wider FFC consisting of all formations that have yielded a primate fossil; (iii) a comprehensive FFC consisting of all formations that have yielded a terrestrial macromammal fossil; and (iv) a proxy for collection effort: the number of years that have yielded a hominin fossil. Using time series and multivariate analysis, we show that early hominin TDE is greatly affected by temporal heterogeneity in fossil sampling, and that the pattern of diversification frequently linked to discrete climatic events is more apparent than real. Lastly, we demonstrate that each PDE shows little relation to sampling and supports gradual change as the primary mode of diversification in the hominin lineage.

Results and Discussion

Early Hominin Diversity Dynamics.

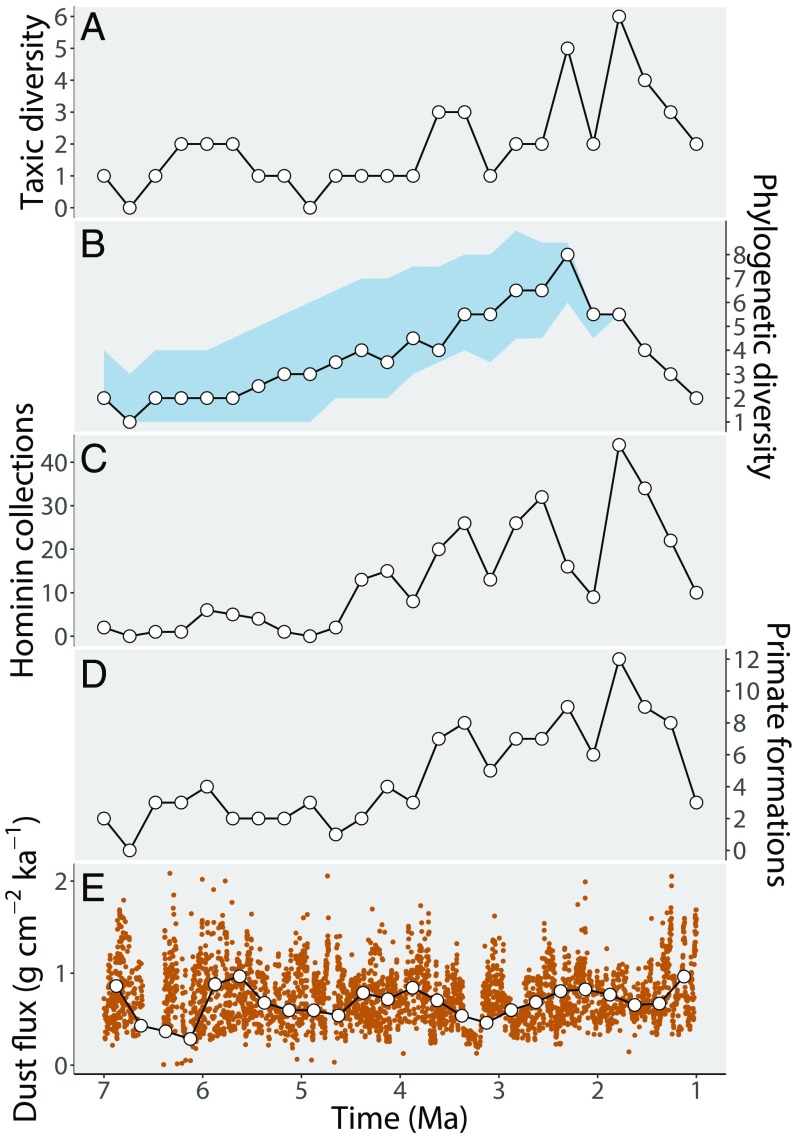
The updated TDE (Fig. 1) is similar to the diversity curve of previous analyses (e.g., ref. 3), displaying three peaks: first, 3.6 million years ago (Ma); second, 2.4 Ma; and third, 1.9 Ma (date refers to the midpoint age of each time bin). Peak TDE (n = 6) occurs at 1.9 Ma. These peaks are separated by troughs at 3.0 Ma and 2.0 Ma, and low-standing diversity during the late Miocene and early Pliocene. Two time bins in the late Miocene to early Pliocene (6.75–6.5 Ma and 5.0–4.75 Ma) do not contain any identifiable hominin fossils and therefore have zero taxic diversity. Overall, TDE displays a classic spiky curve (27), indicative of a genuine signal of speciation and extinction overlain by major fluctuations in sampling.

Fig. 1.

Early hominin diversity estimates, sampling metrics, and terrigenous dust flux through geological time. (A) Taxic diversity estimate (TDE). (B) Phylogenetic diversity estimate (PDE) based on the median of the four estimates shown in SI Appendix, Fig. S1. The blue envelopes represent upper and lower 95% CIs based on the median of 1,000 time-scaling replicates. (C) Hominin-bearing collections (HBCs). (D) Primate-bearing formations (PBFs). (E) Terrigenous dust flux curve (5). Original data appear in orange; interpolated means are shown in white circles with black outline. Data points are plotted at the midpoint age of each time bin.

The PDEs for Strait and Grine (ref. 30; SPDE), Dembo et al. (ref. 31; D1PDE), Haile-Selassie et al. (ref. 32; HPDE), and Dembo et al. (ref. 33; D2PDE) are shown in SI Appendix, Fig. S1; a composite PDE is shown in Fig. 1 (see SI Appendix, Table S1 for a list of abbreviations). Each PDE correlates strongly with one other, both before and after false discovery rate (FDR) correction, and converge on a diversification pattern qualitatively different to the TDE (SI Appendix, Table S2). SPDE, D1PDE, and D2PDE display a long-term increase in diversity from the late Miocene to the early Pleistocene, each reaching peak diversity (n = 7, 8, and 8, respectively) at 2.4 Ma. HPDE differs from the other curves in two aspects. First, although it also displays a long-term increase from the late Miocene onwards, peak diversity occurs during the mid-Pliocene (3.4 Ma). Second, where diversity peaks and then begins to decline in SPDE, D1PDE, and D2PDE, HPDE remains high from 3.4 to 2.4 Ma, after which diversity then begins to decline. Finally, each PDE generally implies one or two more taxa per bin than the TDE (Fig. 1 and SI Appendix, Fig. S1) and thus no time bins have zero diversity.

The composite PDE (Fig. 1) does not display the high-frequency fluctuations that are typical of sampling-driven TDEs (27). However, this does not mean that PDEs are immune from sampling biases. The gradual increase in PDE from 7.0 to 2.4 Ma (SI Appendix, Fig. S1), followed by an eightfold decline from 2.4 to 1.0 Ma, are features of early hominin diversity that require explanation. The steady increase in diversity from 7.0 to 2.4 Ma could reflect the general increase in fossil record quality toward the present (i.e., a long-term sampling signal). Alternatively, early hominin diversity could have increased due to a genuine evolutionary (adaptive) radiation subsequent to the origin of the clade. The post-2.4 Ma fall in PDE from 1.9 to 1.0 Ma, on the other hand, represents a sequence of gradual or coordinated extinctions. However, it is not possible to distinguish between a gradual or rapid extinction scenario for this poorly sampled dataset.

Is Hominin Diversity Controlled by Sampling?

After generalized differencing all time series to remove long-term trends (see Methods and Fig. 1), TDE correlates significantly with both hominin-bearing collections (HBCs) (ρ = 0.457, P = 0.030) and hominin-bearing formations (HBFs) (ρ = 0.618, P = 0.002; SI Appendix, Table S2). Both correlations, however, become nonsignificant after the application of the FDR procedure, and these relationships disappear entirely when HBC and HBF are compared with each PDE (SI Appendix, Table S2). This result could indicate (i) major geological and anthropogenic controls on the sampling of the early hominin fossil record, or (ii) redundancy between early hominin taxic diversity and sampling metrics based solely on counts of early hominin fossils (26, 34). Hominins, like apes today, were probably a minor component of terrestrial ecosystems during their earliest evolution (35) and are therefore expected to be found in a small number of collections/formations during periods of genuine relative low diversity. Conversely, during periods of genuine relative high diversity, hominin fossils are expected to make their way into a greater number of collections/formations. The drive–response relationship between TDE and HBC/HBF is therefore most likely bidirectional, given their interdependence (SI Appendix), and this is corroborated by the fact that the discovery of new hominins and new hominin-bearing formations are intimately linked, having grown in concert through research time (SI Appendix, Fig. S2). This nonindependence (HBFs are as likely to drive TDE as TDE is HBF) calls into question their usefulness as a meaningful sampling metric (26, 34, 36).

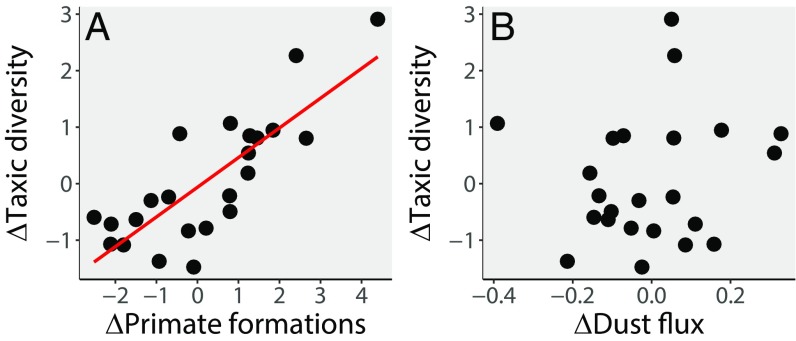
To mitigate the issue of redundancy between TDE and HBFs and more accurately quantify the extent to which sampling controls diversity, we compared TDE to both a wider FFC based on the number of primate-bearing formations (PBFs) and a comprehensive FFC based on the number of terrestrial (i.e., nonmarine) macromammal-bearing formations (MBFs) (SI Appendix). FFCs that include both HBFs and those PBFs/MBFs that have not yielded a hominin, are a priori better sampling metrics than HBFs alone, because they represent a closer approximation of supposed total sampling effort (i.e., collection effort and its underlying driver, the availability of sedimentary rock capable of preserving hominin fossils; ref. 36). HBF alone, in contrast, ignores all sampling opportunities that failed to find a hominin (nonoccurrence) and is therefore not an approximation of total sampling effort (36). When TDE is compared with PBF, it shows a remarkably strong correlation (ρ = 0.742, P < 0.001; Fig. 2) which remains highly significant after FDR correction, implying that observed TDE at any given time is largely controlled by the likelihood of sampling a primate fossil. This correlation completely disappears for each PDE (SI Appendix, Table S2), indicating that the application of only a partial correction for sampling (the addition of cladistically implied, as yet unsampled ghost lineages) produces diversity estimates that show little relation to PBF. On the other hand, when MBF is compared with TDE and PDE, no significant correlations emerge (SI Appendix, Table S2).

Fig. 2.

Scatter plots showing the relationship between early hominin taxic diversity and possible explanatory variables. ∆ indicates that the time series has undergone generalized differencing before statistical testing. (A) Taxic diversity estimate (TDE) against primate-bearing formations (PBFs). (B) TDE against aridity (5). See SI Appendix, Table S2 for correlation coefficients and P values.

Because of its combination of layer-cake stratigraphy and exposure of late Miocene to Holocene fossiliferous sediments through rifting and incision, the East African Rift System (EARS) provides a stratigraphically constrained exemplar for understanding the interaction between Neogene climate and mammal diversification (e.g., refs. 37 and 38). When Plio-Pleistocene eastern African (here including Ethiopia, Kenya, and Tanzania) taxic diversity (TDE_EA) is analyzed separately, the pervasive nature of sampling is also apparent (see also refs. 37 and 39). Here, TDE_EA correlates significantly with both HBC_EA (ρ = 0.546, P = 0.038) and PBF_EA (ρ = 0.575, P = 0.027) (SI Appendix, Table S3). However, these correlations are rendered nonsignificant after FDR correction. Once again, we find no significant correlation between TDE_EA and MBF_EA (ρ = 0.064, P = 0.822).

A highly significant correlation between TDE and PBF on the one hand, and lack of a correlation between TDE and MBF on the other could have three possible explanations: (i) PBF is information redundant with respect to TDE, and MBF (= sampling) does not control diversity; (ii) PBF is information redundant with respect to TDE, and MBF is too broad a measure of the amount of sampling effort in rock suitable for the preservation of a hominin; or (iii) PBF captures a genuine signal of fossil sampling that MBF does not, and largely controls observed TDE. If redundancy were the main cause of these correlations, we would expect the correlation to become weaker the more inclusive the FFC. However, the positive correlation actually increases from HBF to PBF (SI Appendix, Table S2). Further, it is unlikely that TDE drives PBF to the same extent that PBF drives TDE; 39% of PBFs are nonhominin bearing and fossiliferous formations are defined purely on lithostratigraphic grounds. We know of no formations subdivided more finely based on the occurrence of primate fossils, or fluctuations in primate taxic diversity.

For rare and sporadically sampled clades such as hominins, comprehensive FFC might not capture the idiosyncratic nature of fossil preservation and discovery that wider FFC can (but see the case of pterosaurs; refs. 19 and 26). A lack of correlation between TDE and MBF may be a product of most macromammals living in, or being preserved in, habitats that lacked hominins or were unsuitable for them in some way. For example, periods with high MBF could have high TDE if the mammals suitable for preservation in those formations are taphonomically comparable to hominins; but equally, periods with high MBF could have low TDE if the majority of formations preserve habitats unsuitable for hominins, no matter the amount of collection effort a formation receives. This appears to be the case for MBF which, despite containing PBF, correlates weakly with it (ρ = 0.419, P = 0.048; SI Appendix, Table S2). While cercopithecoid and hominoid primates are taphonomically comparable to hominins in terms of body size, morphology, and habitat preference (40), macromammals differ markedly in body size (by several orders of magnitude) and ecomorphology and, as a result, enter the fossil record via different taphonomic pathways. Consequently, the distribution of body sizes in terrestrial mammal assemblages differs markedly by habitat, agent of accumulation, and climate (41). Mammals larger than 180 kg (e.g., Bovidae, Elephantidae, Rhinocerotidae) are overrepresented relative to modern faunas, while the abundance of medium-sized taxa, including large-bodied primates, does not deviate significantly from modern analogs (42). An FFC such as MBF, based on a clade that is preferentially preserved, is therefore less likely to depict a signal of sampling relevant to a rarely preserved and poorly sampled clade.

Defining which formations might preserve a hominin is complex and, to a certain extent, subjective. Although it is better to define a more inclusive clade of interest and compose an FFC based upon its occurrences, the question remains of how wide a clade is required to reach an optimum estimate of sampling intensity (36). Recent model simulations have found that comprehensive FFCs are the best predictor of true sampling, closely followed by all possible formations suitable for the clade of interest and a FFC based on a wider clade of interest (36). Our data indicate that a wider FFC based on primate fossils represents the most meaningful count of the number of preserved depositional environments suitable for the preservation of a hominin. FFCs have been argued (e.g., refs. 16 and 34) to be poor predictors of sampling because they do not consistently correlate with collection effort (but see refs. 21 and 24). However, we find a highly significant correlation between PBF and our proxy for human sampling effort both at the continental (ρ = 0.629, P = 0.002; SI Appendix, Table S2) and regional (ρ = 0.864, P < 0.001; SI Appendix, Table S3) scales.

These findings are of critical importance for climate-forcing hypotheses of early hominin evolution that interpret global and regional climate events, particularly in the EARS, as causal agents in hominin diversification (e.g., refs. 10–12 and 43). Given the strong relationship between early hominin TDE and sampling found here, purported links between diversification and climate need to be reassessed in a paleobiological framework inclusive of this knowledge.

Did Climate Drive Hominin Diversification?

Apparent speciation pulses at 3.6, 2.7–2.5, and 1.9 Ma, coincident with step changes in global cooling and African aridification, were first reported in African Bovidae and inferred in early hominins (ref. 4; but see refs. 44 and 45). More recently, these periods have also been argued to correspond with episodes of intense climatic instability in regional dust flux records and the EARS lake variability index (LVI) (e.g., refs. 11, 46, and 47). The timing of these apparent speciation pulses in bovids does, indeed, coincide with peaks in early hominin TDE (Fig. 1). However, peaks in TDE at 3.6, 2.4, and 1.9 Ma map directly onto peaks in both HBC and PBF (Fig. 1), and in the latter case, MBF. In contrast, we find no evidence of pulsed diversification using any PDE (Fig. 1 and SI Appendix, Fig. S1)—diversity estimates that show no significant relation to sampling (SI Appendix, Table S2). Incidentally, peak MBF at 1.9 Ma also coincides with peak diversity of both EARS bovids and Turkana Basin large mammals (37).

To assess whether early hominin diversification dynamics were controlled by climate, we used time series and multivariate analysis to isolate short-term (i.e., bin-to-bin) fluctuations in early hominin TDE and compared this to HBC, PBF, and a record of terrigenous dust flux (henceforth aridity) to the Arabian Sea (5). We repeated the analysis using TDE_EA plus a record of West African aridity (48) and LVI (11). This differs from previous research (e.g., refs. 10, 11, 43, and 47) by (i) including metrics for sampling, an aspect of the fossil record hitherto ignored in tests of climate-driven hypotheses of human evolution; and (ii) including an intercept-only null model, equivalent to entirely stochastic evolutionary dynamics, into each analysis.

After generalized differencing, we find no link between diversity (either taxic or phylogenetic) and the interpolated aridity curve (Figs. 1 and 2 and SI Appendix, Table S2). This indicates that aridity had little effect on short-term fluctuations in early hominin diversity. We also found no link between aridity and any sampling metric, indicating that the observed relationship between TDE and PBF cannot be explained by a common-cause mechanism at the continental scale (at least for the Arabian Sea aridity curve; ref. 5). The common-cause hypothesis proposes that sampling metrics are driven by the same environmental factors that drove paleodiversity. In the case of hominins, a common-cause mechanism could be implied if aridity controlled both the likelihood of a hominin fossil becoming preserved (via changes in the rate of fluvio-lacustrine sediment deposition) and also diversification rates (i.e., by habitat fragmentation and niche expansion). Such a mechanism could have resulted in a significant but misleading correlation between TDE and PBF, if both were actually independently being driven by a third common cause (24, 25). Despite a causal relationship between aridity and TDE being proposed (e.g., refs. 5 and 6) and reported (e.g., ref. 11), we do not find a relationship here (SI Appendix, Table S2).

To disentangle the underlying mechanism linking the rock record, fossil record, true diversity, and extrinsic abiotic factors, we used generalized least squares (GLS) regression modeling to explore the possibility of multiple explanatory variables driving early hominin TDE. GLS regression modeling has the benefit of assessing the fit of multiple dependent variables while simultaneously accounting for temporal autocorrelation using a first-order autoregressive model. We used both the Akaike information criterion corrected for finite sample sizes (AICc) and Akaike weights (w_i) to assess model fit (Methods). No model fits TDE better than PBF and aridity combined. The removal of aridity from the most supported model yields an approximately equivalent but slightly lower w_i (SI Appendix, Table S4). However, a model including only aridity is the least supported model overall, with an w_i less than the null. In every model with a nonnegligible weight (w_i > 0.01), the only significant predictors of TDE are PBF and HBC. However, HBC is only significant in a single predictor model. The four models with the highest rank all contain PBF, while the lowest four contain collections and aridity. Thus, rather than a common-cause explanation in which aridity drove both diversity and sampling, our results support a simpler relationship in which TDE is controlled by sampling, and aridity does not appear to drive either of these parameters.

In the EARS, the appearance and disappearance of precessionally driven deep lakes has been causally linked to peaks and troughs in early hominin diversity (11). Lake high stands are argued to promote population isolation and allopatric speciation in a spatially constrained landscape, while lake low stands are thought to increase competition and extinction, given the limited resources (11). However, any such correlation can also be interpreted as reflecting the impact of lake levels on preservation rates. For example, during lake high stands, deposition of fluvio-lacustrine sediments will increase and the remains of terrestrial organisms will be more likely to reach aquatic environments and fossilize; conversely, during lake low stands or desiccation, sediment deposition will decrease, erosion rates will increase, and terrestrial remains will be less likely to reach aquatic environments and fossilize. Peaks and troughs in TDE_EA could represent a taphonomic bias imposed by the impact of fluctuating lake levels and wetter local conditions on the preservation potential of terrestrial taxa. Pairwise tests revealed no correlation between TDE_EA and LVI, expressed as either the mean or maximum value per time bin (SI Appendix, Table S3). In addition, we found no correlation between sampling metrics and LVI (SI Appendix, Table S3), once again ruling out a common-cause mechanism underlying the relationship between taxic diversity and sampling metrics. The lack of a correlation between TDE and aridity/LVI could be a result of (i) different datasets used to estimate TDE, (ii) different first and last appearance dates, (iii) temporal resolution (i.e., time bin size), or (iv) the use of generalized differencing. Of these explanations, the use of generalized differencing appears to be the key factor: TDE_EA (r = −0.521, P = 0.039) and LVI (mean: r = −0.683, P = 0.007; maximum: r = −0.572, P = 0.021) both display a significant linear trend (note the negative sign as time decreases toward the present). Indeed, TDE_EA and mean LVI correlate significantly before generalized differencing (ρ = 0.687, P = 0.003), suggesting that much of the support for a link between TDE_EA and LVI may relate to the comparison of two positive long-term trends which in reality show no tendency to increase or decrease in tandem over the short term, as would be expected if they had a cause-and-effect relationship.

We repeated the multiple regression modeling including only those data from the Plio-Pleistocene of eastern Africa plus the 5-My West African aridity record (48) and LVI (11). Here TDE_EA is best explained by PBF_EA (SI Appendix, Table S5). However, a combination of PBF_EA + Arabian Sea aridity is the second-best model with a difference in w_i of less than 0.001, and a combination PBF_EA + West African aridity the third-best model. In the four models with the highest rank, three contain PBF and one HBC. In these models, the only significant predictors are PBF and HBC. The four models with the lowest rank contain aridity as single predictors and in combination, plus a model combining LVI and both aridity proxies. These results indicate that sampling heterogeneity has a considerably greater influence on apparent diversification patterns in the early hominin fossil record than regional climate records. We find no quantitative support for the pulsed turnover hypothesis (4), aridity hypothesis (5), variability selection hypothesis (7, 8), or pulsed climate variability hypothesis (46) in the early hominin lineage. Instead, we find strong evidence that rock record bias is largely responsible for the pattern of early hominin diversity that each of these climate-forcing hypotheses purport to explain. By failing to account for the temporal heterogeneity in fossil sampling, artifactual fluctuations in early hominin taxic diversity have erroneously been linked to climate. Given the immaturity of the early hominin fossil record (SI Appendix, Fig. S2), a sustained and major increase in sampling intensity is undoubtedly required before an accurate understanding of the link between climate and early hominin diversification can be determined.

Conclusion

Long-term variation in aridity and climatic instability probably played a key role in the emergent adaptive strategies taken by hominins in the Plio-Pleistocene. However, we find no evidence that short-term fluctuations in climate relate to changes in hominin diversity. Instead, our data support a direct, causal relationship between TDE and fossil sampling. The near-linear increase in PDE from 7.0 to 2.4 Ma negates any explanation based on climate-driven pulsed turnover and corroborates recent interpretations that events in human evolution once thought to be major transitions, when viewed in a phylogenetic (i.e., lineage) context, actually represent gradual adaptive shifts (e.g., 3 and 49). The identification of a major sampling component in the early hominin fossil record indicates that the pattern of diversification which many climatic forcing hypotheses purport to explain is more apparent than real. This should come as no surprise: approximately one-quarter of early hominin species are point occurrences and the remainder have considerable uncertainties on their known stratigraphic durations. Radiometric dating error associated with a first (last) appearance date is not equivalent to statistical uncertainty that the date represents a speciation (extinction) event. Nor is the finding that radiometric dating error is random with respect to a climate event (47) an appropriate test of the quality of the fossil record. If error were randomly distributed in the early hominin fossil record, any genuine evolutionary signal would be degraded not distorted (50). However, runs tests demonstrate that collection effort (P = 0.004) and rock availability (P < 0.012 for each FFC) are nonrandomly distributed in the early hominin fossil record. The starting point for macroevolutionary analyses in paleoanthropology ought to be that, before any pattern in the fossil record is causally linked to climate, it is demonstrably shown that that pattern is not an artifact of sampling or poor fossil record quality. This requirement has been overlooked by paleoanthropologists, archaeologists, and climatologists alike, and has severely impacted the interpretation of macroevolutionary pattern and process in the early hominin fossil record (51). Becoming cognizant of the rapidly advancing study of fossil record quality in paleobiology, particularly since the pioneering work of Raup (13, 23), should be at the center of 21st century paleoanthropology.

Methods

Taxic Diversity Estimate.

Taxic methods assess diversity by counting the number of observed taxa in a series of time bins based on their stratigraphic range. We used the first-appearance datum (FAD) and last-appearance datum (LAD) of 18 species in Wood and Boyle (52) to compile TDE in 0.25-My time bins between 7 and 1 Ma (SI Appendix, Table S6). If a FAD or LAD falls on the boundary of a time bin (e.g., 2 Ma), that taxon is deemed present only in the younger bin (in this case, 2–1.75 Ma).

Phylogenetic Diversity Estimate.

Phylogenetic methods assess diversity by counting the number of lineages (observed and inferred) in a series of time bins using a dated (i.e., time scaled) phylogeny. We generated PDEs in equivalent time bins using four comprehensive hominin phylogenies (30–33) that sample the largest number of taxa included in the TDE. Polytomies in the strict consensus (30) and majority-rule (32) cladograms were resolved based on the order of first appearance. To maximize comparability between datasets, Eurasian taxa and taxa younger than 1 Ma were pruned from each cladogram after time scaling, as the focus here is early hominin diversity dynamics.

The phylogenetic method requires that branch lengths are proportional to time. To do this we time scaled each tree using taxon duration data and the three-rate-calibrated time-scaling (cal3) method (53). The cal3 method constrains the age of each node between the date of the previous node (except for the root) and the FAD of daughter lineages. The age of each node is then calculated by the probability density of the amount of unobserved evolutionary history implied by each node age, a probability dependent on rates of speciation, extinction, and sampling in the fossil record (53). These densities are then used to stochastically sample the possible ages for each node (53). Speciation, extinction, and sampling rates were first determined empirically in the R package paleotree (54). This function applies a maximum likelihood optimization to the distribution of taxon durations and returns the best fitting sampling probability and extinction rates to explain the distribution (55). Speciation and extinction rates are assumed equal, given the tight relationship observed in the fossil record (56). Results presented for the calculation of speciation, extinction, and sampling rates are based on the taxon durations shown in SI Appendix, Table S6, as the main interest here is the sampling and diversification of early hominin taxa. This method, however, produced an estimated sampling rate that differed markedly from previous estimates for mammals (57). Moreover, the frequency-ratio method (58) did not provide a meaningful estimate of sampling because the frequency distribution of taxon durations violated model assumptions (the equations of ref. 58 require that the frequency distribution of the log of taxon durations is linear). To combat this, the sampling rate reported for primates (0.023 per lineage My; ref. 59) was used plus a maximum root age of 8 Ma. Because node ages are stochastically picked from a distribution defined by the probability of different amounts of unobserved evolutionary history, no single time-scaled tree is correct. Therefore, to account for uncertainty in the age of each node and improve analytical rigor, 1,000 time-scaled trees were generated. The median diversity across all 1,000 trees was calculated along with CIs based on two-tailed 95% upper and lower quantiles (54). It is this median PDE which is used in the statistical tests. Interestingly, the cal3 method produced median node ages that correlate strongly with the node ages produced by Dembo et al. (31) (r > 0.98, P < 0.001) and Dembo et al. (33) (r > 0.94, P < 0.001) in their Bayesian tip-dating analyses. Tip-dating methods tend to produce node ages that are several million years older than the minimum (i.e., fossil) divergence date (60), while cal3 node age distributions tend to be similar to the minimum divergence date (57). The agreement between tip dating and cal3 is, therefore, likely a result of the range of possible node ages being tightly constrained by the input topologies and FAD.

Sampling Metrics.

Rock outcrop.

Temporally resolved information on sedimentary rock outcrop area is not available at the continental level for the late Neogene, so instead, we use FFCs. FFCs summarize aspects of rock volume, facies heterogeneity, geographical and temporal dispersion, and collection effort (16, 22) and have been shown to correlate with rock outcrop area (e.g., ref. 21) and gap-bound packages (e.g., ref. 24 but see ref. 61). FFCs represent an estimate of the number of discrete depositional environments known to contain fossils and are thus a proxy for the amount of rock available for sampling in a given time bin. HBF counts were taken from an exhaustive survey of the published literature. Fossil-bearing deposits in the Cradle of Humankind, South Africa, were counted as one “formation” (SI Appendix). This had minimal effect on the results as HBF and a count including each deposit as a distinct formation correlate strongly (ρ = 0.941, P < 0.001). The same treatment is applied to other primate- and mammal-bearing karst deposits. PBF counts were taken from the chapters on cercopithecoids (62), hominins (63), and lorisoids (64) in Cenozoic Mammals of Africa (65) and corroborated using the Paleobiology Database (PBDB). MBF counts were similarly gathered from the PBDB and Cenozoic Mammals of Africa (65), and excluded small (i.e., Chiroptera, Eulipotyphla, Hyracoidae, Lagomorpha, Macroscelidea, and Rodentia) and nonterrestrial (i.e., Cetacea and Sirenia) mammals (SI Appendix).

Collecting effort.

In-bin counts of the number of HBCs were compiled as a proxy for collecting effort. A collection is defined as an assemblage of fossils from one locality that were amassed in a single effort and is roughly equivalent to a field season. Information on the duration and number of field seasons at a locality are not commonly provided so, instead, we used the number of years that have produced a hominin fossil per formation per bin (SI Appendix). For example, Sahelanthropus tchadensis is known from the 7-Ma Anthracotheriid Unit (Chad) and the fossils that compose its hypodigm were collected in 2002 and 2005. The 7.0–6.75 Ma time bin therefore has a HBC count of 2. The number of HBCs in a given time bin thus represents the number of discrete episodes of field study (i.e., paleoanthropological collection effort) that have yielded a hominin fossil. These data are up to date as of November 1, 2017.

Climate proxies.

TDE and PDE were compared with the 8-My Arabian Sea (5) and 5-My West African (48) terrigenous dust flux records, and the LVI (11). Dust flux data were interpolated to 50-kiloannum (ka) intervals using the shape-preserving piecewise cubic hermite interpolating polynomial, enabling us to calculate the mean and SD of each time bin. To convert the LVI into our time bins (in the original publication, LVI is given in 50-ka time bins; see figure 1 in ref. 11) we took the mean and maximum value in each time bin.

Statistical Tests.

Spearman’s rank (ρ) and Kendall’s tau rank (τ) correlation coefficient were used to compare all diversity estimates, sampling metrics, and climate proxies (66). Time series were detrended and corrected for autocorrelation by generalized differencing before regression (ref. 67, R code from www.graemetlloyd.com/methgd.html). Long-term trends and autocorrelation tend to result in spurious detection of correlation between time series (67) and thus must be removed before performing statistical tests (68). The significance of correlations was evaluated based on original P values and P values adjusted for the implementation of multiple tests using the FDR procedure (69). GLS model fitting was performed to explore the possibility of multiple variables explaining taxic diversity, with model fit assessed using the second-order AICc, corrected for finite sample sizes, and the relative likelihood of each model based on w_i (70). Models were created for all possible combinations of variables plus an intercept-only null model, representing statistically random variation around a constant mean. The Breusch–Pagan test was used to assess heteroskedasticity of residuals. Heteroskedasticity may cause overestimation of model fit; however, no cases of heteroskedasticity were found. We also used Wald–Wolfowitz runs tests to investigate the null hypothesis of randomness and data independence in a time series (66). All analyses were performed in R 3.4.3 (71).