Suppressing viscous fingering in structured porous media

Significance

Viscous fingering commonly takes place during injection of one fluid that displaces a resident fluid in a porous medium. Fingering normally is promoted where the injected fluid is less viscous than the resident fluid being displaced. We propose a design of a porous medium in the form of an ordered structure to suppress or trigger (depending on the application) viscous fingering in porous media without modifying fluid properties or wettability. We utilize pore-scale direct numerical simulations, state-of-art experiments and analysis to derive predictive tools to evaluate effects of various parameters on controlling viscous fingering in porous media. Moreover, we propose generalized analytical solutions and a phase diagram for the parameter space affecting viscous fingering patterns.

Abstract

Finger-like protrusions that form along fluid−fluid displacement fronts in porous media are often excited by hydrodynamic instability when low-viscosity fluids displace high-viscosity resident fluids. Such interfacial instabilities are undesirable in many natural and engineered displacement processes. We report a phenomenon whereby gradual and monotonic variation of pore sizes along the front path suppresses viscous fingering during immiscible displacement, that seemingly contradicts conventional expectation of enhanced instability with pore size variability. Experiments and pore-scale numerical simulations were combined with an analytical model for the characteristics of displacement front morphology as a function of the pore size gradient. Our results suggest that the gradual reduction of pore sizes act to restrain viscous fingering for a predictable range of flow conditions (as anticipated by gradient percolation theory). The study provides insights into ways for suppressing unwanted interfacial instabilities in porous media, and provides design principles for new engineered porous media such as exchange columns, fabric, paper, and membranes with respect to their desired immiscible displacement behavior.

The unstable growth of fluid−fluid interfacial perturbations has been the subject of a large literature owing to its many applications: for example, fluid mixing in microfluidics (1), chromatographic separation of solvents (2), infiltration of water into soils (3), oil recovery from underground reservoirs (4, 5), carbon dioxide sequestration (6, 7), and the formation of plumes in midocean ridges (8), to list a few. For viscously dominated flows, Hill (9) and Saffman and Taylor (10) were the first to quantify the highly ramified morphology of an interface resulting from displacement of a viscous fluid by a fluid of lower viscosity and so document the emergence of finger-like invasion patterns [viscous fingering (VF)]; Hill (9) investigated the process using a packed bed, while Saffman and Taylor (10) employed fluid-filled Hele-Shaw cells to study VF. An excellent review on VF is provided by Homsy (11). Although the fundamental principles governing interfacial instability are relatively well understood, their manifestation in porous media with rich morphologies of displacement fronts remains an active field of research.

Fluid VF during immiscible displacement in porous media is relevant to a variety of applications. In oil recovery from geologic reservoirs, VF can result in early breakthrough of the invading fluid (often water or brine), thus diminishing the efficiency of oil recovery and at times rendering it uneconomical (4, 5). In environmental applications, VF has been implicated in the potential for early arrival of pollutants to underlying groundwater resources. The technological challenges presented by VF have prompted numerous theoretical and experimental studies (12–20). Some of the studies have shown that the use of non-Newtonian fluids (13) or nonlinear control of injection rate (17) stabilize the fluid−fluid interface. Other studies (14–16) suggest that alteration of wetting properties of the porous medium offers a potential remedy for eliminating VF. However, for many applications, the alteration of wetting characteristics of the porous medium is not trivial; hence other solutions must be developed to control VF.

In this research, we demonstrate the influence of regular pore size variations in a porous medium as a means for suppressing the growth of viscous fingers during immiscible displacement. Such a statement may appear counterintuitive at first glance, because, in the literature, pore size variations are considered to be a factor that enhances the frequency of fluid front tip splitting and thus intensifies the fingering phenomenon (15). We report a structure in the form of an “ordered porous medium” in which pore size varies monotonically along the direction of flow. From the physical point of view, such an ordered porous medium allows simultaneous control over viscous and capillary forces in the same direction, which is otherwise rare in random porous media and has not been studied before. The prescribed structure of the porous media is inspired by the theory of percolation under a gradient introduced by Wilkinson (21) which has been used to describe displacement patterns in porous media (22–24). The work of Xu et al. (23) combines gradient percolation with conventional invasion percolation to derive the now classic phase diagram of Lenormand et al. (25) for the fluid front stability in random porous media. In addition, Yortsos et al. (24) extended the approach to model flow profiles in spatially correlated pore networks. In the studies above, a percolation gradient was introduced in the form of an externally applied pressure drop using a set of local pore filling rules. In particular, Yortsos et al. (24) conjectured that a gradient of pore network correlations could act to trigger or suppress VF, yet, to date, no experimental or theoretical evidence supports this conjecture. Although recent studies (18, 19) have indicated that gradual variation in the thickness of a Hele-Shaw cell can significantly restrain VF, no studies have shown how gradual pore size variation would affect VF in porous media (which is a more complicated system than a Hele-Shaw cell).

In this study, we combine experiments, numerical simulations, and theoretical analysis to demonstrate how a porous medium with ordered pore sizes controls (i.e., triggers or suppresses) VF during immiscible flow in porous media. We begin with a porous medium (uniform and ordered) saturated with high-viscosity defending fluid where low-viscosity invading fluid displaces the defending fluid at various flow rates. Our results show that fluid fronts traversing a porous medium where the pore size is gradually reduced along the flow direction results in a velocity-dependent morphological transformation of the front from unstable to stable. Moreover, we show that stabilization of the invasion front at high injection rates requires an increase in the pore size gradient along the flow path. These results provide a means for inhibiting or triggering VF and interfacial instability in engineered porous materials. The insights gained from this study pave the way to new designs of chromatographic columns, membranes, sensors, and other porous media such that the displacement front morphology is unconditionally stable (under prescribed operations conditions), and improve fundamental understanding of VF in porous media. This study is limited to drainage conditions only.

Results and Discussion

Experiments.

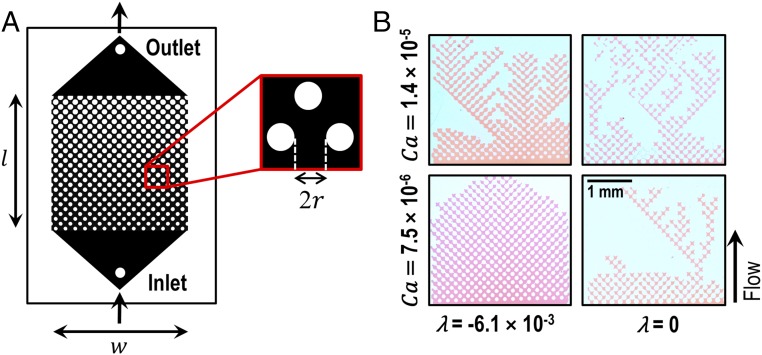
We conducted fluid displacement experiments in micromodels of ordered porous media [Fig. 1A; all four sides were made from polydimethylsiloxane (PDMS)]. We first filled the device with silicone oil (viscosity ${\mu }_2$ = 200 mPa⋅s), and then injected water (colored with red dye, viscosity ${\mu }_1$= 1 mPa⋅s) at a constant flow rate $Q$ to displace the silicone oil, which wetted the surface. The experimental results for two different capillary numbers $Ca$ = 7.5 × 10⁻⁶ and 1.4 × 10⁻⁵ are shown in Fig. 1B. The capillary number is defined as $Ca={\mu }_{1}U/\sigma$, where $U$ is the area-averaged (Darcy) velocity, and σ = 28.2 mN/m is the interfacial tension between the two fluids. The displacement is unstable at both $Ca$ for a uniform porous medium ($\lambda =0$), as expected according to the traditional VF criterion. Note that $\lambda =(r_o-r_i)/l$ represents the pore size gradient where $2r_o=520\mathrm{\mu }\text{m}$ is the pore width at the outlet, $2r_i$ = 880 μm is the pore width at the inlet, and $l=$ 29.5 mm is the length of the ordered region. However, for a nonuniform porous medium ($\lambda =$ −6.1 × 10⁻³), stable displacement is achieved at the lower $Ca$, and becomes unstable at higher $Ca$. These results suggest that there is a capillary number range where the reduction in pore size along the flow direction can stabilize the displacement of a fluid with higher viscosity during injection of a fluid with lower viscosity. We next turn to numerical simulations to develop more understanding of the macroscopic and microscopic features of these observations.

Fig. 1.

(A) Design of the microfluidic device. The lengths of the ordered medium l and the pore radius r are indicated. (B) Experimental results for Ca = 7.5 × 10⁻⁶ and 1.4 × 10⁻⁵ for a uniform porous medium with λ = 0 and a nonuniform medium with λ = −6.1 × 10⁻³. The invading fluid is water with red dye, and the displaced fluid is transparent silicone oil; the flow is from the bottom to the top.

Numerical Simulations.

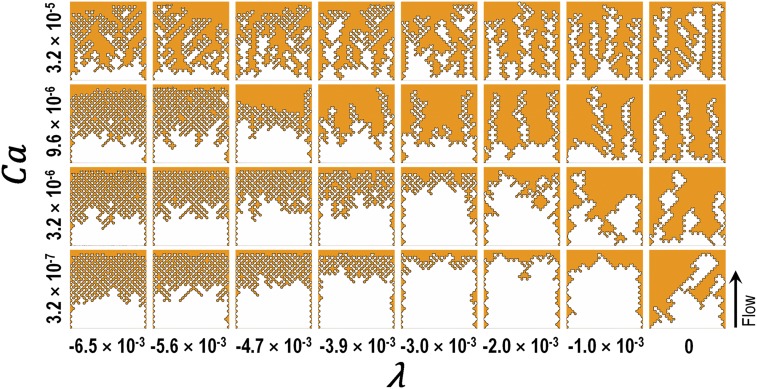
Details about the numerical setup and boundary conditions are presented in Materials and Methods. Fig. 2 shows the morphology of the displacement patterns obtained from the numerical simulations at different values of $Ca$ and $\lambda$. Note that, in the present study, capillary fingering is absent and therefore does not play a role in controlling the displacement patterns.

Fig. 2.

Simulation results demonstrating displacement fluid front morphologies for different values of the capillary number Ca and the pore size gradients λ at the time where the invading fluid reaches the outlet (the direction of displacement is from bottom to top). The white, orange, and black colors represent invading fluid, defending fluid, and the interface, respectively. The viscosities of the invading fluid µ₁ and defending fluid µ₂ were kept constant at 10⁻³ Pa⋅s and 10⁻¹ Pa⋅s, respectively. The viscosity ratio of defending fluid over invading fluid M = 100. The results illustrate that fingering is suppressed as λ becomes more negative. Moreover, for λ = −1.0 × 10⁻³, −3.0 × 10⁻³, and −4.7 × 10⁻³, the critical capillary numbers Ca_C at which the crossover from VF to CD takes place are 3.2 × 10⁻⁷, 3.2 × 10⁻⁶, and 9.6 × 10⁻⁶, respectively.

The morphology of the invading fluid−fluid interface reflects the combined effects of $Ca$ and $\lambda$, as shown in Fig. 2. Results show that, at high displacement rates with $Ca$ = 3.2 × 10⁻⁵, there is no stabilizing effect of negative $\lambda$ on VF (for the range of $\lambda$ values considered), resulting in almost similar displacement patterns for all cases. However, at lower capillary numbers, there exists a critical capillary number ($C{a}_c$) that indicates a transition in front propagation from VF to compact displacement (CD) for a prescribed value of the pore size gradient $\lambda$. The simulation results in Fig. 2 suggest that $\lambda$ is related to $C{a}_c$ approximately as $C{a}_c\approx {\lambda }^2$ (we will expand upon this in Theoretical Analysis).

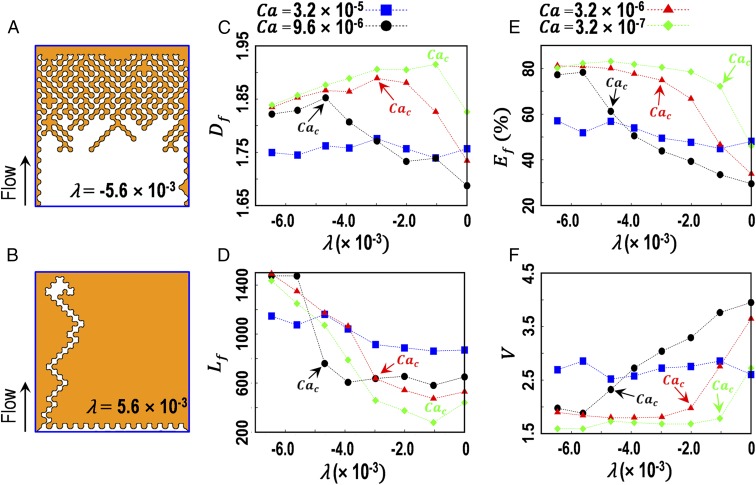
The experiments and simulations shown in Figs. 1 and 2, respectively, highlight the interplay of capillary and viscous forces on multiphase flow (immiscible) displacement in porous media and the role of the pore size gradient that may affect both forces simultaneously and the resulting front morphology. To provide additional insights, we performed simulations where all of the properties are kept constant except for changing the sign of $\lambda$ (in essence, reversing the direction of fluid injection). Typical examples in Fig. 3 A and B depict displacement front patterns in porous media with $\lambda$ = −5.6 × 10⁻³ and $\lambda$ = 5.6 × 10⁻³, respectively. Based on its definition, positive and negative values of $\lambda$ correspond to cases where, respectively, either smaller or larger pores are present at the injection location. Inspection of the patterns in Fig. 3 A and B illustrates the dramatic effect of displacement front flow direction with respect to the pore size gradient. Although the pore size distribution, porosity, wetting, and fluid properties were identical in the two cases, Fig. 3 A and B shows that the gradient in pore size relative to the front flow direction resulted in significantly different displacement patterns. For the scenario where $\lambda$ = 5.6 × 10⁻³ with continuously increasing pore sizes along the direction of flow, VF is accentuated as the lower viscosity fluid preferentially flows through the least resistant pathway. In contrast, when the flow direction is reversed and $\lambda$ = −5.6 × 10⁻³, the fluid−fluid interface becomes more stable (compact), and the front spans the entire width of the domain. For a range of negative $\lambda$, we observe local short fingers on the order of pore sizes (an example is presented in Fig. 3A), which is referred to as “microfingering” in this study.

Fig. 3.

(A and B) Effects of the sign of λ on the morphology of displacement patterns (white) in porous media. Negative (A) and positive (B) values of λ correspond to the cases when the large and small pores, respectively, are placed at the injection point. In both cases, the capillary number was kept constant at Ca = 3.2 × 10⁻⁶, and the viscosities of the invading and defending fluids were constant at 10⁻³ Pa⋅s and 10⁻¹ Pa⋅s, respectively. The direction of displacement is from bottom to top. The white, orange, and black colors represent invading fluid, defending fluid, and interface, respectively. The observed contrast in the displacement patterns indicates the substantial impact of the sign of λ on the interface morphology and dynamics and the resulting macroscopic response. (C) Fractal dimension D_f, (D) interface length L_f normalized with respect to r_i, (E) displacement efficiency E_f (%) defined as the ratio of the recovered volume of the defending fluid to its initial volume, and (F) normalized fingertip velocity V.

To systematically quantify front behaviors observed in Fig. 2, we computed four metrics aimed to characterize front displacement patterns as functions of the prescribed $Ca$ and $\lambda$: (i) front fractal dimension $D_f$ (Fig. 3C), computed using the box-counting method following Shokri et al. (26), which measures the interface roughness; (ii) the fluid−fluid interface length $L_f$ (Fig. 3D) spanning the length of the interface between invading and defending fluids normalized with respect to $r_i$; (iii) displacement efficiency $E_f$ (%), defined as the ratio of the recovered volume of the defending fluid relative to its initial volume (Fig. 3E); and (iv) normalized fingertip velocity $V$ (Fig. 3F). To calculate $L_f$ and $E_f$, each image shown in Fig. 2 was segmented in ImageJ (27) and used to calculate these parameters. The fingertip velocity was directly measured as the ratio of the distance traveled by the interface over time_, and then normalized with respect to the injection velocity.

As shown qualitatively in Fig. 2, all metrics corresponding to $Ca$ = 3.2 × 10⁻⁵ remained insensitive to $\lambda$ for $\lambda <0$, while, for other values of $Ca$, the pore size gradient $\lambda <0$ exerted a significant impact on each of the metrics presented in Fig. 3 C–F. Closer inspection of the results displayed in Figs. 2 and 3 reveals that the maximum value of $D_f$ as a function of $\lambda$ corresponds to the case when a transition from a stable to an unstable displacement pattern is observed. This maximum value is used to classify the observed patterns as stable or unstable, with the corresponding critical capillary number denoted $C{a}_c$.

Theoretical Analysis.

Our experimental and numerical results confirm that a prescribed gradient in pore size ($\lambda <0$) along the fluid displacement flow direction can significantly affect the onset of VF. In this section, we develop a generalized capillary number $C{a}^{\ast }$ that incorporates the contribution of the pore size gradient $\lambda$ and quantifies the relative importance of viscous and capillary forces. Furthermore, using linear stability analysis, we derive a criterion for the conditions that separate stable and unstable displacement patterns. Such a stability criterion can aid in the design of structured porous media to achieve desired results (fingering or stability, depending on the application) under given boundary conditions. A schematic of the porous medium used to formulate the theoretical framework is presented in Fig. S1. Note that, while inertia was considered in the direct numerical simulations (DNSs) using computational fluid dynamics (CFD), following Saffman and Taylor (10) and Al-Housseiny et al. (18), in the analytical analysis presented below, effects of inertia on two-phase displacement were neglected (justified by the relatively slow flows in porous materials). It should be noted that the gravitational force is included in the theoretical analysis.

The generalized capillary number $C{a}^{\ast }$ is derived by applying a force balance (28–30) as the interface moves from position a to position b (see Fig. S1). The stress balance is expressed as (the subscripts correspond to the positions a and b)

$${\tau }_{v_a}+{\tau }_{v_b}+{\tau }_g={\tau }_{c_a}+{\tau }_{c_b}$$ [1]

where ${\tau }_v$ is the viscous stress over a unit interfacial length, ${\tau }_g$ is the gravitational stress that drives the interface forward, and ${\tau }_c$ is the local resistive capillary stress. Viscous stresses over a characteristic length $l_x$ can be evaluated as ${\tau }_v\approx \mu v{l}_x/r{\left(x\right)}^2$, while capillary stresses are described by the Young−Laplace equation as ${\tau }_c\approx 2\sigma \cos \left(\theta \right)/r\left(x\right)$ and gravitational stresses ${\tau }_g\approx \left({\rho }_1-{\rho }_2\right)\left(l-l_a\right)g$. Expressing $v=U/\omega$ (with $\omega$ being the porosity), ${\rho }_1-{\rho }_2=\Delta \rho$, and implementing the boundary conditions $l_a$ = 0, $l_b$ = $l$, $r_a=r_i$, and $r_b=r_o$ enabled us to develop an equation for a generalized capillary number $C{a}^{\ast }$ that quantifies the relative importance of each stress.

The generalized capillary number $C{a}^{\ast }$ is defined as

$$C{a}^{\ast }=\left(\frac{{\mu }_{1}Ul}{2\sigma r_o^2\hspace{0.17em}\cos \left(\theta \right)\omega }+\frac{\mathrm{\Delta }\rho gl}{2\sigma \hspace{0.17em}\cos \left(\theta \right)}\right)\left[\frac{r_i{r}_o}{r_i+r_o}\right].$$ [2]

Substituting ${\mu }_{1}U/\sigma$ and $\Delta \rho g{r}_i{r}_o/2\sigma \cos \left(\theta \right)$, respectively, with the capillary number $Ca$ and Bond number $Bo$ (ratio of gravitational to capillary forces) in the derived expression for $C{a}^{\ast }$ and using $r_o=r_i+\lambda l$ gives rise to

$$C{a}^{\ast }=\frac{Ca\hspace{0.17em}{r}_{i}l}{\cos \left(\theta \right)\omega (4r_i^2+6r_i\lambda l+2{\lambda }^2{l}^2)}+\frac{Bol}{2r_i+\lambda l}.$$ [3]

Eq. 3 represents the generalized capillary number $C{a}^{\ast }$ in the form of the conventional capillary number $Ca$ and Bond number $Bo$.

Furthermore, using linear stability analysis, we derived an analytical solution capable of distinguishing between the stable and unstable displacement patterns that takes into account the gradient of pore size $\lambda$ along the flow direction (among other parameters). The approach we adopted to derive the stability criterion is similar to that described by Saffman and Taylor (10). However, we have modified the dynamic boundary conditions to include the effect of $\lambda$ on VF; see Supporting Information for further details about the derivation of the stability criterion represented by Eq. 4. This is an analytical tool that enables us to predict the critical value of the generalized capillary number $C{a}_{\text{c}}^{\text{*}}$ that distinguishes stable and unstable displacement patterns. In particular, we find

$$C{a}_{\text{c}}^{\text{*}}=\frac{2\lambda r_{i}l}{n\left(2r_i^2+3r_i\lambda l+{\lambda }^2{l}^2\right)\left[1-M-G\right]}+\frac{Bol}{2r_i+\lambda l}$$ [4]

where $G=2\omega \lambda \Delta \rho r\left(x\right)g{h}^{\text{'}}/nU{\mu }_1$ represents the ratio of gravitational to viscous forces, $M={\mu }_2/{\mu }_1$, indicating viscosity ratio of defending fluid over invading fluid, and $n$ is the number of pores perpendicular to the displacement direction (transverse direction). When $C{a}^{\ast }<C{a}_{\text{c}}^{\text{*}}$, the displacement pattern is stable and $C{a}^{\ast }>C{a}_{\text{c}}^{\text{*}}$ is unstable. It is important to note that, although contact angle $\theta$ is not included in Eq. 4, it will strongly influence $C{a}^{\ast }$ (Eq. 3) and therefore whether $C{a}^{\ast }<C{a}_{\text{c}}^{\text{*}}$ or $C{a}^{\ast }>C{a}_{\text{c}}^{\text{*}}$ will be dependent upon $\theta$. The theoretical results illustrating how $C{a}^{\ast }$ varies as a function of $\lambda$ (both positive and negative) under different capillary numbers $Ca$ along with the stability criterion $C{a}_{\text{c}}^{\text{*}}$ are presented in Fig. 4.

Fig. 4.

Semilog plot showing the relationship between the generalized capillary number Ca* and λ. The solid line indicates the analytically predicted critical value of the generalized capillary number, which is a solution of the stability criterion derived from linear stability analysis. The symbols are the results obtained by the direct numerical simulations, where filled, half-filled, and open symbols represent the stable front, critical value of the generalized capillary number, and unstable front, respectively. Yellow and red regions mark analytically predicted stable and unstable regions, respectively, separated by the solid line predicted by Eq. 4. Insets illustrate the displacement front morphology at Ca = 3.2 × 10⁻⁶ computed by the direct numerical simulation.

Fig. 4 illustrates that the analytically predicted $C{a}_{\text{c}}^{\text{*}}$ agrees well with the numerical results in distinguishing between stable and unstable displacement fronts for all combinations of the capillary number $Ca$ and pore size gradient $\lambda$. The validation of Eq. 4 at different viscosity ratio M, contact angle $\theta$, and length scale $l$ is also presented in Figs. S2–S4 respectively. The slight discrepancy in the classification of some points is attributed to the simplifying assumptions made for the derivation of the analytical stability criterion [e.g., ignoring thin wetting films (18) and trapped fluids behind the displacement front]. Examination of Eqs. 3 and 4 suggests that during imbibition (the displacement of a nonwetting phase by a wetting phase), a positive $\lambda$ would delay the onset of VF, whereas unstable fronts would always persist for negative $\lambda$; such a conclusion is experimentally supported by the results of Al-Housseiny et al. (18).

An important result of our simulations is that, for the same capillary number, when $\lambda >0$, the competition between capillary and viscous forces remains the same (as reflected in the constant value of $C{a}^{\ast }$ for $\lambda >0$ in Fig. 4); therefore, VF continues. However, for $\lambda <0$ and the same capillary number, $C{a}^{\ast }$ increases, which results in a stable displacement front. The results presented in Fig. 4 further show that there is an analogy between viscosity of the invading fluid ${\mu }_1$ and negative $\lambda .$ According to the phase diagram introduced by Lenormand et al. (25), increasing μ₁ transforms the invasion behavior from VF to a stable regime. Similarly, our results indicate that increasing the gradient of pore size $\lambda$ (more negative values) stabilizes the displacement front. Therefore, the overall trend observed in Fig. 4 suggests that it is the viscous dissipation that governs stability of the displacement front (due to increase in $C{a}^{\ast }$ as $\lambda$ gets more negative), in agreement with the previous investigation (20). Negative $\lambda$ (meaning decreasing pore size along the flow) enhances the viscous forces. This further promotes lateral growth in disturbances and results in development of a smooth invasion pattern.

Conclusion

Our results demonstrate the impact of λ on the nature of immiscible displacement in porous media. We show that the VF, which is traditionally considered as a function of flow rate, viscosity ratio, and wetting properties of porous media, is controlled by the pore size gradient λ as well. Depending upon the wettability of the porous medium, for a given $Ca$ of the invasion process, both positive and negative λ can inhibit or trigger the growth of viscous fingers. Our numerical and experimental analyses at the pore scale enabled us to identify two pore-scale invasion mechanisms responsible for suppressing VF. More detailed discussions are presented in Supporting Information.

In this research, we have employed a design of a porous medium in the form of an ordered structure to suppress VF. This study has implications in a number of industrial applications, from the design of stable exchange porous columns for analyses and separation science to designing new membranes and porous products for suppression of spurious VF. We envision potential applications related to optimization of reactant transport and phase distribution in fuel cells, sensors and control of fluid flow in spacecraft under microgravity (31), and more. In addition, this research may also contribute toward reconciling pore-scale flow behavior with capillary dispersion phenomena observed during immiscible displacement at the continuum scale (6).

Materials and Methods

Experimental Setup.

The PDMS microfluidic device was made by photolithography. Positive photoresist and plasma etching were used to make the silicone mold for the PDMS to obtain uniform height of the channels. The ratio between the cross-linker and the elastomeric base was chosen as 1.5:10 to enhance the stiffness of the channels. The finished channel was hydrophobic and oleophilic. The triangular area at the inlet (Fig. 1) was designed for stabilizing the interface before it reached the porous medium. The displaced fluid was phenylmethylsiloxane oligomer (PDM-7050) purchased from Gelest Inc. The invading fluid was deionized water mixed with 0.1 wt % food dye for visualization. Considering the small weight ratio of the dye, its effects on the water viscosity and the water−oil interfacial tension were negligible.

The microfluidic device consists of pillar arrays with height H = 160 μm and variable pillar diameter spanning the width of the ordered region w = 30 mm. The pillar diameters and pores were ordered along the direction of the flow, with a pore size gradient $\lambda =-6.1\times {10}^{-3}$. We denote by $\lambda <0$ a reduction in pore size along the flow path, and vice versa for $\lambda >0$. The capillary number is defined as $Ca={\mu }_{1}U/\sigma$, where $U=Q/\left(Hw\right)$ is the area-averaged (Darcy) velocity and σ = 28.2 mN/m is the interfacial tension between the two fluids. We started the experiment at a low capillary number $Ca$ = 6.1 × 10⁻⁷ until a stable interface reached the first row of the pillars. Then, the flow rate was increased to a specified value, and the time evolution of the displacement process was recorded by a Nikon camera.

Numerical Setup.

DNS where volume-of-fluid method (interface tracking approach) is coupled with a Navier−Stokes equation has emerged as a powerful tool for diagnosing pore-scale multiphase flow problems with complex boundary conditions (32–35), enabling parameterization of macroscopic quantities (36). In the present study, we utilized DNS within a CFD framework to investigate how the proposed pore size arrangement influences the general dynamics of two-phase flow in porous media and stability of the displacement front. Additional details regarding the numerical algorithm employed in this study are provided in Deshpande et al. (37) and Rabbani et al. (35).

For the 2D simulations performed in the present study, we assumed an invading fluid of viscosity ${\mu }_1$ = 10⁻³ Pa⋅s, displacing an immiscible fluid (defending fluid) of viscosity ${\mu }_2$ = 10⁻¹ Pa⋅s. The resulting viscosity ratio of defending fluid with respect to invading fluid was $M$ = 100. The contact angle $\theta$ between interface and the solid surface measured along the defending fluid was kept uniform at 30° (i.e., the defending fluid acts as the wetting phase). The values of $l$ and $r_i$ were kept constant at 8 mm and 0.17 $\text{mm}$, respectively, while $r_o$ was allowed to vary based on the simulated $\lambda$ value. In the case of simulations, the width of ordered region $w$ is equal to $l$. The simulations were performed at several capillary numbers $Ca$ ranging from 3.2 × 10⁻⁷ to 3.2 × 10⁻⁵ and the pore size gradients $\lambda$ ranging from 6.5 × 10⁻³ to −6.5 × 10⁻³, respectively. The data, code, and materials used in this analysis will be available freely via sending a request to the corresponding author.