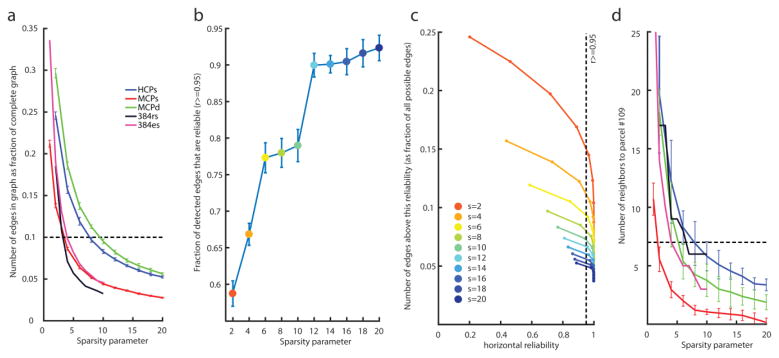
Figure 6.

Causal graph sparsity and reliability. These panels justify how we chose the particular sparsity settings for all subsequent causal discovery analyses. a: Number of edges produced (as proportion of the complete graph) as a function of different sparsity parameters across our five datasets. As an example, the densest graph in the HCP_s dataset is obtained with the lowest sparsity value we tested (a sparsity of 2) and produces graphs that are about 25% complete. For our analyses in this paper, we chose a criterion of producing about 10% of the complete graph (dashed line) across all datasets as a reasonable value that permitted comparisons in all subsequent analyses. b: Fraction of edges in the HCP_s graph with horizontal reliability ≥0.95 (see Methods for a description of our horizontal reliability measure). As sparsity increases (blue dots towards the right) so does the fraction of reliable edges. c: The number of edges in the HCP_s graph (as a proportion of the maximal number of edges that would be present in the complete graph) seen above a given horizontal reliability. Sparsity is encoded as line color. The leftmost point of each curve corresponds to observing a given edge only in 1 of the 11 datasets. Observing an edge in a sparse graph (large sparsity parameter s) is more surprising than observing an edge in a dense graph (small s), which our statistic for horizontal reliability captures (see Methods, and Supplementary Figure S3): hence the leftmost point of each curve shifts to the right for a higher sparsity parameter s. The second leftmost point corresponds to observing one repeat, i.e. to an edge repeating across 2 out of 11 datasets. Very high sparsity parameters (a sparsity of 20, blue curve) produce very reliable graphs. d: Same as a, except showing number of edges to the right amygdala (parcel #109), which is the node that we electrically stimulated in the neurosurgical patient. The dashed line corresponds to the number of edges to #109 obtained on average in the HCP_s datasets with s=8 (as in a). Equating the number of edges to #109 is another way to set the sparsity parameters across datasets, which we also explored (see Figure 8).