Abstract
Introduction
Non-interventional and other observational studies have become important in medical research. In such observational, non-randomized studies, groups usually differ in some baseline covariates. Propensity scores are increasingly being used in the statistical analysis of these studies. Stratification, also called subclassification, based on propensity scores is one of the possible methods. There is the quasi-standard of using five strata. In this paper we focus on a binary outcome and evaluate the above-mentioned standard of using five strata.
Material and methods
Bias and power for different numbers of strata are investigated with a simulation study. The methods are illustrated using data from a study where patients with diabetes mellitus and triple vessel disease undergoing coronary artery bypass surgery with and without previous percutaneous coronary intervention were compared.
Results
We show that more than five strata can be more powerful and give less biased results. However, using more than ten strata hardly gives any further benefit.
Conclusions
When applying a stratification, more than five strata may be preferable, especially because of increased power. Our simulation study does not show a clear winner; hence a useful strategy could be to work with five as well as with ten strata.
Keywords: logistic regression, propensity score, stratification
Introduction
Non-interventional studies have become important for the continuous benefit-risk assessment of medicines [1]. In non-interventional studies and other observational studies, treatments are not randomly assigned, and, as a consequence, any difference in outcome variables between treatment groups could be caused by differences between groups that existed prior to treatment. In such observational, non-randomized studies, groups usually differ in some baseline covariates. Often, randomized studies are not possible for ethical or practical reasons and the question arises how to reliably analyze a non-randomized trial. Methods based on the propensity score to adjust for between-group differences in observational studies have become increasingly popular in different areas, including cardiovascular research; see for instance a study about abdominal aortic aneurysm repair [2].
The propensity score is defined as the conditional probability of receiving the treatment given the observed baseline covariates. It can be estimated using logistic regression and then be used to balance the covariates within the two groups in order to reduce the bias in estimating the treatment effect. Common techniques using the propensity score are matching, stratification, regression adjustment and inverse probability weighting [3–6]. Guo and Fraser [5] demonstrated that the bias can be substantial if key covariates are not controlled in the analysis of data from observational studies.
In this paper we focus on stratification based on the propensity scores and consider a binary outcome variable. When applying stratification, also called subclassification, it is assumed that the different groups have a similar distribution of baseline covariates within each stratum. Usually five strata are created [7, 8], even for substantial sample sizes [9]. Rosenbaum and Rubin [3] referred to Cochran [10], who showed that five strata can remove 90% of the bias due to the stratifying variable. However, Cochran’s results are based on a linear regression. Hence, the results do not necessarily also hold for a logistic regression, which is carried out when a binary outcome is analyzed. In combination with a stratification, a conditional logistic regression is appropriate for a binary outcome. However, the stratification variable, i.e. the propensity score, is continuous. When categorizing such a continuous confounder, its effect is only partly controlled. Neuhäuser and Becher [11] investigated the residual confounding and found that the more strata are formed, the better the effect is controlled. It should be noted that distinct reductions of residual confounding were observed when using more than five strata [11].
Lunceford and Davidian [9], who investigated a normally distributed outcome, noted that the bias due to residual confounding becomes more serious with increasing sample size for a fixed number of strata. They showed that the bias can be reduced when doubling the strata from 5 to 10, and concluded that establishing guidelines for choosing the number of strata is an interesting topic for future research [9]. However, Lunceford and Davidian [9] did not consider a binary outcome. In this note we show that increasing the number of strata can reduce bias for a binary outcome, and we show that increasing the number of strata can also raise the power.
Material and methods
In a simulation study performed with SAS (version 9.3, SAS Institute Inc., Cary, NC), we simulated propensity scores using different beta distributions. The binary outcome was simulated with Bernoulli distributions with varying dependence on group and on the propensity score. A stratification was performed based on the propensity scores. Different numbers of strata were used. The values of the propensity score for both groups combined were used to define strata boundaries in order to obtain approximately equally sized strata. A conditional logistic regression was applied to compare the two groups with respect to the binary outcome. In this model the group was used as a class variable and the categorized propensity score as a stratification variable. For each configuration, 10 000 simulation runs were performed. The investigated total sample sizes were 2000 (balanced with 1000 per group, and unbalanced with n 1 = 500 and n 2 = 1500) and 1000 (balanced with 500 per group). The power was estimated as the proportion of simulated data sets with a p-value not larger than 0.05 for the null hypothesis that the regression coefficient for a difference between groups is zero.
Instead of simulating propensity scores directly, as in this study, one can simulate covariates and compute the values of the propensity scores in a following step (see e.g. [12]). However, the aim of this study was to investigate whether a larger number of strata than five may be preferable. This question can be approached with a direct simulation of propensity scores.
In addition to the simulation study we consider a study presented by Thielmann et al. [13]. In this study patients with diabetes mellitus and triple-vessel disease undergoing coronary artery bypass surgery were investigated. In group 1 (n 1 = 621) the bypass grafting was the primary revascularization procedure whereas patients in group 2 (n 2 = 128) were treated with a previous percutaneous coronary intervention (PCI) before the bypass surgery. The aim therefore was to determine whether previous PCI has a prognostic impact on the surgical outcome when finally referred to coronary artery bypass grafting. Two binary outcome variables were analyzed: in-hospital mortality and major adverse cardiac events (MACE), both determined in hospital during the index hospitalization. The hospital stay ranged from 7 to 13 days [13]. Regarding both death and MACE, it was found that prior PCI adversely affects the outcome of the subsequent bypass surgery. This link between previous PCI and coronary artery bypass graft risk was later confirmed in a large multi-center study with approximately 30 000 patients [14].
Results
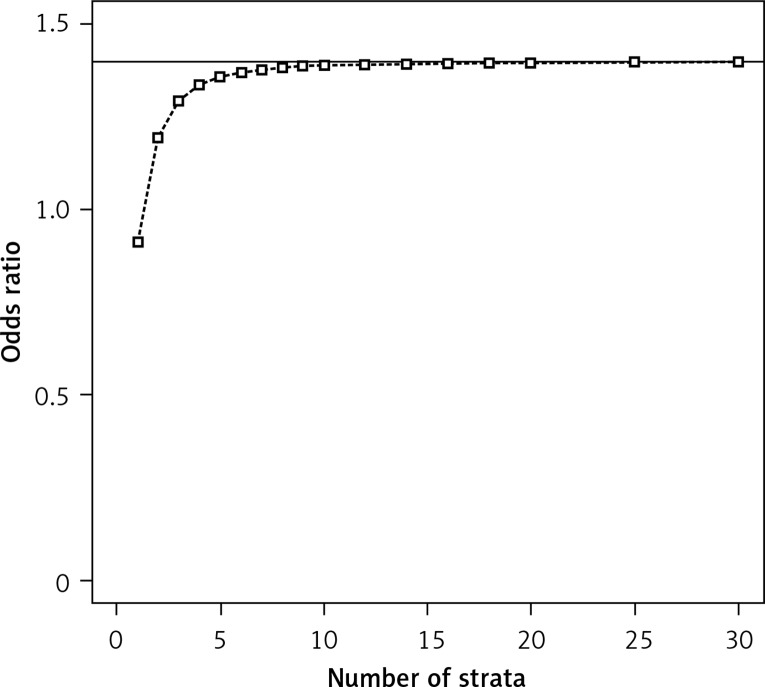
Figure 1 presents the decrease in bias when increasing the number of the strata, consistent with published results for a normally distributed response [9]. Our results in Figure 1 indicate that the choice of five strata is not always ideal. The bias is smaller for a larger number of strata such as 10; between 10 and more strata there is hardly any difference in bias. However, the focus of this note is on power.
Figure 1.
Mean of the estimated odds ratios (simulated using conditional logistic regression with stratification based on propensity scores, sample size per group = 1000, distributions of the propensity score (PS): beta(4,2) in group 1 and beta(7,1) in group 2, binomial proportions for success: 0.18 + PS/2 in group 1 and 0.1+PS/2 in group 2); the true odds ratio is 1.4 (indicated with the horizontal line)
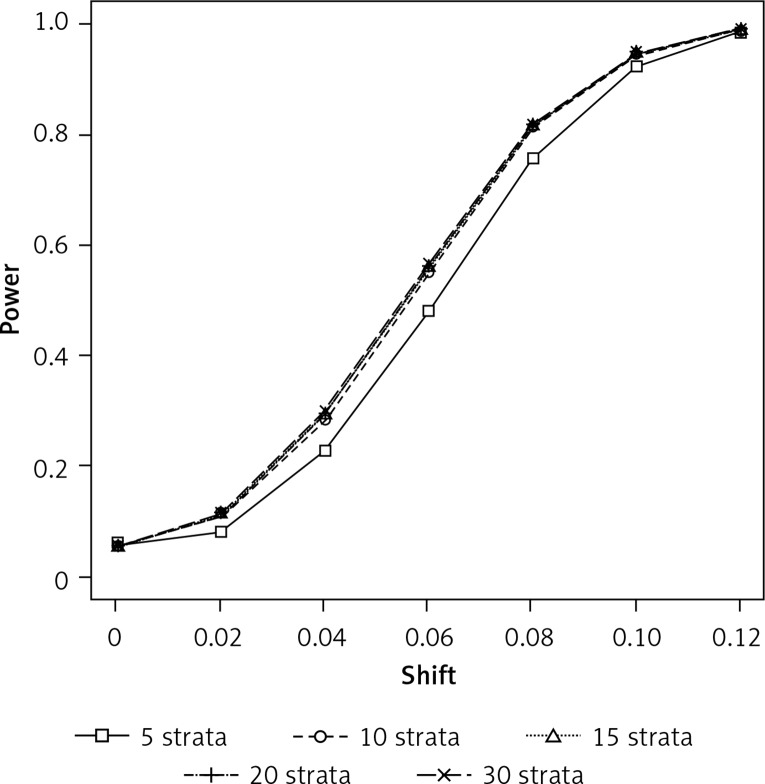
In Figure 2 we show that the power can be distinctly larger when using more than five strata, but again using more than 10 strata only gives a very small gain. However, there are also scenarios where five strata give more power, as scenarios 4, 5, and 8 in Table I exemplarily demonstrate. When there is no need for a propensity score adjustment, as in scenarios 9 and 10 in Table I, a smaller number of strata gives slightly greater power, although the difference in power is marginal. This is consistent with results presented by Neuhäuser and Becher [11] showing that an unnecessarily refined stratification is disadvantageous.
Figure 2.
Simulated power for detecting a between- group difference using conditional logistic regression with stratification based on propensity scores (sample size per group = 1000, significance level: 0.05, distributions of the propensity score (PS): beta(4,2) in group 1 and beta(7,1) in group 2, binomial proportions for success: 0.1 + shift + PS/2 in group 1 and 0.1 + PS/2 in group 2)
Table I.
Simulated power for detecting a between-group difference using conditional logistic regression with stratification based on propensity scores (sample size per group = 1000, significance level: 0.05)
| Variable | Number of strata | Group 1 | Group 2 | Number of strata | Group 1 | Group 2 | |
|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | ||||||
| Distribution of PS | Beta(2,4) | Beta(7,1) | Beta(2,4) | Beta(7,1) | |||
| Binomial proportion for success | 0.1 | 0.1 | 0.1 + PS/2 | 0.1 + PS/2 | |||
| 5 10 15 20 30 |
0.05 0.05 0.05 0.05 0.05 |
5 10 15 20 30 |
0.21 0.06 0.05 0.05 0.05 |
||||
| Scenario 3 | Scenario 4 | ||||||
| Distribution of PS | Beta(4,2) | Beta(2,4) | Beta(4,2) | Beta(2,4) | |||
| Binomial proportion for success | 0.1 + PS/2 | 0.19 + PS/2 | 0.19 + PS/2 | 0.1 + PS/2 | |||
| 5 10 15 20 30 |
0.76 0.83 0.84 0.84 0.84 |
5 10 15 20 30 |
0.93 0.88 0.87 0.86 0.86 |
||||
| Scenario 5 | Scenario 6 | ||||||
| Distribution of PS | Beta(4,2) | Beta(2,4) | Beta(4,2) | Beta(2,4) | |||
| Binomial proportion for success | 0.1 + PS/8 | 0.1 | 0.1 | 0.1 + PS/8 | |||
| 5 10 15 20 30 |
0.87 0.85 0.85 0.84 0.84 |
5 10 15 20 30 |
0.86 0.86 0.86 0.86 0.85 |
||||
| Scenario 7 | Scenario 8 | ||||||
| Distribution of PS | Beta(2,4) | Beta(7,1) | Beta(4,2) | Beta(7,1) | |||
| Binomial proportion for success | 0.3 + PS/2 | 0.1 + PS/2 | 0.1 + PS/2 | 0.18 + PS/2 | |||
| 5 10 15 20 30 |
0.88 0.92 0.93 0.94 0.94 |
5 10 15 20 30 |
0.89 0.84 0.83 0.82 0.82 |
||||
| Scenario 9 | Scenario 10 | ||||||
| Distribution of PS | Beta(4,2) | Beta(7,1) | Beta(4,2) | Beta(2,4) | |||
| Binomial proportion for success | 0.1 | 0.15 | 0.1 | 0.15 | |||
| 5 10 15 20 30 |
0.78 0.77 0.77 0.77 0.76 |
5 10 15 20 30 |
0.70 0.69 0.68 0.68 0.68 |
||||
PS – propensity score, Beta(α,β): beta distribution with parameters α and β.
When there is no difference at all in the probability of success between the groups, the actual type I error rate is close to α = 0.05 (see scenario 1 in Table I). However, when the difference is caused solely by the difference in the distribution of the propensity score, five strata might be insufficient to control for this, as scenario 2 with more than 20% significances in the case of five strata indicates; for 10 or more strata the proportions of significances are close to 5%.
Table II demonstrates that similar results can be obtained for smaller sample sizes or unbalanced groups.
Table II.
Simulated power for detecting a between-group difference using conditional logistic regression with stratification based on propensity scores (sample size per group = 500 for scenarios 1–6, and 500 in group 1 and 1500 in group 2 for scenarios 7–8, significance level: 0.05)
| Variable | Number of strata | Group 1 | Group 2 | Number of strata | Group 1 | Group 2 | |
|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | ||||||
| Distribution of PS | Beta(2,4) | Beta(7,1) | Beta(2,4) | Beta(7,1) | |||
| Binomial proportion for success | 0.1 | 0.1 | 0.1 + PS/2 | 0.1 + PS/2 | |||
| 5 10 15 20 30 |
0.05 0.05 0.05 0.05 0.05 |
5 10 15 20 30 |
0.13 0.05 0.05 0.05 0.05 |
||||
| Scenario 3 | Scenario 4 | ||||||
| Distribution of PS | Beta(4,2) | Beta (2,4) | Beta (4,2) | Beta(2,4) | |||
| Binomial proportion for success | 0.1 + PS/2 | 0.3 + PS/2 | 0.3 + PS/2 | 0.1 + PS/2 | |||
| 5 10 15 20 30 |
0.88 0.90 0.90 0.90 0.89 |
5 10 15 20 30 |
0.94 0.92 0.91 0.90 0.89 |
||||
| Scenario 5 | Scenario 6 | ||||||
| Distribution of PS | Beta(4,2) | Beta(7,1) | Beta(4,2) | Beta(7,1) | |||
| Binomial proportion for success | 0.25 + PS/2 | 0.1 + PS/2 | 0.1 + PS/2 | 0.2 + PS/2 | |||
| 5 10 15 20 30 |
0.74 0.76 0.76 0.76 0.75 |
5 10 15 20 30 |
0.79 0.74 0.73 0.72 0.72 |
||||
| Scenario 7 | Scenario 8 | ||||||
| Distribution of PS | Beta(4,2) | Beta(2,4) | Beta(4,2) | Beta(2,4) | |||
| Binomial proportion for success | 0.1 + PS/2 | 0.2 + PS/2 | 0.2 + PS/2 | 0.1 + PS/2 | |||
| 5 10 15 20 30 |
0.70 0.80 0.82 0.83 0.83 |
5 10 15 20 30 |
0.95 0.88 0.86 0.85 0.84 |
||||
PS – propensity score, Beta(α,β) – beta distribution with parameters α and β.
Thielmann et al. [13] computed the propensity score using a logistic regression based on 12 covariates including major preoperative risk factors such as presence of obesity (defined as body mass index (BMI) > 30 kg/m2) and renal disease (serum creatinine > 2.0 mg/dl). As shown in Table I of Thielmann et al. [13], at the 5% level three of the 12 covariates (presence of a renal disease, a previous myocardial infarction, and antiplatelet therapy) were significantly different between the groups. In addition, presence of hypertension was borderline significant with p = 0.07. All these differences disappear when testing in a stratified analysis with five strata based on the propensity score.
However, five strata are not enough for another reason: there seems to be heterogeneity between the stratum-specific odds ratios. The Breslow-Day test for homogeneity of odds ratios gives p = 0.061 for in-hospital death when using five strata. Zelen’s exact test for equal odds ratios, an exact counterpart to the Breslow-Day asymptotic test, gives p = 0.077. Eleven strata are necessary in order to obtain a p-value of the homogeneity tests larger than 0.2. Regarding MACE, the other outcome variable, there is no indication of heterogeneity. Note that there are significant differences between the groups regarding both outcome variables irrespective of whether one uses five or eleven strata, or twenty strata as in the original analysis [13]. The p-values displayed in Table III indicate that using more than five strata can be more powerful.
Table III.
Results of the conditional logistic regression with stratification based on propensity scores applied to the data of Thielmann et al. [13]
| Number of strata | P-values for a between-group difference | |
|---|---|---|
| In-hospital death | MACE | |
| 5 | 0.033 | 0.035 |
| 11 | 0.023 | 0.032 |
| 20 | 0.028 | 0.016 |
One might argue that only pretreatment covariates that show a between-group difference should be included in the logistic regression model for calculating the propensity score. In this example, one would therefore consider presence of a renal disease, a previous myocardial infarction, antiplatelet therapy and hypertension. With these four dichotomous variables, only 24 = 16 different combinations of covariate values are possible. Actually 15 out of the 16 possible combinations occur. Thus, there are only 15 different values for the propensity score, five of which occur in less than 10 patients only. Therefore, more than 10 strata are not appropriate in this case.
Again there are significant differences regarding both outcomes: for death the p-values are 0.015 (5 strata) and 0.016 (10 strata); for MACE the p-values are 0.023 (5 strata) and 0.024 (10 strata). The related homogeneity tests are not significant. In summary, the significant differences between the two groups reported by Thielmann et al. [13] can be confirmed using different analyses based on propensity score stratification.
Discussion
Propensity scores are commonly applied using matching, stratification, or regression adjustment. Austin [7] also investigated inverse probability of treatment weighting using the propensity score. He compared these four methods and found that matching and weighting with the inverse probability can be slightly better than the other two propensity score methods. However, Austin [7] investigated a stratification with five strata only, which might be a limitation of his work. Because it can be an improvement to create a larger number of strata, the stratification might be more competitive. In addition, stratification has another advantage: the propensity scores can only be estimated; therefore a stratification might be preferable because then small variations in the estimated values of the propensity score hardly have any influence [15].
When applying a stratification, using five strata, i.e. quintiles, has become a widely used approach. In this paper, we demonstrate that a larger number of strata may be preferable, especially because of increased power. The simulation study does not show a clear winner; hence we cannot present a clear strategy for how to choose the number of strata in general. Nevertheless, choosing five strata, just because this approach is common, seems to be not an optimal approach. Heinze and Jüni [16] suggested more than five strata for large data sets, without giving any clear advice. We can reconfirm the statement that establishing guidelines for choosing the number of strata is an interesting avenue for future research [9].
In principle, one could increase the number of strata up to a 1 : 1, or 1 : R, matching. However, already in 1986 it was shown that it is preferable “to pool comparable matched pairs into strata and perform a stratified rather than a paired analysis” [17]. This conclusion to combine patients with similar attributes into one stratum before performing a conditional logistic regression also applies to more general designs [11, 17]. Moreover, one should avoid a stratification which is too fine for a further reason: this increases the probability of there being patients of one group only within a stratum; such a stratum would have no influence in the stratified analysis [11].
Pending further research, a useful strategy could be to work with five as well as with ten strata, especially when a statistical analysis based on the propensity score is carried out as an additional analysis to confirm (or not confirm) the findings of alternative analyses. If the estimates based on five and 10 strata deviate, especially when this causes a different conclusion, the estimates based on ten strata might be preferable, because the bias usually decreases with the number of strata. The bias can be caused by the heterogeneity of patients within strata. For very small studies it might be inappropriate to use more than 5 strata. Furthermore, when there is only a limited number of different combinations of discrete covariate values, a large number of strata is not appropriate, as illustrated using the example data set.
One might argue that the numbers 5 and 10 are arbitrary. However, five strata is the quasi-standard, while using more than ten strata gives no benefit according to our simulation study. Regarding our example data, the estimates based on different numbers of strata are similar: the estimated odds ratios for in-hospital death are 2.85 (5 strata), 3.09 (10 strata), 3.07 (11 strata), and 2.97 (20 strata).
Conflict of interest
The authors declare no conflict of interest.
References
- 1.Hartmann M, Schaffner P. Legal requirements, definitions, and standards for non-interventional drug studies: a global picture of variability – results and conclusions from a single-institution survey. Therap Innov Regulat Sci. 2013;47:684–91. doi: 10.1177/2168479013497033. [DOI] [PubMed] [Google Scholar]
- 2.Piffaretti G, Mariscalco G, Riva F, et al. Abdominal aortic aneurysm repair: long-term follow-up of endovascular versus open repair. Arch Med Sci. 2014;10:273–82. doi: 10.5114/aoms.2014.42579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. J Am Stat Assoc. 1984;79:516–24. [Google Scholar]
- 4.D’Agostino RB. Propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Stat Med. 1998;17:2265–81. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 5.Guo S, Fraser MW. Propensity score analysis. 2nd edition. Thousand Oaks, CA: Sage Publications; 2014. [Google Scholar]
- 6.Austin PC. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate Behav Res. 2011;46:399–424. doi: 10.1080/00273171.2011.568786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Austin PC. The relative ability of different propensity score methods to balance measured covariates between treated and untreated subjects in observational studies. Medical Decision Making. 2009;29:661–77. doi: 10.1177/0272989X09341755. [DOI] [PubMed] [Google Scholar]
- 8.Stürmer T, Rothman KJ, Avorn J, et al. Treatment effects in the presence of unmeasured confounding: dealing with observations in the tails of the propensity score distribution – a simulation study. Am J Epidemiol. 2010;172:843–54. doi: 10.1093/aje/kwq198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Stat Med. 2004;23:2937–60. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- 10.Cochran WG. The effectiveness of adjustment by subclassification in removing bias in observational studies. Biometrics. 1968;24:295–313. [PubMed] [Google Scholar]
- 11.Neuhäuser M, Becher H. Improved odds ratio estimation by post hoc stratification of case-control data. Stat Med. 1997;16:993–1004. doi: 10.1002/(sici)1097-0258(19970515)16:9<993::aid-sim505>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 12.Austin PC. The performance of different propensity score methods for estimating marginal hazard ratios. Stat Med. 2013;32:2837–49. doi: 10.1002/sim.5705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thielmann M, Neuhäuser M, Knipp S, et al. Prognostic impact of previous percutaneous coronary intervention in patients with diabetes mellitus and triple-vessel disease undergoing coronary artery bypass surgery. J Thorac Cardiovasc Surg. 2007;134:470–6. doi: 10.1016/j.jtcvs.2007.04.019. [DOI] [PubMed] [Google Scholar]
- 14.Massoudy P, Thielmann M, Lehmann N, et al. Impact of prior percutaneous coronary intervention on the outcome of coronary artery bypass surgery: a multi-center analysis. J Thorac Cardiovasc Surg. 2009;137:840–5. doi: 10.1016/j.jtcvs.2008.09.005. [DOI] [PubMed] [Google Scholar]
- 15.Rubin DB. On principles for modeling propensity scores in medical research. Pharmacoepidemiol Drug Saf. 2004;13:855–7. doi: 10.1002/pds.968. [DOI] [PubMed] [Google Scholar]
- 16.Heinze G, Jüni P. An overview of the objectives of and the approaches to propensity score analyses. Eur Heart J. 2011;32:1704–8. doi: 10.1093/eurheartj/ehr031. [DOI] [PubMed] [Google Scholar]
- 17.Brookmeyer R, Liang KY, Linet M. Matched case-control designs and overmatched analyses. Am J Epidemiol. 1986;124:693–701. doi: 10.1093/oxfordjournals.aje.a114443. [DOI] [PubMed] [Google Scholar]