Automatic quantification framework to detect cracks in teeth

Abstract

Studies show that cracked teeth are the third most common cause for tooth loss in industrialized countries. If detected early and accurately, patients can retain their teeth for a longer time. Most cracks are not detected early because of the discontinuous symptoms and lack of good diagnostic tools. Currently used imaging modalities like Cone Beam Computed Tomography (CBCT) and intraoral radiography often have low sensitivity and do not show cracks clearly. This paper introduces a novel method that can detect, quantify, and localize cracks automatically in high resolution CBCT (hr-CBCT) scans of teeth using steerable wavelets and learning methods. These initial results were created using hr-CBCT scans of a set of healthy teeth and of teeth with simulated longitudinal cracks. The cracks were simulated using multiple orientations. The crack detection was trained on the most significant wavelet coefficients at each scale using a bagged classifier of Support Vector Machines. Our results show high discriminative specificity and sensitivity of this method. The framework aims to be automatic, reproducible, and open-source. Future work will focus on the clinical validation of the proposed techniques on different types of cracks ex-vivo. We believe that this work will ultimately lead to improved tracking and detection of cracks allowing for longer lasting healthy teeth.

1. INTRODUCTION

Epidemiologic studies report that cracked teeth are the third most common cause for tooth loss in industrialized countries.[1] Histological studies demonstrate that all cracks are colonized by bacteria, which have the potential to cause pulpal and periapical disease.[2,3] Pain associated with these diseases is intense and is the most common reason for seeking emergency dental care.[4,5] Five types of longitudinal fractures have been identified. From least to most severe, these are: 1) craze line; 2) fractured cusp; 3) cracked tooth; 4) split tooth (see figure 1); and 5) vertical root fracture (VRF)[6,7].

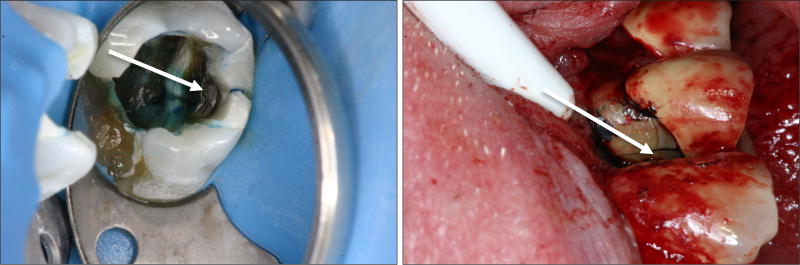
Figure 1.

Clinical pictures showing fractures detected by first (a) accessing the root canal system or (b) surgically reflecting a flap followed by the use of a special dye and a surgical operating microscope. Both of these procedures are invasive and expensive. Patients experience pain and suffering for a long time before these procedures are done and a definitive diagnosis made. By which time it is usually too late to save the tooth resulting in tooth extraction.

Cracked teeth present a complex, diagnostic dilemma. They may present with sharp pain on biting, cold sensitivity or deep probing depths.[8,9] The symptoms are often discontinuous with periods of remission. If left undetected, cracks continue to progress and ultimately result in tooth loss. Early and accurate detection of cracks will reduce the pain and suffering experienced by patients and help them retain their teeth longer. Available clinical tools used to detect cracks have limitations and often cannot determine the extent of the crack.

Imaging modalities used to detect cracks include conventional intraoral radiography and Cone Beam Computed Tomography (CBCT). The accuracy of both modalities for the detection of cracks remains low because the diagnosis depends ultimately upon scanner resolution, crack orientation and the observers' interpretation.[10] Thus, there is an imperative need to develop an objective, automated and reliable method to detect cracks and their extent that does not solely rely on the observer’s clinical observations and radiographic interpretation of an image.

The purpose of this paper is to develop reliable, reproducible and automatic techniques for the detection and quantification of cracks using high-resolution CBCT (hr-CBCT) imaging. Recent developments on hr-CBCT scanners and imaging protocols with a small field of view and isotropic voxels with sub-millimeter resolution have the potential to allow clinically viable quantitative assessments of tooth pathology with reduced effective radiation doses.[11] Furthermore, our preliminary work demonstrates that an advanced image analysis method called 3D Steerable Wavelets[12] can be used to automatically detect and quantify cracks in teeth from hr-CBCT data. (Steerable wavelets are mathematical tools used in digital signal processing that can be “steered” in any direction). This technique can perform a multiscale analysis of a signal. The spatial resolution of wavelets can be modulated, retaining more 3D information from the original image.

We believe that hr-CBCT combined with advanced quantitative image analysis has the potential to accurately, objectively and automatically measure cracks.

2. MATERIALS

We have performed preliminary data analysis using the proposed method on synthetic data [13]. A set of 6 healthy second molars obtained from hr-CBCT scans were analyzed. These scans were collected using the Kodak Carestream 9000 scanner with the parameters FOV: 37.5 × 50 mm, 90 kVp, 12 mA and a 0.085 mm isotropic voxel size. Specifically, the hr-CBCT isotropic resolution used in this study (0.085mm) provides superior visualization of fine radicular and filament-like structures with radiation dose much lower than conventional CT exams. This resolution will also minimize the partial volume effects, and will be able to detect cracks with sub-mm accuracy. The ability of hr-CBCT to generate reconstructions of complex 3D pathology will help reconstructing any fracture orientation, without any concern about alignment of the entire fracture to a single X-ray projection. We plan to use the high resolution with a small FOV (3.75 cm × 5 cm) that delivers an effective dose of 56 µSv[11].

Relevant anatomy of the teeth was segmented using 3DSlicer[16] Segment Editor[17]. We performed intensity based segmentation and refined that segmentation using smoothing, morphological operators and filtering. We then simulated a small longitudinal crack (0.1mm, 1.17 voxels wide) with different orientations, by using a custom script that, given a plane equation, will generate a deformation field that displaces the gray level intensities of the tooth structure by a given amount (in this case, 0.1mm). We generated 6 different cracks in each molar (36 simulated scans total). All scans went through a Gaussian smoothing filter using a sigma of 0.1 to make fractures discontinuous and thus look more realistic (see figure 2).

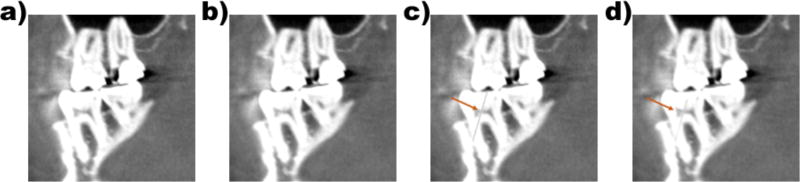
Figure 2.

Example of synthetic simulated dataset for a (a) healthy second molar, and(c) simulated crack sample. Data was post-processed to improve realism. (b) Healthy second molar after smoothing and (d) simulated crack sample after smoothing. Arrow points to the simulated crack.

3. METHODS

Our analysis algorithm is based on the Isotropic Wavelets theory[18], fine-tuned for cracked teeth detection. Wavelets are very important in signal analysis as they can perform a multiscale analysis of a signal. This is similar to a windowed Fourier Transform (FFT), but with the advantage that the spatial resolution (the window) can be modulated, retaining more information from the original image. As illustrated by our preliminary results, the method can detect synthetic cracks in the high frequency component of the wavelet responses. The proposed method performs high-resolution analysis in both the frequency and the spatial domains. The proposed wavelet framework presents a superior flexibility and computational performance compared to other methods for filament-like feature detection, such as the Frangi’s vessel enhancement algorithm [19]. This method has the advantage of providing an isotropic wavelet backbone, which is sensitive to features in any orientation, the ability to provide a directionality analysis when coupling with non-isotropic functions, (e.g derivatives or Riesz Functions) and having the steerablity property with which the response at any orientation can be computed as a linear combination of a basis of functions (at different frequency scales and orientations).

Also, because the number of wavelet scales and frequency phases can be configured, we are proposing an extremely customizable method for the detection of cracks of any size and in any possible orientation given the steerable nature of the wavelets. Depending on the type of crack to detect, we could design different wavelets for different types of lesions in the future.

3.1 Quantification of cracked teeth

For the quantification of cracked teeth, we used the Isotropic Wavelet package[20] developed in the Insight Toolkit (ITK)[21]. ITK is an open-source, cross-platform system that provides developers with an extensive suite of software tools for image analysis. The ITKIsotropicWavelets module is available as an optional external module for ITK since version ITK-4.13, and can also be downloaded from the development site[20]. Following the same practices as other ITK functions and external modules, it provides Python wrappings for the C++ code to facilitate its use. These python wheels have been generated for three main operating systems: Mac, Linux and Windows, and three versions of python: 2.7, 3.5 and 3.6. They can be installed using pip install (see equation 1).

$$\text{pip install itk}-\text{isotropicwavelets}$$ (1)

We believe python wheels will ensure that other research labs will be able to adopt this technology for their own custom biomedical applications.

The package ITKIsotropicWavelets implements a Steerable Wavelet Pyramid [20] in the frequency domain. The wavelet pyramid (figure 3) represents a multi-resolution analysis (MRA) framework, providing information at multiple scales, from small details to bigger features. The wavelet coefficients generated at each scale can be analyzed and modified independently depending on the task at hand (e.g registration, segmentation, denoising), and then used to reconstruct a new image with no aliasing or loss of information. This property of perfect reconstruction is one of the strongest advantages of wavelet analysis but is only fulfilled when using a specific set of functions as mother wavelets (e.g Haar, Daubechies, Simoncelli, etc).

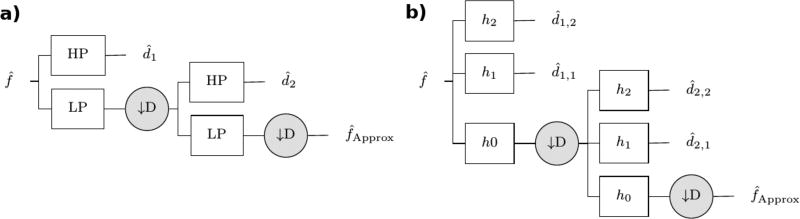
Figure 3.

Schematic of a 2-level Steerable Wavelet Pyramid with: a) 1 high frequency band; b) 2 high frequency sub-bands. The wavelet coefficients d are the result of applying high-frequency band-pass filters (HP) to the input image in the frequency domain (see Fig 2b). The process is recursive for the desired number of scales after applying a low-pass frequency filter (LP) to the input and a down-sampling operator (D).

The pyramid (figure 3) starts with an input in the frequency domain, the wavelet coefficients are the result of applying a high-frequency band-pass filter derived from the chosen mother wavelet (figure 4). A complementary low-frequency pass filter is used to scale the input by a factor of two (dyadic), acting as a zoom-out and ignoring the high-frequency features in the new level. The user, having an upper limit based on the size of input, can select the number of levels. In order to get even higher frequency resolution than the regular pyramid of figure 3a, the module optionally allows splitting the high-pass filter into multiple high frequency sub-bands (figure 4b – figure 4b). We use high frequency band wavelet responses from this filter to localize, quantify and detect cracks in teeth.

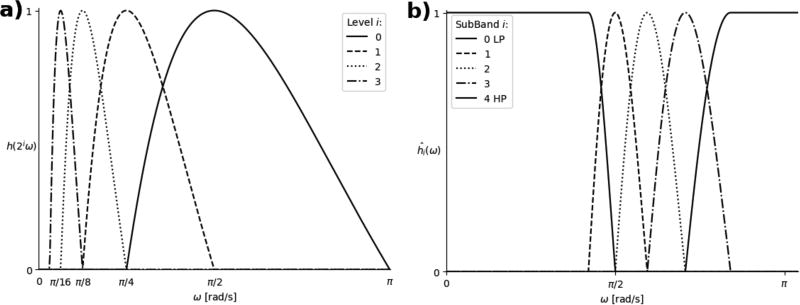
Figure 4.

a) Simoncelli Mother Wavelet. Original profile at l=0, and iteratively scaled profiles for successive levels. b) Band-limited filters in the first level of the pyramid using 4 high-frequency sub-bands.

3.2 Detection of cracked teeth

For the detection of cracks, we trained a binary classifier based on Support Vector Machines (SVM)[22] using the open-source Python package called scikit-learn[23]. SVM is a two-group classifier that seeks to find a separating hyperplane that maximizes the distances between the two groups. SVM’s often outperform competing methods on binary classification tasks, especially if few labeled training data points are available. Wavelet responses in the highest frequencies are used to train the classifier. Using this learning-based classification approach on the training data that includes wavelet features computed on healthy tooth samples will aid reducing false positives and verify the existence of cracks on the wavelet frequency domain.

4. RESULTS

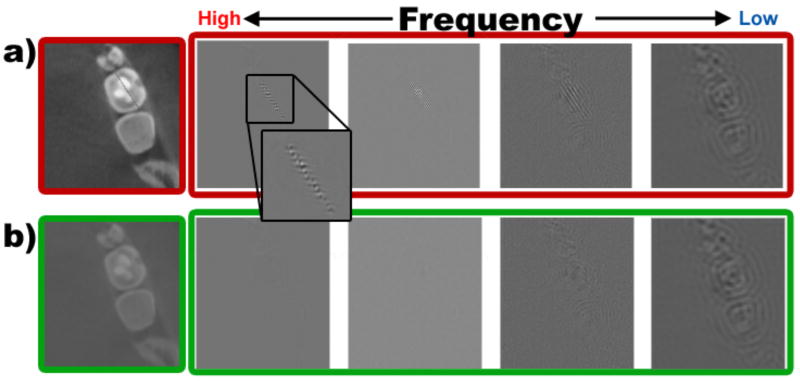
From the different available steerable wavelets we configured a bank of Simoncelli wavelets[24] with 4 levels or scales (each level zooms out the image with half the resolution), and 4 high-frequency sub-bands per level to improve the resolution, resulting in 16 outputs per scan containing the different wavelet coefficients. Figure 5 displays the absolute maximum wavelet coefficient values in the first 4 level wavelet output images. The discontinuous nature of the cracks results in a localized signal with high frequency components. The wavelet coefficients at small scales accurately capture and localize the high frequency signal components associated with the crack (figure 5a). This response is not found in the healthy tooth (figure 5b).

Figure 5.

Spatial representation of wavelet coefficients used to train the classifier. a) Simulated cracked and b) healthy tooth. The crack has a strong response in the high frequency bands, unlike the healthy tooth. This distinctive behavior demonstrates the sensitivity of the proposed method.

We then generated L-dimensional feature vectors (see equation 2, with L=4, the number of levels) comprising the absolute maximum wavelet coefficient values among all the high-frequency sub-bands (bands = 4 in our case, see figure 5).

$$w_{\mathit{\text{level}}}=\mathit{\text{max}}(|w_{\mathit{\text{level}},b}|)\mathit{\text{forb}}\in [1,\mathit{\text{bands}}].$$ (2)

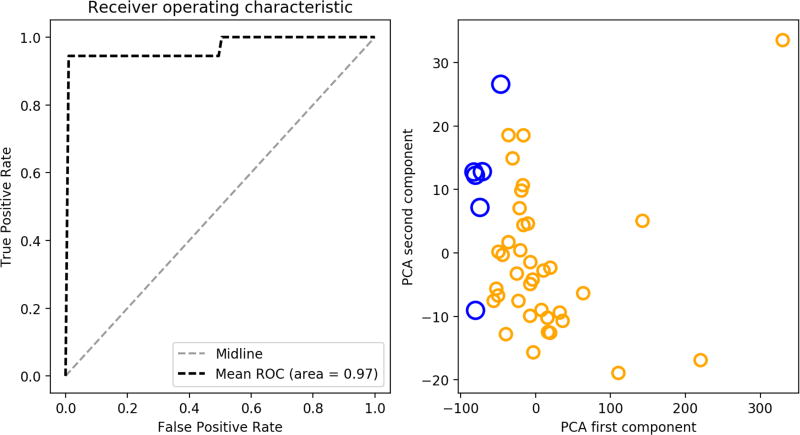
These vectors are used to train our classifier to detect cracked teeth. Because of an unbalanced healthy/simulated sample size we used bagged classification, which forms an ensemble of 6 different SVM[22] classifiers trained over randomly chosen balanced samples (i.e. 6 healthy and 6 randomly chosen cracked scans). Classification for a single sample is based on majority voting over all classifier responses. Receiver operating characteristic (ROC) curve analysis was done using K-fold cross validation (see figure 6). The ROC and discriminant plot using principal component analysis (PCA)[25] demonstrate that the method proposed has discriminatory properties with both high sensitivity and specificity for detecting cracks.

Figure 6.

Preliminary data analysis results (left) mean ROC curve of a 3-fold cross validation with a 0.97 are under the curve (right) class discrimination by plotting the first two components of PCA done on the 4-dimensional features. Healthy (blue dots) and simulated (yellow dots) samples have very distinct variability values

5. DISCUSSION

The US Surgeon General’s report on oral health documented profound disparities in the oral health status of older Americans[26]. It is well known that the incidence of cracks increases with age[27,28]. As cracks progress, they result in pulpal and periapical disease, which often necessitates root canal treatment and full coverage restoration or extraction. Given the lack of accurate diagnostics to determine the extent of the crack and the substantial cost of the treatments involved, many patients choose to have their teeth extracted. Even for those patients who can afford root canal treatment and subsequent full coverage restoration, the prognosis remains uncertain.

In this paper we present a novel technique based on an innovative use of Isotropic Wavelets, which is aimed to accurately detect the presence and extent of cracks in teeth in any location and orientation. There are some clear influences of image quality on the results of the algorithm proposed. Resolution wise, our framework relies on the use of new hr-CBCT systems including sub-mm accuracy resolutions and small field of view set ups to generate the input data necessary for the analysis. A recent position statement jointly issued by the American Association of Endodontists and the Academy of Oral and Maxillofacial Radiology recommends the use of small field of view (FOV) CBCT as the imaging modality of choice for diagnosis in patients who present with contradictory or non-specific signs and symptoms including suspicion of cracked teeth[29]. This may lead to a more widely adoption of this technology. We do not expect to experience a huge influence from scatter noise due to the underlying design of the analysis methodology. 3D steerable wavelets differentiate between high frequency and low frequency components in an image and due to that property they have been used as noise reduction methods for years. However, we expect beam-hardening artifacts[30] to cause challenges for the proposed algorithm during the clinical validation of this project (Phase II). Beam-hardening artifacts occur in the presence of radiopaque root canal obturation and other radiopaque restorative materials. Cracks often occur in teeth with long-standing restorations. Algorithmic correction during reconstruction is one correction route for these defects[31,32], but post-reconstruction correction is also common, especially in CT. Artifacts have been corrected in CT using different analytical approaches such as morphological operations[33,34], level set methods, registration[34] or, geometrical methods[35]. Specifically, geometrical methods have been successful in the past to trace the artifact rays. Once the artifact rays, usually straight lines, have been detected, it is easy to interpolate from the surrounding tissue type via majority voting in order to reconstruct the underlying anatomy. Post-processing algorithms such as this one will be performed to all images prior to the application of our crack detection algorithm.

While cracks are not the only cause for tooth loss, the proposed analytical framework is relevant to public health because the early detection and timely intervention will help prevent tooth loss and maintain oral health and function in our aging population while reducing the pain and suffering associated with cracked teeth.

Future work will focus on the clinical validation of the proposed methodology on different types of cracks ex-vivo and to couple the wavelet backbone with functions to study directionality. We believe this work will ultimately lead to better preventive strategies and improved tracking of the progression of cracks. The ability to relate treatment choices with clinical outcomes for teeth with cracks will lead to targeted interventions and better clinical outcomes.