Effect of BGM Accuracy on the Clinical Performance of CGM: An In-Silico Study

Abstract

Background:

Standard management of type 1 diabetes (T1D) relies on blood glucose monitoring based on a range of technologies from self-monitoring of blood glucose (BGM) to continuous glucose monitoring (CGM). Even as CGM technology matures, patients utilize BGM for calibration and dosing. The question of how the accuracy of both technologies interact is still not well understood.

Methods:

We use a recently developed data-driven simulation approach to characterize the relationship between CGM and BGM accuracy especially how BGM accuracy impacts CGM performance in four different use cases with increasing levels of reliance on twice daily calibrated CGM. Simulations are used to estimate clinical outcomes and isolate CGM and BGM accuracy characteristics that drive performance.

Results:

Our results indicate that meter (BGM) accuracy, and more specifically systematic positive or negative bias, has a significant effect on clinical performance (HbA1c and severe hypoglycemia events) in all use-cases generated for twice daily calibrated CGMs. Moreover, CGM sensor accuracy can amplify or mitigate, but not eliminate these effects.

Conclusion:

As a system, BGM and CGM and their mode of use (use-case) interact to determine clinical outcomes. Clinical outcomes (eg, HbA1c, severe hypoglycemia, time in range) can be closely approximated by linear relationships with two BGM accuracy characteristics, namely error and bias. In turn, the coefficients of this linear relationship are determined by the use-case and by CGM accuracy (MARD).

While current standards of care for the management of type 1 diabetes (T1D) rely on blood glucose monitoring based largely on self-monitoring of blood glucose (BGM), continuous glucose monitoring (CGM) is becoming a strong alternative to BGM. CGM technology has significantly matured since its advent in the early 2000s, and advanced from retrospective review of glucose variations to real-time display of glucose (usually every 5 minutes)¹ and potentially insulin dosing decision making, either through artificial pancreas like systems^2-4 or through standard functional insulin therapy.^5,6

Parallel to these advances, CGM system accuracy has greatly increased over the same decade, from systems commonly making errors of 20% to 50% of the reference value⁷ to current system with 90% or more of readings within 20% of the reference.^8,9 Despite of this, current CGM accuracy does not meet the required accuracy standards for regulatory approval of BGM systems.^10,11 This is also masked by the reliance on MARD as a descriptive parameter. While MARD provides an average measure of accuracy, it does not fully quantify the ability of a CGM to provide trustworthy results. Furthermore, until additional technical and regulatory developments are introduced, CGM systems will be required to utilize BGM for calibration and dosing decisions.

The question of how the accuracies of BGM/CGM interact is still not well understood, and while commonly accepted measures of accuracy for BGM are available,^10,11 CGM accuracy remains difficult to assess.^12-18 How the errors of BGM can propagate to CGM either through its use for insulin dosing decision making in calibration, cannot be easily assessed in the field. In addition, the impact of BGM accuracy on the performance of CGMs with different accuracy levels has yet to be studied. Simulation technologies have made such exploration feasible, and allow for the prediction of clinical outcomes associated with such imperfect devices and their potential interactions.^19,20

Materials and Methods

Data Sources

Data compiled during a National Institutes of Health/National Institute of Diabetes and Digestive and Kidney Diseases grant R01 DK 085623 were the basis for replay simulation.²¹ In the study, 56 T1D patients were asked to collect glucose, insulin, and meal data. Subjects were between the ages of 21 and 65 years old (mean of 41 and standard deviation [SD] of 12.1). Duration of T1D was a minimum of 2 years, with the mean duration of 24.1 (SD 11) years. The study required use of an insulin pump for a minimum of 6 months, with an average interval of 10 (SD 5.8) years. Their average HbA1c level was 7.7% (SD 1.2%), and 59% were female, with most of them white (95%), and 50% had a professional occupation. Protocol for building the database was approved by the local Institutional Review Board.²² Data collection was designed to be unobtrusive and minimize burden, distractions, or alterations to participants’ typical daily routines and allowed them to maintain typical daily behaviors.

Replay Simulators

This work is conceptually similar to a previous effort,²³ where the UVA/Padova simulator^24,25 was adapted for ICU patients. Stress-action curves were identified via deconvolution to characterize metabolic changes. A similar principle is applied to quantify unique metabolic characteristics of the 56 patients, obtaining an individualized simulator.²¹ This approach has been successfully used in therapy optimization.²⁶

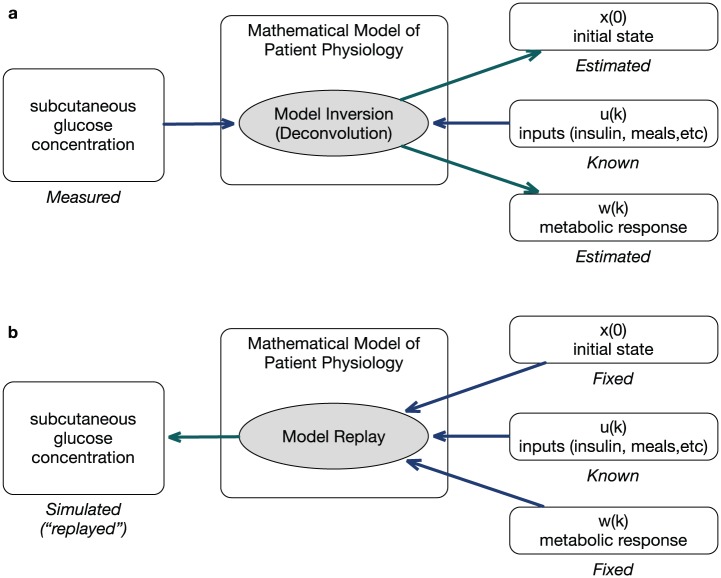
The approach is illustrated in Figure 1. Given measurable subcutaneous glucose concentrations, model inversion is used to characterize the difference between the glucose predicted by a personalized linear time-invariant model and observed data, quantified as a rate of appearance of glucose in plasma.²¹ This rate of appearance is used to assess the effect of alternate dosing decisions. This naturally lends itself to the evaluation of sensor accuracy.¹⁹ In this work, we explore clinical effects of meter accuracy by simulating the same 56 subjects in alternate BGM/CGM use-cases.

Figure 1.

(a) Known inputs and model are used to identify metabolic response and initial state. (b) The reconstructed metabolic response and initial state are applied to a new set of inputs for simulation.

Modeling BG Monitoring Systems

Published data on meter accuracy^27,28 was used to model commercially available meters. The model is a mixture of models for high and low glucose ranges to provide more accuracy. Specifically, in the low glucose range (<100 mg/dL), the parameters of a Johnson distribution of the form

$$Y_L={\chi }_L+{\lambda }_L\sinh \left(\frac{N-{\gamma }_L}{{\delta }_L}\right),$$

are estimated so that $P\left(Y_L\le l_i\right)\approx p{l}_i$, where $l_i$ is one of the thresholds in 15, 10, 5 mg/dL, and $p{l}_i$ is the reported^27,28 percentage of measurements and $N$ is a standard normal variate. On the high range, a similar model is created for $Y_H.$ Simulated glucose readings are generated by evaluating the expression

$$BGM=\left(1-\alpha \right)\left(G+Y_L\right)+\alpha G\left(1+\frac{Y_H}{100}\right),$$

where $\alpha =max\left\{0,min\left\{1,\frac{G-70}{130-70}\right\}\right\}$. We also simulate 21 ideal meters, that is, meters with a Gaussian distribution with no bias and where 95% of measurements falling within 5% to 25%.

A CGM Model

This approach is based on previous CGM modeling approaches,^20,29,30 with some modifications to provide finer error characterization. It takes the form

$$CG{M}_{mod}=\alpha +\beta BG\left(t-\tau \left(t\right)\right)+\mathrm{T}\left(t\right)+N\left(t\right)+n,$$

where $\alpha$ is a systematic bias, $\beta$ represents sensor gain, the series $\tau \left(t\right)$ represents time-varying sensor lag (delay), series $T\left(t\right)$ is a polynomial trend, series $N\left(t\right)$ is a low frequency (possibly auto-correlated) noise, and $n$ is a high frequency noise, assumed to be independent with constant variance. The model is identified sequentially, starting signal delay $\tau \left(t\right)$, followed by bias $\alpha$ and gain $\beta$. At this point, residuals

$$re{s}_k=\alpha +\beta BG\left(t-\tau \left(t_k\right)\right)-CGM\left(t_k\right),$$

are used to compute the trend $\mathrm{T}\left(t_k\right)$. Once this trend is removed, low frequency noise is estimated using an ARMA process, with low frequency noise characterized from the residuals of this process. Note that time is assumed to referenced to calibration time ($t=0$).

CGM Calibration Algorithm

A simplified calibration algorithm was implemented. During the first calibration period bias and gain identified from data are used. Subsequent calibrations use simulated readings from a virtual fingerstick. Given the last five readings, a new bias/gain pair is identified by solving a MSE problem.

Scaling CGM Error

To quantify the interaction between fingerstick and CGM accuracies, we use a scaled CGM model with parameter $\gamma >0$, is computed as

$$\begin{array}{l}CG{M}_{mod}\left(\eta \right)=\gamma \left[\alpha +{\rm T}\left(t\right)+N\left(t\right)+n\right]+\\ \left[\left(\beta -1\right)\gamma +1\right]BG\left(t-\tau \left(t\right)\right).\end{array}$$

Thus, a scale parameter of $\gamma =1$, will result in the original model, while other values were used to obtain a target MARD.

Behavioral Components

The simulation implements self-treatment behaviors related to bolusing and hypoglycemia treatment. Some simulation arms will use CGM for decision making. Meals and other activities are taken directly from the recorded activity of the patients.

Bolus Behavior

Meal corrections and corresponding fingersticks are skipped for 20% of the meals. Also, if glucose readings were consistently high (>250 mg/dL for two consecutive hours), patients will fingerstick and bolus if necessary. There is a 2-hour postprandial correction.

Hypoglycemia Treatment

Fingersticks are triggered by CGM readings below 70 mg/dL (except in Arm 4). Upon a reading of hypoglycemia (<70 mg/dL) a rescue carb (20 g) is administered every 30 minutes until the patients recovers. In some simulation arms, fingerstick confirmation is required, while others use CGM nonadjunctively.

Low Glucose Suspend Algorithm

Arm 4 uses a low glucose suspend algorithm.³¹ In this approach, low glucose (<70 mg/dL) leads to a 2-hour suspension of insulin infusion if patient ignores an alert. After this 2-hour period, insulin delivery resumes for 4 hours. If during this 4-hour interval glucose reaches the hypoglycemia threshold again, it is followed by a new 120-min insulin suspension cycle.³¹

Four In-Silico Trials

In each of the four in-silico trials described below, the 56 subjects in our database use each of the 43+9 available meters^27,28 in addition to the ideal meters. Each of the trials was replicated a total of 16 times to obtain enough precision to significantly compare meters. Insulin boluses were calculated using patient-specific carbohydrate ratio and correction factors, and per the following definitions, also summarized in Table 1:

Table 1.

Use of BGM and CGM in the Different Simulation Arms.

	Arm 1	Arms 2, 5, 6	Arm 3	Arm 4
Calibration	BGM	BGM	BGM	BGM
Dosing	BGM	CGM	CGM+ROC	CGM+LGS
Threshold alerts	CGM	CGM	CGM	CGM
CGM MARD	13%	13% 8% 20%	13%	13%

• Arm 1: BGM is used for CGM calibration and bolus decisions. CGM used only for alarms.

• Arm 2: BGM is used for CGM calibration. CGM is used for alarms, bolus, and rescue decisions.

• Arm 3: BGM is used for CGM calibration. CGM and ROC are used to make decisions.

• Arm 4: BGM is used for CGM calibration. CGM-based alarms, bolus decisions, and LGS.

A CGM model with an MARD of 13% was used in the Arms 1-4, and was modified in two additional arms to assess sensitivity of the results to CGM accuracy. Arm 5, identical to Arm 2, uses a highly accurate CGM (8% MARD). Arm 6, identical to Arm 2, uses a low accuracy CGM (20% MARD).

Simulation Outcomes

Clinical Outcome Estimates

Each 1-month patient simulation produced a month-long glucose trace. We used the average glucose concentration to estimate HbA1c.³² To estimate severe hypoglycemia events, which cannot be defined directly by glucose levels, we estimate the low BG index and used this to estimate severe hypoglycemia events.³³

Meter Characteristics

For each meter, we computed its error and bias per the following definitions:

1. Error: fraction of measurements exceeding 5% of the reference value.

2. Bias: mean difference between meter reading and reference. This should be distinguished from the manufacturer’s definition where bias may be dependent on glucose range.

Results

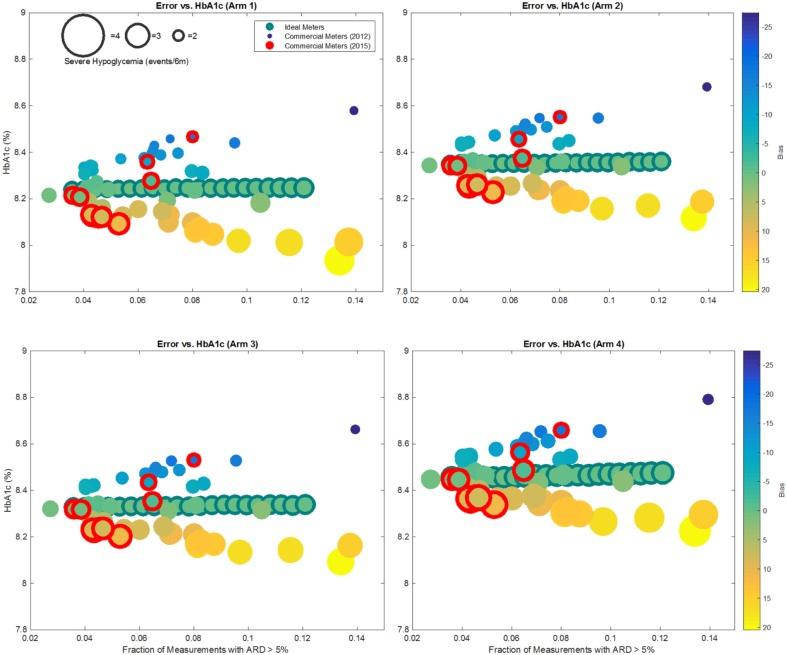
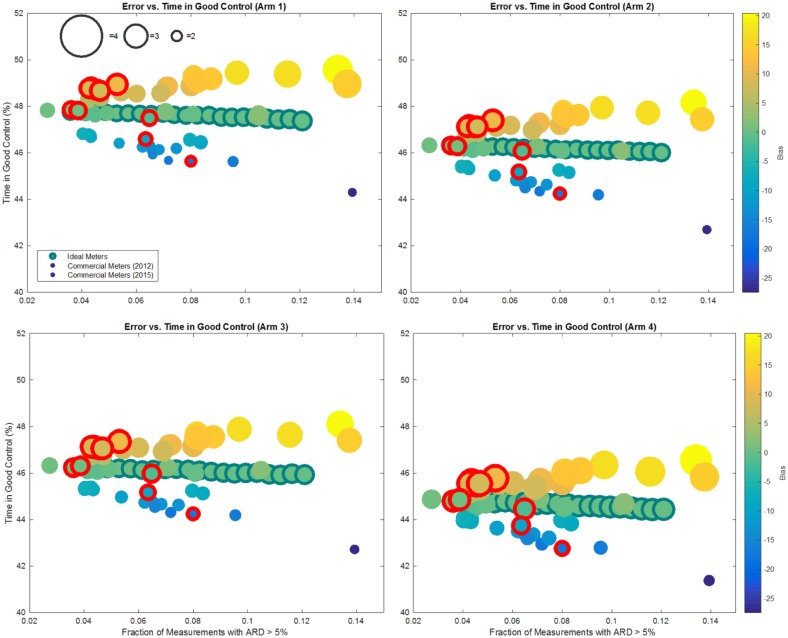
In Figure 2, results of Arms 1-4 are presented for all meters. Each bubble represents average results for a fixed meter across all 56 subjects and 16 replicates. The x-coordinate represents meter error, with HbA1c on the y-axis. Bubble size depicts the average number of predicted severe hypoglycemia per person per 6 months. Finally, fill color denotes systematic meter bias (as defined above) with blue, green, and yellow representing negative, neutral, and positive bias, respectively. Meters reported in 2015²⁸ are represented with a red outline. Time in range is presented in Figure 3, with the y-coordinate corresponding to time in good control (70-180 mg/dL). Actual numerical values are reported in Tables 2-4.

Figure 2.

Influence of meter accuracy on HbA1c and the number of severe hypoglycemic events. Figure presents results for 43 m reported in Freckmann et al 2012, average results for 9 meters reported in Freckmann et al 2015, and 21 ideal meters. The size of the bubble is proportional to the number of expected severe hypoglycemia events, while its color represents meter bias, with blue corresponding to a negative bias, green to zero bias, and orange-yellow to positive bias. The full color range is depicted in the color bar to the right of the figures.

Figure 3.

Average time in good control for all arms. Figure presents results for 43 m reported in Freckmann et al 2012, average results for 9 meters reported in Freckmann et al 2015, and 21 ideal (Gaussian, unbiased) meters. The size of the bubble is proportional to the number of expected severe hypoglycemia events, while its color represents meter bias with blue corresponding to a negative bias, green to zero bias, and orange-yellow to positive bias. The full color range is depicted in the color bar to the right of the figures.

Table 2.

Average Results for Meters Reported in Freckmann et al 2012.

Meter	Meter characteristics		Arm 1			Arm 2			Arm 3			Arm 4
	Error (%)	Bias (mg/dL)	HbA1c (%)	Severe hypo (events/6m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6m)	Time in range (%)
1	4.3	−8.3	8.3	2.2	46.7	8.4	2.3	45.3	8.4	2.3	45.3	8.5	2.5	44.0
2	4.4	−0.1	8.2	2.4	47.7	8.4	2.5	46.1	8.3	2.6	46.1	8.5	2.8	44.7
3	4.3	−8.5	8.3	2.1	46.7	8.4	2.3	45.3	8.4	2.3	45.3	8.5	2.5	43.9
4	4.5	−1.0	8.3	2.3	47.6	8.4	2.4	46.1	8.3	2.5	46.0	8.5	2.7	44.5
5	3.9	0.7	8.2	2.5	47.8	8.3	2.5	46.3	8.3	2.6	46.3	8.4	2.8	44.9
6	4.0	−8.1	8.3	2.2	46.8	8.4	2.3	45.4	8.4	2.3	45.3	8.5	2.5	43.9
7	2.7	0.5	8.2	2.5	47.8	8.3	2.5	46.3	8.3	2.6	46.3	8.4	2.8	44.9
8	5.4	−10.9	8.4	2.1	46.4	8.5	2.2	45.0	8.5	2.3	44.9	8.6	2.4	43.6
9	6.8	−13.0	8.4	2.1	46.1	8.5	2.2	44.7	8.5	2.2	44.6	8.6	2.4	43.3
10	8.2	15.6	8.1	2.9	49.2	8.2	3.0	47.8	8.2	3.1	47.7	8.3	3.3	46.0
11	8.0	−7.4	8.3	2.3	46.5	8.4	2.3	45.2	8.4	2.4	45.2	8.5	2.5	44.0
12	11.6	17.0	8.0	3.3	49.4	8.2	3.1	47.7	8.1	3.2	47.6	8.3	3.4	46.0
13	8.1	−0.2	8.2	2.6	47.6	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.5
14	8.0	10.5	8.1	2.9	48.9	8.2	2.8	47.2	8.2	2.9	47.1	8.3	3.2	45.6
15	13.9	−27.4	8.6	1.9	44.3	8.7	1.9	42.7	8.7	1.9	42.7	8.8	2.1	41.4
16	9.7	17.2	8.0	3.1	49.4	8.2	3.0	47.9	8.1	3.1	47.9	8.3	3.3	46.3
17	6.2	−12.2	8.4	2.1	46.2	8.5	2.2	44.8	8.5	2.2	44.7	8.6	2.4	43.5
18	8.4	−8.2	8.3	2.4	46.4	8.4	2.3	45.1	8.4	2.4	45.1	8.5	2.5	43.8
19	5.5	8.2	8.1	2.7	48.6	8.3	2.7	47.1	8.2	2.8	47.0	8.4	3.0	45.6
20	8.8	14.0	8.0	3.0	49.2	8.2	2.9	47.6	8.2	3.0	47.5	8.3	3.2	46.1
21	7.2	−17.3	8.5	1.9	45.7	8.5	2.0	44.3	8.5	2.1	44.3	8.7	2.2	42.9
22	13.4	20.4	7.9	3.4	49.5	8.1	3.2	48.1	8.1	3.3	48.1	8.2	3.5	46.5
23	10.5	2.0	8.2	2.8	47.6	8.3	2.6	46.1	8.3	2.7	46.1	8.4	2.9	44.7
24	7.1	1.6	8.2	2.6	47.7	8.3	2.6	46.3	8.3	2.6	46.2	8.4	2.8	44.9
25	6.5	−0.6	8.3	2.4	47.6	8.4	2.5	46.0	8.3	2.6	46.0	8.5	2.8	44.6
26	7.1	10.2	8.1	2.8	48.8	8.2	2.8	47.2	8.2	2.9	47.2	8.3	3.1	45.7
27	4.2	−0.5	8.3	2.4	47.6	8.4	2.5	46.1	8.3	2.5	46.1	8.5	2.8	44.6
28	7.2	11.1	8.1	2.7	48.8	8.2	2.8	47.3	8.2	2.9	47.2	8.4	3.1	45.6
29	4.3	−8.0	8.3	2.1	46.8	8.4	2.3	45.4	8.4	2.3	45.4	8.5	2.5	43.9
30	7.5	−13.2	8.4	2.1	46.2	8.5	2.2	44.6	8.5	2.2	44.6	8.6	2.4	43.2
31	4.9	−0.1	8.2	2.4	47.7	8.4	2.5	46.2	8.3	2.6	46.1	8.5	2.8	44.7
32	9.6	−16.3	8.4	2.1	45.6	8.5	2.1	44.2	8.5	2.2	44.2	8.7	2.4	42.8
33	8.1	14.2	8.1	2.9	49.3	8.2	3.0	47.6	8.2	3.0	47.5	8.3	3.3	46.0
34	4.2	4.8	8.2	2.5	48.3	8.3	2.6	46.7	8.3	2.7	46.7	8.4	2.9	45.1
35	4.7	5.4	8.2	2.6	48.3	8.3	2.6	46.8	8.3	2.7	46.7	8.4	2.9	45.3
36	8.3	13.0	8.1	2.9	49.0	8.2	2.9	47.5	8.2	3.0	47.4	8.3	3.2	45.9
37	6.5	−12.6	8.4	2.1	46.3	8.5	2.2	44.7	8.5	2.2	44.8	8.6	2.4	43.4
38	4.0	−7.2	8.3	2.2	46.8	8.4	2.3	45.4	8.4	2.3	45.3	8.5	2.5	44.0
39	6.9	8.4	8.1	2.7	48.6	8.3	2.8	47.0	8.2	2.8	46.9	8.4	3.1	45.4
40	6.0	9.2	8.2	2.7	48.5	8.3	2.8	47.2	8.2	2.8	47.1	8.4	3.1	45.6
41	6.6	−13.7	8.4	2.0	46.1	8.5	2.1	44.6	8.5	2.2	44.7	8.6	2.4	43.3
42	6.6	−14.8	8.4	2.0	45.9	8.5	2.1	44.5	8.5	2.2	44.5	8.6	2.3	43.2
43	13.8	15.2	8.0	3.3	48.9	8.2	3.1	47.4	8.2	3.1	47.4	8.3	3.4	45.8

Table 3.

Results for Ideal Meters (Unbiased).

Meter		Arm 1			Arm 2			Arm 3			Arm 4
	Meter error (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)
5	3.6	8.2	2.4	47.7	8.3	2.5	46.3	8.3	2.5	46.2	8.5	2.7	44.8
6	4.0	8.2	2.4	47.7	8.3	2.5	46.2	8.3	2.5	46.2	8.5	2.7	44.9
7	4.5	8.2	2.4	47.7	8.3	2.5	46.3	8.3	2.5	46.2	8.5	2.7	44.8
8	4.9	8.2	2.4	47.7	8.3	2.5	46.3	8.3	2.5	46.2	8.5	2.7	44.8
9	5.3	8.2	2.4	47.7	8.3	2.5	46.2	8.3	2.5	46.2	8.5	2.7	44.7
10	5.7	8.2	2.4	47.7	8.4	2.5	46.2	8.3	2.5	46.2	8.5	2.7	44.8
11	6.1	8.2	2.4	47.7	8.4	2.5	46.2	8.3	2.6	46.1	8.5	2.8	44.7
12	6.6	8.2	2.4	47.6	8.4	2.5	46.2	8.3	2.6	46.1	8.5	2.7	44.7
13	7.0	8.2	2.5	47.7	8.4	2.5	46.2	8.3	2.6	46.1	8.5	2.8	44.7
14	7.4	8.2	2.5	47.6	8.4	2.5	46.2	8.3	2.5	46.1	8.5	2.8	44.7
15	7.8	8.2	2.5	47.6	8.4	2.5	46.1	8.3	2.6	46.1	8.5	2.8	44.7
16	8.3	8.2	2.5	47.6	8.4	2.5	46.1	8.3	2.6	46.1	8.5	2.8	44.6
17	8.7	8.2	2.5	47.6	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.6
18	9.1	8.2	2.5	47.5	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.6
19	9.5	8.2	2.5	47.5	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.5
20	10.0	8.2	2.6	47.5	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.5
21	10.4	8.2	2.6	47.5	8.4	2.5	46.1	8.3	2.6	46.0	8.5	2.8	44.5
22	10.8	8.2	2.6	47.5	8.4	2.5	46.0	8.3	2.6	45.9	8.5	2.8	44.5
23	11.2	8.2	2.6	47.4	8.4	2.5	46.0	8.3	2.6	45.9	8.5	2.8	44.4
24	11.6	8.2	2.6	47.4	8.4	2.5	46.0	8.3	2.6	46.0	8.5	2.8	44.4
25	12.1	8.2	2.7	47.4	8.4	2.5	46.0	8.3	2.6	45.9	8.5	2.8	44.4

Table 4.

Average Results for Meters Reported in Freckmann et al 2015.

		Meter characteristics		Arm 1			Arm 2			Arm 3			Arm 4
Meter	Lot	Error (%)	Bias (mg/dL)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)	HbA1c (%)	Severe hypo (events/6 m)	Time in range (%)
1	1	4.4	−7.7	8.3	2.2	46.8	8.4	2.3	45.4	8.4	2.3	45.4	8.5	2.5	44.0
	2	4.6	−7.9	8.3	2.2	46.8	8.4	2.3	45.3	8.4	2.4	45.3	8.5	2.5	43.9
	3	4.9	0.4	8.2	2.5	47.8	8.3	2.5	46.2	8.3	2.6	46.2	8.4	2.8	44.8
	Average	4.6	−5.1	8.3	2.3	47.1	8.4	2.4	45.6	8.4	2.4	45.6	8.5	2.6	44.2
2	1	5.0	−0.1	8.2	2.4	47.7	8.4	2.5	46.1	8.3	2.6	46.1	8.5	2.8	44.7
	2	5.0	−9.5	8.4	2.1	46.6	8.5	2.2	45.2	8.4	2.3	45.1	8.6	2.5	43.8
	3	6.0	−10.8	8.4	2.1	46.5	8.5	2.2	45.0	8.5	2.3	44.9	8.6	2.4	43.6
	Average	5.3	−6.8	8.3	2.2	46.9	8.4	2.3	45.4	8.4	2.4	45.4	8.5	2.6	44.0
3	1	3.1	0.5	8.2	2.5	47.8	8.3	2.5	46.3	8.3	2.6	46.3	8.4	2.8	44.8
	2	2.8	0.3	8.2	2.4	47.8	8.3	2.5	46.3	8.3	2.6	46.2	8.4	2.8	44.8
	3	4.6	−9.0	8.3	2.2	46.5	8.4	2.2	45.2	8.4	2.3	45.2	8.6	2.5	43.9
	Average	3.5	−2.7	8.3	2.4	47.4	8.4	2.4	45.9	8.4	2.5	45.9	8.5	2.7	44.5
4	1	3.9	10.0	8.1	2.7	48.9	8.2	2.8	47.4	8.2	2.8	47.2	8.4	3.1	45.7
	2	3.5	0.8	8.2	2.5	47.8	8.3	2.5	46.3	8.3	2.6	46.3	8.4	2.8	44.9
	3	2.3	0.3	8.2	2.4	47.8	8.3	2.5	46.3	8.3	2.6	46.2	8.4	2.8	44.8
	Average	3.2	3.7	8.2	2.5	48.2	8.3	2.6	46.7	8.3	2.7	46.6	8.4	2.9	45.1
5	1	2.9	−0.3	8.2	2.4	47.8	8.4	2.5	46.2	8.3	2.5	46.2	8.5	2.7	44.8
	2	3.4	−0.7	8.3	2.3	47.7	8.4	2.5	46.2	8.3	2.5	46.1	8.5	2.7	44.6
	3	4.5	−10.2	8.4	2.0	46.6	8.5	2.2	45.2	8.4	2.3	45.1	8.6	2.4	43.8
	Average	3.6	−3.7	8.3	2.2	47.4	8.4	2.4	45.9	8.4	2.5	45.8	8.5	2.6	44.4
6	1	10.3	−24.1	8.5	1.7	44.8	8.6	1.9	43.4	8.6	1.9	43.4	8.7	2.1	42.1
	2	7.8	−6.8	8.3	2.2	46.9	8.4	2.3	45.4	8.4	2.4	45.3	8.5	2.6	43.8
	3	6.5	−1.0	8.3	2.4	47.6	8.4	2.5	46.0	8.3	2.6	45.9	8.5	2.8	44.4
	Average	8.2	−10.6	8.4	2.1	46.4	8.5	2.2	44.9	8.5	2.3	44.9	8.6	2.5	43.5
7	1	6.9	−5.5	8.3	2.4	46.9	8.4	2.4	45.5	8.4	2.4	45.4	8.5	2.6	44.1
	2	6.9	−14.8	8.4	2.0	45.8	8.5	2.1	44.6	8.5	2.2	44.5	8.6	2.3	43.2
	3	6.6	−12.4	8.4	2.1	46.2	8.5	2.2	44.7	8.5	2.2	44.7	8.6	2.4	43.5
	Average	6.8	−10.9	8.4	2.2	46.3	8.5	2.2	44.9	8.5	2.3	44.9	8.6	2.4	43.6
8	1	4.9	6.8	8.2	2.6	48.4	8.3	2.7	46.9	8.3	2.8	46.8	8.4	3.0	45.3
	2	4.7	−0.1	8.2	2.4	47.7	8.4	2.5	46.1	8.3	2.6	46.1	8.5	2.8	44.7
	3	4.0	−0.7	8.3	2.4	47.7	8.4	2.5	46.1	8.3	2.5	46.1	8.5	2.7	44.6
	Average	4.5	2.0	8.2	2.5	48.0	8.3	2.5	46.4	8.3	2.6	46.3	8.4	2.8	44.9
9	1	6.8	9.2	8.1	2.8	48.6	8.2	2.8	47.2	8.2	2.9	47.1	8.4	3.1	45.6
	2	6.9	10.4	8.1	2.8	48.7	8.2	2.8	47.3	8.2	2.9	47.2	8.3	3.1	45.7
	3	5.5	0.9	8.2	2.5	47.7	8.3	2.5	46.2	8.3	2.6	46.2	8.4	2.8	44.8
	Average	6.4	6.8	8.1	2.7	48.3	8.3	2.7	46.9	8.2	2.8	46.9	8.4	3.0	45.4

The BGM\CGM System and Its Impact on Clinical Outcomes

Our results show the interplay between BGM and CGM accuracies. To better quantify the effect of CGM accuracy, we fitted a linear regression model to clinical outcomes. In each Arm, clinical outcomes can be explained with a linear relationship to BGM bias and error (see Tables 5-6). Moreover, the coefficients of this linear relationship are determined by the use-case and by CGM accuracy (MARD). For example, consider HbA1c outcomes for Arm 2. A linear regression shows that, if CGM accuracy and use-case are fixed, HbA1c has a linear relationship to meter error and bias. In turn, the coefficients for this relationship (see Table 5) are determined, to a small extent, by the simulation arm (use-case), and by CGM MARD (see Table 6). For example, consider a meter with high error rate and large negative bias (small blue-dot on the top-right corner of Figure 2). The combination of bias and error results in an increase of 0.4 in HbA1c (higher y-axis position), and at the same time a reduction of severe hypoglycemia events (smaller bubble size) with respect to an ideal meter. On the other hand, a meter with similar error but large positive bias (yellow circle at the bottom right corner of Figure 2), results in the opposite, namely an increase in severe hypoglycemia events with respect to an ideal meter, but also a small reduction in HbA1c of 0.3 with respect to an ideal meter.

Table 5.

Linear Regression Coefficients for simulation Arms 2 Through 4.

		Arm 1	Arm 2	Arm 3	Arm 4
Severe hypoglycemia	(Intercept)	1.246***	1.263***	1.202***	1.322***
	BGM bias	0.0328***	0.0327***	0.0295***	0.034***
	BGM error	2.816***	2.7***	2.023***	2.569***
HbA1c	(Intercept)	7.90***	7.94***	7.91***	8.033***
	BGM bias	−0.00495***	−0.0102***	−0.0105***	−0.010***
	BGM error	0.0655	0.0879	0.186***	0.299***

^***P < .001.

Table 6.

Linear Regression Coefficients for Arms 2, 5, and 6.

		Arm 5—MARD 8%	Arm 2—MARD 13%	Arm 6—MARD 20%
Severe hypoglycemia	(Intercept)	1.171***	1.263***	1.430***
	BGM bias	0.0152***	0.0327***	0.0516***
	BGM error	0.651***	2.7***	3.927***
HbA1c	(Intercept)	7.90***	7.94***	7.96***
	BGM bias	−0.00495***	−0.0102***	−0.0162***
	BGM error	0.0655*	0.0879	0.602***

For instance, severe hypoglycemia outcomes associated with a specific meter in Arm 5 can be approximated by the formula Severe Hypoglycemia = 1.171 + 0.0152*Bias + 0.651*Error.

^*P < .05. ***P < .001.

BGM Impact on HbA1c

Maintaining fixed CGM accuracy, meter accuracy can produce a change of up to 0.65 % in HbA1c and the range holds across all arms. This shift is primarily a function of bias (see Table 5), and confirmed by the linear regression: increases in error in unbiased (ideal) meters yield nonsignificant changes in HbA1c. We also show that newer meters will reduce the impact on HbA1c to a maximum range of 0.4%, down from 0.6%.

BGM Impact on Time in Good Control

Figure 3 shows that a parallel between HbA1c and time in good control can be drawn. The range of time in good control is only 5% across all arms, primarily due to meter bias. An increase in meter error (Table 3) in absence of bias will not affect time in good control.

BGM Impact on Severe Hypoglycemia

Tables 2 and 3 show that BGM error has a significant effect on the rate of predicted severe hypoglycemia events. While the range of severe hypoglycemia increase for the 2012 meters varies from 1.3 to 1.5 (depending on the arm), ideal meters (no bias) can generate changes of 0.1 to 0.3 events per 6 months. While small, this could be clinically significant.

Impact of CGM Accuracy

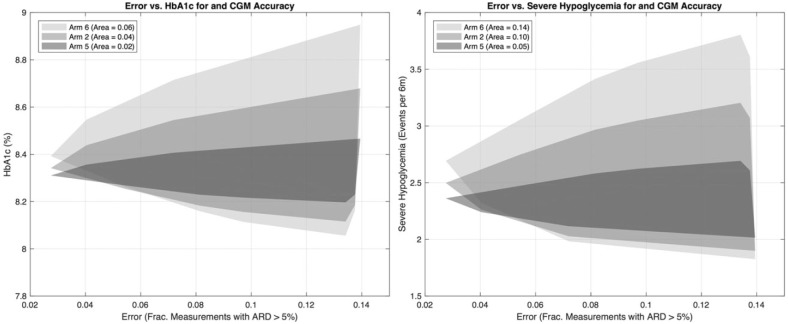
Figure 4 reports the results for Arms 5 and 6, which are identical to Arm 2, but use CGM models of two different accuracies replacing our standard CGM model. Arms 5 and 6 use CGM models with a MARD of 8% and 20% versus the default CGM model with a MARD of approximately 13%. We show in the left panel the minimal polygon enclosing the collection of points (error vs HbA1c). Similarly, the right panel shows polygon for points (error vs severe hypoglycemia). The relative areas of these are a measure of variability introduced by inaccurate BGM devices. For example, the area in the (error vs HbA1c) plane goes from .02 with highly accurate CGM, to .04 (reference CGM), to .06 (low accuracy CGM).

Figure 4.

Results for Arms 5 and 6, low and highly accurate continuous glucose monitors using meters in Freckmann et al 2012 for calibration. Arms 5 and 6 are identical to Arm 2 with less (more) accurate CGM. Left panel shows impact of CGM on BGM performance in terms of HbA1c. Right panel reports severe hypoglycemia effects.

The coefficients in Table 6 support this: higher CGM accuracy mitigating the effects of BGM accuracy. It is important to note that high CGM accuracy cannot completely compensate for BGM error. CGM systems with MARD larger than 13% seem to be more sensitive to BGM errors, an effect previously reported,¹⁹ where CGM with MARD larger than 10% result in rapidly degrading glucose control when used nonadjunctively. More specifically, the effect of BGM bias goes from −0.00495 of (HbA1c per mg/dL) in Arm 5, to −0.0102 in Arm 2, to −0.0162 in Arm 6. Thus, low CGM accuracy (MARD = 20%) triples the impact of BGM accuracy. Similarly, a highly accurate CGM (MARD = 8%) can reduce the effect of BGM error on severe hypoglycemia to a sixth.

Discussion

The above results while not clinically large, show that the impact of BGM accuracy on CGM performance for a broad range of treatment paradigms is consequential, and clinically relevant when comparing highly accurate versus low accuracy BGM systems: Predicted HbA1c changes between 0.5% and 1% and predicted rate of severe hypoglycemia increase of approximately 0.5 events per 6 months. This effect was observed in all tested scenarios, but with different amplitudes. Bias seems to be the driving factor of simulated clinical outcomes in all cases, with BGM error impacting the rate of severe hypoglycemia, but not HbA1c (see linear regression for confirmation). Simulated zero-bias meters confirmed these findings as well.

Not surprisingly, the maximum effect was observed in Arm 1 where BGM was used for both calibration and dosing. The amplitude of the BGM accuracy impact seems to diminish as more CGM features were enabled (Arm 2 and 3). Interestingly, the low glucose suspend (LGS) use case (Arm 4) seemed to be particularly sensitive to high BGM bias as it pertains to exposure to hypoglycemia.

The relative effect of BGM accuracy, bias in particular, may dominate the accuracy of CGM, that is, even a highly accurate CGM can perform poorly if paired with an inaccurate BGM. It also appears that CGM accuracy lends some robustness to the overall system: that is, the changes in HbA1c between a high performance versus low performance meter are more profound in the case of an inaccurate than an accurate CGM. The range in HbA1c variation drops from 0.9% on Arm 6 (20% MARD), to 0.6% in Arm 2 (13% MARD), to 0.3% in Arm 5 (8% MARD). At 8% CGM MARD, a point is reached where the predicted impact of highly accurate BGM on HbA1c has little clinical significance. A similar effect can be observed for severe hypoglycemia (see right panel of Figure 4), where due to changes in CGM accuracy the range of severe hypoglycemia values drop from 2 events per 6 months in low accuracy CGM (MARD = 20%), to 1.2 in the reference scenario (MARD = 13%), and 0.7 events for a highly accurate CGM (MARD = 8%).

A limitation of our approach is the lack of simulated long-term behavioral adjustments which are common in patients facing persistent hyper or hypoglycemia. Unfortunately, we are not aware of an available dataset to model this behavior explicitly. Another limitation is our estimation of severe hypoglycemia events, which are based on a result showing that the low blood glucose index can be used to predict severe hypoglycemia. The number of severe hypoglycemia events estimated this way is large compared to research literature that show an average of one severe hypoglycemia event per year. As mentioned above, the discrepancy may be a result of assuming no behavioral changes around hypoglycemia. It is also possible that the precision of the model has been affected by changes in both clinical practice and sensing technology since this publication.³³

Finally, results assume two CGM calibrations per day, as required by currently available systems. We did not explore how the effect of BGM errors, through calibration, may change as the number of calibrations per day diminishes. It is reasonable to expect that sensitivity to BGM error will increase to match the bias effect as calibration frequency is reduced: infrequent calibrations may result in fewer opportunities to quickly compensate for a larger error. Furthermore, the total BGM accuracy requirements may very well improve, resulting in fewer calibration measurements, ultimately peaking at a single calibration case. Should such a phenomenon occur it would be important to understand the BGM and CGM interaction effect prior to CGM calibration becoming less frequent.

Conclusions

In this paper, we described an in-silico approach to characterize the relationship between BGM and CGM accuracy as it manifests itself in clinical outcomes. Our approach leverages a recently introduced simulation approach that makes it possible to evaluate the performance of an insulin delivery algorithm in close to real-life scenarios. We analyzed the interaction of these two glucose monitoring technologies in a set of use-cases (arms) that range from BGM calibration and bolus decisions, to scenarios where CGM is used nonadjunctively to make dosing decisions, and scenarios where in addition to decision making and alarms, CGM is used to implement a low glucose suspend algorithm, and where BGM is used only for calibration.

Our results show that BGM accuracy has a significant effect in clinical performance of the patient as measured in HbA1c and the frequency of severe hypoglycemia in all scenarios generated for twice daily calibrated CGMs. We identified two accuracy characteristics of a meter (error and systematic bias) that drive clinical performance and showed that systematic bias has the most important effect in clinical performance. In the absence of bias, error has a very limited effect on both HbA1c and severe hypoglycemia. Our results also show that higher CGM accuracy mitigates, but does not eliminate, BGM accuracy effects on both HbA1c and more markedly on severe hypoglycemia.