The p-Median Model as a Tool for Clustering Psychological Data

Abstract

The p-median clustering model represents a combinatorial approach to partition data sets into disjoint, non-hierarchical groups. Object classes are constructed around exemplars, manifest objects in the data set, with the remaining instances assigned to their closest cluster centers. Effective, state-of-the-art implementations of p-median clustering are virtually unavailable in the popular social and behavioral science statistical software packages. We present p-median clustering, including a detailed description of its mechanics, a discussion of available software programs and their capabilities. Application to a complex structured data set on the perception of food items illustrate p-median clustering.

Introduction

In general terms, clustering might be characterized as a collection of methods concerned with the identification of homogenous groups of objects, based on whatever data are available. Cluster analysis represents an obvious choice for developing a taxonomy for any kind of object domain, be that subjects, psychological disorders, test and questionnaire items, experimental stimuli, behavioral patterns, and so on. Cluster analysis can also serve as a preliminary means to identify potential group differences in a sample, subsequently addressable through hypotheses-driven statistical analysis. However, for many statisticians, the “shady history” of early approaches to clustering, “usually just convenient algorithms devoid of any associated representational model or effort at optimizing a stated criterion”, was a long-standing cause of concern and reservation, as Arabie and Hubert (1996, p. 9) observed more than a decade ago.

The situation today is markedly different: a researcher can choose among a large variety of clustering methods ranging from the ‘standard’ algorithms still found in some commercial software packages to state-of-the-art, high-end implementations. Many non-casual cluster analysis users in Psychology have moved to sophisticated statistical computational environments such as MATLAB or R (the latter is freely available). Both platforms provide the flexibility to program special purpose routines/toolboxes that are often ‘open-source’. As examples, we mention the mclust toolbox in R for model-based clustering (Fraley, 1998; Fraley & Raftery, 1999, 2002, 2003, 2006; see McLachlan & Basford, 1988; McLachlan & Peel, 2000, for a comprehensive presentation of model-based clustering), or the suite of MATLAB routines for combinatorial (graph-theoretic) clustering through fitting ultrametric and additive tree structures by Hubert, Arabie, and Meulman (2006, Chapters 5–8; see also Hubert, Köhn, & Steinley, in press — for a thorough treatment of graph-theoretic clustering methods, see Barthélemy & Guénoche, 1991). The books by Martinez and Martinez (2004, 2008) provide detailed technical descriptions and user instructions for the up-to-date mainstream clustering algorithms implemented in the MATLAB statistics toolbox, as well as less common clustering routines available in their own toolboxes. Lastly, we reference the software packages Mplus (Muthén & Muthén, 1998–2007), and Latent GOLD (Vermunt & Magidson, 2005) offering model-based clustering, and a diverse collection of (discrete) latent-class models that can fairly be subsumed as special instances of clustering.

Among advanced (multivariate) statistical methods, clustering probably represents the least abstract and intuitively most accessible procedure, since its rationale emulates a major cognitive process: concept-based object categorization. In fact, the classic dichotomy of theories in concept research, prototype and exemplar models (see Murphy, 2002; Ross, Taylor, Middleton, & Nokes, 2008), attribute to classificatory acts distinct structures and principles of operation having direct counterparts in the logic and computational mechanics of certain clustering algorithms.

Prototype models conceptualize object categorization as the result of evaluating and integrating information about all the possible properties of an item in reference to the prototype of a category, an abstraction of the features shared by all its instances. “Mathematically, the prototype is the average or central tendency of all category members” (Love, 2003, p. 648). A novel object is postulated to be assigned to the category centered around the prototype most similar to the item. The observation of additional instances of a category can induce an update of the prototype feature profile. Eventually, in case of a poor match to all existing prototypes, a newly encountered object might establish a category of its own. Most notable, the prototype of a category can be a virtual object that does not even need to exist. Consequently, the prototype model of object categorization corresponds exactly to the computational logic of the popular K-means clustering method (Forgy, 1965; Hartigan & Wong, 1979; MacQueen, 1967; for a comprehensive review, see Steinley, 2006) that produces a partition of a set of objects into exhaustive and disjoint/non-hierarchical groups based on measures on some variables characterizing the objects.

The exemplar view on object categorization refutes the idea of a representation encompassing an entire concept that summarizes all individual instances of a category. Rather, a person’s concept is postulated to consist of the entire set of category members ever encountered and remembered. A novel object is classified in the category where the total sum of its similarities to all recalled exemplars is largest. As Murphy (2002) illustrates:

“The Irish terrier in my yard is extremely similar to some dogs that I have seen, is moderately similar to other dogs, but is mildly similar to long-haired ponies and burros as well. It has the same general shape and size as a goat, though lacking the horns or beard. It is in some respects reminiscent of some wolves in my memory as well. How do I make sense of all these possible categorizations: a bunch of dogs, a few goats, wolves, and the occasional pony or burro? — When you add up all the similarities, there is considerably more evidence for the object’s being a dog than for its being anything else” (p. 49).

Does the exemplar model of object categorization translate directly into a statistical clustering method like the prototype model into K-means? Not exactly. Yet, techniques known as exemplar-based clustering represent the closest equivalent to object categorization in light of the exemplar view: given a set of objects, a subset is selected as cluster centers (‘exemplars’), and the remaining objects are allocated to their most similar exemplar such that a given loss criterion is optimized (for instance, maximizing the total sum of similarities between exemplars and ‘satellites’).

In this case, the corresponding clustering method for exemplar-based categorization is the p-median model (alternatively referred to as Partitioning Around Medoids [PAM], Kaufman & Rousseeuw, 1990). As K-means, p-median clustering generates a disjoint, non-overlapping partition of a set of objects. In further exploiting the analogy to the competing prototype and exemplar models in cognitive theory, we mention that quantitative researchers have recurrently advocated p-median clustering as a viable procedure for partioning a data set (Alba & Domíguez, 2006; Brusco & Köhn, 2008a, 2008b; Hansen & Mladenoviĉ, 2008; Klastorin, 1985; Mulvey & Crowder, 1979; Rao, 1971; Vinod, 1969). Since the medians represent manifest objects that form the centers for the p groups, it has been argued that clusters built around real objects facilitate substantive interpretation; as an illustration, consider clustering instructional institutions in educational psychology, where groups constructed around existing schools offer an immediate and vivid picture, as opposed to the “virtual” centers found when using a prototype based clustering model. Or recall Murphy’s (2002) example of categorizing dogs: classes that are characterized by centroids of variables representing weight, height, maximal running speed, costs of keeping, friendliness-aggressiveness ratings, life expectancy, and so on, might be less catching and intuitively accessible than clusters centered around actual dogs such as German shepherd, poodle, boxer, or pekinese. In addition, p-median clustering is applicable to a wide range of data formats, be that square-symmetric/-asymmetric or rectangular proximity matrices; whereas, the usual clustering algorithms are usually constrained either to square-symmetric proximity matrices (in the case of hierarchical clustering) or a standard, rectangular data matrix (in the case of K-means clustering or model-based clustering). Lastly, Kaufman and Rousseeuw (2005, Chapter 2) emphasize the remarkable robustness of the p-median approach to outliers.

The unavailability of state-of-the-art implementations of p-median clustering through popular social and behavioral science statistical software packages might present the main cause for the lack of its awareness among researchers (sole exception: Kaufman and Rousseeuw, 2005, provide code written in R for a standard p-median implementation). In an attempt to make p-median clustering more accessible, we offer an introduction to p-median clustering in an effort to help bridge the gap between the theory of clustering based on exemplars and the pragmatic needs of a sophisticated user in psychological research. The next section briefly reviews several integral concepts such as proximity data, loss function, heuristics, and clustering as a combinatorial optimization problem. A detailed description of the rationale underlying the p-median clustering algorithm, illustrating its key features by a small-scale example, is given in the third section. Afterwards, an application to real-world data sets are presented for the perception of a vast collection of food items. We conclude with a discussion of the specific merits of p-median clustering and an outlook onto directions for future methodological developments of the p-median model.

Theoretical Preliminaries: Concepts and Terminology

Proximities

Tversky’s (1977) seminal paper on similarity gives a most thorough theoretical treatment of the concept, emphasizing its eminent and ubiquitous role in psychological “theories of knowledge and behavior” (p. 327). Similarity and its complement, dissimilarity, are typically subsumed under the notion of proximity. In its broadest sense, the term ‘proximity’ refers to any numerical measure of relationship between the elements of a pair from two (possibly distinct) sets of entities or objects. Proximities are typically collected into a matrix, with rows and columns representing the respective sets of objects, and the numerical cell values the observed pairwise proximity scores. By assumption, proximities are restricted to be nonnegative, and are, henceforth, consistently interpreted as dissimilarities so that larger numerical indices pertain to less similar pairs of objects. Cluster analytic methods depend on proximity data as key information and basis for identifying maximally homogenous subgroups.

Loss Function

As a common example, consider the least-squares loss function of the simple (linear) regression model: estimation of model parameters is determined by the objective of minimizing the sum of the squared deviations (residuals) between estimated and observed criterion values. In general, a loss function quantifies how well a fitted model approximates the original data. Thus, model estimation governed by a loss function offers the enormous advantage of a solid criterion for evaluating the quality of an obtained solution, and is nowadays considered a mandatory standard for statistical modeling, including the task of clustering a data set.

Global/Local Optima

Loosely speaking, the global optimum of a loss function denotes its unique absolute minimum/maximum value across the entire set of admissible (‘feasible’) solutions, as opposed to a local optimum pertaining to the minimum/maximum on a subset of the solution space; the associated solutions are said to be globally- or locally-optimal. The former simply indicates that we cannot ‘do any better’ for a given data-analytic task; whereas the latter, typically, but not necessarily, is inferior to the globally-optimal solution.

Related to the definitions of optima are the solution methods, or algorithms, themselves. Specifically, for optimization problems, algorithms can be broadly divided into two classes: exact and approximate. Exact algorithms (e.g., dynamic programming, branch and bound, etc.) produce guaranteed globally-optimal solutions; whereas, approximate algorithms (alternating least squares, expectation-maximization algorithm, etc.) cannot provide this guarantee.

Clustering as a Discrete Optimization Problem

The p-median problem is conceptualized as a combinatorial, discrete optimization problem where either an object an object falls into class C_k or class C_k′ (where 1 ≤ k, k′ ≤ K, with K denoting the total number of classes). Combinatorial optimization problems are characterized by non-smooth functions involving discrete or integer variables; combinatorial optimization problems are said to be discrete (the terms combinatorial and discrete optimization are often used interchangeably in the literature). The set of feasible solutions is finite, and a globally-optimal solution always exists (typically, a set of integers, a permutation, or partition of N objects), implying the misrepresentation that these problems are ‘easy’ and solvable through the explicit search of the entire solution space (‘complete enumeration’). The number of feasible solutions, however, grows exponentially with problem size. Even for small-scale problems, the computational effort of an exhaustive enumeration of all feasible solutions is prohibitive. For example, a seemingly plausible strategy for finding the best fitting cluster representation for a data set would aim at evaluating all possible combinations of assigning objects to groups, and choose the solution that provides a global optimum of the associated loss function. From a certain number of objects onward, this does not offer a realistic option, because the number of distinct partitions of N objects into K clusters increases approximately as K^N/K!. In short, complete enumeration of all possible object groupings is not computationally feasible for most practical applications.

Sophisticated partial enumeration strategies such as dynamic programming (see Hubert, Arabie, & Meulman, 2001, Chapter 3), and branch-and-bound methods (Brusco & Stahl, 2005, Chapters 2–5) can often facilitate globally-optimal solutions of larger clustering problems, without the need for explicit enumeration of the entire solution set, but do face serious limitations on the sizes of problems that can be handled. Thus, despite significant advancement in the development of exact solution procedures, heuristic algorithms remain necessary for combinatorial clustering problems of practical size, with no guarantee of identifying a global optimum, but often producing solutions at least within a close neighborhood of the desired global optimum.

p-Median Clustering

The p-median clustering model originated in operations research from attempts to optimize the planning of facility locations (Hanjoul & Peters, 1985; Kuehn & Hamburger, 1963; Maranzana, 1964; Mladenoviĉ, Brimberg, Hansen, & Moreno-Pérez, 2007). For example, consider the task of rolling-out a network of medical emergency wards in a densely populated area, with multiple candidate sites. Budget constraints limit the actual number of facilities to be installed; at the same time, the choice of locations should guarantee maximal accessibility within minimal time for the entire population across all communities. The search for the most suitable facility sites requires the evaluation of numerous combinations of community assignments to potential facility locations; in operations research known as the p-median facility location problem. The p-median clustering method is molded from this optimization problem: given a set of N objects, p exemplars (‘medians’) are selected, and the remaining N – p objects (‘satellite’) are assigned to medians such that the loss function of the total sum of median-to-satellite dissimilarities is minimized. In its most general form, p-median clustering can be used on data represented by a rectangular matrix containing proximities between two distinct sets of entities (such as in the previous example, where cell entries correspond to distances between communities and location candidates). Many data sets in the social sciences, however, focus on documenting the relationship between entities from a single set, often expressed as pairwise interobject dissimilarities and collected into a square-symmetric proximity matrix. As an aside, pairwise dissimilarity scores can either be directly elicited from subjects, say, through ratings on a scale, or derived from integrating multiple attribute ratings. Without loss of generality, we develop the logic of p-median clustering in application to square-symmetric proximity matrices.

Concretely, the p-median clustering problem can be formulated as a (linear) integer programming problem (IP) and formalized through an objective function (comparable to a loss function) subject to constraints imposed on the function variables (often referred to as ‘decision variables’). The specific IP formulation of p-median clustering is given as the minimization problem

$$(\text{IP})\underset{\mathbf{X}}{min}\left\{f(\mathbf{X})=\sum _{i=1}^N\sum _{j=1}^N{d}_{ij}{x}_{ij}\right\},$$

where d_ij represent the given input proximities, and x_ij denote binary decision variables restricted to take on only values of zero or one (thus, the name ‘integer program’). Let D represent the collection of interobject dissimilarities, D_N×N = {d_ij}_N×N. Then the decision variables, x_ij, are collected into an analogous matrix, X_N×N = {x_ij}_N×N. The decision variables in X split into two sets: the first, {x_jj}, refers to the entries along the main diagonal of X. They represent the candidate medians (the subscript j follows from the convention that medians are chosen among the column objects). The second set of decision variables, {x_ij}_i≠j, denotes the off-diagonal entries in X; they indicate whether a remaining (row) object O_i is assigned to a median O_j. Since the decision variables are constrained to values of zero or one, they operate as ‘switches turning on or off’ a specific object, either as a median or a satellite. If a decision variable is set to a value of one, then the dissimilarity value in the corresponding cell in D enters the objective function. As a technical detail, notice that an object selected as a median itself always contributes a value of d_jj = 0 to the objective function, with the immediate implication that any p-median clustering problem can be ‘solved’ trivially by simply setting p = N. In other words, changing the problem structure from p to p + 1 will automatically decrease the loss function.

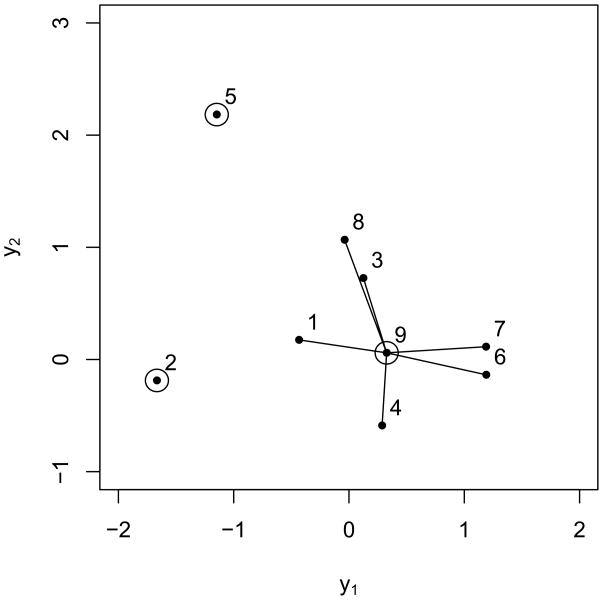
As an example, consider Figure 1. In this figure, there is a set of N = 9 objects located in a plane. For illustrative purposes, assume the goal then is to assign these nine objects to p = 3. Despite the striking simplicity of its rationale, p-median clustering poses a very difficult partitioning problem because, for each particular choice of p, the globally-optimal solution must be identified among $\left(\begin{array}{c}N\\ p\end{array}\right)$ different candidates (note that a candidate solution is well-defined as soon as a particular set of medians has been selected, because the subsequent assignment of remaining objects to medians is fully determined by their row minima across median columns). In our example, we must evaluate $\left(\begin{array}{c}9\\ 3\end{array}\right)=\frac{9!}{6!3!}=84$ different choices for selecting cluster centers.

Figure 1.

Scatter plot of the globally-optimal solution for the nine-object set with p = 3 medians.

The globally-optimal solution for p = 3 medians (represented as dots with circles around them) is shown in Figure 1, with the total sum of median-to-satellite Euclidean distances (represented as the lines connecting the satellites to the medians) equalling .77 + .70 + .65 + .89 + .86 + 1.07 = 4.94, which corresponds to the partition = {C₁, C₂, C₃} = {(2), (5), (9, 1, 3, 4, 6, 7, 8)}.

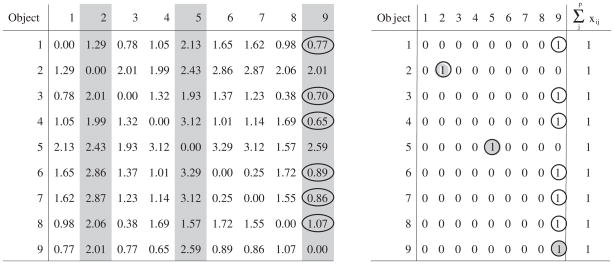
Figure 2 presents matrices D and X side-by-side to illustrate the underlying mechanics for the globally-optimal solution of our small-scale example, {(2), (5), (9, 1, 3, 4, 6, 7, 8)}. Observe that only entries x₂₂, x₅₅, and x₉₉ along the main diagonal of X (corresponding to medians 2, 5, and 9) equal one. The distribution of 0–1-values among the off-diagonal cells indicates that all remaining objects, 1, 3, 4, 6, 7, and 8, have been assigned to median object 9. The value of the objective function is simply computed as the total sum of products of corresponding cells in D and X: f(X) = d₁₁x₁₁ + d₂₁x₂₁ + ··· + d₈₉x₈₉ + d₉₉x₉₉ = 4.94. More succinctly, solving the p-median IP amounts to searching for a specific 0–1-pattering of X that will yield a global minimum of the objective function.

Figure 2.

Dissimilarities and matrix of binary decision variables, with entries corresponding to the globally-optimal solution marked by circles.

As an additional complication, the choice of the 0–1-values for the decision variables must conform to a set of constraints that ensure the identification of an at least feasible solution (a formal listing of these conditions is given below). First, the sum of the x_jj variables along the main diagonal must equal p to guarantee that exactly p objects are selected as medians (see constraint 1). Second, the value of any decision variable, x_ij, can at most equal the value of the median variable, with corresponding index j, x_jj. Thus, a remaining object, O_i, can be assigned to median j if and only if object O_j has been selected as a median (see constraint 2). Third, for each row object, O_i, of X, the sum of the x_ij variables across the j columns is limited to equal 1, which translates into the requirement that a remaining object can only be assigned to one median (i.e., multiple assignments are blocked, because the resulting sum across columns then would exceed one; see constraint 3). Note that for selected medians this condition is automatically fulfilled, because then x_jj always equals 1. In formal notation, the constraints are summarized by

$$\sum _{j=1}^N{x}_{jj}=p,$$ (1)

$$x_{ij}\le x_{jj}\forall i,j,$$ (2)

$$\sum _{j=1}^N{x}_{ij}=1\forall i.$$ (3)

The crucial question remains how to find the optimal values for the decision variables that conform to the stated constraints.

Solving the p-Median IP Globally Optimal

Brusco and Köhn (2008b) proposed a three-stage method for obtaining globally-optimal solutions to p-median clustering problems. The three stages are: (1) multiple restarts of a vertex substitution (VS) heuristic (the term ‘vertex’ simply refers to an object as a candidate median), (2) Lagrangian relaxation/subgradient optimization, and (3) a branch-and-bound algorithm. The three-stage method has obtained globally-optimal solutions to problems with up to N = 1, 400 objects and p = 30 clusters. We provide only a brief non-technical account of Brusco and Köhn’s three-stage procedure; for an in-depth technical description, the interested reader is encouraged to consult the original source, which also provides detailed performance results for a collection of test data sets.

Originally proposed by Teitz and Bart (1968), the VS heuristic is an efficient, effective, and widely applied method for p-median problems. VS performs a systematic, but succinct iterative search among all possible median candidates through consecutively replacing selected medians by unselected objects until an exchange step will not yield any further reduction of the objective function (i.e., the total sum of median-to-satellite distances). The resulting solution is locally optimal with respect to all replacement operations, but not necessarily globally optimal. Hence, as p-median clustering represents a minimization problem, VS provides at least an upper bound to the optimal solution of the p-median clustering IP. The procedure proposed by Brusco and Köhn for p-median clustering employs an especially efficient implementation of VS developed by Hansen and Mladenoviĉ (1997,2005) drawing on earlier work by Whitaker (1983).

Cornuejols et al. (1977; see also, Mulway & Crowder, 1979) introduced an elegant (exact) solution for relatively large p-median clustering problems through Lagrangian relaxation (LR). ‘Relaxation’ means to simplify an optimization problem by removing those constraints that are ‘difficult’ to meet. Thus, in the case of a minimization problem, dropping constraints will automatically lead to a reduction in the value of the objective function. Hence, the solution for the ‘relaxed’ problem can be considered as a lower bound to the solution of the original optimization problem. In case of LR, the relaxed constraints are not simply discarded from the optimization problem, but are attached with a weighting coefficient (‘Lagrangian multiplier’), and incorporated as penalty terms into the objective function. In other words, LR represents a rather ‘conservative’ form of relaxation. Still, the LR optimization problem is typically ‘easier’ to solve than the original IP version, and provides at least a ‘tight’ lower bound to the optimal solution of the original IP of p-median clustering (see also Christofides & Beasley, 1982; Fisher, 1981; Hanjoul & Peeters, 1985). LR optimization problems can be solved efficiently by iterative subgradient optimization (see Agmon, 1954; Held & Karp, 1970; Motzkin & Schoenberg, 1954), provided a tight upper bound on the solution for the original IP is available (say, through VS). Loosely speaking, subgradient optimization iteratively cycles through estimating values for the decision variables in X, subsequently updating the penalty coefficients for the relaxed constraints and the value of the objective function of the LR problem, then followed by another estimation-update step until the value of the objective function can no longer be reduced. The combination of VS and LR results at least in a narrow interval bracing the globally-optimal solution of the original p-median clustering IP. Very often, however, a verifiably globally-optimal solution is identified for the original IP if the subgradient iterations converge to updated constraint weights all equal to zero (which is equivalent to neutralizing the LR relaxation, and, therefore, identical to the original p-median clustering IP).

If the solution obtained through VS/LR-subgradient optimization is not globally optimal (i.e., the subgradient iterations do not converge to zero LR weights), then a subsequent search through branch-and-bound (BAB) is initialized that guarantees a globally-optimal solution if convergence is attained. The general idea of BAB is straightforward: the optimization problem (as forwarded from VS/LR-subgradient) is decomposed into subproblems (‘branching’), thereby allowing for a structured ‘incremental’ enumeration. Starting from a particular subproblem, the algorithm explores various stepwise completion scenarios (‘nodes’) of the initial partial problem; results are constantly monitored against an initial upper bound from a candidate solution for the entire problem (i.e., the locally-optimal solution obtained through VS/LR-subgradient optimization). If at a specific node the partial solution exceeds the bound, then the node is discarded along with all subsequent branches emanating from it (‘pruning’). The algorithm terminates when all nodes of the search tree have been pruned/solved (‘convergence’), yielding the global optimum.

Choosing the Number of Medians (i.e., Clusters)

As with most clustering procedures, p-median clustering requires the user to pre-specify the number of clusters and the question often arises about the correct way to choose the number of clusters. Rousseeuw (1987) introduced the widely accepted silhouette index for choosing the number of clusters in the context of p-median clustering. The silhouette index is given as

$${SI}_k=\sum _{i=1}^N\frac{b(i)-a(i)}{max\{a(i),b(i)\}})/N,$$ (4)

where a(i) is the average dissimilarity of object i to all other objects of the cluster to which it is assigned and b(i) is the minimum distance from object i to any object that is in a different cluster. Different numbers of clusters are fit to the data, and k is chosen to the value that maximizes SI_k. The minimum value for SI_k is zero, while the maximum value is unity.

Example: Data Set on Perception of Food Items

Our application uses data collected by Ross and Murphy (1999) asking 38 subjects to sort 45 foods into as many categories as they wished, based on perceived similarity. The data were aggregated into proportions of subjects who did not place a particular pair of foods together in a common category (thus, these proportions are keyed as dissimilarities in which larger proportions represent the less pairwise similar foods). The pairwise dissimilarity scores were collected into a 45 × 45 square-symmetric proximity matrix. The ultimate substantive question involves the identification of the natural categories of food that may underlie the subjects’ classification judgements. The types of categorizations given by the subjects can be diverse, implying an intricate, potentially multi-criteria evaluation of the stimuli. For example, these might involve the differing situations in which food is consumed, or possibly, a more basic notion of what type of food it is. For a few illustrations, ‘egg’ might be subsumed among foods that involve breakfast as a common consumption situation, or that are dairy products (type). Similarly, ‘spaghetti’ appears related either to those objects that are entrees and particularly to those that are Italian (consumption situation), or apparently when relying on a different interpretation for the word, to those foods that are cereal-based (type). We obtained globally-optimal solutions for 2 ≤ p ≤ 14 clusters. The final number p of clusters was determined based on the silhouette index and the percentage reduction in the value of the objective function resulting from an increase of the number of medians from p to p + 1 (see Table 1). Although the absolute maximum average silhouette index occurs at p = 11, the values increase steeply until p = 8 and then begin to become quite flat. The value of .5514 for p = 8 also falls within Kauffman and Reusseeuw’s (1990, p. 88) range of “reasonable structure”, which is .51 – .70.

Table 1.

Globally-optimal p-median solutions for 2 ≤ p ≤ 14, percentage reduction in the objective function, and silhouette indices

p	Global Optimum	Reduction p to p + 1 in %	Silhouette Index (SIk)
2	2871	—	.1630
3	2385	16.93	.2227
4	1946	18.41	.3129
5	1619	16.80	.3843
6	1358	16.12	.4330
7	1119	17.60	.4884
8	964	13.85	.5514
9	885	8.20	.5535
10	817	7.68	.5580
11	751	8.08	.5594
12	696	7.32	.5454
13	641	7.90	.5292
14	591	7.80	.5196

The solution with eight clusters, is provided in Table 2 (foods representing cluster centers, ‘medians’, are listed in the top line in bold face). In summary, the eight clusters can be characterized as fruit (cluster 1), vegetables (cluster 2), grain-based foods (cluster 3), ‘munchies’ (cluster 4), pastries/tarts/dessert (cluster 5), dairy products (cluster 6), water (cluster 7), and animal-based foods (cluster 8).

Table 2.

Globally-optimal food clustering solution, with p = 8 medians. Foods representing cluster centers, ‘medians’, are listed in the top line in bold face — the numbers in parentheses refer to the original numerical codes used by Ross and Murphy (1999).

Cluster	1	2	3	4
	Apple (1)	Broccoli (7)	Bagel (14)	Pretzels (22)
	Watermelon (2)	Lettuce (6)	Rice (12)	Crackers (20)
	Orange (3)	Carrots (8)	Bread (13)	Popcorn (23)
	Banana (4)	Corn (9)	Oatmeal (15)	Nuts (24)
	Pineapple (5)	Onions (10)	Cereal (16)	Potato Chip (25)
		Potato (11)	Muffin (17)
			Pancake (18)
			Spaghetti (19)
			Granola Bar (21)
Cluster	5	6	7	8
	Pie (30)	Cheese (35)	Water (38)	Pork (42)
	Doughnuts (26)	Yogurt (33)	Soda (39)	Hamburger (40)
	Cookies (27)	Butter (34)		Steak (41)
	Cake (28)	Eggs (36)		Chicken (43)
	Chocolate Bar (29)	Milk (37)		Lobster (44)
	Pizza (31)			Salmon (45)
	Ice Cream (32)

Discussion and Conclusion

The choice among the myriad of available clustering methods — model- or (combinatorial) nonmodel-based, hierarchical or non-hierarchical, and so on (for a recent documentation, see Gan, Ma, & Wu, 2007) — represents an often difficult decision. Sometimes, theoretical considerations can help; for example, is the continuity assumption underlying most model-based clustering methods justifiable for the given data? Or, were the data generated by a discrete process such that combinatorial clustering or discrete latent class models should be preferred? Many practical applications, however, lack unequivocal theoretical support for such a complex decision; instead, after exploring the results of multiple clustering methods applied to a particular data set, one might simply go with what ‘works best’.

K-means clustering and model-based clustering provide a very reasonable choice if object categorization is to be analyzed in light of a prototype theory. Contrastingly, p-median classification incorporates a clustering rationale, most closely related to a perspective on object categorization elaborated by the exemplar model in cognitive theory (i.e., object categories are constructed around manifest objects). So, researchers studying exemplar-driven object classification, might, indeed, consider p-median clustering as a viable clustering technique. In addition, Kaufman and Rousseeuw’s (2005, Chapter 2) statement, referenced earlier, that the p-median approach is more robust and less sensitive to outliers than K-means partitioning might recommend the former as particularly suitable for clustering data potentially contaminated by such distorting observations.

One of its biggest advantages is that the p-median algorithm can handle flexibly a large variety of input formats of proximity matrices, be they square-symmetric, square-asymmetric, or rectangular, containing interval-scale or categorical data (Brusco & Köhn, 2008a). Contrastingly, most model-based clustering procedures (and non-model based clustering procedures) typically only accommodate rectangular input matrices, with rows referring to objects, and columns to variables having at least interval scale level.

p-median clustering represent combinatorial optimization problems. Hence, it suffers from an explosive growth of feasible solutions, as the number of objects increases, and for realistically-sized data sets, each method must rely on heuristics that often produce locally-optimal rather than globally-optimal solutions. For most researchers, who use clustering as a means to an end for an applied data-analytic task, a ‘good’ locally-optimal solution will be perfectly fine.

Fortunately, the three-stage p-median clustering procedure proposed by Brusco and Köhn (2008b) identifies guaranteed globally-optimal solutions for object sets of a size roughly up to N = 1, 400, and at most 30 clusters (depending on the complexity of the problem structure).

The fast VS heuristic (Hansen & Mladenoviĉ, 1997, 2005; Whitaker, 1983), the first module in Brusco and Köhn’s (2008a, 2008b) three-stage p-median procedure, generally performs well for problems where the number of clusters equals 20 or fewer; however, computation time explodes, accompanied by a degrading performance as an increasing function of p > 20. Still, for most practical applications in the behavioral and social sciences, partitions with more than 20 classes are seldom interpretable. Avella, Sassano, and Vasil’ev (2007) describe a branch-cut-price algorithm that guarantees globally-optimal clustering solutions for two-dimensional Euclidean p-median problems (corresponding to our small-scale introductory example) as large as N = 3, 795 and p = 500; so far, however, the performance of their method on higher-dimensional or non-Euclidean proximity data is unknown.

In summary, if obtaining the globally-optimal solution to a clustering task is mandatory, then, depending on the size of the given data set, a researcher would likely fare well using the p-median method.

Computational Logistics

The VS- and LR-subgradient optimization modules of Brusco and Köhn’s (2008a, 2008b) three-stage procedure for p-median clustering have been written in MATLAB; the BAB-module, is currently only available as an executable FORTRAN file.

We already mentioned that Kaufman and Rousseeuw (2005, Chapter 2) provide R-code for a heuristic p-median routine, pam, (Kaufman and Rousseeuw refer to p-median clustering as ‘partitioning around medoids’) that represents an implementation of VS, refined by the innovations proposed by Whitaker (1983), but does not offer the advanced stage 2 and 3 modules, LR-subgradient optimization and BAB, of Brusco and Köhn’s (2008a, 2008b) implementation (pam is available from http://finzi.psych.upenn.edu/library/cluster/html/pam.html).

Although considerable progress has been made in the development of large-scale exact and approximate procedures for the p-median problem (Avella et al., 2007; Hansen, Mladenoviĉ, & Pérez-Brito, 2001; Resende & Werneck, 2004) most of the reported results for large test problems correspond to two-dimensional Euclidean data, and little is known about their performance on a broader class of proximity data. In addition, the aforementioned authors implemented their methods on workstations using optimized compilation of FORTRAN and C++ codes, respectively, that most practitioners might find difficult to operate.

Directions of future research on the p-median clustering algorithm will focus on accessible computer implementations that produce high-quality solutions for problems of large set sizes, N (and a further increase in the number of medians, p), as well as diversified data structures. For example, most recently, Brusco and Köhn (2008c) proposed a p-median heuristic based on simulated annealing that was successfully applied to test problems with 6,000 or more objects, constrained only by computer RAM limitations.