Abstract
Establishing blockmodels for one- and two-mode binary network matrices has typically been accomplished using multiple restarts of heuristic algorithms that minimize functions of inconsistency with ideal block structure. Although these algorithms likely yield exceptional performance, they are not assured to provide blockmodels that optimize the functional indices. In this paper, we present integer programming models that, for a prespecified image matrix, can produce guaranteed optimal solutions for matrices of nontrivial size. Accordingly, analysts performing a confirmatory analysis of a prespecified blockmodel structure can apply our models directly to obtain an optimal solution. In exploratory cases where a blockmodel structure is not prespecified, we recommend a two-stage procedure, where a heuristic method is first used to identify an image matrix and the integer program is subsequently formulated and solved to identify the optimal solution for that image matrix. Although best suited for ideal block structures associated with structural equivalence, the integer programming models have the flexibility to accommodate functional indices pertaining to regular equivalence. Computational results are reported for a variety of one- and two-mode matrices from the blockmodeling literature.
Keywords: Combinatorial data analysis, Blockmodeling, Integer programming
1. Introduction
Blockmodeling of social network data has a well-established history in the quantitative behavioral sciences (Arabie, Boorman, & Levitt, 1978; Arabie & Hubert, 1990; Arabie, Hubert, & Schleutermann, 1990; Borgatti & Everett, 1997; Brieger, Boorman, & Arabie, 1975; Doreian, Batagelj, & Ferligoj, 2004, 2005; Hartigan, 1972; Wasserman & Faust, 1994). A blockmodel is established by clustering the objects that define the rows and columns of a network matrix such that the intersection of the row and column clusters create blocks of matrix elements. Blockmodeling applications can be classified on various dimensions; however, two of the most critical features are: (1) the modality of the network data, and (2) the types of equivalence relationships under investigation. One-mode blockmodeling problems are characterized by a single set of N objects and an N × N binary matrix, S = [sij], measured on those objects. The network matrix, which can be either symmetric (an undirected network) or asymmetric (a directed network), contains entries of sij = 1 when there is a tie (or bond) between elements i and j and sij = 0 in the absence of a tie. In the two-mode blockmodeling context, there are two object sets consisting of N1 and N2 elements, respectively. The N1 × N2 network matrix, T = [tij], contains entries of tij = 1 when there is a tie (or bond) between element i of object set one and element j of object set two, and tij = 0 in the absence of a tie.
The two most important types of equivalence relationships in blockmodeling are structural (Lorrain & White, 1971) and regular (White & Reitz, 1983). Structurally equivalent objects exhibit the same ties to the same objects in the network. A structurally equivalent blockmodel of a matrix produces blocks that are either null or complete. Generally, null blocks consist of elements that are all zero, whereas complete blocks consist of elements that are all one. In the case of one-mode blockmodeling, where ties of an object to itself may or may not be considered, null (complete) blocks may permit ones (zeros) along the main diagonal of a block.
Structural equivalence is a very rigid condition that is difficult to achieve. White and Reitz (1983) proposed regular equivalence as a less restrictive alternative. Regularly equivalent objects exhibit similar types of ties to the same, or possibly different, objects in the network. A regularly equivalent blockmodel of a matrix produces blocks that are either null or regular. A regular block must possess at least one entry of one in each row and column of the block (i.e., the block is row-covered and column-covered). Clearly, the presence of row-coverage and column-coverage in a block that is needed for regular equivalence is much less stringent than the presence of complete blocks that is required for structural equivalence.
The development of a blockmodel for a network matrix can be approached in a variety of ways. One alternative is to permute the rows and columns of the matrix in a manner that tends to produce large bands of ones and zeros. For example, Arabie and Hubert (1990) and Arabie et al. (1990) describe a permutation method based on the bond-energy algorithm (McCormick, Schweitzer, & White, 1972) that induces a blockmodel-type structure. Drawing from pioneering work on incidence matrices and interval graphs (Fulkerson & Gross, 1965; Hubert, 1974; Kendall, 1969), Brusco and Steinley (2006) described a permutation approach for two-mode blockmodeling that attempts to establish Robinson (Robinson, 1951) patterning for TT′ and T′T. A matrix exhibiting Robinson patterning is characterized by non-increasing entries when moving away from the main diagonal within a row or column. Whereas Brusco and Steinley described exact procedures for modestly-sized network matrices, the heuristic procedures for Robinson patterning described by Hubert, Arabie, and Meulman (2006) can be applied to much larger matrices. Although permutation methods provide insight with respect to blockmodel structure, they do not formally establish blocks because objects are not explicitly assigned to clusters. Accordingly, their greatest value might be the provision of visual information for determining an ideal block structure.
A second approach to blockmodeling is the direct partitioning of one or more object sets to minimize some objective function associated with inconsistencies in an ideal blockmodel structure. This approach has been employed in a one-mode context for both structural (Batagelj, Ferligoj, & Doreian, 1992) and regular (Batagel, Doreian, & Ferligoj, 1992) equivalence. The extension of the direct partitioning approach to two-mode blockmodeling based on structural, regular, and other equivalence relationships was offered by Doreian et al. (2004). A thorough coverage of these developments is provided by Doreian et al. (2005, Chapters 6-8).
The cornerstone of the blockmodeling approach championed by Doreian et al. (2005) is a heuristic transfer and exchange algorithm (TEA). Objects are relocated across clusters until no further improvement in the objective function can be realized. Because this procedure is sensitive to the initial clustering of row and column objects, Doreian et al. recommend using a very large number of randomly generated initial solutions. Although metaheuristics such as simulated annealing, tabu search, genetic algorithms, and variable neighborhood search could possibly yield slightly better performance, computational experiments (see, for example, Brusco & Steinley, 2007) suggests that the TEA proposed by Doreian et al. performs exceptionally well when the number of restarts is large (e.g., at least 500). Although generally efficient and effective, heuristic methods such as the TEA, simulated annealing, genetic algorithms, tabu search, and variable neighborhood search are not guaranteed to provide optimal solutions.
Heuristic algorithms for partitioning object sets to establish blockmodels can be implemented in either an exploratory (inductive) or confirmatory (deductive) context. In the case of exploratory blockmodeling, heuristic algorithms are implemented such that the locations of the permitted block types (i.e., null, complete, regular, etc.) are established via the solution process. Contrastingly, in the case of confirmatory blockmodeling, a prespecified image matrix is assumed, wherein the locations of the blocks have been identified in advance. In this context, the heuristic algorithms attempt to obtain the best possible fit for the assumed structure. Accordingly, confirmatory blockmodeling is especially useful when network analysts have à príori knowledge regarding structure and can prespecify the placement of blocks in the image matrix. Doreian et al. (2005, p. 349) describe the importance of confirmatory blockmodeling as follows: “By putting social knowledge into the prespecification of a blockmodel, we are able to test the blockmodel and the knowledge that went into its prespecification.”
In this paper, we present integer programming models that can be used to obtain globally-optimal one- and two-mode blockmodels based on structural and regular equivalence. The objective functions of these models are concordant with those described by Doreian et al. (2005, Chapter 6), imposing penalties on inconsistencies that occur in null, complete, and regular ideal blocks. We apply the integer programming models to a variety of matrices from the social network literature, demonstrating that a number of previously published blockmodeling solutions are optimal with respect to their selected objective function index.
We perceive our contribution as important from both a mathematical and pragmatic perspective. First, from a mathematical standpoint, the representation of the direct partitioning problems described by Doreian et al. (2005, Chapters 6-8) as integer programs has an inherent classificatory value. Given that integer programming models for blockmodeling are not discussed in Doreian et al.'s comprehensive text, we believe that our contribution in this regard is unprecedented in the literature. Second, unlike heuristic algorithms for blockmodeling, the solutions to our integer programming models provide guaranteed globally-optimal solutions. The assurance of global optimality provided by our models represents both a mathematical and practical contribution. Third, the proposed integer programming framework is generally capable of accommodating a variety of side constraints and objective functions and this flexibility would likely have practical relevance for many blockmodeling applications.
Why are our proposed integer programming models useful for applied blockmodeling? We believe that our models are especially constructive in the important case of confirmatory blockmodeling, where they can be applied gainfully to obtain optimal solutions. Consider, for example, a social network analyst conducting a confirmatory blockmodeling analysis. The analyst could apply our integer programming models directly to obtain a blockmodeling solution without any need to qualify the results with respect to potential sub-optimality. This optimality guarantee is not afforded by heuristic algorithms.
We believe that our integer programming models can also play a role in exploratory blockmodeling. If the number of blocks is small, an analyst could implement the appropriate integer programming model for all possible image matrices, thus enabling the identification of a globally-optimal blockmodel across all image matrices. When the formulation and solution of model for all possible image matrices is impractical, the integer programming models will need to be used in conjunction with heuristic procedures that provide guidance regarding the location of ideal blocks. More specifically, we recommend a two-stage procedure where a heuristic method is first used to identify the placement of ideal blocks and the integer program is subsequently formulated and solved to identify the optimal solution for that prespecified ideal structure. Again, from the standpoint of an applied social network analyst, the key justification for using integer programming in the second stage is to ensure that the solution obtained for the prespecified structure is, in fact, globally optimal.
In Section 2, we present an integer programming formulation for one-mode blockmodeling based on structural equivalence. In Section 3, we adapt the model for one-mode regularly equivalent blockmodeling. Sections 4 and 5 present formulations for two-mode blockmodeling based on structural and regular equivalence, respectively. Computational results and numerical examples are interspersed throughout Sections 2-5 to demonstrate the capabilities of the models. The paper concludes with a discussion and suggestions for future research in Section 6.
2. A formulation for one-mode blockmodeling based on structural equivalence
2.1. Model formulation
A structurally equivalent one-mode blockmodel consists of ideal blocks that are either null or complete. Approximation of structural equivalence is accomplished by minimizing a function of inconsistencies with the ideal structure. The required inputs for our integer programming model are: (1) a desired number of blocks, K, (2) a K × K image matrix, B, that defines the placement of ideal blocks, and (3) a K × K penalty matrix, P, that defines the consequences of an inconsistency in each ideal block. An entry of bkl = 1 (bkl = 0) in the image matrix indicates that the block formed by the intersection of clusters k and l should be complete (null). Together, matrices S, P, and B are used to construct the penalty parameters δijkl, which are computed as follows for all 1 ≤ i ≤ N, 1 ≤ j ≤ N, 1 ≤ k ≤ K, and 1 ≤ l ≤ K:
| (1) |
For any given i, j, k, and l, δijkl reflects the penalty associated with placing object i in cluster k and object j in cluster l. If bkl = sij, then the ideal block type is concordant with the network matrix entry and the term in parentheses in equation (1) is zero. However, if bkl = 1 and sij = 0, or vice versa, the value in parentheses is one, reflecting a lack of concordance and resulting in the collection of the penalty term, pkl.
There are two sets of decision variables for the integer linear programming model. The first set consists of cluster assignment variables, xik, for 1 ≤ i ≤ N and 1 ≤ k ≤ K. The variable xik = 1 if object i is assigned to cluster k, otherwise xik = 0. The second set of variables, which facilitates the establishment of blocks, is denoted yijkl, for 1 ≤ i ≤ N, 1 ≤ j ≤ N, 1 ≤ k ≤ K, and 1 ≤ l ≤ K. A value of yijkl = 1 indicates that object i is placed in cluster k and object j is placed in cluster l, otherwise yijkl = 0. The yijkl variables are penalized in the objective function of the mathematical programming model in accordance with the δijkl parameters. The mathematical program for one-mode blockmodeling based on structural equivalence, SE1, can now be stated as follows:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The objective function (2) of SE1 is to minimize a function corresponding to inconsistencies in ideal blocks. Constraint set (3) ensures that each object is assigned to exactly one of the K clusters. Constraint set (4) guarantees that each cluster is assigned at least one object. Constraint set (4) is often (but not always) superfluous when constructing blockmodels based on structural equivalence; however, its inclusion can be imperative in the case of regular equivalence. Constraint set (5) requires that each yijkl variable assumes a value of one if xik and xjk are both equal to one. Accordingly, the yijkl variables provide a linearization of the quadratic term xikxjk, which is a strategy that has also been used for integer programming models developed for the quadratic assignment problem (Kaufman & Broeckx, 1978; Lawler, 1963) and subset extraction (Brusco & Stahl, 2001; Theise, 1989). Some of the constraints in set (5) are superfluous and can be eliminated because i = j ⇒ k = l in the one-mode blockmodeling context. Constraint set (6) places integer restrictions on the cluster assignment variables, and constraint set (7) establishes bounds on the linearization variables.
2.2. Computational results
We developed SE1 formulations for each of four one-mode matrices from the social network literature. A Fortran program was written to generate the SE1 formulation, which was solved using CPLEX 12.1 (ILOG, 2009). All computational results were obtained using a 2.2GHz Pentium IV PC with 1 GB of RAM. The network matrices, which were published by Doreian et al. (2005, Chapters 2, 6) include: (a) the Transatlantic Industries little league baseball team network published by Fine (1987), (b) the Sharpstone little league baseball team network published by Fine (1987), (c) the political actor network studied by Doreian and Albert (1989), and (d) the Kansas search and air rescue (SAR) network collected by Drabek, Tamminga, Kilijanek. and Adams (1981). Each problem was solved using image and penalty matrices consistent with those considered by Doreian et al. (2005, Chapter 6). In all instances, the penalty matrix was a K × K matrix of ones. The computational results, which include the image matrix used for each network, are displayed in Table 1.
Table 1.
Computational results for SE1: one-mode blockmodeling based on structural equivalence
| Network matrix | N | K | Image matrix | Penalty matrix | Optimal objective value | CPU Time |
|---|---|---|---|---|---|---|
| Little League, Transatlantic | 13 | 4 | 1000 | 1111 | 20 | 6.77 |
| 0000 | 1111 | |||||
| 0000 | 1111 | |||||
| 0101 | 1111 | |||||
| Little League, Sharpstone | 13 | 4 | 1000 | 1111 | 14 | 0.66 |
| 1000 | 1111 | |||||
| 1000 | 1111 | |||||
| 0101 | 1111 | |||||
| Political Actor | 14 | 3 | 100 | 111 | 26 | 0.33 |
| 010 | 111 | |||||
| 000 | 111 | |||||
| Kansas Search and Air Rescue | 20 | 5 | 11100 | 11111 | 57 | 867.59 |
| 11000 | 11111 | |||||
| 11000 | 11111 | |||||
| 10000 | 11111 | |||||
| 11110 | 11111 |
Optimal one-mode blockmodeling solutions were efficiently obtained for both of the little league baseball networks (N = 13, K = 4), as well as the political actor network (N = 13, K = 3). For each of these three networks, the solution was obtained in less than seven seconds and confirmed the optimality of the heuristic solutions obtained by Doreian et al. (2005, Chapter 6). The larger Kansas SAR network (N = 20, K = 5) was solved in 867.59 seconds and verified the optimality of Doreian et al.'s solution.
3. A formulation for one-mode blockmodeling based on regular equivalence
Adapting the integer programming model for structural equivalence to accommodate regular blocks is nontrivial. In the case of structural equivalence, an inconsistency for a complete or null ideal block is easily captured by the presence of zeros and ones in these blocks, respectively. For regular equivalence, however, inconsistency corresponds to absence of ones in entire rows or columns. In other words, inconsistency is associated with an inability to achieve row-coverage and/or column-coverage in the regular block.
To enable clarity of presentation, we assume that ideal blocks are either regular or complete. This means that entries of ‘one’ in the image matrix now reflect regular blocks. We adapted SE1 for regular equivalence by introducing binary variables αikl and βjkl for the rows and columns, respectively, of regular ideal blocks. The binary variables αikl, which are defined for 1 ≤ i ≤ N and all (k, l) pairs such that bkl = 1, must assume values of one if the row corresponding to object i in a regular block (k, l) does not contain at least one entry of one. The βjkl variables provide a similar function for columns. Penalties for row (column) violations in regular blocks are denoted λkl (ωkl) for all (k, l) pairs such that bkl = 1. The resulting formulation for one-mode blockmodeling based on regular equivalence, RE1, is as follows:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
and constraint sets (3), (4), (5), and (6).
The objective function of RE1 (8) requires several modifications of (2). For example, the first term in (8) is restricted to null blocks (i.e., {(k, l) : bkl = 0}) because ones in the image matrix represent regular blocks, not complete blocks. The second and third terms in (8) penalize null rows and columns, respectively, in regular ideal blocks. Constraint sets (9) and (10) are designed to capture these null rows and columns, respectively, when they occur. To illustrate, consider constraint set (9) for the ideal regular block defined by the intersection of cluster k for the rows and cluster l for the columns. The first term in (9) collects the ‘ones’ accumulated in row k of this block. If this sum is greater than zero, then the constraint is satisfied regardless of the values of xik and αikl. However, if the sum of the yijkl values equals zero, then there are no ones in the block for object i in row cluster k, column cluster l. This is not an inconsistency if object i is not assigned to cluster k (i.e., xik = 0). On the other hand, if xik = 1, then an inconsistency is present for the row and, to ensure that the constraint holds, αikl must assume a value of one and the penalty for the violation in the regular block is collected in the objective function.
Although constraint set (5) requires yijkl = 1 if xik = xjl = 1, it does not prohibit yijkl = 1 if xik and xjl are not both equal to one. This can be problematic in RE1 because there is the potential for the yijkl variables to erroneously assume nonzero values in an effort to ensure satisfaction of the conditions for regular blocks. To prevent this from occurring, we use constraint sets (11) and (12), which together guarantee that the yijkl values can only be nonzero if both xik and xjl are equal to one. Constraint sets (13) and (14) place binary restrictions on the row and column regular-block inconsistency variables, respectively.
3.2. Computational results
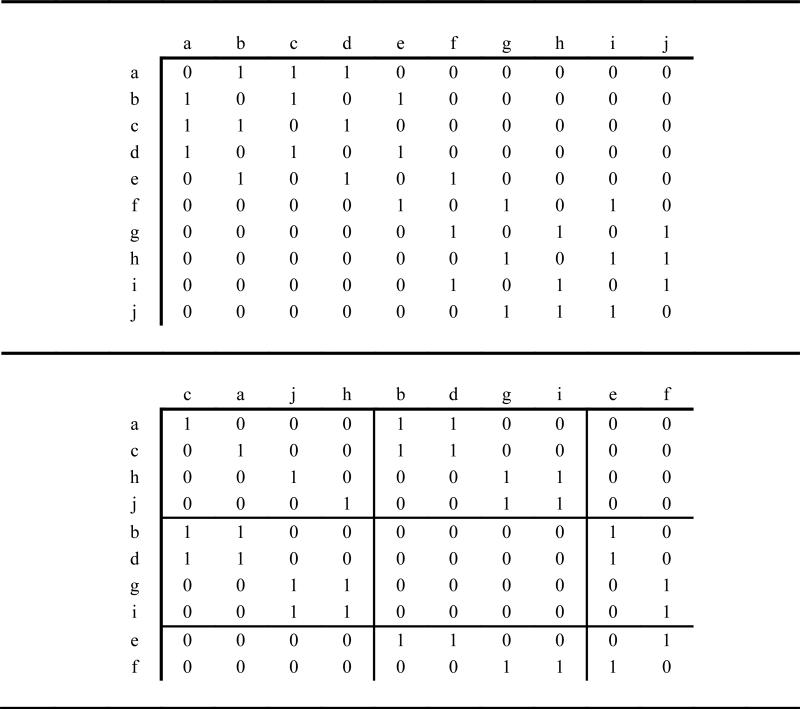
To demonstrate RE1, we developed a formulation for the ‘Everett network’ (Borgatti & Everett, 1989), which was also studied by Doreian et al. (2005, Chapter 6). The adjacency matrix for Everett's network is displayed in the top panel of Table 2. The formulation was developed for K = 3 clusters. All objective function penalty parameters were set to one, and the selected image matrix was:
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
Table 2.
Results for RE1: Everett's network matrix in top panel, and the 3-cluster blockmodel produced by RE1 in the bottom panel.
The RE1 formulation was solved using CPLEX. The required computation time was 1.30 seconds, and the resulting regularly equivalent blockmodel is displayed in the bottom panel of Table 2.
4. A formulation for two-mode blockmodeling based on structural equivalence
4.1. Model formulation
Adaptation of SE1 for two-mode blockmodeling requires several modifications. In the case of two-mode blockmodeling, the columns of the network matrix correspond to a (possibly) different set of objects. We index the row objects as 1 ≤ i ≤ N1 and the column objects as 1 ≤ j ≤ N2, and the network matrix, T, is of dimension N1 × N2. It is necessary to cluster both the row objects and the column objects to obtain a blockmodel for T. Moreover, the number of clusters for the row objects, K1, need not be the same as the number of clusters for the column objects, which we denote as K2. The image and penalty matrices, B and P, are of dimension K1 × K2. A structurally equivalent one-mode blockmodel consists of ideal blocks that are either null or complete. Matrices T, P, and B are used to construct penalty parameters ηijkl, which are computed as follows for all 1 ≤ i ≤ N1, 1 ≤ j ≤ N2, 1 ≤ k ≤ K1, and 1 ≤ l ≤ K2:
| (15) |
The extension to two-mode blockmodeling necessitates two distinct sets of cluster assignment variables, one set each for the row and column objects. For the row objects, the binary cluster assignment variables are denoted as vik for 1 ≤ i ≤ N1 and 1 ≤ k ≤ K1. The binary cluster assignment variables for the column objects are indicated as wjl for 1 ≤ j ≤ N2 and 1 ≤ l ≤ K2. The linearization variables are defined as zijkl, for 1 ≤ i ≤ N1, 1 ≤ j ≤ N2, 1 ≤ k ≤ K1, and 1 ≤ l ≤ K2. A value of zijkl = 1 indicates that row object i is placed in row cluster k and column object j is placed in column cluster l; otherwise zijkl = 0. The zijkl variables are penalized in the objective function of the integer programming model in accordance with the ηijkl parameters. The mathematical program for two-mode blockmodeling based on structural equivalence, SE2, can now be stated as follows:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
The objective criterion (16) of SE2 is to minimize a function of the inconsistencies in the ideal null and complete blocks. Constraint set (17) guarantees that each row object is assigned to exactly one row cluster, whereas constraint set (18) enforces the same type of restriction for column objects and clusters. Constraint sets (19) and (20) ensure that there are no empty clusters for row and column objects, respectively. Constraint set (21) requires the zijkl variables to assume values of one if vik = wjl = 1. Constraint sets (22) and (23) place binary restrictions on the row object and column object assignment variables, respectively. The zijkl variables are bounded in constraint set (24).
4.2. Computational results
We developed SE2 formulations for two prominent two-mode network matrices from the extant literature. The first matrix pertains to the participation (or non-participation) of N1 = 18 women at N2 = 14 social events (Davis, Gardner, & Gardner, 1941, pp. 146-151). Although this matrix has been analyzed ad nauseum in the social network literature (e.g., Borgatti & Everett, 1997; Brieger, 1974; Brieger et al., 1975; Brusco & Steinley, 2006, 2007; Doreian et al., 2005, 2005, Chapter 8; Freeman, 2003; Homans, 1950, pp. 82-86), we deemed it important to apply our optimal methods to these data. The second network matrix corresponds to the voting patterns of the N2 = 9 Supreme Court Justices (Breyer, Ginsburg, Kennedy, O'Connor, Rehnquist, Scalia, Souter, Stevens, and Thomas) on N1 = 26 cases. The binary measurements in this matrix are one (zero) if the justice in the column voted with the majority (minority) on the case in the row.
We formulated SE2 for the southern women event participation and Supreme Court voting networks under a variety of conditions. Specifically, we selected image and penalty matrices that were consistent with those that have recently been used in analyses of these data (Borgatti & Everett, 1997; Brusco & Steinley, 2006, 2007; Doreian et al., 2004, 2005). These image and penalty matrices are displayed in the fourth and fifth columns of Table 3, respectively. Each formulation was solved to optimality using CPLEX, and the objective functions and CPU times are shown in the last two columns of Table 3.
Table 3.
Computational results for SE2: two-mode blockmodeling based on structural equivalence
| Network matrix | N1, N2 | K1, K2 | Image matrix | Penalty matrix | Optimal objective value | CPU Time |
|---|---|---|---|---|---|---|
| Southern women event participation | 18, 14 | 2, 3 | 110 | 111 | 63 | 23.39 |
| 011 | 111 | |||||
| Southern women event participation | 18, 14 | 2, 3 | 100 | 111 | 53 | 9.50 |
| 001 | 111 | |||||
| Southern women event participation | 18, 14 | 2, 3 | 110 | 111 | 52 | 2.39 |
| 010 | 111 | |||||
| Southern women event participation | 18, 14 | 3, 3 | 110 | 111 | 40 | 78.20 |
| 011 | 111 | |||||
| 010 | 111 | |||||
| Southern women event participation | 18, 14 | 3, 3 | 110 | 1 1 100 | 63 | 1.61 |
| 011 | 100 1 1 | |||||
| 010 | 100 1 100 | |||||
| Supreme Court voting data | 26, 9 | 5, 3 | 011 | 111 | 22 | 4.27 |
| 111 | 111 | |||||
| 110 | 111 | |||||
| 110 | 111 | |||||
| 110 | 111 | |||||
| Supreme Court voting data | 26, 9 | 5, 4 | 0111 | 1111 | 16 | 8.39 |
| 1111 | 1111 | |||||
| 1110 | 1111 | |||||
| 1010 | 1111 | |||||
| 1100 | 1111 | |||||
| Supreme Court voting data | 26, 9 | 7, 4 | 0111 | 1111 | 11 | 111.55 |
| 0011 | 1111 | |||||
| 1111 | 1111 | |||||
| 1001 | 1111 | |||||
| 1110 | 1111 | |||||
| 1010 | 1111 | |||||
| 1100 | 1111 |
The results in Table 3 indicate that solutions for the southern women event participation network were efficiently realized for all conditions tested. The results obtained have verified the optimality of solutions produced by previous heuristic implementations, such as exchange algorithms (Doreian et al. 2004, 2005, Chapter 8) and variable neighborhood search (Brusco & Steinley, 2007). The Supreme Court voting data provided a more formidable challenge for our mathematical programming model because of the relatively larger number of row and column clusters tested. The (K1 = 5, K2 = 3) or (5, 3) blockmodel was solved in just over four seconds, and the (5, 4) blockmodel was solved in roughly eight seconds. However, achieving an optimal solution for the (7, 4) blockmodel required nearly two minutes of CPU time. As was the case for the social event network, the blockmodels we obtained for the Supreme Court voting network have confirmed the optimality of heuristic solutions produced in previous studies.
5. A formulation for two-mode blockmodeling based on regular equivalence
5.1. Model formulation
Adaptation of SE2 for regular equivalence is accomplished using the same approach described for modifying SE1 to yield RE1, as discussed in Section 3. We use the same definitions for penalty variables (αikl and βjkl) and parameters (λkl and ωkl) for regular block inconsistencies as described for RE1; however, the index ranges for the variables are appropriately modified as 1 ≤ i ≤ N1 and 1 ≤ j ≤ N2. The formulation for two-mode blockmodeling based on regular equivalence, RE2, is as follows:
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
and constraint sets (17)-(23).
Like RE1, the objective function (25) of RE2 consists of three terms: (a) penalties for entries of one in null blocks, (b) penalties for null rows in regular blocks, and (c) penalties for null columns in regular blocks. Constraints (26) and (27) are analogous to (9) and (10), capturing any null rows and columns in regular blocks, respectively. Constraint sets (28) and (29) ensure that the zijkl values can only be nonzero if both vik and wjl are equal to one. Constraint sets (30) and (31) place binary restrictions on the αikl and βjkl variables, respectively.
5.2. Computational results
To demonstrate RE2, we developed a formulation for a network matrix based on data originally collected by Baker (1992) and subsequently analyzed by Borgatti and Everett (1999) and Doreian et al. (2005, pp. 265-269). The data pertain to 1985-1986 citation patterns among 18 journals in the field of social work. Prior to analysis, we converted the original citation matrix to an 18 × 18 binary asymmetric matrix, T, by setting tij = 1 if the journal corresponding to row i cited the journal corresponding to column j at least once and setting tij = 0 otherwise. Although this network matrix can be analyzed using one-mode blockmodeling methods, we adopt the two-mode perspective followed by Doreian et al., which considers the rows as “consuming” (or citing) journals and the columns as “producing” (or cited) journals.
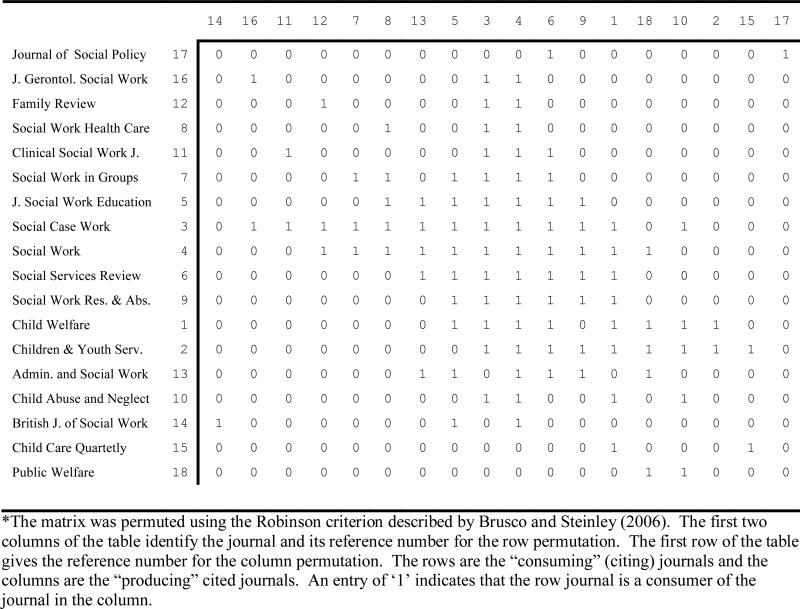
In the absence of à priori choices for K1 and K2 when applying RE2 to the journal citation network matrix, we began our analysis by applying the permutation procedure developed by Brusco and Steinley (2006). The optimally permuted matrix, which is displayed in Table 4, reveals large bands of ones in the rows and columns of the reordered matrix. Based on a visual inspection of this permuted matrix, we decided to evaluate blockmodels with two or three row clusters and three column clusters. In addition, we decided to evaluate different image matrices in conjunction with different integer programming models (SE2, RE1, and RE2). Objective function values and CPU times for several of the models we tested are displayed in Table 5.
Table 4.
Permuted network matrix* for Baker's (1992) social work journal citation data.
Table 5.
Computational results for Baker's (1992) citation matrix using different integer programs, image matrices, and penalty matrices.
| Integer program | N1, N2 | K1, K2 | Image matrix | Penalty matrix | Optimal objective value | CPU Time |
|---|---|---|---|---|---|---|
| SE2 | 18, 18 | 2, 3 | 010 | 111 | 53 | 2.25 |
| 110 | 111 | |||||
| RE2 | 18, 18 | 2, 3 | 010 | 1 100 1 | 1 | 12.48 |
| 110 | 100 100 1 | |||||
| SE2 | 18, 18 | 3, 3 | 000 | 111 | 47 | 84.39 |
| 110 | 111 | |||||
| 010 | 111 | |||||
| RE2 | 18, 18 | 3, 3 | 000 | 1 1 1 | 2 | 67.80 |
| 110 | 100 100 1 | |||||
| 010 | 1 100 1 | |||||
| RE1 | 18, 18 | 3, 3 | 000 | 1 1 1 | 23 | 21.03 |
| 110 | 100 100 1 | |||||
| 010 | 1 100 1 | |||||
| SE2 | 18, 18 | 3, 3 | 010 | 111 | 55 | 237.59 |
| 110 | 111 | |||||
| 011 | 111 | |||||
| RE2 | 18, 18 | 3, 3 | 010 | 1 100 1 | 0 | 125.07 |
| 110 | 100 100 1 | |||||
| 011 | 1 100 100 | |||||
| RE1 | 18, 18 | 3, 3 | 010 | 1 100 1 | 415 | 34.06 |
| 110 | 100 100 1 | |||||
| 011 | 1 100 100 |
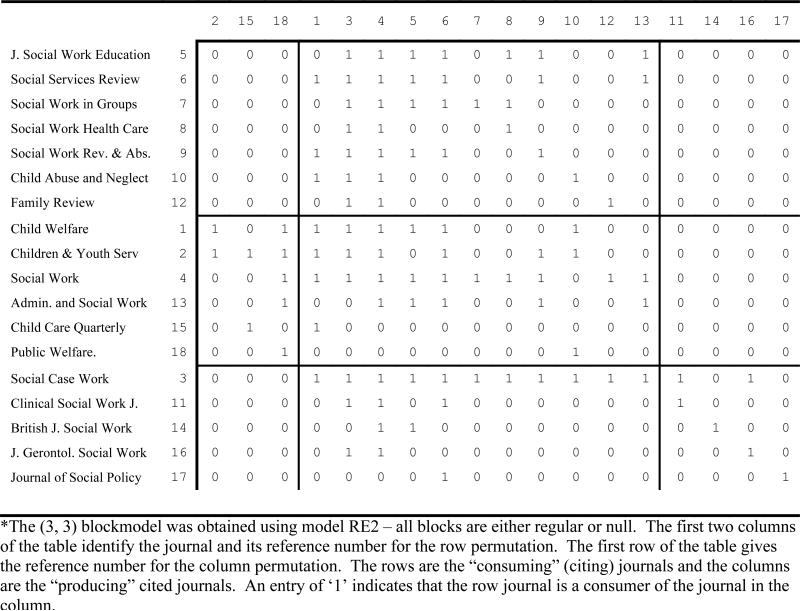
Among the solutions obtained in our blockmodeling evaluation process, we believe that the most interesting was produced by RE2 using the following image matrix:
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
The penalty matrix used with this image matrix was:
| 1 | 100 | 1 |
| 100 | 100 | 1 |
| 1 | 100 | 100 |
The solution time for the RE2 formulation of our selected blockmodel was 125.78 CPU seconds. The optimal solution yielded an objective function value of zero (no inconsistencies), resulting in the regularly equivalent blockmodel shown in Table 6. The most salient aspect of this blockmodel is that there are two modestly-sized clusters of producers, {2, 15, 18} and {11, 14, 16, 17}, which are not cited by two sizable clusters of consumers. For example, journals in producer cluster {2, 5, 18} are not cited by journals in consumer cluster {3, 11, 14, 16, 17} and, similarly, journals in producer cluster {11, 14, 16, 17} are not cited by journals in consumer cluster {1, 2, 4, 13, 15, 18}. Moreover, both producer clusters {2, 15, 18} and {11, 14, 16, 17} are not cited by the large consumer cluster {5, 6, 7, 8, 9, 10, 12}. It is also interesting to observe that the consumer cluster {5, 6, 7, 8, 9, 10, 12} is a proper subset of the producer cluster {1, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13}, which consists of journals that do not define any null blocks.
Table 6.
A (3, 3) regularly equivalent blockmodel for Baker's (1992) social work journal citation data obtained using RE2.
Using RE2, we were able to identify the (3, 3) regularly equivalent blockmodel displayed in Table 6. We also attempted to identify a regularly equivalent blockmodel using RE1 along with the same image and penalty matrices used for RE2. As shown by the objective function value of 415 in the last row of Table 5, we were unsuccessful in our effort to establish a regularly equivalent blockmodel for RE1. This is not especially surprising given that the two-mode blockmodel is much less restrictive because it does not require the same clustering solution for both rows and columns. Although it is possible that a regularly equivalent blockmodel for RE1 might be realized using a different 3 × 3 image matrix, we did not identify such a solution during our experiments.
6. Summary
We have presented a collection of integer programming models for direct blockmodeling of one- and two-mode binary network matrices. The proposed integer programming models are formulated to optimize criteria pertaining to inconsistencies from prespecified ideal block structures associated with structural and regular equivalence. We demonstrated the models using a variety of one- and two-mode matrices from the social network literature. Using the integer programming approach, we were able to achieve guaranteed optimal solutions for these network matrices, verifying the optimality of previously reported solutions obtained using heuristic methods (Brusco & Steinley, 2007; Doreian et al, 2004, 2005, Chapters 6-8). In most, but not all cases, optimal solutions were obtained within a few minutes of microcomputer CPU time.
It is important to reiterate that we are not purporting integer programming methods as a replacement for previously proposed heuristic solution strategies for blockmodeling, such as the TEA (Doreian et al., 2005, Chapter 6) and variable neighborhood search (Brusco & Steinley, 2007). Relative to integer programming, the heuristic methods have the advantage of not requiring prespecification of the image matrix. Contrastingly, unlike the heuristics, the integer programming method has the advantage of guaranteeing an optimal solution for a given image matrix. These relative strengths and weaknesses of the heuristic and integer programming approaches suggest the following recommendations: (1) in the case of confirmatory blockmodeling, the integer programming approach can be applied directly to obtain globally-optimal solutions, (2) in exploratory blockmodeling applications where the total number of blocks is small (e.g., K ≤ 3 in one-mode blockmodeling), the integer programming model can be implemented for all possible image matrices to yield a globally-optimal solution, and (3) in exploratory blockmodeling applications where the number of blocks precludes consideration of all possible image matrices, a two-stage procedure is advised, where a heuristic method is first used to identify an image matrix and the integer program is subsequently formulated and solved to identify the optimal solution for that image matrix.
With respect to efficiency of the integer programming approach, in the one-mode context, the viability of the integer programming approach is particularly affected by the number of objects and the number of clusters. In addition we have observed that modifications of the image and/or penalty matrices can have a pronounced effect on CPU time. We have also observed greater difficulty in obtaining solutions for regular equivalence relative to structural equivalence. This is not surprising in light of the greater complexity (i.e., more integer variables and more constraints) of RE1 relative to SE1. Increased solution times are also evident when moving from one-mode to two-mode blockmodeling. Two-mode blockmodeling problems are generally more difficult to solve than one-mode problems because of the need for partitions of two object sets.
In spite of the aforementioned limitations, we are encouraged by the initial success of the integer programming models proposed in this paper. We believe that there are a variety of possible research extensions that could stem from our work. These extensions fall under three categories: (1) improved formulations for the same blockmodeling criteria considered in this paper, (2) computational enhancements to expedite solution time, (3) the development of formulations that accommodate other types of ideal block structures, and (4) the development of models that will simultaneously select the image matrix. Although the formulations presented herein have provided reasonably efficient results, it is possible that different formulations could yield optimal solutions in less time. There are also a variety of computational actions that can accelerate the solution process. For example, CPLEX and other commercial mathematical programming software packages allow an advanced starting solution to be supplied to the integer programming solver. We have found that using a heuristic solution obtained by TEA as a starting point for the integer programming routine can, in some cases, greatly reduce computation time.
The extension of the integer programming method for different objective criteria pertaining to structural or regular equivalence, as well as other forms of equivalence, remains an avenue for future research. For example, the necessary components of SE1 and RE1 (or SE2 and RE2) could be incorporated in the same model if it were necessary to develop a blockmodel that contained both complete and regular ideal blocks. There are some important adaptations of our models for alternative penalty functions, however, which are appreciably more difficult to handle. Most notable among these are the penalty functions for row-dominant, column-dominant, row-regular, column-regular, row-functional, and column-functional blocks described by Doreian et al. (2005, Chapter 7), which require multiplying the number of inconsistencies by the number of rows (or columns) in the block.
Consider, for example, the case of a non-diagonal row-dominant block, where a zero penalty is realized only if there is a row in the block that consists of all ones. If there is no row in the block with a one in each column, then the penalty is computed by multiplying the number of rows in the block by the difference between the number of block columns and the maximum number of ones in any row of the block. Thus, each row contributes to the penalty function and, accordingly, a smaller block that does not satisfy row dominance occurs a less serious penalty than a larger block. In light of its direct implications for cluster/block size, this type of penalty function could be quite useful in applied blockmodeling; however, it would be difficult to accommodate such a function in our formulations because the number of rows and columns in the block is a function of other decision variables. Although the development of new integer programming models for blockmodeling applications that require these more complex penalty functions presents a formidable challenge, it is our sincerest hope that our initial findings will stimulate further progress in this area.
Footnotes
Disclaimer: “This article may not exactly replicate the final version published in the Journal of Mathematical Psychology. It is not the copy of record
Contributor Information
Michael J. Brusco, Florida State University.
Douglas Steinley, University of Missouri-Columbia.
References
- Arabie P, Boorman SA, Levitt PR. Constructing blockmodels: How and why. Journal of Mathematical Psychology. 1978;17:21–63. [Google Scholar]
- Arabie P, Hubert LJ. The bond energy algorithm revisited. IEEE Transactions on Systems, Man, and Cybernetics. 1990;20:268–274. [Google Scholar]
- Arabie P, Hubert L, Schleutermann S. Blockmodels from the bond energy algorithm. Social Networks. 1990;12:99–126. [Google Scholar]
- Baker DR. A structural analysis of the social work journal network. Journal of Social Service Research. 1992;15:153–167. [Google Scholar]
- Batagelj V, Doreian P, Ferligoj A. An optimizational approach to regular equivalence. Social Networks. 1992;14:121–135. [Google Scholar]
- Batagelj V, Ferligoj A, Doreian P. Direct and indirect methods for structural equivalence. Social Networks. 1992;14:63–90. [Google Scholar]
- Borgatti SP, Everett MG. The class of all regular equivalences: algebraic structure and computation. Social Networks. 1989;11:65–88. [Google Scholar]
- Borgatti SP, Everett MG. Network analysis of 2-mode data. Social Networks. 1997;19:243–269. [Google Scholar]
- Borgatti SP, Everett MG. Models of core/periphery structures. Social Networks. 1999;21:375–395. [Google Scholar]
- Brieger RL. The duality of persons and groups. Social Forces. 1974;53:181–190. [Google Scholar]
- Brieger RL, Boorman SA, Arabie P. An algorithm for clustering relational data with applications to social network analysis and comparison to multidimensional scaling. Journal of Mathematical Psychology. 1975;12:328–383. [Google Scholar]
- Brusco MJ, Stahl S. Compact integer programming models for extracting subsets of stimuli from confusion matrices. Psychometrika. 2001;66:405–420. [Google Scholar]
- Brusco MJ, Steinley D. Inducing a blockmodel structure for two-mode binary data using seriation procedures. Journal of Mathematical Psychology. 2006;50:468–477. [Google Scholar]
- Brusco MJ, Steinley D. A variable neighborhood search method for generalized blockmodeling of two-mode binary matrices. Journal of Mathematical Psychology. 2007;51:325–338. [Google Scholar]
- Davis A, Gardner B, Gardner MR. Deep south. University of Chicago Press; Chicago: 1941. [Google Scholar]
- Doreian P, Albert LH. Partitioning political actor networks: some quantitative tools for analyzing qualitative networks. Journal of Quantitative Anthropology. 1989;1:279–291. [Google Scholar]
- Doreian P, Batagelj V, Ferligoj A. Generalized blockmodeling of two-mode network data. Social Networks. 2004;26:29–53. [Google Scholar]
- Doreian P, Batagelj V, Ferligoj A. Generalized blockmodeling. Cambridge University Press; Cambridge, UK: 2005. [Google Scholar]
- Drabek TE, Tamminga HL, Kilijanek TS, Adams CR. Managing multi-organizational emergency responses. University of Colorado, Institute of Behavioral Science; Boulder: 1981. [Google Scholar]
- Fine GA. With the boys: Little league baseball and preadolescent culture. University of Chicago Press; Chicago: 1987. [Google Scholar]
- Freeman LC. Finding social groups: a meta-analysis of the Southern Women data. In: Brieger R, Carley C, Pattison P, editors. Dynamic social network modeling and analysis: workshop summary and papers. The National Academies Press; Washington, DC: 2003. pp. 39–97. [Google Scholar]
- Fulkerson DR, Gross OA. Incidence matrices and interval graphs. Pacific Journal of Mathematics. 1965;15:835–855. [Google Scholar]
- Hartigan J. Direct clustering of a data matrix. Journal of the American Statistical Association. 1972;67:123–129. [Google Scholar]
- Homans GC. The human group. Harcourt-Brace; New York: 1950. [Google Scholar]
- Hubert L. Problems of seriation using a subject by item response matrix. Psychological Bulletin. 1974;81:976–983. [Google Scholar]
- Hubert L, Arabie P, Meulman J. The structural representation of proximity matrices with MATLAB. SIAM; Philadelphia: 2006. [Google Scholar]
- ILOG, Inc. CPLEX 12.1. Author; Sunnyvale, CA: 2009. [ http://www.ilog.com/products/cplex/news/whatsnew.cfm] [Google Scholar]
- Kaufman L, Broeckx F. An algorithm for the quadratic assignment problem using Benders’ decomposition. European Journal of Operational Research. 1978;2:204–211. [Google Scholar]
- Kendall DG. Incidence matrices, interval graphs, and seriation in archaeology. Pacific Journal of Mathematics. 1969;28:565–570. 1969. [Google Scholar]
- Lawler EL. The quadratic assignment problem. Management Science. 1963;9:586–599. [Google Scholar]
- Lorrain F, White HC. Structural equivalence of individuals in social networks. Journal of Mathematical Sociology. 1971;1:49–80. [Google Scholar]
- McCormick WT, Schweitzer PJ, White TW. Problem decomposition and data reorganization by a clustering technique. Operations Research. 1972;20:993–1009. [Google Scholar]
- Robinson WS. A method for chronologically ordering archeological deposits. American Antiquity. 1951;16:293–301. [Google Scholar]
- Theise ES. Finding a subset of stimulus-response pairs with minimum total confusion: a binary integer programming approach. Human Factors. 1989;31:291–305. [Google Scholar]
- Wasserman S, Faust K. Social network analysis: methods and applications. Cambridge University Press; Cambridge: 1994. [Google Scholar]
- White DR, Reitz KP. Graph and semigroup homomorphisms on networks of relations. Social Networks. 1983;5:193–234. [Google Scholar]