Abstract
In this paper, the relationship between the static and dynamic elastic modulus of concrete and the relationship between the static elastic modulus and compressive strength of concrete have been formulated. These relationships are based on investigations of different types of concrete and take into account the type and amount of aggregate and binder used. The dynamic elastic modulus of concrete was tested using impulse excitation of vibration and the modal analysis method. This method could be used as a non-destructive way of estimating the compressive strength of concrete.
Keywords: concrete, dynamic elastic modulus, elastic modulus, non-destructive testing
1. Introduction
The compressive strength and modulus of elasticity are the most important properties of concrete from the viewpoint of structural design. Commonly, these parameters are determined by the uniaxial compression of cylindrical or cube-shaped specimens, according to standard procedures, and so values obtained that way are considered to be the reference values. However, it is not always possible to use these methods in practice because they are destructive and require the collection of numerous test samples during concreting operations. In addition, properly conducted modulus of elasticity testing using cylindrical specimens is a relatively time-consuming process. Therefore, we seek non-destructive methods in order to estimate these parameters for hardened concrete, such as: the sclerometric method, the ultra-sound pulse velocity method, and the impulse excitation and modal analysis method.
Technological developments and better access to more appropriate apparatus has resulted in significant progress in the dynamic testing methods used in structural health monitoring. These methods could also be used in concrete material parameter testing (especially compressive strength) or to monitor its increase over time. A significant disadvantage of non-destructive methods is the fact that the values are achieved indirectly, i.e., the results of each test have to be converted to a certain parameter (e.g., the compressive strength of concrete) using a previously assumed relationship between these values.
The natural frequencies obtained using impulse excitation testing and modal analysis methods are very good indicators of the state of concrete elements because the fundamental resonant frequency of vibration decreases with an increasing degree of material degradation [1]. This also allows monitoring of the concrete parameters as they change over time, especially in the first few days after sampling [2]. As mentioned above, results obtained through non-destructive methods have to be converted to the parameters required, using experimentally obtained relationships. The relationship between the compressive strength and modulus of elasticity of concrete has been the subject of numerous investigations, which have resulted in many equations linking these parameters.
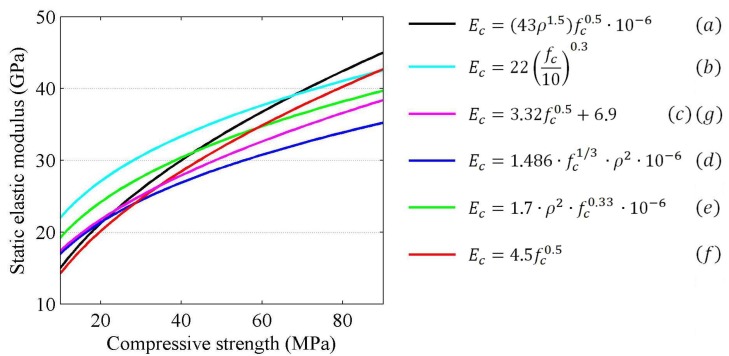
The most commonly used equations were presented by Neville (2000) [3]. Selected equations from the different standards are presented in Figure 1. These were derived by matching the coefficients of predetermined equations (commonly exponential or similar functions) in order to obtain the best fit model for the experimental results.
Figure 1.
The selected relations between compressive strength and elastic modulus of concrete: (a) ACI 318-95; (b) Eurocode 2; (c) ACI 363R-92; (d) Noguchi et al. (2009); (e) BS 8110-2:1985; (f) CSA A23.3-04; (g) NZS 3101-2006 [4,5,6,7,8,9,10].
The equations mentioned above are convenient to use when calculating the compressive strength for a known modulus of elasticity because the compressive strength and concrete density are the only parameters required however, their accuracy in predicting the modulus of elasticity value is not sufficient for all kinds of concrete. This indicates that the relationship between elastic modulus and compressive strength is influenced by a number of factors, such as: the type of aggregate, humidity, age of the concrete, and the type of binder used. As preliminary research shows [11], the equations which take into account the value of static modulus of elasticity as well as concrete density provide better accuracy. However, the values calculated in this way could also be significantly different from the ones determined experimentally. It should be noted that concrete density is strongly correlated to the type of aggregate used.
The effect of aggregate type on the elastic properties of concrete is widely discussed in the literature e.g., [12,13]. These authors demonstrated the effect of aggregate type and also its volume content in concrete. Different models, treating concrete as a two phase material, were also considered [14]. While the effect of aggregate on the relationship between compressive strength and modulus of elasticity seems to be recognized, the influence of cement matrix type on this dependency is discussed in very few publications.
A comprehensive analysis, based on the results of more than 3000 concrete samples, is presented in paper [7]. Those authors proposed a relationship taking into account the aggregates used and the binder type. These parameters were determined for different types of aggregate and for selected kinds of binders.
An interesting model is presented in [15]. The M5′ algorithm was used to achieve a multi-parameter relationship and this allows the Young’s modulus of concrete to be estimated. The M5′ is one of the algorithms in the model tree method which is relatively easy to use; this is further described in [16]. The proposed model is based on equations derived from many experimentally obtained results and application of the M5′ model tree algorithm indicates which one is appropriate for a specific kind of concrete. It should be mentioned that the paper refers to concrete containing recycled aggregate.
The values calculated using the equations proposed in the literature usually provide satisfactory results for specific kinds of concrete only. On the rare occasion that an attempt has been made to provide relationships that take into account the influence of binder and aggregate type, the results have been significantly different from the ones determined experimentally. Additionally, most of the equations proposed in the literature refer to ‘normal’ strength concrete, although high strength concrete is also investigated [17].
An additional problem when calculating the compressive strength of concrete using the impulse excitation method is the difference between the static and dynamic modulus of elasticity of concrete. The studies clearly show that the dynamic modulus is significantly greater than the static one. It could be the result of large differences in the strain rates associated with the static and dynamic testing methods [18] or it could be a result of the multi-phase nature of concrete [19].
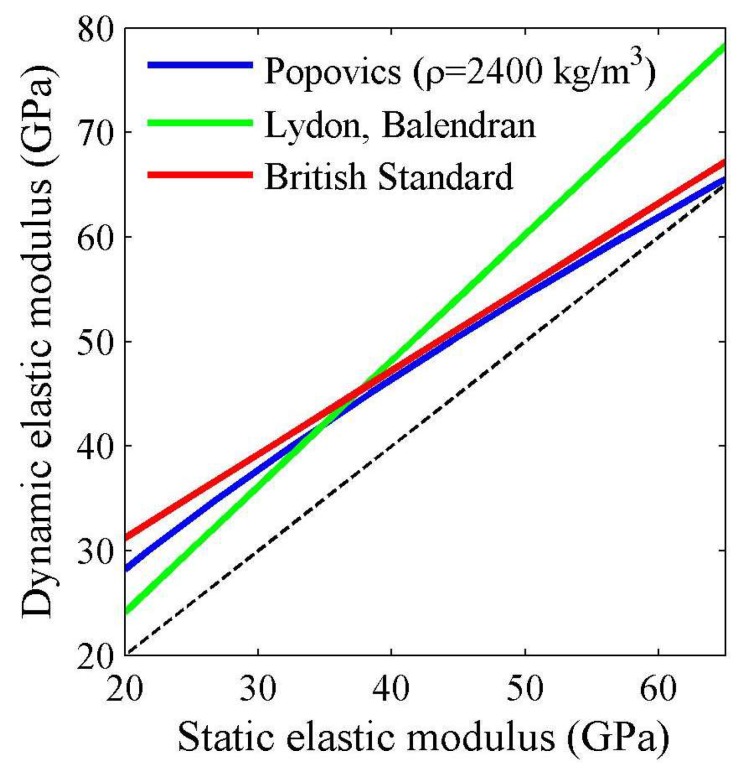
The literature survey revealed equations that describe the relationship between the static and dynamic modulus of elasticity. The most common are equations proposed by Lyndon and Balendran [20], Popovics [21], and by British Standard CP 110-1:1972 [22]. The relationship between the static and dynamic modulus of elasticity is presented in Figure 2. The estimation of the elastic modulus of concrete using non-destructive methods requires the application of a relationship between the dynamic and static elastic modulus as well as a relationship between the static elastic modulus and compressive strength of concrete.
Figure 2.
A relationship between the static and dynamic elastic modulus of concrete proposed by: Lyndon and Balendran [20], Popovics [21], and CP 110-1:1972 standard [22].
The relationship between static and dynamic modulus was investigated e.g., in [23,24,25]. The authors demonstrate that this relationship depends highly on the specimen shape [23], concrete type and composition [24], as well as the testing methodology [25]. In [26], the relationship based on nonlinear deformation of concrete theory is proposed. The authors state that the relationship between static and dynamic modulus depends on the applied stress level in the static test as well as on the rate of loading.
The comprehensive study of the relationship between dynamic elastic modulus and compressive strength of concrete is presented in [27]. The authors demonstrate that the main factors which affect the relationship between static and dynamic elastic modulus are aggregate volume content and maximum size of the coarse aggregate. On the other hand, the water to cement ratio and curing temperature had no significant influence. The authors propose a linear relationship between static and dynamic elastic moduli.
The method of dynamic elastic modulus testing preferred in this paper is based on excitation of a concrete specimen using a hammer and then analysis of its dynamic response. Recommendations for concrete testing methods using impulse excitation methods and modal analysis can be found in [28] and the standards [29,30,31]. A comparison of these standards shows that all of them present similar testing procedures. The main differences are concerned with calculating correction factors to account for the finite thickness of a specimen.
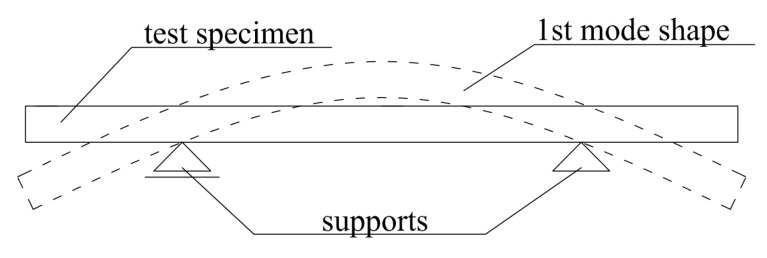
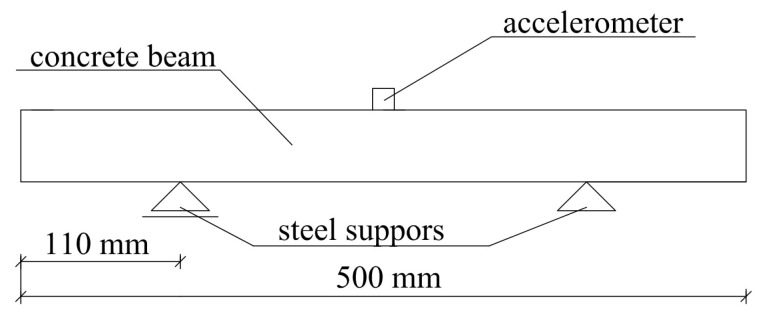
It is most convenient to test beam-shaped samples of concrete. Commonly, these specimens are supported in vibration nodes to form a so-called ‘free-free’ configuration (Figure 3). In the case of testing concrete samples which are relatively blocky, it is acceptable to support them on rubber pads, in order to isolate the sample from the ground. The investigation into how this form of support influences the dynamic elastic modulus results was described in [32]. It was demonstrated that the resonant frequencies of concrete beams supported on rubber pads are about 2% higher when compared to beams supported on steel supports in vibration nodes. This difference is more significant in the case of relatively slender beams. In addition, it was stated that the location of the accelerometer (on the edge or in the middle of the span) had no significant effect on the value of fundamental vibration frequency of concrete samples.
Figure 3.
Free-free beam configuration.
Non-destructive methods of concrete testing are commonly based on experimentally derived relationships. The accuracy of the methods mentioned is highly dependent on the assumptions made. The literature survey, as well as experimental tests, demonstrated that widely used relationships are not appropriate to all types of concrete, especially in the case of concrete containing mineral additives.
In case of concrete at early-age, values of compressive strength and elastic modulus increase significantly. In practice, it is of interest to know when the framework can be removed or when a construction element can be loaded without excessive deflections or cracking. Therefore, non-destructive methods are highly demanded in the situ testing. The accuracy of the estimated values in this way depends on the relationship between dynamic elastic modulus (obtained from the non-destructive testing), static elastic modulus, and compressive strength. In this paper, the investigation of different concrete compositions and properties, including different types of cement matrix, is presented. Based on static and dynamic elastic modulus and compressive strength testing results, the relationship between these parameters was formulated, taking into account the age of the concrete and the type and volume content of each ingredient (especially binder type). The impulse excitation and modal analysis method were used as a non-destructive method to determine the dynamic elastic modulus of concrete. It should be noted that values of initial and stabilized elastic modulus (introduced recently in EN 12390-13:2014 standard) were included to the proposed relationship between elastic modulus and compressive strength of concrete, which is the novelty in this field.
2. Materials and Methods
In order to formulate the relationship between dynamic elastic modulus and compressive strength, different types of concrete were investigated. The tested concrete compositions varied in terms of the amount and type of each aggregate and also the type of binder. The chemical composition of the cements and metakaolin used is presented in Table 1.
Table 1.
The chemical composition of cements and metakaolin.
| Cement/Additive | SiO 2 | Al 2 O 3 | Fe 2 O 3 | CaO | MgO | K 2 O | Na 2 O | SO 3 | TiO 2 |
|---|---|---|---|---|---|---|---|---|---|
| (%) | |||||||||
| CEM I | 17.9 | 5.8 | 2.9 | 63.1 | 1.2 | 0.8 | 0.1 | 2.1 | - |
| CEM III | 28.8 | 6.9 | 1.8 | 51.0 | 5.3 | 0.6 | 0.3 | 1.9 | - |
| Metakaolin | 52.7 | 40.6 | 1.93 | 0.3 | 0.3 | 1.6 | 0.0 | - | 0.4 |
In concrete mixes M1–M3, the same aggregate type (natural aggregate) and the same volume content of aggregate were maintained. These mixes varied in the type of binder used. In order to increase the effect of cement type on the elastic properties of the concrete, an increased binder content was applied. This was carried out on self-compacting concrete (M4 and M5) and high strength concrete (M6).
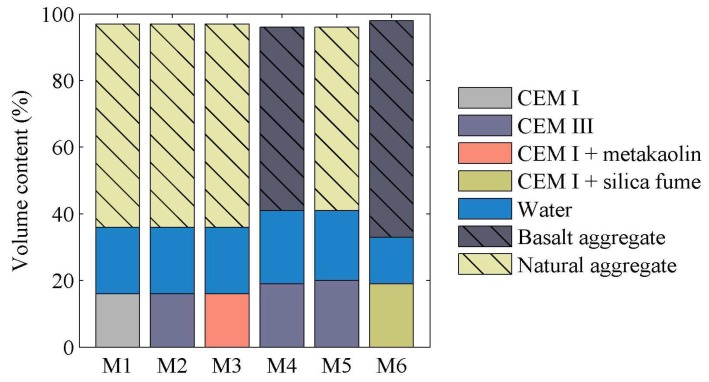
The concrete mixes M4 and M5 varied only by the aggregate type. The same volume content of basalt aggregate (M4) and natural aggregate (M5) was applied. The composition of concrete M1–M6 is presented in Table 2. Figure 4 presents the volume composition of the M1–M6 mixes. For all designed concrete mixes the compressive strength, static, and dynamic elastic modulus testing was conducted in a timescale of 4 to 28 days.
Table 2.
Concrete mixes composition .
| Concrete | Binder | Water | Natural Aggregate | Basalt Aggregate | SP | |||
|---|---|---|---|---|---|---|---|---|
| CEM I | CEM III | Metakaolin | Silica Fume | |||||
| M1 | 500 | - | - | - | 200 | 1600 | - | - |
| M2 | - | 501 | - | - | 200 | 1600 | - | - |
| M3 | 387 | - | 97 | - | 193 | 1600 | - | 0.5 |
| M4 | - | 582 | - | - | 232 | - | 1692 | 2.0 |
| M5 | - | 585 | - | - | 202 | 1493 | - | 2.0 |
| M6 | 500 | - | - | 50 | 135 | - | 2008 | 1.25 |
Figure 4.
Volume composition of concrete mixes.
The dynamic elastic modulus was determined using procedures based on EN ISO 12680-1:2008. In this method, the vibration of the concrete beam is induced by a random force hitting the beam. The recorded signal is subjected to fast Fourier transform (FFT) and the fundamental resonant frequency was then determined.
The dimensions of the concrete samples were: 500 mm length, 100 mm width, and 100 mm height. Each specimen was supported by steel tubes, positioned in such a way so as to coincide with the theoretical occurrence of fundamental vibration mode nodes. An illustration of the apparatus used in the dynamic elastic modulus testing is presented in Figure 5.
Figure 5.
Scheme of test stand used for testing dynamic elastic modulus.
The values of dynamic elastic modulus were calculated using the analytical relationship between the rigidity of the test sample, its geometry and mass and the fundamental resonant frequency, using the equation
| (1) |
where is the dynamic elastic modulus in Pa, —is the fundamental resonant frequency in Hz, —is the length of the tested specimen in m, —is the cross section moment of inertia in m4, and —is a constant that is dependent on the vibrating mode (equal to 22.373). In order to take into account such factors as the finite thickness of the specimen and Poisson’s ratio, the results of Equation (1) were multiplied by the correction factor, according to [26].
Compressive strength was determined using the method described in European standard EN 12390-3.
The static elastic modulus was determined using cylindrical specimens—150 mm diameter and 300 mm high—in accordance to EN 12390-13:2014. Standard method ‘A’ was applied and then two kinds of static elastic modulus were determined: initial and stabilized (designated as EC,0 and EC,S, respectively). The parallelism of the top and bottom surfaces was obtained using the steel caps and fine sand layer method, in accordance with Appendix ‘A’ of PN-EN 12390-3.
The specimens used in all of the experiments were cured in water at a temperature of 20 °C and then tested in the surface-dried state, from 4 to 28 days.
3. Experimental Results and Discussion
The results of compressive strength and static and dynamic elastic modulus testing are presented in Table 3. The selected trends in the results achieved are presented in Figure 6 and Figure 7.
Table 3.
The concrete specimen test results.
| Concrete | Age (days) | Compressive Strength fc,cube | Static Elastic Modulus | Dynamic Elastic Modulus ED | |
|---|---|---|---|---|---|
| Initial | Stabilized | ||||
| (MPa) | (GPa) | (GPa) | (GPa) | ||
| M1, CEM I, natural aggregate | 4 | 47.5 | 33.1 | 36.8 | 40.1 |
| 7 | 52.7 | 34.1 | 37.7 | 41.3 | |
| 14 | 55.8 | 35.5 | 38.2 | 42.6 | |
| 21 | 57.2 | 35.4 | 38.5 | 43.2 | |
| 28 | 58.1 | 36.3 | 39.4 | 43.6 | |
| M2, CEM III, natural aggregate | 4 | 27.3 | 25.3 | 27.8 | 34.7 |
| 7 | 36.0 | 29.9 | 31.9 | 39.4 | |
| 14 | 45.1 | 33.9 | 36.2 | 42.3 | |
| 21 | 49.9 | 35.3 | 38.5 | 43.5 | |
| 28 | 52.5 | 38.2 | 39.1 | 43.9 | |
| M3, CEM I + metakaolin, natural aggregate | 4 | 34.7 | 26.3 | 29.3 | 34.0 |
| 7 | 41.5 | 30.2 | 32.7 | 37.9 | |
| 14 | 50.5 | 32.3 | 35.1 | 40.6 | |
| 21 | 52.2 | 33.7 | 36.8 | 41.8 | |
| 28 | 53.9 | 36.6 | 37.7 | 41.8 | |
| M4, CEM III, basalt aggregate | 7 | 36.9 | 33.9 | 35.9 | 40.8 |
| 14 | 51.5 | 39.8 | 41.2 | 44.3 | |
| 28 | 62.4 | 42.9 | 43.7 | 46.7 | |
| M5, CEM III, natural aggregate | 7 | 40.4 | 29.3 | 31.9 | 37.6 |
| 14 | 52.9 | 31.4 | 34.0 | 39.7 | |
| 28 | 64.6 | 35.4 | 37.3 | 42.1 | |
| M6, CEM I + silica fume, basalt aggregate | 7 | 84.8 | 53.1 | 55.0 | 56.9 |
| 14 | 98.3 | 56.6 | 59.3 | 60.3 | |
| 28 | 106.5 | 57.8 | 59.5 | 60.5 | |
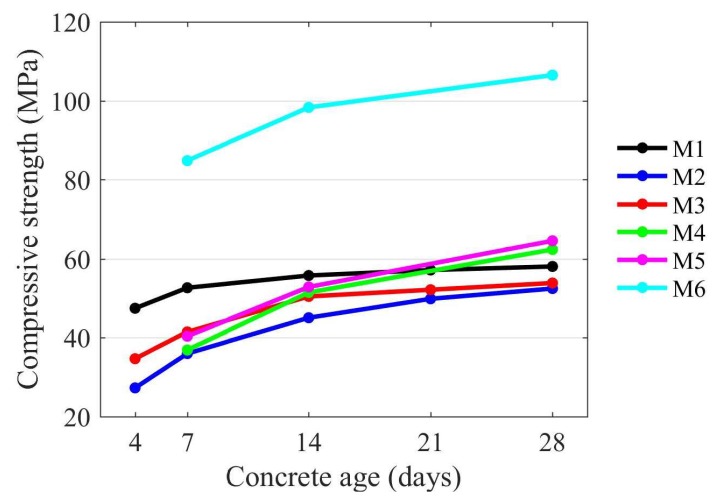
Figure 6.
Compressive strength of concrete mixes M1–M6.
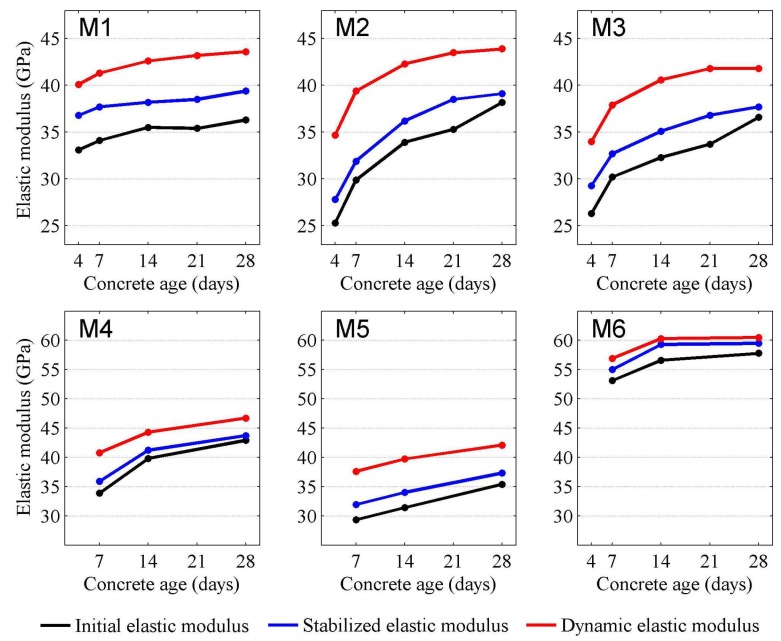
Figure 7.
The comparison of static and dynamic elastic modulus of concrete mixes M1–M6.
As Figure 6 shows, after 28 days of curing, the compressive strength exceeds 50 MPa for all of the concrete tested. The highest values of compressive strength were reached by the high strength concrete (M6). The self-compacting concrete (M4 and M5) achieved similar compressive strength (approximately 60 MPa) although they were made using a different type of aggregate.
The comparison of static and dynamic elastic modulus (Figure 7) shows that, for the time interval of 4 to 28 days, the values of initial static elastic modulus were lower and proportional to the stabilized elastic modulus for all of the concrete tested. In the case of M1–M3 concrete, the difference between these values is approximately 10%, regardless of age. Considering the M1–M3 concrete mix composition, indicates that the EC,0/EC,S ratio depends on the aggregate type rather than cement matrix.
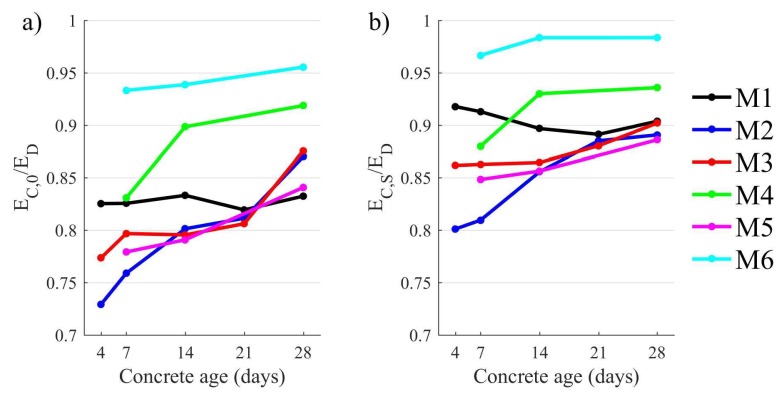
Figure 8 shows the differences between the initial and stabilized static elastic modulus and dynamic elastic modulus of concrete obtained using the impulse excitation and modal analysis method. It could be concluded that these differences generally decrease with time and this could be connected with increasing compressive strength. It should be stressed that relative differences between static and dynamic elastic modulus are smallest in the case of high strength concrete (M6), where these values tend to be nearly equal.
Figure 8.
The relative differences between dynamic and static elastic modulus of concrete: (a) initial; (b) stabilized.
4. Relationship between Elastic Modulus and Compressive Strength
In order to formulate the relationship between the dynamic elastic modulus, obtained using the impulse excitation and modal analysis method, and compressive strength of concrete, we first need to establish the relationship between dynamic elastic modulus () and initial static modulus (). In order to take into account the concrete’s composition, Equation (2) is proposed, in which and are functions related to the kind of aggregate and the type of binder, respectively.
| (2) |
where
| (3) |
where is the volume content of aggregate in the concrete mix, is the proportionality ratio between the initial () and stabilised static elastic modulus () depending on the kind of aggregate used. It was observed that these values appeared to be proportional (Figure 8), so it can be stated that
| (4) |
The results show that the difference between and decreases with an increase in compressive strength. In order to take this into account, the function of the compressive strength increase () was used. Originally, is the function used to estimate the concrete’s compressive strength depending on its age, according to Eurocode 2 Equation (5). The parameters of this function are age (t) in days and the coefficient depends on the binder type ()
| (5) |
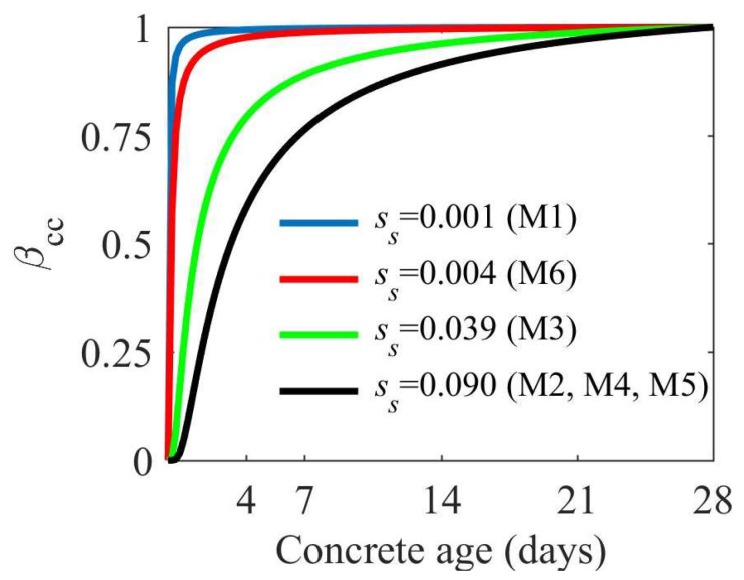
This exponential function reflects the rate of increase in concrete parameters over time. The rate of this increase is regulated by the coefficient, which was determined for all binder types used in the tested concrete (M1–M6). Figure 9 presents the shape of the function for the following binder types: CEM I, CEM III, CEM I with metakaolin, and CEM I with silica fume.
Figure 9.
Increase in the compressive strength of tested concrete, as described by the function.
The values of the coefficients and were determined using the least-squares method, taking as a criterion the smallest difference between values of stabilized elastic modulus calculated using Equation (2) and those determined experimentally. The values of the and coefficients are presented in Table 4.
Table 4.
Determined values of the coefficients depending on aggregate and binder type.
| Concrete | Aggregate | Binder | Concrete Density | Volume Content of Aggregate | Coefficients Determined Using Least Squares Method | |
|---|---|---|---|---|---|---|
| M1 | Natural | CEM I | 2360 | 0.61 | 0.926 | 0.001 |
| M2 | Natural | CEM III A | 2340 | 0.61 | 0.926 | 0.090 |
| M3 | Natural | CEM I + metakaolin | 2310 | 0.61 | 0.926 | 0.039 |
| M4 | Basalt | CEM III A | 2560 | 0.55 | 0.964 | 0.090 |
| M5 | Natural | CEM III A | 2320 | 0.55 | 0.926 | 0.090 |
| M6 | Basalt | CEM I + silica fume | 2650 | 0.65 | 0.964 | 0.004 |
Knowing the values of static elastic modulus () allows for the calculation of the compressive strength of concrete using the relationships outlined in the literature. In this work, the relationship given in ASTM 318-95 was used
| (6) |
where is the density of concrete, thus the compressive strength is equal to
| (7) |
Taking into account the coefficients that are dependent on the type of aggregate and binder (Table 4), the compressive strength was calculated using Equation (7). The calculated values were compared to the values obtained experimentally and these were then assessed using the Pearson correlation coefficient (R2 = 0.921). The largest differences between the calculated and experimental values are approximately 30%. This indicates that the relationship between static elastic modulus and compressive strength is influenced by the type of binder used. Thus, the parameter related to binder type and volume content was introduced to Equation (7)
| (8) |
where —is the experimentally determined coefficient dependent on the type of binder and is the volume content of cement matrix in the concrete. The relationship then takes the form
| (9) |
The values of the coefficient for all of the binders used were calculated based on the investigation results (Table 3) and they are presented in Table 5.
Table 5.
The values of coefficient
| Binder | |
|---|---|
| CEM I 42.5R | 2.31 |
| CEM III A 42.5N | 2.09 |
| CEM I + metakaolin | 2.19 |
| CEM I + silica fume | 2.76 |
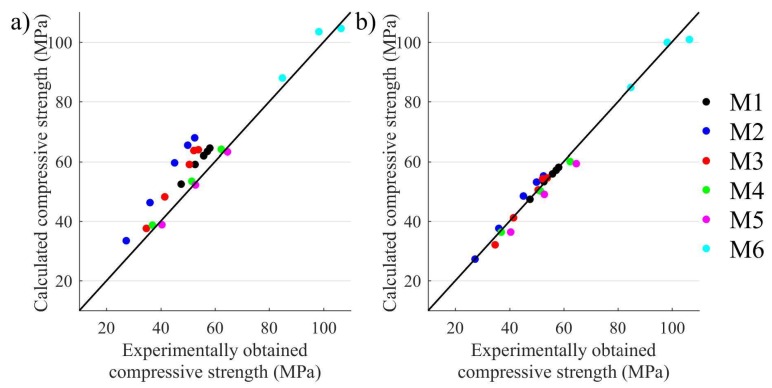
The comparison of calculated compressive strength (according to ASTM 318-95 and using the relationship proposed in this paper) with the experimentally obtained values is presented in Figure 10. It is evident that introduction of the coefficient, which takes into consideration the type of binder Equation (9), allows a significantly improved correlation between the analyzed material parameters of concrete to be achieved. In this case, the Pearson correlation coefficient equals R2 = 0.950.
Figure 10.
Comparison of calculated and experimentally obtained compressive strength of concrete values (a) using relationship (7); (b) using relationship (9).
Based on the investigations carried out, it can be stated that the proposed relationship allows the compressive strength of concrete to be calculated with better accuracy. The differences between calculated values and those obtained experimentally (Figure 10a) indicates the type of binder used and this influences the elastic properties of concrete significantly.
5. Conclusions
Based on the results of our investigation, the relationship between the static and dynamic elastic modulus and the relationship between the static elastic modulus and compressive strength of concrete were formulated.
The proposed relationship between dynamic elastic modulus and compressive strength takes into account the type and amount of aggregate and binder type. It was demonstrated that consideration of these factors allows compressive strength to be calculated with better accuracy.
The investigation results showed that the stabilized elastic modulus is proportional to the initial elastic modulus and that the proportionality coefficient between them is dependent on the type of aggregate used.
The proposed relationship between dynamic elastic modulus and compressive strength could allow the use of impulse excitation and modal analysis method as a non-destructive method of compressive strength testing for concrete. However, the relationship should be developed through further experimental analysis of the results achieved for different types of concrete.
Author Contributions
Krystian Jurowski and Stefania Grzeszczyk performed the general conception of the work. Krystian Jurowski planned and carried out the experiments, data collection, interpretation of results and article draft. Stefania Grzeszczyk made the revision and the final approval of the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Wang Z., Man X.T.C., Finch R.D., Jansen B.H. The Dynamic Behavior and Vibration Monitoring of Reinforced Concrete Beams. J. Test. Eval. 1998;26:405–419. [Google Scholar]
- 2.Azenha M., Ramos L.F., Aguilar R., Granja J.L. Continuous monitoring of concrete E-modulus since casting based on modal identification: case study for in situ application. Cem. Concr. Res. 2012;34:881–890. doi: 10.1016/j.cemconcomp.2012.04.004. [DOI] [Google Scholar]
- 3.Neville A.M. Properties of Concrete. 4th ed. Polski Cement; Cracow, Poland: 2000. (In Polish) [Google Scholar]
- 4.American Concrete Institute . ACI 318-95 Building Code Requirements for Structural Concrete. American Concrete Institute; Detroit, MI, USA: 1996. ACI manual of concrete practice Part 3: Use of concrete in buildings—Design, specifications, and related topics. [Google Scholar]
- 5.European Commitee for Standardization . EN 1992-1-1 Eurocode 2: Design of Concrete Structures Part 1—NA, 1. General Rules and Rules for Buildings. European Commitee for Standardization; Brussels, Belgium: 2004. [Google Scholar]
- 6.American Concrete Institute . ACI 363R-08 State of the Art Report on High Strength Concrete. American Concrete Institute; Detroit, MI, USA: 2008. [Google Scholar]
- 7.Noguchi T., Tomosawa F., Nemati K.M., Chiaia B.M., Fantilli A.P. A Practical Equation for Elastic Modulus of Concrete. ACI Struct. J. 2009;106:690–696. [Google Scholar]
- 8.British Standards Institution . British Standard BS 8110-2: 1985 Structural Use of Concrete. Part 2: Code of Practice for Special Circumstances. British Standards Institution; London, UK: 1985. [Google Scholar]
- 9.CSA Technical Committee . Reinforced Concrete Design, A23.3-04, Design of Concrete Structures. Canadian Standards Association; Rexdale, ON, Canada: 2004. [Google Scholar]
- 10.Standards New Zealand . NZS 3101:2006 The Design of Concrete Structures. Standards New Zealand; Wellington, New Zealand: 2006. New Zealand Standard, Concrete Structures Standard. [Google Scholar]
- 11.Jurowski K., Grzeszczyk S. The influence of concrete composition on Young’s modulus. Procedia Eng. 2015;108:584–591. doi: 10.1016/j.proeng.2015.06.181. [DOI] [Google Scholar]
- 12.Nikbin I.M., Beygi M.H.A., Kazemi M.T., Vaseghi A.J., Rahmani E., Rabbanifar S., Eslami M. A comprehensive investigation into the effect of aging and coarse aggregate size and volume on mechanical properties of self-compacting concrete. Mater. Des. 2014;59:199–210. doi: 10.1016/j.matdes.2014.02.054. [DOI] [Google Scholar]
- 13.Tasdemir M.A., Karihaloo B.L. Effect of type and volume fraction of aggregate on the fracture properties of concrete. Mech. Concr. Struct. 2001:123–129. [Google Scholar]
- 14.Bilir T. Investigation of performances of some empirical and composite models for predicting the modulus of elasticity of high strength concretes incorporating ground pumice and silica fume. Constr. Build. Mater. 2016;127:850–860. doi: 10.1016/j.conbuildmat.2016.10.054. [DOI] [Google Scholar]
- 15.Behnood A., Olek J., Glinicki A. Predicting modulus elasticity of recycled aggregate concrete using M5’ model tree. Constr. Build. Mater. 2015;94:137–147. doi: 10.1016/j.conbuildmat.2015.06.055. [DOI] [Google Scholar]
- 16.Wang Y., Witten I.H. Induction of Model Trees for Predicting Continuous Classes. University of Waikato; Hamilton, New Zealand: 1996. (Working Paper Series 96/23). [Google Scholar]
- 17.Logan A., Choi W., Mirmiran A., Rizkalla S., Zia P. Short-Term Mechanical Properties of High-Strength Concrete. ACI Mater. J. 2009;106:413–418. [Google Scholar]
- 18.Ross A., Tedesco J.W., Kuennen S.T. Effects of strain rate on concrete strength. ACI Mater. J. 1995;92:37–47. [Google Scholar]
- 19.Popovics J.S., Zemajtis J., Shkolnik I. A Study of Static and Dynamic Modulus of Elasticity of Concrete. American Concrete Institute; Detroit, MI, USA: 2008. [Google Scholar]
- 20.Lyndon F.D., Balendran R.V. Some observations on elastic properties of plain concrete. Cem. Concr. Res. 1986;16:314–324. doi: 10.1016/0008-8846(86)90106-7. [DOI] [Google Scholar]
- 21.Popovics S. Verification of relationships between mechanical properties of concrete-like materials. Mater. Constr. 1975;8:183–191. doi: 10.1007/BF02475168. [DOI] [Google Scholar]
- 22.British Standards Institution . CP 110-1:1972 Code of Practice for the Structural Use of Concrete. Design, Materials and Workmanship. British Standards Institution; London, UK: 1972. [Google Scholar]
- 23.Lee B.J., Kee S.H., Oh T., Kim Y.Y. Effect of Cylinder Size on the Modulus of Elasticity and Compressive Strength of Concrete from Static and Dynamic Tests. Adv. Mater. Sci. Eng. 2015;2015:580638. doi: 10.1155/2015/580638. [DOI] [Google Scholar]
- 24.Salman M.M., Al-Amawee A.H. The Ratio between Static and Dynamic Modulus of Elasticity in Normal and High Strength Concrete. J. Eng. Dev. 2006;10:163–174. [Google Scholar]
- 25.Plachy T., Padevet P., Polak M. Comparison of Two Experimental Techniques for Determination of Young’s Modulus of Concrete Specimens; Proceedings of the 5th WSEAS International Conference on Applied and Theoretical Mechanics (MECHANICS ’09); Puerto De La Cruz, Spain. 14–16 December 2009; pp. 68–71. [Google Scholar]
- 26.Shkolnik I.E. Effect of nonlinear response of concrete on its elastic modulus and strength. Cem. Concr. Compos. 2005;27:747–757. doi: 10.1016/j.cemconcomp.2004.12.006. [DOI] [Google Scholar]
- 27.Zhou Y., Gao J., Sun Z., Qu W. A fundamental study on compressive strength, static and dynamic elastic moduli of young concrete. Constr. Build. Mater. 2015;98:137–145. doi: 10.1016/j.conbuildmat.2015.08.110. [DOI] [Google Scholar]
- 28.Brunarski L. Recommendations for use of resonance methods for testing concrete. Meteriaux Constr. 1969;2:269–273. doi: 10.1007/BF02475161. [DOI] [Google Scholar]
- 29.ASTM International . Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens. ASTM International; West Conshohocken, PA, USA: 2002. [Google Scholar]
- 30.Bunke N. Prüfung von Beton, Empfehlungen und Hinweise als Ergänzung zu DIN 1048. Deutscher Ausschauss für Stahlbeton; Berlin, Germany: 1991. (In German) [Google Scholar]
- 31.International Organization for Standardization . EN ISO 12680-1 Methods of Test for Refractory Products—Part 1: Determination of Dynamic Young’s Modulus (MOE) by Impulse Excitation of Vibration. International Organization for Standardization; Geneva, Switzerland: 2008. [Google Scholar]
- 32.Jurowski K., Kokot S., Bobra P., Grzeszczyk S. The method of dynamic elastic modulus of concrete testing using impulse excitation of vibration and the modal analysis. Inżynieria i Budownictwo. 2016;11:612–615. (In Polish) [Google Scholar]