The search for gene-gene interactions in genome-wide association studies: challenges in abundance of methods, practical considerations, and biological interpretation

Abstract

One of the primary goals in this era of precision medicine is to understand the biology of human diseases and their treatment, such that each individual patient receives the best possible treatment for their disease based on their genetic and environmental exposures. One way to work towards achieving this goal is to identify the environmental exposures and genetic variants that are relevant to each disease in question, as well as the complex interplay between genes and environment. Genome-wide association studies (GWAS) have allowed for a greater understanding of the genetic component of many complex traits. However, these genetic effects are largely small and thus, our ability to use these GWAS finding for precision medicine is limited. As more and more GWAS have been performed, rather than focusing only on common single nucleotide polymorphisms (SNPs) and additive genetic models, many researchers have begun to explore alternative heritable components of complex traits including rare variants, structural variants, epigenetics, and genetic interactions. While genetic interactions are a plausible reality that could explain some of the heritabliy that has not yet been identified, especially when one considers the identification of genetic interactions in model organisms as well as our understanding of biological complexity, still there are significant challenges and considerations in identifying these genetic interactions. Broadly, these can be summarized in three categories: abundance of methods, practical considerations, and biological interpretation. In this review, we will discuss these important elements in the search for genetic interactions along with some potential solutions. While genetic interactions are theoretically understood to be important for complex human disease, the body of evidence is still building to support this component of the underlying genetic architecture of complex human traits. Our hope is that more sophisticated modeling approaches and more robust computational techniques will enable the community to identify these important genetic interactions and improve our ability to implement precision medicine in the future.

Introduction

Most rare Mendelian genetic disorders, such as cystic fibrosis, are influenced by the effects of a single gene. However, common complex diseases, such as Alzheimer’s disease, breast cancer, or diabetes, are known to be influenced by more than one gene. Understanding the etiologic architecture of complex traits has remained a nearly insurmountable challenge for decades. Genome-wide association studies (GWAS) are an unbiased survey of common single nucleotide polymorphisms (SNPs) across the human genome, assayed by one of the commercial SNP platforms and tested one by one for association with a phenotype or trait of interest. GWAS have been successful for some traits/phenotypes with the identification of new disease susceptibility genes (1,2), while other diseases have been less successful through GWAS (3,4), which may point to a problem of “missing heritability” (5-7).

The search for the “missing heritability” of complex traits has led many to the path of genetic interactions, as these are a likely source of some of the underlying heritability (5,8). The idea of genetic interactions between loci, or epistasis, is not new, dating back to Bateson in 1909 (9). The most compelling recent evidence comes from studies in model organisms where there is both biological and statistical evidence for epistasis (10-12). Here, there is statistically significant evidence of an association between the epistatic loci and the trait of interest AND there is evidence that the genes biologically interact in a protein-protein, protein-DNA, protein-RNA, or similar type of interaction (10,11). These model organism studies provide evidence that epistasis detected via statistical and computational techniques may be relevant biologically for these organisms. We and others (13) propose that if these genetic interactions are important for model systems, they are similarly important for humans.

Although the concept has been extensively studied and accepted in model systems, the importance of epistasis in humans has continued to be a matter of debate. Based on recent research, epistasis is not merely a theoretical argument, and we have seen that complex interactions (such as interactions between genes that affect the trait of interest through multiplicative, or non-linear, or non-additive, interactions) have been identified as a component of complex phenotypes such as lipid profiles, sporadic ALS, multiple sclerosis, and cataracts to name a few (14-19). Some of these were identified in smaller scale candidate gene studies, but many are emerging from Genome-Wide Association Interaction Studies (GWAIS). These examples of epistasis in complex traits support the evidence seen in model systems. Furthermore, even once considered “simple” Mendelian disorders such as retinitis pigmentosa (20), Hirschsprung disease (21), juvenile-onset glaucoma (22), familial amyloid polyneuropathy (23) and cystic fibrosis (24), are now documented examples of epistasis where modifier genes have been identified which affect the disease phenotype. Thus, even these simple genetic diseases are complex and include epistasis, or genetic interaction, components.

When beginning a new study to discover and analyze the loci involved in a given complex phenotype, one goal is to select the most powerful, robust analysis methods for the problem at hand. Unfortunately, this process is not as simple as one would hope. For various reasons, including the heterogeneity of the underlying models that we are trying to identify, differential correlation patterns between SNPs, different allele frequencies, and other modeling assumptions, it is the case that there is not one, single best tool to use for all analyses. In fact, many different tools have been developed, each with strengths and weaknesses, and optimality for certain types of problems. Thus, rather than trying to make a recommendation for which tool is “best” or “optimal” for the identifying important genetic associations for complex disease in a GWAIS analysis, our goal is to (I) create a general awareness of some of the specific issues that are important in the context of GWAIS projects and (II) to provide pointers or suggestions towards possible solutions so that we might increase the clinical and public health utility of the findings of these studies. We first explain the topics that investigators should consider when selecting the most appropriate tool for a given study. However, a thorough review of all of the available tools is out of the scope of this review; instead we refer readers to the following additional reviews of specific methods (25-29). In the following sections, we discuss the topics for consideration divided into three broad categories: abundance of methods, practical considerations, and biological interpretation. The ultimate utility of our monumental investment in data generation will depend largely on the development of innovative analytical strategies and study designs that allow for the identification of complex genetic effects, like epistasis (or genetic interactions).

Abundance of methods: finding the tree in the forest, but how?

The lack of a consensus in good common practice in GWAIS and clear criteria for performance assessment as well as the lack of realistic synthetic data to rigorously evaluate the strengths and weaknesses of several competing epistasis detection methods has left the researcher interested in GWAIS with a feeling of not being able to see the “trees from the forest”. Moreover, the adoption of different definitions of family-wise error, false positives or power, and/or variations in how to compute them, complicates assessments about the relative efficiency of the different competing methodologies. It is important when comparing methods for GWAIS to identify and understand their core components other than those parts involving data preparation, pre-selection of interesting interactions, and multiple testing correction. Sometimes these parts cannot be disentangled due to the nature of the approach itself or due to the fact that the software source code is inaccessible. However, in some cases, the core of several different methods may be identical; therefore, it would not be useful to run both methods and compare results and be more confident in overlapping resultant models. If the core components of the methods are the same, this is not increased evidence of signal, this is merely what is expected. In addition, too much attention is given to a general simplified picture of epistasis and not the detailed structure it involves. The complexity of the human biological system requires the consideration of complex scenarios in simulation studies, minimally involving higher-order (>2 SNP) interactions, as well as interacting pathways (possibly modified by non-genetic exposures), differential patterns of short- and long-distance relationships between SNPs, varying patterns of genetic architecture, and missingness, as well as trait or genetic heterogeneity. Most of the simulation studies to evaluate novel genetic interaction methods use subsets of the above complexities and custom-tailored, overly simplified synthetic data. We believe that all of these factors may explain the limited number of replicated findings in epistasis research, as well as the poor results on biological a posteriori validation of identified epistasis signals.

Despite these challenges, the opportunities for identifying important interaction models that explain or predict disease susceptibility are immense. Dimensionality reduction strategies are extremely powerful. When the appropriate assumptions are met, ample power is achieved through having a substantial sample size, and a robust analysis tool is implemented, interaction models can be identified. There continue to be more and more examples of epistasis models identified in many complex traits; which emphasizes the importance of considering GWAIS going forward.

Over the past 10 years, several reviews, opinion and perspective papers have emerged (25,29-33), discussing the advantages and limitations of epistasis studies. Nowadays, it is often mandatory to supplement GWAS analysis with some notes about potential interactions between identified predisposing loci or within a particular genomic region. It is therefore not surprising that an increasing number of sophisticated analysis methods have entered the scene, a process that will last for several years to come. This comes with a caveat: clear guidelines are needed to use these methods in a correct way, in the appropriate context, and with a full understanding of what they are able to tell us and what they are not.

We argue that an optimized use of existing methods, as well as the creation of novel methods that better integrate the complexities involved in biological epistasis, are needed in order to make significant and clinically relevant progress and to better understand how the genetic structure and its biological mechanisms may relate to complex traits. A number of such approaches have been developed or are underway.

The abundance of methodological possibilities, developed to tackle the problem of epistasis identification in human genetics, does not make it easy to make an educated decision without going over the details of the method and empirical data supporting their utility. Some practical guidelines that generally apply to most methods will be offered further in this Review. On the positive side, the abundance of possibilities allows for the exploration of the vast modeling space of interactions, including parametric and non-parametric statistical methods as well as machine learning and data mining techniques, using a variety of routes. Each of them is likely to lead to different solutions due to the different representations of the same phenomenon, and thus caution is needed when prioritizing epistasis findings that are consistent across different analytic approaches. This is well-acknowledged within a classical regression framework: if one uses forward, stepwise regression, and backward elimination regression on the same dataset, the resulting models may be very different due to the path taken to construct them (29,34-36).

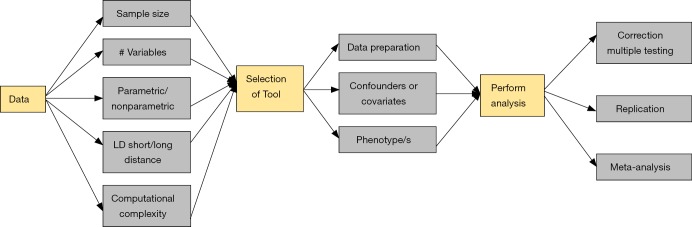
While all of the analytic approaches have their different strengths and weaknesses, there are underlying challenges that are shared amongst many or even all of the approaches. At the very heart of working with genetic interactions is the concept that appropriate modeling tools must be available to maximize our ability to develop models of complex traits. Additionally, due to the technological advances in genotyping and sequencing, we need to join forces to develop new methodologies to perform variable selection to extract the DNA variants associated with our trait of interest from the millions of available SNPs. Reviewing the extensive challenges in variable-selection and providing guidelines on which modeling tool has optimal performance are out of the scope of this review and have been covered in other review papers such as Fan and Lv (37). Instead, we will now draw attention to additional concerns when performing large-scale genetic interaction analyses, and will provide suggestions for scientists and analysts on how to address these in the future. Figure 1 demonstrates these concerns that are discussed below from each step of detecting epistatic interactions in the form of a flowchart.

Figure 1.

Flowchart describing the process of testing for epistatic interactions and challenges necessary to address at each step. A number of important considerations and decisions come into play when performing an epistasis analysis. This flowchart provides an overview of these steps.

Practical considerations

Here, we list a number of important practical considerations which describe part of the challenge the scientific community has experienced when faced with exploring epistasis. Different choices made for each of these may lead to widely varying epistasis results (38).

• ❖ Computational complexity issues arise when scaling up from studies investigating small genomic regions to studies covering the entire genome. The number of combinations of interacting SNPs is reasonable when studies evaluated 100 SNPs from candidate genes. But now that GWAS assays include 1 million SNPs or more, the number of combinations to test has exploded.

• ❖ There is also a major concern with sample size. This is often referred to as the “small n big p” problem (n: number of subjects; p: number of variables/genetic markers); this issue may give rise to curse of dimensionality problems (39).

• ❖ Questions about how to develop the statistical model of epistasis remain. Parametric model mis-specification is a major concern, especially in the presence of high-dimensional confounders. Parametric model mis-specification occurs when the model being used makes certain assumptions (such as dominant inheritance or additive effects), and if the data violate those assumptions, then the model does not effectively capture the effects in the data.

• ❖ How can we best exploit short-distance [i.e., linkage disequilibrium (LD)] or long-distance associations between genetic markers in epistasis studies? These patterns of LD should be able to enhance our ability to identify epistasis models, but thus far has not been capitalized on to the fullest extent.

• ❖ Multiple testing correction has been a huge focus of research in biostatistics applications in general, and in GWAS in particular, but more work is needed to optimize these in the context of epistasis screening (e.g., when hierarchically building 2-order, …, k-order interaction models).

Given the large amount of available data, the field has seen a shift from purely parametric (e.g., multiple regression) to semi-parametric interaction models (e.g., estimating interactions without modeling main effects) or “data mining” types of strategies [e.g., MDR (40) or MB-MDR (41,42)] and the exploitation of multiple different methods and statistical tools to combine their strengths. These shifts are exciting and have begun to lead to the identification of epistasis that replicates across studies (43). However, careful and thorough analyses are essential to detect and model these epistasis effects. In the following sections, we describe important areas of consideration when embarking on a GWAIS.

Checking assumptions

Most statistical methods have assumptions of some sort that should be considered prior to analysis. Failure to evaluate assumptions can lead to false positive associations or false negative associations. Statistical analyses are based on modeling strategies, each of which make certain assumptions about the data. For example, in a Student’s t-test, the assumptions include: (I) normal distribution of the dependent variable, (II) homogeneity of variance, and (III) independence of the samples. If the samples violate one or more of these assumptions, methods such as paired t-test or Wilcoxon rank sum test must be implemented as an alternative.

Whether the aim is to model genetic interactions or to explicitly test for them, the validity of model or test assumptions needs to be verified. Especially when data mining approaches are adopted this step in the data analysis flow is often forgotten. This can be explained by the fact that these methods are often termed non-parametric, and thus “model-free”. Parametric methods tend to have very specific model assumptions, which lead to our ability to determine statistical significance under such assumptions. In a non-parametric test, we often have fewer assumptions to evaluate, but also differences in how statistical significance is determined. For example, with a t-test, a P value can be assigned based on a table from a statistics textbook. However, if we run a non-parametric test, such as MDR, there is no P value table in the back of any textbook. Thus, care has to be given to what non-parametric means in the light of a particular analysis method. For instance, both MDR and MB-MDR are usually referred to as non-parametric approaches, but the term non-parametric here refers to these methods making no assumptions about genetic modes of inheritance. MB-MDR involves association testing, which may be either non-parametric (e.g., based on ranks) or parametric (i.e., relying on data distributional properties which may or may not be valid).

Complex analyses often rely on resampling-based methodologies to assess significance rather than on theoretical (often large-sample) reference distributions. Thus significance assessment and multiple testing correction methods may rely on assumptions that in principle need to be verified. In particular, both MDR and MB-MDR adopt permutation-based resampling methods to obtain empirical distributions of the relevant test statistic under a null hypothesis by rearranging trait labels of observed data records and recalculating test statistics accordingly. These resampling strategies can be tricky when studies are using hierarchical or sequential testing of models. Here, the process includes a first phase that tests a set of models; models that pass some threshold proceed to the next stage of analysis, and so on. Performing a permutation test of this process and creating the appropriate null distribution can be quite complicated. Apart from issues related to hierarchical or sequential testing of multiple models (e.g., 2-order, 3-order, …, k-order interaction models in MDR) and correctly describing “null” for a test statistic’s null distribution, applicability of the “exchangeability” premise or the assumption of “subset pivotality” may need to be checked. Subset pivotality refers to an assumption made about the exchangeability of matrices (44). Permutation-based step-down MaxT algorithms (45) do take into account the joint distribution of epistasis test statistics for significance assessment and are less conservative than Bonferroni correction, but need the subset pivotality (exchangeability) property in order to guarantee strong control of family-wise error rate (FWER). FWER considers not just the multiple tests with respect to one set of variables, but the tests over all combinations of variables and models. It was suggested in Mahachie John et al. (2013) (46) that this may be a problem for epistasis screening; a problem that may become even more pronounced in the presence of increased LD between markers (such as in whole genome sequencing data) and rare variants (47). Indeed, these particular data characteristics may induce quite different joint distributions of test statistics for different selections of equally sized joint hypotheses throughout the genome, making them non-exchangeable. The issue can be overcome by adopting a gene-centric analysis (48).

Selection of the tool

Several criteria are used to classify existing methodologies in epistasis studies, such as those based on whether (I) the strategy is exploratory in nature or not, (II) whether modeling or testing is the primary aim, (III) the epistasis effect is tested indirectly or directly, (IV) the approach is parametric or non-parametric in nature, (V) the strategy uses exhaustive search algorithms or takes a reduced set of input-data, that may be derived from prior expert knowledge or some filtering approach (49). These classification criteria show the diversity of available epistasis detection methods and approaches and indicate the complexities involved when trying to compare them (30).

The regression framework has long been, and still is, one of the most commonly used frameworks when modeling the effects of two susceptibility loci influencing disease status, allowing the easy inclusion of a main effect for each locus (50). After the realization of the HapMap project (51), there was a growing interest in haplotype analyses for GWAS, and the regression framework may also be used to model individual effects from multiple genetic markers that are putatively in LD with a susceptibility locus, allowing an effect to be studied for each marker haplotype that occurs (52,53). However this interest rapidly cooled down, mainly due to the limited additional power advantages it could offer to multiple regression based approaches (54). In addition, the increased computational burden haplotype construction itself would involve, despite the fact that haplotype-based methods for GWAS naturally account for correlations between markers in close proximity. The continuing popularity of parametric modeling (i.e., regression analyses) is somewhat surprising, given the several disadvantages it exhibits (55), such as the inclusion of that many parameters in a model (high-order interaction) which, in combination with small data sets may lead to overfitting (50); correlated predictors may further degrade the models and may lead to harmful multicollinearity; (nearly) empty cells (multi-locus genotype combinations with little or no data) require special parameterization; and the significance of the interaction parameters in fully saturated models largely depends on the underlying genetic model, allele frequency and multiple testing correction used (56).

Each of the aforementioned aspects may differentially impact the performance of an epistasis analysis method, where performance is usually assessed via power and notions of false positives on simulated data that may or may not well represent reasonable biological mechanisms. Here, power should be defined as the probability of detecting a statistically significant signal, given a particular epistasis model. The goal in most studies is to have maximal statistical power possible so that all true associations can be identified. In effect, some authors use “specific” power to indicate the probability to identify the causal interactive pair(s) and nothing else (no false positive SNPs). Others rather use the more general concept of “sensitivity” rather than “statistical power”. Different forms of sensitivity may apply depending on what is being tested for, against which alternative. For instance, Grady et al. (2011) (57) use “exact sensitivity” to refer to the simultaneous detection of the functional pair of markers in 2-locus epistasis studies versus “signal sensitivity”, which may refer to any sensitivity which is not exact. This means that while the method detected the correct 2-locus model, it may have also included one or more additional SNPs which are actually false positives. In contrast, false positive rate is defined as the probability that an error is made, either under a global null hypothesis of no association between genetic markers and trait or under the alternative of a particular epistasis model. Type I errors assess the probability of making at least one false-positive inference under the null hypothesis, but depending on the stated null, several Type I error definitions may apply within the same application. The goal is to use a method which has a low false positive rate (does not detect too many SNPs that are not truly associated). Using different performance criteria obviously further complicates making comparisons between several methodologies and clearly there is a need for a consensus and correct usage of them in simulation studies. When evaluating simulation studies, a researcher can determine if they are more focused on power, type I error, or both. Is it most important to find all of the true signals, and it is okay to also detect a few false positive signals? Is it most important to find only true signals and no false positives - even if you may miss some true signals? These considerations will allow an investigator to balance power and type I error and select the appropriate tool for their project.

Notably, some methodologies generate a ranking of results without a threshold above which results are “significant”. For instance, Random Forests or Conditional Inference Forests (58,59) provide variable importance scores for input variables or pairs of input variables, but generally no statistical significance is assigned to these scores. User dependent thresholds complicate the comparison of power and false positive rates with methodologies that do generate a fixed threshold or rule of significance assignment. In addition, there are numerous ways for genetic interactions to manifest themselves in tree-based models. Currently adopted criteria such as “two variables should appear on the same branch” are not sufficient proof for interaction. This concept has been explained in more detail in (60) and can be seen in Figures 1 and 2 of (60).

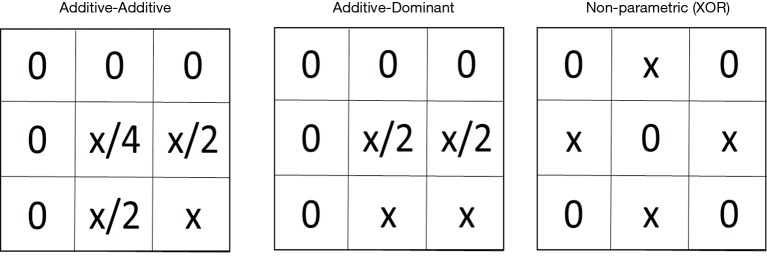
Figure 2.

Examples of genetic models represented as penetrance functions. Genetic interaction models can be represented as penetrance functions based on many different types of underlying genetic models. Three examples are shown here. The value in each box indicates the penetrance, or the probability of disease given that genotype combination. The value, x, can be any value such that the resulting penetrance value is between 0 and 1.

While methods are often selected on the basis of easy-to-access software availability or required IT-infrastructure to run the software, we believe that selecting the most appropriate method(s) for epistasis detection for particular biomedical data should be driven by characteristics of the “core component” of the epistasis detection approach; that is, the part of the method not related to data preparation, variable selection or multiple testing. The body, or core component, of an approach is defined as the primary statistical or computational model that is developed, assumptions made, optimization strategies implemented, and how results are provided and interpreted. Unfortunately, far too often, the source code of the related software tool does not allow manipulations to get to the core of the method, or the essential programming expertise is not available in the lab, or researchers having generated the initial software code have moved on and are no longer available to provide help. This issue has been discussed by others such as (61). In what follows, we discuss why it is important to align methodologies with respect to data preparation, variable selection, and multiple testing handling, so as to be able to better evaluate the relative performance of different epistasis detection methods.

Data preparation

Because of the computational complexity, big n small P, and multiple testing issues mentioned earlier, most epistasis methods employ some type of filtering method prior to analysis so that the computation time and number of tests are reduced. Several methods to pre-filter data in preparation for subsequent epistasis analysis exist and although the theoretical properties of these are fairly well understood in machine learning or bioinformatics communities, the potential of using biological knowledge to assist the filtering has re-opened the debate about the best ways to filter in the context of epistasis screening and whether we should do so in the first place (62). Many filter techniques assess the relevance of features by looking only at the intrinsic properties of the data (63,64). In most cases a feature relevance score is calculated, and low-scoring features are removed. Wrapper techniques involve a search procedure in the space of possible feature subsets, and an evaluation of specific subsets of features. The evaluation of a specific subset of features is obtained by training and testing a specific classification model. Embedded techniques involve a search in the combined space of feature subsets and hypotheses. Hence, the search for an optimal subset of features is built into the classifier construction, reviewed by Saeys et al. (2007) (65).

Some of the specific strategies being applied to prepare the data and make these analyses feasible can be categorized into two-stage approaches and space-pruning approaches. In two-stage approaches, SNPs are filtered through the use of an initial screen, to then move on to the second stage analysis. This can be done through single-locus GWAS (main effect) testing and only those SNPs that are statistically significant based on some P value threshold move on to the epistasis testing in stage 2, as performed in Sha et al. (66). Two-stage analysis can also be done through filtering based on biological knowledge including pathways, networks, and protein-protein interactions (49,67,68). There are also many methods developed for space-pruning; this includes strategies to reduce the search space using computationally efficient approach such as FastANOVA (69) or TEAM (70). When screening and testing involve two separate steps, and these steps are not independent, then proper accounting should be made for this dependence, in order to avoid overly optimistic test results.

Aligning the correct method for multiple testing

Several multiple testing methods exist, each of which have been evaluated at length via theoretical simulation studies in biostatistics settings. Interestingly, especially for small-scaled genetic association studies, family-wise type I error control still is often implemented as a Bonferroni correction, despite it being too conservative as it does not account for the correlation among multiple SNP pairs and may lead to an increase in type II errors. Type I error is the probability of identifying a SNP that is not truly associated (false positive). Type II error is the probability of missing a true association signal (lack of power—false negative). Balancing type I and type II error is a critically important aspect to the multiple testing approach selected. If one is more concerned with identifying as many potential associations as possible, even if some are false, they will have a lower type II error, but higher type I error. If a researcher does not want to be wrong and identify anything that is a false positive, they will have a low type I error, and a higher type II error. This also means that they will have lower power and may miss true association signals. There are strong motivations that would determine which is the appropriate balance for a given study; but it is a very individualized decision. Alternatively, genome-wide correction procedures focus on controlling the percentage of statistical significant tests that are false positives [false discovery rate (FDR) (71)] or on the false positive report probability (72), which refers to the posterior probability that a null hypothesis is true, given a statistic at least as extreme as the one observed, but are hardly used in genome-wide epistasis screening. Approaches such as the permutation-based step-down maxT adjustment of Westfall and Young (45) or adaptions using sample-based approximations, implemented MB-MDR (73), unifies the advantages of test significance assessment via resampling-based null distributions for test statistics, with an adequate control of type I error when multiple tests are performed. A discussion about the utility of a selection of multiple testing procedures in GWAIS applications falls outside the scope of this work. For more information, see Steen et al. (30), amongst others.

Characterizing and comparing the body or core components

Our ongoing work to incorporate features of MB-MDR in BOOST (in particular, integrating MB-MDR’s ways to handle missing data, covariate correction, score association testing, etc., with BOOST methodology) in a new umbrella tool called EpiShell (http://bio3.giga.ulg.ac.be/index.php/software/), highlights the benefits of evaluating methods on the basis of their “core” components in order to better understand the relative merits of each method (unpublished data). Methods that are conceptually quite different (for instance parametric and non-parametric methods) may actually give quite similar performances when they are properly “aligned”. We have also performed some simulations to characterize the performance of different methods and attempted to integrate them in PLATO (74). PLATO is the Platform for Analysis, Translation, and Organization of large scale data. It is a complementary analysis tool to PLINK, using the same file formats and some similar commands. However, PLATO has many analysis methods for epistasis, gene-environment interactions, and phenome-wide association study (PheWAS) analysis (74). Strategies like these will optimally allow for the best use of multiple analytic strategies.

Biological interpretation

Correction for confounding factors and covariates

When disease prevalence and genetic exposures differ among populations, spurious results may arise when testing the association between disease outcome and the genetic exposure of interest. To what extent genetic interactions exhibit different architectures between populations is largely unknown, making it uncertain how to best account for population substructure in GWAIS. Also, correcting for population stratification is relatively easy in a regression context (e.g., adding principal components as additional covariates to the association model), but it is far less obvious for certain dimensionality reduction or pattern recognition methods. In the context of dimensionality reduction or non-parametric data mining methods, only a limited number of groups have addressed the issue of adjusting for lower-order genetic effects during epistasis screening. This is understandable when the emphasis is on identifying a global signal from multiple loci, ignoring whether the joint signal is mainly explained by the highest possible order interaction or lower-order effects. Here the focus is on using a composite null hypothesis, where both main effects and interaction effects are tested jointly. This is an approach that has been seen to be rather efficient in gene-environment interaction studies when a locus is expected to only have residual marginal effects conditional on other factors tested for interaction (75). The quest for gene-gene interaction signals, above and beyond lower-order interactions or main effects, implies a shift towards the parametric paradigm or an integration of parametric or semi-parametric ideas in intrinsic non-parametric data mining approaches. Consequently, this shift comes with a cost of checking the validity of additional assumptions related to the approach. Results from a study performed by Mahachie John et al. (42) confirmed highly increased type I errors (i.e., false epistasis findings in data with main effects but no interaction effects) when main effects were not taken into account or when they were not properly accounted for. For instance, MB-MDR’s type I error and false positive rates are under control when there is no additional main effect on the trait or when adjustment is made under a genotype model (i.e., biallelic genetic markers are coded as variables with 3 factor levels), but the latter also depends on the strategy used for adjustment. To attain sufficient power, these authors point out that adjusting for the main effects in the two genetic markers that are under investigation for epistasis using a genotype coding scheme as part of MB-MDR screening is the most appropriate strategy. Clearly, when higher-order interactions are envisaged, the previously mentioned disadvantages of parametric modeling will outweigh the advantages of using a semi-parametric correction instead. To our knowledge, the latter has not been considered in combination with non-parametric data mining methods for epistasis to condition on lower-order effects. This would be feasible though, given that there does not seem to be a power advantage of correcting for genetic markers other than those included in the higher-order interaction in the absence of LD between markers (42). Obviously, a detailed investigation of the effects of LD and long-distance correlations between markers on epistasis screening results may lead to quite different conclusions, and such an investigation is work in progress and has been discussed for MDR previously (57).

Replication

The gold standard in genetic epidemiology for accepting genetic association results is replication (76). In this context, for a SNP to replicate in a GWAS, we must observe the same SNP associated in two or more independent datasets drawn from the same population, ideally with the same study design, and with the same direction of effect. Replication is one strategy to minimize type I errors, as if we observe the same finding in multiple independent datasets, we can be more confident that the finding is real. Replication is typically seen as confirmation of results from the discovery set in an independent dataset. It differs from validation in subtle but important ways. First, validation refers to the concept that we observe the same SNP-phenotype association in two or more datasets collected in different populations (77). These different populations can be the result of different ethnic or ancestry backgrounds, different phenotype definitions, or different sample strategies. This is also known as an external cross-validation design (77). Although the necessity of replication and validation analysis and the procedures to carry them out is no longer under debate for GWAS, how to consider these types of analyses in GWAIS contexts may be regarded to be trivial but is—in our opinion—largely under-examined.

Genome-wide SNP genotyping platforms consist predominantly of tagSNPs from across the genome. Most of these SNPs are not causal and have no functional consequences. When two or more tagSNPs are combined in a genetic interaction model, is it reasonable to assume that the same combination of tagSNPs interacts in an independent dataset? We postulate that due to variation in allele frequency and underlying LD patterns between two datasets, it is highly unlikely that the same combination of tagSNPs would be associated in the same statistical model across both datasets. Rather, we would expect that the combination of underlying signals that those SNPs are tagging would replicate across datasets than the tagSNPs themselves. We have observed this in simulation studies (57). Also, when aligning two independent datasets by imputing missing markers, one SNP in a SNP-pair may be imputed in one dataset, whereas it is actually observed in another dataset. So even when the same SNP pair is highlighted in a significant genetic interaction in this setting, can we really talk about “replication”? Hence, it is necessary to expand the definition of replication and validation to better accommodate the aforementioned scenarios and to better consider the reality of the data we are working with, which are indirect association signals due to LD or signals that would never have emerged without data imputation. One such expansion considers gene-based replication instead of SNP-based replication (78,79), and is often the only feasible approach when evidences from different heterogeneous published studies need to be combined. Other more refined expansions may be thought of, that may better reflect a more detailed gene structure and function.

Leaving aside for the moment what replication means or should mean in the context of GWAIS even for the currently so-called replicated genetic interactions, it is unclear to what extent a potentially false positive model has been replicated due to the adopted methodological strategy itself or whether the replication of epistasis is not solely attributed to main effects (such as HLA effects) not properly accounted for. Clearly, effects such as those arising from the HLA region will be strong in whatever independent data are analyzed (80,81).

Meta-analysis

As described earlier, the goal is to identify associations that exist in multiple independent datasets as a way to rule out false positive findings. One strategy is to replicate or validate those findings. An alternative strategy is meta-analysis. Like replication and validation analysis, meta-analysis is also an approach to look for confirmation of signals, but with a very different analytic approach: however, it may establish statistical significance of genetic interaction studies with conflicting results. It looks to combine signals across multiple smaller datasets to increase statistical power and/or to develop more precise estimates of effect magnitudes. In addition, meta-analysis allows us to explicitly investigate study heterogeneity and to analyze datasets that on their own would not give statistically significant results due to too small sample sizes. Hence, the meta-analysis framework is particularly relevant for GWAIS. In the context of GWA studies, meta-analysis has mostly been applied to single SNP analysis of a given phenotype, although more advanced meta-analysis strategies also account for genome-wide multiple testing and population stratification issues (82,83). Alternatively, the Principal Components based meta-analysis approach proposed by Wang et al. 2012 (84) to deal with the ineffectiveness of double genomic control while accounting for population stratification in meta-studies, assumes the availability of per-study datasets. In ‘double genomic control’, genomic control is calculated in each study separately to generate the corrected P values and then also once again in the meta-analysis. Even with the original data of different centers being available for GWAIS analysis, genetic interaction signals may reveal themselves in different multi-locus patterns depending on the nature of the data (see also the previous section on replication, and the suggestion that gene-gene interactions may be modeled in a variety of ways, such as additive-additive, additive-dominant, or non-parametric, to name a few [shown in Figure 2 and more in (85-87)].

Future directions for success

We have examined some of the thought processes around the abundance of tools available, practical considerations for GWAIS (including checking assumptions and selection of analytic tools), as well as biological interpretation (including replication and meta-analysis). These are a few of the issues facing the community as we explore genome-wide datasets to elucidate genetic interaction signals that we expect to detect. For each of these topics, there are specific points to consider, selections to make to design a study, and conclusions that can be drawn based on these decisions. We have provided important points to consider, but unfortunately not strict recommendations. As mentioned throughout the review, many choices made for GWAIS with respect to analytic tool, replication, and meta-analysis strategy, will be study-specific. The appropriate tool and replication strategy for one study may not be the right choice for a different study. In addition, the continued development of new methods and evaluation and comparison of methods is critical to move the field forward. Method comparisons require data simulation studies where the simulated data are challenging and complicated, much like natural biological data. Fortunately, tools for data simulation also continue to be developed and evolve including GAMETES (88) and SELAM (89), both of which were developed explicitly for simulating epistasis. We are optimistic that both the simulation approaches and analysis approaches will continue to improve as we learn and understand more about the complexity of human disease biology.

While the simulation aspect of genetic interactions is important, specifically developing representative datasets and designing appropriate in silico protocols, we also need to better align in silico approaches with experimental work. In most current studies, experimental work is integrated into genetic interactions as either prior knowledge or as a posteriori confirmation of results. However, to truly take advantage of the experimental techniques along with the computational techniques, we should surpass these simple uses of experimental information. Strategies to fully integrate experimental and computational work, as well as the community acceptance of the integration of these two very different worlds into collaborative projects, will facilitate our detection and understanding of genetic interactions in the future.

An overarching goal for this review is to point out the challenges in the search for genetic interactions, along with some thought provoking perspectives, to provide context that may explain why successful genetic interactions from GWAIS have been lagging behind single SNP associations from GWAS. The challenges facing GWAIS are considerably greater than those for standard GWAS (one SNP association at a time). However, the potential for uncovering more of the underlying heritability of complex traits, and improving our understanding of genetic architecture is considerable. Thus, the efforts being spent by many researchers in the community to improve our ability to detect genetic interaction signals are critical.