Personalized Network Modeling in Psychopathology: The Importance of Contemporaneous and Temporal Connections

Abstract

Recent literature has introduced (a) the network perspective to psychology and (b) collection of time series data to capture symptom fluctuations and other time varying factors in daily life. Combining these trends allows for the estimation of intraindividual network structures. We argue that these networks can be directly applied in clinical research and practice as hypothesis generating structures. Two networks can be computed: a temporal network, in which one investigates if symptoms (or other relevant variables) predict one another over time, and a contemporaneous network, in which one investigates if symptoms predict one another in the same window of measurement. The contemporaneous network is a partial correlation network, which is emerging in the analysis of cross-sectional data but is not yet utilized in the analysis of time series data. We explain the importance of partial correlation networks and exemplify the network structures on time series data of a psychiatric patient.

Recent years have witnessed an emergence of two distinct trends in the fields of psychopathology and psychiatry. The first trend is the network perspective on psychopathology, in which mental disorders are interpreted as the consequence of a dynamical interplay between symptoms and other clinically relevant variables (Borsboom, 2017; Borsboom & Cramer, 2013; Cramer & Borsboom, 2015; Cramer, Waldorp, van der Maas, & Borsboom, 2010). This literature uses symptom networks in an attempt to understand and predict the dynamics of psychopathology (Borsboom, 2017). From this perspective, symptoms are not seen as passive indicators of a mental disorder but rather play an active role, making symptoms prime candidates for interventions (Fried, Epskamp, Nesse, Tuerlinckx, & Borsboom, 2016). Since its introduction, the network perspective has grown into an extensive field of research in clinical psychology and psychiatry (Hofmann, Curtiss, & McNally, 2016; McNally, 2016; for an overview of recent literature, we refer the reader to the review of Fried et al., 2017). Second, technological advances have permitted the gathering of intensive measurements of symptoms, moods, and other daily fluctuating factors in patients and healthy controls with the experience sampling method (ESM; Aan het Rot, Hogenelst, & Schoevers, 2012; Myin-Germeys et al., 2009; Wichers, Lothmann, Simons, Nicolson, & Peeters, 2012). With ESM, participants are measured repeatedly within short time intervals during daily life. For example, someone is queried five times a day during a period of 2 weeks on his or her level of rumination, depressed mood, and fatigue since the previous measurement. We will term the time frame on which one reports the window of measurement. The resulting time series data allow for the investigation of intraindividual processes (Reis, 2012).

Time series data of a single individual offer a promising gateway into understanding the psychological dynamics that may occur within that individual over time (Bak, Drukker, Hasmi, & van Os, 2016; Fisher & Boswell, 2016; Kroeze et al., 2017; Wichers & Groot, 2016). With such time series data, one can estimate network structures that are unique to the patient: personalized symptom networks. Such networks are typically estimated using a statistical technique called vector autoregression (VAR; van der Krieke et al., 2015), which has recently grown popular in analyzing larger data sets of multiple subjects (e.g., Bringmann et al., 2013; Bringmann, Lemmens, Huibers, Borsboom, & Tuerlinckx, 2015; Fisher Reeves, Lawyer, Medaglia & Rubel, 2017; Pe et al., 2015; Wigman et al., 2015). Predominantly, VAR analyses have focused on the estimation of temporal relationships (relationships that occur between different windows of measurement). However, the residuals of the VAR model can be further used to estimate contemporaneous relationships (relationships that occur in the same window of measurement), which are not yet commonly used in the field. In this article, we argue that both network structures generate valuable hypothesis-generating information that can be directly applied in clinical practice. We focus the majority of the discussion on explaining contemporaneous partial correlation networks, as these are often ignored in the literature of intraindividual analysis.¹ We exemplify the utility of investigating both network structures by analyzing ESM data of a patient.

Temporal and Contemporaneous Networks

In time series data analysis with an average time interval of a few hours, a typical default statistical assumption is violated: Consecutive responses are not likely to be independent (e.g., someone who is tired between 9:00 and 11:00 is likely to still be tired between 11:00 and 13:00). The minimal method of coping with this violation of independence is the lag-1 VAR model (van der Krieke et al., 2015). In this model, a variable in a certain window of measurement is predicted by the same variable in the previous window of measurement (autoregressive effects) and all other variables in the previous window of measurement (cross-lagged effects; Selig & Little, 2012).² This model does not assume that autocorrelations between larger differences in time (e.g., lag-2) are zero, but merely that such relationships can be fully explained by the lag-1 model. These autoregressive and cross-lagged effects can be estimated and visualized in a network (Bringmann et al., 2013). In this network, measured variables (such as symptoms) are represented as nodes. When one variable predicts another in the next window of measurement, we draw a link with an arrowhead pointing from one node to the other. We term this network the temporal network. Temporal prediction has been termed Granger causality in the econometric literature (Granger, 1969), as evidence for temporal prediction can potentially be indicative of causality, at least satisfying the condition that the cause precedes the effect. With indicative of causality we mean that we would expect a temporal link if a causal relationship is true, although a link may also arise for other reasons (e.g., a unidimensional autocorrelated factor model would lead to every variable predicting every other variable over time). Important to note is that although a temporal relationship is to be expected if a causal relationship is true, we might not be able to detect such a temporal relationship from data because of a lack of statistical power or a different sized lag interval: A relationship that unfolds in seconds is not likely to lead to a temporal relationship when the lag interval is a few hours.

Only interpreting temporal coefficients does not utilize VAR to its full potential. The residuals of the temporal VAR model are correlated; correlations in the same window of measurement remain that cannot be explained by the temporal effects. These correlations can be used to compute a network of partial correlations (Wild et al., 2010). In such a network, each variable is again represented as a node. Links (without arrowhead) between two nodes indicate the partial correlation obtained after controlling for both temporal effects and all other variables in the same window of measurement. We term this network the contemporaneous network (Epskamp, Waldorp, Mõttus, & Borsboom, 2017; Fisher, Reeves, Lawyer, Medaglia, & Rubel, 2017). The contemporaneous network should not be confused with a network of lag-0 (partial) correlations. Such a network (a) does not take into account that responses are not independent and (b) presents a mixture of temporal and contemporaneous effects (Epskamp, Waldorp, et al., 2017). Thus, we compute the contemporaneous network from the residuals of the VAR model because only then relationships between windows of measurement and relationships within windows of measurement are separated.³ Modeling contemporaneous effects of a VAR model by using a partial correlation network is termed graphical VAR (Wild et al., 2010).

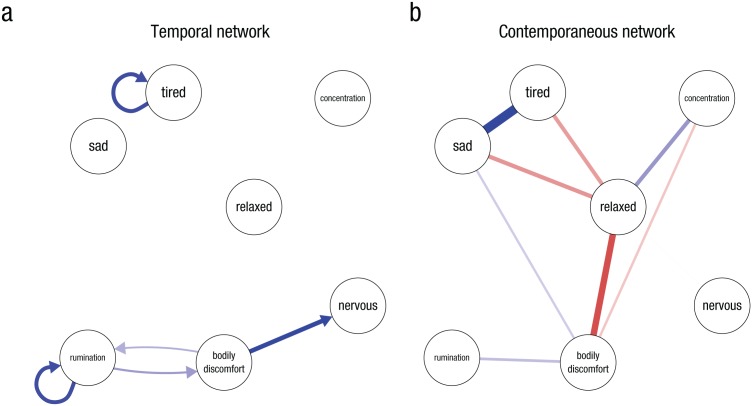
Figure 1 shows an example of the two symptom networks obtained from a graphical VAR analysis. These networks are estimated using ESM data of a clinical patient, and estimation and results are further described and interpreted in the Clinical Example section. The temporal network (a) shows autoregressions (an arrow of a node pointing at itself) of two variables: tired and rumination. These autoregressions indicate that when this patient is tired she is likely still tired during the next window of measurement. There are cross-lagged relationships between several variables. For example, for this patient, experiencing bodily discomfort predicts higher nervousness in the next measurement. The contemporaneous network (b) shows, among other relationships, a negative relationship between sad and relaxed: When this patient reported being sad she reported feeling less relaxed, during the same window of measurement. This predictive relationship may be the direct consequence of a plausible causal relationship: Being sad might lead you to feel less relaxed (or vice versa). There is no reason why such a causal relationship should take a few hours to materialize.

Fig. 1.

Two network structures that can be estimated with time series data analysis, based on data of a clinical patient (n = 47) measured over a period of 2 weeks. The model was estimated using the graphicalVAR package for R. Circles (nodes) represent variables, such as symptoms, and connections (links, both undirected drawn as simple lines or directed drawn as an arrow) indicate predictive relationships. Blue links indicate positive relationships, red links indicate negative relationships, and the width and saturation of a link indicates the strength (absolute value) of the relationship. The network on the left (Panel a) shows a temporal network, in which a link denotes that one variable predicts another variable in the next window of measurement. The network on the right (Panel b) shows a contemporaneous network, in which links indicate partial correlations between variables in the same window of measurement, after controlling for all other variables in the same window of measurement and all variables of the previous window of measurement.

Causation at the Contemporaneous Level

In a typical ESM study, the time between consecutive measurements is a few hours (e.g., Janssens, Bos, Rosmalen, Wichers, & Riese, 2017).⁴ Thus, the temporal network will only contain predictive effects of measured variables on other measured variables about a few hours later. However, it is likely that many causal relationships occur much faster than within a timeframe of a few hours. Take for example a classical causal model:

• Turn on sprinklers → grass is wet

In this representation, an arrow indicates that whatever is on the left causes whatever is on the right: Turning on the sprinklers causes the grass to become wet. This causal effect occurs very fast: After turning on the sprinklers it takes perhaps a few seconds for the grass to become wet. If we take measures of sprinklers (“on” or “off”) and the wetness of the grass every 2 hr, it would be rather improbable to capture the case in which the sprinklers were turned on just before the grass became wet. As a result, the temporal network would not contain a connection between turning on the sprinklers and the grass being wet, and likely would only contain a temporal autoregression of the grass being wet (because it takes time for grass to dry). However, after controlling for this autoregression, we most likely would find a connection between these variables in the contemporaneous network: In windows of measurement where the sprinklers were on, we are likely to find that the grass is wet.

We can think in a similar vein about psychopathological relationships. Consider the following hypothetical example: a patient suffering from panic disorder might anticipate a panic attack by experiencing somatic arousal (e.g., sweating, increased heart rate):

• Somatic arousal → anticipation of panic attack

This patient anticipates a panic attack, because the patient is experiencing somatic arousal. This causal effect would likely occur within minutes, not hours. Someone who experiences somatic arousal between 13:00 and 15:00 might still experience somatic arousal between 15:00 and 17:00. Thus, we might expect to find autoregressions. However, between somatic arousal and anticipation of panic attack we are likely to only find a contemporaneous connection.

In sum, relationships between symptoms and other clinically relevant variables can plausibly unfold faster than the typical timeframe of measurement, and such relationships can then be captured in the contemporaneous network. Figure 1 shows, however, that the contemporaneous network has no direction (links have no arrowheads). To understand how such undirected networks can still highlight potential causal pathways, we need to delve into the literature on estimation of networks in psychopathology.

Partial Correlation Networks

As outlined above, the contemporaneous relationships can be interpreted and drawn as a network of partial correlations. In this section, we describe how such partial correlation networks can be interpreted and how links in a network may be indicative of causal relationships. Partial correlation networks are not yet utilized in intraindividual time series analysis, but have gained considerable following in the analysis of cross-sectional psychopathological data.⁵ These networks are part of a more general class of undirected (i.e., no arrows) networks (formally called Markov random fields; Lauritzen, 1996) that have been introduced to psychopathology in response to the call for conceptualizing psychopathological behavior (e.g., symptoms) as complex networks (Borsboom, Cramer, Schmittmann, Epskamp, & Waldorp, 2011; Cramer et al., 2010). After the introduction of easy-to-use estimation methods and publicly available software packages for both estimation and visualization of networks (Epskamp, Cramer, Waldrop, Schmittmann, & Borsboom, 2012; van Borkulo et al., 2014), the use of undirected networks in psychopathology gained considerable traction. Ever since, such network structures have extensively been applied to research topics in the fields of psychopathology and psychiatry, including comorbidity (Boschloo et al., 2015), autism (Ruzzano, Borsboom, & Geurts, 2015), posttraumatic stress disorder (McNally et al., 2015), psychotic disorders (Isvoranu, Borsboom, van Os, & Guloksuz, 2016; Isvoranu et al., 2016), major depression (Cramer et al., 2016; Fried et al., 2015; van Borkulo et al., 2015), and clinical care (Kroeze et al., 2017).

Partial correlation networks present a relatively easy method to estimate and visualize potential causal pathways, while taking into account that observational data (i.e., no experimental interventions) contain limited information about such relationships. In observational data, causality is reflected only in the conditional independence structure (Pearl, 2000). Conditional independence means that two variables are no longer correlated at fixed levels of a third variable. A partial correlation network features conditional independence when two nodes are not connected by an edge (the partial correlation is estimated to be zero).

Taking again the panic disorder patient described above, suppose we expand the causal structure to include the pathway related to avoiding feared situations:

• Somatic arousal → anticipation of panic attack → avoidance of feared situations

Anticipating a panic attack might cause this patient to avoid feared situations, such as malls or busy shopping streets where panic would be especially inconvenient.⁶ The causal structure indicates that we would expect to be able to predict this patient avoiding feared situations if we know he or she is experiencing somatic arousal. However, if we also know this patient is anticipating a panic attack, we can already predict that this patient will avoid feared situations regardless of our knowledge about the experienced somatic arousal. Our knowledge about somatic arousal will no longer improve this prediction. Thus, we would expect nonzero partial correlations between somatic arousal and anticipation of panic attack, and between anticipation of panic attack and avoidance. We would furthermore expect a partial correlation of zero between somatic arousal and avoidance behavior; somatic arousal and avoidance behavior are conditionally independent given the anticipation of a panic attack. Consequently, we would expect the following partial correlation network:

• Somatic arousal → anticipation of panic attack → avoidance of feared situations

Finding such a partial correlation network often does not allow one to find the true direction of causation for two reasons: (a) different models are compatible with the exact same conditional independence structure and (b) assessing the direction of effect often requires an assumption that the causal structure is acyclic (i.e., contains no feedback loops). Concerning the first argument, we can summarize the above causal structure as A → B → C, in which A and C are conditionally independent given B. This conditional independence, however, also holds for two other models: A ← B ← C and A ← B → C (Pearl, 2000). In general, we cannot distinguish between these three models using only observational data. Adding more variables only increases this problem of potentially equivalent models, making it difficult to construct such a network only from observational data. Even when such a network can be constructed, we need to assume that the structure is not self-enforcing (Reason b). That is, a variable cannot cause itself via some chain (e.g., A → B → C → A). In psychopathology, however, this assumption likely does not hold (in our example above: anticipating a panic attack might cause more somatic arousal). In an undirected network, the observation that A and C are conditionally independent given B is represented by only one model: A – B – C (Lauritzen, 1996).

As a result of these problems with finding directed causal structures when temporal or experimental information is lacking, undirected networks have been more successful in the analysis of cross-sectional data. For the same reasons, we expect undirected networks also to be more successful than directed networks in gaining exploratory insight in the contemporaneous level of time series analysis. It should be noted that methodology to confirmatively test or exploratively find directed network structures at the contemporaneous time level exists as well, and that temporal information may help identify the direction of effect at the contemporaneous time level (Chen et al., 2011; Gates & Molenaar, 2012; Gates, Molenaar, Hillary, Ram, & Rovine, 2010). A more detailed discussion on this topic is beyond the scope of this article (we refer the reader to Epskamp, Waldorp, Mõttus, & Borsboom, 2017).

To summarize, the contemporaneous network is an undirected network without arrowheads. This network shows a link when two variables are not conditionally independent given responses from the previous window of measurement and responses from the current window of measurement. If a causal relationship were present, we would expect such a link. If a causal relationship were not present, we would often not expect such a link if all relevant variables are assumed to be included in the model (i.e., no latent variables causing covariation).⁷ Therefore, the links in the contemporaneous network can be indicative of causal relationships.

Generating Hypotheses

The connections in both the temporal and contemporaneous network cannot be interpreted as true causal relationships except under strong assumptions (for example, one needs to assume that every variable of the causal system has been measured without measurement error). The pathways shown can only be indicative of potential causal relationships. Such a pathway is a necessary condition for causality (we would expect such relationships when there is a true causal effect), but not sufficient (the relationship can also be spurious and due to, e.g., unobserved causes; Pearl, 2000). Edges in both the temporal and the contemporaneous network can arise for many different reasons. For example, an edge in a temporal network can arise as a result of unmodeled nonstationarity in the mean (see the Supplemental Material available online), and edges in both the temporal and contemporaneous networks can arise as a result of unmodeled (uncorrelated or correlated) measurement error or the influence of latent variables. Therefore, these networks can only be seen as hypothesis generating. To test for causality one needs to investigate what happens after experimentally changing one variable; it is hard to infer causality from observational data, no matter how often and intensive someone is measured and how intensive the sampling rate is.

In addition to generating hypotheses on potential causal links, both networks also generate hypotheses on which nodes are important. The importance of nodes in a network can be quantified with descriptive measures called centrality measures (Costantini et al., 2015; Newman, 2010; Opsahl, Agneessens, & Skvoretz, 2010). A node with a high centrality is said to be “central,” indicating the node is well connected in the network. Such a central node may be a prime candidate for intervention, as targeting this node will influence the rest of the system. This is the case not only for central nodes in the temporal network, but also for central nodes in the contemporaneous network. Even when a node has no outgoing temporal connections, it can still carry a lot of information on subsequent measurements, purely by being central in the contemporaneous network. For example, if a central node in the contemporaneous network predicts other nodes well in the same window of measurement, and all nodes predict themselves at the next measurement (autoregressions), then as a result the central node indirectly predicts other nodes at the next measurement.

Although experimental intervention is needed to test causal hypotheses, such hypotheses on causal relationships and central nodes might be hard to verify in clinical practice for a single patient, especially if one assumes the dynamics to be different per patient. For example, one cannot wait with the construction of treatment plans until after lengthy experimental designs have been tested in a clinical patient. In addition, in intensive treatments for example, multiple nodes are likely to be targeted simultaneously; that is, the causal effect of one particular node is hard to test. Furthermore, it might not be known how certain symptoms can be treated at all (e.g., feelings of derealization when the patient is also suffering from depersonalization). These considerations may also make the application of promising methodological developments incorporating both observational and experimental data (Magliacane, Claassen, & Mooij, 2017) hard if not impossible in clinical practice. Still, the obtained insights are useful: The personalized symptom networks can be discussed with the patient and, when the patient recognizes the discovered relationships, it can help to generate working hypotheses and choose interventions that target these nodes (Fisher & Boswell, 2016; Kroeze et al., 2017).

Clinical Example

To exemplify how the described symptom networks can be utilized in clinical practice, we analyzed ESM data obtained from a patient treated in a tertiary outpatient clinic at the Universitair Medisch Centrum Groningen (UMCG), the Netherlands. The patient was a female patient, aged 53 suffering from major depressive disorder, in early partial remission after having received electroconvulsive therapy (ECT). Data collection started one day after her last ECT session.

Method

The patient received an extensive briefing plus written user instructions for the ESM measurements. Direct support was available 24/7. Patient data were gathered during normal daily life with an ESM tool developed for an ongoing epidemiological study. With a secured server system (RoQua; roqua.nl; Sytema & van der Krieke, 2013), text messages with links to online questionnaires were sent to the patient’s smartphone. All items could be answered on a 7-point Likert-type scale varying from 1 (not at all) to 7 (very much). Measurement occasions were scheduled five times a day every 3 hr for 2 weeks (maximal number of possible measurement is 70), and took 3 to 5 min to complete. The timing of the measurements was adjusted to the patient’s personal daily rhythm with the last measurement timed 30 min before going to bed. The patient was instructed to fill out the questionnaires as soon as possible after receiving the text message. The patient received a reminder after 30 min, and after 60 min the link was closed. The protocol used was submitted to the ethical review board of the UMCG, who confirmed that formal assessment was not required. Prior to participation, the patient was fully informed about the study, after which he or she gave written informed consent.

The analyses in this article aim to exemplify an exploratory methodology that can be used in clinical practice. To that end, we opted to analyze only a subset of all administered items to obtain more easily interpretable network structures. We selected seven of the administered variables that usually should interact with each other: feeling sad, being tired, ruminating, experiencing bodily discomfort, feeling nervous, feeling relaxed, and being able to concentrate. Before analyzing the data, we removed the linear trend of variables that featured a significant linear trend on time (Fisher et al., 2017), and we did not regress the first response of the day on the last response of the previous day.⁸

The networks were estimated using the graphicalVAR (Version 0.2.1) package (Epskamp, 2017a) for R (Version 3.3.1), which uses penalized maximum likelihood estimation to estimate model parameters (strength of connections) while simultaneously controlling for parsimony (which links are removed; Abegaz & Wit, 2013; Rothman, Levina, & Zhu, 2010). The graphicalVAR package estimates 2,500 different models, varying 50 levels of parsimony in the temporal network and 50 levels of parsimony in the contemporaneous network. Bayesian information criterion (BIC) model selection was used to select the best fitting model. We refer the reader to Epskamp and Fried (2017) for an introduction to model selection of regularized networks; to Epskamp, Waldorp, et al. (2017) for a methodological introduction to the model used; and to Abegaz and Wit (2013) for the estimation procedure used. Network structures were standardized as described by Wild et al. (2010) to avoid misleading parameter estimates in the network structure (Bulteel, Tuerlinckx, Brose, & Ceulemans, 2016).

After estimating the network structures, the estimated models were refitted as a latent network model (LNM; Epskamp, Rhemtulla, & Borsboom, 2017) using the lvnet (Version 0.3.2) package for R. An LNM is a generalization of structural equation modeling that allows for the inclusion of undirected links. Fitting the model as an LNM allows one to obtain unpenalized parameter estimates and fit indices of both the graphical VAR model and a dynamic factor model (Molenaar, 1985). The graphical VAR model and dynamic one-dimensional factor models were fitted to the Toeplitz matrix, the covariance matrix of lagged and current responses (Chow, Ho, Hamaker, & Dolan, 2010). Thus, a good fit indicates that the model explains lag-0 and lag-1 (co)variances well. The variance-covariance structure between lagged variables was left unmodeled in both the graphical VAR and one-factor models. Furthermore, residuals of each variable were allowed to correlate with residuals of the same variable over time in the one-factor models. Full R codes of the analyses are available in the Supplemental Material.

Results

Figure 1 shows the two symptom networks of the patient (response rate: 93%, final n after removing nights and missing data = 47). The model fitted the lag-0 and lag-1 covariances well, χ²(56) = 54.36, p = .54, root mean square error of approximation (RMSEA) = 0, 95% CI = [0, .09], Akaike information criterion (AIC) = 1592.8, BIC = 1683.4, and fitted better than a one-factor model, χ²(54) = 128.55, p < .001, RMSEA = .17, 95% CI = [.13, .21], AIC = 1671, BIC = 1765.3. The temporal network in Panel a featured fewer connections than the contemporaneous network in Panel b. The temporal network shows the effects over time and highlights a potential feedback loop, where rumination (in her case, depressive thinking patterns where she keeps wondering why she is unable to change the way things are going) leads to more attention to bodily discomfort, leading to more rumination. In the contemporaneous network, the nodes “bodily discomfort” and “relaxed” featured central roles, based on the number of nodes they are connected with in the network. Whenever the patient experienced bodily discomfort (in her case, physical tiredness and pain), she felt less relaxed, was sadder, ruminated more, and was less able to concentrate within the same window of measurement. Therapy sessions revealed that intensively cleaning her house was her way of coping with stress. This led to bodily discomfort and eventually rumination about her inability to do the things in the way she used to do things, resulting in a sad mood. Specific interventions aiming at teaching her other ways to cope with stress broke this negative pattern.

Challenges to Personalized Network Modeling in Clinical Practice

Recent literature on network modeling in psychopathology has highlighted that this fast-growing field of research is still very young and not without challenges (Epskamp, Kruis, & Marsman, 2017; Fried & Cramer, 2017; Guloksuz, Pries, & van Os, 2017). Directly applying network modeling to clinical practice, therefore, also suffers from several pitfalls and challenges yet to be overcome. In this section, we list a few of the most prominent challenges we see.

Lag interval and model complexity

A main limitation of the (graphical) VAR method is that, even when contemporaneous networks are estimated, the results depend on the lag interval used. If the lag interval is shorter than the time frame of the dynamics, meaningful relationships might not be retrieved (e.g., some dynamics might occur within days or weeks rather than hours, such as loss of appetite leading to weight loss). Conversely, if the relationship is too fast, and dissipates fast, it might also not be retrieved (e.g., if the effect of a relationship dissipates after minutes, it might not be captured in a design that measures individuals hourly or at even larger time intervals). The optimal lag interval is often unknown and can even differ between individuals and notably also for different variables. The lag interval used is typically chosen in part for practical reasons; it may not be feasible for a patient to fill out a questionnaire more often during a day (e.g., 20 times a day). The data gathering can also not take too long (e.g., more than 2 weeks), especially not when the analyses are used directly in clinical practice, although notable exceptions exist as well (e.g., Bak et al., 2016; Wichers & Groot, 2016). In large-scale studies the data gathering may take longer if sophisticated statistical methods are used to deal with violations of stationarity (allowing the model to change over time; e.g., Bringmann et al., 2017; Haslbeck & Waldorp, 2017; Wichers & Groot, 2016), but such studies can be costly. Although effects that are slower than the lag interval could be captured in a second temporal network (e.g., a network between days in addition to a network between measurements; de Haan-Rietdijk, Kuppens, & Hamaker, 2016), such methods require more observations. This brings us to the next challenge.

Required number of observations

Many researchers wish to know the required number of observations needed to compute network models. This is a complicated question, as the performance of network estimation methods strongly depend on the true network structure—the network equivalent of a true effect size in power analysis studies. Even in the seven-node networks used in this network, required sample size to discover the true network model is a complicated function of 49 potential temporal links and 21 potential contemporaneous links. Large-scale simulation studies can and should be performed (e.g., Epskamp, Waldorp, et al., 2017, show adequate performance for estimating eight-node networks using 50 observations); however, these strongly depend on specifics of the simulated network structure. Epskamp and Fried (2017) propose a simulation-based approach per study to obtain a recommendation on the number of observations: simulate data under the number of nodes and an expected network structure, and check the performance of an estimation method under different sample sizes. An expected network structure can, for example, be obtained from prior literature. Network estimation techniques, such as the regularization method used in this article, aim to have high specificity (not detect false edges) and sensitivity improving with sample size (the ability to detect true edges). With few observations, estimated edges can still be interpreted to represent true edges, but one might miss on estimating other true edges (Epskamp, Kruis, et al., 2017).

Prior knowledge

In clinical practice, it is not always feasible to obtain more observations of a patient, as the patient cannot fill out too many responses throughout the day, and extending the data-gathering time period might not be desirable for the patient or the clinician and also comes with making the assumption of stationarity less plausible. A potential method for improving the network estimation in such limited sample sizes is to incorporate prior knowledge in a Bayesian analysis (O’Hagan & Forster, 2004). Prior knowledge on the network structures is readily available in this setting from both the expertise of the clinician and the experiences of the patient (Frewen, Schmittmann, Bringmann, & Borsboom, 2013). Incorporating such prior knowledge in an estimation technique such as used in this article, however, is still a topic of future research. In addition, exploratory model selection of graphical VAR models in a Bayesian context itself is still to be worked out. New promising Bayesian methods in exploratory network structure estimation are rapidly being developed (e.g., Hinne, Lenkoski, Heskes, & van Gerven, 2014; Pan, Haksing Ip, Dubé, Ip, & Dube, in press; Wang, 2012), which can potentially be extended to estimating graphical VAR models incorporating prior knowledge.

Centrality analysis

Thus far in the literature centrality analysis has mostly been performed using only temporal networks, which does not take the full model into account. Incorporating both contemporaneous and temporal connections in a centrality analysis is a topic of future research (Epskamp, 2017b, chap. 12). An additional caveat for using common centrality indices (e.g., strength, closeness, betweenness and eigenvector centrality; Newman, 2010) is that these are based on entirely different kinds of network models as analyzed here, such as social networks or railroad networks (Epskamp, Borsboom, & Fried, 2017). Although the utility of such centrality indices is debatable in analyzing such networks already (Borgatti, 2005), it is also questionable how these measures behave when computed on the basis of estimated statistical graphical models (Bringmann, 2016, chap. 8; Epskamp, 2017b, chap. 12). Finally, the sampling variability of centrality indices has been shown to potentially be large (Bringmann et al., 2013; Epskamp, Borsboom, et al., 2017), especially when sample size is low. To this end, we have not estimated and interpreted centrality indices on the network models presented in this article.

Conclusion

In this article we argued that when analyzing intraindividual time series data in clinical settings, researchers should focus on both temporal and contemporaneous relationships. Although temporal networks are commonly estimated and interpreted in the network approach to psychopathology (e.g., Bringmann et al., 2013), contemporaneous networks, especially when drawn as a partial correlation network, are not commonly used. We have argued that both contemporaneous and temporal networks can highlight meaningful relationships, interpretable and useable by patients and clinicians in treatment, as well as present researchers with hypothesis generating exploratory results on potential causal relationships. Such personalized knowledge can be used for intervention selection (e.g., choosing which symptoms to treat) and to generate hypotheses pertaining to the individual patient. In addition to temporal relationships, contemporaneous relationships are also important in discovering psychological dynamics, as such relationships can also occur at a much faster time scale than the typical lag interval used in ESM studies.

The aim of this article is not to argue against interpreting temporal coefficients—both temporal and contemporaneous effects contain information on how the observed variables can relate to one-another. Regardless, we strongly argue that the temporal and contemporaneous relationships should not be overinterpreted, as these merely show predictive effects and can at most only highlight potential causal pathways. A true causal interpretation of both temporal and contemporaneous edges requires assumptions to be met that are not tenable in clinical practice. So what is the use then of contemporaneous and temporal networks if they do not allow for causal interpretation? We argue that, for an individual patient, what matters is that both types of symptom networks give the clinician as well as the patient a personalized and visualized window into a patient’s daily life. Networks allow for a unique system view on person-specific associations obtainable from data rather than categorizing patients. Moreover, this personalized window comes with a host of opportunities to arrive at tailor-made intervention strategies (e.g., treating central symptom of patient), and to monitor progress (e.g., will “deactivating” a central symptom indeed result in the deactivation of other symptoms?). In addition, discussing the intricacies of personalized networks with the patient may offer ample opportunities for the patient to gain insight into his or her strengths and pitfalls and for reinforcing a sense of participation in one’s own care.