Abstract
Photosensitizer fluorescence excited by photodynamic therapy (PDT) treatment light can be used to monitor the in-vivo concentration of the photosensitizer and its photobleaching. The temporal integral of the product of in-vivo photosensitizer concentration and light fluence is called PDT dose, which is an important dosimetry quantity for PDT. However, the detected photosensitizer fluorescence may be distorted by variations in the absorption and scattering of both excitation and fluorescence light in tissue. Therefore, correction of the measured fluorescence for distortion due to variable optical properties is required for absolute quantification of photosensitizer concentration. In this study, we have developed a fourchannel PDT dose dosimetry system to simultaneously acquire light dosimetry and photosensitizer fluorescence data. We measured PDT dose at four sites in the pleural cavity during pleural PDT. We have determined an empirical optical property correction function using Monte Carlo (MC) simulations as well as measurements of fluorescence for a range of physiologically relevant tissue optical properties. Parameters of the optical property correction function for Photofrin fluorescence were determined experimentally. In-vivo measurements of photosensitizer fluorescence showed negligible photobleaching of Photofrin during the PDT treatment, but large intra- and inter-patient heterogeneities of in-vivo Photofrin concentration are observed. PDT doses delivered to 22 sites in the pleural cavity of 8 patients were different by 2.9 times intra-patient and 8.3 times inter-patient.
Keywords: Photodynamic therapy, Photofrin, PDT dose, optical properties correction, Monte Carlo simulation
1. Introduction
Type II photodynamic therapy (PDT) is a treatment based on the generation of highly reactive singlet oxygen (1O2) through the interactions of light, photosensitizer, and oxygen (3O2). PDT has been approved by the U.S. Food and Drug Administration to treat patients with a variety of cancers and precancers including esophageal cancer and non-small cell lung cancer as well as Barrett’s esophagus, a precancerous lesion that can lead to esophageal cancer (Huang, 2005; Zhu and Finlay, 2006; Triesscheijn et al., 2006). Although PDT has emerged as a viable minimally-invasive treatment modality for a variety of malignant and premalignant conditions, many clinical PDT treatment outcomes are suboptimal due to the lack of a reliable dose metric which will effectively predict treatment outcomes (Weersink et al., 2005; Gross and Wolfsen, 2010; Penjweini et al., 2016; Qiu et al., 2017; Kim et al., 2017a). Tremendous amounts of research have been done over the past three decades to understand the underlying biophysical mechanism of PDT in the effort to establish a robust dosimetry method (Kim et al., 2017a).
Future use of PDT depends on the development of improved dosimetry methods. Defining a PDT treatment dose can be complex since it involves a combination of local light fluence, local photosensitizer (PS) concentration, and local tissue oxygenation, which are highly interdependent and dynamic. Inadequate treatment doses may lead to insufficient treatment with residual dysplasia or carcinoma, while excessive doses may result in severe damage to the surrounding healthy tissues. Currently, most PDT treatments have been performed based on administered photosensitizer dosage and delivered light fluence (Zhu and Finlay, 2008; Wilson and Patterson, 2008; Jarvi et al., 2012). Zhou et al. (Zhou et al., 2006) reported animal-to-animal variation in PDT treatment response due to large intra- and inter-animal variations in PS uptake for benzoporphyrin derivative monoacid ring A (BPD-MA)-mediated PDT. The variation in treatment response was reduced when PDT dose, defined as the product of photosensitizer concentration and light fluence, was kept constant among animals. These results for BPD are consistent with our recent studies (Kim et al., 2016b; Kim et al., 2017b).
When PDT treatment is delivered with fixed incident light dose, the PDT dose delivered between sites can vary markedly due to the large inter- and intra-patient variability in the photosensitizer pharmacokinetics and tissue optical properties (Finlay et al., 2006b; Ong et al., 2017). Our previous work has shown PDT dose to be a better dosimetry quantity than light fluence or photosensitizer dose alone for Photofrin-mediated (Qiu et al., 2017) and 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide-a (HPPH)-mediated (Penjweini et al., 2016) PDT treatment. Under well-oxygenated conditions, PDT dose is a good predictor of PDT treatment outcome as it accounts for the variations in local PS concentration and light fluence.
In conjunction with an ongoing Phase II clinical trial of Photofrin-mediated PDT* (Friedberg et al., 2017) for pleural mesothelioma (Simone and Cengel, 2014), we have developed an instrument capable of measuring light fluence rate and photosensitizer concentration simultaneously during PDT. The goal of pleural PDT is to target the residual microscopic disease on or near the surface of the pleural cavity after surgical resection of the gross disease. PDT is chosen because it kills tumor cells directly through apoptosis and necrosis and by damaging tumor vasculature within a limited depth within target surface, and it also induces an inflammatory reaction capable of stimulating antitumor immune response which contribute to better treatment outcome. (Simone and Cengel, 2014) Light fluence and Photofrin fluorescence measured at tissue surface are used to calculate the PDT dose delivered to superficial tissue of the pleural cavity. Spatial heterogeneities in delivered PDT dose are observed within and among patients.
Quantifying measurement of fluorescence emission in vivo is difficult due to the influence of the background tissue optical properties. The interplay of absorption and scattering of both excitation and emission light within the tissue can severely alter the measured fluorescence. Variations in tissue optical properties may be mistaken for different PS concentration. However, in our current implementation, the excitation light (630nm) and emission light (650–700 nm) are close enough that same optical properties at the excitation wavelength (630 nm) can be used to represent the tissue optical properties at both emission and excitation wavelengths. There are several methods in the literature to reduce the effects of tissue optical properties on measured fluorescence, such as specially design optical probes (Diamond et al., 2003; Middelburg et al., 2015) or by applying a correction to the measured fluorescence based on independent measurements of tissue optical properties (Gardner et al., 1996; Muller et al., 2001; Finlay and Foster, 2005; Finlay et al., 2006b; Lambson et al., 2013; Sharikova et al., 2013; Kim et al., 2016a; Qiu et al., 2016; Penjweini et al., 2016; Kim et al., 2017b). Here, we report an empirical method to eliminate the effects of tissue optical properties on measured fluorescence spectra based on MC modeling of excitation and fluorescence light propagation in tissue. An empirical optical properties correction function is determined such that it corrects the measured fluorescence at any tissue optical properties to the one measured at the reference tissue optical properties. The validity of this optical properties correction approach was tested experimentally using tissue simulating phantoms for a wide range of clinically relevant optical properties. We have determined the parameters in this model experimentally for Photofrin fluorescence detected on the surface with broad beam irradiation similar to the excitation and detection geometries of our Photofrin fluorescence measurement during PDT treatments.
2. Materials and Methods
2.1. Monte Carlo simulation
Monte Carlo modeling is used to simulate the fluorescence signal collected by an isotropic detector placed on the tissue surface. The range of tissue optical properties simulated (absorption coefficient (μa) between 0.1 and 1 cm−1 and reduced scattering coefficient (μs’) between 5 and 40 cm−1) was based on a review of previously published in vivo tissue optical properties (Sandell and Zhu, 2011). The Monte Carlo algorithm used here was written in Matlab (The Mathworks Inc., Natick, MA, USA) as described previously (Lambson et al., 2013). This code uses the implicit capture method (Prahl et al., 1989) to improve the efficiency of the MC simulation.
In the code, we model the tissue in the cavity as a semi-infinite medium with uniform optical properties (μa and μs’), scattering anisotropy (g = 0.9) and refraction index mismatch (n1/n2 = 1.4). Photons are launched normal to the air-tissue interface along the z direction with initial weight of 1. Specular reflection at the surface, resulting from the refraction index mismatch, is calculated by the Fresnel reflectance for unpolarized light. The code traces each photon step by step from launch through multiple scattering events until it either escapes the medium or falls below a threshold weight, triggering a random ‘roulette’ process in which a photon has a one in ten chance of surviving with ten times its initial weight and a nine in ten chance of being terminated. At the end of each step, the weight of the photon is reduced by a factor of 1-a’, where a' = μs'/(μa+μs'). The photon’s new direction is determined based on the Henyey-Greenstein phase function with anisotropy g = 0.9.
To model fluorescence, assuming homogeneous fluorophore distribution in the medium, a new fluorescence photon with a weight 1/100 the weight of the incoming photon is generated at each step and is followed by the same algorithm until it escapes the medium or is terminated. The MC code records the distribution of light fluence rate in the medium (ϕ), the diffuse components of the reflected light (Rd) and the fluorescence light at the surface (FMC) in a cylindrical geometry consisting of rings of thickness dz and width dr. Reciprocity theorem is used to calculate the ϕ, Rd, and FMC on the central axis of a circular field as a function of radius R as described elsewhere (Attix, 1986; Zhu et al., 2003; Ong and Zhu, 2016). The magnitude of ϕ, Rd, and FMC are normalized to the light fluence rate in-air (ϕair), which is proportional to the total number of incident photons.
2.2. Patient treatment and PDT dose detection
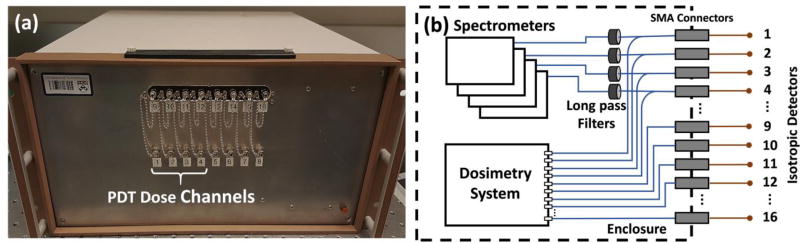
The patients in this study were enrolled in a Phase II randomized clinical trial of Photofrin-mediated PDT for pleural mesothelioma treatment. Having given informed consent, they were administered Photofrin (Pinnacle Biologics, Chicago, IL, USA) at 2 mg/kg of body weight as an intravenous infusion 24 hours prior to intra-operative PDT. PDT was performed in the operating room, immediately following radical pleurectomy and debulking of tumor. PDT treatment was performed with 632 nm light provided by a KTP-pumped dye laser (model 630 XP, Laserscope, Inc., San Jose, CA, USA) to a total fluence of 60 J/cm2. Light was delivered to the pleural cavity via an optical fiber inserted into modified endotracheal tube filled with 0.1% intralipid to produce an extended isotropic light source. The pleural cavity was filled with 0.01% intralipid solution during PDT treatment. As the intralipid solution became contaminated with blood as observed by the treating physician, it was repeatedly removed by suction pump and replaced with fresh solution to minimize light absorption by hemoglobin. The light source was circulated around in the lung cavity by the physician during the PDT. The instantaneous light fluence rate and the cumulative light dose were monitored continuously using 8 isotropic detectors (Medlight, Switzerland) sutured to 8 strategic locations within the pleural cavity wall. Light was delivered until the prescribed light dose of 60 J/cm2 was reached at each site. Isotropic detectors 1 to 4 were connected to four photodiodes of the multichannel dosimetry system and four spectrometers (Exemplar, B&W Tek, Inc., Newark, DE, USA) via a 1 by 2 bifurcated fiber (Ocean Optics, Dunedin, FL, USA), as shown in Fig. 1b, to monitor the fluence rate of the treatment light and Photofrin fluorescence simultaneously. Each spectrometer has wavelength range of 200 nm–1050 nm and resolution of 0.42 nm using a diode array of 2048×1 elements and 14 µm × 200 µm per element. The spectral resolution achieved was 0.47 nm. Isotropic detectors 9 to 12 were connected to the multichannel dosimetry system only. The dosimetry system records light fluence rate using photodiodes. Light fluence rate at surface is measured directly with an isotropic detector placed on the surface. The measured light fluence rate is not reflective of intra-tissue light fluence rate, which may be higher or lower than the value on the tissue surface depending on the tissue optical properties. Fluorescence collected by the fibers was collimated and passed through long pass filters (Semrock, Inc., Rochester, NY, USA) to block the treatment light before the transmitted fluorescence was recorded by the spectrometers, whereas no filtration was required for the treatment-light signal in the other arm of the bifurcated fibers. The front view and the schematic diagram of the system setup are shown in figure 1. There are 16 channels on the system enclosure as shown in Fig. 1(a). Channels 9 to 16 (top row) are connected to the dosimetry system only whereas Channels 1 to 4 (bottom row) are connected to both the dosimetry system and the spectrometers. Channels 5 to 8 (bottom row) are currently not used. In this study, Channels 1 to 4 are used to measure fluence rate of the treatment light and Photofrin fluorescence concurrently, while Channel 9 to 12 are used to measure light fluence rate only.
Figure 1.
(a) The front view of the 4-channel PDT dose dosimetry instrument and (b) the schematic diagram of the system setup.
2.3. Optical properties measurements
Diffuse reflectance measurements were acquired before and after PDT treatment using a specially designed fiber optic-based contact probe consisting of one source fiber, coupled to an air-cooled quartz-tungsten-halogen (QTH) lamp (Avalight HAL-S, Avantes, Inc., Louisville, CO, USA), and 9 detection fibers spaced at distances from 1.4 to 8.7 mm from the source. Measurements were made with the probe in contact with the interior surface of the pleural cavity. The reflected light was collected by the detection fibers which are imaged via a spectrograph onto a CCD, to measure radially-resolved diffuse reflectance. Background signal was measured in the same tissue with the white light source turned off, and then subtracted from each measurement. Each tissue spectrum is divided by the spectrum obtained with the same light source and detector in an integrating sphere to account for the wavelength-dependence of the white light source power and CCD response. The diffuse reflectance spectra are fitted with a nonlinear fitting algorithm implemented in the Matlab programming environment to extract the values of tissue optical properties. Details of the probe design and fitting algorithm have been described previously (Finlay et al., 2006a).
2.4. Optical properties correction
2.4.1. Monte Carlo determination of optical properties correction function
MC simulated fluorescence light at the surface was divided by the total light fluence rate on the surface. This normalization is done so that our MC results are consistent with our PDT dose dosimetry results, in which the measured fluorescence was normalized to the fluence rate measured on the tissue surface. Light fluence rate at a tissue surface is calculated based on a previous study (Zhu et al., 2003). The normalized MC simulated fluorescence light is referred to as FMC in this paper, and is given by
| (1) |
To account for the differences in fluorescence due to the variation in optical properties, a set of empirical correction factors, CFMC, were computed using the relationship shown in Eq (1). CFMC is defined as the ratio of FMC,ref to FMC, where FMC,ref is the fluorescence simulated at the reference optical properties (μa,ref = 0.3 cm−1 and μs’,ref = 9.6 cm−1). The product of CFMC and FMC at any optical properties (μa, μs’) is equal to FMC,ref. The correction factor at the reference optical properties is by definition equal to 1.
The built-in fitting functions in OriginPro 2017 (OriginLab Corp., Northampton, MA, USA) were used to fit CFMC with two independent variables, μa and μs’. The best fit of data yields a 4-parameter power function of the form:
| (2) |
2.4.2. Experimental determination of OP correction factor for Photofrin fluorescence
A series of tissue mimicking phantoms with Photofrin concentration of 3mg/kg and a range of optical properties (μa = 0.1 – 0.9 cm−1 and μs’ = 5 – 24 cm−1) were used to determine the correction factor for Photofrin fluorescence measured using the 4-channel PDT dosimeter. Intralipid was added as light scatterer and India ink was added as light absorber. The raw fluorescence spectra collected from each spectrometer were fitted to the basis spectra of Photofrin, laser and Fourier components using a single value decomposition (SVD) fitting algorithm described previously (Finlay et al., 2001). The SVD amplitude of Photofrin fluorescence was divided by the SVD amplitude of laser to account for the difference in excitation light fluence rate between measurements. The normalized SVD amplitude of Photofrin, referred to as Ap in this paper, is correlated to FMC by a conversion constant δ (Ap = δ · FMC). Ap was fitted directly using Eq. (3) to determine parameters C1, C2, b1 and b2.
| (3) |
The reference optical properties used in this study were μa,ref = 0.3 cm−1 and μs’,ref = 9.6 cm−1, close to the mean of the measured tissue optical properties. Ap,ref was determined from the average of Ap obtained from Photofrin fluorescence measured at the reference optical properties using four PDT dose channels. The denominator of the term on the right hand side of Eq. (3) is the optical correction factor for Photofrin in phantoms, and is referred to as CFp in this paper. To correct for the variation in optical properties in the measured fluorescence, Ap is multiplied by CFp.
2.5. Data analysis
The raw fluorescence spectra collected during PDT are corrected for the spectral response of the individual spectrometer and analyzed using the SVD fitting algorithm (Finlay et al., 2001). This algorithm requires the basis spectra of the known components that comprise the measured fluorescence emission spectrum. The first basis spectrum is the emission of the excitation source that passes through the optical filter. This basis is created by recording the spectrum from a nonfluorescing scattering solution of 20% Intralipid diluted (1:20) in water to 1% concentration, excited with the 630 nm laser used for treatment. A background spectrum, recorded from the same solution with excitation laser turned off in a dark room, was subtracted from the source spectrum. The laser component arises primarily from the autofluorescence of isotropic detector and the low frequency tail of the excitation laser spectrum, which passes the long pass filter. Extensive experiments have been performed to verify the peak at 675 nm is caused by the isotropic detector. The laser component is therefore independent of the sample being measured and can be used as a measure of the excitation light intensity. The second basis spectrum is the fluorescence of Photofrin, measured at a concentration of 3 mg/kg in the same phantom, with both the excitation source and background spectra subtracted. Each basis spectrum is the average of 10 measurements and is smoothed using a 5-point moving average.
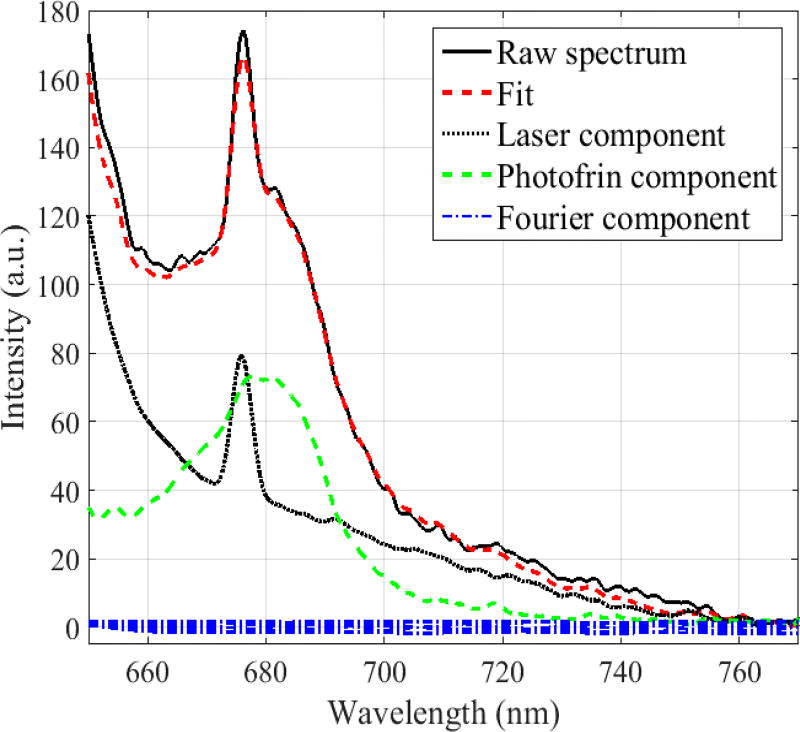
A 21-term Fourier series is included in the SVD algorithm to account for any unknown spectroscopic components, e.g. tissue autofluorescence and ambient room light, in the measured spectra (Finlay et al., 2001). The Fourier components are given a much lower weight in the fitting routine than that of the excitation source and Photofrin components to restrict their application to the unknown components of the spectrum that cannot be fit by combinations of these known components. In the cases presented here, the basis spectra of the two known components adequately account for the measured fluorescence, and the Fourier components constitute only a minor contribution to the fit. Spectra of the basis components and an example of the SVD fit to one fluorescence spectrum measured from patient #020 are shown in figure 2.
Figure 2.
Measured raw fluorescence spectrum and its SVD fit using the laser, Photofrin and Fourier basis spectral components. The peak at 675 nm arises from fluorescence of the isotropic detector.
The SVD fitting algorithm reduces the measured spectrum to a set of unitless SVD amplitudes, one for each basis component. The SVD amplitude of Photofrin is normalized to the SVD amplitude of the laser component to account for the variation in the excitation light fluence rate due to the movement of the treatment light source during PDT treatment. The normalized Photofrin SVD amplitude, after applying the optical properties correction, provides a quantitative measure of the local Photofrin concentration and is regarded as Ap in this paper for the purpose of convenience. The advantage of using Ap value instead of taking the intensity at a particular emission wavelength to quantify local Photofrin concentration is that Ap is less sensitive to noise at individual wavelengths because it is determined by fitting to the entire measured spectrum. The use of SVD value in our application here is particularly advantageous in reducing the uncertainties in the quantification of local Photofrin concentration as a considerable number of the measured fluorescence spectra have low SNR due to the moving excitation light source. The relationship between Ap,ref (CFp*Ap) and Photofrin concentration is obtained through a series of measurements from tissue simulating phantoms with increasing and known Photofrin concentration, as described in section 2.6.
2.6. PDT dosimeter calibration and phantom verification
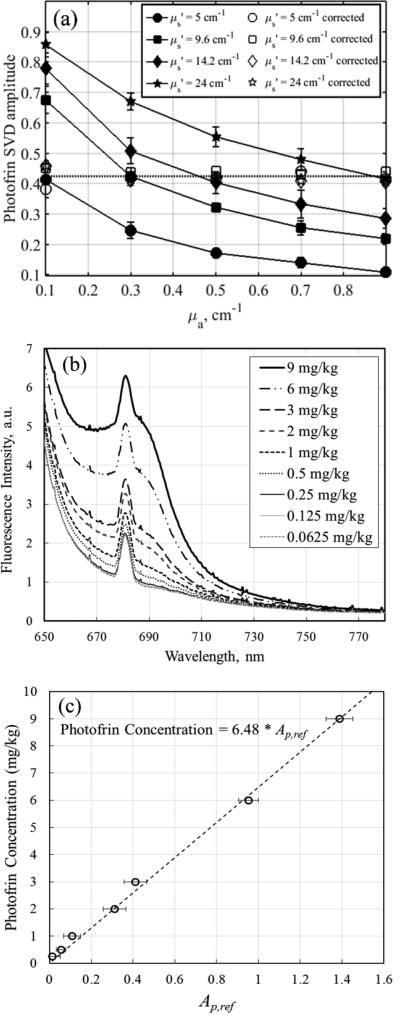
To quantify absolute in vivo Photofrin concentration, a calibration curve which relates the Ap,ref to the concentration of Photofrin was established using tissue simulating phantoms with increasing Photofrin concentration (0.0625mg/kg to 9mg/kg). Fluorescence spectra were measured and processed as described above to obtain a set of Ap,ref amplitudes with known concentrations of Photofrin. Fluorescence spectra measured using Channel 1 of the PDT dosimeter are shown in figure 3(b). Photofrin concentrations of the measured fluorescence are plotted against Ap,ref as shown in figure 3(c). The error bars represent the standard deviation of Ap,ref obtained from the fluorescence measured using 4 different PDT dose channels. Photofrin concentration is found to be Ap,ref*6.48 mg/kg and the minimum detectable level of Photofrin concentration of the instrument is 0.5 mg/kg.
Figure 3.
(a) Fluorescence SVD amplitude for Photofrin in tissue-simulating phantom experiments with different optical properties (μa = 0.1 – 0.9 cm−1 and μs’ = 5 – 24 cm−1) but constant Photofrin concentration of 3mg/kg. Photofrin SVD amplitudes were corrected for optical properties using Eq. (3) to obtained corrected SVD amplitude, Ap,ref (b) Fluorescence spectra of Photofrin at concentrations ranging from 0.0625 mg/kg to 9 mg/kg in tissue simulating phantom with μa,ref = 0.3 cm−1 and μs,ref’ = 9.6 cm−1 and (c) Photofrin concentration calibration curve.
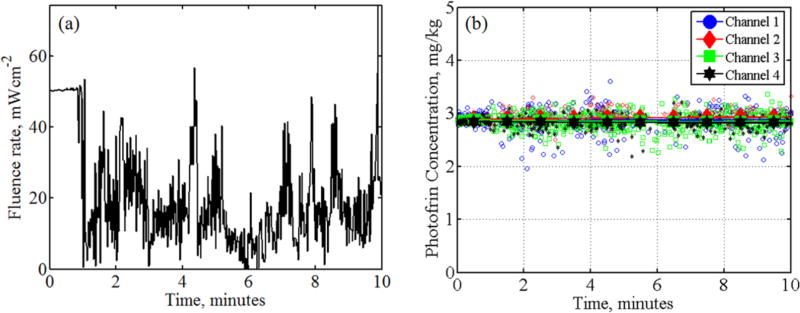
Excitation light intensity varies vastly during PDT as the light source was constantly circulated around in the lung cavity by the physician. To test the performance of the PDT dosimetry system in measuring Photofrin fluorescence with varying excitation light intensities, a 10-minute mock treatment was performed using liquid tissue-simulating phantom (μa = 0.3 cm−1 and μs’ = 9.6 cm−1) with known Photofrin concentration of 3 mg/kg and a moving light source. The fluorescence spectra were measured at the surface of the phantom using isotropic detectors as described above. The treatment started with the treatment light wand positioned at a fixed distance above the phantom for 1 minute. The average fluence rate measured on the surface was 50 mWcm−2. Then the light wand was moved randomly over the top of the phantom to simulate the variations in the light fluence rate due to the movement of treatment light source in the pleural cavity during PDT treatment. The light fluence rate measured at the surface of the phantom, averaged over the 4 channels, as plotted in figure 4(a) shows constant light fluence rate at 50mWcm−2 for the first minute and varying light fluence rate between 0 – 70mWcm−2 for the following 9 minutes. The Photofrin concentrations obtained from measured Photofrin fluorescence spectra using data analysis method described above are plotted as a function of treatment time as shown in figure 4(b). Each data point represents Photofrin concentration obtained from one fluorescence spectrum and the solid lines represent the average Photofrin concentration calculated for every 1-minute of data. The results in figure 4(b) show there is negligible photobleaching of Photofrin during the time course of the measurements. The uncertainty of measurements between channels is around 3% as the Photofrin concentrations recovered from 4 channels vary between 2.84 and 2.92 mg/kg.
Figure 4.
(a) Average light fluence rate of 4 channels measured during 10 minutes of mock treatment (b) Photofrin concentrations obtained from fluorescence measured using 4 channels.
2.7. Diffuse reflectance measurements
To assess the validity of our fluorescence spectroscopy method, absolute Photofrin concentrations obtained from fluorescence measurements were compared to those obtained from diffuse reflectance spectra measured using DRS contact probe as described in Section 2.3 from the same locations before and after PDT treatment. This technique has been validated using phantoms with known photosensitizer concentrations (Solonenko et al., 2002) and was used to recover photosensitizer concentration from in vivo reflectance measurements (Wang et al., 2005). Interested readers can refer to (Solonenko et al., 2002; Wang et al., 2005) for more details about the instrumentation and data analysis of this method. Briefly, a multi-wavelength algorithm based on diffusion approximation equation was employed to fit all reflectance spectra between 600nm to 800 nm simultaneously using multiple source-detector separations to extract μa (λ) and μs’ (λ). Then, the concentration of Photofrin (and other chromophores) were obtained from μa (λ) using μa (λ) = Σiciεi (λ), where εi (λ) is the extinction coefficient of i’th chromophore and ci (λ) is the molar concentration of the i’th chromophore. The major chromophores in the spectral region of interest are oxy-(HbO2), deoxy-hemoglobin (Hb), water, and Photofrin and their extinction coefficients are obtained from the literature (Wang et al., 2005). The concentrations of all chromophores, cwater, cHb, cHbO2 and cPhotofrin are reconstructed directly using a nonlinearly constrained optimization method, fminsearch, implemented in Matlab. The spatial distributions of oxy-, deoxy-hemoglobin and water in the pleural cavity are beyond the scope of this study and only cPhotofrin will be reported.
3. Results and discussion
3.1. Monte Carlo determination of parameters for fluorescence correction
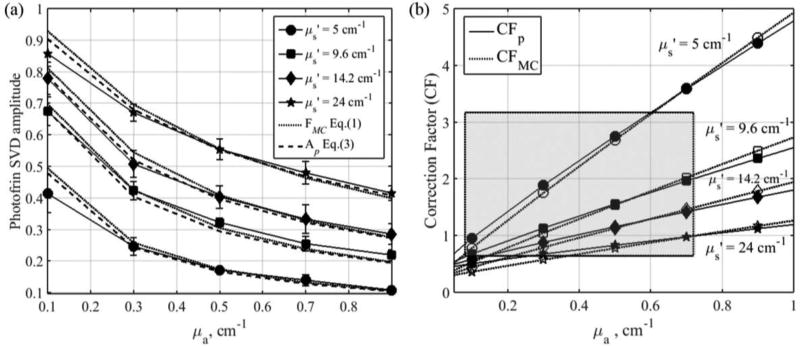
MC simulated fluorescence (FMC), detected by an isotropic detector placed at the surface of tissue with varying optical properties, are represented by dotted lines in figure 5(a). A circular beam with radius = 7 cm is used in the simulation as the incident light field to represent the broad beam illumination used in the clinic. To facilitate the comparison of MC and experimental results, the amplitudes of FMC are scaled by a constant so that the amplitude of FMC matches that of Ap at the reference optical properties (μa,ref = 0.3 cm−1 and μs’,ref = 9.6 cm−1). Variations in fluorophore concentration and optical properties can both alter the intensity of the detected fluorescence. To investigate and account for the effect of optical properties alone on the fluorescence intensity, fluorophore concentration is kept constant in all of our simulations. The simulated fluorescence intensity increases with tissue reduced scattering coefficient and decreases with absorption coefficient. A set of correction factors, CFMC, is computed using Eq. (1) to correct for the change in fluorescence intensity due to optical properties so that FMC is equal to value measured at the reference tissue optical properties (FMC,ref). We found that Eq. (2) can fit CFMC very well, where C1 = 22.43, C2 = 0.011, b1 = 0.943, and b2 = −0.973. The empirical correction factors are plotted as a function of optical properties as represented by dotted lines in figure 5(b). Parameters b1 and b2 describe the behavior of the fluorescence alteration due to light scattering and absorption in the tissue while C1 is a scaling factor which accounts for the difference in fluorescence detection efficiency due to spectrometer’s sensitivity and optical components along the light path. No optical properties correction is needed for fluorescence measured at the reference optical properties, as CFMC is equal to 1.
Figure 5.
(a) MC simulated fluorescence, FMC, (dotted lines), average Photofrin SVD amplitude obtained from fluorescence measured in phantoms using 4-channel PDT dosimeter (solid lines) and Ap fits using Eq. (3) (dashed lines); (b) Comparison of CFMC (dotted lines) and CFp (solid lines).
We found that the exponential form of correction factor formula suggested in our earlier publication (Sharikova et al., 2013; Kim et al., 2016a; Qiu et al., 2016; Penjweini et al., 2016; Kim et al., 2017b) works well within a narrower range of tissue optical properties (absorption coefficients between 0.1 and 1 cm−1 and reduced scattering coefficients between 5 and 15 cm−1). The exponential form of the correction factor formula is not able to fit the Monte Carlo results when the reduced scattering coefficient is larger than 15cm−1. The power form of correction factors are used in this study, but it should be noted that the exponential form of correction factors used in earlier publications are valid for the range of reduced scattering coefficient of most measured tissue sites in this study (5.8 – 16.6 cm−1). The correction factors calculated using both the power form, CFp, and exponential form, CFa, are listed in table 2 for comparison.
3.2. Phantom determination of parameters for Photofrin fluorescence correction function
The average amplitudes of Ap obtained from fluorescence measured in tissue-simulating phantoms using 4 different channels of the PDT dosimeter are represented as solid lines in figure 5(a). The error bars are the standard deviation of the Ap for 4 different channels. Similar trend in the fluorescence alteration is observed as the amplitude of Ap decreases with absorption coefficient and increases with reduced scattering coefficient. Equation (3) is used to fit Ap using Ap,ref = 0.423 at the reference optical properties (μa,ref = 0.3 cm−1 and μs’,ref = 9.6 cm−1). The parameters of CFp are C1 = 25.49, C2 = 0.016, b1 = 0.902, and b2 = −1.094 and the empirical CFp are plotted as a function of optical properties in figure 5(b), represented by solid lines. The fit of Ap using Eq. (3) are plotted on figure 5(a) for comparison, as represented by the dashed line, and has a goodness of fit of R2=0.9608. The parameters for correction factors obtained from Monte Carlo simulations and phantom measurements are summarized in Table 1.
Table 1.
Optical properties correction function parameters
| Parameters | C1 | b1 | b2 | C2 |
|---|---|---|---|---|
| CFMC | 22.43 | 0.943 | −0.973 | 0.011 |
| CFp | 25.49 ± 0.65 | 0.902 ± 0.1 | −1.094 ± 0.12 | 0.016 ± 0.05 |
The empirical correction method described above requires accurate knowledge of the tissue optical properties. As the difference in optical properties at the excitation (630nm) and emission wavelength (650–700nm) is rather small in this study, we have applied the correction based on the optical properties at the excitation wavelength of 630 nm obtained from diffuse reflectance spectroscopy measurements. There are significant variations in optical properties inter- and intra-patients according to our measurements. The correction factors used in analyzing our in vivo data correspond to excitation wavelength absorption coefficients of 0.08 to 0.72 cm−1 and reduced scattering coefficients of 5.8 to 16.6 cm−1, as indicated by the shaded area in figure 5(b).
3.3. Tissue optical properties and spatial distribution of Photofrin
In this study, we measured in vivo diffuse reflectance and fluorescence spectra for 22 sites in the pleural cavities of 8 patients. The PDT dose dosimetry system had two channels that were capable of measuring light fluence rate and fluorescence simultaneously for the first 5 patients, later expanded to 4 channels. Tissue absorption and reduced scattering coefficients at excitation wavelength of 630nm from all measurement sites where fluorescence spectra were taken are presented in figure 6. We saw large heterogeneity in the tissue optical properties within and among patients. The contribution of haemoglobin to the tissue absorption at the emission wavelength, close to the NIR biological window, is rather small. The large spatial heterogeneity in tissue optical properties, especially the high absorption coefficient observed in some patients, could be due to the thermal damage to the measured tissue caused by electrosurgery during tumor resection. Figure 6(c) shows correction factors obtained for all sites based on the measured optical properties. The magnitude of correction factors range from 0.59 to 3.13 for 22 sites, with mean and median values of 1.26 and 1.04, respectively. It should be noted that the values of CF are susceptible to uncertainties in the measurement of tissue optical properties. Nevertheless, we observed small variation in CF within patients but large variation in CF between patients. The largest intra-patients difference in CF is 1.6 times, as in the locations of posterior chest wall and posterior diaphragmatic sulcus of patient #020, while the CF can vary by 4.9 times among patients. Variations in CF among and within patients clearly demonstrates the importance of optical property correction for absolute quantification of in vivo Photofrin concentration.
Figure 6.
(a) Tissue absorption coefficients, (b) reduced scattering coefficients at excitation wavelength of 630 nm and (c) CFp at 22 different sites in the pleural cavities of 8 patients. ACW = anterior medial chest wall; PCW = posterior chest wall; AS = anterior diaphragmatic sulcus; PS = posterior diaphragmatic sulcus; PM = posterior mediastinum; Peri = pericardium.
3.4. Temporal and spatial distribution of Photofrin and PDT dose
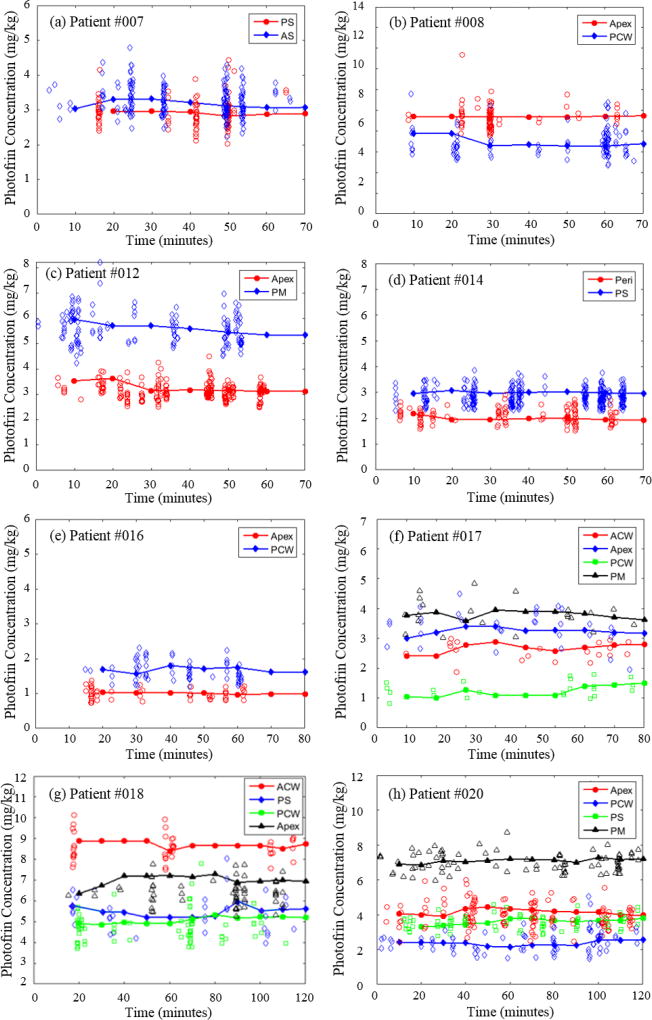
Figure 7 shows the temporal changes of local Photofrin concentrations at 22 different sites in the pleural cavities of 8 patients during the course of PDT treatment. Patient #007 and #020 are the first and the most recent patients for whom we obtained PDT dose measurements, respectively, at the time when this paper is being written. Each data point in figure 7 represents Photofrin concentration obtained from one fluorescence spectrum using the method described above. Data smoothing was performed by taking the average of all the data points every 10 minutes of treatment time.. The smoothed results show no significant photobleaching of Photofrin, in all measurement sites, during the time course of PDT treatment. The maximum (standard) uncertainty of the smoothed Photofrin concentrations for all patients is ± 17.2% (9.5%). The uncertainty arises mainly from 1) low signal-to-noise ratio of measured fluorescence spectra due to the short acquisition time used (300ms), and 2) the variation in treatment light fluence rate due to the movement of the light source during PDT treatment. We increased the acquisition time of the fluorescence measurements up to 2.5 seconds in patient #020 to improve the signal-to-noise ratio of the measured fluorescence spectra and the maximum (standard) uncertainty of the smoothed Photofrin concentrations was reduced to ± 11.5% (7%).
Figure 7.
(a) – (h) Temporal changes of Photofrin concentrations measured from 22 sites in pleural cavity of 8 patients during the PDT treatments. To convert from mg/kg to µM, one can use 1 mg/kg = 1.65 µM.
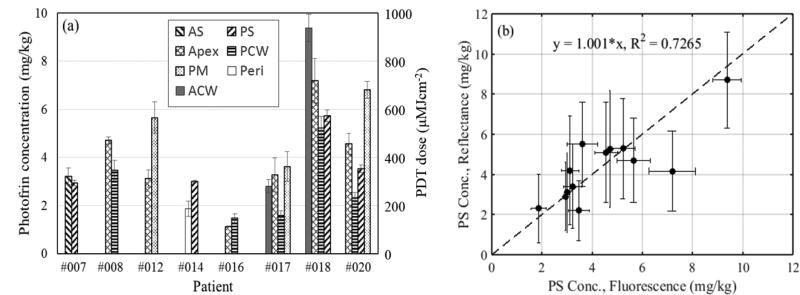
The mean Photofrin concentrations measured from all 22 sites are presented in figure 8(a). The error bars represent the uncertainties of the smoothed Photofrin concentrations assuming no photobleaching of Photofrin during the time course of the PDT treatment. As expected, we see large spatial heterogeneities of Photofrin due to the difference in pharmacokinetics within and among patients. With the same administered Photofrin dose of 2 mg/kg, the local sensitizer concentrations can be different by 2.9 times within the same patient (#020) and 8.3 times between patients (#016 and #018). The range of the measured local Photofrin concentration is 1.13 to 9.38 mg/kg; the lowest was measured from the apex location in the pleural cavity of patient #016 while the highest was recorded from the anterior chest wall location in patient #018. The mean and median of the local Photofrin concentrations measured from all sites are 3.94 ± 2.01 mg/kg and 3.37 ± 2.01 mg/kg, respectively. To convert the unit of Photofrin concentration from mg/kg to µM, one can use the molecular weight of Photofrin (605.691gmol−1)* and assume the average density of human body of 1 kg/L. Thus 1 mg/kg = 1×10−3 g / 605.691 gmol−1 / 1 L = 1.65×10−6 molL−1 = 1.65 µM.
Figure 8.
(a) Mean Photofrin concentrations and PDT dose delivered to 22 different sites in the pleural cavities of 8 patients; (b) Comparison of Photofrin concentration determined by reflectance and fluorescence measurements. To convert from mg/kg to µM, one can use 1 mg/kg = 1.65 µM.
Figure 8(b) shows the comparison of Photofrin concentrations obtained from fluorescence measurements and broadband reflectance measurements. Assuming no photobleaching of Photofrin during PDT treatment as suggested by our fluorescence measurements, reflectance measurements from 9 out of the total 22 sites, which show large discrepancy (~2.5 times difference) in Photofrin concentration before and after PDT treatments, are excluded from the comparison. Linear fit of y=1.001× (shown as dashed line) with a goodness of fit of R2=0.7265 shows reasonable agreement between the data, validating the in vivo fluorescence measurements method using PDT dose dosimetry system.
PDT doses delivered to each measurement site are calculated by taking the product of the local Photofrin concentration and delivered light dose. As each treatment site received the same light dose of 60 J cm−2, the delivered PDT dose can be shown on the same plot in figure 8(a) with a secondary axis on the right. Since the total light fluence is the same in all sites, the marked variations in effective PDT doses observed were caused solely by intra- and inter-subject heterogeneities in photosensitizer uptake. Large intra- and inter-patient variations in the measured Photofrin concentrations of various tumors and normal tissues have been reported in earlier studies (Busch et. al, 2004; Hahn et. al., 2006). The mean and median PDT dose of all sites in this study are 390.1 ± 198.9 µMJ/cm2 and 333.6 ± 198.9 µMJ/cm2, respectively. Tissue optical properties, total light fluence, the mean and standard deviation of smoothed Photofrin concentration and the PDT dose delivered at tissue surface of each pleural site for all patients are summarized in Table 2. Light fluence rate and PDT doses delivered at 3 mm below tissue surface, calculated using the analytical equation reported earlier (Ong and Zhu, 2016) based on the measured tissue optical properties and mean Photofrin concentrations, are included for comparison.
Table 2.
Tissue optical properties, correction factors, mean Photofrin concentration, light fluence at 3mm below surface, PDT dose at surface and 3 mm below surface for 8 patients. The light fluence on surface is the same at 60 J/cm2 for all patients.
| Patient | Site | Optical Properties |
CFp | CFa† | Mean Photofrin Concentration (mg/kg) |
Light fluence at 3mm (J/cm2) |
PDT dose at surface (µMJ/cm2) |
PDT dose at 3mm (µMJ/cm2) |
|
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| μa (cm−1) |
μs’ (cm−1) |
||||||||
|
| |||||||||
| #007 | AS | 0.24 | 11.6 | 0.89 | 0.87 | 3.22 ± 0.35 | 73.7 | 318.8 ± 34.7 | 391.8 ± 42.6 |
| PS | 0.37 | 16.6 | 0.89 | 0.68 | 2.94 ± 0.12 | 48.1 | 291.1 ± 11.9 | 233.5 ± 9.5 | |
|
| |||||||||
| #008 | Apex | 0.32 | 7.7 | 1.39 | 1.47 | 4.71± 0.15 | 77.4 | 466.3 ± 14.9 | 601.7 ± 19.2 |
| PCW | 0.16 | 9.1 | 0.84 | 0.93 | 3.47 ± 0.42 | 94.0 | 343.5 ± 41.6 | 538.2 ± 65.1 | |
|
| |||||||||
| #012 | Apex | 0.12 | 14.7 | 0.61 | 0.51 | 3.12 ± 0.35 | 87.4 | 308.9 ± 34.7 | 449.8 ± 50.5 |
| PM | 0.24 | 13.1 | 0.83 | 0.76 | 5.65 ± 0.67 | 69.7 | 559.4 ± 66.3 | 650.1 ± 77.1 | |
|
| |||||||||
| #014 | Peri | 0.09 | 12.5 | 0.59 | 0.56 | 1.87 ± 0.31 | 100.7 | 185.1 ± 30.7 | 310.6 ± 51.5 |
| PS | 0.15 | 13.4 | 0.68 | 0.61 | 3.01 ± 0.05 | 83.7 | 298.0 ± 5.0 | 415.7 ± 6.9 | |
|
| |||||||||
| #016 | Apex | 0.08 | 7.1 | 0.71 | 0.83 | 1.13 ± 0.02 | 119.1 | 111.9 ± 2.0 | 221.9 ± 3.9 |
| PCW | 0.09 | 11.9 | 0.60 | 0.59 | 1.47 ± 0.20 | 102.1 | 145.5 ± 19.8 | 247.8 ± 33.7 | |
|
| |||||||||
| #017 | ACW | 0.33 | 12.4 | 1.00 | 0.95 | 2.80 ± 0.27 | 61.2 | 277.2 ± 26.7 | 282.9 ± 27.3 |
| Apex | 0.42 | 9 | 1.46 | 1.52 | 3.27 ± 0.71 | 63.5 | 323.7 ± 70.3 | 342.7 ± 74.4 | |
| PCW | 0.26 | 8.8 | 1.11 | 1.18 | 1.58 ± 0.21 | 80.1 | 156.4 ± 20.8 | 208.7 ± 27.7 | |
| PM | 0.24 | 10.9 | 0.92 | 0.93 | 3.62 ± 0.61 | 75.8 | 358.4 ± 60.4 | 452.6 ± 76.3 | |
|
| |||||||||
| #018 | ACW | 0.72 | 5.9 | 3.13 | 3.13 | 9.38 ± 0.57 | 57.4 | 928.6 ± 56.4 | 887.7 ± 53.9 |
| Apex | 0.44 | 5.8 | 2.18 | 2.21 | 7.19 ± 0.92 | 74.9 | 711.8 ± 91.1 | 888.6±113.7 | |
| PCW | 0.7 | 7.4 | 2.48 | 2.61 | 5.23 ± 0.47 | 52.1 | 517.8 ± 46.5 | 449.7 ± 40.4 | |
| PS | 0.44 | 5.9 | 2.15 | 2.18 | 5.73 ± 0.24 | 74.4 | 567.3 ± 23.8 | 703.8 ± 29.5 | |
|
| |||||||||
| #020 | Apex | 0.27 | 9 | 1.12 | 1.18 | 4.56 ± 0.45 | 78.1 | 451.4 ± 44.6 | 587.9 ± 58.0 |
| PCW | 0.32 | 10.9 | 1.08 | 1.07 | 2.32 ± 0.23 | 66.4 | 229.7 ± 22.8 | 254.3 ± 25.2 | |
| PS | 0.57 | 9 | 1.79 | 1.88 | 3.54 ± 0.16 | 53.3 | 350.6 ± 15.8 | 311.1 ± 14.1 | |
| PM | 0.33 | 8.5 | 1.31 | 1.38 | 6.81 ± 0.35 | 73.4 | 674.2 ± 34.7 | 824.3 ± 42.4 | |
CFa = ((P1+P2 μs’)/μs’)exp((S1+S2 μs’)μeff) (Sharikova et al., 2013; Kim et al., 2016a; Qiu et al., 2016; Penjweini et al., 2016; Kim et al., 2017b); where P1 = 3.881; P2 = 0.0103; S1 = 0.5043; S2 = −0.01622.
The current dosimetry system is equipped with four PDT dose channels that measure both light fluence rate and photosensitizer fluorescence using the same isotropic detectors. As the isotropic detectors are sutured onto the patients’ tissues during PDT treatment, they allow for continuous monitoring of light fluence and photosensitizer concentration from the same locations throughout the PDT treatment. This is advantageous compared to broadband reflectance spectroscopy in which reflectance spectra can only be taken before and after PDT treatment using our current contact probe. Our fluorescence measurements show that Photofrin concentrations are mostly unchanged during PDT treatment, but high discrepancies in Photofrin concentrations before and after PDT treatment can be observed using reflectance spectroscopy. These variations in Photofrin concentration can arise due to spatial heterogeneity of tissue and the difference in the exact locations of the two measurements. Continuous measurements of reflectance spectra during PDT treatment are not feasible in the current clinical setting. Therefore, the PDT dose dosimetry system provides a better means to monitor temporal changes in photosensitizer concentration during treatment.
Improvements to the PDT dose dosimetry system will further reduce the uncertainty in the measured Photofrin concentration. This uncertainty currently limits our confidence in measuring photobleaching, as any photobleaching in the order of uncertainty cannot be resolved. The normalization method that we employed in data analysis, in which the Photofrin SVD amplitude is divided by the laser SVD amplitude, is insufficient to completely eliminate the effect of varying excitation light fluence rate from measurements. Replacing the current long-pass filters with ones that permit a fraction of the treatment light to be collected by fluorescence spectrometer could provide a direct means to normalize the measured fluorescence to the fluctuating intensity at the excitation wavelength. In addition, we are also working on improving the detection limit of the current system by replacing the spectrometers with more sensitive ones. Work is in progress to expand the system to 16 channels capable of measuring both light fluence rate and fluorescence simultaneously and to develop real-time data analysis capability, which will incorporate input of tissue optical properties from diffuse reflectance measurement, to calculate delivered PDT dose in real time. PDT dose has been proven to be a better predictor of outcome than PDT light dose or administered photosensitizer dose alone in our preclinical studies (Qiu et al., 2016). It takes into account both the patient-to-patient and site-to-site variations in tumor uptake of photosensitizer and the variation in optical properties of different tissues, and could potentially serve as a useful predictor of pleural PDT treatment outcome. In the future, PDT dose dosimetry can be used to guide and stop treatment when the desired PDT dose, rather than desired light dose, has been reached.
4. Conclusion
A 4-channel PDT dose dosimeter was developed and used during Photofrin-mediated pleural PDT. Light dosimetry and photosensitizer fluorescence were acquired simultaneously using the same isotropic detectors sutured on pleural cavity wall during PDT treatment. The Photofrin concentration could be determined from fluorescence data using optical properties correction function. The minimum detectable Photofrin concentration of the instrument was determined to be 0.5 mg/kg. Our results showed that the local concentration of Photofrin in tissues did not change significantly during the treatment time. However, large variations in the mean Photofrin concentration are observed within and among patients. With the same administered Photofrin dose and light dose, PDT doses can be different by 2.9 times in intra-patient comparisons and 8.3 times in inter-patient comparisons. PDT dose delivered during PDT treatment could serve as a useful predictor of treatment outcome as it takes into account both the patient-to-patient and site-to-site variations in specific tumor uptake of photosensitizer and the variation in optical properties of different tissues. Also, this suggests that care must be taken by the physician to create a homogenous PDT dose at all areas of the disease in order to achieve the desired treatment goal.
Acknowledgments
The authors would like to thank all the PDT group members at the hospital of the University of Pennsylvania, Arjun G. Yodh, Carmen Rodriguez, Rozhin Penjweini, Arash Darafsheh, Theresa M. Busch, Charles B Simone II, Jess Appleton, Sally McNulty, Joann Miller, and Min Yuan. This work was supported by NIH grants R01 CA154562 and P01 CA87971 and by the Department of Radiation Oncology.
Footnotes
ClinicalTrials.gov [Internet]. Bethesda (MD): National Library of Medicine (US). Identifier NCT02153229, MPM PDT Phase II Trial; 2014 May 28; Available from: https://clinicaltrials.gov/ct2/show/NCT02153229
National Center for Biotechnology Information. PubChem Compound Database; CID=3086257; 2017 June 19; Available from: https://pubchem.ncbi.nlm.nih.gov/compound/3086257
References
- Attix FH. Introduction to Radiological Physics and Radiation Dosimetry. Wiley-VCH Verlag GmbH. 1986:38–60. [Google Scholar]
- Busch TM, Hahn SM, Wileyto EP, Koch CJ, Fraker DL, Zhang P, Putt ME, Gleason K, Shin DB, Emanuele MJ, Jenkins K, Glatstein E, Evans SM. Hypoxia and photofrin uptake in the intraperitoneal carcinomatosis and sarcomatosis of photodynamic therapy patients. Clin. Cancer Res. 2004;10:4630–38. doi: 10.1158/1078-0432.CCR-04-0359. [DOI] [PubMed] [Google Scholar]
- Diamond KR, Patterson MS, Farrell TJ. Quantification of fluorophore concentration in tissue-simulating media by fluorescence measurements with a single optical fiber. Appl. Opt. 2003;42:2436–42. doi: 10.1364/ao.42.002436. [DOI] [PubMed] [Google Scholar]
- Finlay JC, Conover DL, Hull EL, Foster TH. Porphyrin bleaching and PDT-induced spectral changes are irradiance dependent in ALA-sensitized normal rat skin in vivo. J. Photochem. Photobiol. 2001;73:54–63. doi: 10.1562/0031-8655(2001)073<0054:pbapis>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Finlay JC, Foster TH. Recovery of hemoglobin oxygen saturation and intrinsic fluorescence with a forward-adjoint model. Appl. Opt. 2005;44:1917–33. doi: 10.1364/ao.44.001917. [DOI] [PubMed] [Google Scholar]
- Finlay JC, Zhu TC, Dimofte A, Friedberg JS, Hahn SM. Diffuse reflectance spectra measured in vivo in human tissues during Photofrin-mediated pleural photodynamic therapy. Proc. SPIE. 2006a;6139:61390O. doi: 10.1117/12.647016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finlay JC, Zhu TC, Dimofte A, Stripp D, Malkowicz SB, Busch TM, Hahn SM. Interstitial Fluorescence Spectroscopy in the Human Prostate During Motexafin Lutetium–Mediated Photodynamic Therapy. J. Photochem. Photobiol. 2006b;82:1270–8. doi: 10.1562/2005-10-04-RA-711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedberg JS, Simone CB, Culligan MJ, Barsky AR, Doucette A, McNulty S, Hahn SM, Alley E, Sterman DH, Glatstein E, Cengel KA. Extended pleurectomy-decortication-based treatment for advanced stage epithelial mesothelioma yielding a median survival of nearly three years. Ann. Thorac. Surg. 2017;103:912–919. doi: 10.1016/j.athoracsur.2016.08.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner CM, Jacques SL, Welch AJ. Fluorescence spectroscopy of tissue: recovery of intrinsic fluorescence from measured fluorescence. Appl. Opt. 1996;35:1780–92. doi: 10.1364/AO.35.001780. [DOI] [PubMed] [Google Scholar]
- Gross SA, Wolfsen HC. The role of photodynamic therapy in the esophagus. Gastrointest. Endosc. Clin. N Am. 2010;20:35–53. vi. doi: 10.1016/j.giec.2009.07.008. [DOI] [PubMed] [Google Scholar]
- Hahn SM, Putt ME, Metz J, Shin DB, Rickter E, Menon C, Smith D, Glatstein E, Fraker DL, Busch TM. Photofrin uptake in the tumor and normal tissue of patients receiving intraperitoneal photodynamic therapy. Clin. Cancer Res. 2006;12:5464–70. doi: 10.1158/1078-0432.CCR-06-0953. [DOI] [PubMed] [Google Scholar]
- Huang Z. A review of progress in clinical photodynamic therapy. Techno. Cancer Res. Treat. 2005;4:283–93. doi: 10.1177/153303460500400308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvi MT, Patterson MS, Wilson BC. Insights into photodynamic therapy dosimetry: simultaneous singlet oxygen luminescence and photosensitizer photobleaching measurements. Biophys. J. 2012;102:661–71. doi: 10.1016/j.bpj.2011.12.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MM, Ashwini AG, Alexander G, Zhu TC. On the in vivo photochemical rate parameters for PDT reactive oxygen species modeling. Phys.Med. Biol. 2017a;62:R1–R48. doi: 10.1088/1361-6560/62/5/R1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MM, Darafsheh A, Ahmad M, Finlay JC, Zhu TC. PDT Dose Dosimeter for Pleural Photodynamic Therapy. Proc. SPIE. 2016a;9694:96940Y. doi: 10.1117/12.2213401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MM, Penjweini R, Liang X, Zhu TC. Explicit macroscopic singlet oxygen modeling for benzoporphyrin derivative monoacid ring A (BPD)-mediated photodynamic therapy. J. Photochem. Photobiol. B: Biol. 2016b;164:314–22. doi: 10.1016/j.jphotobiol.2016.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MM, Penjweini R, Zhu TC. Evaluation of singlet oxygen explicit dosimetry for predicting treatment outcomes of benzoporphyrin derivative monoacid ring A-mediated photodynamic therapy. J. Biomed. Opt. 2017b;22:028002. doi: 10.1117/1.JBO.22.2.028002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambson K, Liang X, Sharikova AV, Zhu TC, Finlay JC. A theorectical and experimental examination of fluorescence in enclosed cavities. Proc. SPIE. 2013;8568 doi: 10.1117/12.2004314. 85680B-B-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middelburg TA, Hoy CL, Neumann HAM, Amelink A, Robinson DJ. Correction for tissue optical properties enables quantitative skin fluorescence measurements using multi-diameter single fiber reflectance spectroscopy. J. Dermatol. Sci. 2015;79:64–73. doi: 10.1016/j.jdermsci.2015.03.017. [DOI] [PubMed] [Google Scholar]
- Muller MG, Georgakoudi I, Zhang Q, Wu J, Feld MS. Intrinsic fluorescence spectroscopy in turbid media: disentangling effects of scattering and absorption. Appl. Opt. 2001;40:4633–46. doi: 10.1364/ao.40.004633. [DOI] [PubMed] [Google Scholar]
- Ong YH, Kim MM, Finlay JC, Dimofte A, Cengel KA, Zhu TC. Four-channel PDT dose dosimetry for pleural photodynamic therapy. Proc. SPIE. 2017;10047:1004717–1. [Google Scholar]
- Ong YH, Zhu TC. Analytic function for predicting light fluence rate of circular fields on a semi-infinite turbid medium. Opt. Exp. 2016;24:26261–26281. doi: 10.1364/OE.24.026261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penjweini R, Kim MM, Liu B, Zhu TC. Evaluation of the 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide (HPPH) mediated photodynamic therapy by macroscopic singlet oxygen modeling. J. Biophoton. 2016;9:1344–54. doi: 10.1002/jbio.201600121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prahl SA, Keijzer M, Jacques SL, Welch AJ. A Monte Carlo model of light propagation in tissue. Proc. SPIE. 1989;IS5:102–11. [Google Scholar]
- Qiu H, Kim MM, Penjweini R, Finlay JC, Busch TM, Wang T, Guo W, Cengel KA, Simone CB, Glatstein E, Zhu TC. A Comparison of Dose Metrics to Predict Local Tumor Control for Photofrin-mediated Photodynamic Therapy. J. Photochem. Photobiol. 2017 doi: 10.1111/php.12719. Published online on Feb 22 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu H, Kim MM, Penjweini R, Zhu TC. Macroscopic singlet oxygen modeling for dosimetry of Photofrin-mediated photodynamic therapy: an in-vivo study. J. Biomed. Opt. 2016;21:88002. doi: 10.1117/1.JBO.21.8.088002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandell JL, Zhu TC. A review of in-vivo optical properties of human tissues and its impact on PDT. J. Biophoton. 2011;4:773–87. doi: 10.1002/jbio.201100062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharikova AV, Finlay JC, Liang X, Zhu TC. PDT dose dosimetry for pleural photodynamic therapy. Proc. SPIE. 2013;8568:856817. doi: 10.1117/12.2005198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simone CB, Cengel KA. Photodynamic Therapy for Lung Cancer and Malignant Pleural Mesothelioma. Semin. Oncol. 2014;41:820–30. doi: 10.1053/j.seminoncol.2014.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solonenko M, Cheung R, Busch TM, Kachur A, Griffin GM, Vulcan T, Zhu TC, Wang HW, Hahn SM, Yodh AG. In vivo reflectance measurement of optical properties, blood oxygenation and motexafin lutetium uptake in canine large bowels, kidneys and prostates. Phys. Med. Biol. 2002;47:857–73. [PubMed] [Google Scholar]
- Triesscheijn M, Baas P, Schellens JHM, Stewart FA. Photodynamic Therapy in Oncology. The Oncologist. 2006;11:1034–44. doi: 10.1634/theoncologist.11-9-1034. [DOI] [PubMed] [Google Scholar]
- Wang HW, Zhu TC, Putt ME, Solonenko M, Metz J, Dimofte A, Miles J, Fraker DL, Glatstein E, Hahn SM, Yodh AG. Broadband reflectance measurements of light penetration, blood oxygenation, hemoglobin concentration, and drug concentration in human intraperitoneal tissues before and after photodynamic therapy. J. Biomed. Opt. 2005;10:14004. doi: 10.1117/1.1854679. [DOI] [PubMed] [Google Scholar]
- Weersink RA, Bogaards A, Gertner M, Davidson SR, Zhang K, Netchev G, Trachtenberg J, Wilson BC. Techniques for delivery and monitoring of TOOKAD (WST09)-mediated photodynamic therapy of the prostate: clinical experience and practicalities. J. Photochem. Photobiol. B: Biol. 2005;79:211–22. doi: 10.1016/j.jphotobiol.2005.01.008. [DOI] [PubMed] [Google Scholar]
- Wilson BC, Patterson MS. The physics, biophysics and technology of photodynamic therapy. Phys. Med. Biol. 2008;53:R61–R109. doi: 10.1088/0031-9155/53/9/R01. [DOI] [PubMed] [Google Scholar]
- Zhou X, Pogue BW, Chen B, Demidenko E, Joshi R, Hoopes J, Hasan T. Pretreatment photosensitizer dosimetry reduces variation in tumor response. Int. J. Rad. Oncol. Biol. Phys. 2006;64:1211–20. doi: 10.1016/j.ijrobp.2005.11.019. [DOI] [PubMed] [Google Scholar]
- Zhu TC, Dimofte A, Hahn SM, Lustig RA. Light Dosimetry at Tissue Surfaces for Small Circular Fields. Proc. SPIE. 2003;4952:56–67. doi: 10.1117/12.474144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu TC, Finlay JC. Prostate PDT dosimetry. Photodiag. Photodyn. Ther. 2006;3:234–46. doi: 10.1016/j.pdpdt.2006.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu TC, Finlay JC. The role of photodynamic therapy (PDT) physics. Med. Phys. 2008;35:3127–36. doi: 10.1118/1.2937440. [DOI] [PMC free article] [PubMed] [Google Scholar]