DNP-Enhanced MAS NMR: A Tool to Snapshot Conformational Ensembles of α-Synuclein in Different States

Abstract

Intrinsically disordered proteins dynamically sample a wide conformational space and therefore do not adopt a stable and defined three-dimensional conformation. The structural heterogeneity is related to their proper functioning in physiological processes. Knowledge of the conformational ensemble is crucial for a complete comprehension of this kind of proteins. We here present an approach that utilizes dynamic nuclear polarization-enhanced solid-state NMR spectroscopy of sparsely isotope-labeled proteins in frozen solution to take snapshots of the complete structural ensembles by exploiting the inhomogeneously broadened line-shapes. We investigated the intrinsically disordered protein α-synuclein (α-syn), which plays a key role in the etiology of Parkinson’s disease, in three different physiologically relevant states. For the free monomer in frozen solution we could see that the so-called “random coil conformation” consists of α-helical and β-sheet-like conformations, and that secondary chemical shifts of neighboring amino acids tend to be correlated, indicative of frequent formation of secondary structure elements. Based on these results, we could estimate the number of disordered regions in fibrillar α-syn as well as in α-syn bound to membranes in different protein-to-lipid ratios. Our approach thus provides quantitative information on the propensity to sample transient secondary structures in different functional states. Molecular dynamics simulations rationalize the results.

Introduction

Intrinsically disordered proteins (IDPs) are characterized by their high degree of conformational freedom, which is due to a rather flat free energy landscape, comprising low energy barriers and many local minima. These allow IDPs to fluctuate rapidly over an ensemble of conformations in solution instead of adopting a well-defined three-dimensional structure (1, 2, 3, 4, 5). The structural heterogeneity of IDPs is closely related to their biological functions, e.g., in signaling and regulation (6). Essential biological processes rely on IDPs and elucidating the link between composition of the conformational ensemble and function is required for a complete comprehension of IDPs.

For studying conformational ensembles of IDPs, both experimental and computational methods have been developed in recent years. On the experimental side, far-ultraviolet circular dichroism is used for the determination of secondary structure content of proteins in solution, small-angle x-ray scattering (SAXS) can provide overall dimensions and shape of the molecules, and fluorescence resonance energy transfer and electron paramagnetic resonance spectroscopy can provide quantitative distance distributions (7, 8, 9, 10, 11). On the theoretical side, a number of methods have evolved in recent years to overcome two of the main problems of molecular dynamics (MD) simulations of IDPs: the lack of conformational sampling due to hardware restraints, and the limited performance of available force-field parameters for representation of the protein ensemble (12, 13, 14).

A well-established experimental method for studying structure, dynamics, and function of IDPs is solution NMR spectroscopy. NMR chemical shifts and residual dipolar couplings are sensitive to conformational sampling of IDPs. Conformational ensembles of IDPs were previously studied by generating large arrays of molecules by Monte Carlo-based methods and subsequently selecting conformers in agreement with predicted NMR parameters (15, 16, 17, 18, 19, 20, 21, 22), or by MD simulations using experimental data as restraints (23). Furthermore, longitudinal relaxation rate dispersion profiles of protein protons at low magnetic fields give information on long-range correlated motions in IDPs (24).

Studying the proportion of secondary structure motifs of an IDP is impeded by conformational averaging on the timescales of many biophysical methods, and conformational distributions in many cases can be detected only indirectly. We therefore use an approach that allows simultaneous observation of the entire conformational ensemble and quantification of the amount of transient secondary structure sampled. For this aim, the sample is frozen in solution, and hyperpolarized solid-state NMR (ssNMR) experiments are performed at cryogenic temperatures as low as 100 K (25, 26, 27, 28, 29). In such a frozen solution, the molecules are statistically trapped in different conformations and consequently, a continuum of chemical shifts is observed for each nucleus. The obtained spectrum reflects the entire conformational ensemble covered, representing a snapshot of its momentary composition (27). Changes in composition of the structural ensemble due to different functional states of the IDP can be tracked by this method, which is applied here on the IDP α-synuclein (α-syn).

The 140 amino-acid-residue protein α-syn possesses a remarkable conformational flexibility. α-Syn is able to adjust its conformation to the environmental conditions and is thus called a “protein-chameleon” (30). Its natural function is supposed to involve membrane and lipid vesicle binding, driven by the properties of lipids (mainly headgroups’ charge density), and inducing α-helical structural features (31). This propensity is thought to play a role in SNARE-like vesicle fusion mechanisms (32, 33, 34). Membrane binding of α-syn critically depends on membrane properties, such as curvature and charge, as well as molecular crowding. Different membrane affinities have been determined for different regions of the protein (35).

Moreover, it is well established that α-syn can adopt β-strand conformations along the energetically favorable pathway of protein aggregation and fibril formation (36). At least five different polymorphic forms have been observed for α-syn amyloid fibrils (37, 38, 39, 40). The conformational characteristics of the heterogeneously structured α-syn are not yet completely understood. Aggregation of α-syn into amyloid fibrils is linked to a number of neurodegenerative diseases, known as synucleopathies, of which the most widely known is Parkinson’s disease (41). As the conformational ensembles of IDPs critically report on their propensities to form transient secondary structural elements and thus may predict early aggregation and membrane binding events, monomeric α-syn has been extensively studied (42). The intrinsically disordered monomer was found to be stabilized by long-range intramolecular contacts between the C terminus and the hydrophobic center region of the protein (43), and β-strand propensities in monomeric α-syn were found to correlate well with β-sheet regions in mature fibrils (44).

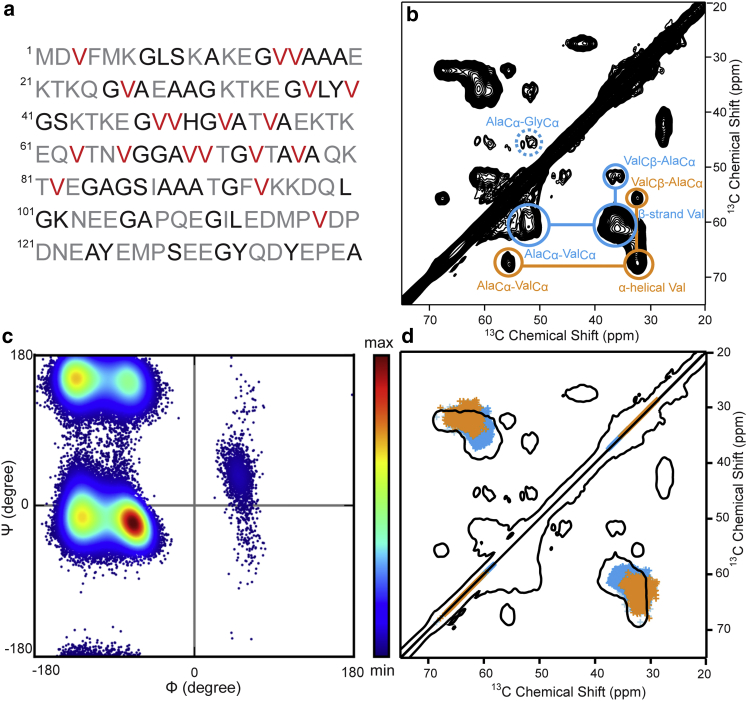
In this work, we studied different conformational ensembles of the IDP α-syn in frozen solution. The study was performed on recombinantly expressed α-syn in its monomeric, fibrillar, and membrane-associated forms. Additionally, we quantified the amount of α-helical secondary structure features in α-syn bound to membranes in different protein-to-lipid ratios. As ssNMR spectra of diluted biological samples suffer from low sensitivity, we made use of dynamic nuclear polarization (DNP) for signal enhancement (45, 46, 47, 48). To reduce spectral overlap in the inhomogeneously broadened NMR spectra, α-syn was expressed using the previously described TEASE labeling strategy (Fig. 1 a), simplifying ¹³C-¹³C spectra to valine Cα/Cβ and leucine Cβ/Cγ correlations (49). We used the backbone chemical shifts of the 19 valine residues as a reporter for the conformational ensemble of α-syn. Furthermore, we explored the valine conformational ensemble and chemical shifts from MD simulations with different force fields and solvent models.

Figure 1.

(a) Primary sequence of α-syn indicating the labeling scheme obtained by addition of [2-¹³C]-glucose to the M9 medium: simultaneous ¹³C enrichment of Cα and Cβ is only achieved for valine residues (red); amino acid residues labeled only in Cα position (except for leucine, which is labeled in Cβ and Cγ position) are printed in black. (b) 2D ¹³C-¹³C PDSD DNP-NMR spectrum of specifically ¹³C-labeled α-syn monomers are shown. Intra- and interresidual crosspeaks involving β-strand or α-helical valine residues are highlighted in blue and orange, respectively. (c and d) Conformational sampling and NMR shifts of the valine residue in a representative AGKTKEGVAGGA peptide using the AMBER99SB^∗-ILDN force field in TIP3P explicit solvent are shown. (c) Ramachandran plot indicating relative probabilities of different secondary structures is shown. (d) NMR spectrum of monomeric α-syn in frozen solution (black) overlaid with chemical shifts of the simulated ensemble is shown. The positions of β-sheet (blue) and right-handed α-helix (orange) regions are also annotated. Further analysis is given in Fig. S4.

Materials and Methods

Recombinant expression and purification of α-syn

α-Syn was expressed recombinantly in Escherichia coli cells from pT7-7, as described previously (50). The labeling strategy, adopted from the TEASE approach (49), was applied by growing cells in M9 minimal medium containing [2-¹³C]-glucose and ¹⁵NH₄Cl as sole carbon and nitrogen sources. The ¹³C labeling of the amino acids Phe, Gln, Glu, Pro, Asn, Asp, Met, Thr, Lys, and Ile was suppressed by supplementing sufficient quantities (150 μg/mL of each) of these unlabeled amino acids to the expression media. The cells were harvested 4 h after inducing with IPTG to a final concentration of 1 mM. Harvesting was followed by cell lysis performed by sonication in lysis buffer (20 mM Tris-HCl, 1 mM EDTA, pH 8.0). Purification of α-syn started with ammonium sulfate precipitation at 4°C for 15 min under nutation, with centrifugation for 30 min at 15,000 × g at 4°C to pellet precipitated α-syn. Further purification was achieved by anion exchange chromatography on a 5 mL HiTrap Q FF column (GE Healthcare, Little Chalfont, UK) where α-syn eluted at ∼300 mM NaCl in 50 mM Tris-HCl pH 8. Finally, it was purified by size-exclusion chromatography (SEC) on a HiLoad 16/60 Superdex 75 column (GE Healthcare), equilibrated in 20 mM sodium phosphate, 50 mM NaCl, pH 7.4.

Membrane scaffold protein expression and purification

As reported in Bayburt et al. (51), E. coli BL21 (DE3) were transformed with MSP1D1 plasmid DNA in vector pET28a. Cells were grown in LB medium, induced by 1 mM IPTG at an optical density of 0.7 and incubated 5–6 h at 37°C, then pelleted down. Cells were resuspended in 50 mM Tris-HCl pH 8, 500 mM NaCl (buffer B) supplemented with 6 M Gdn-HCl and EDTA-free Complete protease inhibitors (Macherey-Nagel, Düren, Germany) lysed by sonication (Sonopuls MS72 probe; Bandelin, Berlin, Germany), centrifuged at 17,000 × g for 1 h (Cat. No. J2-21 rotor JA-20.1; Beckman Coulter, Brea, CA) and incubated 1 h with previously equilibrated 2.5 mL Ni-NTA agarose resin/3L culture (Macherey-Nagel). The column was washed subsequently with 4 CV buffer B; 4 CV buffer B supplemented with 1% Triton X-100; 4 CV buffer B + 60 mM Na-cholate; and 4 CV buffer B, 4 CV buffer B + 20 mM imidazole. Four fractions of 1 CV were eluted with 250 mM imidazole. The whole process was kept at 4°C in a cold room. The elution fractions were pooled and dialyzed against 100-fold 200 mM Tris-HCl pH 7.5, 100 mM NaCl. N-terminal His-tag was cleaved using TEV protease incubated overnight at 4°C. ΔHis MSP was separated from MSP by immobilized metal ion affinity chromatography and concentrated to the desired molarity using a Vivaspin centrifugal device (Vivaproducts, Littleton, MA) of 10 kDa MWCO.

Nanodisc assembly

Nanodiscs (NDs) were assembled according to established protocols (52, 53). In short, lipid chloroform stocks (Avanti Polar Lipids, Alabaster, AL) were dried under nitrogen flow to obtain a lipid film and stored under vacuum overnight. ΔHis MSP1D1 and the appropriate amount of 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) solubilized in 60 mM Na-cholate were mixed together in 20 mM Tris-HCl pH 7.5, 100 mM NaCl, 5 mM EDTA. The scaffold-to-lipids molar ratio was calculated from geometrical considerations. A quantity of 20% w/v of previously washed (methanol, water, buffer twice) Biobeads SM-2 (BioRad, Hercules, CA) was added and the mixture incubated at room temperature overnight. The Biobeads were removed by centrifugation and once again 20% w/v was added for an additional 4–5 h. Finally, they were purified by SEC on a HiLoad 16/600 Superdex 200 pg column (GE Healthcare) equilibrated with 20 mM sodium phosphate pH 7.4, 50 mM NaCl using an Äkta pure device (GE Healthcare) run at 1 mL/min. The quality of ND preparation was evaluated by the SEC chromatogram as well as by DLS (Nicomp system; Particle Sizing Systems, Port Richey, FL). NDs were concentrated to the desired molarity using a Vivaspin centrifugal device of 10 kDa MWCO.

DNP experiments

DNP experiments were conducted using a wide-bore Avance 600 MHz spectrometer (Bruker, Billerica, MA) connected to a 395-GHz gyrotron as a source of continuous microwaves. The samples were suspended in d₈-glycerol/D₂O/H₂O solutions (60:30:10 volume ratio) and 2.5 mM AMUPol (54) was added as a radical source. The samples were filled into 3.2-mm sapphire rotors and experiments were performed at a temperature of 100 K. All experiments were recorded using a recycle delay of 5 s. Two-dimensional (2D) ¹³C-¹³C proton-driven spin diffusion (PDSD) spectra with 1 s mixing time were recorded using 300 t₁ increments with 16 or 48 scans (16 scans for monomeric and fibrillated form, 48 scans for membrane-associated α-syn). All PDSD spectra were recorded at a magic angle spinning frequency of 9 kHz during a total experimental time of 8 h for the monomeric and fibrillar form and 24 h for α-syn in contact with a membrane. 2D ¹³C-¹³C double quantum/single quantum (DQ/SQ) SPC5 spectra were recorded at a magic angle spinning frequency of 8.2 kHz and with 64 or 128 scans (64 scans for monomeric and fibrillated form, 128 scans for all the α-syn in contact with membrane samples). The number of t₁ increments was 86 for the monomeric form and 128 for the others. The maximum evolution time was set to 1.3 ms for all samples. Total experimental times were 8, 11, and 24 h for monomeric, fibrillar, and membrane-bound α-syn, respectively. DNP enhancement factors of ∼32 were obtained for the protein signals in all samples (Fig. S1).

¹H decoupling using SPINAL-64 with a decoupling field of 104 kHz was employed during evolution and detection periods. All NMR spectra were processed with the software TopSpin 3.2 (Bruker).

To integrate the crosspeaks in DQ/SQ NMR spectra, one-dimensional projections from the respective regions were summed up. For the monomeric, fibrillary, and membrane-bound forms, the regions in between 85–103, 86–101, and 86–107 ppm on the double-quantum axis were summed up, respectively. The respective region is shown in Fig. S2). The program DMfit (dmfit2015_vs32) (55) was used for deconvolution of overlapping peaks with a Gaussian distribution. The integrals were calculated from the deconvoluted spectra. The crosspeak intensities were evaluated for both sides of the diagonal.

MD simulations

The replica exchange MD simulations were initialized from a linear conformation of the AGKTKEGVAGGA peptide, protected with N-terminal acetyl and C-terminal N-methyl amide capping groups. We performed simulations with five different force-field/solvent model combinations: 1) AMBER99SB^∗-ILDN (56, 57) with implicit generalized Born solvent (58), 2) AMBER99SB^∗-ILDN with TIP3P explicit solvent (59), 3) AMBER99SB^∗-ILDN with TIP4P-D explicit solvent (60), 4) CHARMM22^∗ (61) with TIP4P-Ew explicit solvent (62), and 5) CHARMM36m (63) with CHARMM-modified TIP3P explicit solvent (64). In addition, we performed an MD simulation of the GGVGG peptide with the CHARMM36m force field and CHARMM-modified TIP3P solvent (Fig. S3).The peptide was capped with an N-terminal acetyl and a C-terminal –NH₂ group.

The explicit solvent simulations were performed using GROMACS v. 4.6.7 (65) patched with PLUMED v. 2.1 (66, 67). The peptide was centered in a cubic box, at least 10 Å away from each edge, and the net charge of the system was neutralized with one chloride ion. The system was simulated under periodic boundary conditions, where particle mesh Ewald (68) was used to treat electrostatic interactions. The short-range nonbonded interactions were calculated using a cutoff of 9 Å. Bond lengths were constrained with the LINCS algorithm (65). The system was minimized with the steepest descent and conjugate gradient minimizers, until the maximal force was smaller than 500 and 100 kJ mol⁻¹ nm⁻¹, respectively. During the 0.1 ns NVT equilibration, the system was heated to 300 K using a v-rescale thermostat (69), and the main-chain atoms were restrained with a force of 1000 kJ mol⁻¹ nm⁻². An additional 0.4-ns restrained NpT equilibration was performed keeping the pressure at 1 bar with a Berendsen barostat (70). The equilibrated system was used as starting structure for the subsequent Hamiltonian replica exchange-MD simulations involving eight replicas at 300 K and 1 bar. As before, a v-rescale thermostat was used together with Parrinello-Rahman barostat (71). An effective temperature range of 300–500 K was achieved by scaling the Hamiltonians of the replicas with λ-values of 1.000, 0.930, 0.864, 0.803, 0.747, 0.694, 0.645, and 0.600. Replica exchanges were attempted every 4 ps during the 1 μs simulation with a 2-fs time step (note: for AMBER99SB^∗-ILDN with TIP4P-D and CHARMM22^∗ only 300 ns/replica were simulated), which led to exchange rates of 30–45%.

The implicit solvent simulation was performed with GROMACS v. 5.1.1, using the Still algorithm and a dielectric constant of 80 (57). Bond lengths were constrained with the LINCS algorithm and infinite cutoffs were used for the calculation of nonbonded interactions. The peptide was minimized with the steepest-descent minimizer (maximum force smaller than 250 kJ mol⁻¹ nm⁻¹). Before the temperature replica exchange-MD simulation was started, each of the 12 replicas was equilibrated for 0.2 ns at the desired temperature ranging from 300 to 525 K. The exact temperatures were 300.0, 315.3, 331.5, 348.5, 366.5, 385.5, 405.5, 426.6, 448.8, 472.2, 496.8, and 522.4 K. The temperature was controlled with a v-rescale thermostat. Each replica was simulated for 2 μs (with a 2-fs time step), and the exchange between the replicas was attempted every 2 ps, which led to exchange rates of ∼58%.

The analysis was performed on the unperturbed replica (λ = 1 or T = 300 K). The α_R-helix region was defined as −100° < ϕ < −30° and −67° < Ψ < −7°, α⁺ as −160° < ϕ < −20° and −120° < Ψ < 50°, whereas the β-sheet was defined as −180° < ϕ < −90° and 50° < Ψ < 180° plus −180° < Ψ < −120°, the Pp^II region covers −90° < ϕ < −20° and 50° < Ψ < 180° or −180° < Ψ < −120°, and the left-handed α-helix region is defined as 30° < ϕ < 100° and 7° < Ψ < 67° (63). Chemical shifts were calculated with SPARTA+ (72) for conformations sampled every 10 ps of the trajectory. Data analysis was performed with the software MATLAB R2015b (The MathWorks, Natick, MA).

Results and Discussion

Conformational ensemble of the IDP elucidated by DNP-enhanced solid-state NMR at cryogenic temperature

α-Syn is found predominantly as a disordered monomer in solution, with a very high conformational plasticity. Solution-state NMR spectra of monomeric α-syn yield random-coil chemical shift values that represent averages over the full conformational ensemble sampled by the protein (31); however, there is no corresponding random-coil conformation area in the Ramachandran plot. Instead, “random-coil state” refers to a rapid sampling of the energetically favored parts of the Ramachandran space that predominantly consists of conformations typically found in left- and right-handed α-helices and β-strand/polyproline-like conformations (Fig. 1 c) (73). Upon freezing the sample, each monomer is trapped in its conformation, and thus, every conformer gives rise to a chemical shift typical for its conformation, and, as a consequence, inhomogeneously broadened lines that contain information on the conformational distribution, are obtained. Fig. 1 b shows a DNP-enhanced 2D ¹³C-¹³C PDSD spectrum (1 s mixing-time) acquired on monomeric α-syn in glycerol/water solution at a temperature of ∼100 K. The 19 valine residues (shown in red in Fig. 1 a) of this IDP contribute to one inhomogeneously broadened Cα-Cβ crosspeak. Due to the labeling approach, no other intraresidual Cα-Cβ crosspeaks are expected. Note that due to the low resolution attained at cryogenic temperatures, discrimination between individual valine residues is not possible and site-specific information cannot be extracted from this spectrum. Instead, the crosspeak shows a characteristic and reproducible 2D shape reporting on the entire conformational ensemble adopted by the 19 valine residues in the α-syn sequence. Two peak maxima can be distinguished, one located in the typical α-helical chemical-shift region, and the other in the typical β-strand chemical-shift region. The static snapshot of the entire ensemble thus contains backbone conformations that are typical of α-helical and β-strand conformations. Note that we report here on the propensity of single residues to adopt conformations similar to those found in α-helices or β-strands and not on the secondary structures. We keep these denominations for the sake of simplicity.

It is visible in Fig. 1 b that the contribution from the β-strand part of the valine Cα-Cβ crosspeak is higher than the α-helical part. These data are in line with conformational propensities of α-syn derived from NMR and SAXS results, in which valine residues roughly sampled 70% β-sheet/polyproline and 30% α-helix conformation (74).

To gain further insight into this conformational sampling of valine residues inside disordered monomeric α-syn, we decided to pursue MD simulations. For the sake of computation time, we focused on the highly conserved KTKEGV motif of the α-syn primary sequence that repeats four times. The dodecapeptide AGKTKEGVAGGA contains a sole valine residue that was used to monitor the conformational changes. We performed long replica exchange MD simulations whose nature allows the molecule to cross energy barriers efficiently, and thus to thoroughly sample the conformational ensemble (75).

A structural ensemble generated with the AMBER99SB^∗-ILDN force field with TIP3P explicit solvent samples the full allowed region of the Ramachandran space (Figs. 1 c and S5). Chemical shifts were predicted from these structures with the help of the simulation program SPARTA+ (72). The comparison of the experimental and simulated chemical shifts shows good mutual agreement (Figs. 1 d and S5); however, simulated chemical shifts do not cover the full area of the experimental crosspeak. This observation may partly be explained either by the fact that 1) the single valine in the model peptide is not representative for all 19 valine residues in the sequence, or 2) that the conformational space sampled by the IDP exceeds that sampled by MD simulations, or 3) by shortcomings of the shift calculations. The coverage of the experimental crosspeaks becomes even smaller when using SHIFTX2 (76) instead of SPARTA+ for the chemical shift calculations. We also checked the influence of the force field and the water model on the sampled Ramachandran space and found that the relative ratio between α-helical and β-sheet-like conformations obtained from MD simulations strongly depends on both the force field and the water model (Fig. S6). The usage of TIP4P-D, a water model that was developed to produce more expanded protein structures for disordered states due to increased water dispersion interactions (60), shifts the equilibrium toward the β-state while not changing the sampled Ramachandran space otherwise, as the comparison between AMBER99SB^∗-ILDN/TIP3P and AMBER99SB^∗-ILDN/TIP4P-D shows (Fig. S6). The two CHARMM force fields disfavor the α-helical state and instead prefer the polyproline II conformation. Moreover, the left-handed helix is sampled at somewhat higher ψ-values than AMBER99SB^∗-ILDN predicts for this helix, which has already been observed in a previous study (77). Not quite unsurprisingly, AMBER99SB^∗-ILDN combined with an implicit solvent encourages intrapeptide hydrogen bonds, causing a gain in population of the α-helix.

We were further interested in probing the propensity of neighboring residues to adopt similar conformations. Notably, interresidual crosspeaks between ¹³C atoms of adjacent amino acids can be observed in PDSD spectra acquired with a long mixing time (here 1 s). In the case of sparsely labeled α-syn, isotope-labeled neighbors of the valine residues are 7 ¹³Cα-labeled alanine and 8 ¹³Cα-labeled glycine residues. Interresidual valine-glycine cross-correlation signals were surprisingly weak, which may originate from the relatively large flexibility of glycine residues reflected by a larger array of backbone conformations and thus also increased heterogeneous line broadening of the glycine Cα resonance peak. On the other hand, two distinct interresidual valine-alanine crosspeaks can be found, located at chemical shifts typical for either α-helical or β-strand conformation for both amino acids. This indicates that neighboring valine and alanine residues have a strong propensity to adopt the same secondary structure in the majority of conformers and that a correlation between local conformations can be observed (Fig. S7). Previous ensemble descriptions of the Tau protein and of α-syn by NMR, SAXS, and molecular ensemble approaches are consistent with such a local structural correlation within a conformer, even though the ensemble selection treats each amino acid independently (74). Also, in our MD simulations, we could observe a weak but nonnegligible correlation between backbone conformations of neighboring amino acids. If the valine residue is found in a β-sheet-like conformation (definition given in the Materials and Methods), the subsequent alanine residue is found in a β-sheet-like conformation with a likelihood of 32%, whereas this likelihood is reduced to 24% when the preceding valine residue is in an α-helical conformation. Likewise, the alanine residue adopts an α-helical conformation with a likelihood of 24% if the preceding valine residue is in α-helical conformation, and only 11% if the preceding valine is in β-sheet conformation. Transient secondary structure elements have been observed and predicted in other IDPs as well (78, 79, 80).

Visualizing the conformational ensemble of α-syn in different states

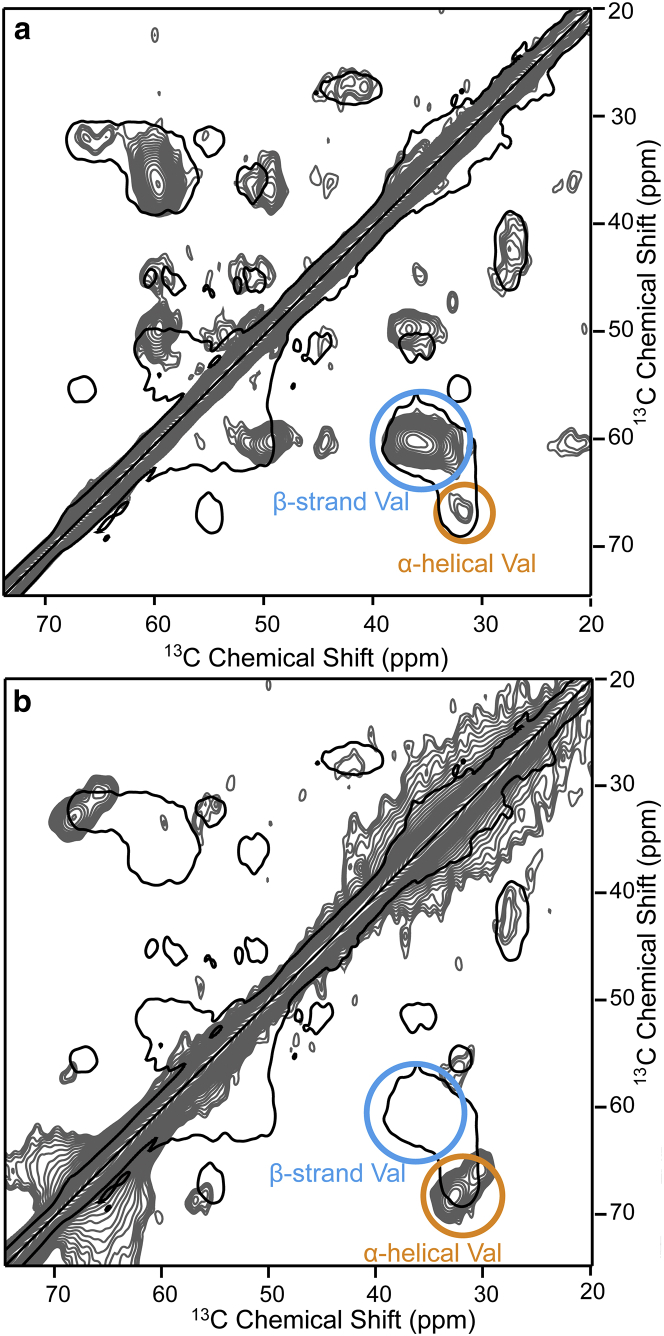
α-Syn is able to spontaneously aggregate into amyloid fibrils, a species rich in β-sheet content (81). Misfolded and aggregated α-syn plays an important role in the neurodegenerative Parkinson’s disease. We studied fibrillar α-syn under the same conditions as the monomeric α-syn to observe the conformational change due to fibrillation. As expected, the valine chemical shifts were shifted strongly toward the region typical of β-sheet conformation after fibrillation (Fig. 2 a). Nevertheless, a fraction of the valine signal remains in the α-helical region of the spectrum. As α-helical secondary structures per se are highly unexpected in amyloid fibrils, these are likely to stem from disordered regions protruding from the fibril core. It has indeed been reported before that the C-terminal region is mobile. Likewise, for most polymorphs, the β-sheet core region was found to start only around residue 38 (37, 38, 39, 82), therefore, a substantial fraction of the valine residues can still be expected to be located in disordered regions of the protein.

Figure 2.

2D ¹³C-¹³C PDSD DNP-NMR spectra of specifically ¹³C-labeled α-syn (a) fibrils and (b) α-syn monomers bound to nanodiscs in a molar ratio of 2:1 of protein to nanodisc. Intra- and interresidual crosspeaks involving β-strand or α-helical valine residues are highlighted in blue and orange, respectively. Both spectra were recorded with a longitudinal mixing time of 1 s. The outline (i.e., the lowest contour level) of the spectrum of monomeric α-syn (Fig. 1b) is given in black for comparison. To see this figure in color, go online.

α-Syn is also known to bind to lipid vesicles and membranes, with a binding mode strongly influenced by the charge density of lipids and other physical properties (35). Moreover, α-syn undergoes a significant conformational transition with some regions of the protein adopting a high degree of α-helical structure (35, 83, 84). We therefore mixed α-syn with negatively charged lipid bilayers in the form of NDs (100% 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol), more information in Materials and Methods) and characterized its conformational ensemble. In Fig. 2 b, the DNP-enhanced PDSD spectrum of α-syn bound to NDs in a protein-to-ND molar ratio of 2:1 is shown (one protein per membrane leaflet). We almost exclusively observe α-helical signals in this spectrum. The β-sheet content is dramatically decreased and could only be observed at the noise level.

Additionally, interresidual crosspeaks between α-helical valine and α-helical alanine are observed. This further confirms a correlation between local α-helical conformations of neighboring residues binding to the membrane bilayer and is in line with the α-helix structural model (35, 85, 86).

Notably, the α-helical crosspeak of membrane-bound α-syn (Fig. 2 b) has a distinct shape that exceeds the α-helical region covered by the random-coil ensemble. We observe two peak maxima in the α-helical signal region of the valine residues. This surprising fact could be attributed to two distinguishable populations of valine residues, e.g., those buried inside the lipid bilayer versus those residues facing more the charged headgroups, thus experiencing different chemical environments. Alternatively, it may also be feasible that α-syn can bind to the membrane surface in different ways, which also would lead to differences in the chemical environment of different valine residues.

Quantification of conformational populations in different states

PDSD or similar ¹³C/¹³C correlation spectra are considered as “protein fingerprints” in solid-state NMR. They are very useful, e.g., to visualize differences between samples, as we did above. Nevertheless, this type of experiment relies on a proton-proton dipolar network around the carbon nuclei to transfer magnetization. This has, in our hands, two disadvantages. The magnetization transfer is rather inefficient under DNP conditions, because the glycerol/water glassy matrix used contains only 10% protons to optimize enhancement factors. Thus, long mixing times are required during which relaxation processes can take place. Secondly, the relative intensities of crosspeaks are affected by different local densities of protons (e.g., at the protonated membrane and in the bulk solution), which may lead to variation in magnetization transfer efficiency and, thus, also in crosspeak intensity for amino acid residues located in different environments. For those reasons we decided to use a proton-independent magnetization transfer scheme for accurate quantification, i.e., the DQ/SQ experiment using SPC5 recoupling (87).

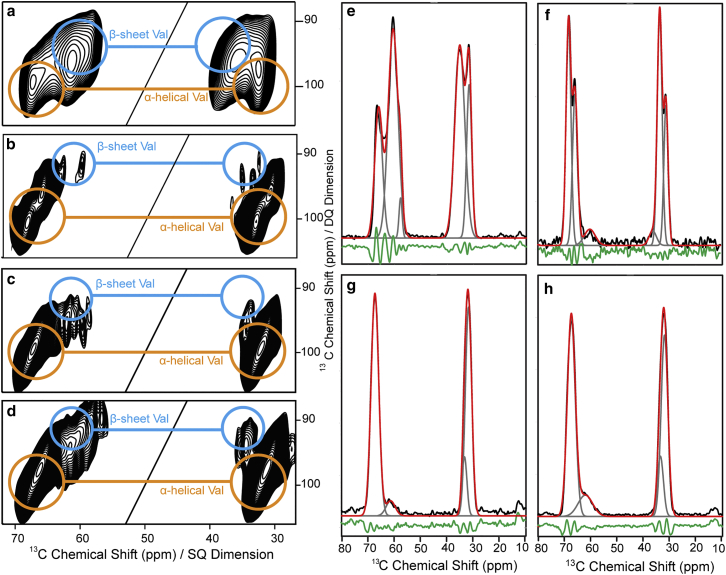
In the case of monomeric disordered α-syn, we do not expect those effects to play a significant role because all parts of the protein should experience the same proton density. Indeed, for both PDSD (Fig. 1 b) and DQ/SQ (Fig. 3 a), quantification of α-helical and β-strand contributions to the signal led to amounts of 30 and 70%, respectively, after deconvolution of the projected crosspeaks (Fig. 3 e). The discrepancy between the populations determined from the two experiments was <5%. These numbers are well in line with previously reported studies, as mentioned above.

Figure 3.

2D ¹³C-¹³C correlation DQ/SQ spectra of specifically ¹³C-labeled (a) α-syn monomers, and α-syn monomers mixed with nanodiscs in (b) 2:1, (c) 8:1, and (d) 16:1 protein-to-nanodisc molar ratio. For one-dimensional projections (black lines in e–h), the Cα-Cβ crosspeak region of valines of the 2D spectra was summed up. The projections were deconvoluted using Gaussian line shapes with the help of the DMfit program. The projections are given in black, the single deconvoluted peaks in gray, the resulting fitting curve is shown in red for each sample, and the difference spectrum is given in green. The simulations were done for the monomeric form (e); for α-syn monomers mixed with nanodiscs in a protein-to-nanodisc molar ratio of (f) 2:1, (g) 8:1, and (h) 16:1; and for the fibrillar form (Fig. S2).

For fibrillar α-syn, the quantification in the DQ/SQ spectrum (Fig. S2) gives a β-strand content of 89% and an α-helical content of 11%. Based on the intrinsic conformational propensity of disordered residues stated above (i.e., assuming that 30% of all valine residues located in unstructured regions contribute to the α-helical signal intensity I_α), we can now quantify P_rc, the fraction of valine residues that remain disordered in the fibrillary state from I_α, as follows:

$$P_{rc}=\frac{I_{\alpha }}{0.3}=\frac{0.11}{0.3}=\mathrm{0.36.}$$ (1)

Thus, 36% of all 19 valines (corresponding to six to seven valine residues) in the α-syn sequence are expected to be disordered, which is very well in line with the six valines N-terminal of position 38 and one valine residue (V118) in the disordered C-terminus.

In the ND-bound state (one α-syn molecule per membrane leaflet), as the membrane is fully protonated, the fraction of α-syn bound to the membrane is in close vicinity to a dense proton network, which leads to a higher transfer efficiency in PDSD than for the unbound, unstructured part. Indeed, almost exclusively, the α-helical signal could be detected in PDSD spectra for membrane-bound α-syn, whereas β-sheet signals are hardly visible (Fig. 2 b). However, these signals can be observed in a DQ/SQ spectrum (Fig. 3 b), and after quantification (Fig. 3 f) give a β-strand to α-helix ratio of 6:94. The propensity of valine residues in unstructured regions of the protein can, in a similar way as in Eq. 1, be calculated as follows:

$$P_{rc}=\frac{I_{\beta }}{0.7}.$$ (2)

Therefore, the amount of valines remaining disordered is ∼8%, corresponding to one or two valine residues in the sequence of α-syn. At such a low protein-to-lipid ratio and high lipid negative charge density, α-syn is expected to bind to the membrane with its N-terminal 92 residues (85, 86), indeed leaving one valine residue in the disordered C-terminal region.

To challenge our quantitative approach further, we prepared samples of α-syn in different molar ratios with the NDs: 8:1 and 16:1, corresponding to 4 and 8 proteins per membrane leaflet (composed of roughly 77 lipids), respectively. As visible in the DQ/SQ spectra shown in Fig. 3, c and d, increasing protein-to-ND ratios lead to higher signal intensities at chemical shifts typical for β-strands. The deconvolution (Fig. 3, g and h) gives β-strand contents of 11 and 21%, corresponding to fractions of disordered valines of 15 and 30%, respectively. This agrees well with the previously reported decrease in α-helical secondary structures when the lipid availability is lowered (88). Moreover, our previous solution NMR titration experiments on the same samples (89) allowed observing the behavior of α-syn association with NDs. The signal intensities from all unbound valine residues were summed up, and the ratios obtained this way are 7, 19, and 29% for protein-to-ND ratios of 2:1, 8:1, and 16:1, respectively. These numbers are in very good agreement (4% off for the highest discrepancy) with our DNP results, corroborating the ability of DNP-enhanced solid-state NMR to quantify conformational propensities and secondary structures with high accuracy.

Conclusions

The definition of representative conformational ensembles sampled by IDPs usually requires the combination of different methodologies. In this article, we have shown that it is possible to study conformational ensembles of IDPs with one experiment (and in 1 d) by DNP-enhanced ssNMR spectroscopy in frozen solution. Different conformational ensembles were obtained under different environmental conditions for our conformationally versatile model protein α-syn, and our results are in good agreement with previous studies.

DNP spectra were shown to faithfully report on expected conformational distribution of α-syn in different states of physiological relevance, i.e., unstructured free monomeric, β-sheet fibrillary, and α-helical membrane bound α-syn in different protein-to-lipid ratios, with very good agreement with the structural models.

Our analysis of 2D ¹³C/¹³C correlation spectra allowed accurate quantification of the expected structural features in different membrane binding modes of α-syn, which is also in line with our previously performed solution NMR titration experiments and current MD simulations.

In summary, we have demonstrated the power of DNP-enhanced solid-state NMR at cryogenic temperatures for the study of conformational ensembles and anticipate that this technique will also be useful for the study of interactions of proteins exhibiting flexible regions with other proteins, ligands, or membrane surfaces.

Author Contributions

M.E., W.H., and H.H. designed the experiments. B.U., T.V., H.S., F.W., and A.G. performed experiments. B.U., T.V., and H.H. analyzed the NMR data. D.P. and B.S. performed and analyzed MD simulations. B.U. and H.H. wrote the manuscript with input from all authors. All authors discussed the results and commented on the manuscript.

Editor: Jill Trewhella.