Skip to main content
PMC home page
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences logoLink to Philosophical transactions. Series A, Mathematical, physical, and engineering sciences
. 2018 May 14;376(2122):20170166. doi: 10.1098/rsta.2017.0166

A simplified method to estimate the run-off in Periglacial Creeks: a case study of King George Islands, Antarctic Peninsula

Ulrike Falk 1,✉, Adrián Silva-Busso 2,3, Pablo Pölcher 2
PMCID: PMC5954467  PMID: 29760111

Abstract

Although the relationship between surface air temperature and glacial discharge has been studied in the Northern Hemisphere for at least a century, similar studies for Antarctica remain scarce and only for the past four decades. This data scarcity is due to the extreme meteorological conditions and terrain inaccessibility. As a result, the contribution of glacial discharge in Antarctica to global sea-level rise is still attached with great uncertainties, especially from partly glaciated hydrological basins as can be found in the Antarctic Peninsula. In this paper, we propose a simplified model based on the Monte Carlo method and Fourier analysis for estimating discharge in partly glaciated and periglacial hydrological catchments with a summer melt period. Our model offers the advantage of scarce data requirements and quick recognition of periglacial environments. Discharge was found to be highly correlated with surface air temperature for the partially glaciated hydrological catchments on Potter Peninsula, King George Island (Isla 25 Mayo). The model is simple to implement and requires few variables to make most versatile simulations. We have obtained a monthly simulated maximum flow estimates between 0.74 and 1.07 m3 s−1 for two creeks (South and North Potter) with a very good fit to field observations. The glacial mean monthly discharge during summer months was estimated to 0.44±0.02 m3 s−1 for South Potter Creek and 0.55±0.02 m3 s−1 for North Potter Creek.

This article is part of the theme issue ‘The marine system of the West Antarctic Peninsula: status and strategy for progress in a region of rapid change’.

Keywords: glacial discharge, permafrost hydrology, run-off, climatic change, Antarctic Peninsula

1. Introduction

The South Shetland Islands (SSI) are located at the northern tip of the Antarctic Peninsula (AP), which has been among the fastest warming regions on the Earth in the past decades [1–4]. Surface air temperature increase is concurrent with retreating glacier fronts, an increase in melt areas, ice surface lowering and rapid break-up and disintegration of ice shelves [5–8], among others. Ice shelves and glaciers along the AP generally show disintegration and retreat over the past five decades [7,9–17], but systematic glaciological field studies are scarce for the region. The warming trend has come to a halt, but the response of glacier ice masses lags behind climatic conditions, and glacial discharge can still be expected to increase [16].

The periglacial environment is primarily conditioned by the regional climatic conditions and has a great diversity in the SSI, depending on local relief geomorphology, lithology, hydrogeology and presence of permafrost [18]. Permafrost is ubiquitous in ice-free areas of Antarctica and its offshore islands [19]. The SSI show permafrost temperatures slightly below 0°C in altitudes near sea level and are, thus, located close to the climatic boundary of permafrost, proving it highly sensitive to climate change [20].

The behaviour of stream discharge in permafrost environments is not yet completely understood [21]. It can show large fluctuations of amplitude on a daily or even hourly scale [22]. Although the relationship between glacial ablation and discharge in the Northern Hemisphere has been studied for at least a century, few exist for Antarctica. Chinn [23] is one of the first to investigate the relationship between air temperature and discharge from firn/ice ablation to the Ross Sea, Antarctica. His study determines that the discharge of the the Rio Onyx into lakes in the Dry Valley is largely dependent on changes in the summer energy balance at the surface and to a minimal degree on winter temperatures. Chinn [23] also highlights the impact of extreme events such as heavy snow and short periods of high positive air temperatures, the control of ablation by altitude, albedo and air temperature. As a result of climate variability studies, several authors have also recently addressed the influence of other climatic factors [4,24]. At higher latitudes, in the Valley of Miers near Scott Base, solar incidental radiation instead of air temperature proved to be the main driver of hydrological discharge [25]. Similar results were found for streams in the Dry Valleys [26] and for Tierney Creek in East Antarctica by Bronge [27].

For the AP region, Vaughan [24] reports a strong positive trend in the annual duration of melting conditions, i.e. the number of positive degree days. He argues, however, that most of the resulting increase in melt water does not drain into the sea, but refreezes and it is thus difficult to predict the fraction of ablation that results in run-off. Owing to the complexity of the driving variables and the terrain, continental scale melt models are subject to large uncertainties when applied to the AP. Hydrological studies on more detailed spatial scales are prerequisite for understanding water systems in Antarctica and the relationship between ablation and run-off. At the Dry Valley lakes, warmer summer conditions are caused by strong wind systems, a consequence of unusual low barometric pressure observed above Ross Sea, and that results in an increase of discharge and lake water levels [28]. The authors suggest that strong summer winds may have even been responsible for the genesis of large glacial lakes during the last glacial maximum, although surface air temperatures were considerably colder than concurrent.

Periods with positive surface air temperature and rainfall events are a permanent feature in the climatology of the SSI and its effect on hydrological systems in the area has not been studied yet in detail. To understand their influence, we can resort to Nowak & Hodson [29], who discuss the influence of rainfall in the autumn—winter for the Bayelva glacier in Svalbard (Arctic). Rain events produce ablation outside the summer period and can have a major impact on glacier mass balance calculations [16]. The resulting ablation is a significant part of the discharge, even in areas of continuous permafrost and cold-base glaciers. The geographical location of the SSI determines less stringent conditions on hydrological systems. On Livingston Island (SSI), Mangin et al. [30] constituted the air temperature as the main factor controlling the run-off in streams of partly glaciated basins. Inbar [31] found a strong correlation between run-off and discharge water temperature for Deception Island (SSI) and distinguishes between two periods in the annual hydrological regime: first, run-off during a short period resulting from firn and glacier ice melt, and, second, ablation of the winter snow layer in the entire drainage area.

The estimation and calculation of discharge in glaciated or partly glaciated hydrological basins has been the objective of many recent studies in cold environments or high mountains in the Northern Hemisphere (e.g. [32]). To assess this discharge, a number of studies have resorted to complex analyses using remote sensing, sophisticated numerical models in combination with long-term time series of hydrological and meteorological data. For Antarctica, however, this abundance of information on the investigated hydrological basins is not available. More specifically, time series of in situ data usually cover only short periods within summer months (e.g. [33]). Additionally, the missing spatial terrain information can generate huge uncertainties when embarking on process modelling. Therefore, we propose here a simplified model to assess catchment discharge that offers the advantage of being economical in terms of data need and that requires a rapid recognition of periglacial environments, but still yields a reasonable complexity in the numerical implementation.

The case of the Potter Creek catchment on King George Island (KGI), Antarctica, provides an adequate and environmentally proper context typical for hydrological catchment areas at the Northern AP dominated by maritime climate and governed by the Southern Annual Mode. In the basin under investigation, the run-off is composed of a glacial component, a contribution from permafrost, but also from precipitation in the form of rain and/or snow. During the annual course, the relative and absolute contributions of these run-off components can change. Throughout summer months, all other situations are possible, thus complicating the methodology to study such systems. The discharge rates can vary strongly depending on soil and air temperature, solar incidental radiation and, to a lesser degree, on precipitation in form of rain. Climatological in situ data are available in acceptable spatial and temporal resolution. Thus, it offers easy access to a good comprehension of the hydrological systems during summer periods, which is the focus of the model proposed here.

The work presented here is based on fieldwork conducted on Potter Peninsula, KGI, during the austral summer of 2010/2011 and contributes to an improved understanding of the response of Antarctic permafrost to changing climate conditions. On the basis of the comprehensive dataset presented here, a time series analysis was carried out to investigate the correlations between the air temperature, soil temperature, incidental solar radiation and discharge in two creeks on Potter Peninsula as proposed by Silva-Busso [22] and French [34], and to discuss the cyclical nature of the hydrological systems by Fourier analysis and Monte Carlo method.

2. Data and methods

(a). Study area

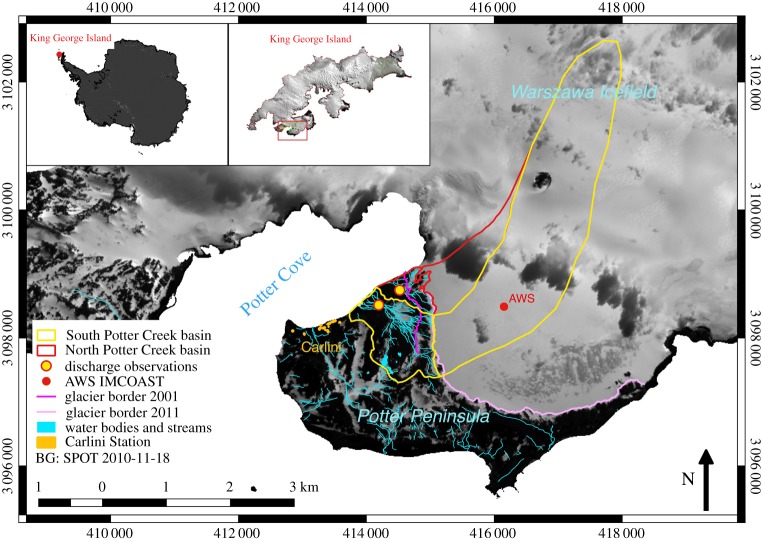
The study area is on the Potter Peninsula (S 62°14′10′′ W 58°39′01′′), KGI, the largest of the SSI (figure 1). Mean annual surface air temperatures in the northern part of the AP range between −2°C and −5°C, mean summer air temperature between 0°C and +2°C, and mean winter air temperatures between −6°C and −10°C [4,35]. The Potter Stream basin is a hydrological system that is fundamentally fed by the discharge from the polythermal Fourcade Glacier, which is part of the Warszawa ice field. Surface and subsurface hydrological processes are observed to be strongly influenced by the present glacial retreat and active permafrost processes. To facilitate the hydrologic analysis, the Potter Stream basin was distinguished into two different basins, North Potter (NP) Creek and South Potter (SP) Creek, and the respective discharge is measured separately (figure 1). The complete Potter Stream basin covers 8.42 km2, of which the non-glaciated part has the rather small area of 1.54 km2, divided into SP creek with 1.2 km2 and NP creek with 0.34 km2. Its drainage network is composed of ephemeral, short, shallow and unstable channels that develop a sub-dendritic design on top of modern glacial deposits of high lithological homogeneity. The basin area is characterized by discontinuous permafrost. Hence, the river network shows a direct strong response to glacial dynamics and an intermediate linkage to water supply from the active layer of the permafrost and snow melt. The latter is negligible during mid- and late summer.

Figure 1.

Figure 1.

Open in a new tab

Map of research area on King George Island (South Shetland Islands, AP) including the locations of own installations and the AWS, North and South Potter Creek basins with drainage channels in the catchment area. Background: SPOT-4, 18 November 2010, © ESA TPM, 2010.

(b). Hydrological and climatological data

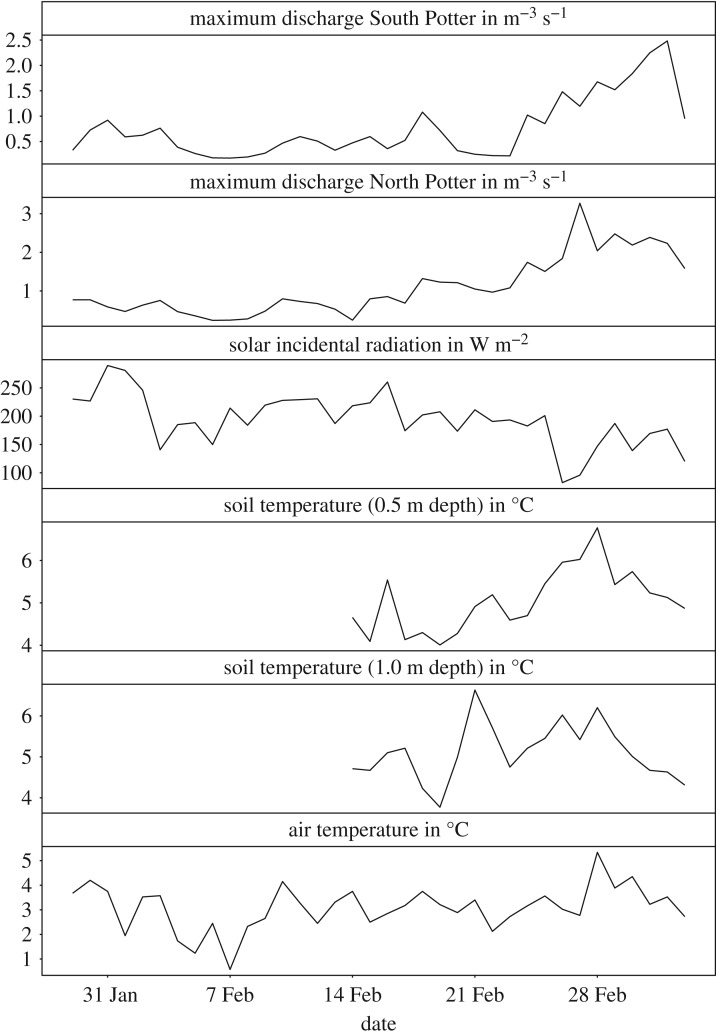
During the time period 25 January to 18 March 2011 in the austral summer 2010/2011, a variety of hydrological and geomorphological measurements were carried out in the Potter Creek basins on KGI (figure 1). The boundaries of the basins as well as the watercourses and divides of the basins were analysed (figure 1) using the topographic terrain model by Lusky et al. [36] and complemented with own GPS in situ observations. The discharge was measured at carefully assessed and defined cross-sections at the confluence of SP and NP creek, respectively, and at times of expected maximum discharge. As the highest amounts of discharge were expected to occur between 16.00 and 18.00 local time, the times of measurements were arranged to approximately meet the time of maximum discharge. To investigate the underlying processes of energy exchange between soil reservoir and atmospheric surface layer and parametrize in the hydrological discharge model presented here, a 24 h period was chosen according to the forecast of no liquid precipitation and with expected around long-term average temperatures. According to these criteria, the time period 2–3 March 2011 was chosen, where hydrological measurements were obtained in 3 h intervals.

The greatest care was taken to provide precise measurements considering the challenging conditions and local geomorphological characteristics. In this region, creeks alter their channels very quickly and frequently, sometimes activating palaeo-channels, or eroding new channels while abandoning the previous one. This occurred twice during the field campaign in January–March 2011. In cases where the old channel was abandoned, the measurement site was moved to the new channel and a new assessment of the cross-sectional area carried out. In the case of a transition period with coexistence of old and new channels, measurements were continued at the old channel while establishing cross-sections and measurements at the new site. Thus, data of 3 h and daily hydrographs were collected to describe the total discharge of both creeks. Continuous discharge measurements by automated sensor installations were not possible due to the highly variable water courses.

Soil temperature data were recorded in a well near the SP gauging site (figure 1). Soil temperature was measured at two different depths (0.5 m and 1.0 m) in the soil’s active layer. Incidental solar radiation data were provided by an automated weather station (AWS) installed on the Fourcade Glacier [4] at a distance of approximately 2 km to the discharge measurements. Air temperature was taken from the standard meteorological observations of Carlini station [37]. The uncertainty of the measured discharge accumulates to approximately 0.1 m3 s−1, based on the sensor precision of 0.01 m s−1 for stream velocity (OTT, Kempten, Germany) and an assumed error of 0.01 m2 in the stream’s cross-section assessment. Accuracy of air temperature measurements is 0.01°C and of the incidental solar radiation is 10 W m−2 (Campbell Scientific, Logan, USA). All data are displayed in figure 2.

Figure 2.

Figure 2.

Open in a new tab

The maximum discharge measurements in South and North Potter Creek, as well as daily averages of soil temperature measurements at South Potter Creek (18.00 local time), solar incidental radiation from the AWS on Fourcade glacier and air temperature at Carlini station on King George Island, AP, during the time period 25 January to 18 March 2011. For locations refer to figure 1.

(c). A simplified hydrological model for run-off estimation

(i). Model concept

The assessment of hydrological and environmental systems by mathematical models is becoming increasingly important. At the same time, the high complexity of numerical models representing natural systems makes it more difficult to understand the behaviour of the underlying conceptual models to define their sensitivities and uncertainties. Several authors have discussed the importance of appropriate modelling and assessment of the underlying uncertainties to evaluate the possibilities of interpretation [38–41]. Gómez et al. [42] use Seasonal Copula Models to analyse the relationship between air temperature and glacier discharge using a discharge time series in the Collins Glacier basin on the Fildes Peninsula, KGI. They proposed a set of Bayesian inference procedure for the model parameters and predict discharge from air temperature distribution to allow for simultaneous estimation of marginal and copulation parameters in contrast to classical approaches. Their approach encompasses a multivariate model using more environmental variables (e.g. rain, humidity, solar radiation or atmospheric pressure). Gómez et al. [42] conclude that the discharge time series is clearly nonlinear and not constant over time, which is their conceptual argument to apply a Bayesian model. A quick survey based on satellite imagery data suggests, however, that the catchment area above their observations contains a very complex drainage network, containing overflowing reservoirs that are being fed by three lakes located upstream that have little direct connection to glacial supply and where water supply is probably predominantly from ablation of snow and permafrost. The complex geomorphology and mixed water supply sources make a proper analysis difficult or even mask the direct relationship between variables like air temperature and solar incidental radiation. In this case, the use and interpretation of more complex models has probably very limited possibilities of validation a the influences of permafrost or glacial discharge itself are not represented.

The in situ data time series presented here were used to develop a hydrological model based on Fast Fourier analysis and Monte Carlo method to yield discharge estimations for the Potter Stream basin, and were validated with another independent subset of field-acquired data. The numerical model presented here was developed and implemented in Python v. 2.7 and used to extend the discharge time series data using meteorological in situ data, i.e. the data time series of air temperature and incidental solar radiation. These variables were determined to be the main drivers of hydrological discharge for partly glaciated basins at the Northern AP.

(ii). Model equations

Hydrological discharge is interpreted as a cyclic process throughout the austral summer with a variability on an hourly basis with changing amplitude and also periodicity. Thus, the time-dependent discharge (Q(t)) can be expressed by a general sinusoidal equation, where A is the amplitude, f the ordinary frequency and φ the phase

(ii). 2.1

The discharge time series can be interpreted as a set of overlying signals attributable to different drivers with different weight coefficients. This allows the use of the Fourier analysis method thereby obtaining a harmonic signal that represents the discharge fluctuations. The discharge behaviour is oscillatory due to energy fluxes in the system that have a cyclic behaviour mathematically defined by a finite summation of sinusoidal signals. The first parsimonious approach is to fit a linear relation between the discharge and the air and soil temperatures. If we assume a modulated base discharge Q0, we can propose

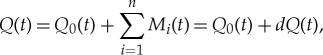(ii). 2.2

where Mi(t) is the individual contribution along the time t and dQ(t) is the total sum of contributions of the different variables, which can be seen as the delta that modulates the discharge oscillator. M stands for every single unadjusted variable used to calculate a contribution (i.e. air and soil temperature, radiation, etc). dQ can also be seen as the difference between the discharge value that the oscillator predicts and the real discharge value. Under the assumption that air and soil temperatures are the main drivers in the discharge time series and neglecting the influence of solar incidental radiation, expanding dQ yields

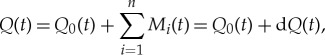(ii). 2.3

where the indices (a, s) denote the contribution of a=air temperature and s=soil temperature. The individual contributions Ma,s are expressed as functions of the air and soil temperatures (Ta and Ts), respectively:

(ii). 2.4

with i=a,s and Si are the constants that relate the discharge with the individual contribution of air and soil temperatures (ka and ks) are the contribution coefficients giving the scale of the impact of changes in air and soil temperature on discharge. A value close to one means a high contribution and close to zero a low contribution. Replacing Ma and Ms in equation (2.3) using equation (2.4), dQ can be expressed as follows:

(ii). 2.5

Both temperatures influence the discharge in the same way as long as the contact between both physical environments has equal properties, meaning the energy transfer elapses in identical processes. In this way, the condition S=Sa=Ss and dQ(t) is defined by

(ii). 2.6

In agreement with the assumption that only the energy transfer process modifies the contribution meaning ka+ks=1, equation (2.6) can be written as

(ii). 2.7

For ka≠ks, a weighted temperature (Tp(t)) is introduced

(ii). 2.8

and equation (2.7) can be rewritten as

(ii). 2.9

In a second step, S and Q0(t) are empirically calculated from the discharge and the respective temperatures measured in the field. As the contribution coefficients are not known, the solution is found by searching for a pair of ka and ks values that yield the best fit of the discharge equation to a set of empirically measured discharge values.

To keep the empirical model simple, a Monte Carlo method [43] is chosen here for fitting the coefficients. In this way, starting with two random values for ka and ks, the adjusted parameters were calculated using the least-squares method. The goodness of fit was estimated from the regression coefficient r, resulting for the preceding analysis in values of r≥0.85. According to the form of the original function, this kind of analysis can possibly lead to several solutions by converging to a local minimum that is not optimal for a set of solutions, as it is not a global minimum. The number of initial conditions was set to two (air temperature ka and soil temperature ks). Under the assumption that ka+ks=1, a number of three or four sets of pairs of (ka, ks) were chosen. Starting from large ka values (ka=0.7) yields an especially high ka>0.9 and low ks<1×10−3. Starting from small values for ka=0.3 leads to the same results. Intermediate initial values and making the dart size small enough, again, show the same results. Thus, the current results suggest that the equation has a single minimum. Hence, it is assumed that no other set of two values for ka and ks exists that would yield an optimal solution. The use of more contribution terms could lead to a more complex scenario, but the model focuses on the impact of the two main drivers: soil and air temperatures.

As a third step, carried out to reframe the discharge time series, equation (2.2) can be rewritten as

(ii). 2.10

where Q(t) is the actual discharge, Q0(t) the base discharge and S×Tp(t) is the difference in the discharge supply depending on the derived consolidated temperature. In turn, Q0(t) is modelled as the base signal of the sinusoidal contributions. Q0(t), thus, takes the following:

(ii). 2.11

by disregarding the harmonic terms of higher orders than i=2. Here, ω is the angular frequency, A is the amplitude and k the scalar coefficient for the harmonics terms, and k0=1. The actual discharge Q(t) can then be written as

(ii). 2.12

This is a complete equation that describes the relation between discharge, air and soil temperatures with time and that can be integrated to obtain the approximate total discharge over a finite time interval using the empiric temperatures of the same period.

(iii). Model adaption to the Potter Creek basins

The integration procedure of equation (2.12) for analytical methods, though possible, is impractical and tedious in data-sparse environments. To obtain a fast estimation, a numerical integration method can be used to solve

(iii). 2.13

Initially, the 3 h discharge data taken at both Potter Creeks (NP and SP) on the 2 and 3 March 2011 were analysed. Understanding the daily course and variability of meteorological and hydrological variables is the key to understanding and modelling the discharge along the summer. This data subset was used as parametric data in the development of the numerical model. As might be expected, the measured discharge data do not perfectly agree with the superposition of the sinusoidal signals and a more careful look on the original discharge signal reveals that the sinusoidal components are modulated by other discharge signals. These model results are a consequence of the physical processes depending on climate variables, and show a relation with the irradiative and conductive energy transfer processes at the air–soil interface [22,34].

The parameters that primarily define the energy content in the air and the soil layers are the respective temperatures. In the following, the correlation between measured soil and air temperatures and the discharge time series is investigated further. In contrast to the air temperature time series, measurements of soil temperature are not available for the whole period. This time series contains only data along the period of the field measurements simultaneously with the discharge time series data. However, solar incidental radiation time series data are available every 10 min continuously over the whole austral summer 2010/2011 from the AWS meteorological station on Fourcade Glacier. With a satisfactory correlation between soil temperature data and solar incidental radiation data, it is possible to use the longer data time series of the latter in replacement of the first.

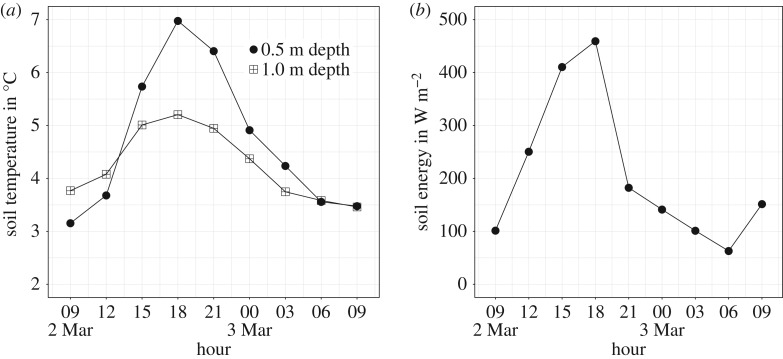
According to Penman [44], the available energy can be expressed by the difference between net radiation (Rn) and soil heat flux (G), where a possible impact of vegetation is negligible for this research site. This allows for the establishment of a relationship between G/Rn, or in this case, of a direct relationship between solar incidental radiation (Rs) and soil temperature (Ts). The underlying assumption is, that albedo is approximately constant during the considered time period, i.e. no snow fall on the moraine region in austral summer. The soil is considered a huge heat reservoir in which the upper layers are in contact with the atmosphere via the surface to allow for the exchange of energy. Penman [44] assigns a resistance to the energy transfer between surface air and soil as in an electrical circuit, which describes the amount of energy to be transferred per unit time from the surface to the deeper soil layers. This approach allows for a better adjustment of the simulation along the whole summer period. Analysis of soil temperature and solar incidental radiation shows a clear correlation and can be expressed by

(iii). 2.14

where krs is assumed constant depending on basin characteristics, e.g. soil properties and terrain. Now, the reservoir is considered to have an infinite heat capacity. Starting from an energy value of E0 (supplied by irradiation) at a time t0 to an energy value E1 at a time t1. If E1 in t1 is greater than E0, then the amount of energy stored in the reservoir will grow proportionally. As long as the energy change is positive (ΔE>0), the energy content and soil temperature of the reservoir will increase proportionally (figure 3). If the energy change turns out to be negative (ΔE<0), the upper soil layer that has been conducting energy to deeper layers will still do so while it is not in thermal equilibrium. Once it runs out of stored energy, it will start to drain energy from the soil storage as long as (ΔE<0). The soil exchanges energy by heat transfer processes to the atmospheric layer, but the most important energy loss of the soil is through water run-off. Water acts as a heat exchange fluid and is taken a constant amount of thermal energy per unit time and volume. Equation (2.14) leads to a description of heat exchange by calculating the change in stored energy (ΔE) from the energy balance equation at the surface between soil and atmosphere. In all cases, there is the energy loss due to the heating of water contained in the soil that is flowing and draining into water courses, etc. Finally, one possible validation method is to analyse the residuals, i.e. the differences between the observed and simulated discharge values. French [34] proposes the use of the r2-method, or model fit efficiency, to verify the goodness of fit at maximum and average values by the adjustment correlation coefficient r:

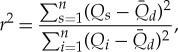(iii). 2.15

where Qs is the daily simulated discharge, Qi is the daily measured discharge and 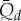Inline graphic average daily measured discharge value for the whole data series. We have estimated the average daily measured discharge (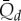Inline graphic) by

(iii). 2.16

where d is the total number of days in the time series. To obtain the average monthly (30 days) measured discharge (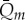Inline graphic), the average daily measured discharge data were multiplied by the days of the month:

(iii). 2.17
Figure 3.

Figure 3.

Open in a new tab

Shown are 3 h soil temperature measurements (a), calculated soil energy flux (b) at South Potter Creek, King George Island, AP, during the time period 2–3 March 2011. Hour is in local time (GMT − 3).

3. Results

(a). Application of the hydrological model to the Potter Creek basins, KGI

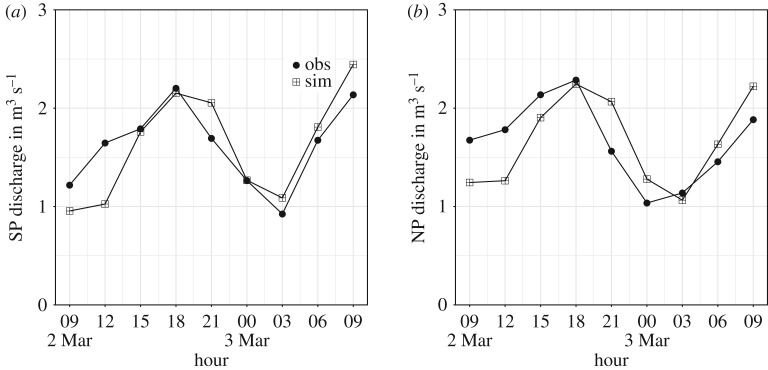
The application of the proposed simplified hydrological model (§2c) to the study area on the Potter Peninsula, KGI, requires a more thorough analysis of the relationship between discharge in the Potter creeks and soil temperature with regard to groundwater contribution to the stream flow. Figure 4 shows observed and simulated discharge of the 3 h datasets from 2 to 3 March 2011 for NP and SP creeks. These datasets were used only for the adjustment and calibration of the hydrological discharge model presented here.

Figure 4.

Figure 4.

Open in a new tab

Three-hourly discharge data from measurements (obs) and simulation (sim) during calibration period 2 March to 3 March 2011 in the North Potter Creek (a) and South Potter Creek (b). Hour is in local time (GMT − 3).

Empirical data are fitted to the mathematical model discussed in §2c to calculate coefficients for equations (2.12) and (2.13). The simulated discharge data that are obtained by feeding observed time series into the model are corrected by a factor fc. This tuning factor, fc, has been estimated by considering that the magnitudes calculated by the Cooley–Tukey fast Fourier transform (FFT) algorithm [45] used in the model are a multiple of N of the actual magnitudes estimated by the complex discrete Fourier transformation (DFT), where N is the number of samples. Thus, fc scales down these magnitudes to the values that a DFT would yield, which can then be used throughout the rest of the model. As there may be other factors influencing the difference between the expected magnitudes and the ones calculated by the FFT algorithm before being scaled down, the naming of a correction factor fc would be appropriate, because it could later be expressed as a linear combination of effects that contribute to the model, as long as these effects are linear in nature. This factor fc takes into account all unknown factors influencing the discharge and scales the discharge values calculated by integrating the discharge function (equation (2.13)). A value of fc=2.5×10−2 was found to be acceptable.

The analysis of the discharge in SP creek shows an adjustment correlation coefficient of r=0.92. The air temperature contribution coefficient was estimated to be ka=0.9986 and soil temperature contribution coefficient to beks=0.0014. The high difference in contribution coefficients ka and ks shows that discharge in SP creek is predominantly supplied by melt processes on the glacier. Thus, the main driver is identified as surface air temperature [22,34]. The contribution coefficient derived for the soil temperature, ks, is low, almost negligible, compared with the air temperature contribution coefficient ka. The soil’s contribution to discharge can be associated with the supply by melt processes in the active layer of the permafrost and/or the groundwater supply from the talik zone to the creek channel. These aspects may have an influence on the hydrological discharge model and on the turbulent flow regime, sediment particle freight and, thus, on measurement uncertainties. This must be taken into account when quantifying the total run-off in the basin. This argumentation incorporates to some degree of uncertainty in the proposed model.

The analysis of the NP creek discharge yields an adjustment correlation coefficient of r=0.86, an estimated air temperature contribution coefficient of ka=0.9983 and soil temperature contribution coefficient of ks=0.0017. As mentioned before, the different contribution coefficients indicate that the discharge process has its greatest contribution from glacial melt. Again, the contribution coefficient of the soil temperature is almost negligible, and represents the relationship of the water supply from melt processes in the active layer of the permafrost and/or the groundwater supply through the talik zone to the creek channel. These aspects influence the hydrological discharge model as previously discussed for the SP creek case. The NP creek has a more turbulent flow that is reflected in the lower adjustment correlation coefficient and a higher measurement error of discharge flow than for the SP creek flow assessment.

The adjustments between the measurements and model runs of the hydrological discharge are in good agreement for both creeks and the resulting fits can be considered satisfactory and reasonable. The discharge rates can vary strongly depending on air temperature, and to a lesser degree on soil temperature. The dependency on solar incidental radiation is given via the soil temperature, as discussed before. The impact of precipitation in the form of rain on discharge quantities will be discussed in the analysis of the daily discharge time series (§3b).

(b). Analysis of daily discharge

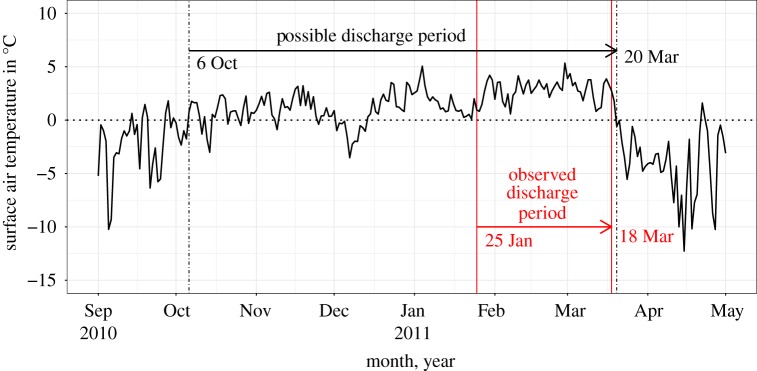
The hydrological discharge model derived in the previous chapter (figure 4) proved to be adequate for estimating the discharge in both creeks, SP and NP, throughout the time period in the austral summer using air temperature and incidental solar radiation data together with empirically obtained discharge data. The variation in surface air temperature can be seen in the data time series for the extended period of the austral summer 2010/2011. Figure 5 shows the possible run-off activity periods related to both Potter creeks in the basin, and the measured actual discharge time period.

Figure 5.

Figure 5.

Open in a new tab

Average daily surface air temperature during austral summer 2010/2011, time period 1 September 2010 to 1 May 2011, at Carlini Base Station based on measurements by the National Meteorological Service of Argentina [37].

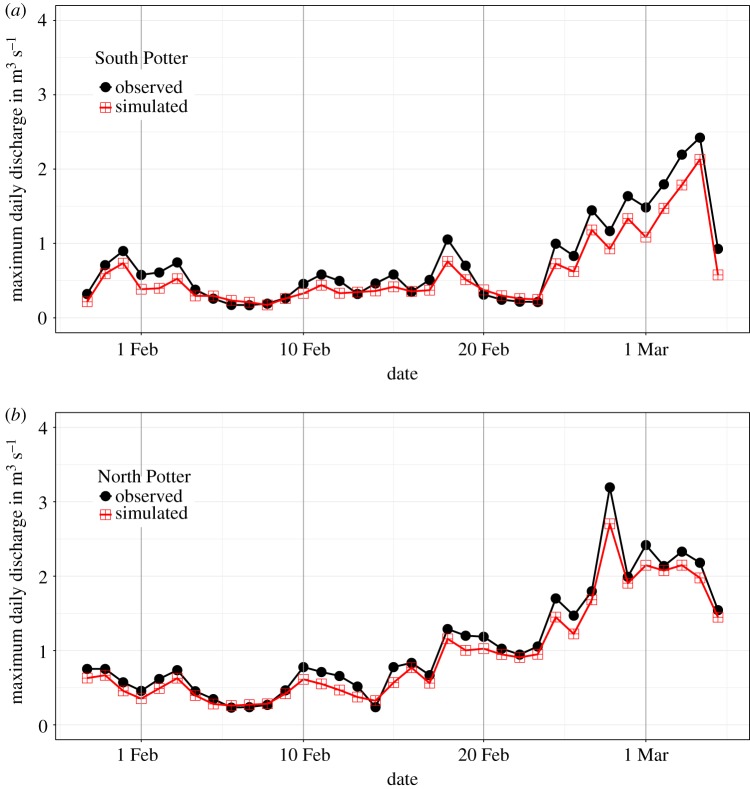
The model presented here estimates the total discharge amounts and their variability for both creeks along the austral summer, when ablation is most intense and the underlying assumptions apply. The data time series used for the analysis are the meteorological observations from Carlini Station [37] and the IMCOAST AWS on the Fourcade Glacier [4]. The maximum daily discharge time series derived from the daily hydrological measurements and model simulations for NP and SP creeks within the period 30 January 2011 to 5 March 2011 are shown in figure 6 and include the period during which the measurements used in the calibration of the hydrological discharge model were taken. It needs to be taken into account that the values correspond to times of daily maximum discharge. As can be seen, the pattern of the simulation curves are in good agreement with the patterns of the measurement curve for both Potter creeks, but that the hydrological model systematically underestimates discharge. This will be discussed later in the following paragraphs.

Figure 6.

Figure 6.

Open in a new tab

Comparison of observed and simulated maximum hydrological discharge from the partly glaciated hydrological Potter Creek basins: (a) South Potter Creek and (b) North Potter Creek, on Potter Peninsula on King George Island, as defined in the map (figure 1) during the austral summer 2010/2011, time period 29 January to 5 March 2011.

Several of the features and anomalies of the simulated data, however, need further explanation. There are several statistical methods for this purpose as the average error between measured and simulated data time series. The error in calculated total monthly discharge, 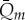Inline graphic (equation (2.13)), amounts to 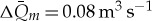Inline graphic for NP creek, which means a typical percentage error of 7.5% was obtained. For the SP creek, the error in 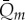Inline graphic is slightly higher with 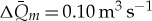Inline graphic, i.e. a percentage error of 12%. The lower error in discharge for NP creek indicates a satisfactory parametrization of the hydrological system. The higher error in SP creek discharge estimations can be related to the contribution of discharge water from other processes.

The adjustment parameters, however, prove the simulation results for both SP and NP creeks are acceptable. The obtained results from both series (simulated and measured) for NP and SP creeks are summarized in table 1. In this table, r2 is the correlation coefficient and represents the goodness of fit of observed daily maximum discharge Qd,obs to simulated daily maximum discharge Qd,sim, and observed monthly discharge, Qm,obs to simulated monthly discharge, Qm,sim. The measured discharge values are maximum values, while the simulated ones are in fact the maximum values estimated by the simulation and taking into account the daily amplitude of variation of discharge. This amplitude is driven by changes in temperature and incidental radiation. Finally, the mean discharges were calculated taking into consideration the daily variation of simulated discharge (figure 4).

Table 1.

Summary of monthly discharge analysis from simulation and observations, including results of fitting efficiencies.

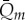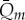Inline graphic (observed) Inline graphic (simulated) error 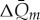Inline graphic Pearson’s
creek in m3 s−1 in m3 s−1 in m3 s−1 r2 coefficient
South Potter 0.74 0.60 0.10 0.97 0.98
North Potter 1.07 0.95 0.08 0.98 0.99
Open in a new tab

Main precipitation events happened on only four days during the time period 25 January to 18 March 2011. Total amount of precipitation during the whole observation period added up to 63.8 mm. A great part of the catchment area is glaciated, and precipitation falls mostly in the form of snow, especially at higher elevations of the glacier. The precipitation on glaciated parts of the catchment area is, thus, not directly available for discharge processes but adds to the mass balance of the glacier. Counting only the precipitation falling on the non-glaciated catchment parts, and disregarding completely evaporation and latent heat fluxes, this would translate to a total amount over the whole time period of 0.89 m3 s−1 for SP creek and 0.25 m3 s−1 for NP creek. This is not realistic, as latent heat fluxes will probably take up a substantial amount of water from the dark heated moraine landscape. Hence, these values can be considered maximum errors in total discharge amounts. Considering that 74% of the precipitation occurred on only four days (2 February, 23 February, 24 February and 25 February), the error in simulated daily discharge for the remaining bulk of the time period amounts to 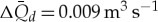Inline graphic for the complete Potter basin. Each of the later rainfall events accounted for 21% of the total precipitation throughout the whole discharge measurement period, but in the discharge time series the response to the rainfall events is not evident (figure 6). The hydrological discharge model systematically underestimates the discharge by neglecting precipitation.

On 2 February 2011, rainfall contributed 6.8 mm to the total discharge, translating into a maximum possible contribution to a daily discharge of 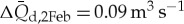Inline graphic for SP creek and 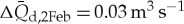Inline graphic for NP creek. On 23, 24 and 25 February 2011, precipitation amounted to 13.2 mm on each day. This leads to an maximum possible contribution in daily discharge of 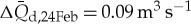Inline graphic for SP creek and 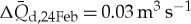Inline graphic for NP creek. It can be considered of particular interest that rainfall events occurring in the later part of the measurement period (23–25 February) also fell in the form of rain on the glacial surface at altitudes of 250 m.a.s.l. These rainfall events may have contributed to a greater extent to the discharge because of the associated erosion of the snow layer. The calculated correlation coefficients of r2=0.97 for SP and r2=0.98 for NP does not indicate a significant mismatch between the simulated and measured values, even when using only data after 24 February 2011. This points to a contribution of precipitation to discharge that could be incorporated into our model as a contribution to the base discharge Q0(t) (equation (2.11)).

Nonetheless, the model proposed here responds robustly, especially when used in periods of scarce or no rainfall. However, it should also be considered that the daily oscillations of the discharges are not limited and can show significant variations [22]. Moreover, the hydrological discharge model presented here gives estimates of discharge using in situ observations of air temperature and solar incidental radiation without committing to a full glaciological survey required for spatially distributed modelling efforts of glacierized and partly glacierized catchments. The mean glacial discharge simulated was estimated to a monthly discharge of 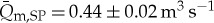Inline graphic (i.e. 1.13±0.05 hm−3 month−1) for the SP creek and 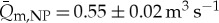Inline graphic (i.e. 1.43±0.05 hm3 month−1) for the NP creek during summer months January–March 2011. Melt processes can explain about 98–99% of the water supply in the NP and SP creeks on the glaciated parts of the catchment according to the proposed hydrological discharge model. We conclude that hydrological discharge in partly glaciated hydrological catchments with a summer melt season is mainly driven by air temperature, and to a lesser degree by soil temperature and solar incidental radiation.

4. Discussion and conclusion

In recent literature, there have been important contributions to the subject of modelling the discharge of glacier ablation in partly glaciated hydrological basins (e.g. [46–48]). Most of the models are very sophisticated, spatially distributed and physical process based, and, thus, very demanding when it comes to input spatial and temporal data resolution. Lindström et al. [48] present a model developed for water basins in the Northern Hemisphere that include agricultural land use by simulating the flow of water, but also the transport and rotation of nitrogen and phosphorus. Designed and tested in Sweden with its application on mountain glacier basins in the Scandinavian Peninsula, it is unlikely to be representative for or implementable in the Antarctic continent. Engelhardt et al. [49] conclude that marine glaciers are more strongly influenced by winter precipitation and air temperature variability in summer. Glaciers that are less influenced by the marine environment, on the other hand, proved to be less sensitive to rainfall and more sensitive to summer air temperatures. A different degree of marine influence could have a significant impact on the discharge from glaciated or partly glaciated hydrological basins. This statement is important as many glaciers in the AP region are under proven marine influence [4].

Tanguang et al. [50] integrated two glaciological and three snow models into a spatially distributed hydrological model for basins in the Tibetan plateau. Their results show a better adjustment of glacial discharge from temperature index method compared with positive degree day (PDD) methods. Parametrizing air temperature and global radiation, the use of Monte Carlo models to estimate hydrological parameters has more examples in the literature (e.g. [51]). They also proposed the use of Monte Carlo analysis for spatial analysis and/or population in the parameter space of the respective conceptual model for any case with appropriate sampling. Engelhardt et al. [49] identified air temperature as an important factor in hydrological discharge models, and emphasize the importance of air temperature observations and the use of Monte Carlo methods.

The hydrological discharge model presented here was validated by the observations conducted during austral summer 2010/2011 at Potter Peninsula, with high correlation coefficients between simulated and observed discharge. It can be used in the estimation of discharge in streams whose supply is primarily water from glacier ablation. The model includes a Monte Carlo statistical method and Fourier numeric series analysis. It has been verified that this simulation can be run on meteorological observation records of air temperatures and solar incidental radiation. The hydrological discharge model was calibrated and validated using a comprehensive dataset of discharge values derived from field measurements. It was proved to be adequate for estimating discharge of partly glacierized hydrological catchment areas that have a summer melt season and above-freezing air temperatures. The next step in the model development would be to include a parametrization of liquid precipitation and the response of discharge to rainfall events.

The simple parametrization of this model makes it a valuable and important contribution for its application in areas with scarce hydrological and meteorological data availability, as well as difficult access to the terrain. It is thus especially versatile in parts of the Antarctic continent. The proposed model allows a first estimate of discharge without detriment to the subsequent use of more complex models that require more complete data series. Its implementation is simple and requires few variables to yield reasonable discharge simulations. High variability in discharge flow was driven by air temperature at the beginning of the ablation season and resulted from extensive rain events at the end of the ablation season. Warm and wet winters prolonged the occurrence of early and late run-off. The results can be used interdisciplinary for validation of glacier mass balances and, in this particular case, the derived time series of discharge are of great importance to the marine biology and biological diversity in the coastal areas of Potter Cove and its sensitivity to recent climate change in polar regions. The model was developed and adapted to the Potter Creek basins, but it should be easily transferable to other similar basins. We expect it to be adaptable to a wide variety of glaciated and partly glaciated hydrological basins that are driven either by surface air temperature, solar incidental radiation or soil temperature.

Acknowledgements

The authors thank Hernán Sala (Argentinean Antarctic Institute), the IAA (Argentinean Antarctic Institute), the INA (Argentinean Water Institute) and the logistics support of the Argentinean Army. All graphs in this paper were produced using the R programming language (R Core Team, 2014) and QGIS software (QGIS, 2016). We thank Damián López for the careful reading of and his very helpful comments on the manuscript.

Data accessibility

All supplementary data are available under the following links and on request to the authors. Hydrological data and discharge model: http://dx.doi.org/10.1594/PANGAEA.887836; climatological data: http://dx.doi.org/10.1594/PANGAEA.848704; glaciological data: http://dx.doi.org/10.1594/PANGAEA.874599.

Authors' contributions

A.S.-B. was PI of the hydrological project on the Potter Peninsula, leading the field work, the data processing and interpretation and also the first draft of the manuscript. P.P. took part in the fieldwork and led the development and implementation of the hydrological model. U.F. was PI of the climatological and glaciological project on Potter Peninsula, contributed to the data processing and data analysis, and implementing the results into the figures shown in this manuscript. U.F. is responsible for the final version of this manuscript.

Competing interests

We declare we have no competing interests.

Funding

This research was funded by ESF Europolar programme (IMCOAST, BMBF award AZ 03F0617B) and EU FP7-People-2012-IRSES programme (IMCONet, agreement no. 318718).

References

  • 1.Vaughan DG, Marshall GJ, Connolley WM, Parkinson C, Mulvaney R, Hodgson DA, King JC, Pudsey CJ, Turner J. 2003. Recent rapid regional climate warming on the Antarctic Peninsula. Clim. Change 60, 243–274. ( 10.1023/A:1026021217991) [DOI] [Google Scholar]
  • 2.Steig EJ, Schneider DP, Rutherford SD, Mann ME, Comiso JC, Shindell DT. 2009. Warming of the Antarctic ice-sheet surface since the 1957 International Geophysical Year. Nature 457, 459–462. ( 10.1038/nature07669) [DOI] [PubMed] [Google Scholar]
  • 3.Barrand N, Vaughan D, Steiner N, Tedesco M, Kuipers Munneke P, Broeke M, Hosking J. 2013. Trends in Antarctic Peninsula surface melting conditions from observations and regional climate modeling. J. Geophys. Res.: Earth Surface 118, 315–330. ( 10.1029/2012JF002559) [DOI] [Google Scholar]
  • 4.Falk U, Sala H. 2015. Winter melt conditions of the inland ice cap of King George Island, Antarctic Peninsula. Erdkunde 69, 341–363. ( 10.3112/erdkunde.2015.04.04) [DOI] [Google Scholar]
  • 5.De Angelis H, Skvarca P. 2003. Glacier surge after ice shelf collapse. Science 299, 1560–1562. ( 10.1126/science.1077987) [DOI] [PubMed] [Google Scholar]
  • 6.Rau F, Mauz F, de Angelis H, Jaña R, Neto JA, Skvarca P, Vogt S, Saurer H, Gossmann H. 2004. Variations of glacier frontal positions on the northern Antarctic Peninsula. Ann. Glaciol. 39, 525–530. ( 10.3189/172756404781814212) [DOI] [Google Scholar]
  • 7.Braun M, Humbert A, Moll A. 2009. Changes of Wilkins Ice Shelf over the past 15 years and inferences on its stability. Cryopshere 3, 41–56. [Google Scholar]
  • 8.Rignot E, Mouginot J, Scheuchl B. 2011. Antarctic grounding line mapping from differential satellite radar interferometry. Geophys. Res. Lett. 38, L10504 ( 10.1029/2011GL047109) [DOI] [Google Scholar]
  • 9.Rott H, Skvarca P, Nagler T. 1996. Rapid collapse of northern Larsen ice shelf, Antarctica. Science 271, 788 ( 10.1126/science.271.5250.788) [DOI] [Google Scholar]
  • 10.Skvarca P, Rack W, Rott H, DonáNgelo Y, IbarzáBal T. 1998. Evidence of recent climatic warming on the eastern Antarctic Peninsula. Ann. Glaciol. 27, 628–632. ( 10.3189/S0260305500018164) [DOI] [Google Scholar]
  • 11.Shepherd A, Wingham D, Payne T, Skvarca P. 2003. Larsen ice shelf has progressively thinned. Science 302, 856–859. ( 10.1126/science.1089768) [DOI] [PubMed] [Google Scholar]
  • 12.Skvarca P, De Angelis H, Zakrajsek AF. 2004. Climatic conditions, mass balance and dynamics of Larsen B ice shelf, Antarctic Peninsula, prior to collapse. Ann. Glaciol. 39, 557–562. ( 10.3189/172756404781814573) [DOI] [Google Scholar]
  • 13.Scambos T, Ross R, Bauer R, Yermolin Y, Skvarca P, Long D, Bohlander J, Haran T. 2008. Calving and ice-shelf break-up processes investigated by proxy: Antarctic tabular iceberg evolution during northward drift. J. Glaciol. 54, 579–591. ( 10.3189/002214308786570836) [DOI] [Google Scholar]
  • 14.Sobota I, Kejna M, Araźny A. 2015. Short-term mass changes and retreat of the Ecology and Sphinx glacier system, King George Island, Antarctic Peninsula. Antarctic Sci. 27, 500–510. ( 10.1017/S0954102015000188) [DOI] [Google Scholar]
  • 15.Pȩtlicki M, Sziło J, MacDonell S, Vivero S, Bialik RJ. 2017. Recent deceleration of the ice elevation change of ecology glacier (King George Island, Antarctica). Remote Sensing 9, 520 ( 10.3390/rs9060520) [DOI] [Google Scholar]
  • 16.Falk U, López DA, Silva-Busso A. 2018. Multi-year analysis of distributed glacier mass balance modelling and equilibrium line altitude on King George Island, Antarctic Peninsula. Cryosphere 12, 1–22. ( 10.5194/tc-2017-232) [DOI] [Google Scholar]
  • 17.Fieber KD, Mills JP, Miller PE, Clarke L, Ireland L, Fox AJ. 2018. Rigorous 3D change determination in Antarctic Peninsula glaciers from stereo WorldView-2 and archival aerial imagery. Remote Sens. Environ. 205, 18–31. ( 10.1016/j.rse.2017.10.042) [DOI] [Google Scholar]
  • 18.López-Martínez J, Serrano E, Schmid T, Mink S, Linés C. 2012. Periglacial processes and landforms in the South Shetland Islands (northern Antarctic Peninsula region). Geomorphology 155, 62–79. [Google Scholar]
  • 19.Bockheim JG, Hall KJ. 2002. Permafrost, active-layer dynamics and periglacial environments of continental Antarctica: periglacial and permafrost research in the Southern Hemisphere. South African J. Sci. 98, 82–90. [Google Scholar]
  • 20.Vieira G. et al. 2010. Thermal state of permafrost and active-layer monitoring in the antarctic: advances during the international polar year 2007–2009. Permafrost Periglacial Process. 21, 182–197. ( 10.1002/ppp.685) [DOI] [Google Scholar]
  • 21.Matthew B, Neil G (eds). 2009. Glacial geology. Ice sheets and landforms. Chichester, West Sussex, UK: Wiley Blackwell Publisher. [Google Scholar]
  • 22.Silva-Busso A. 2009. Aguas superficiales y subterráneas en el área norte de la Península Antártica. In el agua en el norte de la Península Antártica, pp. 47–82, 3rd edn. Buenos Aires, Argentina: Vázquez Mazzin and Fundación de Historia Natural Félix de Azara.
  • 23.Chinn T. 1981. Hydrology and climate in the Ross sea. J. R. Soc. New Zealand 11, 373–386. ( 10.1080/03036758.1981.10423328) [DOI] [Google Scholar]
  • 24.Vaughan DG. 2006. Recent trends in melting conditions on the Antarctic Peninsula and their implications for ice-sheet mass balance and sea level. Arctic Antarctic Alpine Res. 38, 147–152. ( 10.1657/1523-0430(2006)038%5B0147:RTIMCO%5D2.0.CO;2) [DOI] [Google Scholar]
  • 25.Mc Conchie J, Winchester D, Hawke R, Campbell H. 1990. The hydrology, glaciology and sediment transport monitoring programme in the Miers Valley (K046). New Zealand Antarctic Record 10, 23–25. [Google Scholar]
  • 26.Chinn T, Woods A. 1984. Hydrology and glaciology, Dry Valleys, Antarctica. Annual report for 1981–1982. Christchurch, New Zealand: Ministry of Works and Development.
  • 27.Bronge C. 1989. The hydrology of Proglacial Chelnok Lake. Vestfold Hills, Antarctica: Stockholms Universitet, Naturgeografiska Institutionen. [Google Scholar]
  • 28.Doran PT, McKay CP, Fountain AG, Nylen T, McKnight DM, Jaros C, Barrett JE. 2008. Hydrologic response to extreme warm and cold summers in the McMurdo Dry Valleys, East Antarctica. Antarctic Sci. 20, 499–509. [Google Scholar]
  • 29.Nowak A, Hodson A. 2013. Hydrological response of a High-Arctic catchment to changing climate over the past 35 years: a case study of Bayelva watershed, Svalbard. Polar Res. 32, 19691 ( 10.3402/polar.v32i0.19691) [DOI] [Google Scholar]
  • 30.Mangin A, Romero AE, Auzmendi IA. 1992. Características del drenaje de un lóbulo del Glaciar Hurd, Isla Livingston, Islas Shetland del Sur. In Simposios. III. Congreso geológico de España y VIII Congreso Latinoamericano de Geología, pp. 325–336. Universidad de Salamanca.
  • 31.Inbar M. 1995. Fluvial morphology and streamflow on Deception Island, Antarctica. Geografiska Annaler: Ser. A, Phys. Geography 77, 221–230. ( 10.1080/04353676.1995.11880442) [DOI] [Google Scholar]
  • 32.Magnusson J, Farinotti D, Jonas T, Bavay M. 2011. Quantitative evaluation of different hydrological modelling approaches in a partly glacierized Swiss watershed. Hydrol. Process. 25, 2071–2084. ( 10.1002/hyp.7958) [DOI] [Google Scholar]
  • 33.Sziło J, Bialik RJ. 2017. Bedload transport in two creeks at the ice-free area of the Baranowski Glacier, King George Island, West Antarctica. Polish Polar Res. 38, 21–39. ( 10.1515/popore-2017-0003) [DOI] [Google Scholar]
  • 34.French HM. 2017. The periglacial environment. New York, NY: John Wiley & Sons. [Google Scholar]
  • 35.King J, Turner J, Marshall G, Connolley W, Lachlan-Cope T. 2003. Antarctic Peninsula climate variability and its causes as revealed by analysis of instrumental records. Wiley Online Library. [Google Scholar]
  • 36.Lusky J, Vallverdú E, Gómez I, del Valle R, Felske H. 2001. Map of Potter Peninsula. King George Island, South Shetland Islands, Antarctica. Buenos Aires, Argentina: Instituto Antártico Argentino. [Google Scholar]
  • 37.SMN. 2016. Meteorological observations at Carlini base. Argentinean Meteorological Service, Argentina, Buenos Aires.
  • 38.Jakeman AJ, Letcher RA, Norton JP. 2006. Ten iterative steps in development and evaluation of environmental models. Environ. Modell. Softw. 21, 602–614. ( 10.1016/j.envsoft.2006.01.004) [DOI] [Google Scholar]
  • 39.Beven K. 2006. A manifesto for the equifinality thesis. J. Hydrol. 320, 18–36. ( 10.1016/j.jhydrol.2005.07.007) [DOI] [Google Scholar]
  • 40.Wagener T. 2003. Evaluation of catchment models. Hydrol. Process. 17, 3375–3378. ( 10.1002/hyp.5158) [DOI] [Google Scholar]
  • 41.Jolma A, Norton J. 2005. Methods of uncertainty treatment in environmental models. Environ. Modell. Softw. 20, 979–980. ( 10.1016/j.envsoft.2004.10.004) [DOI] [Google Scholar]
  • 42.Gómez M, Ausín MC, Domínguez MC. 2017. Seasonal copula models for the analysis of glacier discharge at King George Island, Antarctica. Stoch. Environ. Res. Risk Assess. 31, 1107–1121. ( 10.1007/s00477-016-1217-7) [DOI] [Google Scholar]
  • 43.Robert CP. 2004. Monte carlo methods. Wiley Online Library. [Google Scholar]
  • 44.Penman HL. 1948. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 193, 120–145. ( 10.1098/rspa.1948.0037) [DOI] [PubMed] [Google Scholar]
  • 45.Van Loan C. 1992. Computational frameworks for the fast Fourier transform, vol. 10 Philadelphia, PA: SIAM. [Google Scholar]
  • 46.Klok E, Jasper K, Roelofsma K, Gurtz J, Badoux A. 2001. Distributed hydrological modelling of a heavily glaciated Alpine river basin. Hydrol. Sci. J. 46, 553–570. ( 10.1080/02626660109492850) [DOI] [Google Scholar]
  • 47.Reijmer C, Hock R. 2008. A distributed energy balance model including a multi-layer sub-surface snow model. J. Glaciol. 54, 61–72. ( 10.3189/002214308784409161) [DOI] [Google Scholar]
  • 48.Lindström G, Pers C, Rosberg J, Strömqvist J, Arheimer B. 2010. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 41, 295–319. ( 10.2166/nh.2010.007) [DOI] [Google Scholar]
  • 49.Engelhardt M, Schuler T, Andreassen L. 2014. Contribution of snow and glacier melt to discharge for highly glacierised catchments in Norway. Hydrol. Earth Syst. Sci. 18, 511–523. ( 10.5194/hess-18-511-2014) [DOI] [Google Scholar]
  • 50.Tanguang G, Shichang K, Cuo L, Tingjun Z, Guoshuai Z, Yulan Z, Sillanpää M. 2015. Simulation and analysis of glacier runoff and mass balance in the Nam Co basin, southern Tibetan Plateau. J. Glaciol. 61, 447–460. ( 10.3189/2015JoG14J170) [DOI] [Google Scholar]
  • 51.Wagener T, Kollat J. 2007. Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox. Environ. Modell. Softw. 22, 1021–1033. ( 10.1016/j.envsoft.2006.06.017) [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

All supplementary data are available under the following links and on request to the authors. Hydrological data and discharge model: http://dx.doi.org/10.1594/PANGAEA.887836; climatological data: http://dx.doi.org/10.1594/PANGAEA.848704; glaciological data: http://dx.doi.org/10.1594/PANGAEA.874599.

Articles from Philosophical transactions. Series A, Mathematical, physical, and engineering sciences are provided here courtesy of The Royal Society

RESOURCES