Probing Position-Dependent Diffusion in Folding Reactions Using Single-Molecule Force Spectroscopy

Abstract

Folding of proteins and nucleic acids involves a diffusive search over a multidimensional conformational energy landscape for the minimal-energy structure. When examining the projection of conformational motions onto a one-dimensional reaction coordinate, as done in most experiments, the diffusion coefficient D is generally position dependent. However, it has proven challenging to measure such position-dependence experimentally. We investigated the position-dependence of D in the folding of DNA hairpins as a simple model system in two ways: first, by analyzing the round-trip time to return to a given extension in constant-force extension trajectories measured by force spectroscopy, and second, by analyzing the fall time required to reach a given extension in force jump measurements. These methods yielded conflicting results: the fall time implied a fairly constant D, but the round-trip time implied variations of over an order of magnitude. Comparison of experiments with computational simulations revealed that both methods were strongly affected by experimental artifacts inherent to force spectroscopy measurements, which obscured the intrinsic position-dependence of D. Lastly, we applied Kramers’s theory to the kinetics of hairpins with energy barriers located at different positions along the hairpin stem, as a crude probe of D at different stem positions, and we found that D did not vary much as the barrier was moved along the reaction coordinate. This work underlines the difficulties faced when trying to deduce position-dependent diffusion coefficients from experimental folding trajectories.

Introduction

Physically, structure formation in biological macromolecules involves a diffusive search over a landscape representing the energy of the molecule as a function of all possible conformations (1, 2, 3, 4). The rate at which this search proceeds is determined by the diffusion coefficient, D, which thus encapsulates critical information about the microscopic dynamics during folding, effectively connecting the thermodynamics of landscapes to the kinetics of folding. Because of the large number of degrees of freedom associated with even a small protein or nucleic acid, folding landscapes are inherently multidimensional. Experimentally, however, folding reactions are typically monitored using a single observable, such as the radius of gyration or the distance between probes attached to the molecule, which then becomes the reaction coordinate used to describe the progress of the structural transition. As a result, the full dynamics on the multidimensional landscape are projected onto a one-dimensional (1D) energy profile (5).

One of the consequences of this projection is that the value of the diffusion coefficient may vary with position along the reaction coordinate. The nature of this position-dependence for D depends on the details of the 1D projection and thus on the particular reaction coordinate chosen (6). Given the significance of D as a determinant of the speed at which dynamical processes occur—for example, both kinetic rates and the transition times for barrier-crossing depend linearly on D (7, 8, 9)—it is important to characterize its behavior. A number of computational studies have explored the position-dependence of D, with results that appear sometimes to conflict; in some cases, D was found to vary significantly with position (10, 11), whereas in other cases, the effects were smaller (6, 12, 13). These differences may relate to differences in the type of model used in the simulations or to the choice of reaction coordinate, as different projections can yield very different position-dependence (6, 11, 13). Various strategies can be used to change reaction coordinates in computations to find an “optimal” projection (5), but the same is not true in experiments, in which the reaction coordinate is typically imposed by the choice of experimental assay. Exploring the position-dependence of D in the context of experiments is thus important to ensure proper interpretation.

Experimentally, it is challenging enough to measure D, let alone its position dependence, and thus there is relatively little quantitative information on this question. The relaxation time for intrachain dynamics measured with fluorescent probes such as fluorescence resonance energy transfer pairs or quenchers has been used to study D within unstructured or denatured proteins, which has found intriguingly that D tends to decrease as denaturant is reduced (14, 15, 16). The position-dependence of D has also been assessed experimentally by combining kinetic measurements with modeling, finding that D decreases as the folded state is approached (17).

An especially powerful approach to studying the position-dependence of diffusion is provided by single-molecule methods because individual folding and unfolding trajectories can be monitored directly, avoiding ensemble averaging (18). In single-molecule force spectroscopy (SMFS), for example, a force is applied across an individual molecule by a force probe like optical tweezers or atomic force microscope (AFM), and the extension of the molecule—the reaction coordinate in these measurements—is measured as its structure changes in response to the load (19). SMFS is particularly useful for studying position-dependent diffusion because data can be collected during the actual transition events themselves (20, 21, 22, 23). Furthermore, SMFS is a powerful tool for measuring energy landscapes experimentally (24).

A few methods have been proposed for determining the dependence of D on the molecular extension, D(x). One is based on the average “round-trip” time, which is the time required to return to a given initial extension value for the first time after hitting a fixed reference point on the reaction coordinate, like the folded or unfolded state, when the system is in equilibrium (25). Another is based on the average “fall time,” which is the time required to reach a given extension from the unfolded state during a nonequilibrium refolding transition after a force jump (26). The fall time method has been applied to protein folding using AFM, finding that D appears constant for polyubiquitin (26), but it has never been validated by comparison to other methods. The round-trip time method has not yet been applied to experimental data, to our knowledge. Here, we have applied both methods to the folding of a simple model system, a DNA stem-loop hairpin (27, 28), to test how well they work. We found that the analyses were confounded by measurement artifacts from the experimental apparatus, such that the position-dependence of D remained difficult to determine experimentally.

Methods

Sample preparation and measurement

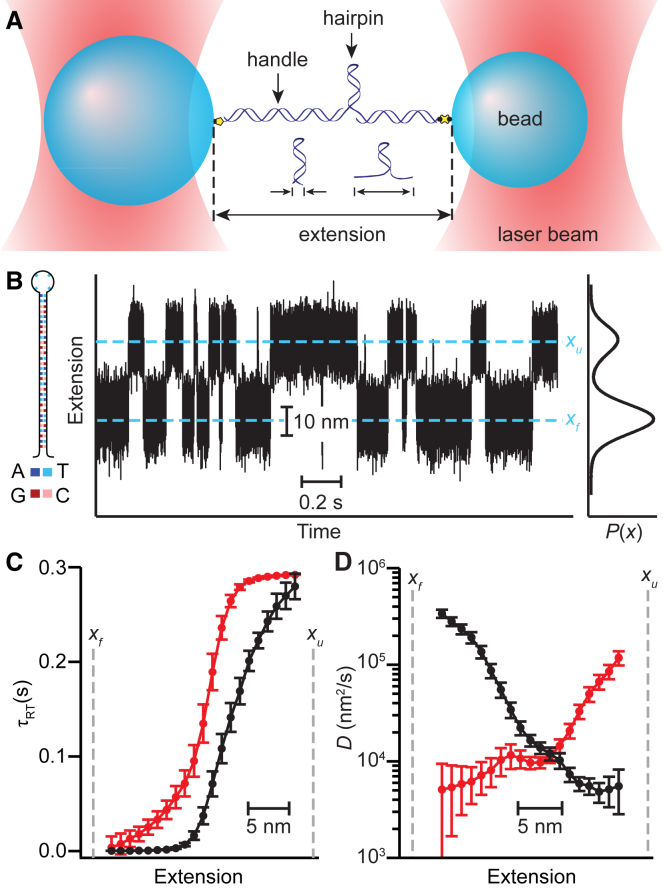
DNA hairpins with specified stem and loop sequence were made as described previously (27), attached to 842-bp and 1289-bp handles of double-stranded DNA that were in turn bound respectively to 600-nm diameter avidin-coated polystyrene beads and 820-nm diameter antidigoxigenin-coated beads, forming dumbbells (Fig. 1 A). Samples were measured in 50 mM MOPS (3-(N-morpholino)propanesulfonic acid) (pH 7.0), 130 mM KCl, with an oxygen-scavenging system consisting of 40 U/mL glucose oxidase, 185 U/mL catalase, and 8.3 mg/mL D-glucose. The sequences of the DNA hairpins are listed in Table 1. All measurements were done using a custom dual-trap optical tweezers instrument described previously (29). Constant-force measurements were made using a passive force clamp (30) to maintain a constant tension on the hairpin near F_1/2, the force at which the hairpin spent equal time in each state (Fig. 1 B). The trap stiffness was 0.5 pN/nm for the force-sensing trap; the zero-stiffness anharmonic region of the trapping potential was used for the other trap to implement the passive force clamp (30). Data were sampled at 100–256 kHz during trajectories of length 90–520 s and filtered online at the Nyquist frequency. Force jump measurements were implemented using the passive force clamp to maintain a constant force after jumping down to the refolding force to avoid artifacts arising from feedback loops (31, 32). The force was changed during force jumps by acousto-optical modulation of the laser intensity in the anharmonic trap.

Figure 1.

Round-trip time diffusivity analysis of DNA hairpin (color online). (A) A schematic of measurement shows that a single DNA hairpin is connected to double-stranded DNA handles that are attached to beads held by optical traps. The extension of the DNA construct is measured as the hairpin structure changes. (B) A representative section of an extension trajectory measured at constant force for hairpin 30R50/T4 is shown. The left inset shows the hairpin sequence, and the right inset shows the equilibrium probability density. Dashed lines indicate the locations of the unfolded (x_u) and folded (x_f) states. (C) The average round-trip times calculated from the extension trajectory with respect to reference points x_f (black) and x_u (red, inverted for ease of comparison) are qualitatively similar but do not agree quantitatively. (D) The diffusivity profile calculated from the round-trip time depends on the choice of reference point (black: reference point x_f, red: reference point x_u). Error bars represent SE. To see this figure in color, go online.

Table 1.

DNA Hairpin Sequences

30R50/T4	5′-GAGTCAACGTACTGATCACGCTGGATCCTATTTTTAGGATCCAGCGTGATCAGTACGTTGACTC-3′
20TS06/T4	5′-GCCGGCTATTATTTATATTCTTTTGAATATAAATAATAGCCGGC-3′
20TS10/T4	5′-GACTGAAGCGTATTATATTATTTTTAATATAATACGCTTCAGTC-3′
20TS16/T4	5′-GACTGTGTAGGTCACGGCTATTTTTAGCCGTGACCTACACAGTC-3′
20M07/T4	5′-GAGTCATCGTCTGGATCCTGTTTTCAGGATCCAGACGTTGACTC-3′
20M10/T4	5′-GAGTCAACGTCTGGATCCTGTTTTCAGGATCCTGACGTTGACTC-3′

Round-trip time analysis

The round-trip time analysis is based on the assumption of diffusive dynamics along the reaction coordinate, whose time-evolution is described by the 1D Fokker-Planck equation. Under this assumption, the average time required to start at extension x, reach some fixed reference point x₀ for the first time, and then subsequently return to x for the first time is given by the following (25):

$${\tau }_{\text{RT}}\left(x,x_0\right)=Z\underset{x_0}{\overset{x}{\int }}\left\{\exp \left[\beta G\left(x^{\prime }\right)\right]/D\left(x^{\prime }\right)\right\}d{x}^{\prime },$$ (1)

where τ_RT(x,x₀) is the average round-trip time between x and x₀, Z is the partition function, β is the inverse thermal energy, and G(x) is the 1D free-energy profile governing the motion. The solution for the diffusion coefficient is thus written as follows:

$$D\left(x\right)={\left[P\left(x\right)\frac{\partial {\tau }_{\text{RT}}\left(x,x_0\right)}{\partial x}\right]}^{-1},$$ (2)

where P(x) is the extension probability distribution. P(x) was found from the histogram of extension values in constant-force trajectories (Fig. 1 B, inset). τ_RT(x,x₀) was calculated empirically from the trajectories for x between the positions of the folded and unfolded states, respectively x_f and x_u (Fig. 1 C), by doing the calculation once with the reference point x₀ located at x_f and then testing for consistency a second time with the reference point at x_u. The calculations were done for x in steps of ∼1 nm, starting and ending ∼2 nm from the boundaries to avoid edge effects. To reduce noise in the calculation of D(x) using Eq. 2, we fit τ_RT with a monotonic smoothing spline before differentiating numerically. The analysis was applied separately to each extension record at constant force.

Fall time analysis

The fall time analysis of force jump trajectories was based on the assumption of overdamped diffusive dynamics over a 1D energy landscape (33). Under this assumption, the diffusivity is given by the following (26):

$$D\left(x\right)={\left[{\tau }_{\text{c}}\left(x\right)\frac{d\rho \left(x\right)}{dx}\right]}^{-1},$$ (3)

where the fall time τ_c(x) is the average time after the force was jumped that was required to reach extension x for the first time during a refolding trajectory starting from the unfolded state, and ρ(x) is the nonequilibrium extension distribution from the force jump trajectories when each individual curve was terminated once the extension x is reached for the first time. ρ was calculated by pooling the trajectories from all repeated force jump measurements on a given molecule, terminating each curve at x the first time it was reached. The exit flux ρ′ was then found by applying a kernel smoother to ρ and differentiating numerically. τ_c was found by averaging the time required in each individual curve after the force jump to reach a given extension x for the first time, measured from the last time the extension of the unfolded state, x_u, was crossed.

Kramers’s theory rate analysis

The diffusion coefficient for barrier-crossing calculated via Kramers’s theory for the two-state hairpins 20TS06/T4, 20TS10/T4, and 20TS16/T4 from (28) was reported previously (34). Briefly, free-energy profiles were reconstructed from the equilibrium extension distribution P(x) via the inverse Boltzmann transform while deconvolving the effects of the dumbbell compliance as described (28). The barrier height ΔG^‡ and harmonic curvatures of the potential wells (κ_w) and barrier (κ_b) were measured directly from the reconstructed profiles, the microscopic rates (k) for folding and unfolding were measured from the distribution of lifetimes in each state via thresholding (27), and D was then calculated from Kramers’s rate equation:

$$D=\frac{2\text{π}k}{\beta \sqrt{{\kappa }_{\text{b}}{\kappa }_{\text{w}}}}\exp \left(\beta \Delta G^{\text{‡}}\right).$$ (4)

For the three-state hairpins 20M07/T4 and 20M10/T4 from (28), free-energy profiles were reconstructed and analyzed in the same way. The microscopic rates for each interstate transition were obtained by signal-pair correlation analysis (35), and Kramers’s equation was applied to each barrier separately.

Simulations

Brownian dynamics simulations of folding measurements under constant force and force jump conditions were performed similarly to previous work (36, 37). Diffusive motion of a molecule over a 1D free-energy profile was assumed, with the molecule tethered at one end to a bead of radius r via a spring with stiffness k, while a constant force F was applied to the bead. The bead radius was r = 400 nm, similar to the measurements, leading to a bead diffusion coefficient of 5.5 × 10⁵ nm²/s (assuming viscosity of 10⁻³ Pa · s as for water). The free-energy profile was similar to that of hairpin 30R50/T4 used in measurements (28), but with energies scaled down to allow for more frequent transitions and hence more rapid simulations. Stochastic forces on the molecule and bead were generated from the expression (2/D)^1/2W(t)/β, where W(t) represents Gaussian white noise. For equilibrium simulations, the nonstochastic forces on the molecule and bead were –V′(x₁) + k(x₂ – x₁) and k(x₁ – x₂) – F, respectively, where x₁ is the extension of the molecule, x₂ the position of the bead, and V(x₁) is the energy profile for the molecule. Simulations were run for 2–5 s for each condition studied, containing ∼400–1200 transitions. Force jumps were simulated by selecting the initial position of the molecule randomly from the equilibrium distribution of positions in the unfolded state calculated from the landscape at the initial force, 2.5 pN above F_1/2. After 0.1 ms at the initial force, the force was jumped down by 5 pN. In all simulations, a 0.1-ns time step was used, and the data were down-sampled to 0.1 μs for analysis. Approximately 100 force jumps were simulated for each condition studied. All simulation data were analyzed in the same way as the experimental data.

Results

We first applied round-trip time analysis to constant-force measurements of the hairpin 30R50/T4 (Fig. 1 B, left inset) from (27). The force was kept constant in these measurements with a passive force clamp (30) to avoid artifacts in the dynamics that can be caused by the use of a feedback loop (32). The reference point for calculating the average round-trip time, τ_RT, from the extension trajectory (Fig. 1 B) was first chosen to be the location of the folded-state peak, x_f, in the extension distribution (Fig. 1 B, right inset). Calculating τ_RT (Fig. 1 C, black) and hence D(x) from Eq. 2 (Fig. 1 D, black), we found that D(x) was roughly constant over the range of extensions corresponding to unfolding the upper half of the stem and then rose over an order of magnitude as x approached the folded state, indicating distinct position-dependence of D. To test for self-consistency, we also calculated τ_RT using the unfolded state at x_u as the reference point (Fig. 1 C, red), obtaining a separate estimate of D(x). Surprisingly, this second calculation resulted in a diffusivity profile that was quite different from the first (Fig. 1 D, red): D(x) was roughly constant for unfolding the lower half of the hairpin stem but increased by over an order of magnitude as x approached the unfolded state, which was the reverse of the pattern of position-dependence found using the other reference point.

Naively, the value of D(x) should not depend on the choice of the reference point unless the dynamics along the reaction coordinate are non-Markovian (25), arising for example from the choice of a poor reaction coordinate (38). In such a case, the assumption underlying the calculation—that the motion is well described in terms of 1D diffusion—breaks down. Although multiple dimensions may be needed to describe hairpin folding in its full phase space (39), previous work analyzing the statistics of the transition paths (40) during the folding of this very same hairpin under mechanical tension showed that, in fact, the dynamics agree quantitatively with 1D diffusive motion under the conditions of this measurement (22). Indeed, a study of the splitting probability, p_fold(x)—the probability at a given reaction-coordinate value x that the molecule will reach the folded state before the unfolded state—not only confirmed that extension was a good reaction coordinate but also suggested that D(x) was close to constant (41). Hence, the inconsistency most likely arises from some alternate cause.

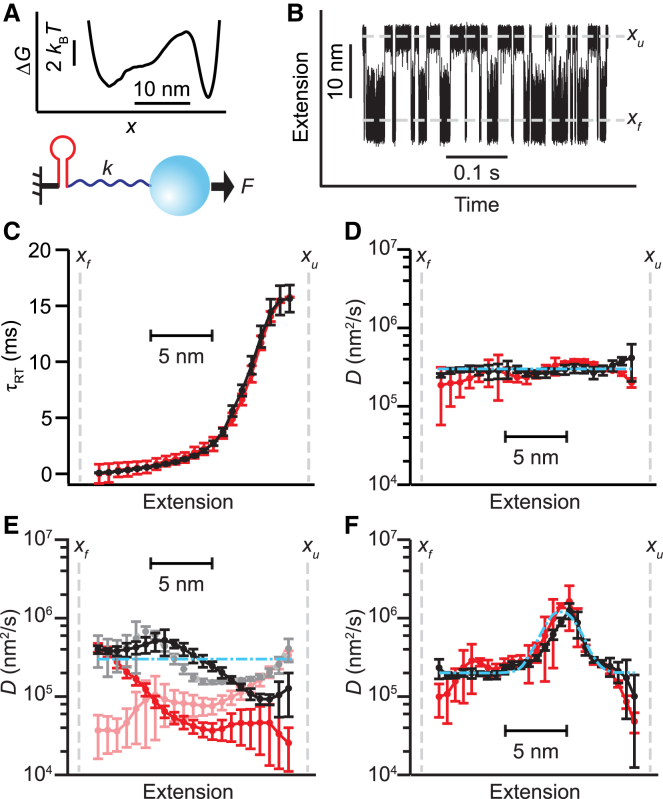
Previous studies have found that the dynamics observed in force spectroscopy measurements can be affected by the properties of the handle linkers and probe (in this case, beads) used to apply force to the molecule (30, 31, 36, 37, 42, 43, 44). Given the possibility for convolution of the dynamics of the molecule with the dynamics of the handles and beads, we investigated whether this effect might cause the inconsistency of the round-trip time calculation by using Brownian dynamics simulations of a model system. This model encapsulated the principal elements of the measurement: a molecule with a given 1D landscape (Fig. 2 A, inset) attached to a bead subjected to a constant force F ∼ F_1/2 via a linker of stiffness k (Fig. 2 A). Extension trajectories (Fig. 2 B) were simulated for two k values, 0.2 and 1 pN/nm, with a bead radius of 400 nm (similar to the experiment), as well as for the case in which there were no linkers or beads and the force was applied directly to the end of the molecule. For simplicity, a constant value D = 3 × 10⁵ nm²/s was imposed in the calculation. The simulation parameters were chosen to match the numbers expected from the experiments: the experimental handle stiffness was 0.2–0.3 pN/nm (equivalent to the low-stiffness condition used in the simulation), and the experimental values for D in DNA hairpin folding have been reported from single-molecule fluorescence and force studies to be in the range 1 × 10⁴ to 5 × 10⁵ nm²/s (20, 21, 34, 45, 46).

Figure 2.

Round-trip time analysis of folding simulations (color online). (A) Extension trajectories for folding of a hairpin with the given energy landscape (inset) were simulated by assuming a constant force applied to the end of the hairpin, either directly or via a 400-nm radius bead attached to the hairpin by a handle of stiffness k. (B) A simulated extension trajectory in the absence of beads and handles is shown. Dashed lines indicate the locations of the unfolded (x_u) and folded (x_f) states. (C) The average round-trip times calculated from the trajectory in (B) with respect to reference points x_f (black) and x_u (red, inverted for ease of comparison) agree well. (D) The diffusivity profiles calculated from the round-trip times in (C) agree well for both choices of reference point (black: x_f, red: x_u), and recover the constant diffusion coefficient imposed in the simulation (cyan) except near the reference points. (E) After repeating the analysis for simulations including a stiff (black/gray: k = 1 pN/nm) or compliant (red/pink: k = 0.2 pN/nm) handle, the results for the two choices of reference point (black/red: x_f, gray/pink: x_u) are somewhat similar for the stiff handle but differ substantially for the compliant handle. The diffusivity profile is degraded only slightly for the stiff handle compared to the no-handle simulation but significantly for the compliant handle. (F) When the folding is simulated without handles while imposing a spatially varying diffusivity (dot-dashed line), the diffusivity profile is again recovered reasonably well for both reference points (black: x_f, red: x_u). Error bars represent SE. To see this figure in color, go online.

Considering first the case in which the handle and bead were removed, τ_RT (Fig. 2 C) and D(x) (Fig. 2 D) were calculated from the trajectory in the same way as for the experimental data, using as the reference points x_f (black) and x_u (red). The results for this simulation were much more self-consistent than the results from the experimental data; the calculations based on the two different reference points (x_f and x_u) both showed a diffusivity profile that was effectively flat, with a value of D equal within error to that imposed in the simulation (Fig. 2 D, dot-dashed line). By repeating the calculations with the simulations containing handles and beads, however, we found that this self-consistency began to degrade as the handles became more compliant. At k = 1 pN/nm, the diffusivity profile was fairly consistent between the calculations with different reference points (Fig. 2 E, black: reference point x_f, gray: reference point x_u) and still somewhat close to the expected result (dot-dashed line) over most of the extension range. However, at k = 0.2 pN/nm (Fig. 2 D, red: reference point x_f, pink: reference point x_u), the results for the two reference points diverged more significantly from each other, and D(x) began to look at least qualitatively similar to the profiles seen in the experimental result (Fig. 1 D). The D(x) values recovered in the latter case were generally lower than the value imposed in the simulation, except for those close to the reference point.

These simulations support the notion that the methodology for reconstructing the diffusivity profile from the round-trip time is sound but also that the calculations are being confounded by the influence of the linkers and beads attached to the molecule such that an incorrect profile for D(x) is recovered. To further confirm the essential soundness of the methodology for reconstructing D(x) from round-trip times, we altered the diffusivity profile imposed in the simulation without handle/beads to be Gaussian rather than constant (Fig. 2 F, dot-dashed line). The imposed diffusivity profile was indeed recovered by the round-trip time analysis (Fig. 2 F). Note that we expect to see such quantitative agreement between the simulation result and the imposed diffusivity in the case of the simulations of the isolated molecule. However, when comparing the simulations that include beads and linkers with the experiments, quantitative agreement cannot be expected: the diffusivity of the hairpin is likely different from what was assumed in the simulations, and the simulation model is a simplified representation of the actual measurement. Instead, only qualitative agreement with the general trends should be expected, as indeed was seen.

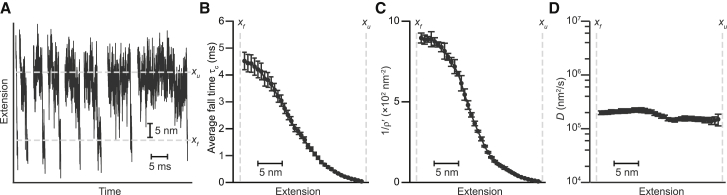
We next investigated an alternate approach for measuring D(x) based on fall time analysis of force jump refolding measurement (26). The same hairpin was remeasured under nonequilibrium conditions, jumping the force down from 5 pN above F_1/2, where the hairpin was unfolded, to 5 pN below F_1/2, where it folded rapidly (Fig. 3 A). As in the constant-force experiments, the force was kept constant using a passive force clamp to avoid feedback-loop artifacts. The average fall time to reach a given reaction-coordinate value x, τ_f(x), was calculated directly from the trajectories (Fig. 3 B), as was the reciprocal of ρ′ (Fig. 3 C), yielding D(x) from Eq. 3 (Fig. 3 D). The result this time was relatively independent of position, featuring variations of only ∼20%. The value for D was similar to the low end of estimates for D from measurements of transition path times (20, 21) and roughly half the value estimated from rates using Kramers’s theory (34). Notably, the fall time method yielded a diffusivity that differed significantly from the round-trip time results for the same hairpin (Fig. 1 D), both in terms of the profile of the position-dependence as well as the magnitude of D.

Figure 3.

Fall time analysis of diffusivity profile. (A) Force jump refolding trajectories measured with a passive force clamp are shown. (B) The average fall time calculated from the force jump trajectories is shown. (C) 1/ρ′, reciprocal of the exit flux. (D) The diffusivity profile from Eq. 3 is close to constant and disagrees with the results from the round-trip time analysis. Error bars represent SE.

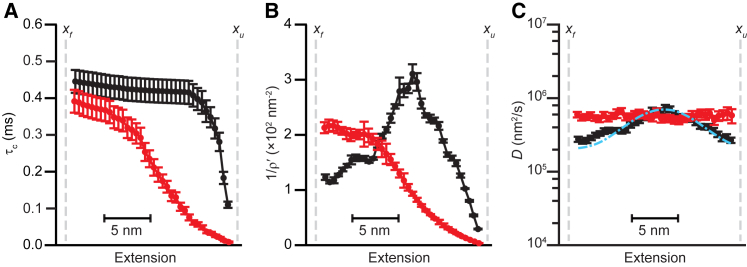
To assess whether the fall time method is affected by artifacts arising from the handles and beads in a way analogous to the round-trip time method, we simulated force jump measurements using the same model as for the equilibrium-hopping simulations. Simulations were done for an isolated molecule and for the same molecule attached to a bead via a tether of compliance 0.2 pN/nm, in both cases using a nonconstant diffusivity profile. From τ_c (Fig. 4 A, black: molecule alone, red: molecule tethered to bead) and 1/ρ′ (Fig. 4 B, black: molecule alone, red: molecule tethered to bead), we calculated D(x) as above. The result from the simulation without beads and linkers (Fig. 4 C, black) recovered both the magnitude and position-dependence of the imposed diffusivity (Fig. 4 C, cyan) quite well. However, including the linkers and beads in the simulation yielded a result (Fig. 4 C, red) that, although close to the correct magnitude, did not capture any of the position-dependence. The result was qualitatively similar to what was observed experimentally, indicating that the constant D deduced from experiments could just reflect the confounding effects of beads and linkers on the fall time method.

Figure 4.

Fall time analysis of force jump simulations (color online). (A) The average fall time calculated from force jump trajectories simulated using the same energy landscape as in Fig. 2A is shown for an isolated hairpin (black) and hairpin connected to bead via linker with stiffness k = 0.2 pN/nm (red). (B) The reciprocal of the exit flux for simulated trajectories is shown (black: isolated hairpin, red: 0.2 pN/nm linker stiffness). (C) The diffusivity profile calculated for the isolated hairpin (black) recovers the position-dependent diffusivity imposed in the simulation (cyan), but the profile calculated for the hairpin linked to a bead (red) does not recover the position-dependence and is instead close to constant. Error bars represent SE. To see this figure in color, go online.

Given the inability to determine D(x) reliably from the round-trip and fall time methods, we sought another approach to give insight into the question of position-dependence in D: we used Kramers’s theory to deduce D from rates and free-energy profiles for barriers located at different positions along the stem (34). Kramers’s rate equation (7) is sensitive primarily to D in the vicinity of the energy barrier, but the barrier can be moved within the stem by engineering the hairpin sequence (28). Because the projection of the full multidimensional landscape onto the reaction coordinate should be similar for hairpins having the same stem-tetraloop structure and being unfolded/refolded in the same way (via force applied to the termini), any strong position-dependence of D arising from landscape projection effects within a single hairpin (e.g., D lower for smaller x) ought to show up as a similar trend when the barrier position is moved within different hairpins. Hence, moving the barrier within the stem should provide a crude window into how D varies when measured at different locations along the stem, even if this approach does not truly measure D(x).

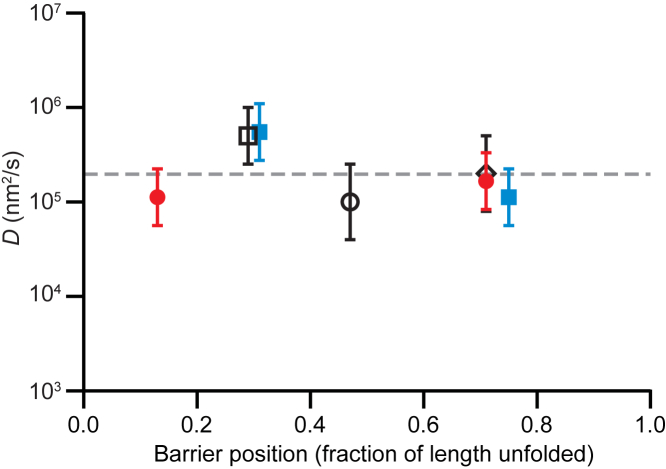
Equilibrium extension measurements of a series of two-state and three-state hairpins of the same length with barriers in various locations from (28) (two-state hairpins 20TS06/T4, 20TS10/T4, and 20TS16/T4; three-state 20M07/T4 and 20M10/T4), for which energy landscapes were measured previously using the inverse Boltzmann transform (28), were used to determine the folding and unfolding rates across each barrier in the landscape. In the case of the two-state hairpins, rates were found using thresholding analysis (27); in the case of the three-state hairpins, the microscopic rates for all transitions were found via signal-pair correlation analysis (35). Measuring the barrier heights directly from the reconstructed landscapes and determining the stiffness of the potential wells and barriers from harmonic fits of the landscape (34), D was then calculated for each barrier using Eq. 4. The values for unfolding and refolding across each given barrier agreed within error and were therefore averaged. The results, plotted as a function of the relative position of the barrier along the reaction coordinate (Fig. 5), show that D at the barriers is effectively constant for different barrier positions, D ∼2 × 10⁵ nm²/s (Fig. 5, dashed line). This result is close to the value found near the barrier for hairpin 30R50/T4 from the fall time analysis (2 × 10⁵ nm²/s) but larger than the values from the round-trip time analysis (10⁴–10⁵ nm²/s, depending on the reference point).

Figure 5.

Kramers’s analysis of D for barriers at different positions (color online). The diffusion coefficient for barrier-crossing, determined from Kramers’s theory (Eq. 4) via landscape analysis of hairpins with barriers located at different positions, is the same within error for barrier positions spanning the range from close to the folded state to close to the unfolded state, which is consistent with a diffusivity that is roughly flat (dashed line). The open square shows hairpin 20TS06/T4, the open circle shows hairpin 20TS10/T4, the open diamond shows hairpin 20TS16/T4, the filled circle shows hairpin 20M07/T4 (two barriers), and the filled square shows hairpin 20M10/T4 (two barriers). Error bars represent SE. To see this figure in color, go online.

Discussion

By evaluating the performance of these methods for determining the position-dependence of D, we see that the round-trip time method yields results that are not self-consistent when calculated in ways that should be the same. Moreover, the results found in the region near the barrier (located ∼7 nm from x_u (27)) disagree with the values obtained previously from other methods applied to the same hairpin: analysis of the rates using Kramers’s theory, the average transition path time, and the distribution of individual transit times over the barrier all indicate D ∼2–5 × 10⁵ nm²/s in the barrier region (20, 34). Based on simulations of the experiment, these problems appear to arise from the effects of instrumental artifacts in the measurements. The results for the fall time analysis, in which D is constant with a value that agrees reasonably well with previous work, look more promising. Other work has found that hairpin folding can be modeled well assuming constant D, suggesting that a strongly position-dependent D is unlikely (21, 41). Nevertheless, there are reasons for concern about these results, too: the simulations show that the fall time analysis is also affected by instrumental artifacts that confound the results in ways that obscure the position-dependence of D.

The above considerations suggest that determining the diffusivity profile from experimental single-molecule folding trajectories is less straightforward than hoped. Although the round-trip and fall time methods both work when applied to simulated data without including any instrumental effects (25, 26, 33), careful consideration of how the details of the experimental assay may affect the analysis is required before these methods can be applied reliably to experimental data. Optical trapping experiments like those described above, for example, measure not the extension of the hairpin itself, but rather the position of the beads that are attached via compliant linkers to the ends of the hairpin. The compliance of the bead/linker system broadens the distribution of extension values observed beyond what would be expected simply from fluctuations of the ends of the hairpin in isolation, whereas the viscous drag on the bead (and to a lesser extent, the linkers) limits the response speed for detecting extension changes in the hairpin (37, 42). Furthermore, the linker compliance couples the diffusion coefficient of the beads to the diffusion coefficient for the hairpin and can therefore influence the hairpin dynamics—both the rates and transition times (36, 37, 44, 47).

These instrumental effects are expected to alter the outcomes of both the round-trip and fall time analyses. In the case of the fall time analysis, the viscous drag will tend to increase τ_c by reducing the local velocity that is reached in the transition paths (effectively convolving the conformational dynamics of the hairpin with the response function of the beads/linkers and thus possibly altering the shapes of the transition paths), whereas the compliance tends to have an averaging effect on ρ′; the slow response time of the beads/linkers may also alter ρ. In the case of the round-trip time analysis, any drag-induced increase in the transition path times will reduce ∂τ_RT/∂x; the compliance will tend not only to broaden the equilibrium extension distribution P(x) but also to alter τ_RT, especially in the transition region (where compliance-induced noise will introduce new nonproductive level-crossings), and hence ∂τ_RT/∂x. Instrumental artifacts may thus affect all the terms in both Eqs. 2 and 3.

The effects of compliance can sometimes be removed empirically by using deconvolution methods, for example based on the measured compliance-dependent point-spread-function (28, 48) or theoretical models of the system dynamics (49). However, the coupling of compliance and dynamic effects in the analyses above represents a more difficult problem in deconvolution. It might be possible, in principle, to use dynamical models of the measurement mechanics (50) to separate the dynamics of the different components of the mechanical network (beads, linkers, and molecule), but the full effects of bead-linker coupling on the paths followed during individual transitions remain incompletely understood (36, 37).

Reliable application of the round-trip and fall time methods for measuring D(x) thus awaits future developments in theory that will permit the instrumental effects to be accounted for more robustly. We note that these instrumental effects help to explain not only why the round-trip and fall time methods may yield incorrect results when applied to experimental data but also why they produce mutually inconsistent results even when applied to measurements on the same individual molecule; the parameters used in the two methods, τ_c and ρ′ for the fall time method as opposed to ∂τ_RT/∂x and P(x) for the round-trip time method, are presumably affected differently by the compliance and drag, leading to different outcomes.

Although we have discussed the issue of instrumental effects in the specific context of optical trapping measurements, similar considerations will apply to other types of force spectroscopy assays of conformational dynamics, such as AFM and magnetic tweezers, in which compliant linkers connect the molecule of interest to a force probe subject to viscous drag (18). Differences in the properties of the linker and probe geometries in different assays, however, may change the ways in which the instrumental effects alter the results. For example, the linkers used in AFM studies are generally much shorter and stiffer than the linkers in optical tweezer measurements, and thus compliance-induced broadening of extension distributions is less important. However, stiffer linkers couple the dynamics of the molecule more closely to the dynamics of the force probe (36, 37): indeed, in the stiff-linker regime, the dynamics of the molecule become limited by the dynamics of the cantilever so that the effective diffusivity observed is simply that of the cantilever (36, 37). These observations may help explain the results of AFM studies of diffusivity in folded and unfolded polyubiquitin, which found notably low but constant values for D, ∼10^2–3 nm²/s (26, 51). These values are much lower than those found by other methods for protein unfolding (52) and chain reconfiguration times (14, 15, 53), D ∼10^6–8 nm²/s, and also inconsistent with the fast Kramers’s rate prefactor found for the same polyubiquitin construct from temperature-dependent AFM dynamic force spectroscopy kinetics (54). In contrast, the stiffness of the kilobase-long DNA handles typically used in optical tweezers is sufficiently low that the intrinsic molecular diffusivity can in principle be recovered (36, 37, 42, 47), but compliance-induced extension broadening can still have significant effects.

Considering the hairpin folding results found above, the Kramers’s rate analysis can be interpreted as suggesting that D(x) is close to constant (Fig. 5). Of course, this analysis is only a crude probe of how D may vary with position because Kramers’s theory is effectively only sensitive to D in the region close to the barrier—it does not yield the diffusivity profile. As argued above, however, large position-dependent changes in D arising from effects that are common to all the hairpins (like projection effects) ought to be detectable this way. Our results, which show that moving the barrier to different locations in the hairpin stem does not significantly change the value of D near the barrier, are thus consistent with the view that D(x) is roughly constant but are not conclusive because the method does not directly probe the diffusivity profile for a given choice of barrier location. We note that other results also suggest that D(x) is roughly constant for DNA hairpins, including models using constant D that replicate experiments well (55) and studies of the splitting probability (p_fold) showing that p_fold calculated empirically from extension trajectories agrees well with p_fold calculated from the measured energy landscape under the assumption of constant D (41). Again, however, such evidence is indirect. Recent measurements of sequence-dependent transition times in DNA hairpin folding found that D is faster for G:C pairs than for A:T pairs (21), implying some position-dependence from sequence variations, but this effect is relatively small (less than a factor of two) compared with the 10-fold or greater variations in D suggested by the round-trip time analysis. More direct measurements of D(x) may be possible in future work that studies the shape of transition paths (20, 56) because the position-dependence of the velocity along the reaction coordinate during transition paths can be related to the diffusivity profile (57); however, such approaches have yet to be developed and tested.

Conclusions

This work shows that methods that have been proposed for determining the diffusivity profile along the reaction coordinate for biomolecular folding from single-molecule trajectories yield unreliable results because of experimental artifacts—in this case, the effects of the coupling of the force probe in force spectroscopy measurements to the molecule of interest. It is essential to understand better how the measurement method affects the data so that these effects may be removed to obtain reliable results. Measuring the position-dependence of the diffusion coefficient directly from experiment thus remains a technically challenging problem that has yet to be solved. Continued advances in understanding how instrumental effects alter the experimentally observed behavior (31, 36, 37, 42, 43, 44) hold the promise that these challenges can be overcome in the future.

Author Contributions

M.T.W. designed the research. D.A.N.F. performed the experiments. R.P. and A.G.T.P. performed the simulations. D.A.N.F., A.H., R.P., and A.G.T.P. analyzed the data. F.W. and D.A.N.F. provided the reagents. M.T.W., D.A.N.F., R.P., A.G.T.P., and A.H. wrote the manuscript.

Editor: Thomas Perkins.