Fast-Folding Pathways of the Thrombin-Binding Aptamer G-Quadruplex Revealed by a Markov State Model

Abstract

G-quadruplex structures participate in many important cellular processes. For a better understanding of their functions, knowledge of the mechanism by which they fold into the functional native structures is necessary. In this work, we studied the folding process of the thrombin-binding aptamer G-quadruplex. Enabled by a computational paradigm that couples an advanced sampling method and a Markov state model, four folding intermediates were identified, including an antiparallel G-hairpin, two G-triplex structures, and a double-hairpin conformation. Likewise, a misfolded structure with a nonnative distribution of syn/anti guanines was also observed. Based on these states, a transition path analysis revealed three fast-folding pathways, along which the thrombin-binding aptamer would fold to the native state directly, with no evidence of potential nonnative competing conformations. The results also showed that the TGT-loop plays an important role in the folding process. The findings of this research may provide general insight about the folding of other G-quadruplex structures.

Introduction

Structures are crucial for proteins and nucleic acids to carry out their biological functions. In recent years, it has been found that noncanonical nucleic acid structures are involved in many cellular processes (1, 2, 3). An example is the G-quadruplex, which is a family of quadruple helix structures (3). Accumulated experimental evidence has indicated that G-quadruplex structures are effective in the regulation of telomere maintenance, replication, transcription, and translation (4, 5, 6). Likewise, it has been stated that they are attractive for use as drug-designing targets for cancer therapy because of their impedance of telomere-continuous elongation (7, 8).

G-quadruplex structures are formed through a recurring unit named the G-tetrad, which arises from Hoogsten hydrogen bonding between four guanines (Fig. 1 a). For enhanced stabilization of four-stranded helical structures, two or more G-tetrads stack on top of each other along with the positioning of monovalent cations (typically K⁺ or Na⁺) between G-tetrad units (9, 10). Until now, various G-quadruplex folding topologies have been recognized. Influenced by sequence, loops, type of monovalent cations, and other factors, G-quadruplex structures may adopt parallel, antiparallel, and (3+1) hybrid conformations (11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24). Although these structures offer the static snapshots of functional native conformations, the mechanism by which they fold to the native state cannot be effectively understood. Knowledge of the folding mechanism is necessary for a better understanding of how G-quadruplexes fulfill their functions. In addition, the study of the folding process of G-quadruplex structures is scientifically beneficial for understanding the dynamics of the structures of other nucleic acids. This is because they involve many important physical or chemical interactions that affect the dynamics of nucleic acids, such as the hydrogen bonds, the electrostatic effect associated with metal ions, and the syn/anti reorientation of the glycosidic bonds.

Figure 1.

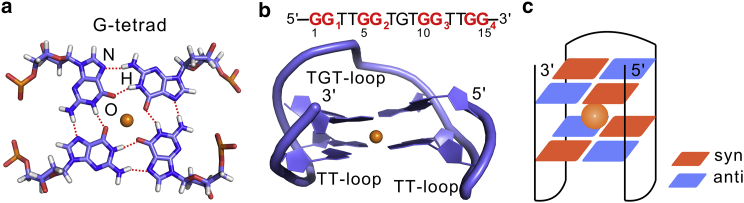
Illustration of the G-tetrad and TBA native structure. (a) A schematic representation of the G-tetrad is shown. The Hoogsten hydrogen bonds are plotted as dashed lines. The metal ions are shown as spheres. (b) The sequence and native structure of TBA (PDB: 1QDF) is shown. The four G-tracts are defined as GG₁∼GG₄, respectively. (c) A schematic representation of the TBA native structure is shown. The syn and anti guanines are labeled by different colors. To see this figure in color, go online.

Many studies have examined the folding mechanism of G-quadruplex structures (25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45). For instance, Gray et al. conducted an experimental study to monitor the folding process of the human telomeric hybrid-1 and hybrid-2 G-quadruplexes (32). They found that a complex pathway with the involvement of a prefolded G-hairpin and a G-triplex exists. In another study, Li and co-workers also reported a G-triplex intermediate in the folding process of human telomeric G-quadruplex using magnetic tweezers (35). Molecular dynamics (MD) simulations were also used to provide much detailed information or insights on the folding of G-quadruplexes. As highlighted by Sponer et al., the folding of G-quadruplexes occurs by multipathway mechanisms. This observation was achieved after performing extended sets of MD simulations to study the dynamics of various potential G-hairpin and G-triplex structures (38, 39). Unfortunately, despite these and other pioneering studies, even the folding process of the simplest G-quadruplex topology, thrombin-binding aptamer (TBA), remains unclear. Kim et al. suggested that the folding of TBA is a two-state process (42). However, Limongelli and co-workers reported that the G-triplex conformation must be involved in the folding protocol as an intermediate (43).

The aim of this study is to decipher the folding mechanism of the TBA G-quadruplex by incorporation of all-atom MD simulations. Because TBA is the simplest G-quadruplex topology, some general nature of the G-quadruplex (such as free-energy landscape, the possible folding mechanism, and potential folding intermediates) could be explored as a benchmark to study the folding process of other G-quadruplex structures. The determination of the solution structure of TBA revealed that TBA adopts an antiparallel topology containing two G-tetrads: a TGT-loop and two TT-loops (Fig. 1, b and c) (46). In addition, the stability of the structure is enhanced by a cation coordinating between the consecutive G-tetrads. In this study, the four G-tracts were labeled as GG₁∼GG₄ in the 5′–3′ direction, and the guanine nucleotides in the G-tetrads and TGT-loop were defined as G-tetrad–forming guanines and loop-guanines, respectively (Fig. 1 b). Because the experimental folding timescales of TBA and other similar two–G-tetrad G-quadruplexes range from dozens of milliseconds to several seconds (47, 48, 49), which is well beyond the timescale of traditional all-atom MD simulations, a paradigm that couples an advanced sampling method termed bias-exchange metadynamics (BEMD) (50) with the Markov state model (MSM) (51) was employed in this study to overcome this problem. Several metastable states were identified, and transition path theory (TPT) (52) analysis was performed to determine the folding pathways. The contribution of this research is to propose the presence of multiple folding pathways for the TBA G-quadruplex. Its relevance to the reported experimental and theoretical observations is discussed.

Methods

An unfolding MD simulation was performed to acquire an ensemble of unfolded structures. Then, a BEMD simulation was carried out to sample the conformational space by randomly choosing a structure from the unfolded ensemble as the starting conformation (Fig. S1 a). After that, a set of unbiased MD simulations were conducted by selecting a series of seeds from the BEMD simulation. Finally, an MSM was built to identify the metastable states, and a TPT analysis was performed to determine the folding pathways. All simulations were performed with the Groningen Machine for Chemical Simulations (GROMACS) 4.6.2 package (University of Groningen, Groningen, the Netherlands) (53) and the latest version of the Assisted Model for Building with Energy Refinement (AMBER) DNA force field ff99bsc0εζ_OL1χOL4 (University of California at San Francisco, San Francisco, CA) (54, 55, 56), which greatly improves the accuracy of simulations for G-quadruplexes. The force field format was converted from AMBER to GROMACS using the Antechamber Python Parser Interface script (57). The Python Emma’s Markov Model Algorithms package was used to build the MSM and to perform the TPT analysis (58). Details of the unfolding simulation are documented in Supporting Material.

Preparation of the system

The unfolded structure was solvated within a periodic box of 4783 transferable intermolecular potential with 3 points water molecules. K⁺ and Cl⁻ were added to neutralize the system and to maintain a salt concentration of 100 mM. The electrostatic interaction was treated using the particle mesh Ewald method with a cutoff of 1.0 nm. The cutoff of the van der Waals interactions was also selected as 1.0 nm. The MD time step was set to 2 fs, as all bonds were constrained using the linear constrain solver algorithm. The Berendsen algorithm was used for both temperature and pressure coupling. The whole system was first subjected to a minimization of 1000 steps, followed by an equilibrium run with an NPT ensemble at 1 atm and 300 K for 20 ns. The last conformation was utilized as the initial structure for the BEMD simulation.

BEMD simulation

Metadynamics is a widely used method in molecular simulation to accelerate the barrier-crossing events (59). In metadynamics, the system is forced to escape from local energy minima by periodically adding external repulsive Gaussian potentials, as follows:

$$\text{V}\left(\text{S}\left(\text{x}\right),\text{t}\right)=\mathit{\omega }\sum _{t^{\prime }=\Delta t,2\Delta t\dots ,t^{\prime }<t}\text{exp}\left(\frac{{\left(S\left(x\right)-S\left(t^{\prime }\right)\right)}^2}{2\delta s^2}\right),$$ (1)

where s(t) is the value of the collective variables (CVs) at time t, ω is the Gaussian height, δ is the Gaussian width, and Δt is the time interval of the addition of Gaussian potentials. BEMD is an extension of the metadynamics method. It enlarges the conformational sampling space by employing multiple replicas that exchange their configurations and velocities periodically according to the metropolis-like criterion.

Four replicas were used in this study, with each biased on a different CV. The CVs were chosen as 1) the number of native hydrogen bonds formed by the H and O/N atoms in the two G-tetrads (N_hb), 2) the coordination number between the K⁺ and O atoms of the G-tetrad–forming guanine bases (N_KO), 3) the number of native contacts formed by the heavy atoms of G-tetrad–forming guanines (Q), and 4) the distance mean-square deviation of the backbone (C4’ atoms) with respect to the native structure. The details of the CVs are documented in Supporting Material.

The height of the Gaussian potential was set to 0.5 kJ/mol, and the widths were chosen as 0.5, 0.5, 1.8, and 0.02 nm for the four CVs, respectively. The time interval for depositing the Gaussian potentials was 1 ps, and the exchange-attempting interval between replicas was 30 ps. The simulation time of each replica was 100 ns. The PLUMED GROMACS plugin (60) was used for the BEMD simulation.

Seeding conventional MD simulations

All the conformations obtained from BEMD simulation were clustered using a simple algorithm. The i-th conformation with the representative structures of the clusters was obtained previously one-by-one. If a root mean-square deviation defined by the heavy atoms of the G-tetrad–forming guanines smaller than a cutoff of 0.3 nm was detected, the i-th conformation was deemed to belong to the corresponding cluster. Otherwise, if this conformation did not belong to any existing clusters, it was assumed to be the representative structure of a new cluster. After that, three structures were randomly chosen from each cluster as starting points to generate a set of 20 ns conventional MD simulations. When constructing MSMs, the first 5 ns frames of each trajectory were discarded. All the conventional MD simulations were performed at 300 K with an NPT ensemble. The setup and the parameters were identical to those described above.

MSM and validation

MSM is a powerful tool to investigate the conformational dynamics of biological macromolecules (61, 62). In an MSM, the conformational space is transformed into a set of discrete microstates. When choosing a reasonable time unit, termed the lag time, which is longer than the relaxation time within each discrete state, the jumps between these microstates can be regarded as a Markov chain. Under this condition, the time evolution of the ensemble probabilities can be modeled by the following master equation:

$$\text{p}\left(\text{n}\mathit{\tau }\right)=T^n\left(\tau \right)p\left(0\right),$$ (2)

where τ is the lag time, p(τ) is the probability distribution of the states, and T(τ) is the transition probability matrix at the given lag time.

Numerous metrics have been used to coarse-grain the conformational space. These include the root mean-square deviation, distances between sets of atoms, Cartesian coordinates of atoms, and others. Likewise, a dimension-reduction method like principle components analysis can be employed to reduce the high-dimension conformational space. Recently, another method termed time-lagged independent component analysis (TICA) has been successfully used to reduce the dimension (63, 64). It is able to identify the coordinates of maximal autocorrelation at a lag time and differentiates between slowly equilibrating populations. Thus, TICA is a good choice to reduce the dimension of space in the construction of MSMs by projecting the input coordinates onto dominant independent components. After clustering the MD dataset into discrete microstates, the transition probability matrix, T(τ), at the given lag time is estimated using the maximal likelihood reversible transition matrix based on the quadratic optimizer (65). The microstates that quickly interconvert can be further grouped into the same macrostate using a hidden MSM (hMSM) (66), which is a useful method to find the hidden metastable states. In addition, a conformation was randomly chosen from each metastable state to conduct an additional 300 ns conventional MD simulation to investigate the structural dynamics. The parameters of the additional MD simulations are the same as those above. The mean first passage time (mfpt) from the metastable state I to J is estimated as follows:

$$\text{mfpt}\left(\text{I},\text{J}\right)=\frac{1}{{\pi }_i}\sum _{i\in I}{\pi }_{i}mfpt\left(i,J\right),$$ (3)

where π_i is the stationary probability of microstate i.

We validated our model in two ways. We first examined the behavior of the implied timescales t_i as a function of the lag time τ, as follows:

$$t_i=-\frac{\tau }{\ln \left|{\lambda }_i\left(\tau \right)\right|},$$ (4)

where λ_i is the i-th eigenvalue of the transition probability matrix at the given lag time τ. The Markovian lag time was determined by identifying the value after which the implied timescales reach a plateau. Then, we further validated our model by conducting a Chapman-Kolmogorov test, which compares the system’s residence probability of remaining in a certain metastable state predicted by the MSM and that directly computed from the MD simulations.

TPT

The folding pathway can be identified from the analysis of TPT (52). In TPT, by defining a reactant state A and a product state B, the probability flux along microstates i and j is estimated by the following equation:

$$f_{ij}={\pi }_i{q}_i^{-}{T}_{ij}{q}_i^{+},$$ (5)

where π_i is the stationary probability of microstate i, T_ij is the transition probability from microstate i to j, $q_i^{+}$ is the forward-committor probability that is defined as the probability that the system will reach the product state next rather than the reactant state from microstate i, and $q_i^{-}$ is the backward-committor probability $q_i^{-}=1-q_i^{+}$. The net flux $f_{ij}^{+}$, which defines the folding flux leaving state A and entering state B, is computed as follows:

$$f_{ij}^{+}=\max \left(0,f_{ij}-f_{ji}\right).$$ (6)

For the macrostate model, the conformational space is coarse-grained into a few metastable states {M_i}. The net flux is estimated by $F_{ij}^{+}=\text{max}\left\{0,F_{ij}-F_{ji}\right\}$, where $F_{ij}={\sum }_{k\in M_i,l\in M_j}{f}_{kl}$. Based on a previously published algorithm (52), the net fluxes can be further decomposed into a set of pathways along with their fluxes {f_i}. The probability of pathway i is obtained by computing the ratio of f_i over the total flux:

$$p_i=\frac{f_i}{{\sum }_j{f}_j}.$$ (7)

Results

MSM

As shown in Fig. S1, beginning from an unfolded structure, the BEMD simulation sampled a sufficiently large conformational space. The folded state could be sampled by the four replicas (Fig. S1, b–e), and jumps between the unfolded and folded states were observed in the reconstructed continuous trajectory (Fig. S1 f). Likewise, clusters of the conformations also covered the unfolded and folded states, as shown in Fig. S2. All these results indicated that the BEMD simulation provides a broad distribution of seeds to build the MSM. It is worth mentioning that the BEMD simulation was not employed to obtain the free-energy landscape. Thus, its convergence was not focused on in this study.

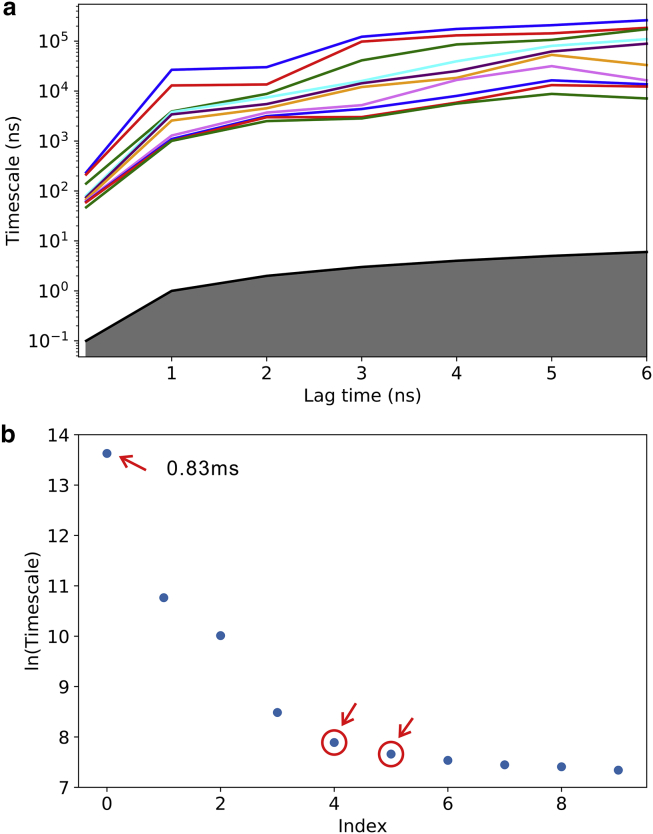
Overall, 1260 conventional MD trajectories were collected with a total simulation time of 25.2 μs. Rototranslationally aligned Cartesian coordinates of all heavy atoms were considered as input features to determine the conformational changes (945 dimensions). Then, the high-dimension space was reduced to 187 dimensions using the TICA method at a lag time of 2 ns (90% of the total kinetic variance was retained). After that, the conformations were clustered into 250 microstates through the k-means clustering algorithm. These 250 microstates were sufficient to cover unfolded and folded states (Fig. S3 a). The arrangement of these conditions indicated that the implied timescales were continuously constant after ∼3 ns (Fig. 2 a). This further indicates that the jumping between these microstates was Markovian after 3 ns. Thus, this lag time was used to build the MSM. Furthermore, there was a gap between the zero-based fourth and the fifth implied timescales (Fig. 2 b). This allows grouping of the 250 microstates into six metastable states using the hMSM method (Fig. S3 b). Fig. S4 shows that the steady-state probability of the system could be predicted by the MSM, in agreement with the estimated condition by MD simulations. Based on this achievement, it could be concluded that the six-macrostate model could reproduce the dynamics of MD simulations. Structures of the metastable states are shown in Fig. 3, and the dynamics of each state obtained from the additional conventional MD simulation is demonstrated in Fig. S5.

Figure 2.

Construction of the MSM. (a) Implied timescales as a function of the lag time are shown. (b) A sorted eigenvalue spectrum estimated from a lag time of 3 ns (zero-based) is shown. The slowest implied timescale (predicted folding timescale) is ∼0.83 ms. To see this figure in color, go online.

Figure 3.

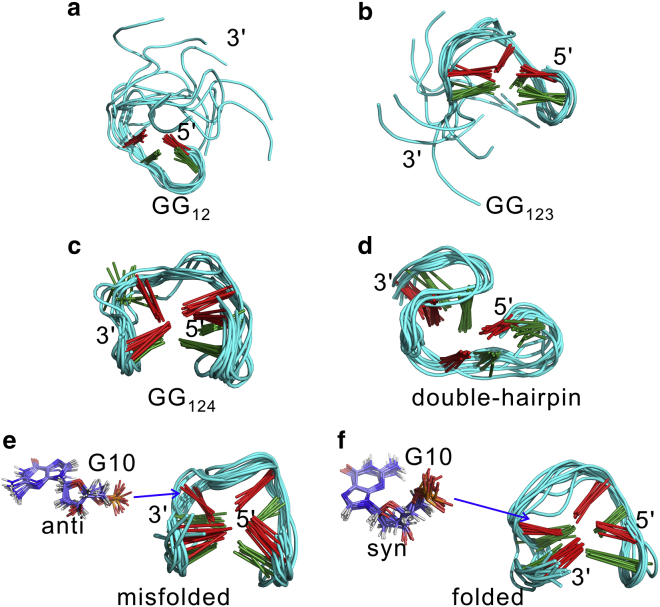
Structures of the metastable states obtained from hidden Markov state model. Panels (a–f) respectively denote the six metastable states. For each state, 10 aligned structures were randomly selected. To see this figure in color, go online.

Structures and dynamics of the metastable states

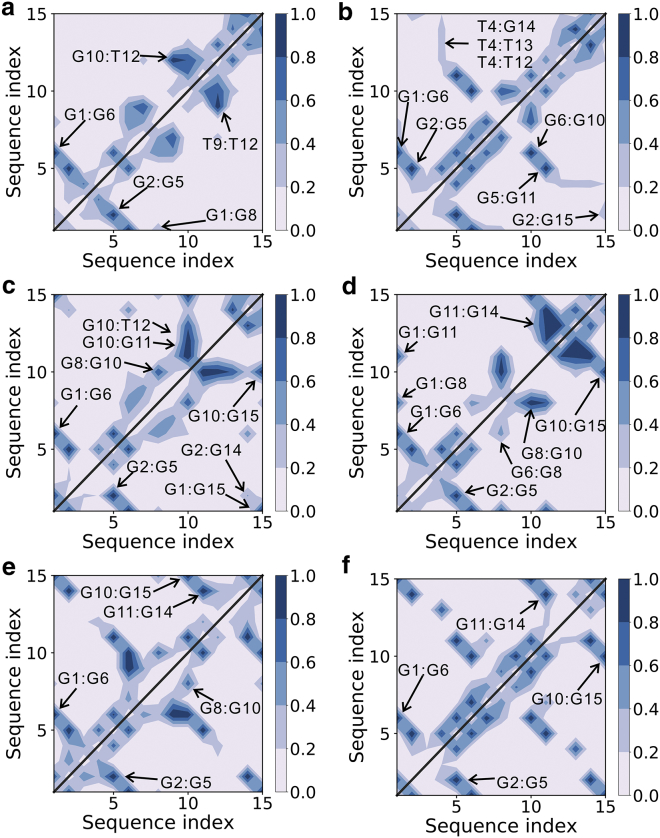
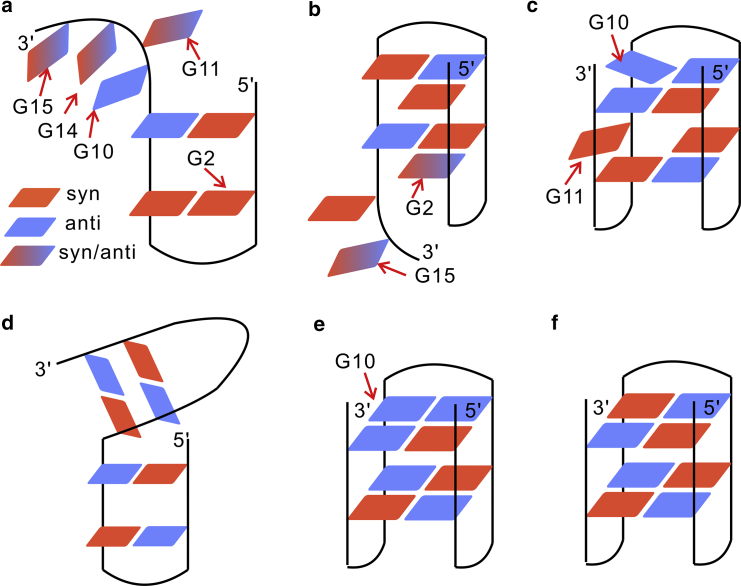
G-hairpins are potential early-stage folding intermediates of G-quadruplexes. We identified a structure that can be characterized as an antiparallel hairpin. As shown in Fig. 3 a, Fig. S5 a, and Fig. 4 a, G-tracts GG₁ and GG₂ established a hairpin at the 5′-terminus through the two native basepairs G1:G6 and G2:G5. For simplification, this state is hereafter expressed as GG₁₂. The additional MD simulation on this state demonstrated that large dynamic changes occurred at the 3′-terminus, whereas the remaining segments of the structure were stable (Fig. S5 a). This would be due to the markedly reduced flexibility of corresponding nucleotides by the interactions G1:G6, G2:G5, G1:G8, T9:T12, and G10:T12 (Fig. 4a; Fig. S5 a). These interactions also stabilized the G-tetrad–forming guanines (G1, G5, and G6) to remain in the fixed syn/anti configuration, the same as the native state, whereas the guanines G2 and G10 adopted a nonnative pattern (Fig. 5 a; Fig. S6). In contrast, other free guanine nucleotides (G11, G14, and G15) were altered between both the syn and anti configurations (Fig. 5 a; Fig. S6).

Figure 4.

The hydrogen-bonding maps for the metastable states obtained from additional conventional MD simulations. Panels (a–f) respectively denote the six metastable states. The formation probabilities in each metastable state are averaged on all the structures collected from the corresponding 300 ns conventional MD simulations. To see this figure in color, go online.

Figure 5.

The distribution of syn/anti guanines of the metastable states. Panels (a–f) respectively denote the six metastable states. The syn and anti guanines are labeled by different colors. The gradient color indicates a fluctuating configuration between syn and anti. The nucleotides indicated by arrows correspond to either fluctuating or nonnative syn/anti configuration. To see this figure in color, go online.

G-triplexes are key potential folding intermediates of G-quadruplexes. Two G-triplex states were detected in this study. The structure of the first triplex state is displayed in Fig. 3 b and Fig. S5 b. Two triad planes were built by two group hydrogen-bonding interactions: G1:G6:G10 and G2:G5:G11 (Fig. 4 b). In other words, the arrangement of this triplex could be contemplated as G-tracts GG₁, GG₂, and GG₃, or, in a simpler form, GG₁₂₃. From the MD simulation results of GG₁₂₃, it was observed that the triplex structure was stable, whereas the 3′-overhang was swung freely with respect to the well-formed triplex structure (Fig. S5 b). However, Fig. S5 b also shows that the overhang can dock upon the triplex formed by two nonnative base interactions (G2:G15 and T4:G14). At the same time, the two TT-loops can be bridged together via the interactions T4:T12 and T4:T13. All these interactions pulled the G-tract GG₄ close to the well-formed triplex structure and facilitated the finding of the native state by limiting the searching space. Concerning the configuration of G-tetrad–forming guanines, although most of them adopted the native patterns, G2 and G15 were found to occur in both the syn and anti configurations in the simulation (Fig. 5 b; Fig. S7).

The structure of the second triplex state is demonstrated in Fig. 3 c and Fig. S5 c. Two triad planes were built by the G15:G1:G6 and G14:G2:G5 interactions (Fig. 4 c). Generally, this triplex is generated by G-tracts GG₁, GG₂, and GG₄ and can be abbreviated GG₁₂₄. Based on the achieved MD simulation results for GG₁₂₄, this triplex structure was rather stable. However, firm structuring of the G-tract GG₃ was also detected and was due to interactions of nucleotide G10 with other nucleotides (G8, G11, T12, and G15). These interactions pulled GG₃ close to the triplex structure (Fig. 4 c; Fig. S5 c). Furthermore, a nonnative configuration of the guanine nucleotides G10 and G11 was also observed in the MD simulation of the GG₁₂₄ triplex structure (Fig. 5 c; Fig. S8).

A metastable state that can be characterized as a double-hairpin conformation was also identified (Fig. 3 d; Fig. S5 d). Stable hairpin structures were found at both the 5′- and 3′-termini. Fig. S5 d demonstrates that this structure was rather stable, and the TGT-loop played a significant role in providing this stability. As shown in Fig. S5 d and Fig. 4 d, the loop-guanine G8 established several interactions with the two hairpins (G1:G8, G6:G8, and G8:G10). These interactions could pull the two hairpins close to each other and drastically reduce their flexibility. In addition, the additional MD simulation also showed that the native syn/anti configuration of each G-tetrad–forming guanine was achieved during the whole simulation (Fig. 5 d; Fig. S9).

Interestingly, all native G:G pairs were observed in two states (Fig. 4, e and f), from which two “native-like” metastable states could be identified, as depicted in Fig. 3, e and f and Fig. S5, e and f. However, MD simulations showed that these metastable structures adopted different distributions of syn/anti guanine nucleotides. In the former state (Fig. 3 e; Fig. S5 e), all G-tetrad–forming guanines except G10 adopted the correct syn/anti configurations (Fig. 5 e; Fig. S10). In the latter state (Fig. 3 f; Fig. S5 f), each G-tetrad–forming guanine adopted its native pattern (Fig. 5 f; Fig. S11). Therefore, we defined them as the misfolded and folded states, respectively. Fig. 4 e shows that loop-guanine G8 interacted with the base group of G10 and played an important role for the stabilization of the misfolded state. To some extent, G8 could prevent nucleotide G10 from finding the native configuration.

Folding pathways

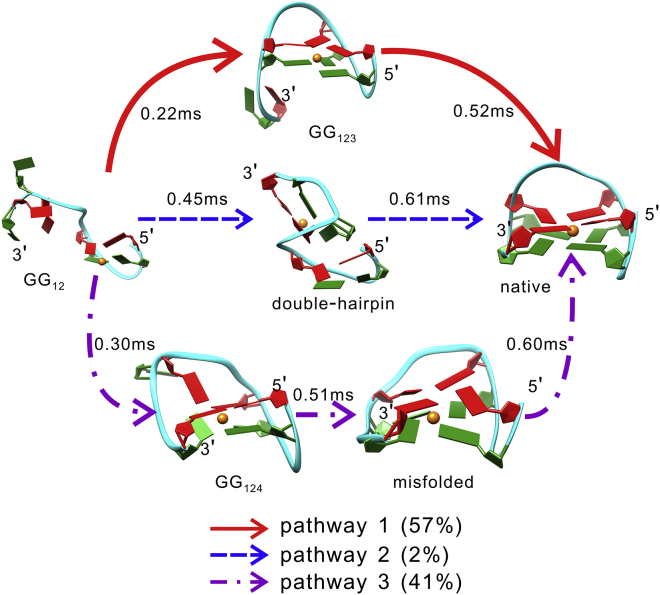
By defining the hairpin/folded state as the reactant/product state, three possible folding pathways could be affirmed through the TPT analysis (Fig. 6). A sequential manner of folding was obtained in the first pathway (pathway 1), through which the formation of TBA proceeded through the G-hairpin GG₁₂ into the G-triplex state GG₁₂₃, followed by construction of the native topology. In contrast, the second pathway (pathway 2) demonstrated a nonsequential folding process, in which the DNA formed a double-hairpin conformation after visiting the G-hairpin ensemble. The folding process was completed by the docking of the two hairpins. Remarkably, another pathway (pathway 3) was detected. In this pathway, the TBA experienced misfolding in the initial stage. The DNA folded into the misfolded state before forming the native structure and after traversing through the ensembles of G-hairpin GG₁₂ and G-triplex GG₁₂₄. Ultimately, the folding process was completed by the guanine with the nonnative pattern adopting its correct configuration. Based on the pathway probabilities, pathway 1 was found to be dominant compared with the other two recognized pathways.

Figure 6.

The folding pathways and their probabilities revealed by transition path theory. Also shown are the mfpt values associated with the conformational transitions along the pathways. To see this figure in color, go online.

To study the folding dynamics of TBA, we computed the mfpt associated with the conformational transitions along the pathways. It is clear from Fig. 6 that these transitions take place in the order of sub-milliseconds, indicating that the metastable states are well separated kinetically. Moreover, the mfpt computations identified the triplex state GG₁₂₃ as the most kinetically accessible intermediate after the formation of hairpin GG₁₂ (∼0.22 ms), whereas the triplex state GG₁₂₄ was demonstrated to form faster than the double-hairpin state (0.30 vs. 0.45 ms). This could be the reason why pathway 1 was determined to be the dominant pathway and why pathway 3 was more probable than pathway 2. In addition, because of the structural stability of the misfolded state, a glycosidic bond with a nonnative pattern slowly adopts the correct configuration (∼0.60 ms). The reorientation may occur on the same order of magnitude as that of the transitions from GG₁₂₃ and double-hairpin to the native state (0.52 and 0.61 ms, respectively).

Discussion

The combined power of BEMD and MSM enabled us to investigate the folding process of TBA. The relevance of our results to the findings of previous studies is discussed subsequently.

Knowledge of the structures of folding intermediates is essential to understand the folding process. Several metastable states could be involved in the folding of TBA. First, an antiparallel hairpin was identified as the early-stage intermediate. This is in agreement with the results of a previous MD simulation on various forms of G-hairpins (38), which suggested that antiparallel G-hairpins can form spontaneously at the early stage in the folding of different G-quadruplex structures. Second, two G-triplex structures, identified as GG₁₂₃ and GG₁₂₄, were observed in this study. It is worth mentioning that the former conformation has been validated by experimental data (43, 67). Through nuclear magnetic resonance, circular dichroism, and differential scanning calorimetry examinations, Limongelli et al. observed that the 3′-truncated TBA sequence (11-mer oligonucleotide) can form a G-triplex conformation (43). Subsequently, the structure of the G-triplex was determined by Cerofolini et al. (67). In addition to experimental observations, our simulation provides more atomistic details of the structure. For example, the simulations demonstrated that the well-formed triplex structure was stable, whereas the 3′-overhang swung freely with a probability of docking upon the triplex through nonnative interactions. In contrast to GG₁₂₃, GG₁₂₄ was previously unidentified. We also found another intermediate characterized as a double-hairpin conformation that has not been previously observed. Likewise, MD simulation results showed that the two newly detected intermediates are stable enough to participate in the folding of TBA. It can be concluded that similar intermediates are involved in the folding of other forms of G-quadruplexes. Validation of this conclusion will be sought in further studies.

The reorientation of the glycosidic bonds is an important aspect to complicate the G-quadruplex folding. Stadlbauer et al. reported that folding of G-quadruplexes is likely to be slowed by trapping in the misfolded states that are adopted with an inappropriate combination of syn/anti guanines (68). Their proposal is supported by observations from an MD simulation of the structures of the late-stage folding intermediates. We found a similar misfolded state that involved a nonnative distribution of syn/anti guanines. In addition, our results indicate that this distribution may be seeded at the early stage, as it was found that the nonnative configuration of G10 occurred in the hairpin structure.

Concerning TBA, we identified three possible folding pathways involving multiple intermediates. This multipathway mechanism has been observed for the folding of other G-quadruplex structures. Recently, Aznauryan et al. used single-molecule fluorescence resonance energy transfer microscopy and MD simulations to achieve a direct view of the multipathway folding process of the human telomeric G-quadruplex (33). Similar to our results, they also found that the pathways involve several stable folding intermediates. This complexity of folding was highlighted in a recent review article, which suggested that the folding of G-quadruplexes follows a kinetic partitioning mechanism (69). In such a folding process, accompanied by the interaction with metal ions, the nucleotides could form numerous hydrogen bonds. This could produce a very rugged folding energy landscape because many deep local minima would be separated by a high energy barrier. As a result, many well-separated conformation ensembles would compete with each other, and the folding process of G-quadruplexes could be partitioned into multiple pathways with different folding timescales. Previous experiments showed that the folding timescales of TBA and other similar two–G-tetrad G-quadruplex structures range from dozens of milliseconds to a few seconds (47, 48, 49). In this study, the predicted folding timescale of TBA is ∼1 ms, which is close to some of the experimental observations (48, 49). Therefore, our results offer some insights into the millisecond folding dynamics of TBA. To discriminate with the folding dynamics on the order of seconds, the identified pathways in this study were termed “fast-folding pathways.”

Knowledge of the timescale associated with the formation of the G-triplex structure is important to understand the folding dynamics of the G-quadruplex because such a structure was suggested to be one of the most plausible folding intermediates. In this research, formation of the simplest G-triplex structure, which is composed of two triad planes, was predicted to take place on the order of sub-milliseconds. In the absence of direct experimental measurements of the folding time of this structure, we cannot make concrete conclusions regarding this issue. However, it is conceivable that the estimated timescale presented here may represent the lower limit, based on the following reason. In the BEMD simulation, the employed CVs were based on the native structure. This led to the elimination of some potential nonnative kinetic traps that may hold the DNA for a long time in the conformational transition from the unfolded ensemble to the triplex state. Therefore, taking into account this weakness, the formation of the simplest G-triplex structure was expected to occur on a timescale longer than sub-milliseconds. Furthermore, it can be concluded that more complex G-triplex structures can form on a timescale of milliseconds or longer. Consistent with our prediction, a previous experiment for human telomeric G-quadruplex revealed the millisecond dynamics of the formation of G-triplex structure (70). We await more experimental measurements for the folding timescale of G-triplex structure to make a comparison.

The TGT-loop is important for the stability of the native structure of TBA (71). This study additionally reveals a role for the TGT-loop in the misfolding and folding protocols. In both the structures of triplex GG₁₂₄ and misfolded state, the loop-guanine G8 interacted with G10 and stabilized it to remain in the nonnative configuration. This implicates that the TGT-loop has a significant role in the misfolding process. The interactions formed by the TGT-loop were also found in the double-hairpin conformation. Without these interactions, the two hairpins may drift away from each other, and TBA must search a larger conformational space to find the native structure.

Concerning the folding of TBA, previous studies sampled the conformational space through using the replica-exchange MD method (42) or well-tempered metadynamics with two CVs (43). Our simulations could provide much more reasonable insights. First, rather than starting simulations from the native conformation, as in the two previous studies, we performed a conformational sampling from an unfolded structure by employing BEMD with four CVs. This enabled us to capture a wider free-energy landscape along real folding trajectories. This revealed a folding picture that was much closer to the real conditions. Second, instead of inferring the folding thermodynamics from the free-energy landscape, we used the MSM and TPT based on unbiased MD simulations to explore the folding kinetics. This approach could provide more details of the folding process and could be useful to interpret the experimental results. Moreover, BEMD was not employed in this investigation to estimate the free-energy landscape. In fact, it was performed to obtain a first guess of the folding process as the first step of conventional MSM construction. This strategy avoided the problem of poor convergence, which is a normal drawback of metadynamics when studying complex systems.

The limitations of this study should be discussed. In the BEMD simulation, we employed several native-structure–based CVs. Although these CVs enabled us to find some possible folding events quickly, some potential nonnative kinetic traps, such as the alternative folding topology, were eliminated because they biased the sample in favor of the native state. As a result, we only captured a part of the folding-energy landscape along which TBA directly folds to the native basin without visiting potential competing conformations. Moreover, we built the MSM on the basis of the BEMD simulation, from which the model merely reflected the folding kinetics on the narrow-energy landscape and produced a markedly faster timescale of prediction compared to that of the experiments. This limitation was due to a long folding timescale. It should be noted that these limitations would not be considered as weaknesses of the utilized methods. The capture of the full folding-energy landscape of TBA remains a formidable challenge because the landscape is so rugged that contemporary MD simulations cannot sample thoroughly within an acceptable simulation time. Likewise, such a long folding timescale can also easily result in the computation dropping in a data-poor regime, where there are no single trajectories connecting the unfolded and folded states. The MSM built from this dataset can qualitatively reflect the original dynamics. However, it inaccurately estimates many quantitative details. To analyze the datasets in a kinetically meaningful way, MSMs must be built in a data-rich regime. For instance, Islam et al. recently constructed an MSM in a data-rich regime and successfully investigated the slow conformational transitions in the propeller loops of G-quadruplexes (72). Their system featured a much simpler energy landscape than that of TBA, and thus it would be much easier to obtain the data-rich regime. We assume that our data is rich for the sampled narrow-energy landscape. However, it poorly characterized the full landscape.

In summary, although only several fast-folding events were captured, our results provide some general insights into the folding of TBA. Because of the rugged free-energy landscape, multiple folding pathways involving different intermediates were detected. The major pathway involved a G-triplex state, which was in good agreement with previous experimental and computational results. Moreover, a misfolded state with nonnative distribution of syn/anti guanine conformations could additionally participate in the folding process. Furthermore, the TGT-loop was implicated as being important in the folding protocols. These findings increase the knowledge of the TBA folding process and shed light on the folding mechanism of other types of G-quadruplexes.

Author Contributions

Y.B. and J.W. designed the research; Y.B. performed the research; Z.C., L.Z., J.Y., and X.G. contributed analytic tools; Y.B. and F.S. analyzed the data; and Y.B. and F.S. wrote the manuscript.

Editor: Andrew Spakowitz.