Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2015 Oct 16;7(2):1082–1092. doi: 10.1039/c5sc03088a

A universal chemical potential for sulfur vapours†

Adam J Jackson a, Davide Tiana a,‡, Aron Walsh a,b,✉
PMCID: PMC5954976  PMID: 29896372

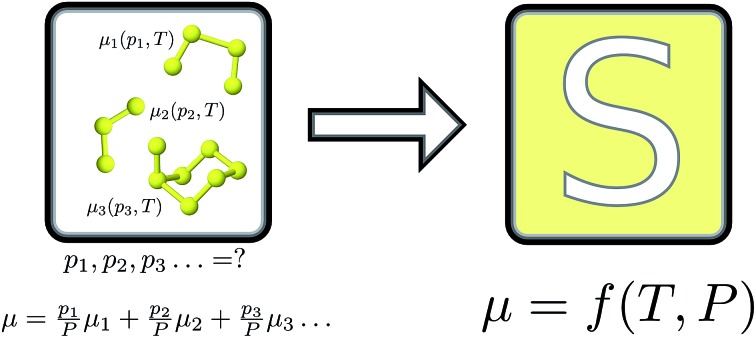
graphic file with name c5sc03088a-ga.jpgThe equilibrium thermochemistry of mixed vapour-phase sulfur allotropes is computed and solved to obtain a single chemical potential function.

Abstract

The unusual chemistry of sulfur is illustrated by the tendency for catenation. Sulfur forms a range of open and closed Sn species in the gas phase, which has led to speculation on the composition of sulfur vapours as a function of temperature and pressure for over a century. Unlike elemental gases such as O2 and N2, there is no widely accepted thermodynamic potential for sulfur. Here we combine a first-principles global structure search for the low energy clusters from S2 to S8 with a thermodynamic model for the mixed-allotrope system, including the Gibbs free energy for all gas-phase sulfur on an atomic basis. A strongly pressure-dependent transition from a mixture dominant in S2 to S8 is identified. A universal chemical potential function, μS(T,P), is proposed with wide utility in modelling sulfurisation processes including the formation and annealing of metal chalcogenide semiconductors.

1. Introduction

Sulfur is an abundant resource exploited by industry on a scale of tens of millions of tonnes per year.1 While it may be found in its elemental form, the primary industrial source is hydrogen sulfide, a byproduct of the oil and gas industry. The vast majority of industrial sulfur is converted to sulfuric acid or sulfur dioxide before further use; this may explain the surprising shortage of data in the thermochemical literature regarding the vapour phase of elemental sulfur.

Historically, the thermochemistry of sulfur has been studied experimentally and has been understood to be associated with a variable composition for over a century; Lewis and Randall remarked in 1914 that “no other element is known to occur in as many different forms as sulfur” while studying the free energy of a number of these forms.2 (Carbon now has a higher number of known allotropes but the majority of these are not naturally-occurring.) However, contemporary reference data for sulfur still does not present a complete picture; the NIST-JANAF thermochemical tables (1998) give thermochemical data for two solid phases, one liquid phase, the ions S+ and S– and eight gas allotropes S1–8.3 Of these, only S2 and S8 are from spectroscopic data. The allotropes S3–7 are assumed to exist and are assigned energies following an interpolation scheme suggested by Rau et al. (1966), which also makes use of experimental data for S6.4 That paper rules out the significant presence of tautomers, finding little evidence of a tautomer contribution and assuming that they have relatively high energy. The authors generally reserve speculation on the actual structures of the components of their equilibrium model.

In recent years considerable attention has turned to metal chalcogenides; II–VI semiconductors such as ZnS, CdS, PbS are widely studied in many contexts.5 Copper indium gallium selenides (CIGS) and cadmium telluride (CdTe) are used as the basis for “second-generation” thin-film photovoltaic devices, and have seen a dramatic rise in production. Cu2ZnSn(S,Se)4 (CZTS) and Cu2SnS3 (CTS) devices have so far struggled to match these materials in terms of energy conversion efficiencies, but hold significant long-term promise due to their use of highly abundant elements; such availability is a prerequisite for terawatt-scale photovoltaics.6 As such, thin-film processing in sulfur atmospheres is of considerable interest, as the inherent safety of industrial processing may be improved by eliminating the use of toxic H2S. In addition to chalcogen annealing, which is used to increase grain size, substitute other elements or directly form chalcogenides from elements, high-quality single-crystal samples may be produced using chemical vapour transport of elemental chalogens.7–9 Previous work on the thermodynamics of such processing has tended to assume that sulfur adopts one particular gaseous allotrope (either S2 or S8), but the validity of this assumption has not been explored in depth.10–12 It is undermined however by the model derived by Rau et al., which predicts that no one component makes more than 50% of the gas mixture at temperatures between 800–1100 K.4

Mass spectrometry at a relatively mild 105 °C has observed a series of charged clusters with the form (S8n)+.13 In the mid 1980s, a number of cyclic allotropes had been identified by crystallisation and X-ray diffraction, but this only covered the range n = 6–20.14 An ab initio study was carried out for S2 through to S13 in an early application of the Car–Parrinello simulated annealing method.15 Energies were calculated using density-functional theory with the local density approximation (LDA). While limited by the inherent difficulties in exploring the entire potential energy surface of the atomic positions, this thorough study generated 21 allotropes, finding a local maximum in the atomisation energy at n = 8. A later (1990) paper used coupled-cluster electronic structure calculations to study the proposed tautomers of S4 in depth, concluding that the planar structure with C2v symmetry is lowest in energy, with a trans (C2h) structure also visible in experimental spectra; a more recent ab initio study reached similar conclusions regarding stability while challenging the spectroscopic assignment of the phases.16,17 The C2v structure was ruled out in the simulated annealing study with LDA, although the authors noted the experimental evidence for its existence.15 A 2003 review by Steudel et al.18 collects more recent data, including both experimental and theoretical studies of vapour-phase allotropes; this review notes the weakness of the widespread assumption that each size is represented by a single species.18 The work compares several sets of enthalpies relative to S8 that have been obtained experimentally; variability is high for the smaller allotropes while there is fairly good agreement for the larger allotropes. Studies are generally carried out at a single temperature, such that the temperature and pressure dependence of the thermochemistry must be derived from statistical mechanics and analysis of vibrational information.

In this study, we develop a set of structures for S2–S8, compute their Gibbs free energy from first-principles and with empirical corrections, and solve the temperature-dependent chemical potential to describe the gaseous mixture. The potential function will be important for quantitative investigations of defect formation and phase stability in metal sulfide materials.

2. Methods

2.1. Density functional theory

Energies and forces of arbitrary clusters of sulfur atoms were computed within Kohn–Sham density-functional theory (DFT).19 A range of exchange–correlation functionals were used in this work: PBE is a popular and elegant implementation of the Generalised Gradient Approximation (GGA) and PBEsol restores a periodic exchange contribution leading to improved performance for solids;20,21 B3LYP§ is a widely-used “hybrid” functional which combines pre-existing gradient corrections with “exact” Hartree–Fock exchange;23 PBE0 is applies similar principles to the parameter-free PBE functional.24 (While PBE is generally preferred to PBEsol for molecular calculations, PBEsol was included in this study for its compatibility with other all-electron work using this functional.)

Calculations for the evolutionary algorithm search used the Vienna Ab Initio Simulations Package (VASP) with the PBE exchange–correlation functional and a plane-wave basis set with a 500 eV energy cutoff.25,26 As calculations in VASP employ a periodic boundary condition, orthorhombic bounding boxes were employed with 10 Å of vacuum between each molecule and its periodic images. Electronic structure iteration used only the Γ-point of this large cell.

Further calculations used the Fritz Haber Institute ab initio molecular simulations package (FHI-aims) to carry out all-electron DFT calculations with numerically-tabulated basis sets.27,28 All calculations were open-shell with S2 adopting its low-energy triplet spin configuration. The recommended “tight” basis set was employed for initial relaxation and study with PBEsol, which extends the minimal set of occupied orbitals with 6 additional functions. This was extended further to the full “tier 2” set of 9 additional functions for calculations with the LDA, PBE0, and B3LYP functionals.

2.2. Global structure search

Global structure optimisation was carried out with the USPEX package, which was originally developed for crystalline systems and has been adapted for use with clusters.29–31 At this stage, molecules with n > 8 were disregarded, as experimental results anticipate high- and low-temperature limits dominated by S2 and S8, respectively. Clusters were generated for S3–7, and refined with an evolutionary algorithm to minimise the ground-state energy until a number of seemingly distinct clusters were identified by inspection. The atomic positions of these clusters were then optimised in FHI-aims calculations with PBEsol, using the BFGS algorithm to minimise the atomic forces to less than 10–4 eV Å–1 and converge energy to within 10–6 eV. Point groups were assigned to the structures using Materials Studio version 6.0, a proprietary package developed by Accelrys.

2.3. Vibrational frequencies

Vibrational frequencies were calculated within the harmonic approximation by making finite displacements to each atomic position to obtain the local potential wells, and diagonalising the resulting dynamical matrix to obtain the normal modes and their frequencies. This is implemented as a script and diagonalisation routine provided with FHI-aims.

Improved vibrational frequencies may be obtained by applying an empirically-derived scale factor to the vibrational eigenvalues computed using DFT; collections of such scale factors have been published for large test-sets of molecules.32,33 The use of these factors is somewhat problematic when creating a systematic, transferable set of data but offers an opportunity to create the most realistic thermochemical model possible. Given that the calculations in this work involve a more limited subset of atomic interactions, we choose to fit a scaling factor to the experimentally-reported frequencies of S8 and S2.

2.4. Thermochemistry

2.4.1. Thermochemistry of individual gas species

Thermochemical properties were calculated within the ideal gas, rigid-rotor and harmonic vibration approximations. A set of textbook equations forms the chemical potential μ for a nonlinear molecule from the ground-state electronic energy E0 given a set of vibrational energies ε, the rotational constant σ, moment of inertia I

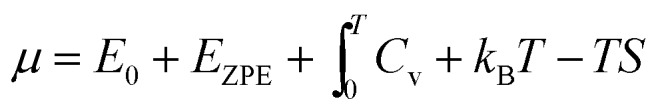2.4.1. 1

where

Cv = Cv,trans + Cv,vib + Cv,rot 2
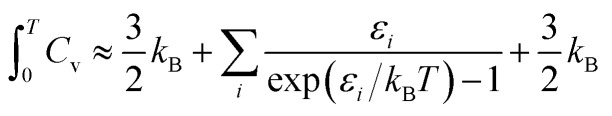2.4.1. 3
S = Svib + Strans + Srot 4
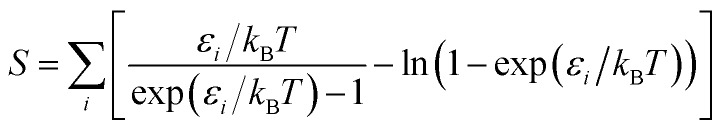2.4.1. 5

These were applied as implemented in the Atomic Simulation Environment (ASE) Python package.34 (Note that the expressions for monatomic and linear molecules are slightly different.) The rotational constants σ were assigned from the point groups.

2.4.2. Reference energies

A number of ab initio methods have been applied. In order to compare the energies, a reference point is needed. Conventionally the enthalpy of the ground state is zero; however, in this case the ground state phase α-sulfur is relatively expensive to compute. We therefore use the experimental sublimation enthalpy 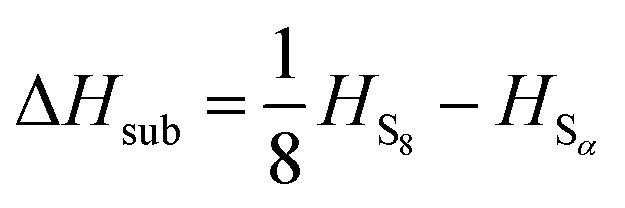Inline graphic to obtain a reference from the calculated enthalpy of S8:

ΔHSx = HSx – xHSα 6
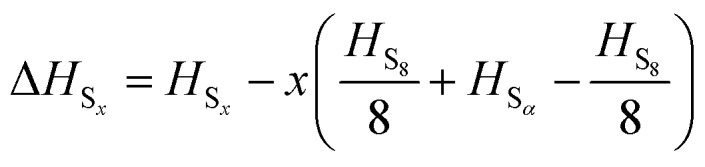2.4.2. 7
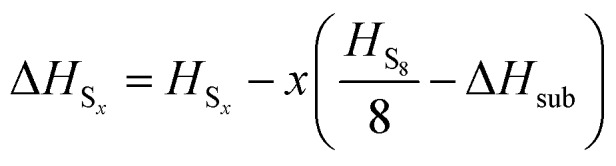2.4.2. 8

The preferred experimental value for ΔHsub is 100.416/8 = 12.552 kJ mol–1, from experiments at 298 K.3 Note that the physical system does not in fact sublime at high temperatures, but passes through a molten phase. Nonetheless, it is more practical (and perfectly valid) to retain α-S as the reference state over the whole temperature range studied.

2.4.3. Equilibrium modelling

The following derivation closely follows the approach and notation of ref. 35, which describes a generalised “non-stoichiometric method” for solving chemical equilibria. This approach is well-established and based on key work in ref. 36–38.

We attempt to minimise the Gibbs free energy

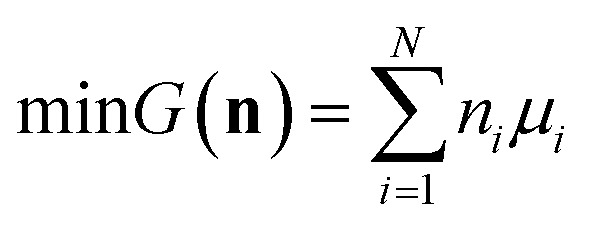2.4.3. 9

subject to the mass balance constraint

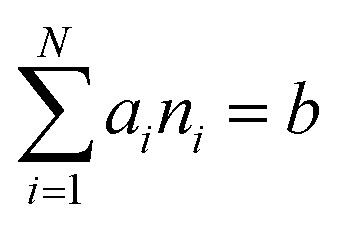2.4.3. 10

where N is the number of unique species i with stoichiometric coefficient ai; n is the quantity of species i and b is the total number of sulfur atoms. The classic approach for a constrained optimisation is the method of Lagrange multipliers. The Lagrangian is formed

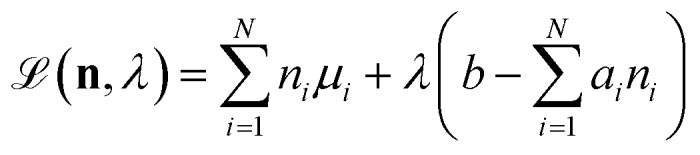2.4.3. 11

and differentiated to form a set of equations defining the equilibrium state.

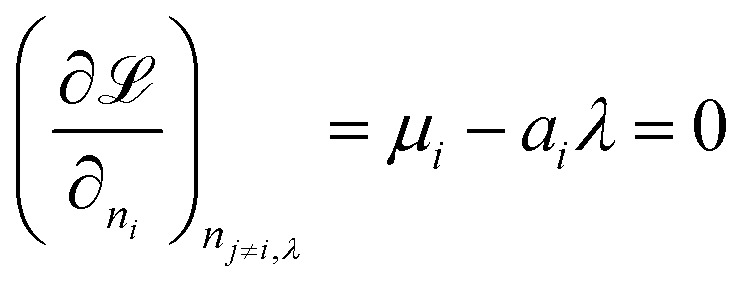2.4.3. 12

and

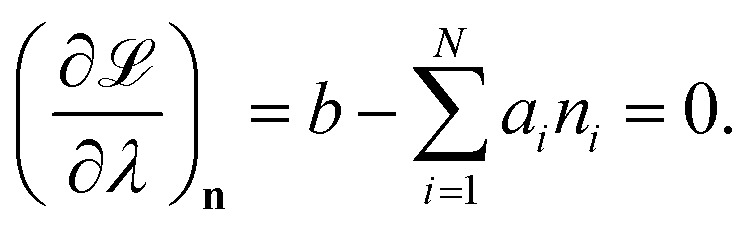2.4.3. 13

The species chemical potential μi calculated as in Section 2.4.1 is a function of both temperature and the partial pressure 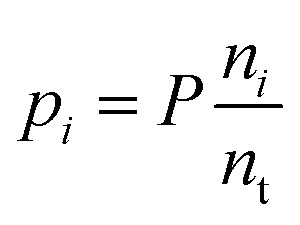Inline graphic where P is the total pressure and the total quantity 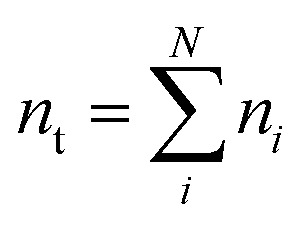Inline graphic. The temperature dependence is complex and we are willing to solve the equilibrium at each temperature of interest, so we form a temperature-dependent standard free energy at a reference pressure P°, μ°i(T) = μi(T,P°).

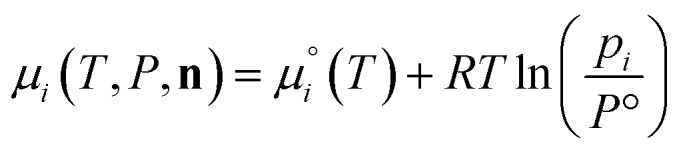2.4.3. 14
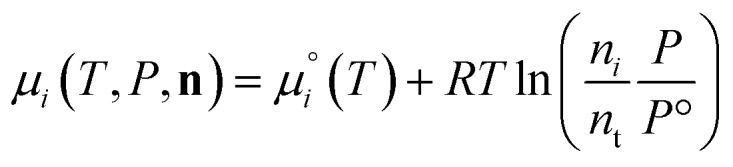2.4.3. 15
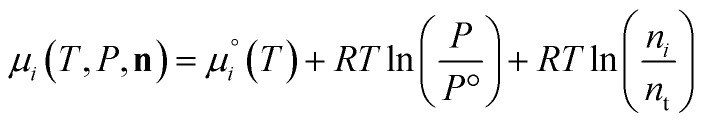2.4.3. 16

From here we drop the parenthetical indication that μ°i is a function of temperature, and define the unit of pressure as the reference pressure, such that P° = 1. Substituting (16) into (12), we obtain

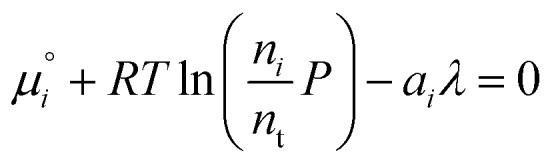2.4.3. 17
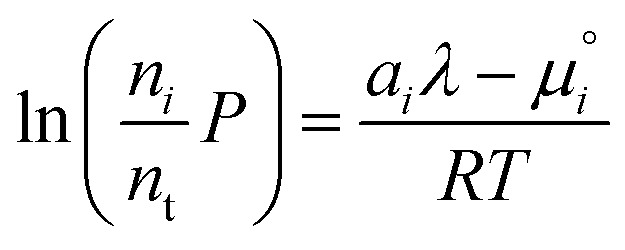2.4.3. 18

and summing over i

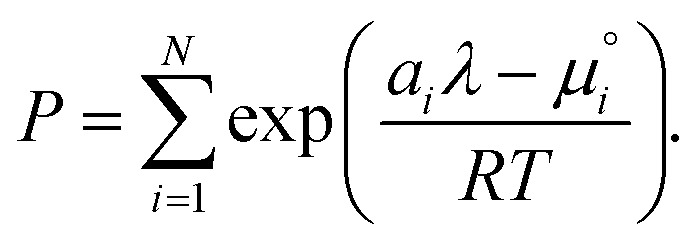2.4.3. 19

The only unknown variable in this expression is λ; rearranging slightly we form a polynomial which is suitable for solving by standard numerical methods. The method employed in this work is the Levenberg–Marquardt least-squares algorithm, as implemented in Scipy.39,40

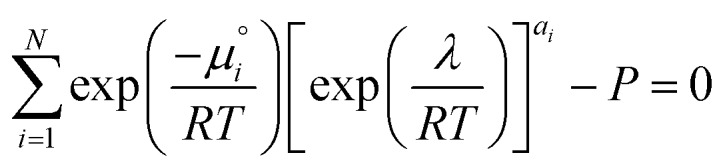2.4.3. 20

To recover the composition n, we rearrange (18):

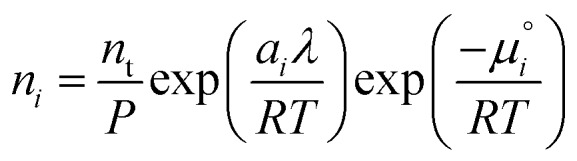2.4.3. 21

and substitute into the second equilibrium condition (10) to obtain

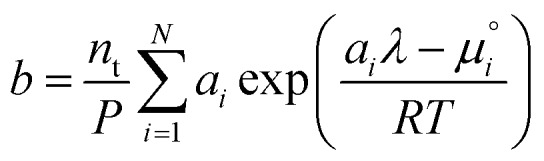2.4.3. 22

combining (21) and (22) we eliminate nt

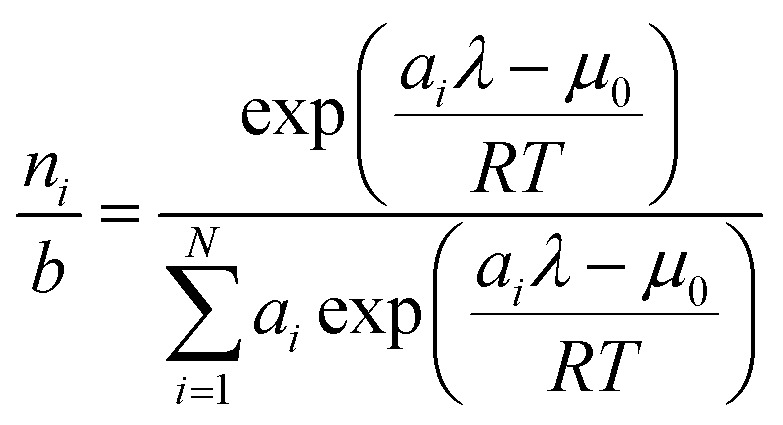2.4.3. 23

and clean up the notation by denoting 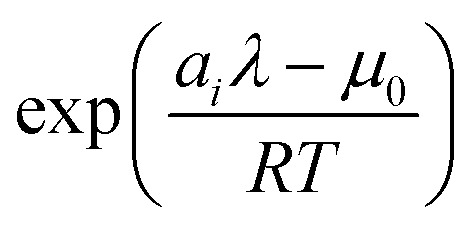Inline graphic as Φi

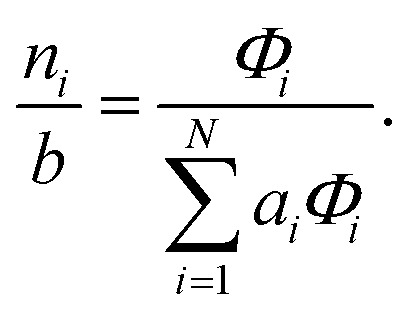2.4.3. 24

Finally, to obtain the chemical potential of the mixture we note from (12) that 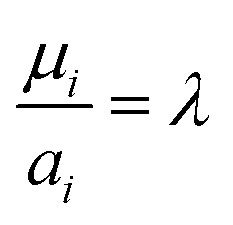Inline graphic for all i. Therefore

λ = μS, 25

the normalised chemical potential of sulfur vapour on an atom basis. (A mathematical derivation is given in the Appendix.)

3. Results

3.1. Sulfur allotropes

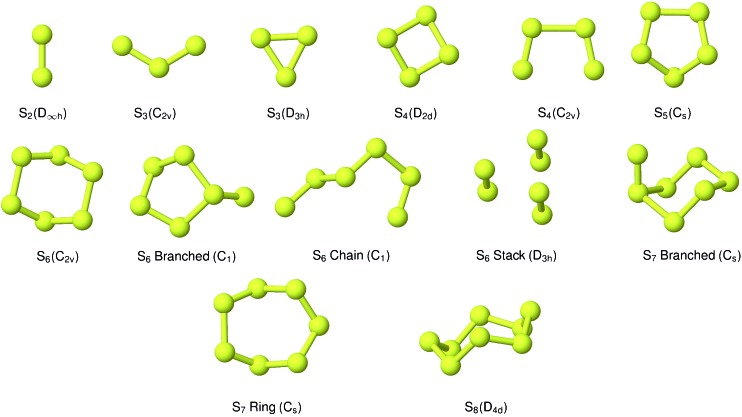
A variety of candidate structures were generated in the evolutionary algorithm study with the PBE functional. The low-energy candidates following geometry optimisation are discussed in this section.

3.1.1. S2

Diatomic sulfur has the point group D∞h, in common with other homonuclear diatomics. The atoms were initially set 2 Å apart, and relaxed to a bond length of 1.91 Å. Studies with other functionals were relaxed either from this distance or from 2 Å. The resulting bond lengths are given in Table 1.

Table 1. Calculated and experimental bond length r in S2. Experimental value is NIST/JANAF-recommended distance3.
DFT functional r/Å
PBE 1.911
PBEsol 1.903
LDA 1.895
PBE0 1.884
Experiment 1.889
Open in a new tab

3.1.2. S3

The evolutionary algorithm process eliminated all but a C2v non-linear chain for S3. This corresponds to “thiozone”, which has a well-characterised structure by rotational spectroscopy (bond length 1.917(1) Å and angle 117.36(6)°; the values from optimisation with PBE0 in this study are 1.901 Å and 118.2°).41 We have also considered the simple triangular allotrope, which is ∼0.5 eV higher in ground-state energy.

3.1.3. S4

A range of branched and cyclic structures were generated in the evolutionary algorithm. The structures included in the equilibrium modelling are shown in Fig. 1. The lowest-energy structure identified was the ‘eclipsed’ C2v chain; this is in agreement with the high-level theoretical studies in ref. 16 and 17. These studies identified a ‘trans’ C2h structure as being likely to exist; there is some spectroscopic evidence for the viability of this isomer as well as a branched chain, but we were not able to reproduce stable structures corresponding to these allotropes through geometry optimisation.42,43 Various cyclic and tetrahedral candidate structures yielded a relatively flat puckered ring with D2d symmetry.

Fig. 1. Predicted low-energy sulfur clusters with symmetry assignment.

Fig. 1

Open in a new tab

3.1.4. S5

Although a wide range of branched and chain structures were generated, the main candidate is the 5-membered ring with Cs symmetry.

3.1.5. S6

In addition to a cyclic C2v allotrope, relatively low-energy branched and chain variations were identified. Of considerable interest is also a structure which may be viewed as a stack of two S3 cycles, or alternatively as a cluster of S2 diatoms. This appears to be the D3h “prism” structure identified by Wong et al.;44 the characteristic S–S bond lengths from that study were 190.1 and 276.2 pm, while the corresponding average distances from optimisation with the same hybrid XC functional (B3LYP) in this work were 189.0 and 275.7 pm. It is worth stressing that no explicit dispersion terms were included in any of the electronic structure calculations.

3.1.6. S7

The evolutionary algorithm results rapidly provided the same Cs cyclic structure as that obtained by energy minimisation from a regular polygon. A branched structure, generated early in the progress of the algorithm, was also selected as an interesting alternative to include. This was about 1 eV lower in energy than the other candidates at that stage. Geometry optimisation by force relaxation yielded a compact structure, also with Cs (mirror-plane) symmetry.

3.1.7. S8

No evolutionary algorithm study was applied for S8, as its ring structure is quite well-known. The initial geometry was extracted from the crystal structure for the condensed α-S phase used in a previous study,45 and relaxed to form an isolated D4d ring.

3.1.8. Ground-state energies

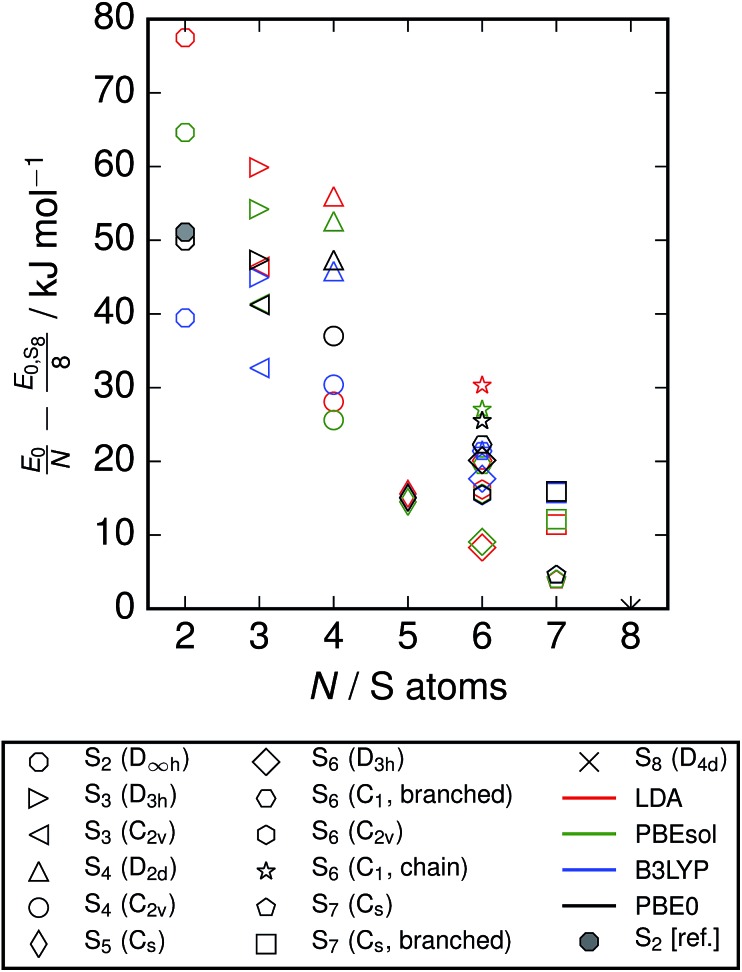
An inspection of the ground-state energies from DFT reveals a trend of smoothly decreasing energy per atom with cluster size for the minimum-energy configuration at each size (Fig. 2). The variation within the clusters included at each size is of the order 10 kJ mol–1 atom, which is comparable to the energy difference between neighbouring cluster sizes.

Fig. 2. Ground-state energies from DFT of clusters included in study. Energies are relative to the energy for S8 with each functional, and normalised to the number of atoms. A point is also included from reference data;3 this is derived from the enthalpies of formation at zero temperature, based on spectroscopic observations and equilibrium studies. While the energies from different exchange–correlation functionals diverge across the series, the S2 energy from PBE0 calculations agrees closely with this reference data.

Fig. 2

Open in a new tab

3.2. Vibrational properties

Vibrational frequencies were calculated for all of the allotropes listed in Section 3.1; frequencies for S2 and S8 are listed in Table 2.

Table 2. Calculated and experimental vibrational frequencies for S2 and S8.3 All frequencies in cm–1.

LDA PBEsol PBE0 PBE0 (scaled) B3LYP Expt
S2 716 713 751 721 714 724
 
S8 73 73 74 71 74 56
73 73 75 72 74 56
136 136 150 144 145 152
136 136 150 144 145 152
188 187 197 189 191 191
188 187 197 189 191 191
217 215 223 214 214 218
228 228 248 238 242 243
248 247 256 246 249 248
248 247 256 246 249 248
391 382 434 417 381 411
418 411 454 436 407 437
418 411 454 436 407 437
473 467 492 472 455 471
473 467 492 472 455 471
479 474 493 473 461 475
479 474 493 473 461 475
486 482 497 477 470 475
Open in a new tab

3.2.1. Empirical corrections

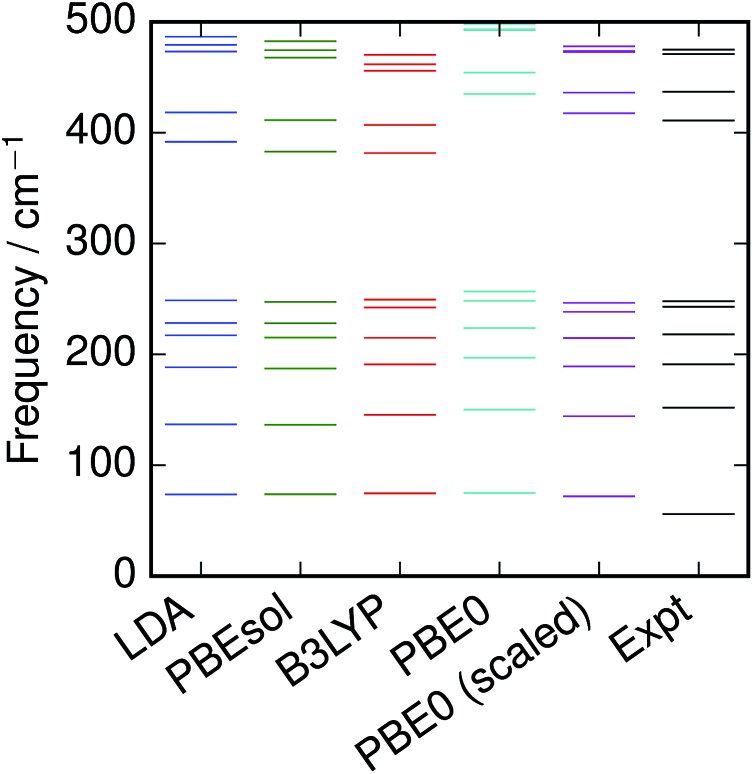
Empirical scale factors were determined by fitting the frequencies to the experimental spectrum for S8. Note that frequencies are linearly proportional to their corresponding zero-point energies 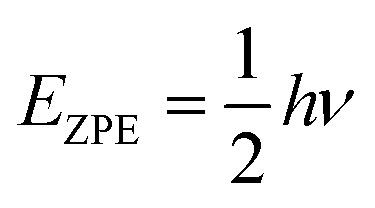Inline graphic and hence this may also be seen as fitting to zero-point energy on a per-mode basis. The factors were calculated for each functional (Table 3); scaling the frequencies from PBE0 by 96% was found to give the best overall fit, and is employed here as the reference “empirically-corrected” method. The resulting set of frequencies is illustrated in Fig. 3 alongside the uncorrected and experimental values. Using this scale factor also gives good agreement (<4 cm–1 error) with the stretching frequency of S2, which was not used in the fit (Table 2).

Table 3. Optimal scale factors for exchange–correlation functionals, fitting to ground-state frequencies of S8.3 Standard deviations s for the least-squares fit are given over the set of frequencies in units of frequency and their corresponding zero-point energies per sulfur atom.
Functional Scale factor s/cm–1 s/eV (ZPE)
LDA 1.0085 11.57 0.00072
PBEsol 1.0201 12.39 0.00077
PBE0 0.9596 6.41 0.00040
B3LYP 1.0332 11.05 0.00068
Open in a new tab
Fig. 3. Vibrational frequencies of S8 calculated with various DFT functionals, compared with recommended experimental values.3.

Fig. 3

Open in a new tab

Least-squares fitting was carried out with the Levenberg–Marquardt algorithm as implemented in Scipy.39,40

3.3. Equilibrium model

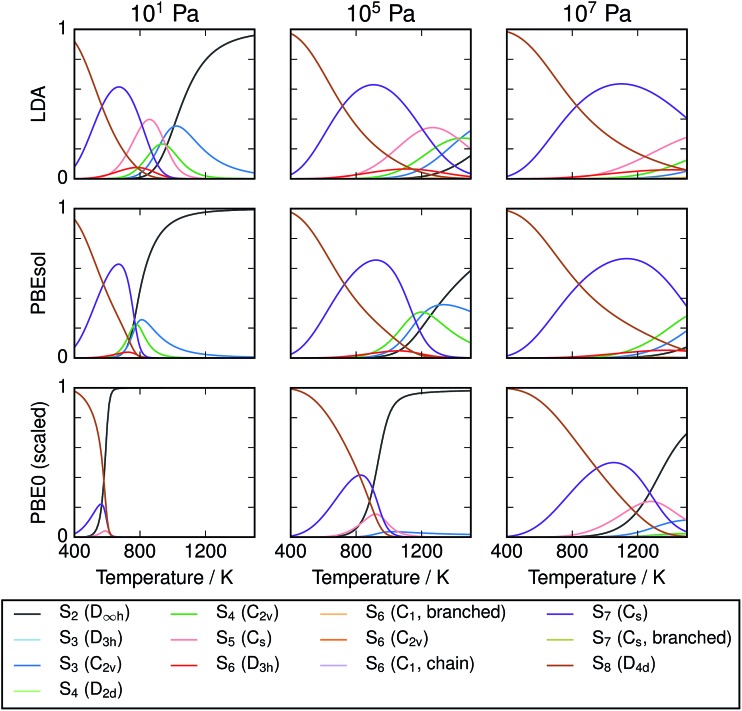
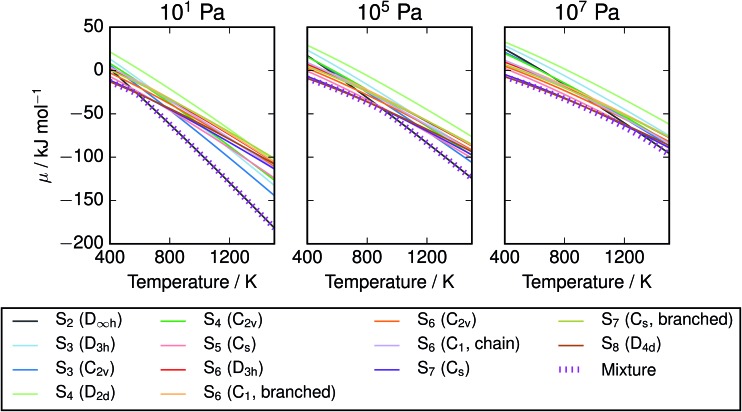
Equilibrium compositions and free energies were computed as a function of temperature and pressure for all the data sets computed (Fig. 4). There is significant disagreement between the predictions of the local exchange–correlation functionals LDA and PBEsol and the predicted composition from the hybrid functional PBE0, both before and after frequency scaling. While the “lower-level” calculations predict a diverse mixture of phases, hybrid DFT strongly supports the dominance of S8 and S2, at low and high temperatures respectively. In all cases, this simplicity is strongest at low total pressure. The other phases which are present in any significant quantity are the cyclic allotropes where N = 4–7, in the range 600–1000 K.

Fig. 4. Compositions of modelled Sx mixtures over range of equilibrium temperatures and pressures. Results are given for one local (LDA), one semi-local (PBEsol) and one non-local exchange–correlation functional with empirical corrections. Composition is given in units of atom fraction. It is expected that the most accurate results are obtained using PBE0 with scaled frequencies.

Fig. 4

Open in a new tab

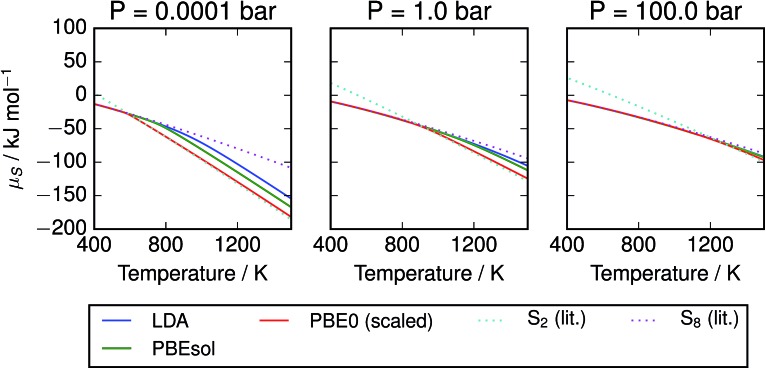
The corresponding free energies are also plotted in Fig. 5; we note that agreement between the methods is much stronger at low temperatures where the mixture is dominated by larger molecules. This may be an artefact of aligning the free energies of the S8 atoms; divergence in the energies of the smaller molecules leads to the disagreement at high temperatures. The other trend of note is the presence of a sharp bend in the μ–T curve, particularly at low pressure, corresponding to the presence of S2 molecules. The point of onset depends on the data source, but the curve for PBE0 with empirical corrections closely tracks the minimum of the two curves from reference data. This represents a challenge to the formation of a simple parameterised model function, as it suggests the presence of a spike in the second derivative. Popular parameterisations of thermochemical properties, such as those in the NIST “WebBook”, employ multiple temperature regions. This is usually viewed as a limitation, as it introduces non-physical discontinuities; with care, they could be aligned to an apparently physical discontinuity in the function. Taking the PBE0 results with empirical corrections as our preferred model, the free energy of the mixture is plotted with the chemical potentials of its component species on an atomic basis (Fig. 6).

Fig. 5. Chemical potential of S vapours per mole of atoms, given at several pressures according to range of calculation methods. Data for S2 and S8 are also provided from the thermochemical literature.3 At low pressures, the free energy diverges by more than 50 kJ mol–1 S atoms between the S2 and S8 allotropes at high temperatures, while at high pressures there is less variation. Results from hybrid DFT calculations with scaled frequencies closely track the minimal value from the literature, while the local and semi-local exchange–correlation functionals diverge from this data due to over-estimation of the formation energy of S2.

Fig. 5

Open in a new tab

Fig. 6. Chemical potential of S vapours over range of T,P, compared with individual allotropes. The equilibrium mixture is lower in energy than any single allotrope, but in most T/P regimes lies close to the chemical potential of S2 or S8. Data from vibrational calculations with PBE0 and empirically-corrected frequencies.

Fig. 6

Open in a new tab

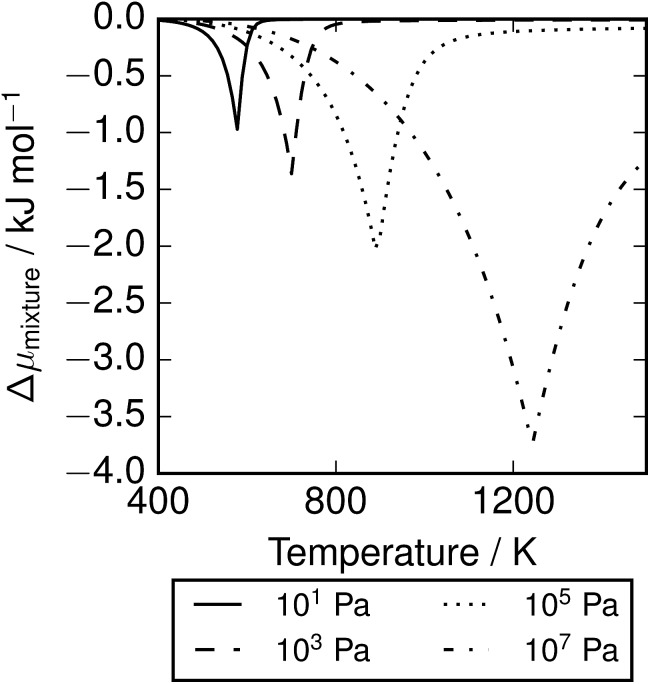
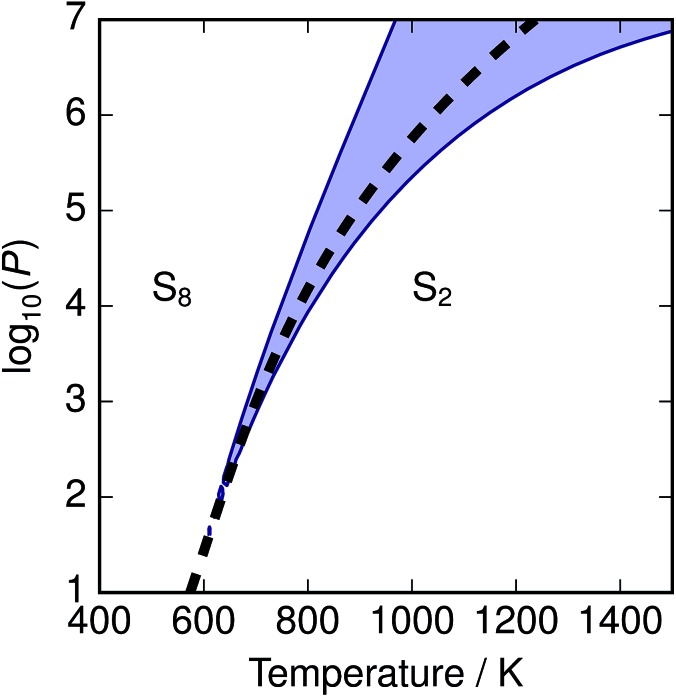
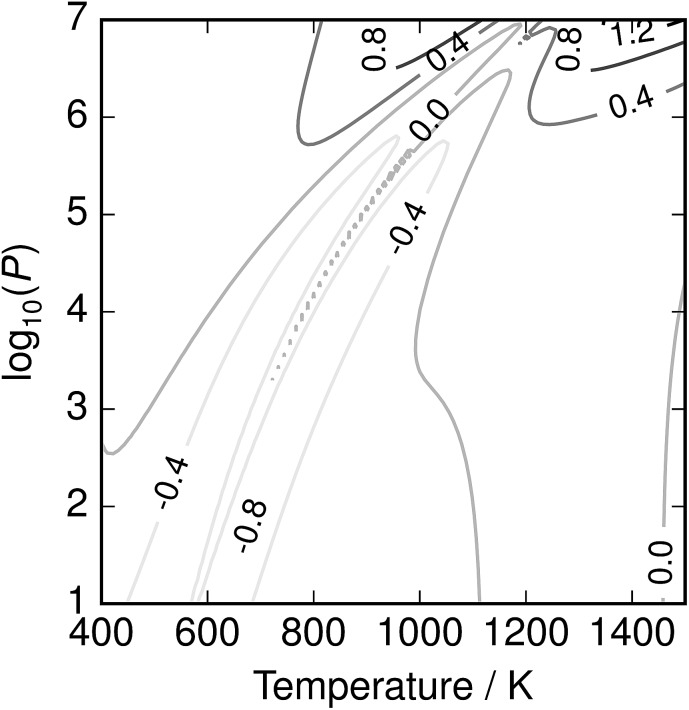
The depression in free energy due to mixing of allotropes and presence of minor components can be quantified by subtracting the chemical potential of the mixture from the minimum of the chemical potentials of the majority components S2 and S8. The resulting plot (Fig. 8) shows that this has an impact ranging from around 1–4 kJ mol–1, depending on the pressure. This is illustrated as a contour plot in Fig. 7; within each unshaded region a single-phase model is adequate to within 1 kJ mol–1 S atoms.

Fig. 8. Depression in chemical potential of sulfur vapour μS due to mixing and presence of minor allotropes. 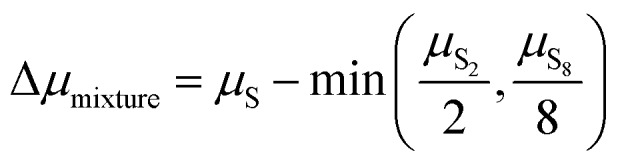Inline graphic.

Fig. 8

Open in a new tab

Fig. 7. Temperature-pressure map of approximations to free energy of mixture. At dashed line 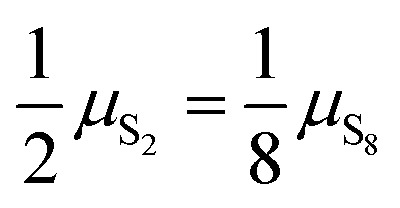Inline graphic; in shaded region the error in chemical potential μ associated with assuming a single phase S2 or S8 exceeds 1 kJ mol–1 S atoms; in unshaded regions the corresponding single-phase free energy is close to the energy of the mixture.

Fig. 7

Open in a new tab

3.4. Parameterisation

For convenience, a parameterised fit has been generated for the chemical potential of S over the T, P range 400–1500 K, 100 to 107 Pa, incorporating an error function “switch” between S2 and S8 dominated regions and a Gaussian correction for the free energy depression where there is substantial mixing of phases. In eV per S atom, for T in K, the form of the parameterisation is

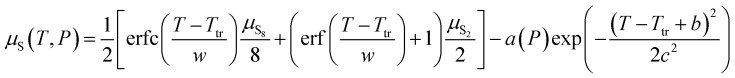3.4. 26

where μS8(T,P) = 7.620 × 10–1 – 2.457 × 10–3T – 4.012 × 10–6T2 + 1.808 × 10–9T3 – 3.810 × 10–13T4 + 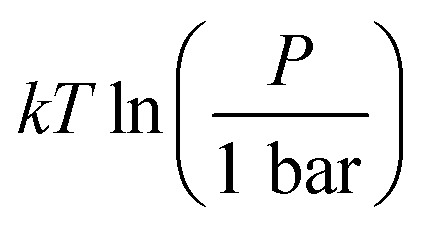Inline graphic, μS2(T,P) = 1.207 – 1.848 × 10–3T – 8.566 × 10–7T2 + 4.001 × 10–10T3 – 8.654 × 10–14T4 + 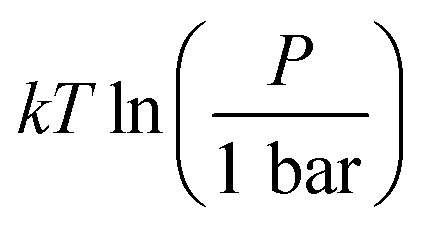Inline graphic. Ttr, the transition temperature obtained by solving Inline graphic is approximated by the polynomial Ttr = 5.077 × 102 + 7.272 × 101 log10 P – 8.295(log10 P)3 + 1.828(log10 P)2. The height of the Gaussian correction a(P) = 1.414 × 103 – 2.041 × 102log10 P + 6.663 × 101(log10 P)2, and the more arbitrarily assigned width and offset parameters b = 10, c = 80, w = 100.

It is noted that this parameterisation contains many fitting parameters; however, given its physically-motivated form the resulting function is smooth and well-behaved over the region studied, while the fits to μS2, μS8 and Ttr have some value in their own right. The fitting error is plotted in Fig. 9, and while somewhat irregular remains below 1 kJ mol–1.

Fig. 9. Error of parameterisation in kJ mol–1. Error is reduced to less than 1 kJ mol–1, but is highly non-uniform. Parameterisation is recommended for convenient application over wide T–P ranges; the full equilibrium solution is required to correctly capture fine detail.

Fig. 9

Open in a new tab

4. Conclusions

The chemical potential of sulfur vapours has been studied by solving the thermodynamic equilibrium of 13 gas-phase allotropes, including the dominant components S2 and S8. Thermochemical data was obtained from first-principles calculations and corrected with an empirical scaling factor for the vibrational frequencies. The transition between these dominating phases is highly pressure-dependent, and the free energy is further depressed at the transition temperature by the presence of additional phases, especially at elevated pressures. Selection of an inappropriate gas phase can lead to errors of the order 50 kJ mol–1 atoms, while the minor phases contribute free energy of the order 1 kJ mol–1 atoms. The resulting chemical potential data is made available through tabulated data, a parameterised model with error of the order 0.5 kJ mol–1 atoms and through open-source code; the reference energy is compatible with the NIST-Janaf thermochemical tables for the solid α-sulfur phase.3 This phase is frequently used as a reference state for thermodynamic studies of defects and stability in metal chalcogenides; the application of this gas-phase potential may allow such studies to examine a wide range of reactions involving sulfur vapours, taking into account the equilibrium within the vapour phase. The selection of appropriate chemical potentials is also critical for the development and interpretation of phase diagrams.

5. Data access statement

The reference implementation of this model, complete with Python 2.7 code to generate all the plots in this paper as well as tabulated data in the form of Table 4, is available online at ; https://github.com/WMD-Bath/sulfur-model and a snapshot of the code at the point of submission of this article is hosted by Zenodo and available with the DOI: ; 10.5281/zenodo.28536. In addition, full tables are provided with this paper in the ESI† for the composition, enthalpy and chemical potential from the calculations with PBE0 and empirical corrections; one set of enthalpy and chemical potential data follows Table 4 and uses the enthalpy of α-S as a reference energy (for use with other tabulated data) while the other employs the ground state of S8 as a reference energy (for use with first-principles calculations.) The code and its dependencies are Free Software, using a range of licenses. Input and output files from DFT calculations with FHI-aims have been deposited with Figshare and are available with the DOI: ; 10.6084/m9.figshare.1513736. A set of data generated during the evolutionary search, consisting of candidate structures and the DFT energies used to rank them, has been deposited with Figshare and is available with the DOI: ; 10.6084/m9.figshare.1513833.

Table 4. Gibbs free energy of S vapours, tabulated from calculations with PBE0 and empirical corrections, with reference state (H = 0) α-sulfur at 298.15 K. Energies in kJ mol–1, column headers in log10(pressure/Pa). Tables are provided with more values and greater decimal precision in the ESI.

T/K log10(p/Pa)
1.00 1.67 2.33 3.00 3.67 4.33 5.00 5.67 6.33 7.00
100 4.73 4.88 5.04 5.20 5.36 5.52 5.68 5.84 6.00 6.16
150 2.29 2.53 2.77 3.01 3.25 3.49 3.72 3.96 4.20 4.44
200 –0.39 –0.07 0.25 0.57 0.89 1.21 1.53 1.85 2.17 2.49
250 –3.27 –2.87 –2.47 –2.08 –1.68 –1.28 –0.88 –0.48 –0.08 0.32
300 –6.34 –5.86 –5.39 –4.91 –4.43 –3.95 –3.47 –2.99 –2.51 –2.03
350 –9.58 –9.02 –8.46 –7.90 –7.34 –6.78 –6.23 –5.67 –5.11 –4.55
400 –12.97 –12.33 –11.69 –11.05 –10.41 –9.77 –9.13 –8.49 –7.85 –7.21
450 –16.50 –15.77 –15.05 –14.33 –13.61 –12.89 –12.17 –11.45 –10.73 –10.01
500 –20.20 –19.37 –18.56 –17.75 –16.94 –16.14 –15.33 –14.53 –13.73 –12.93
550 –24.24 –23.17 –22.22 –21.31 –20.40 –19.51 –18.62 –17.73 –16.85 –15.96
600 –29.74 –27.46 –26.12 –25.03 –24.01 –23.01 –22.03 –21.05 –20.08 –19.11
650 –37.54 –33.52 –30.62 –29.01 –27.78 –26.65 –25.56 –24.49 –23.42 –22.36
700 –45.63 –41.17 –36.83 –33.61 –31.81 –30.45 –29.22 –28.04 –26.87 –25.72
750 –53.78 –49.00 –44.23 –39.63 –36.36 –34.48 –33.03 –31.71 –30.43 –29.18
800 –61.99 –56.89 –51.79 –46.72 –41.99 –38.90 –37.03 –35.51 –34.10 –32.74
850 –70.27 –64.84 –59.43 –54.02 –48.67 –44.06 –41.31 –39.46 –37.88 –36.39
900 –78.59 –72.85 –67.11 –61.38 –55.67 –50.16 –46.04 –43.61 –41.79 –40.15
950 –86.97 –80.91 –74.85 –68.80 –62.75 –56.78 –51.43 –48.04 –45.84 –44.01
1000 –95.39 –89.01 –82.64 –76.26 –69.90 –63.57 –57.48 –52.84 –50.06 –47.98
1050 –103.86 –97.17 –90.47 –83.77 –77.09 –70.43 –63.88 –58.14 –54.50 –52.07
1100 –112.38 –105.36 –98.34 –91.33 –84.32 –77.34 –70.42 –63.91 –59.21 –56.29
1150 –120.94 –113.60 –106.26 –98.93 –91.60 –84.29 –77.03 –70.00 –64.26 –60.68
1200 –129.53 –121.88 –114.22 –106.57 –98.92 –91.29 –83.70 –76.25 –69.65 –65.25
1250 –138.17 –130.19 –122.22 –114.24 –106.28 –98.33 –90.41 –82.60 –75.33 –70.03
1300 –146.84 –138.54 –130.25 –121.96 –113.67 –105.40 –97.16 –89.01 –81.23 –75.04
1350 –155.55 –146.93 –138.32 –129.71 –121.10 –112.51 –103.95 –95.46 –87.25 –80.27
1400 –164.29 –155.36 –146.42 –137.49 –128.57 –119.66 –110.77 –101.95 –93.36 –85.72
1450 –173.06 –163.81 –154.56 –145.31 –136.07 –126.84 –117.63 –108.49 –99.53 –91.33
Open in a new tab

6. Appendix

6.1. Proof that G = λ

We define the molar Gibbs free energy of sulfur atoms in a molecular gas mixture as

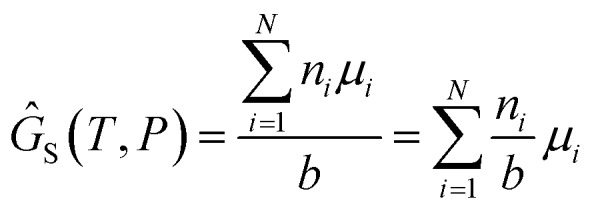6.1. 27

and substitute in (24)

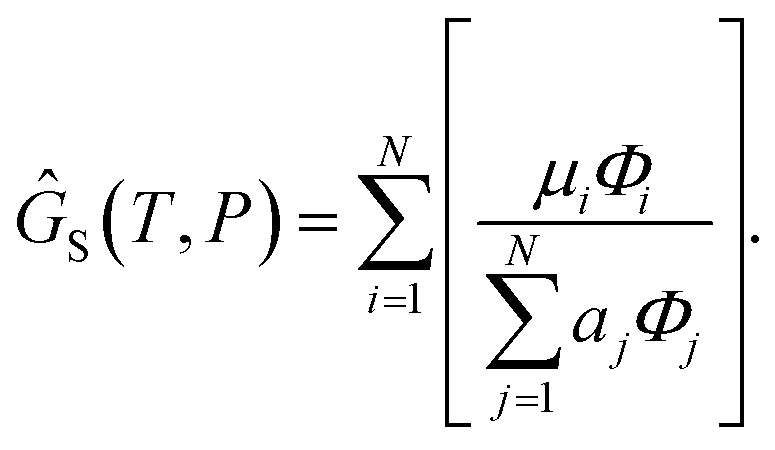6.1. 28

(Notation the same as Section 2.4.3). From (12), μi = aiλ and hence

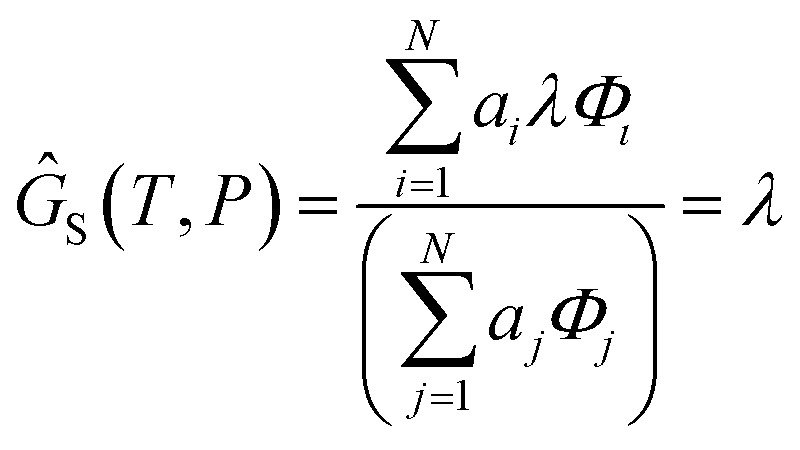6.1. 29

Supplementary Material

Click here for additional data file. (9.4KB, zip)

Acknowledgments

The authors thank J. M. Skelton and J. M. Frost for useful discussions. USPEX/VASP calculations with PBE were carried out using the University of Bath's High Performance Computing facilities. Hybrid DFT calculations were carried out using ARCHER, the UK's national high-performance computing service, via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (grant no. EP/L000202L000202). A. J. J. is part of the EPSRC Doctoral Training Center in Sustainable Chemical Technologies (grant no. EP/G03768XG03768X/11). The contribution of D. T. was supported by ERC Starting Grant 277757.

Footnotes

†Electronic supplementary information (ESI) available: Tabulated free energy and enthalpy data. Additional data and code available in external repositories with DOI: 10.5281/zenodo.28536; DOI: 10.6084/m9.figshare.151373; DOI: 10.6084/m9.figshare.1513833. See data access statement for more information. See DOI: 10.1039/c5sc03088a

§Note that the implementation of B3LYP in FHI-aims uses a parameterisation of the local density contribution based on the random phase approximation in order to match values obtained with Gaussian, another quantum chemistry code.22

References

  1. Nehb W. and Vydra K., Sulfur, Ullmann’s Encyclopedia of Industrial Chemistry, 2006 10.1002/14356007.a25_507.pub2. [DOI] [Google Scholar]
  2. Lewis G. N., Randall M. J. Am. Chem. Soc. 1914;36:2468–2475. [Google Scholar]
  3. Chase M. J. J. Phys. Chem. Ref. Data, Monogr. 1998;9:1–1951. [Google Scholar]
  4. Rau H., Kutty T., Guedes de Carvalho J. J. Chem. Thermodyn. 1973;5:833–844. [Google Scholar]
  5. Yu P. Y. and Cardona M., Fundamentals of Semiconductors, Springer-Verlag, Berlin, Heidelberg, New York, 3rd edn, 2003. [Google Scholar]
  6. Berg D. M., Djemour R., Gütay L., Zoppi G., Siebentritt S., Dale P. J. Thin Solid Films. 2012;520:6291–6294. [Google Scholar]
  7. Lichtenstriger M., Bölsterli H. U., Nitsche R. J. Phys. Chem. Solids. 1961;21:199–205. [Google Scholar]
  8. Colombara D., Delsante S., Borzone G., Mitchels J., Molloy K., Thomas L., Mendis B., Cummings C., Marken F., Peter L. J. Cryst. Growth. 2013;364:101–110. [Google Scholar]
  9. Burton L. A., Colombara D., Abellon R. D., Grozema F. C., Peter L. M., Savenije T. J., Dennler G., Walsh A. Chem. Mater. 2013;25:4908–4916. [Google Scholar]
  10. Jackson A. J., Walsh A. J. Mater. Chem. A. 2014;2:7829. [Google Scholar]
  11. Kosyak V., Mortazavi Amiri N. B., Postnikov A. V., Scarpulla M. A. J. Appl. Phys. 2013;114:124501. [Google Scholar]
  12. Scragg J. J., Ericson T., Kubart T., Edoff M., Platzer-Björkman C. Chem. Mater. 2011;23:4625–4633. [Google Scholar]
  13. Martin T. P. J. Chem. Phys. 1984;81:4426. [Google Scholar]
  14. Steudel R., Studies in Inorganic Chemistry, Elsevier, Amsterdam, 1984, vol. 5, pp. 3–37. [Google Scholar]
  15. Hohl D., Jones R. O., Car R., Parrinello M. J. Chem. Phys. 1988;89:6823. [Google Scholar]
  16. Quelch G. E., Schaefer H. F., Marsden C. J. J. Am. Chem. Soc. 1990;112:8719–8733. [Google Scholar]
  17. Wong M. W., Steudel R. Chem. Phys. Lett. 2003;379:162–169. [Google Scholar]
  18. Steudel R., Stuedel Y., Wong M. W. Top. Curr. Chem. 2003:117–134. [Google Scholar]
  19. Kohn W., Sham L. Phys. Rev. A. 1965;140:1133–1138. [Google Scholar]
  20. Perdew J., Burke K., Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  21. Perdew J., Ruzsinszky A., Csonka G., Vydrov O., Scuseria G., Constantin L., Zhou X., Burke K. Phys. Rev. Lett. 2008;100:136406. doi: 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  22. Hertwig R. H., Koch W. Chem. Phys. Lett. 1997;268:345–351. [Google Scholar]
  23. Becke A. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
  24. Adamo C., Barone V. J. Chem. Phys. 1999;110:6158. [Google Scholar]
  25. Kresse G., Furthmüller J. Comput. Mater. Sci. 1996;6:15–50. [Google Scholar]
  26. Kresse G., Furthmüller J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  27. Blum V., Gehrke R., Hanke F., Havu P., Havu V., Ren X., Reuter K., Scheffler M. Comput. Phys. Commun. 2009;180:2175–2196. [Google Scholar]
  28. Havu V., Blum V., Havu P., Scheffler M. J. Comput. Phys. 2009;228:8367–8379. [Google Scholar]
  29. Oganov A. R., Glass C. W. J. Chem. Phys. 2006;124:244704. doi: 10.1063/1.2210932. [DOI] [PubMed] [Google Scholar]
  30. Oganov A. R., Lyakhov A. O., Valle M. Acc. Chem. Res. 2011;44:227–237. doi: 10.1021/ar1001318. [DOI] [PubMed] [Google Scholar]
  31. Lyakhov A. O., Oganov A. R., Stokes H. T., Zhu Q. Comput. Phys. Commun. 2013;184:1172–1182. [Google Scholar]
  32. Merrick J. P., Moran D., Radom L. J. Phys. Chem. A. 2007;111:11683–11700. doi: 10.1021/jp073974n. [DOI] [PubMed] [Google Scholar]
  33. Alecu I. M., Zheng J., Zhao Y., Truhlar D. G. J. Chem. Theory Comput. 2010;6:2872–2887. doi: 10.1021/ct100326h. [DOI] [PubMed] [Google Scholar]
  34. Bahn S. R., Jacobsen K. W. Comput. Sci. Eng. 2002;4:56–66. [Google Scholar]
  35. Smith W. R. and Nissen R. W., Chemical Reaction Equilibrium Analysis: Theory and Algorithms, John Wiley & Sons, New York, 1982. [Google Scholar]
  36. Brinkley S. R. J. Chem. Phys. 1946;14:563. [Google Scholar]
  37. Brinkley S. R. J. Chem. Phys. 1947;15:107–110. [Google Scholar]
  38. White W. B. J. Chem. Phys. 1967;46:4171. [Google Scholar]
  39. Marquardt D. W. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
  40. SciPy, Open source scientific tools for Python, 2001, http://www.scipy.org/, online; accessed 2015-03-06. [Google Scholar]
  41. McCarthy M. C., Thorwirth S., Gottlieb C. A., Thaddeus P. J. Am. Chem. Soc. 2004;126:4096–4097. doi: 10.1021/ja049645f. [DOI] [PubMed] [Google Scholar]
  42. Boumedien M. S., Corset J., Picquenard E. J. Raman Spectrosc. 1999;472:463–472. [Google Scholar]
  43. Hassanzadeh P., Andrews L. J. Phys. Chem. 1992;96:6579–6585. [Google Scholar]
  44. Wong M. W., Steudel Y., Steudel R. J. Chem. Phys. 2004;121:5899–5907. doi: 10.1063/1.1785143. [DOI] [PubMed] [Google Scholar]
  45. Burton L. A., Walsh A. J. Phys. Chem. C. 2012;116:24262–24267. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (9.4KB, zip)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES