Correlated longitudinal changes across linguistic, achievement, and psychomotor domains in early childhood: Evidence for a global dimension of development

Abstract

An important question within developmental psychology concerns the extent to which the maturational gains that children make across multiple diverse domains of functioning can be attributed to global (domain-general) developmental processes. The present study investigated this question by examining the extent to which individual differences in change across children’s development in five different domains are correlated. Multivariate growth-curve models were fit to longitudinal data on linguistic, mathematics, reading, gross motor, and fine motor skills in 8,950 children ranging in age from 44 to 86 months (3.7 years to 7.2 years). All five rates of change were positively intercorrelated. A common factor accounted for 42% of the individual differences in change. These results suggest that a global dimension underlies substantial proportions of cognitive and psychomotor development.

A primary goal of developmental psychology is to characterize and understand the tremendous gains that children make in many distinct forms of functioning as they grow. Developmental gains are observed in all areas of cognition, ranging from basic psychomotor functions to language acquisition, oral communication, and mathematical reasoning. Each of these domains is highly complex, so it is not surprising that entire research programs are commonly devoted to studying development in a specific domain. As such, research on children’s achievements in mathematics, reading, language, and motor skills frequently focuses on predictors and mechanisms of learning that are specific to one of these domains (e.g., Jordan, Kaplan, Locuniak & Ramineni, 2007; Markman, 1990; Muter, Hulme, Snowling & Stevenson, 2004; Wolpert, Ghahramani, & Flanagan, 2001). The ubiquity of research on domain-specific influences on development, however, gives rise to an important question concerning the extent to which general factors underlie development across many different domains of functioning (Chiappe & Macdonald, 2005; Fuchs, Geary, Compton, Fuchs, Hamlett, & Bryant, 2010; Hecht, Torgesen, Wagner, & Rashotte, 2001; Kail, 2004; Oaks, 2009; Petrill, 1997; Salthouse, 1998; Tucker-Drob, 2009). To the extent that children’s growth across multiple domains is affected by global factors, it may be misleading to construct exclusively domain-specific models and theories of development—development in different domains must at least in part be explained by general mechanisms and processes. In this case, developmental research will profit from considering domain-general mechanisms and predictors in addition to domain-specific ones.

Cognitive psychologists have proposed a number of domain-specific and domain-general accounts of development. On the domain-specific side, Spelke and colleagues have proposed that infants are natively equipped with basic (“core”) knowledge in several domains of reasoning, including numbers, physical objects, and minds (e.g., Carey, 2009; Spelke & Kinzler, 2007). These modular cores of reasoning are hypothesized to provide the framework for children’s early learning in each domain. For example, Leslie, Friedman, and German (2004) proposed that infants have a ‘theory of mind’ mechanism that supports learning to reason about other people’s beliefs and desires, and suggested that deficits in this mechanism can lead to developmental disorders such as autism.

On the domain-general side, a number of researchers have shown that infants and children are able to use general learning mechanisms to acquire knowledge and skills across a vast array of perceptual, cognitive, and motor domains. For example, children can observe probabilistic relations among syllables, words, and objects to parse words from the speech stream, to pair novel words with objects, and to guide inference about hidden properties of object kinds (Kelly & Martin, 1994; Kirkham, Slemmer, & Johnson, 2002; Pelucchi, Hay, & Saffran, 2009; Saffran, Aslin, & Newport, 1996; Tenenbaum, Griffiths, & Kemp, 2006; Vouloumanos & Werker, 2009). Other domain-general learning mechanisms include the use of analogy and comparison (e.g., Gentner & Medina, 1998), attention to causal relations (e.g., Gopnik, Glymour, Sobel, Schulz, Kushnir, & Danks, 2004; Shulz & Gopnik, 2004), and use of social cues (e.g., Csibra & Gergely, 2006). This research has typically examined whether groups of normally-developing infants or children are able to use a particular kind of information or kind of reasoning to learn about the world.

Other researchers have addressed the domain-general versus domain-specific question by examining whether a small set of cognitive mechanisms is responsible for the diverse developmental gains that children experience as they age (Fry & Hale, 1996, 2000; Hale, 2008; Kail, 2000, 2007; Kail & Salthouse, 1994). This line of research has revealed that age-related differences in processing speed and working memory mediate age-related differences in various cognitive domains. Based on these findings, both Kail and Salthouse (1994) and Fry and Hale (1996) suggested that development across many different cognitive domains is driven by increases in processing speed throughout childhood which, in turn, lead to increased working memory capacity. As with the domain-general research reviewed above, this research has focused on group trends; almost none of it has examined whether individual differences in the proposed domain-general processes or mechanisms relate to developmental differences among children.

Surprisingly, few, if any, researchers have addressed the question of generality versus specificity of development from the perspective of longitudinal individual differences, that is, by examining relations among individual differences in rates of change over time. To illustrate why this approach is important, consider the development of reading fluency and mathematics competency. The fact that both reading fluency and mathematics competency increase on average in a population does not mean that reading and mathematics increase in tandem for specific individuals. Similarly, showing that children are able to use a common learning technique (e.g., analogy) to learn new principles in math and reading does not necessarily mean that they can do so with equal alacrity in both domains. To the contrary, folk wisdom suggests that many children who excel in reading may have difficulty learning math, and vice versa.

A long history of research on general intelligence (Spearman, 1904) has examined the relations among individual differences in performance on measures of many different functions at a single point in time (see, e.g., Deary, 2000, for an overview of the concept of general intelligence). But examining individual differences at a static point in time is not directly informative about individual differences in growth and change over time. Examining scholastic performance at a given instance during first grade would represent an unknown admixture of individual differences due to mechanisms that operated prior to school entry (and perhaps even during gestation), and individual differences due to mechanisms that operate during the formal schooling. For example, it is possible that the genes that give rise to individual differences in early infant mental development may not be the same genes as those that determine individual differences in scholastic achievement during the school years. Similarly, it is very likely that the environmental influences that children experience prior to school entry (which mostly exist with the caregiver in the home) differ greatly from those that they experience during the early school years (which include a great deal of time away from the caregiver and outside of the home).

To the extent that these influences differ at different stages of development, learning at different ages may be more or less domain-specific. It is possible that prior to the school years, genes and home experiences broadly affect many different domains of functioning, for example, by influencing children’s working memory, motivation, attention, or other learning skills. For instance, controlled attention might be particularly important for learning in many different arenas (e.g., both walking and talking) during early child development, in which case, genes that affect individual differences in controlled attention might have general effects. Moreover, parental sensitivity might similarly be crucial for early infant verbal and motor learning. Alternatively, genes and experiences that have more specific effects on individual domains of functioning might be more likely to operate during the school years. For example, specific genes for language processing and specific genes for numerical thinking might not be expressed until middle childhood, and the rigor and quality of mathematics courses and language courses might have specific effects on children’s interests and capabilities in particular subjects or domains of learning. For these reasons, correlations between facets of development at a single point in time do not support inferences about whether global mechanisms affect children’s development over time.

By estimating the correlations among individual differences in language, mathematics, and psychomotor growth, the present study is designed to directly test whether a child’s rate of growth in one domain of functioning is related to her rate of growth in other domains of functioning (Baltes & Nesselroade, 1979). Rather than focusing on average trends in performance in a population, our approach investigates individual differences in the developmental process (e.g. whether individuals who change in their reading performance more quickly relative to their peers are also likely to change in their math performance more quickly relative to their peers) to make inferences about the factors affecting growth across domains. We examine development of five cognitive variables in children from preschool through kindergarten. We model children’s change in each variable over time and investigate the extent to which those changes can be accounted for by a single common developmental factor. After reporting our findings, we go on to discuss possible genetic, neurophysiological, and social mechanisms that could underlie correlated individual differences in change.

Method

For the current project we applied the individual differences in change approach described above to data from the Early Childhood Longitudinal Study-Birth Cohort (ECLS-B), which was conducted by the U.S. Department of Education’s National Center for Education Statistics. ECLS-B is a study based on a nationally representative sample of approximately 10,700 children born in the United States in the year 2001. The ECLS-B followed children longitudinally from approximately nine months of age until kindergarten. Children were assessed up to five times between 2001 and 2007. However, because children were too young to be administered multiple cognitive measures at the first two waves (infancy), only data from the latter three assessments were analyzed for the current project.

Participants

Our analyses are based on data from 10200¹ children, of whom 8300 participated at the third wave (Time 1), 6800 at the fourth wave (Time 2), and 1850 at the fifth wave (Time 3). Note that only the subset of children who were not yet attending kindergarten at Time 2 were invited to participate at Time 3, and that missing a wave of measurement did not preclude a child from participating in subsequent waves. The weighted mean age of the children was 4;6 (years; months; SD = 4.11 mo; range = 44 to 65 mo) at Time 1, 5;5 (SD = 3.71 mo, range = 55 to 75 mo) at Time 2, and 6;2 (SD = 2.52 mo, range = 70 to 86 mo) at Time 3. Approximately half of the children were girls (51.1%). The ethnic composition of the sample was as follows: 41.4% white, 15.9% African-American, 20.5% Hispanic, 11.3% Asian, and 10.8% other. All model estimates were weighted to match the population of children born in 2001: 53.1% white, 13.7% African-American, 25.5% Hispanic, 2.8% Asian, and 4.7% other.

Measures

ECLS-B measured five different cognitive and psychomotor domains: reading, mathematics, oral language, gross motor skills, and fine motor skills. More difficult items were added to the reading and mathematics tests at later waves, and item response theory scoring was used to place reading and mathematics scores obtained at different ages on the same metric, such that longitudinal changes could be meaningfully interpreted. Figure 1 displays the developmental trends of each of the five measures.

Figure 1.

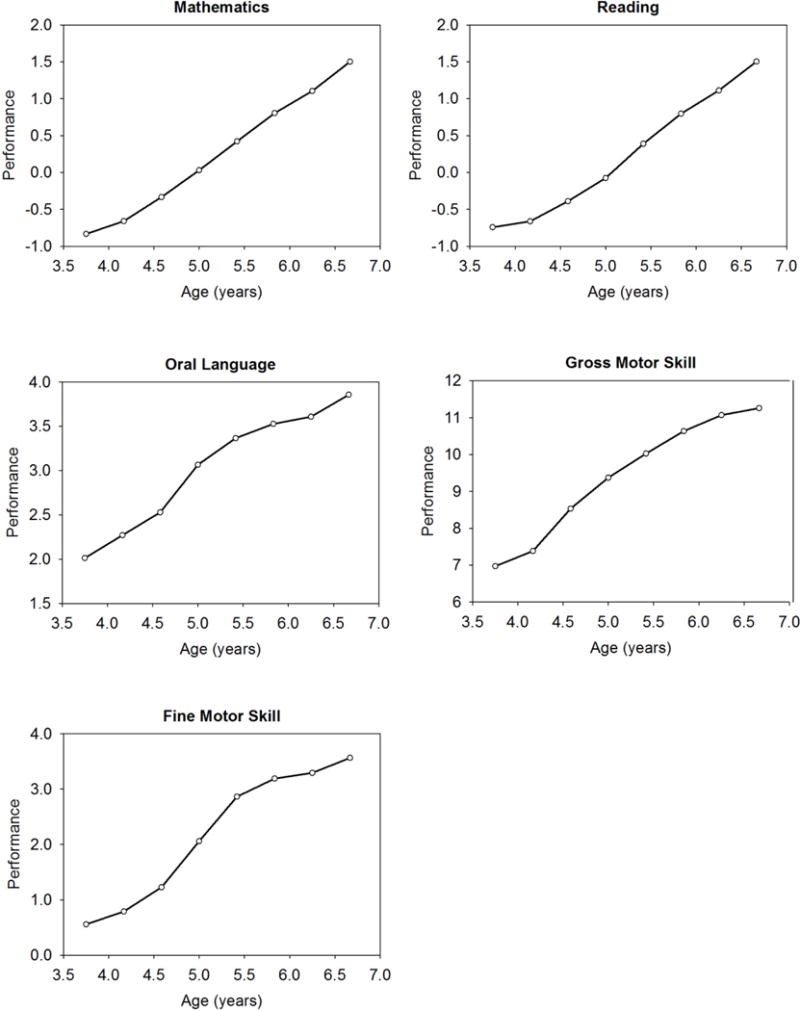
Mean developmental trends for each of five outcomes.

Note. Because each participant was measured at up to three different ages, a multilevel model was used to take into account the nesting of time points within individuals.

Reading

The ECLS-B reading assessment was designed to measure basic skills such as letter recognition and letter sounds (e.g., identifying the names and sounds of letters), phonological awareness (e.g., matching words starting with the same sound), and knowledge of print conventions (e.g., displaying familiarity with left-to-right reading), as well as early reading (e.g., reading simple words) and vocabulary (e.g., matching a word to a picture depicting its referent). Comprehension tasks assessed children’s global understanding of the content of a story that was read to them, the extension of their global understanding to a more complete interpretation of content, and their objective appraisal of the content read. Items to assess each of these constructs were taken from popular reading and language assessments, including the Preschool Language Assessment Scale (PreLAS; Duncan & De Avila 1998), the Preschool Comprehensive Test of Phonological & Print Processing (Pre-CTOPP; Lonigan, Wagner, Torgeson & Rashotte, 2002), and the Peabody Picture Vocabulary Test (PPVT-III; Dunn & Dunn, 1997). IRT trait scores ranged from −2.11 to 2.59.

Mathematics

The ECLS-B mathematics assessment was designed to measure number sense (e.g., cardinality, ordinality, quantity) and operations (e.g., addition, subtraction), as well as more complex skills including measurement (e.g., comparing the lengths or heights of two objects), geometry and spatial sense (e.g., identification and transformation of geometric shapes), statistics and probability (e.g., identifying and describing patterns in data), and pattern recognition. IRT trait scores ranged from −2.84 to 3.12.

Oral Language

The “Let’s Tell Stories” task was adapted from the preLAS subtest of the same name. It was designed to assess children’s expressive and receptive verbal ability. For each of two stories, an experimenter pointed to a series of pictures while telling the child a scripted story. The child then re-told the story, with the help of the pictures as prompts. Children’s responses were audiotaped and transcribed, and subsequently scored on a 0 to 5 point scale by trained coders using standardized procedures. Scores indicated the degree to which the child was able to tell a coherent and grammatically complex story, where a score of 0 indicated that the child made no response, 1 indicated the child’s use of short isolated phrases, 2 indicated the child’s use of disconnected phrases and many grammatical errors, 3 indicated that the child told a recognizable story with limited detail and grammatical errors, 4 indicated that the child told a recognizable story in clear, fluent sentences, and 5 indicated the child was highly articulate, using complex constructions and advanced descriptive vocabulary to tell a story.

Gross Motor Skills

Gross motor skills involve large muscle groups, and represent general musculature, physical skill, and coordination. Trained experimenters assessed a number of gross motor skills including jumping, balancing, hopping, skipping, walking backwards, and catching a bean bag. Experimenters scored children according to standardized procedures. Scores on each task were summed to create a composite score that ranged from 0 to 13, according to the number of tasks children were able to successfully execute.

Fine Motor Skills

Fine motor skills involve smaller muscle groups, and represent both fine motor control and visual-motor integration. Experimenters assessed fine motor skills using two tasks. The first task required the child to build a gate from wooden blocks after watching an experimenter build it out of a second set of blocks. The second task required the child to copy three shapes: a square, a triangle, and an asterisk, using a pencil and paper. Children received 1 point for each subtask they completed successfully, resulting in total scores ranging from 0 to 4.

Covariates

In addition to the primary outcomes of interest, we also made use of a number of a number of covariates. We control for these covariates in our final model to test the robustness of the relations initially identified. The covariates that we included were age at Time 1, Socioeconomic Status (a composite variable composed of maternal and paternal income, education, and job status), parents’ estimates of the number of children’s books in their home), whether the child was ever breastfed, parent rating of the child’s health at Time 1, and the total number of siblings living in the same household with the child at Time 1.

Statistical Methods

We made use of a growth curve modeling approach (McArdle & Nesselroade, 2003). Growth curve models allow repeated measures data for a given variable to be decomposed into three components: an initial level of performance (the intercept), a rate of systematic change in performance over time (the slope), and unsystematic influences on performance that are unique to each time point (disturbances). Individual differences can be manifest in each of these components. When more than one variable is measured repeatedly over time, these individual differences may be allowed to correlate with one another. Correlations among intercepts are directly analogous to concurrent relations measured at a single point in time (e.g. correlations from a cross-sectional study), whereas correlations among slopes indicate that two variables change together over development.

The basic version of the growth curve model can be generally written as,

$$\mathrm{Y}{\left[\mathrm{t}\right]}_{\mathrm{w},\mathrm{n}}={\mathrm{y}}_{0,\mathrm{w},\mathrm{n}}+\mathrm{a}\left[\mathrm{t}\right]·{\mathrm{y}}_{\mathrm{s},\mathrm{w},\mathrm{n}}+\mathrm{e}{\left[\mathrm{t}\right]}_{,\mathrm{w},\mathrm{n}},$$ (Eq. 1)

where Y[t]_w,n is the score of person n on outcome w at time t; y₀,_w,n is the level of performance (or intercept) on outcome w for person n at time 1; y_s,w,n is the rate of longitudinal change (or slope) in performance on outcome w for person n, and e_t,w,n is a residual for person n on outcome w at time t.² The residuals are scaled to each have means of zero and are specified to be uncorrelated. The levels and the slopes are allowed to have nonzero means and to correlate. The a[t] coefficients define the shape of the systematic change. For the current project, these a[t] coefficients were freely estimated as model parameters, such that the shape of the change was determined by the empirical data.

When there is evidence for correlations among the levels and/or among the slopes, a factor model can be useful to account for these relations with just a few dimensions. Such a model can be written for levels and slopes separately as

$${\mathrm{y}}_{0,\mathrm{w},\mathrm{n}}={\mathrm{\upsilon }}_{0,\mathrm{w}}+{\mathrm{\lambda }}_{0,\mathrm{w}}·{\mathrm{F}}_{0,\mathrm{n}}+{\mathrm{u}}_{0,\mathrm{w},\mathrm{n}},$$ (Eq. 2a)

$${\mathrm{y}}_{\mathrm{s},\mathrm{w},\mathrm{n}}={\mathrm{\upsilon }}_{\mathrm{s},\mathrm{w}}+{\mathrm{\lambda }}_{\mathrm{s},\mathrm{w}}·{\mathrm{F}}_{\mathrm{s},\mathrm{n}}+{\mathrm{u}}_{\mathrm{s},\mathrm{w},\mathrm{n}},$$ (Eq. 2b)

where F₀ is the factor on which the levels (y₀) load, and F_s is the factor on which the slopes (y_s) load (cf. Tucker-Drob, 2011). Of particular interest for the current project was the factor pattern of the slopes.

Results

All models made use of full information maximum likelihood (FIML) estimation in the Mplus statistical package (Muthén & Muthén, 1998–2007). FIML estimation takes advantage of all information from all variables and all individuals in the dataset. This results in parameter estimates that are representative of the original population sampled, under the assumption that any patterns of missingness that systematically relate to the outcomes can be accounted for by the available data. The implementation of FIML, and the inclusion of the covariates described above were particularly important for correcting for any bias that would have resulted from the missing data patterns resulting from ECLS-B’s decision to only invite children to participate at Time 3 if they were not yet attending kindergarten at Time 2. All models employed sampling weights, and took nesting within geographic regions into account in the estimation process to correct for the underestimation of standard errors due to clustered sampling.

Modeling Longitudinal Change

We fit the basic growth-curve model in Equation 1 for each dependent measure, allowing the intercepts and slopes of the five outcomes to correlate. Note that this model also included the six covariates, which were allowed to freely correlate with the growth-curve levels and slopes (i.e., while the covariates were included in the model to improve the quality of the model estimates, they were not controlled for). This model fit relatively well; χ² (80) = 884.61, p < .001; Root Mean Square Error of Approximation (RMSEA) = .03; Comparative Fit Index (CFI) = .96. We allowed the time-specific residuals on the two achievement tests (i.e., math and reading) to freely correlate. This considerably improved model fit; χ² (77) = 393.56, p < .001; RMSEA = .02, CFI = .99; χ²_difference (3) = 552.50, p < .001. These residuals were allowed to correlate in all subsequent models. The growth curve parameter estimates of this model are displayed in Table 1. It can be seen that all of the slope means were positive, indicating that children’s performance improved over time, and that all of the intercept variances and slope variances were significantly greater than zero, indicating that children differed from each other both in their initial levels of performance and in their rates of change in performance over time.

Table 1.

Parameter Estimates for Growth Curves of the Five Outcomes, Model 1.

Parameter	Mathematics	Reading	Oral Language	Gross Motor	Fine Motor
a[1]	@0	@0	@0	@0	@0
a[2]	.49 (.01)	.46 (.01)	.75 (.02)	.60 (.01)	.68 (.01)
a[3]	@1	@1	@1	@1	@1
Intercept Mean	−.49 (.03)	−.51 (.02)	2.38 (.02)	7.99 (.07)	1.02 (.02)
Slope Mean	1.79 (.02)	1.89 (.03)	1.31 (.03)	3.25 (.09)	2.59 (.04)
Intercept Variance	.48 (.02)	.45 (.02)	.65 (.08)	4.56 (.32)	.66 (.08)
Slope Variance	.19 (.03)	.28 (.04)	.41 (.11)	2.72 (.61)	.49 (.15)
Variance of e[1]	.14 (.01)	.12 (.01)	.43 (.08)	3.42 (.3)	.53 (.09)
Variance of e[2]	.16 (.01)	.25 (.01)	.44 (.03)	3.10 (.13)	.85 (.03)
Variance of e[3]	.06 (.01)	.04 (.02)	.22 (.04)	2.12 (.26)	.62 (.06)

Note: @ denotes that a parameter was fixed to identify the metric of the factor. Standard errors are in parentheses. All parameters are significant at p < .05.

Examining Change Interrelations

Correlations among the intercepts of each of the outcomes are shown in the upper diagonal of Table 2, and correlations among the slopes are shown in the lower diagonal of the same table. In line with a long history of individual differences research (Carroll, 1993; Spearman, 1904), all intercept correlations (which are directly analogous to concurrent correlations at a single point in time—approximately 4 years of age in this case) were positive and moderate-to-large in magnitude. Of greater interest are the correlations among the slopes. These correlations represent the extent to which different abilities change together as children develop over time. Interestingly, these correlations were also all positive and most were moderate-to-large in magnitude. That is, except for the correlation between oral language and fine motor development (r = .11, ns), all correlations were significantly greater than 0, and ranged in magnitude from .19 to .62. This manifold of positive change inter-correlations is evidence that domain-general components across the five measured domains influence developmental change.

Table 2.

Intercept and Slope Correlations in Early Childhood (Model 1)

	Math	Reading	Oral Language	Gross Motor	Fine Motor
1. Mathematics	—	.90 (.01)	.56 (.04)	.53 (.03)	.70 (.04)
2. Reading	.62 (.08)	—	.55 (.04)	.43 (.03)	.61 (.05)
3. Oral Language	.32 (.08)	.18 (.07)	—	.29 (.03)	.32 (.04)
4. Gross Motor	.56 (.11)	.37 (.09)	.19 (.10)	—	.50 (.04)
5. Fine Motor	.61 (.11)	.37 (.08)	.11 (.08)	.35 (.09)	—

Note. Residual variances of reading and mathematics indicators at each time point were allowed to correlate. Correlations between the intercepts (i.e., static correlations at the initial time point, according to the model) are above the diagonal; correlations between the slopes (i.e., correlations among change) are below the diagonal. Standard errors are in parentheses. Bolded values are significant at p < .05.

Fitting a Common Dimension

We next fit a common factor model in which a common dimension was formally presumed to underlie the level correlations and a second common dimension was formally presumed to underlie the change correlations (see Equation 2b). The control variables in the preceding analysis were allowed to covary with both independent variables (the level factor and the slope factor) in this model. Factor loadings of the individual levels and slopes on these common factors are presented in Table 3. On average, the common factor accounted for 44% of the systematic variance in change over time in cognitive outcomes. Note that, while substantial portions of the variances in these outcomes were accounted for by the common change factor (and therefore by domain-general influences on change), this factor did not account for all variation in change. Domain-specific developmental processes were also apparent.

Table 3.

Standardized Loadings of the Intercepts and Slopes on Common Factors (Model 2)

	Level Factor (F0)	Change Factor (Fs)
1. Mathematics	.98 (.01)	.85 (.08)
2. Reading	.93 (.01)	.53 (.08)
3. Oral Language	.54 (.04)	.30 (.08)
4. Gross Motor	.48 (.03)	.72 (.11)
5. Fine Motor	.73 (.05)	.77 (.17)

Note. Residual variances of reading and mathematics indicators at each time point were allowed to correlate. Bolded values are significant at p < .05.

Controlling for Covariates

In our previous models, we included six non-cognitive variables that were allowed to freely correlate with the independent variables. Next, we were interested in examining whether any of these six variables mediated our correlations of interest, as each of them has been shown to be related to children’s cognitive development (e.g., Anderson, Johnstone, & Remley, 1999; Azmitia & Hesser, 1993; Bing, 1963; Bradley & Corwyn, 2002; Guo & Harris, 2000; Perner, Ruffman, & Leekam, 1994; Sénéchal, LeFevre, Thomas, & Daley, 1998). In the next analysis, therefore, we controlled for the effects of age, socioeconomic status, number of books in the home, breastfed status, child’s health, and number of siblings by regressing the intercept and slope of each of the five growth curves onto each of these covariates while also allowing the intercepts and slopes to load on their respective factors. The results from this analysis are displayed in Table 4. Comparing Table 4 to Table 3, it is apparent that, while controlling for non-cognitive covariates tended to reduce the loadings of intercepts on the common intercept factor, the loadings of the slopes on the common slope factor – that is, the extent to which a global dimension can account for change in each of the cognitive – were relatively unaffected. In other words, the average proportion of variance accounted for (computed as the average squared loading) by the common factor of intercepts was reduced from 58% to 31%, whereas the average proportion of variance accounted for by the common factor of the slopes was only reduced from 44% to 42%. Therefore, the results of this analysis suggest that the common dimension of change was not simply an epiphenomenon of changes in many variables being similarly influenced by the common set of covariates examined.

Table 4.

Standardized Loadings of the Intercepts and Slopes on Common Factors, Controlling for Covariates(Model 3)

	Level Factor (F0)	Change Factor (Fs)
1. Mathematics	.76 (.02)	.86 (.10)
2. Reading	.65 (.01)	.57 (.09)
3. Oral Language	.34 (.03)	.28 (.06)
4. Gross Motor	.37 (.02)	.57 (.10)
5. Fine Motor	.54 (.04)	.78 (.17)

Note. Residual variances of reading and mathematics indicators at each time point were allowed to correlate. Effects of child’s age, socioeconomic status, number of books in the home, breastfed status, child’s health, and number of siblings were controlled for. Bolded values are significant at p < .05.

Discussion

For the current project we simultaneously fit growth models to longitudinal measurements of math, reading, oral language, gross motor, and fine motor achievement in children ranging in age from 3 years 8 months to 7 years 2 months. Six covariates were controlled for, including child’s age, socioeconomic status, number of books in the home, breastfed status, child’s health, and number of siblings. The rates of developmental change in every domain loaded significantly on a common factor, suggesting the existence of a domain-general dimension of individual differences in cognitive and psychomotor development. This factor accounted for an average of 42% of individual differences in change.

The present findings have both practical and theoretical implications for future research. Practically speaking, researchers should be cautious in drawing strong inferences about specific developmental outcomes without taking into account other outcomes that may be related. For example, a model of reading development that only considers the contribution of phonological skills, letter knowledge, and grammatical skills to overall reading proficiency would fail to account for more domain-general contributions to reading development, which might include general capacities such as attention, memory, inhibitory control, or social understanding. If such general processes contribute significantly to the development of reading proficiency, an educational program or intervention that only targets reading-specific skills might not be as effective as one that also aims to improve general learning skills.

Theoretically, these findings are consistent with a balanced global and modular perspective on development. With global influences accounting for an average of 42% of the systematic variance across domains, it is clear that there is still much room for specific influences on development within each domain. These might include children’s natural abilities, their inclinations and motivation with respect to a particular subject, and variance in the amount and quality of exposure, instruction, and practice children have access to in specific domains of development. Marcus and Rabagliati (2006) commented that, “One might ask whether different ‘rooms’ of the brain are all built according to exactly the same plan, or whether they differ in important ways, while depending on common infrastructure” (p. 397). The present work has revealed that the amount of common infrastructure is perhaps greater than some researchers may have expected, while also confirming that there is a large role of domain-specific factors.

Genetic, physiological, and social mechanisms all have potential to lead to correlated changes in multiple domains of functioning, either by acting through domain-general functions, such as attention, motivation, or working memory, or by acting directly on the development of multiple domain-specific skills. Research examining specific global predictors of developmental change has found that cognitive primitives such as executive functioning, working memory, and processing speed broadly affect many different domains of cognition (Fry & Hale, 1996; Hale, 2008; Kail, 2000; 2007; Kail & Salthouse, 2004). Similarly, evidence that infants use probabilistic relations to learn about the world suggests the presence of a low-level statistical processing mechanism that may predict the rate of infant learning (Gómez, 2002). In addition, there is both behavioral and neurological evidence that cognitive and motor neural functioning are deeply intertwined in development. Research on primarily cognitive deficits such as ADHD, language impairment, dyslexia, and autism suggests that these deficits frequently correspond with delayed motor development (Diamond, 2000, 2007). Imaging studies have revealed patterns of activation in the cerebellum and other motor areas of the brain in response to cognitive tasks, suggesting that common patterns of brain activation may underlie performance across motor and cognitive tasks. The cerebellum is particularly involved in tasks that require learning a new skill (Desmond & Fiez, 1998), detecting patterns (Albus, 1971; Marr, 1969; Steuber, Mittman, Hoebeek, Silver, De Zeeuw, Häusser, & De Schutter, 2007) and learning from errors (Fiez, Petersen, Cheney, & Raichle, 1992). Individual differences in the efficiency with which the brain is able to perform these tasks may underlie individual differences in performance across many domains of early development.

Other proposals of domain-general learning mechanisms have focused on higher-level processes such as use of analogy to learn new concepts (Gentner, 1989). There is some evidence that such learning skills may predict individual differences. In one study directly examining the domain-general predictors of success in mathematics, Fuchs et al. (2010) found that 20% of the variance in mathematical word-problem skill in first graders was explained by a set of domain-general factors that included language ability, attention, executive functioning, working memory, concept formation, nonverbal reasoning, and processing speed. In addition, other researchers have found evidence that personality traits such as conscientiousness, achievement-striving, and self-discipline relate to children’s success across many domains of achievement (e.g., Busato, Prins, Elshout, & Hamaker, 2000; Chamorro-Premuzic & Furnham, 2003; Wong & Csikszentmihalyi, 1991). It is possible, therefore, that these factors also predict the correlated growth across domains observed in the present study.

Where might individual differences in the development of these neurobiological and psychological traits come from? Certain global influences on development may be attributable to environmental factors that have widespread effects (Tucker-Drob, 2011a). For example, differences in teacher quality are likely to lead to differences in growth in multiple areas of achievement, such as mathematics, reading, and vocabulary (Rockoff, 2004): children in more stimulating classrooms may experience faster development across all domains than those in duller environments. Similarly, socioeconomic advantage tends to have a broad impact on many factors (e.g., nutrition, quality of schooling, parenting) that may affect development in many domains via both domain-general and domain-specific pathways (e.g., Hoff, 2003). If, however, environmental explanations are responsible for substantial proportions of the global aspect of change, these would have to be explanations unrelated to the covariates included in the analyses described above. Our six covariates were chosen to be broadly reflective of the child’s social environment, including variables that are known to reflect socioeconomic conditions as well as parenting. Recall that, although controlling for these covariates tempered the strength of the correlations among intercepts, it did not have an appreciable effect on the correlations among slopes. In other words, factors affecting the quality of children’s home lives globally affected the levels at which children started out, but not their rates of change.

Factors influencing development across domains may also stem from individual variation in genes. According to “the generalist gene hypothesis” (Kovas & Plomin, 2006), the same genes affect individual differences in the development of many different domains of cognitive functioning (Haworth, Meaburn, Harlaar, & Plomin, 2007; Plomin & Kovas, 2005). As Kovas and Plomin (2007) reason, a gene can have broad (i.e., pleitropic) effects either through 1) influencing one brain region which in turn influences many different domains of functioning, 2) influencing several brain regions, each of which affects a specific domain of functioning, or 3) influencing several brain regions, each of which in turn affects several domains of functioning. Some candidate brain processes that may be broadly affected by pleiotropic genes include neural plasticity, dendritic complexity, myelinization, and nerve conduction speed (Kovas & Plomin, 2006). Although this is a provocative and promising line of inquiry that has received substantial support from twin and adoption studies, research attempting to identify and study specific genes for behavioral development is still very new.

We believe that a comprehensive account of cognitive and psychomotor development will need to account not only for the individual contributions of broadly affecting environmental inputs and pleitropic genetic influences, but also for their interplay. It is straightforward to see how two environmental factors could influence each other: for example, teacher quality may moderate the effects of SES and parenting. Similarly, there is evidence that low-level cognitive processes affect each other: for example, as processing speed improves, it may cause working memory span to increase (Fry & Hale, 2000). More interesting interactions may be found between environmental and genetic processes. A number of authors, for example, have proposed that a dynamic person-environment matching process occurs over the course of child development, whereby genetic variation leads different individuals to seek out and elicit different environmental experiences, which in turn affect many aspects of their abilities and personalities (Bronfenbrenner & Ceci, 1994; Dickens & Flynn, 2001; Scarr and McCartney, 1983; Tucker-Drob & Harden, in press). A major focus of our future work will be to continue to test and document these dynamics empirically.

In sum, the present findings suggest that there are significant relationships between the development of several cognitive and psychomotor skills in childhood. Researchers would do well to consider the interdependence of cognitive phenomena when building developmental models for domain-specific outcomes. Salthouse (1998) cautioned, “if large proportions of the age-related variance were found to be shared with individual differences in other cognitive variables, then many of the task-specific mechanisms that have been inferred to exhibit age-related differences might simply be consequences of a broader developmental phenomenon” (p.851). Our research suggests that this shared variance is notable. Future research on domain-general processes, whether environmental influences, cognitive primitives, genetic effects, or dynamic combinations of these, will be necessary to reveal the sources of the broad developmental influences witnessed here.