Paired split-plot designs of multireader multicase studies

Abstract.

The widely used multireader multicase ROC study design for comparing imaging modalities is the fully crossed (FC) design: every reader reads every case of both modalities. We investigate paired split-plot (PSP) designs that may allow for reduced cost and increased flexibility compared with the FC design. In the PSP design, case images from two modalities are read by the same readers, thereby the readings are paired across modalities. However, within each modality, not every reader reads every case. Instead, both the readers and the cases are partitioned into a fixed number of groups and each group of readers reads its own group of cases—a split-plot design. Using a $U$-statistic based variance analysis for AUC (i.e., area under the ROC curve), we show analytically that precision can be gained by the PSP design as compared with the FC design with the same number of readers and readings. Equivalently, we show that the PSP design can achieve the same statistical power as the FC design with a reduced number of readings. The trade-off for the increased precision in the PSP design is the cost of collecting a larger number of truth-verified patient cases than the FC design. This means that one can trade-off between different sources of cost and choose a least burdensome design. We provide a validation study to show the iMRMC software can be reliably used for analyzing data from both FC and PSP designs. Finally, we demonstrate the advantages of the PSP design with a reader study comparing full-field digital mammography with screen-film mammography.

1. Introduction

In multireader multicase (MRMC) studies, a number of readers (e.g., radiologists) read medical images of a number of patient cases for a specified clinical task (e.g., cancer detection) and the diagnostic performance is evaluated. In the most general case, both readers and cases are treated as random representative samples from their respective populations. By accounting for both reader and case variabilities, the reader-averaged diagnostic performance can be generalized to both the reader and case populations, thereby providing direct evidence of device efficacy. Because both sources of variability are often substantial, sufficiently large numbers of readers and cases are needed to achieve a desired precision such that a difference in performance between two imaging modalities can be found statistically significant. The theme of this paper is to investigate study design strategies for MRMC studies that may allow for reduced cost and increased flexibility.

The most widely used MRMC study design for comparing two modalities is the fully crossed (FC) design: every reader reads every case of both modalities.¹ By pairing both readers and cases across modalities, the FC design builds a positive correlation between the performances of two modalities and reduces the variability of the performance difference.^1,2 Formally, the variance of the performance difference is

$$\mathrm{Var}[{\widehat{A}}^{(1)}-{\widehat{A}}^{(2)}]=\mathrm{Var}[{\widehat{A}}^{(1)}]+\mathrm{Var}[{\widehat{A}}^{(2)}]-2\rho \sqrt{\mathrm{Var}{\widehat{A}}^{(1)}\mathrm{Var}{\widehat{A}}^{(2)}},$$

where ${\widehat{A}}^{(i)}$ is the performance estimate for modality $i$ and $\rho$ is the correlation between ${\widehat{A}}^{(1)}$ and ${\widehat{A}}^{(2)}$. Typically, $\rho >0$ and the correlation reduces the variability of the performance difference.

Throughout the paper, we assume the diagnostic performance metric is the area under the receiver operating characteristic curve (AUC) (unless noted otherwise) as this is a meaningful and widely used metric.¹ Now, by having every reader read every case, the FC design is cost-effective in terms of the total number of readers and the total number of cases.³ However, as Obuchowski³ pointed out for the FC design, “study length (i.e., the number of total readings) and the time commitment of individual readers (i.e., the number of readings per reader) can be great.”

Alternative study designs have been investigated in the literature. Obuchowski³ compared several designs including the traditional FC design, unpaired designs (either the cases or the readers or both are unpaired across modalities), and a hybrid design in which both readers and cases were paired across two modalities, but, within each modality, each reader read his/her own group of cases of both modalities. Obuchowski found that, not surprisingly, the unpaired designs had significant power disadvantages due to lack of correlation as explained in the previous paragraph. The FC design is powerful but requires a long study duration and a heavy workload for each reader. The “hybrid design” was shown to be very competitive in terms of study length and the time commitment of individual readers, but it requires a very large number of patient cases to be collected and truth-verified.

In an effort to reduce the number of cases, Obuchowski⁴ proposed the “mixed” MRMC design in which both readers and cases were paired across two modalities and, within each modality, they were divided into a number of independent reader or case groups and each group of readers read their own group of cases. Obuchowski showed that the “mixed” design was a promising alternative borrowing strengths from both the FC design and the hybrid design. Later, this design was called the split-plot design and different analysis methods were compared⁵ and refined.⁶ In this paper, we call this design the “paired split-plot” (PSP) design to reflect the fact that both readers and cases are paired across modalities, and the split-plot design is used within each modality.

Despite the aforementioned publications showing potential advantages of the PSP design, we have rarely seen its use in real-world studies, either in the peer-reviewed literature or in the premarket applications submitted to the Food and Drug Administration for regulatory review. This is likely due to the deeply rooted notion that the FC design is the “most” powerful and that many validation studies for freely available software tools assume a FC design. However, the notion that the FC design is most powerful only means that, by having all the readers read all the cases, one can obtain the most information possible from the given numbers of readers and cases. This notion essentially considers the sample sizes (readers and cases) as the only resource needed to achieve certain statistical power. However, the workload of the readers (i.e., the number of readings) is another cost of a study, and frequently a major one. In this work, we show that, when both sample sizes and reader’s workload are considered, the PSP design can be more cost-effective than the FC design, which is similar to the notion that Obuchowski⁴ demonstrated by showing how the estimates of certain Obuchowski–Rockette model parameters are affected by different designs. In our work, we provide a mathematical proof with easy-to-understand formulas showing statistical efficiency/power gain of the PSP design compared with the FC design when the number of readings for each reader is the same. We then put the theoretical analysis into practical perspectives by comparing different designs in terms of power and cost trade-off under a variety of simulation conditions. Furthermore, we present a real MRMC study, the VIPER study (validation of imaging in premarket evaluation and regulation),⁷ which used the PSP design. We use the parameters estimated from this real study to further compare different designs. Finally, in the appendix, we present a simulation study validating the freely available iMRMC software⁸ and show that it works equally well for for both FC and PSP designs.

2. Efficiency Gain of Paired Split-Plot Designs

In this section, we present theoretical analyses to demonstrate that, with fixed number of readers and fixed workload per reader, the PSP design is more efficient than the FC design for both measuring the performance of a single modality and for comparing two modalities.

2.1. Theoretical Analysis: Single Modality

In a FC design with $N_R$ readers each reading $N_0$ nondiseased cases and $N_1$ diseased cases, the reader-averaged empirical estimate of AUC for a single modality is

$$\widehat{A}=\frac{{\mathrm{\Sigma }}_{r=1}^{N_R}{\mathrm{\Sigma }}_{i=1}^{N_0}{\mathrm{\Sigma }}_{j=1}^{N_1}s(x_{ir},y_{jr})}{N_R{N}_0{N}_1},$$ (1)

where $x_{ir}$ and $y_{jr}$ are the rating scores (e.g., level of confidence that cancer is present) of reader $r$ on the nondiseased case $i$ and diseased case $j$, respectively, and $s(x,y)$ is the kernel function

$$s(x,y)=\{\begin{array}{ll}1& \text{if}x<y\\ 0.5& \text{if}x=y\\ 0& \text{if}x>y\end{array}.$$

Note that we use the “hat” notation for “an estimate” of a population parameter and we will use upper-case $X$ and $Y$ to denote random variables corresponding to the observations $x_{ir}$ and $y_{jr}$, respectively.

Gallas⁹ showed that the MRMC variance of $\widehat{A}$ can be written as

$$\mathrm{Var}\widehat{A}=\frac{1}{N_R}(c_1{M}_1+c_2{M}_2+c_3{M}_3+c_4{M}_4)+\frac{N_R-1}{N_R}(c_1{M}_5+c_2{M}_6+c_3{M}_7+c_4{M}_8)-M_8,$$ (2)

where $c_i(i=1,\dots ,4)$ are determined by $N_0$ and $N_1$

$$c_1=1/N_0{N}_1,c_2=(N_0-1)/N_0{N}_1,c_3=(N_1-1)/N_0{N}_1,c_4=(N_0-1)(N_1-1)/N_0{N}_1,$$

and the $M_l(l=1,\dots ,8)$ are the second-order moments of the kernel function $s$ ($E$ denotes “expectation”)

• •$M_1=E[s{(X_{ir},Y_{jr})}^2]$,
• •$M_2=E[s(X_{ir},Y_{jr})s(X_{i^{\prime }r},Y_{jr})](i\ne i^{\prime })$,
• •$M_3=E[s(X_{ir},Y_{jr})s(X_{ir},Y_{j^{\prime }r})](j\ne j^{\prime })$,
• •$M_4=E[s(X_{ir},Y_{jr})s(X_{i^{\prime }r},Y_{j^{\prime }r})](i\ne i^{\prime },j\ne j^{\prime })$,
• •$M_5=E[s(X_{ir},Y_{jr})s(X_{i{r}^{\prime }},Y_{j{r}^{\prime }})](r\ne r^{\prime })$,
• •$M_6=E[s(X_{ir},Y_{jr})s(X_{i^{\prime }{r}^{\prime }},Y_{j{r}^{\prime }})](i\ne i^{\prime },r\ne r^{\prime })$,
• •$M_7=E[s(X_{ir},Y_{jr})s(X_{i{r}^{\prime }},Y_{j^{\prime }{r}^{\prime }})](j\ne j^{\prime },r\ne r^{\prime })$,
• •$M_8=E[s(X_{ir},Y_{jr})s(X_{i^{\prime }{r}^{\prime }},Y_{j^{\prime }{r}^{\prime }})](i\ne i^{\prime },j\ne j^{\prime },r\ne r^{\prime })$.

The unbiased estimators of these moments are provided in Gallas.⁹ This approach has been developed based on a probabilistic foundation of MRMC analysis^9–12 and was later found to be identical to the $U$-statistic approach.^13,14

We define two variance-component parameters. The first decreases with the number of readers [Eq. (3)]. The second is independent of the number of readers [Eq. (4)]

$$V_R\equiv c_1(M_1-M_5)+c_2(M_2-M_6)+c_3(M_3-M_7)+c_4(M_4-M_8)$$ (3)

and

$$V_C\equiv c_1{M}_5+c_2{M}_6+c_3{M}_7-(1-c_4)M_8.$$ (4)

Then, the MRMC variance in the FC design as expressed in Eq. (2) can be written as

$${\mathrm{Var}}_{\mathrm{FC}}\widehat{A}=\frac{1}{N_R}{V}_R+V_C.$$ (5)

To understand the meaning of $V_R$ and $V_C$, note that the MRMC variance in Eq. (2) can be decomposed into three components: reader variability purely due to the finite number of readers, case variability purely due to the finite number of cases, and variability due to reader by case interactions, which are expressed as

$${\mathrm{Var}}_{\text{reader}}\widehat{A}=\frac{1}{N_R}(M_4-M_8),$$ (6)

$${\mathrm{Var}}_{\text{case}}\widehat{A}=c_1{M}_5+c_2{M}_6+c_3{M}_7-(1-c_4)M_8,$$ (7)

and

$${\mathrm{Var}}_{\text{reader}\times \text{case}}\widehat{A}=\frac{1}{N_R}[c_1{M}_1+c_2{M}_2+c_3{M}_3-(1-c_4)M_4-c_1{M}_5-c_2{M}_6-c_3{M}_7+(1-c_4)M_8],$$ (8)

respectively. It can be seen that $V_C$ is identical to the case variability [Eqs. (4) and (7)] and $V_R$ (when normalized by $N_R$) is the combination of reader variability and variability due to reader by case interactions.

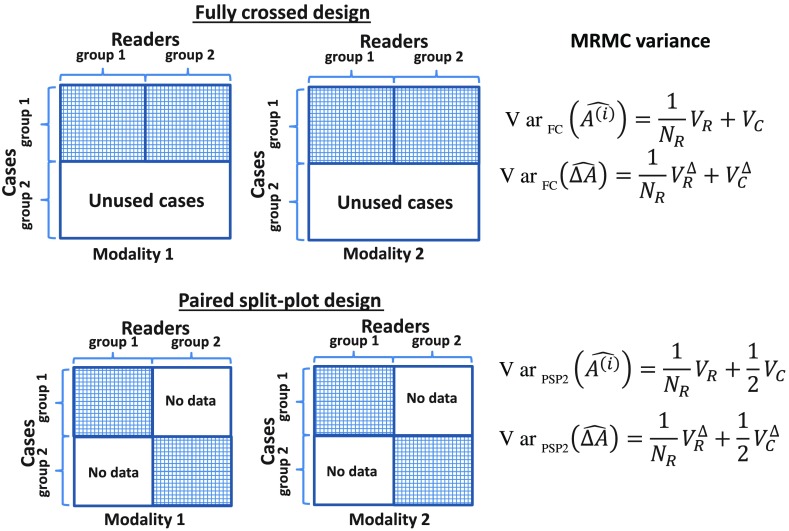
We now consider a PSP design with G groups (PSPG). For comparison, we assume that the total number of readers and the workload of each reader are the same as those in the FC design, i.e., $N_R$ readers each reading $N_0$ nondiseased cases and $N_1$ diseased cases. The difference is that all the readers read the same $N_0+N_1$ cases in the FC design whereas, in the PSP design, different groups of readers read different groups of cases. Within each group, however, all the readers read the same group of cases. These are schematically shown in Fig. 1 for the FC design and a PSP2 design. As each group is FC, the variance of the AUC averaged over the $N_{R_g}$ readers in the $g$’th group is given as

$$\mathrm{Var}{\widehat{A}}_g=\frac{1}{N_{R_g}}{V}_R+V_C.$$

Fig. 1.

Illustration of the FC design and the PSP design (assuming the two groups have the same number of readers and each reader reads the same number of cases).

As all the groups are independent, the performance estimates ${\widehat{A}}_g(g=1,\dots ,G)$ in the $G$ groups are independent (i.e., zero covariance across groups). Noting that ${\mathrm{\Sigma }}_{g=1}^G{N}_{R_g}=N_R$, the variance of the average performance $\widehat{\mathrm{A}}={\mathrm{\Sigma }}_{g=1}^G{N}_{R_g}{\widehat{A}}_g/N_R$ is given as

$$\begin{gathered} {\mathrm{Var}}_{\mathrm{PSPG}}\widehat{A}=\frac{1}{N_R^2}{\mathrm{\Sigma }}_{g=1}^G{N}_{R_g}^2\mathrm{Var}{\widehat{A}}_g \\ =\frac{1}{N_R}{V}_R+\frac{{\mathrm{\Sigma }}_{g=1}^G{N}_{R_g}^2}{N_R^2}{V}_C, \end{gathered}$$ (9)

$$=\frac{1}{N_R}{V}_R+\frac{1}{G}{V}_C(\text{if}{N}_{R_1}=\dots =N_{R_G}).$$ (10)

Comparing Eq. (5) with Eqs. (9) and (10), we see that, for study designs having the same number of readers with each reader reading the same number of cases, ${\mathrm{Var}}_{\mathrm{PSPG}}\widehat{\overline{A}}<{\mathrm{Var}}_{\mathrm{FC}}\widehat{\overline{A}}$, i.e., the PSP design is statistically more efficient in estimating the performance of a single modality. More specifically, we see that the precision gain of the PSP design with G groups is due to the shrinkage of the case variability component $V_C$ by a factor of $1/G$. Of course the gain of efficiency is not free as when the number of cases read by each reader is held constant, the total number of cases in the PSPG design is $G$ times that in the FC design. Basic statistics principles tell us that, when we have more case samples, we gain more information from cases and the uncertainty of the measured performance due to the finite case sample decreases. The theoretical analysis provided here shows how this happens exactly in the MRMC setting. On the one hand, when the total case sample size increases in the PSP design, the case variability decreases correspondingly although the number of cases read by each reader is the same. On the other hand, the other component in the total variance, namely $V_R$, is the same across designs because it is a function of the number of readers and the number of cases read per reader, which are set to be the same across designs.

2.2. Theoretical Analysis: Comparing Two Modalities

To compare two imaging modalities by testing the null hypothesis that the performances of the two modalities, $A^{(1)}$ and $A^{(2)}$, are equal, we need to estimate the performance difference $\widehat{\mathrm{\Delta }A}=\widehat{A^{(1)}}-\widehat{A^{(2)}}$ and its variance $\widehat{\mathrm{Var}\widehat{\mathrm{\Delta }A}}$ and construct a test statistic $z=\widehat{\mathrm{\Delta }A}/\sqrt{\widehat{\mathrm{Var}\widehat{\mathrm{\Delta }A}}}$. Note that we use superscript $(i)$ to denote modality. For the FC design, we have

$$\widehat{\mathrm{\Delta }A}=\frac{{\mathrm{\Sigma }}_{r=1}^{N_R}{\mathrm{\Sigma }}_{i=1}^{N_0}{\mathrm{\Sigma }}_{j=1}^{N_1}[s^{(1)}(x_{ir},y_{jr})-s^{(2)}(x_{ir},y_{jr})]}{N_R{N}_0{N}_1}.$$

Comparing this equation with Eq. (1), we see that we just replace the kernel function $s$ in the single-modality AUC formula with $s^{(1)}-s^{(2)}$ in the AUC difference formula here. It is straightforward to see that the variance formulas in Eqs. (2)–(10) for a single-modality AUC would hold for the variance of $\widehat{\mathrm{\Delta }A}$ if we just replace $s$ with $s^{(1)}-s^{(2)}$ in computing the moment parameters. For example, in the single-modality situation we have $M_1=E[s{(x_{ir},y_{jr})}^2]$. Then for the corresponding moment $M_1^{\mathrm{\Delta }}$ for the variance of $\widehat{\mathrm{\Delta }A}$, we have $M_1^{\mathrm{\Delta }}=E\{{[s^{(1)}(x_{ir},y_{jr})-s^{(2)}(x_{ir},y_{jr})]}^2\}$. Note that $M_1^{\mathrm{\Delta }}=M_1^{(1)}+M_1^{(2)}-2M_1^{(1\times 2)}$, where $M_1^{(i)}=E[s^{(i)}{(x_{ir},y_{jr})}^2]$ is the moment parameter for the variance of AUC of modality $i$ and $M_1^{(1\times 2)}=E[s^{(1)}(x_{ir},y_{jr})s^{(2)}(x_{ir},y_{jr})]$ is the moment parameter for the covariance between the two AUCs. The other seven moment parameters $M_k^{\mathrm{\Delta }}(k=2,\dots ,8)$ are defined similarly with similar properties.

We define $V_R^{\mathrm{\Delta }}$ and $V_C^{\mathrm{\Delta }}$ in a fashion similar to $V_R$ and $V_C$ in Eqs. (3) and (4) by replacing the $M_k$ parameters with $M_k^{\mathrm{\Delta }}(k=1,\dots ,8)$. In the end, under the setting that the FC design and the PSPG design have the same number of readers each reading the same number of cases, we have the variance of AUC difference for these two designs in Eqs. (11) and (12), respectively. Again, we see that the $V_C^{\mathrm{\Delta }}$ component of the variance would shrink by a factor of $G$ in the PSPG design as compared with the FC design. Because statistical power is inversely related to the variance of the AUC difference, the PSPG design is more powerful in comparing two modalities given that the number of readers and the number of cases read per reader (workload) are the same

$${\mathrm{Var}}_{\mathrm{FC}}\widehat{\mathrm{\Delta }A}=\frac{1}{N_R}{V}_R^{\mathrm{\Delta }}+V_C^{\mathrm{\Delta }},$$ (11)

$${\mathrm{Var}}_{\mathrm{PSPG}}\widehat{A}=\frac{1}{N_R}{V}_R^{\mathrm{\Delta }}+\frac{{\mathrm{\Sigma }}_{g=1}^G{N}_{Rg}^2}{N_R^2}{V}_C^{\mathrm{\Delta }}=\frac{1}{N_R}{V}_R^{\mathrm{\Delta }}+\frac{1}{G}{V}_C^{\mathrm{\Delta }}(\text{if}{N}_{R1}=\cdots =N_{Rg}).$$ (12)

3. Comparison of Paired Split-Plot with Fully Crossed Using Analytical Computations under the Roe and Metz Simulation Model

The purpose of this section is twofold. First, we put the theoretical variance analysis in the previous section into a more practical perspective by comparing the statistical power between the PSP design and the FC design under a variety of simulation conditions. This is not a simulation study, but we use a simulation model to explore different levels of reader and case variability (variance-component structures). Second, we show that a trade-off can be made between the total number of cases and the workload per reader in choosing the most cost-effective design for achieving the same power. In practice, the computational procedure presented here can be used to choose a cost-effective design based on real parameters (e.g., measured in a pilot study) rather than the simulation parameters as we do here.

The simulation model and simulation parameters were initially developed by Roe and Metz¹⁵ and have been frequently used in validating analysis methods. Roe and Metz¹⁵ developed a linear mixed effect model to simulate reader study data

$$X_{ijkt}={\mu }_{it}+R_{jt}+C_{kt}+{[RC]}_{jkt}+{[\tau R]}_{ijt}+{[\tau C]}_{ikt}+E_{ijkt},$$ (13)

where $X_{ijkt}$ denotes the rating by reader $j$ using modality $i$ for the likelihood of case $k$ being diseased (e.g., a malignant lesion is present in the image), whereas the truth state is $t$ ($t=0$ for nondiseased and $t=1$ for diseased). The Greek letter $\mu$ denotes a fixed modality effect and the remaining terms denote random effects, which are independent zero-mean Gaussian random variables with variance parameters denoted as ${\sigma }_R^2$, ${\sigma }_C^2$, ${\sigma }_{RC}^2$, ${\sigma }_{\tau R}^2$, ${\sigma }_{\tau C}^2$, ${\sigma }_E^2$, respectively. These variance parameters can vary with the modality and the truth state in general,¹⁶ but, for simplicity, they were set in Roe and Metz¹⁵ to be the same across modalities and across truth states. Roe and Metz¹⁵ provided several sets of variance parameters, which we adopt as shown in Table 1. These parameters have different combinations of high or low data correlation (the first $H$ or $L$ letter in the “structure” column of Table 1) and high or low reader variability (the second $H$ or $L$ letter in the “structure” column of Table 1). To simulate three levels of AUC values (expectation over the population of readers and the population of cases), we change the separation of the scores from nondiseased and diseased cases by setting the ${\mu }_{it}$ parameter as ${\mu }_{i0}=0$ and ${\mu }_{i1}={\mathrm{\varphi }}^{-1}[A^{(i)}]\times \sqrt{2(1+{\sigma }_R^2+{\sigma }_{\tau R}^2)}$, where ${\mathrm{\varphi }}^{-1}$ is the inverse cumulative distribution function of the standard normal distribution and the “1” in this formula comes from the constraint that Roe and Metz¹⁵ set: ${\sigma }_C^2+{\sigma }_{RC}^2+{\sigma }_{\tau C}^2+{\sigma }_E^2=1$.

Table 1.

Simulation parameters for the Roe and Metz model.

Structure	${\mathrm{AUC}}_1$	${\mathrm{AUC}}_2$	${\sigma }_R^2$	${\sigma }_{\tau R}^2$	${\sigma }_C^2$	${\sigma }_{RC}^2$	${\sigma }_{\tau C}^2$	${\sigma }_E^2$
HH	0.65	0.70	0.011	0.011	0.3	0.2	0.3	0.2
	0.80	0.85	0.030	0.030	0.3	0.2	0.3	0.2
	0.90	0.95	0.056	0.056	0.3	0.2	0.3	0.2
HL	0.65	0.70	0.0055	0.0055	0.3	0.2	0.3	0.2
	0.80	0.85	0.0055	0.0055	0.3	0.2	0.3	0.2
	0.90	0.95	0.0055	0.0055	0.3	0.2	0.3	0.2
LH	0.65	0.70	0.011	0.011	0.1	0.2	0.1	0.6
	0.80	0.85	0.030	0.030	0.1	0.2	0.1	0.6
	0.90	0.95	0.056	0.056	0.1	0.2	0.1	0.6
LL	0.65	0.70	0.0055	0.0055	0.1	0.2	0.1	0.6
	0.80	0.85	0.0055	0.0055	0.1	0.2	0.1	0.6
	0.90	0.95	0.0055	0.0055	0.1	0.2	0.1	0.6

Note: HH, high data correlation, high reader variance; HL, high data correlation, low reader variance; LH, low data correlation, high reader variance; LL, low data correlation, low reader variance.

Given the Roe and Metz simulation parameters, we can analytically compute the moment parameters $M_l^{(i)}(i=\mathrm{1,2})$ and $M_l^{(1\times 2)}(l=1,\dots ,8)$ using the method developed by Gallas and Hillis,¹⁶ which has been implemented in the iRoeMetz software.¹⁷ Using these moment parameters and specified sample sizes, we can compute the variance of the AUC difference using the methods described in Sec. 2. Under normal approximation, the statistical power for a two-sided test at the significant level $\alpha$ with critical values $\pm z_{\alpha /2}$ is

$$\text{Power}=\mathrm{\varphi }[\frac{\mathrm{\Delta }A}{\sqrt{\mathrm{Var}(\mathrm{\Delta }A)}}-z_{\alpha /2}]+\mathrm{\varphi }[-\frac{\mathrm{\Delta }A}{\sqrt{\mathrm{Var}(\mathrm{\Delta }A)}}-z_{\alpha /2}],$$ (14)

where $z_{\alpha /2}=1.96$ for $\alpha =0.05$.

Specifying the number of readers $N_R=16$ with each reader reading $N_0=80$ nondiseased cases and $N_1=60$ diseased cases, we computed the variance and statistical power for the FC design and PSP designs (with 2, 4, and 8 groups, respectively) for each set of the Roe and Metz model parameters (Table 1). The results are shown in Table 2.

Table 2.

Comparison between the FC design and PSP designs in terms of statistical efficiency/power by holding constant the number of readings per reader.

Structure	${\mathrm{AUC}}_1$	${\mathrm{AUC}}_2$	$\mathrm{Var}(\mathrm{\Delta }A)\times {10}^3$				Power (%)
			FC	PSP2	PSP4	PSP8	FC	PSP2	PSP4	PSP8
HH	0.65	0.70	1.42	0.83	0.53	0.38	26.4	41.2	58.2	72.3
	0.80	0.85	0.96	0.63	0.46	0.38	36.4	51.4	64.4	73.1
	0.90	0.95	0.42	0.30	0.24	0.21	68.0	82.0	89.5	93.0
HL	0.65	0.70	1.34	0.75	0.45	0.30	27.6	44.9	65.7	82.5
	0.80	0.85	0.77	0.43	0.26	0.17	43.7	67.6	87.7	96.9
	0.90	0.95	0.28	0.15	0.09	0.06	85.1	98.0	99.9	100
LH	0.65	0.70	0.71	0.52	0.43	0.38	46.6	58.9	67.5	72.5
	0.80	0.85	0.55	0.45	0.40	0.38	56.9	65.5	70.6	73.3
	0.90	0.95	0.27	0.23	0.22	0.21	86.5	90.5	92.4	93.3
LL	0.65	0.70	0.63	0.44	0.34	0.30	51.4	66.5	76.9	82.7
	0.80	0.85	0.35	0.25	0.20	0.17	75.8	88.5	94.4	96.8
	0.90	0.95	0.12	0.083	0.067	0.059	99.7	100	100	100

There are two kinds of cost that can be considered in comparing study designs. One is the cost associated with the radiologist’s time, which can be represented by the total number of readings. The other is the cost for collecting and truth-verifying patient cases, which can be represented by the total number of cases. For the results shown in Table 2, we held the total number of readings the same across study designs and showed that the PSP designs gain efficiency/power with increased cost of collecting and truth-verifying more cases. We can also compare the number of readings and the number of cases needed to achieve the same statistical power, allowing a trade-off between the two kinds of cost being made such that the total cost is minimized.

We again assumed 16 readers in each of the four designs: FC, PSP2, PSP4, and PSP8. Utilizing Eq. (14), the fixed number of readers (i.e., 16), and a fixed ratio (3:4) of the number of diseased cases to the number of nondiseased cases, we iteratively solved the number of cases each reader needs to read such that a power of 80% is achieved. The results are shown as “cases per reader” in Table 3. Then, the total number of readings is simply the “case per reader” times 16 and therefore they are equivalent for comparison purpose. The total number of cases that need to be collected and truth-verified is the number of cases per reader times 1, 2, 4, and 8 for the FC, PSP2, PSP4, and PSP8 designs, respectively (shown as “total number of cases” in Table 3). From this table, we can see that one can make a trade-off between “cases per reader” and the “total number of cases” to choose the most cost-effective design. If patient cases are precious, one would certainly choose the FC design as it requires the least number of cases. If many cases are already available and reader’s time is the major cost of the study, which is typical in many retrospective studies, one can choose a PSP design to reduce the workload of readers.

Table 3.

Comparison between the FC design and PSP designs in terms of the number of cases read by each reader and the total number of cases to achieve 80% power (16 readers are assumed for all the designs and so the total number readings is 16 times the “case per reader”).

Structure	${\mathrm{AUC}}_1$	${\mathrm{AUC}}_2$	Cases per reader				Total number of cases
			FC	PSP2	PSP4	PSP8	FC	PSP2	PSP4	PSP8
HH	0.65	0.70	1197	630	352	198	1197	1260	1408	1584
	0.80	0.85	1348	709	410	237	1348	1418	1640	1896
	0.90	0.95	249	137	81	51	249	274	324	408
HL	0.65	0.70	774	398	217	128	774	796	868	1024
	0.80	0.85	385	202	112	67	385	404	448	536
	0.90	0.95	144	77	46	28	144	154	184	224
LH	0.65	0.70	513	333	249	198	513	666	996	1584
	0.80	0.85	578	375	305	237	578	750	1220	1896
	0.90	0.95	104	74	60	51	104	148	240	408
LL	0.65	0.70	333	217	153	125	333	434	612	1000
	0.80	0.85	158	104	79	65	158	208	316	520
	0.90	0.95	56	39	30	27	56	78	120	216

4. VIPER Study

From the results in Sec. 3, we have seen that the relative advantage of one design over the other would depend on the variance-component structure. It is known that some of the Roe and Metz simulation parameters may not be realistic.¹⁸ Thus, it is useful to further compare different designs with realistic variance parameters estimated from real data. We used the iMRMC software⁸ to analyze a real dataset, and, based on the estimated parameters, we compared the PSP design to the FC design. We have validated our software to analyze both FC and PSP data (see Appendix A, for a validation study using simulations).

The real dataset is a study on design methodologies surrounding the validation of imaging premarket evaluation and regulation called VIPER.⁷ The VIPER study compared full-field digital mammography (FFDM) to screen-film mammography (SFM) for women with heterogeneously dense or extremely dense breasts. All cases and corresponding images were sampled from Digital Mammographic Imaging Screening Trial¹⁹ archives. This is a retrospective reader study contracted to Medical University of South Carolina (MUSC). The institutional review board of MUSC approved the study.

Here, we analyze one of the VIPER reader studies and use the estimated variance parameters to compare a PSP design with a related FC design. In this VIPER reader study, we used the PSP4 design with 20 readers divided into four groups (i.e., each group had five readers). Using design, each group of readers were to read 60 cases with an enriched cancer prevalence of $\sim 50\%$. However, the split was not perfectly balanced and the numbers of diseased and nondiseased cases per group are slightly different from the original design. The case sample sizes for the four groups are shown in Table 4. In this table, we also show the moment parameters estimated from this dataset using our iMRMC software along with the AUC values, their difference, and the associated standard errors. The results show that FFDM’s AUC is slightly inferior to the SFM’s by 0.025 with a standard error (SE) of 0.025 and an $\sim 95\%$ confidence interval (CI) of ($-0.07$ and 0.02).

Table 4.

VIPER’s high-prevalence reader study results and sizing new studies based on these results.

Retrospective reader study comparing SFM and FFDM
Sample sizes: 20 readers in four groups
			Group 1	Group 2	Group 3	Group 4	Total
		$N_0$	32	31	32	35	130
		$N_1$	28	29	28	24	109
Estimated moment parameters
	$M_1$	$M_2$	$M_3$	$M_4$	$M_5$	$M_6$	$M_7$	$M_8$
FFDM	0.7091	0.5904	0.5531	0.5060	0.5686	0.5509	0.5202	0.5075
SFM	0.7345	0.61470	0.5922	0.5433	0.59756	0.5774	0.5570	0.5439
Cross	0.5718	0.5549	0.5379	0.5239	0.5625	0.5519	0.5330	0.5257
Estimated AUC (with standard error)
FFDM	0.713 (0.024)		SFM	0.738 (0.022)
	Difference	$-0.025$ (0.025)		$\sim 95\%$ CI		$(-0.07,0.02)$
FC with the same workload for each reader ($N_r=20$, $N_0=32$, $N_1=27$):
$\mathrm{SE}=0.0394$, $\sim 95\%$ CI $(-0.10,0.05)$
Size a noninferiority study (for 80% power, noninferiority margin $\delta =0.05$)
Assume effect size $\mathrm{\Delta }A=0$, diseased to nondiseased case ratio = 0.75
	Cases per reader				Total number of cases
	FC	PSP2	PSP4		FC	PSP2	PSP4
$N_r=16$	408	237	153		408	474	612
$N_r=20$	364	207	132		364	414	528

Given the components of variance in Table 4, we can estimate the variance of an FC study where 20 readers read the same 27 diseased cases and the same 32 nondiseased cases in both modalities [using Eq. (2) or Eq. (5)]. The SE of the AUC difference from such an FC study would be 0.039 [$\sim 95\%$ CI ($-0.10$ and 0.05)]. Compared with the PSP4 study, the FC study has 25% the cases (59/239) and the same number of reads per reader and in total. The trade-off for the reduced cost of collecting and truth-verifying 25% of the cases is more uncertainty: the SE of the AUC difference from the FC study would be 56% larger than the PSP4 study.

For demonstration, we also show how to size a noninferiority study to achieve a specific power. A reasonable hypothesis to establish is that the diagnostic performance of FFDM is noninferior to that of SFM. We assume an effect size $\mathrm{\Delta }A=0$ based on the fact that their technological characteristics are similar and the clinical performance reported in the literature shows that FFDM is generally noninferior to the SFM. We specify a noninferiority margin $\delta$ of 0.05 in AUC. In addition, we assume the ratio of the number of diseased cases to the number of nondiseased cases to be 0.75. Then for a fixed number of readers, we iteratively solve the number of cases needed for a target power of 80%. The computational procedure was similar to that in Sec. 3 except that the power for a noninferiority study is (using normal approximation)

$${\text{Power}}_{\text{noninferiority}}=\mathrm{\varphi }(\frac{\mathrm{\Delta }A+\delta }{\sqrt{\mathrm{Var}(\mathrm{\Delta }A)}}-z_{\alpha /2}).$$

We set the number of readers as 16 or 20 for the following designs: FC, PSP2, and PSP4. The results are shown in the bottom section of Table 4. We demonstrate again that one can assess the following in choosing a cost-effective design: how many readers are available, the cost of collecting and truth-verifying patient cases, and the cost of reading the cases by the readers. If a large number of cases are already available and the cost of collecting and truth-verifying cases is thus minimal, then a PSP design is preferred because the workload of each reader and the total number of reads are substantially reduced. For example, when $N_r=16$, using the PSP4 design each reader would need to read 153 cases as compared with 408 in the FC design.

5. Discussions and Conclusion

In this work, we investigated the PSP design for MRMC reader studies and compared it with the widely used FC design. From the theoretical perspective, we analytically showed how statistical efficiency can be gained by the PSP design as compared with the FC design when the number of readings is the same across designs. We then used analytical computations to compare the two designs under a broad range of model parameters in terms of statistical efficiency/power, the number of reads per reader, and the number of cases that have to be collected and truth-verified. The results in Tables 2 and 3 showed that a trade-off can be made between the reader’s workload and the collection and truth-verification of patient cases. Moreover, such a trade-off would depend on the true variance-component structure. Therefore, we further compared the two designs using variance-components estimated in a real study. The VIPER study results indicated that substantial precision can be gained by the PSP design with the same reading workload and more patient cases.

This means that, when the same cases are read again and again by multiple readers, the benefit of adding readers is subjected to diminishing returns. On the other hand, by having the readers read different cases (PSP) rather than the same cases (FC), substantial precision can be gained with fewer number of reads. In the meantime, it should be noted that this gain of precision may be associated with the extra cost of collecting and truth-verifying more cases. We further note that, in addition to these cost considerations, the PSP design offers practical flexibilities. For example, the study duration may be shortened because each reader reads fewer cases. Furthermore, in a study that involves multiple institutions, the readers may read the cases from their own institution thereby avoiding the need for shipping the cases around the country, assuming the study conditions can be well controlled and readers and patient cases from each institution are representative of their respective population. These findings are consistent with those of Obuchowski⁴ who compared the PSP design with the FC design by showing how the Obuchowski–Rockette (OR) model parameters vary across the two designs. In this work, we employed the U-statistic variance analysis of the AUC to explicitly show the variance difference between the two designs using simple analytical formulas (Fig. 1).

These investigations have important practical implications. When patient cases are precious, one may choose the FC design to take full advantage of the cases that are available. On the other hand, when many cases are available and the study is mainly limited by the cost of the radiologist’s time, one may choose to have the radiologists read fewer but different cases in a PSP design. If variance-component parameters are available (e.g., from pilot studies or previously published similar studies), one can quantify various sources of cost and compare the overall cost of different designs to choose the most cost-effective one.

We have assumed the same number of readers in comparing the FC design with the PSP design throughout this paper. This is mainly to make the analytical comparison easier. For example, in Fig. 1, we show that with the same number of readers each reading the same number of cases, the PSP design is more efficient (less variance) and it requires more cases. Graphically, the shaded area (that represents the number of readings) in this figure for the PSP design is the same as the FC design, but they are split in the vertical direction. Alternatively, we can split the shaded area in the horizontal direction and show that the PSP in that way is more efficient than the FC design. This is a setting that requires more readers. In reality, one may typically collect more cases, recruit more readers, or both, in the PSP design than in the FC design. The benefit is, as we have showed, fewer readings are needed to achieve the same precision (efficiency).

We note that the amount of PSP-versus-FC efficiency gain given the same reader workload depends on the variance components of the problem, as we have showed in Table 2. This is also evident from our analytical results in Eqs. (11) and (12). Because only one variance component, namely $V_C$, is reduced in the PSP design compared with the FC design, the efficiency gain can be small if this component is very small compared with the other variance components (i.e., $V_C\ll V_R$). Similar analytical results may be obtained in terms of the OR model parameters using the marginal-mean ANOVA approach developed by Hillis.⁶ This is interesting future work because one can survey the published studies analyzed by either methods to compare study designs in a broad range of real-world applications. For readers who are familiar with the OR model, we showed a connection between the $U$-statistic parameters ($V_C$ and $V_R$) and the OR model parameters in Appendix B.

The iMRMC⁸ and iRoeMetz¹⁷ software can be used to aid the design process as it can compute the variance and statistical power for different designs and sample sizes. We also validated the iMRMC software’s statistical inference functionality using simulations and showed that it can be reliably used to analyze data from both the FC and PSP designs. However, we should point out that the current version of the iMRMC software only supports the binary performance endpoint (e.g., sensitivity and specificity) and the AUC endpoint estimated by the trapezoidal/Wilcoxon method, which is appropriate for ROC data collected on the multilevel ordinal or the (quasi-)continuous scale. Alternatively, one can use the software from the University of Iowa²⁰ that implements the Obuchowski–Rockette method for MRMC study sizing and analysis,^5,21,22 especially when partial AUC or semiparametric estimate of AUC is the preferred endpoint.

In conclusion, the PSP design is a useful alternative to the widely used FC design in MRMC studies. The PSP design may substantially reduce the cost of reader studies as compared with the FC design in many applications.

Biographies

Weijie Chen received his PhD in medical physics from the University of Chicago, Chicago, Illinois, in 2007. Since then, he has been a scientist at the Center for Devices and Radiological Health, U.S. Food and Drug Administration, Silver Spring, Maryland. His research interests include statistical assessment methodology for diagnostic devices in general, and ROC methodology and reader studies for medical imaging and computer-aided diagnosis in particular.

Qi Gong is a research fellow at the Center for Devices and Radiological Health, U.S. Food and Drug Administration, Silver Spring, Maryland. His research areas include medical image processing, reader studies statistical analysis, and programming. He received his Master in science degree in electrical engineering from the George Washington University in 2014.

Brandon D. Gallas provides mathematical, statistical, and modeling expertise to the evaluation of medical imaging devices at the FDA. His main areas of contribution are in the design and statistical analysis of reader studies, image quality, computer-aided diagnosis (CAD), and imaging physics. Before working at the FDA, he was in Dr. Harrison Barrett’s research group at the University of Arizona, earning his PhD from the Graduate Interdisciplinary Program in Applied Mathematics.

Appendix A: Validation of the iMRMC Software in Analyzing Paired Split-Plot Study Data

The freely available iMRMC software⁸ can be used to aid the design (sizing) of an MRMC study and analyze data for both the FC and PSP designs. The software is platform independent with a graphical user interface (see Fig. 2 for screen shots). It is well documented and actively maintained. In its core, the software uses the trapezoidal/Wilcoxon method to estimate the AUC (a $U$ statistic) and applies the $U$-statistic method to estimate the MRMC variance, which has been validated as an unbiased estimator.^9,13,23 For statistical inference, the test statistic

$$t=\frac{|\widehat{A^{(1)}}-\widehat{A^{(2)}}|}{\sqrt{\widehat{\mathrm{Var}[\widehat{A^{(1)}}-\widehat{A^{(2)}}]}}},$$

is modeled as a Student’s $t$ statistic.⁵

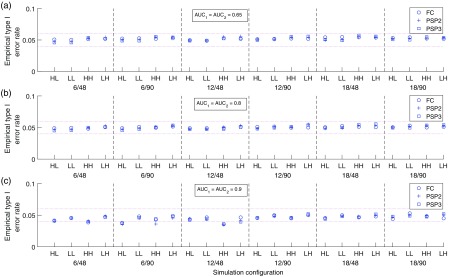
We validated the statistical inference functionality of the software by simulating data under the null hypothesis (i.e., two modalities have equal AUC performance) and investigated the empirical type I error rate, which we expected to be close to the nominal level of 5%. Specifically, we simulated MRMC datasets using the Roe and Metz model [Eq. (13)] with specified parameters and analyzed it with our iMRMC software to see if the difference of performance between the two modalities was statistically significant at the significant level 0.05. We repeated the simulations 100,000 times and computed the proportion of experiments that showed a statistically significant AUC difference, which is the empirical type I error rate. We did such simulation validation for three study designs: FC, PSP2, and PSP3. For each design, we varied the following parameters in a fully factorial fashion:

• •Variance component parameters with three AUC levels: we used the 12 sets of parameters in Table 1 except that we changed the values of ${\mathrm{AUC}}_2$ such that ${\mathrm{AUC}}_2={\mathrm{AUC}}_1$ because we intended to simulate a null hypothesis,
• •The total number of readers: $N_R=\mathrm{6,12},18$, and
• •The total number of cases: $N_C=\mathrm{48,90}$ cases per class.

Fig. 2.

Graphical user interface of the iMRMC software.

The simulation results are plotted in Fig. 3. The results showed that the iMRMC software controlled the type I error rate reliably across a broad range of simulation parameters and study designs.

Fig. 3.

Validation of the iMRMC software for analyzing MRMC data.

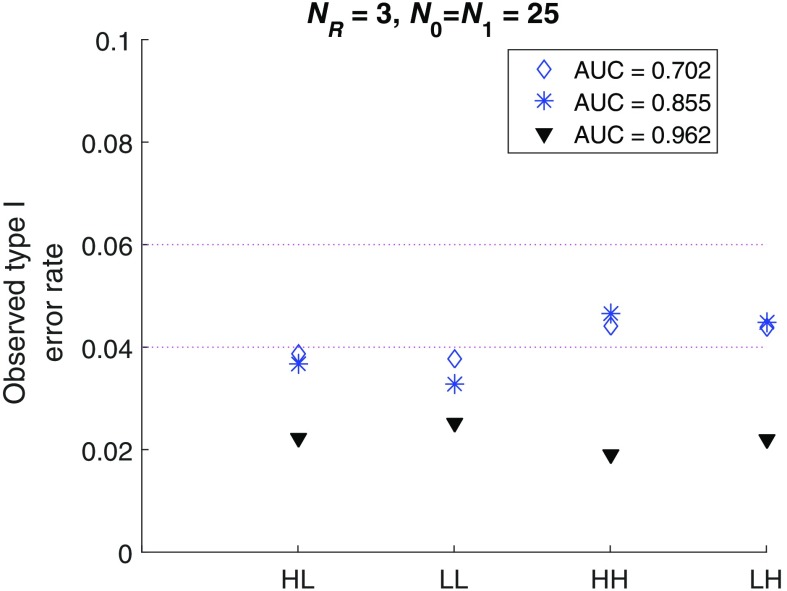
We do not recommend a reader study with too few readers because they may not represent the reader population. But just to test our software with extreme parameter values, we further performed simulation studies simulating only three readers reading $25+25$ cases in an FC fashion. The summary results (Fig. 4) show that the type I error is controlled below the nominal level of 0.05 across all the simulations (though it is a little conservative for some simulation conditions).

Fig. 4.

Small sample size performance of the iMRMC software: FC design.

Appendix B. Relationship between the U-Statistic Variance Parameters and the Obuchowski–Rockette Model Parameters

In Sec. 2.2, we showed that the variance of the estimate of difference in AUC $[\widehat{\mathrm{\Delta }A}={\widehat{A}}^{(1)}-{\widehat{A}}^{(2)}]$ in a FC design can be expressed in terms of $U$-statistic parameters as

$${\mathrm{Var}}_U\widehat{\mathrm{\Delta }A}=\frac{1}{N_R}{V}_R^{\mathrm{\Delta }}+V_C^{\mathrm{\Delta }},$$ (15)

where $N_R$ is the number of readers $V_R^{\mathrm{\Delta }}\equiv c_1(M_1^{\mathrm{\Delta }}-M_5^{\mathrm{\Delta }})+c_2(M_2^{\mathrm{\Delta }}-M_6^{\mathrm{\Delta }})+c_3(M_3^{\mathrm{\Delta }}-M_7^{\mathrm{\Delta }})+c_4(M_4^{\mathrm{\Delta }}-M_8^{\mathrm{\Delta }})$, $V_C^{\mathrm{\Delta }}\equiv c_1{M}_5^{\mathrm{\Delta }}+c_2{M}_6^{\mathrm{\Delta }}+c_3{M}_7^{\mathrm{\Delta }}-(1-c_4)M_8^{\mathrm{\Delta }}$, and $M_k^{\mathrm{\Delta }}=M_k^{(1)}+M_k^{(2)}-2M_k^{(1\times 2)}$.

The estimate of variance of $\widehat{\mathrm{\Delta }A}$ can be expressed in terms of OR parameters as⁶

$$\widehat{{\mathrm{Var}}_{\mathrm{OR}}(\widehat{\mathrm{\Delta }A})}=\frac{2}{N_R}\mathrm{MS}(T*R)+2\mathrm{Max}(\widehat{{\mathrm{COV}}_2}-\widehat{{\mathrm{COV}}_3},0),$$ (16)

where $\mathrm{MS}(T*R)$ is modality × reader mean squares, ${\mathrm{COV}}_2$ is the between-reader within-modality covariance of AUC, ${\mathrm{COV}}_3$ is the between-reader between-modality covariance of AUC, and Max is a constraint of setting $\widehat{{\mathrm{COV}}_2}-\widehat{{\mathrm{COV}}_3}$ to zero if it is negative.

Note that the $U$-statistic variance expression [Eq. (15)] is for population parameters, whereas the OR expression [Eq. (16)] is an estimator. The main purpose of this appendix is to show the expectation (“$E$”) of the latter equals to the former, i.e., $E[\widehat{{\mathrm{Var}}_{\mathrm{OR}}(\widehat{\mathrm{\Delta }A})}]={\mathrm{Var}}_U\widehat{\mathrm{\Delta }A}$. More specifically, we will show that

$$V_R^{\mathrm{\Delta }}=2E[\mathrm{MS}(T*R)]$$ (17)

and

$$V_C^{\mathrm{\Delta }}=2({\mathrm{COV}}_2-{\mathrm{COV}}_3).$$ (18)

Hillis⁶ has shown that

$$E[\mathrm{MS}(T*R)]={\sigma }_{TR}^2+{\sigma }_{\epsilon }^2-{\mathrm{COV}}_1-{\mathrm{COV}}_2+{\mathrm{COV}}_3,$$ (19)

where ${\sigma }_{TR}^2$ is the variance of the modality × reader interaction term in the OR model, ${\sigma }_{\epsilon }^2$ is the expected variance of a fixed-reader AUC, and ${\mathrm{COV}}_1$ is the within-reader between-modality covariance of AUC. Next, we express each of the parameters on the r.h.s of Eq. (19) in terms of $U$-statistic parameters.

The empirical fixed-reader AUC is

$${\widehat{A}}_r=\frac{{\mathrm{\Sigma }}_{i=1}^{N_0}{\mathrm{\Sigma }}_{j=1}^{N_1}s(x_{ir},y_{jr})}{N_0{N}_1},$$

and its $U$-statistic variance is given by Refs. 9 and 14 $\mathrm{Var}({\widehat{A}}_r|r)=c_1{M}_{1|r}+c_2{M}_{2|r}+c_3{M}_{3|r}+(c_4-1)M_{4|r}$, where $M_{k|r}$ is the $M_k$ conditional on reader $r$. For example, $M_{1|r}=E[s{(X_{ir},Y_{jr})}^2|r]$. Then $M_k$ is the expectation of $M_{k|r}$ over the reader population, i.e., $M_k=E_r(M_{k|r})$. In the two-modality FC setting, ${\sigma }_{\epsilon }^2=(E_r\{\mathrm{Var}[{\widehat{A}}_r^{(1)}|r]\}+E_r\{\mathrm{Var}[{\widehat{A}}_r^{(2)}|r]\})/2$. So we have

$${\sigma }_{\epsilon }^2=\frac{1}{2}{\mathrm{\Sigma }}_{i=1}^2[c_1{M}_1^{(i)}+c_2{M}_2^{(i)}+c_3{M}_3^{(i)}+(c_4-1)M_4^{(i)}].$$ (20)

Similarly, we have

$${\mathrm{COV}}_1=c_1{M}_1^{(1\times 2)}+c_2{M}_2^{(1\times 2)}+c_3{M}_3^{(1\times 2)}+(c_4-1)M_4^{(1\times 2)},$$ (21)

$${\mathrm{COV}}_2=\frac{1}{2}{\mathrm{\Sigma }}_{i=1}^2[c_1{M}_5^{(i)}+c_2{M}_6^{(i)}+c_3{M}_7^{(i)}+(c_4-1)M_8^{(i)}],$$ (22)

and

$${\mathrm{COV}}_3=c_1{M}_5^{(1\times 2)}+c_2{M}_6^{(1\times 2)}+c_3{M}_7^{(1\times 2)}+(c_4-1)M_8^{(1\times 2)}.$$ (23)

To express ${\sigma }_{TR}^2$ in terms of $U$-statistic parameters, we first apply the conditional variance identity theorem²⁴

$$\mathrm{Var}[{\widehat{A}}_r^{(1)}-{\widehat{A}}_r^{(2)}]=E\{\mathrm{Var}[{\widehat{A}}_r^{(1)}-{\widehat{A}}_r^{(2)}]|r\}+\mathrm{Var}\{E[{\widehat{A}}_r^{(1)}-{\widehat{A}}_r^{(2)}|r]\},$$

to the OR model, then we have $\mathrm{Var}\{E[{\widehat{A}}_r^{(1)}-{\widehat{A}}_r^{(2)}|r]\}=2{\sigma }_{TR}^2$. On the other hand, based on $U$-statistics, $\mathrm{Var}\{E[{\widehat{A}}_r^{(1)}-{\widehat{A}}_r^{(2)}|r]\}=M_4^{\mathrm{\Delta }}-M_8^{\mathrm{\Delta }}$. So we have

$${\sigma }_{TR}^2=\frac{1}{2}(M_4^{\mathrm{\Delta }}-M_8^{\mathrm{\Delta }}).$$ (24)

By inserting Eqs. (20)–(24) back to Eqs. (17)–(19), one can find Eqs. (17) and (18) hold.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.