Machine learning framework for early MRI-based Alzheimer’s conversion prediction in MCI subjects

Abstract

Mild cognitive impairment (MCI) is a transitional stage between age-related cognitive decline and Alzheimer’s disease (AD). For the effective treatment of AD, it would be important to identify MCI patients at high risk for conversion to AD. In this study, we present a novel magnetic resonance imaging (MRI)-based method for predicting the MCI-to-AD conversion from one to three years before the clinical diagnosis. First, we developed a novel MRI biomarker of MCI-to-AD conversion using semi-supervised learning and then integrated it with age and cognitive measures about the subjects using a supervised learning algorithm resulting in what we call the aggregate biomarker. The novel characteristics of the methods for learning the biomarkers are as follows: 1) We used a semi-supervised learning method (low density separation) for the construction of MRI biomarker as opposed to more typical supervised methods; 2) We performed a feature selection on MRI data from AD subjects and normal controls without using data from MCI subjects via regularized logistic regression; 3) We removed the aging effects from the MRI data before the classifier training to prevent possible confounding between AD and age related atrophies; and 4) We constructed the aggregate biomarker by first learning a separate MRI biomarker and then combining it with age and cognitive measures about the MCI subjects at the baseline by applying a random forest classifier. We experimentally demonstrated the added value of these novel characteristics in predicting the MCI-to-AD conversion on data obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. With the ADNI data, the MRI biomarker achieved a 10-fold cross-validated area under the receiver operating characteristic curve (AUC) of 0.7661 in discriminating progressive MCI patients (pMCI) from stable MCI patients (sMCI). Our aggregate biomarker based on MRI data together with baseline cognitive measurements and age achieved a 10-fold cross-validated AUC score of 0.9020 in discriminating pMCI from sMCI. The results presented in this study demonstrate the potential of the suggested approach for early AD diagnosis and an important role of MRI in the MCI-to-AD conversion prediction. However, it is evident based on our results that combining MRI data with cognitive test results improved the accuracy of the MCI-to-AD conversion prediction.

Introduction

Alzheimer’s disease (AD), a common form of dementia, occurs most frequently in aged population. More than 30 million people worldwide suffer from AD and, due to the increasing life expectancy, this number is expected to triple by 2050 (Barnes and Yaffe, 2011). Because of the dramatic increase in the prevalence of AD, the identification of effective biomarkers for the early diagnosis and treatment of AD in individuals at high risk to develop the disease is crucial. Mild cognitive impairment (MCI) is a transitional stage between age-related cognitive decline and AD, and the earliest clinically detectable stage of progression towards dementia or AD (Markesbery, 2010). According to previous studies (Petersen et al., 2009), a significant proportion of MCI patients, approximately 10% to 15% from referral sources such as memory clinics and AD centers, will develop into AD annually. AD is characterized by the formation of intracellular neurofibrillary tangles and extracellular β-amyloid plaques as well as extensive synaptic loss and neuronal death (atrophy) within the brain (Mosconi et al., 2007). The progression of the neuropathology in AD can be observed many years before clinical symptoms of the disease become apparent (Braak and Braak, 1996; Delacourte et al., 1999; Morris et al., 1996; Serrano-Pozo et al., 2011; Mosconi et al., 2007). AD pathology has been therefore hypothesized to be detectable using neuroimaging techniques (Markesbery, 2010). Among different neuroimaging modalities, MRI has attracted a significant interest in AD related studies because of its completely non-invasive nature, high availability, high spatial resolution and good contrast between different soft tissues. Over the past few years, numerous MRI biomarkers have been proposed in classifying AD patients in different disease stages (Fan et al., 2008; Duchesne et al., 2008; Chupin et al., 2009; Querbes et al., 2009; Wolz et al., 2011; Hinrichs et al., 2011; Westman et al., 2011a,b; Westman et al., 2012; Cho et al., 2012; Coupé et al., 2012; Gray et al., 2013; Eskildsen et al., 2013; Guerrero et al., 2014; Wang et al., 2014). Despite of many efforts, identifying efficient AD-specific biomarkers for the early diagnosis and prediction of disease progression is still challenging and requires more research.

In the current study, we present a novel MRI-based technique for the early detection of AD conversion in MCI patients by using advanced machine learning algorithms and combining MRI data with standard neuropsychological test results. In more detail, we aim to predict whether an MCI patient will convert to AD over a 3 year period (this is referred as progressive MCI or pMCI) or not (this is referred as stable MCI or sMCI) using only data at the baseline. The data used in this work is obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.loni.usc.edu/ADNI) and it includes MRI scans and neuropsychological test results from normal controls (NC), AD, and MCI subjects with a matched age range. Recently, several computational neuroimaging studies have focused on predicting the conversion to AD in MCI patients by utilizing various types of ADNI data such as MRI (e.g. Ye et al., 2011; Filipovych and Davatzikos, 2011; Batmanghelich et al., 2011), positron emission tomography (PET) (Zhang and Shen, 2011, 2012; Cheng et al., 2012; Shaffer et al., 2013), cerebrospinal fluid (CSF) biomarkers (Zhang and Shen, 2011; Cheng et al., 2012; Davatzikos et al., 2011; Shaffer et al., 2013), and demographic and cognitive information (see Tables 1 and 7). Our method is a multi-step procedure combining several ideas into a coherent framework for AD conversion prediction:

1. Semi-supervised learning, using data from AD and NC subjects to help the sMCI/pMCI classification

2. Novel random forest based data integration scheme

3. Removal of age related confound.

Table 1.

Semi-supervised classification of AD using ADNI database. AUC: area under the receiver operating characteristic curve, ACC: accuracy, SEN: sensitivity, SPE: specificity.

Author	Data	Task	Result (supervised)	Result (semi-supervised)
Ye et al. (2011)	MRI, 53 AD, 63 NC, 237 MCI	sMCI vs. pMCI	AUC = 71% ACC = 55.3% SEN = 88.2% SPE = 42%	AUC = 73% ACC = 56.1% SEN = 94.1% SPE = 40.8%
Filipovych and Davatzikos (2011)	MRI, 54 AD, 63 NC, 242 MCI	sMCI vs. pMCI	AUC = 61% SEN = 78.8% SPE = 51%	AUC = 69% SEN = 79.4% SPE = 51.7%
Zhang and Shen (2011)	MRI, PET, CSF 51 AD, 52 NC, 99 MCI	AD vs. NC	AUC = 94.6%	AUC = 98.5%
Batmanghelich et al. (2011)	MRI, 54 AD, 63 NC, 238 MCI	sMCI vs. pMCI	AUC = 61.5%	AUC = 68%

Table 7.

Supervised classification of AD conversion prediction using ADNI database. AUC: area under the receiver operating characteristic curve, ACC: accuracy, SEN: sensitivity, SPE: specificity.

Author	Data	Validation method	Result	Conversion time
Moradi et al. (this paper)	MRI, age and cognitive measures	10-fold cross-validation	AUC = 90% ACC = 82% SEN = 87% SPE = 74%	0–36 months
Misra et al. (2009)	Basic measures and MRI data, 27 pMCI and 76 sMCI	Leave-one-out cross-validation	AUC = 77% ACC = 75%–80%	0–36 months
Davatzikos et al. (2011)	MRI and CSF, 69 pMCI and 170 sMCI	k-fold cross-validation	AUC = 73% Max ACC = 62%	0–36 months
Ye et al. (2012)	Basic measures and MRI data, 177 sMCI and 142 pMCI	Leave-one-out cross-validation	AUC = 86%	0–48 months
Zhang and Shen (2012)	MRI, PET and cognitive scores, 38 pMCI and 50 sMCI	Leave-one-out cross-validation	AUC = 77% ACC = 78% SEN = 79% SPE = 78%	0–24 months
Gaser et al. (2013)	Age and MRI data, 133 pMCI and 62 sMCI	Independent test set	AUC = 78%	0–36 months
Cuingnetet al. (2011)	MRI data, 134 sMIC, 76 pMCI	Independent test set	ACC = 67% SEN = 62% SPE = 69%	0–18 months
Shaffer et al. (2013)	MRI, PET, CSF and basic measurements, 97 MCI	k-fold cross-validation	ACC = 72%	0–48 months
Eskildsen et al. (2013)	Age and MRI data, 161 pMCI, 227 sMCI	Leave-one-out cross-validation	AUC: pMCI6vs sMCI = 81%, pMCI12 vs sMCI = 76%, pMCI24 vs sMCI = 71%, pMC36 vs sMCI = 64%,	0–48 months
Wolz et al. (2011)	Combination of different MR-based features 238 sMCI, 167 pMCI	k-fold cross-validation	ACC = 68% SEN = 67% SPE = 69%	0–48 months
Chupin et al. (2009)	MRI data, 134 sMCI, 76 pMCI	Independent test set	ACC = 64% SEN = 60% SPE = 65%	0–18 months
Cho et al. (2012)	MRI data, 131 sMCI, 72 pMCI	Independent test set	ACC = 71% SEN = 63% SPE = 76%	0–18 months
Coupé et al. (2012)	MRI data, 238 sMCI, 167 pMCI	Leave-one-out cross-validation	ACC = 74% SEN = 73% SPE = 74%	0–48 months
Westman et al. (2011a)	MRI data, 256 sMCI, 62 pMCI	k-fold cross-validation	ACC = 59% SEN = 74% SPE = 56%	0–12 months
Cheng et al. (2012)	MRI, PET, CSF 51 D, 52 NC, 99 MCI Only MRI	k-fold cross-validation	AUC = 73.6% ACC = 69.4% SEN = 64.3% SPE = 73.5% AUC = 70.0% ACC = 63.3% SEN = 59.8% SPE = 66.0%	Not available
Casanova et al. (2013)	Only cognitive measures, 188 NC, 171 AD, 153 pMCI, 182 sMCI Only MRI (GM)	k-fold cross-validation	ACC = 65% SEN = 58% SPE = 70% ACC = 62% SEN = 46% SPE = 76%	0–36 months

In the experimental sections we will demonstrate that all these provide a significant contribution towards the accuracy of the combined prediction model. Our method differs in the following aspects from earlier studies.

Most of the earlier studies were based on supervised learning methods, where only labeled data samples are used for learning the model. Semi-supervised learning (SSL) approaches are able to use unlabeled data in conjunction with labeled data in a learning procedure for improving the classification performance. The great interest in SSL techniques over the past few years (Zhu, and Goldberg, 2009) is related to the wide spread of application domains where providing labeled data is hard and expensive compared to providing unlabeled data. The problem studied in this work, predicting the AD-conversion in MCI subjects, is a good example of this scenario since MCI subjects have to be followed for several years after the data acquisition to obtain a sufficiently reliable disease label (pMCI or sMCI). Few recent studies (listed in Table 1) have investigated the use of different semi-supervised approaches for diagnosis of AD in different stages of the disease. In Zhang and Shen (2011), MCI subjects’ data were used as unlabeled data to improve the classification performance in discriminating AD versus NC subjects. They achieved a significant improvement, the AUC score increased from 0.946 to 0.985, which is high for discriminating AD vs. NC subjects. Ye et al. (2011), Filipovych and Davatzikos (2011), and Batmanghelich et al. (2011) used AD and NC subjects as labeled data and MCI subjects as unlabeled data and predicted disease-labels for the MCI subjects. In all these studies, the improvement in the predictive performance of the model was significant over supervised learning. The best classification performance in discriminating sMCI versus pMCI using only MRI data was achieved by Ye et al. (2011) with the area under the receiver operating characteristic curve (AUC) equal to 0.73 for prediction of conversion within 0–18 month period. We hypothesize that the classification performance of semi-supervised learning approaches could be improved if MCI subjects who have been followed up for long enough would be used as labeled data. In this work, we develop a semi-supervised classifier for AD conversion prediction in MCI patients based on low density separation (LDS) (Chapelle and Zien, 2005) and by using MRI data of MCI subjects. Our results demonstrate applicability of the proposed semi-supervised method in MRI based AD conversion prediction in MCI patients by achieving a significant improvement compared to a state of the art supervised method (support vector machine (SVM)).

We perform two processing steps in between our voxel based morphometry style preprocessing (Gaser et al., 2013) and the learning of the LDS classifier. First, we remove age-related effects from MRI data before training the classifier to prevent the confounding between AD and age-related effects to brain anatomy. Previously, a similar technique has been used for the classification between AD and NC subjects, but this study has not considered AD-conversion prediction in MCI subjects (Dukart et al., 2011). In addition, the impact of age was studied recently for detecting AD (Coupé et al., 2012) as well as for predicting AD in MCI patients (Eskildsen et al., 2013). Second, we perform feature selection on MRI data independently of the classification procedure using the auxiliary data from AD and NC subjects. Feature selection is an essential part of the combined procedure since the number of features (29,852) available after the image preprocessing significantly exceeds the number of subjects. We assume that AD vs. NC classification is a simplified version of the pMCI vs. sMCI and the same features that are most useful for the simple problem are useful for the complex one. This idea is implemented by applying regularized logistic regression (RLR) (Friedman et al., 2010) on MRI data of AD and NC subjects for finding the image voxels that are best discriminated between AD and NC subjects. Next, we use these selected voxels for predicting conversion to AD within MCI patients. Most of existing studies incorporating feature selection rely only on a dataset of MCI subjects by using it for feature selection and classification task. In particular, previous studies (Ye et al., 2011, 2012; Janoušová et al., 2012) have considered feature selection based on RLR for MCI-to-AD conversion prediction, but the feature selection was performed with the data from MCI subjects not utilizing data from AD and NC subjects. Auxiliary data from AD and NC subjects to aid the classification of MCI subjects have been considered by Cheng et al. (2012) in a domain transfer learning method. Briefly, the method utilizes cross-domain kernel build from target data (MCI subjects) and auxiliary data (AD and NC) subjects to learn a linear support vector machine classifier. As Cheng et al. reduced the number of features to 93 by partitioning each MRI into 93 regions of interest and did not consider feature selection, the approach to use the auxiliary data is different from our approach.

We integrate MRI data with age and cognitive measurements, also acquired at the baseline, for improving the predictive performance of MCI-to-AD conversion. As opposed to several other studies combining MRI with other types of data (Davatzikos et al., 2011; Zhang and Shen, 2012; Shaffer et al., 2013; Cheng et al., 2012; Wang et al., 2013), we purposely avoid using CSF or PET based biomarkers, the former because it requires lumbar puncture, which is invasive and potentially painful for the patient, and the latter because of its limited availability compared to MRI, as well as its cost and radiation exposure (Musiek et al., 2012). Previously, the combination of MRI derived information and cognitive measurements has been considered by Ye et al. (2012) who trained an RLR classifier with standard cognitive measurements and volumes of certain regions of interest as features and Casanova et al. (2013) who combined outputs of two classifiers, one trained based on MRI and the other trained based on cognitive measurements, based on a sum-rule for the classifier combination. In order to use more efficiently MRI and basic (age and cognitive) measures, we develop what we call an aggregate biomarker by utilizing two different classifiers, i.e. LDS and random forest (RF), in different stages of the process. We first derive a single real valued biomarker based on MRI data using LDS (our biomarker) and thereafter use this as a feature for the aggregate classifier (RF). We will highlight the importance of using a transductive classifier (e.g., LDS) instead of an inductive one (e.g., a standard SVM) during the first stage of the learning process and provide evidence of the effectiveness of the aggregate biomarker for the AD conversion prediction in MCI patients based on MRI, age and cognitive measures at the baseline.

Materials and methods

ADNI data

Data used in this work is obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu/). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The principal investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California — San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2.

To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow-up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

Data used in this work include all subjects for whom baseline MRI data (T1-weighted MP-RAGE sequence at 1.5 T, typically 256 × 256 × 170 voxels with the voxel size of approximately 1 mm × 1 mm × 1.2 mm), at least moderately confident diagnoses (i.e. confidence > 2), hippocampus volumes (i.e. volumes of left and right hippocampi, calculated by FreeSurfer Version 4.3), and test scores in certain cognitive scales (i.e. ADAS: Alzheimer’s Disease Assessment Scale, range 0–85; CDR-SB: Clinical Dementia Rating ‘sum of boxes’, range 0–18; MMSE: Mini-Mental State Examination, range 0–30) were available.

For the diagnostic classification at baseline, 825 subjects were grouped as (i) AD (Alzheimer’s disease), if diagnosis was Alzheimer’s disease at baseline (n = 200); (ii) NC (normal cognitive), if diagnosis was normal at baseline (n = 231); (iii) sMCI (stable MCI), if diagnosis was MCI at all available time points (0–96 months), but at least for 36 months (n = 100); (iv) pMCI (progressive MCI), if diagnosis was MCI at baseline but conversion to AD was reported after baseline within 1, 2 or 3 years, and without reversion to MCI or NC at any available follow-up (0–96 months) (n = 164); (v) uMCI (unknown MCI), if diagnosis was MCI at baseline but the subjects were missing a diagnosis at 36 months from the baseline or the diagnosis was not stable at all available time points (n = 100). From 164 pMCI subjects, 68 subjects were converted to AD within the first 12 months, 69 subjects were converted to AD between 12 and 24 months of follow-up and the remaining 27 subjects were converted to AD between 24 and 36 month follow-up. Details of the characteristics of the ADNI sample used in this work are presented in Table 2. The subject IDs together with the group information is provided in the supplement (Tables S2 – S5, see also https://sites.google.com/site/machinelearning4mcitoad/ for MATLAB files). The conversion data was downloaded on April 2014.

Table 2.

Characteristics of datasets used in this work. There was no statistically significant difference in age (permutation test, p > 0.05) nor gender (proportion test, p > 0.05) between different MCI groups.

	AD	NC	pMCI	sMCI	uMCI
No. of subjects	200	231	164	100	130
Males/female	103/97	119/112	97/67	66/34	130/81
Age range	55–91	59–90	55–89	57–89	54–90

Image preprocessing

As described in Gaser et al. (2013), preprocessing of the T1-weighted images was performed using the SPM8 package (http://www.fil.ion.ucl.ac.uk/spm) and the VBM8 toolbox (http://dbm.neuro.uni-jena.de), running under MATLAB. All T1-weighted images were corrected for bias-field inhomogeneities, then spatially normalized and segmented into gray matter (GM), white matter, and cerebrospinal fluid (CSF) within the same generative model (Ashburner and Friston, 2005). The segmentation procedure was further extended by accounting for partial volume effects (Tohka et al., 2004), by applying adaptive maximum a posteriori estimations (Rajapakse et al., 1997), and by using an hidden Markov random field model (Cuadra et al., 2005) as described previously (Gaser, 2009). This procedure resulted in maps of tissue fractions of WM and GM. Only the GM images were used in this work. Following the pipeline proposed by Franke et al. (2010), the GM images were processed with affine registration and smoothed with 8-mm full-width-at-half-maximum smoothing kernels. After smoothing, images were resampled to 4 mm isotropic spatial resolution. This procedure generated, for each subject, 29,852 aligned and smoothed GM density values that were used as MRI features.

MRI biomarker

As a preprocessing operation, we removed the effects of normal aging from the MRI data. The rationale for this is related to the fact that the effects of normal aging on the brain are likely to be similar (equally directed) with the effects of AD, which can lead to an overlap between the brain atrophies caused by age and AD. This, in turn, would bring a possible confounding effect on the estimation of disease-specific differences (Franke et al., 2010; Dukart et al., 2011). We estimated the age-related effects on the GM densities of NC subjects by using a linear regression model that is similar to a method applied in earlier studies (Dukart et al., 2011; Scahill et al., 2003). Once estimated, the age-related effects were removed from the MRI data of each subject before training the classifiers. For more details, see the algorithmic description in Appendix B.

The overall structure of the proposed classification method is illustrated in Fig. 1. The method consists of two fundamental stages: a feature selection stage, that uses a regularized logistic regression (RLR) algorithm to select a good subset of MRI voxels for AD conversion prediction; and a classification stage that applies a semi-supervised low density separation (LDS) method to produce the final prediction. The LDS relies on a transductive support vector machine classifier, whose hyperparameters are also learned from the data. Note that, for each test subject, instead of the discrete class, an LDS returns the value of the continuous discriminant function d ∈ ℝ that we call MRI biomarker. If d < 0 then the subject is predicted as sMCI and otherwise pMCI; more details are presented in Appendix A.

Fig. 1.

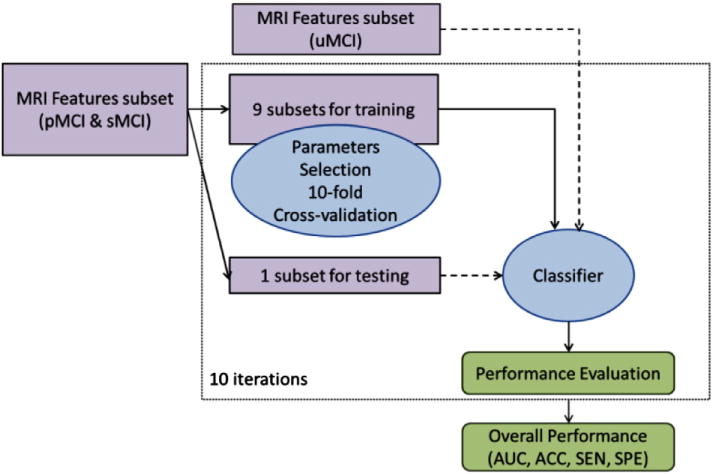
Semi-supervised classification scheme. Dashed arrows indicate data fed to classification process without any label information (in contrast to solid arrows indicating training data with label information). The test subset is used in the classification process without any label information.

More specifically, the first stage of the classification framework selects the most informative voxels (features) among all MRI voxels (features) while discarding non-informative ones. The feature selection uses the regularized logistic regression framework (Friedman et al., 2010) that produces a path of feature subsets with different cardinalities (called regularization path), and has been used widely in previous works (Huttunen et al., 2012, 2013; Ryali et al., 2010) for the multi-voxel pattern analyses of functional neuroimaging data as well as for AD related studies using structural MRI data (Ye et al., 2012; Casanova et al., 2011a,b, 2012; Shen et al., 2011; Janoušová et al., 2012). As the RLR procedure is a supervised learning method, the input has to be fully labeled data. To this aim, we applied RLR on MRI data of AD and NC subjects for determining a subset of features (voxels) with the highest accuracy in discriminating the two classes. The selected voxels (and only them) were then used for predicting conversion to AD in MCI patients. Note that this way we avoided using data about MCI subjects for feature selection and therefore we can use all the MCI data for learning the classifier. The cardinality of the selected subset along the regularization path was determined using 10-fold cross validation, which estimated the most discriminative subset among the candidates found by the RLR. The details of the RLR approach are described in Appendix B.

The second stage trains the final semi-supervised LDS classifier. At this stage, also the unlabeled uMCI samples were fed to the classifier, after the extraction of the most discriminative features. Since the LDS approach is based on the transductive SVM classifier, also the hyperparameters of the transductive SVM have to be selected. The choice of the SVM parameters was done using a nested cross validation approach, where each of the cross validation splits of the feature selection stage was further split into second level of 10 cross validation folds. In this way we were able to estimate the performance of the complete framework and simulate the final training process with all data after the hyperparameters have been selected.

The LDS approach for semi-supervised learning (see Appendix A and Chapelle and Zien, 2005) integrates unlabeled data into the training procedure. The algorithm assumes that the classes (e.g., pMCI and sMCI subjects) form high density clusters in the feature space, and that there are low density areas between the classes. This way the labeled samples determine the rough shape of the decision rule, while the unlabeled samples fine-tune the decision rule to improve the performance. A typical gain due to integrating unlabeled data varies from a few percent to manifold decrease in prediction error. The LDS is a two step algorithm, which first derives a graph-distance kernel for enhancing the cluster separability and then it applies transductive support vector machine (TSVM) for classifier learning. SSL methods previously applied to MCI-to-AD conversion prediction have included TSVM (Filipovych and Davatzikos, 2011) and Laplacian SVM (Ye et al., 2011). Based on experimental results by Chapelle and Zien (2005), LDS can be seen as an improved version of TSVM and related to Laplacian SVM. Moreover, we have provided evidence that the LDS overperforms the semi-supervised discriminant analysis (Cai et al., 2007) in MCI-to-AD conversion prediction in our recent conference paper (Moradi et al., 2014). Finally, we note that as the majority of the semi-supervised classifiers including TSVMs, LDS applies transductive learning, practically meaning that the MRI data (but not the labels) of the test subjects can be used for learning the classifier. We point out that this is perfectly valid and does not lead to double-dipping as the test labels are not used for learning the classifier. For a clear explanation of the differences between transductive and inductive machine learning algorithms, we refer to Gammerman et al. (1998) and relation between semi-supervised and transductive learning is discussed in detail by Chapelle et al. (2006).

In order to examine the applicability of the semi-supervised method, i.e., LDS, we applied it on the MRI data with and without feature selection and compared its performance with the performance of its supervised counterpart, the support vector machine (SVM). SVM is a maximum margin classifier that is widely used in supervised classification problems. In SVM, only labeled samples are used for determining decision boundary between different classes.

Aggregate biomarker

In order to improve AD conversion prediction in MCI patients, we developed a method for the integration of the baseline MRI data with age and cognitive measurements acquired at baseline. The measurements we considered were Rey’s Auditory Verbal Learning Test (RAVLT), Alzheimer’s Disease Assessment Scale—cognitive subtest (ADAS-cog), Mini Mental State Examination (MMSE), Clinical Dementia Rating—Sum of Boxes (CDR-SB), and Functional Activities Questionnaire (FAQ). These standard cognitive measurements, which are widely used in assessing cognitive and functional performance of dementia patients, are explained in the ADNI General Procedures Manual.² The rationale was to include the cognitive assessments that are inexpensive to acquire and available for the MCI subjects in this study. We only considered the composite scores of the measurements that often include several subtests. We did not consider CSF or PET measurements for the reasons outlined in the Introduction section. Since the effects of normal aging on the MRI data were removed, age was again used as a predictor, because it is a risk factor for AD.

The way that MRI data is combined with the cognitive measurements is crucial to achieve a good estimation accuracy of the MCI-to-AD conversion prediction. The simplest way would be to combine the MRI data (only selected voxels) and cognitive measurements as a long feature vector which is as the input of the classifier. We will refer to this as data concatenation. However, this is not the best way, because of the different natures of MRI data (close to continuous) and cognitive measurements (mainly discrete) (Zhang et al., 2011). Therefore, we propose a simple classifier ensemble for constructing the aggregate biomarker. In effect, we used the MRI biomarker, derived using LDS classifier, as a feature/predictor for the aggregate biomarker. The MRI feature was combined with age and cognitive measurements and used as input features for the random forest (RF) classifier. An RF consists of a collection of decision trees all trained with different subsets of the original data. Averaging of the outputs of individual trees renders RFs tolerant to overlearning, which is the reason for their popularity in classification and regression tasks especially in the area of bioinformatics. Note that an RF is an ensemble learning method that outputs vote counts for different classes so the aggregate biomarker value approximates the probability of converting to AD. Random forests are often used for ranking the importance of input variables by randomly permuting the values of each variable at a time, and estimating the decrease in accuracy on out of bag samples (Breiman, 2001; Liaw and Wiener, 2002). The overview of the aggregate biomarker and its evaluation is shown in Fig. 2. Previous applications of RFs in the context of AD classification include Llano et al. (2011) who applied RFs to generate a new weighting of ADAS subscores.

Fig. 2.

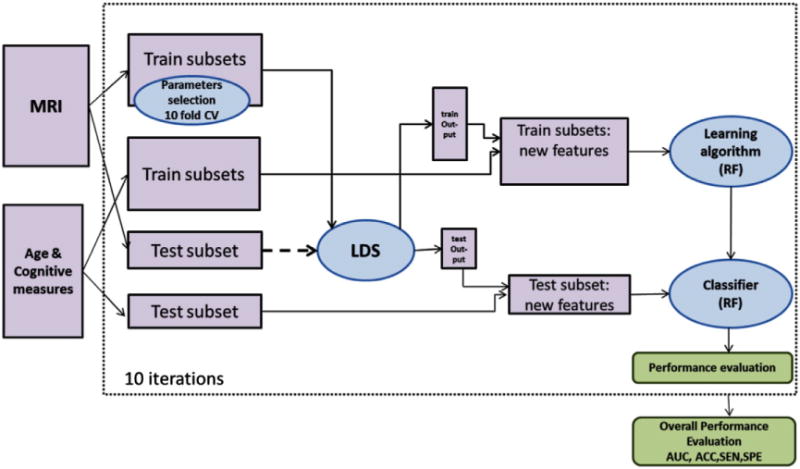
Workflow for the aggregate biomarker and its cross-validation based evaluation. For computing the output of LDS classifier for test subjects, the test subset is used in the learning procedure without any label information (shown with dashed arrow).

Performance evaluation

For the evaluation of classifier performance and estimation of the regularization parameters, we used two nested cross-validation loops (10-fold for each loop) (Huttunen et al., 2012; Ambroise and Mclachlan, 2002). First, an external 10-fold cross-validation was implemented in which labeled samples were randomly divided into 10 subsets with the same proportion of each class label (stratified cross-validation). At each step, a single subset was left for testing and remaining subsets were used for training. Again the train set was divided into 10 subsets that were used for the selection of classifier parameters listed below. The optimal parameters were selected according to the maximum average accuracy across the 10-fold of the inner loop. The performance of the classifier was then evaluated based on AUC (area under the receiver operating characteristic curve), accuracy (ACC, the number of correctly classified samples divided by the total number of samples), sensitivity (SEN, the number of correctly classified pMCI subjects divided by the total number of pMCI subjects) and specificity (SPE, the number of correctly classified sMCI subjects divided by the total number of sMCI subjects) using the test subset of the outer loop. The pooling strategy was used for computing AUCs (Bradley, 1997). The reported results in the Results section are averages over 100 nested 10-fold CV runs in order to minimize the effect of the random variation. To compare the mean AUCs of two learning algorithms, we computed a p-value for the 100 AUC scores with a permutation test.

To perform the survival analysis and estimate the hazard rate for AD conversion in MCI subjects, Cox proportional hazard model was employed (see McEvoy et al., 2011; Gaser et al., 2013; Da et al., 2014 for previous applications of the survival analysis in the sMCI/pMCI classification). The predictor was the real valued output of the classifier (i.e., the value of the discriminant function in the case of LDS and estimated probability of conversion in the case of RF; see the MRI biomarker and Aggregate biomarker sections) and the conversion time to AD in MCI subjects was taken as the time-to-event variable. The duration of follow-up was truncated at 3 years for sMCI subjects and uMCI subjects were not included in the analysis. The Cox models implemented by MATLAB’s coxphfit-function were adjusted for age and gender. The Cox-regression was performed in the cross-validation framework similarly as described above for AUC.

Implementation

The implementation of elastic-net RLR for feature selection was done by using the GLMNET library (http://www-stat.stanford.edu/~tibs/glmnet-matlab/). The support vector machine (SVM) with a Radial Basis Function (RBF) kernel was used as supervised method for a comparison with LDS. The RBF kernel was used with the SVM as this widely used kernel clearly outperformed the linear kernel in a preliminary testing and linear kernels can be seen as a special case of the RBF kernels (Keerthi and Lin, 2003). The implementation of SVM was done using LIBSVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html) running under MATLAB. The implementation of LDS was done by using a publicly available MATLAB implementation (http://olivier.chapelle.cc/lds/). The SVM has two parameters, C (soft margin parameter, see Appendix A) and γ (parameter for RBF kernel function). For tuning these parameters, a grid search was used, i.e., parameter values were varied among the candidate set {10⁻⁴, 10⁻³, 10⁻², 10⁻¹, 10⁰, 10¹, 10², 10³, 10⁴} and each combination was evaluated using cross-validation as outlined above. LDS has more parameters to tune. Since tuning many parameters with grid search is impractical, we considered only the most critical parameters, i.e., C (soft margin parameter) and ρ (softening parameter for graph distance computation) in grid search. For tuning parameter C, its value was varied among the candidate set {10⁻², 10⁻¹, 10⁰, 10¹, 10²} and for parameter ρ among the candidate set {1, 2, 4, 6, 8, 10, 12}. For the other parameters, default values were used except that the 10-nearest neighbor graphs were used for the kernel construction (instead of fully connected graph) and the parameter δ in (Chapelle and Zien, 2005) was set to be 1. The MRI features were normalized to have unit variance before the classification. The implementation of RF was the MATLAB port of the R-code of Liaw and Wiener (2002) available at http://code.google.com/p/randomforest-matlab/. All parameters were set to their default values. The CPU time for training a single classifier (including parameter selection and performance evaluation using cross-validation) was in the order of tens of minutes on an Intel Core 2 Duo processor, 3.00 GHz, 4 GB RAM. The image processing of the Image preprocessing section required on average 8 min per single image (3.4 GHz Intel Core i7, 8 GB RAM).

Results

MRI biomarker

In this section, we consider the experimental results obtained using the biomarker based on solely MRI data as described in the MRI biomarker section. The feature selection reduced the number of voxels in MRI data from 29,852 to 309 voxels. Fig. 3 shows the locations of the selected 309 voxels overlaid on the standard template. Supplementary Table S1 provides the ranking of the brain regions of the loci of the selected voxels according to the Automatic Anatomical Labeling (AAL) atlas. It can be observed that the selected voxels were spread all over the brain (including the hippocampus, the temporal and frontal lobes, the cerebellar areas, as well as the amygdala, insula, and parahippocampus). These locations have been previously reported in studies concerning the brain atrophy in AD (Weiner et al., 2012). The neuropathology of AD is typically related to changes (e.g. atrophy that reflects the loss and shrinkage of neurons) in the entorhinal cortex, that progress then to the hippocampus, the temporal, frontal and parietal areas, before ultimately diffusing to the whole cerebral cortex (Casanova et al., 2011b; Salawu et al., 2011). These brain structures, especially the hippocampus, frontal and temporal areas have been found to be effective in discriminating between AD patients and NC (for a review see Casanova et al., 2011b and references therein). Also, patterns of neuropathology in cerebellar areas have been reported in previous studies (Sjöbeck and Englund, 2001).

Fig. 3.

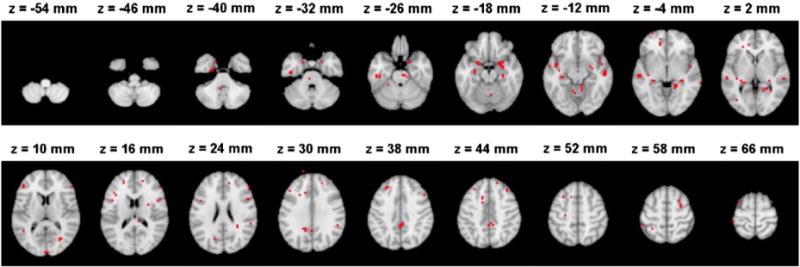
The locations of selected voxels by elastic-net RLR with the highest accuracy in discriminating AD and NC subjects within the brain in MNI (Montreal Neurological Institute) space. One of the voxels appears to be slightly outside the brain due to the effect of smoothing and the larger voxel size of the pre-processed data compared to the voxel size of the template.

We applied LDS on the MRI data with and without feature selection and compared its performance with the performance of its supervised counterpart, the standard SVM. We also evaluated the impact of removing age-related effects from the MRI data for the purpose of early diagnosis of AD. Because the age was used as a parameter for removing age-related effects, the biomarker was based on MRI and age information. However, the age was not used as a feature in the learning process. Table 3 shows the results of the MRI biomarker. First, second and third rows show the performance measures obtained using a SVM without feature selection, with feature selection, and after removing age-related effects, respectively. The fourth, fifth and sixth rows in Table 3 show the performance measures obtained by the LDS. The classification accuracy of both methods without feature selection was only about chance level. After the feature selection, the classification performance based on AUC and ACC obtained by both methods improved. The improvement (in AUC) was statistically significant for both LDS (p < 0.0001) and SVM (p < 0.0001). As a result, the elastic-net RLR was able to select the relevant voxels corresponding to AD in the high dimensional MRI data. In addition, feature selection was done independently of the classification procedure. Using NC and AD datasets for feature selection was a strategy that allowed a larger sample size for the training and validating the MCI classifier.

Table 3.

A comparison of the performances of SVM and LDS methods with and without feature selection, and with and without age-related effects by using MRI data. The results are averages over 100 computation times. For the classification accuracy (ACC), the chance level is 62.12%.

Classifier	Feature selection	Age related effect	AUC	ACC	SEN	SPE
SVM	No	Not removed	66.37%	64.86%	87.90%	27.09%
SVM	Yes	Not removed	69.49%	66.01%	78.88%	44.91%
SVM	Yes	Removed	74.30%	69.15%	86.73%	40.34%
LDS	No	Not removed	67.60%	66.05%	85.67%	33.90%
LDS	Yes	Not removed	72.88%	72.60%	84.16%	53.66%
LDS	Yes	Removed	76.61%	74.74%	88.85%	51.59%

As expected, applying LDS on the MRI data after removing age-related effects increased the AUC score from 0.7288 to 0.7661, which was significant according to the permutation test (p < 0.0001). Removing age-related effects from MRI data improved the classification performance significantly also in the case of SVM (AUC 0.6949 vs. 0.7430, p < 0.0001).

In order to evaluate the performance of the elastic-net RLR for feature selection within MRI data, we compared the classification performance of MRI biomarker based on different feature selection algorithms. For this purpose we used univariate t-test and graph-net (Grosenick et al., 2013) feature selection methods. The AUC of MRI biomarker with the univariate t-test based feature selection (1000 features) was 0.71 and with graph-net based feature selection (354 features) was 0.74. The elastic-net RLR based feature selection led to a significantly improved performance in MRI biomarker as compared to the t-test and graph-net based feature selection methods (p < 0.0001). We experimented with the feature selection directly on MCI subjects’ data for reducing dimensionality of MRI data. More specifically, the feature selection (elastic-net RLR) was performed in the outer loop of two nested cross-validation loops by first performing the feature selection using all features in MRI data (29,852 voxels) and then using these selected features for parameter selection and learning the model. The performance of MRI biomarker with the feature selection using MCI subjects decreased significantly compared to the feature selection using an independent validation set of AD and NC subjects (from 0.7661 to 0.6833, p < 0.0001). When the feature selection was done combining AD and pMCI subjects into one class, and NC and sMCI subjects into other, the performance did not significantly differ from the suggested approach (AUCs of 0.7661 vs. 0.7692). As this approach necessitates an additional CV loop, the suggested feature selection method remained preferable.

We investigated how much unlabeled data improved the classification accuracy. For this, we trained the LDS classifier also without data from uMCI subjects. Note that the LDS is a transductive learning method that uses the test MRI data (but not labels) as unlabeled data. As explained in the MRI biomarker section, because the label information of the test data was not used in the learning process, this does not lead to ‘double-dipping’ or ‘training on the testing data’ problems, and more specifically, to upward biased classifier performance estimates (Chapelle and Zien, 2005; Chapelle et al., 2006). Fig. 4 shows the box plots for AUC, ACC, SEN and SPE of LDS and SVM methods based on MRI data (with feature selection and age-related effects removed). In the case of LDS, the results are shown with and without utilizing uMCI data as unlabeled data in the learning process. As it can be seen from the results, adding uMCI data samples improved classification performance slightly, but the improvement was not statistically significant (p = 0.3072). However, it increased the stability of the classifier by decreasing the variance in AUCs between different cross-validation runs. The LDS method works based on the cluster assumption and utilizes unlabeled data for finding different clusters and placing the decision boundary in low density regions of the feature space. When the cluster assumption does not hold, unlabeled data points do not carry significant information and cannot improve the results (Chapelle and Zien, 2005). Also, the number of unlabeled data might be too small for significant performance improvement. Here, the number of unlabeled data was only 130 which is few compared to number of labeled data (264 subjects). However, LDS either with or without uMCI data samples, clearly outperformed the corresponding supervised method (SVM, AUC 0.7430 vs. 0.7661, p < 0.0001). Even though adding uMCI samples did not significantly improve the predictive performance of the MCI-to-AD conversion, the use of LDS method in a transductive manner led to a higher predictive performance compared to SVM method.

Fig. 4.

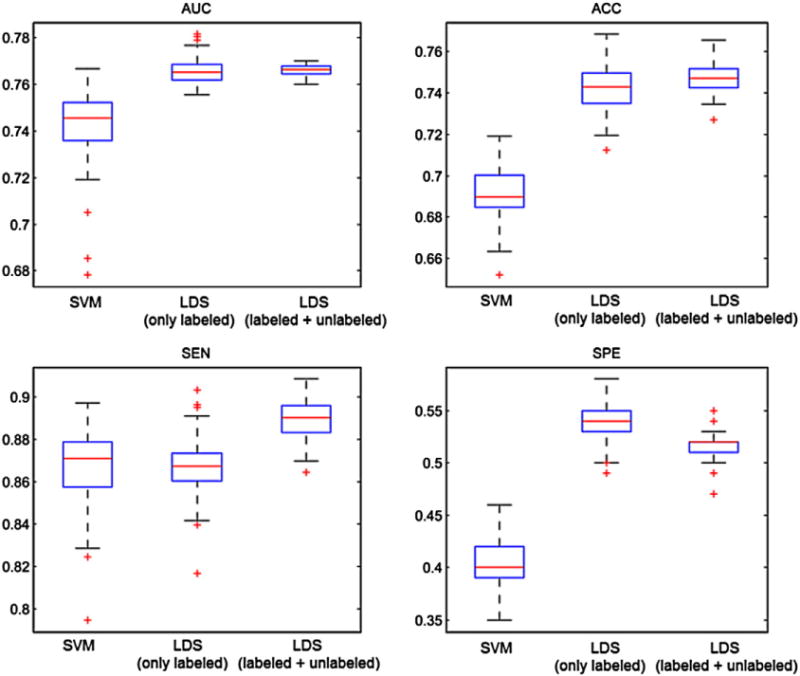
Box plots for AUC, ACC, SEN and SPE of SVM and LDS methods based on MRI data with selected features and removed age-related effects, within 100 computation times. In the case of LDS, the depicted results are obtained with (LDS-labeled + unlabeled) and without (LDS-only labeled) utilizing uMCI subjects in the learning. On each box, the central mark is the median (red line), the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted with a +.

Aggregate biomarker

In this section, we present the experimental results for the aggregate biomarker of the Aggregate biomarker section based on MRI, age, and cognitive measures, all acquired at the baseline. Table 4 shows the correlation between cognitive measurements used in aggregate biomarker to the ground-truth label.

Table 4.

The correlation between cognitive measures to the ground-truth labels. The negative correlation indicates that the higher the value the lower is the risk for AD.

	Age	MMSE	FAQ	CDR-SB	ADAS-cog total-11	ADAs-cog total Mod	RAVLT
Correlation	−0.06	−0.28	0.40	0.34	0.43	0.43	−0.46

In order to demonstrate the advantage of the selected data-aggregation method and the utility of combining age and cognitive measurements with MRI data, we also applied LDS and RF on data formed by concatenating cognitive measurements, age and MRI data (309 selected voxels with age-related effects removed) as a long vector. Further, we applied RF on the age and cognitive measurements to predict AD in MCI patients in the absence of MRI data and combined SVM with RF (abbreviated as SVM + RF) in the same way as LDS is combined to RF in the aggregate biomarker. The box plots for the performance measures of aggregate biomarker (LDS + RF), SVM + RF as well as RF and LDS applied on the concatenated data and the RF without MRI are shown in Fig. 5.

Fig. 5.

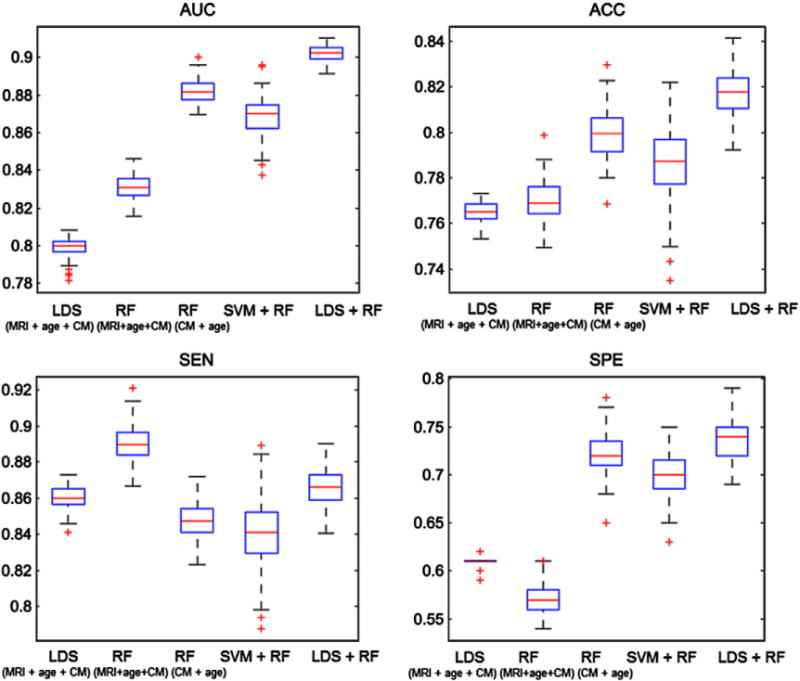
Box plots for AUC, ACC, SEN and SPE of RF, LDS and aggregate biomarker with LDS + RF and with SVM + RF, using MRI with cognitive measurements within 100 computation times. On each box, the central mark shown in red is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted with a +. The abbreviation CM refers to cognitive measurements. The data for LDS (MRI + age + CM) and RF (MRI + age + CM) was formed by simple data concatenation.

The aggregate biomarker achieved mean AUC of 0.9020, which was significantly better than the AUC of LDS with aggregated data (0.7990, p < 0.0001) and the AUC of RF with only cognitive measures (0.8819, p < 0.001). With LDS, there was a significant improvement when integrating cognitive measurements and MRI data (mean AUC increased from 0.7661 to 0.7990, p < 0.0001). However, in the case of RF adding cognitive measurements with MRI data decreased its performance significantly when comparing to RF with only cognitive measurements (mean AUC decreased from 0.8819 to 0.8313, p < 0.0001). These results seem to suggest that RF had difficulties in aggregating MRI data with cognitive measures and supports our decision to use two different learning algorithms when designing the aggregate biomarker. Also, the performance of SVM + RF was clearly worse than the performance LDS + RF (p < 0.001) and even RF with only cognitive measures (p < 0.001). We hypothesize that this is because SVM overlearned and failed to provide a useful input to random forest while the images in the test set regularize LDS in a useful way. Fig. 6 shows the ROC curves of one computation time (of the median AUC within 100 cross-validation runs) of MRI biomarker (LDS with only MRI data), RF with only age and cognitive measures, LDS and RF methods trained on the concatenated data from MRI, age and cognitive measurements, and of the aggregate biomarker with MRI, age and cognitive measurements. The ROC curve of the aggregate biomarker dominates the other ROC curves nearly everywhere. We also calculated the stratified AUC for different pMCI subgroups, i.e., pMCI subjects that are converted to AD in different time points (1, 2 or 3 years), for both MRI and aggregate biomarkers. Results are shown in Fig. 7. Fig. 7 shows, as expected, that the prediction was more accurate the closer the conversion subject was. Additionally, we evaluated the classification performance of the MRI and aggregate biomarkers against a random classifier, where a biomarker value for each subject was drawn randomly from a standard normal distribution. The mean AUC of the random classifier was 0.5016, which was significantly lower than the AUC of the MRI biomarker (AUC = 0.7661, p < 0.0001) as well as the AUC of aggregate biomarker (AUC = 0.9020, p < 0.0001).

Fig. 6.

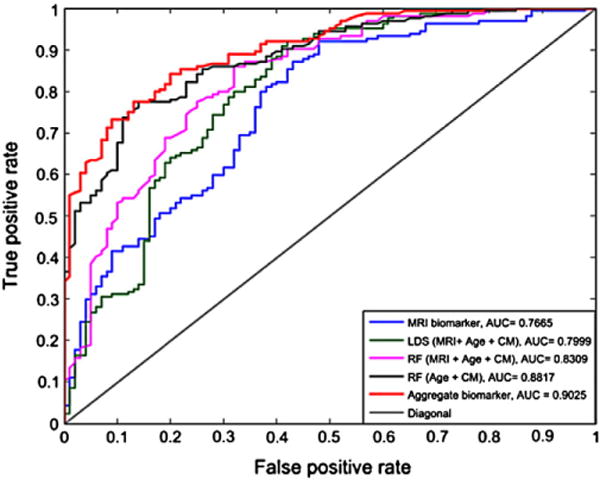
ROC curves of subject’s classification to sMCI or pMCI using classification methods, LDS, SVM and aggregate biomarker using only MRI and MRI with age and cognitive measurements. Each ROC curve is from a cross-validation run with the median AUC within 100 cross-validation runs.

Fig. 7.

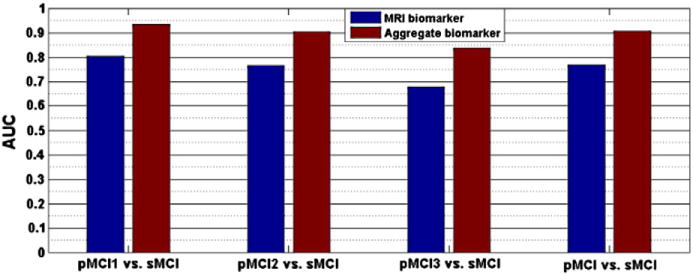
The AUC of MRI biomarker and aggregate biomarker for classification of different pMCI groups. pMCI1: if diagnosis was MCI at baseline but converted to AD within the first 12 months, pMCI2: if diagnosis was MCI at baseline and conversion to AD occurred within the 2nd year of follow-up (24 months), pMCI3: if diagnosis was MCI at baseline and conversion to AD was reported at 36 months follow-up.

Random forests can (without too much extra computational burden) produce of an estimate of feature importance via out-of-bag error estimate (Breiman, 2001; Liaw and Wiener, 2002). Fig. 9 shows the importance of each feature of the aggregate biomarker calculated by the RF classifier. The MRI feature was the combined feature generated by LDS classifier as described in the MRI biomarker section. According to Fig. 9, the MRI biomarker and RAVLT were the most important features followed by ADAS-cog total, FAQ, ADAS-cog total Mod, age, CDR-SB, and MMSE. We computed AUCs for each feature, considered one-by-one, using 10-fold CV. AUCs for MRI, RAVLT, ADAS-cog scores and FAQ were high while age, CDR-SB and MMSE were less significant.

Fig. 9.

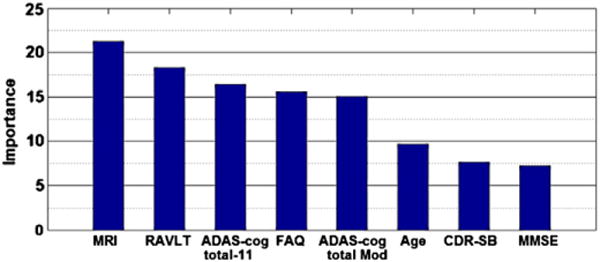
The importance of MRI, age and cognitive measurements calculated by RF classifier. ADAS-cog total 11 and ADAS-cog total Mod are weighted averages of 13 ADAS subscores, ADAS-cog subscore Q4 (delayed word recall) and Q14 (number cancelation) are not included in the ADAS-cog total 11. RAVLT is RAVLT-immediate that is sum score for 5 learning trials. The AUC of each individual feature was calculated using RF except for MRI that LDS was used. MRI: 0.7661, RAVLT: 0.7172, ADAS-cog total-11: 0.7185, FAQ: 0.7290, ADAS-cog total Mod: 0.6554, age: 0.5573, CDR-SB: 0.6789, MMSE: 0.6154.

The survival curve for the aggregate biomarker is shown in Fig. 8. According to Fig. 8 subjects in the first quartile have the lowest risk for conversion to AD and subjects in the last quartile have the highest risk. Table 5 shows the hazard ratios for the continuous predictor and for different quartiles compared to the first quartile. These are shown for the aggregate biomarker, the MRI biomarker and the RF trained with age and cognitive measures. High biomarker values were associated with the elevated risk for Alzheimer’s conversion (p < 0.001 for all three biomarkers). The aggregate biomarker showed over 10 times higher risk of conversion to AD for the subjects in the last quartile as compared to the subjects in the first quartile while for the MRI biomarker and the RF with age and cognitive measures (without MRI) this risk was 3.5 and 5.83 times higher, respectively.

Fig. 8.

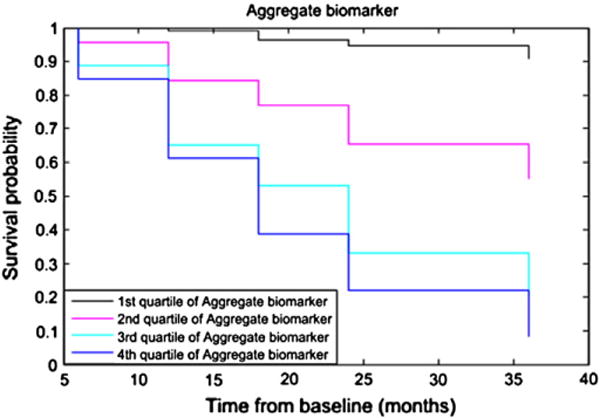
Kaplan–Meier survival curve for aggregate biomarker by splitting the predictor into quartiles. The follow-up period is truncated at 36 months.

Table 5.

Hazard rates (HR) of MCI to AD conversion for aggregate biomarker, MRI biomarker and RF with only age and cognitive measures (all methods adjusted for age and gender). Note that the continuous Hazard rate of MRI biomarker is not comparable to other biomarkers because it results from a different classifier (LDS vs. RF) with a different output (Sections MRI biomarker and Aggregate biomarker) and one-unit change has a different meaning.

	Aggregate biomarker			MRI biomarker			RF with age & CM
	HR	95%CI	p	HR	95% CI	p	HR	95% CI	p
Continuous	24.63	12.2–49.9	<0.001	2.48	1.9–3.3	<0.001	19.85	10.1–39.1	<0.001
1st vs 2nd quartile	5.14			2.84			2.64
1st vs 3rd quartile	9.16			2.72			5.04
1st vs 4th quartile	10.60			3.52			5.83

Comparisons to other methods

Cuingnet et al. (2011) tested ten different methods for classification of pMCI and sMCI subjects. Only four of these methods, listed in Table 6 using the naming of Cuingnet et al. (2011), performed better than the random classifier for the task. However, none of them obtained significantly better results than the random classifier, according to McNemar test. In order to compare the performance of our biomarkers with the work presented by Cuingnet et al. (2011) we performed the experiments using training and testing set used on their manuscript. The Supplementary Tables S7 and S8 explain the differences between ours and Cuingnet’s labeling of the subjects. With aggregate biomarker, one subject was excluded from the training set and two subjects from the testing set in sMCI groups due to missing cognitive measurements. The results are reported in Table 6. The McNemar’s chi square tests with significance level 0.05 were performed to compare the performance of each method with random classifier, as it was done in Cuingnet et al. (2011). We also list the results of Wolz et al. (2011) with the dataset used in Cuingnet et al. (2011) in Table 6. According to McNemar tests, both MRI and aggregate biomarkers performed significantly better than random classifier for this data. Also, with this dataset, the aggregate biomarker provided better AUC than the MRI biomarker. Interestingly, the margin of difference between the AUCs of the two biomarkers was smaller than with our labeling. This is probably caused by the difference in the labeling of subjects detailed in Supplementary Tables S7 and S8.

Table 6.

The performance metrics in the ADNI data used by Cuingnet et al. (2011). Except for MRI and aggregate biomarker, SEN, SPE values and McNemar test p-scores are extracted from Cuingnet et al. (2011) and Wolz et al. (2011). McNemar test p-value is not available for Wolz et al. (2011). Cuingnet et al. and Wolz et al. (2011) did not provide AUCs.

Method	SEN	SPE	AUC	McNemar test
MRI biomarker	64%	72%	75%	p = 0.0304
Aggregate biomarker	40%	94%	81%	p = 0.0013
Cuingnet et al. (2011) Voxel-STAND	57%	78%	–	p = 0.4
Cuingnet et al. (2011) Voxel-COMPARE	62%	67%	–	p = 1.0
Cuingnet et al. (2011) Hippo-Volume	62%	69%	–	p = 0.885
Cuingnet et al. (2011) thickness direct	32%	91%	–	p = 0.24
Wolz et al. (2011) (all)	69%	54%	–	–

Discussion

For the early identification of MCI subjects who are in risk of converting to AD, we developed a new method by applying advanced machine learning algorithms for combining MRI data with standard cognitive test results. First, we presented a new biomarker utilizing only MRI data that was based on a semi-supervised learning approach termed low density separation (LDS). The use of LDS in place of more typical supervised learning approaches based on support vector machines was shown to provide advantages as demonstrated by significantly increased cross-validated AUC scores. Second, we presented a new method for combining MRI-biomarker with age and cognitive measurements. This method combines the score provided by the MRI-biomarker and applies it as a feature for the learning algorithm (RF in this case). This aggregate biomarker provided a cross-validated AUC score of 0.9020 averaged across 100 different cross-validation runs. Since the cross-validation was properly nested, i.e., the testing data was not used for feature nor parameter selection, this AUC can be seen as promising for the early prediction of AD conversion.

The main novelties of the MRI-biomarker were 1) feature selection using only the data from AD and NC subjects without using any data from MCI subjects, thus reserving all the data about MCI subjects for learning the classifier, and 2) removing age-related effects from MRI data by using only data from healthy controls. The feature selection in this way can be seen as a mid-way between whole-brain, voxel-based MCI-to-AD conversion prediction approaches (as in Gaser et al., 2013) and approaches that use the volumes of pre-defined regions of interest (ROIs) (as in Ye et al., 2012) as MRI features. For the feature selection, we applied elastic-net RLR by selecting all the features that had a non-zero coefficient value along the regularization path up to a point which may be considered to provide minimal applicable amount of regularization. This allowed us to detect all the voxels which may be thought to provide relevant information for the classification task with concrete evidence that they indeed are useful for the discrimination. The regularized logistic regression was chosen as a model selection method because it has been widely used in multi-voxel pattern analyses of functional neuroimaging data as well as MRI based AD classification approaches and shown to outperform many other feature selection methods (Huttunen et al., 2012, 2013; Ryali et al., 2010; Ye et al., 2012; Casanova et al., 2011a,b; Janoušová et al., 2012). According to the results presented here (see Table 3), elastic-net RLR was able to select relevant voxels corresponding to AD in the high dimensional MRI data. We note that the number of selected voxels is not sufficient to fully capture the AD atrophy. The elastic net succeeded in this task better than the tested competing methods and provides a voxel set that, although being sparse, was well distributed all over the brain. If our aim would be to capture the full extent of atrophy in AD, a more specialized feature selection method would probably be more adequate (Fan et al., 2007; Cuingnet et al., 2013; Grosenick et al., 2013; Michel et al., 2011).

As normal aging and AD have similar effects on certain brain regions (Desikan et al., 2008; Dukart et al., 2011), we estimated the effects of normal aging on the MRI based on the data of healthy controls in a voxel-wise manner and then removed it from MRI data of MCI subjects before training the classifier. Our results indicated that removing age-related effects from MRI could improve significantly the prediction of AD, especially young pMCI subjects as well as old sMCI subjects were classified more accurately after the age removal. We hypothesize that this is because the AD related atrophy in young pMCI was mixed to the normal age related atrophy. Moreover, due to misidentifying age-related atrophy as AD related atrophy in old sMCI subjects, these subjects could be misdiagnosed as pMCI.

We constructed the aggregate biomarker by a specific ensemble learning method. We first derived the MRI biomarker by using LDS and then added the output of the LDS classifier as a feature together with the age and cognitive measures for RF, which acts as a classifier combiner. This aggregate biomarker was shown to outperform data concatenation with either LDS or RF as a learning algorithm. Moreover, the data concatenation scheme with RF outperformed the MRI biomarker and the data concatenation scheme with LDS. In addition to demonstrating the utility of combining cognitive measurements with MRI, these results suggest that different classifiers were adequate for the different stages of the biomarker design method. LDS performed well with close-to-continuous data (such as MRI) but failed when a part of the data was discrete. Instead, RF was more immune to the data type because it is able to handle discrete data and for continuous data type it applies an efficient discretization algorithm before the learning step. The difficulty of LDS to adapt to discrete features is not surprising because LDS in our implementation applied the Euclidean distance in constructing the graph-based kernel (see Appendix A) that is sub-optimal for discrete features. Recently, Wang et al. (2013), Hinrichs et al. (2011) and Zhang et al. (2011) considered multiple kernel learning algorithms for combining MRI, PET and CSF biomarkers for AD vs. NC and NC vs. MCI classification and showed that the combination of multiple data sources improves the classification performance. All data in these works is close-to-continuous and all the data sources have multiple features. Instead, in our case, only MRI has multiple features and cognitive measurements provide a single feature as we rely on the composite cognitive scores with standard weightings. Interestingly, Zhang et al. (2011) compared the performance of their multiple kernel learning to a simple classifier ensemble (majority vote between three SVMs trained with data from three different modalities, MRI, PET, and CSF), and obtained nearly as good classification accuracy with the classifier ensemble (75.6% for NC vs. MCI) as with the multiple kernel learning (76.4% for NC vs. MCI).

Compared to several previous studies (listed in Table 7) using ADNI database, our aggregate biomarker seems promising with an AUC of 0.9020, ACC of 0.8172, SEN of 0.8665 and SPE of 0.7364, on 164 pMCI and 100 sMCI subjects. To the best of our knowledge, the study by Ye et al. (2012) reported a highest achieved performance (AUC of 0.8587) to date for predicting AD in MCI patients in a relatively large data samples (319 labeled MCI subjects).

The comparison of different methods for MCI-to-AD conversion prediction is hampered by the fact that the nearly all works use a different classification of the subjects into stable and progressive MCI. For example, Wolz et al. (2011) used a simple criterion for labeling where a subject who had not converted to AD before July 2011 was labeled as stable MCI. This labeling provides a label for every MCI subject, but, on the other hand, leads to very heterogeneous stable MCI group that contains subjects with progressive MCI (Runtti et al., 2014) and is not sensible in our semi-supervised learning setup. Our pMCI group is almost the same as in Eskildsen et al. (2013) (156 subjects of 164 are common), but using more recent conversion information, we found that 41 subjects labeled as stable MCI by Eskildsen et al. (2013) had converted to AD or the diagnosis had changed from MCI to NC and we labeled them as uMCI. Finally, the 3-year cut-off period used here is somewhat arbitrary and was decided based on the length of follow-up for the original ADNI-1 project while AD-pathologies might be detectable in MRI even earlier than 3 years before clinical diagnosis (Adaszewski et al., 2013) and setting a fixed cut-off period is difficult due to non-dichotomous nature of the problem, partly caused by the fact that the pMCI group is composed of subjects who convert to AD in different time spans from the baseline. Partial remedies for the problem include the use of more homogeneous groups for the classifier evaluation as we have done in Fig. 7 (following Eskildsen et al. (2013)) and the use of statistical methods from the survival analysis to evaluate AD-prediction biomarkers as we have done in Fig. 8 and Table 5. Survival analysis has been used to evaluate MCI-to-AD conversion prediction previously in McEvoy et al. (2011), Gaser et al. (2013), and Da et al. (2014). Specifically, McEvoy et al. (2011) and Da et al. (2014) build an MRI-based MCI-to-AD conversion prediction biomarkers based on data from AD and NC subjects and compare the biomarker magnitudes in MCI subjects to their time to conversion to AD using either Kaplan–Meier curves and/or Cox hazard models. As Da et al. (2014) noted the results of survival analyses cannot be directly compared to the results of dichotomous classification into pMCI and sMCI groups, but are a complementary approach. As in previous studies (McEvoy et al., 2011; Gaser et al., 2013; Da et al., 2014), we showed that the elevated biomarker values are associated with the higher risk of converting to AD.

An important characteristic of the present study was the use of a semi-supervised classification method for the AD conversion prediction in MCI subjects. The semi-supervised method (LDS) was shown to outperform its counterpart supervised method (SVM) in the design of MRI biomarker. We also found that adding data about uMCI subjects as unlabeled data in the LDS learning procedure improved the classification performance slightly but not enough to reach the statistical significance. This is probably due to a relatively small number of uMCI subjects. Previously, Filipovych and Davatzikos (2011) have found that even a small number of unlabeled data improved the performance of TSVM in AD versus NC classification when the number of labeled data was very small (10 or 20 samples). However, AD vs. NC classification is an easier problem than sMCI vs. pMCI classification (Cuingnet et al., 2011), especially if the number of labeled training data is small (Filipovych and Davatzikos, 2011). Generally, unlabeled data improves the classification performance when the assumed model is correct (Zhang and Oles, 2000) and the amount of improvement depends strongly on the number of labeled data and the problem complexity (Cohen et al., 2002). In our recent conference paper (Moradi et al., 2014) we provided evidence that even a small number of unlabeled data aids the MRI-based AD conversion prediction, but the size of improvement decreases when the number of labeled data increases.

In summary, we developed an approach to predict conversion to AD within MCI patients by combining machine learning approaches including feature selection for selecting most relevant voxels corresponding to AD within MRI data, regression for determining normal aging effects within the brain and supervised and semi-supervised classification methods for discriminating between pMCI vs. sMCI subjects. Our aggregate biomarker achieved a very high predictive performance, with a cross-validated AUC of 0.9020. Our experimental results demonstrated also the important role of MRI in MCI-to-AD conversion prediction. However, the integration of MRI data with age and cognitive measurements improved significantly the AD conversion prediction in MCI patients.

Appendix A

A.1. Low density separation (LDS) (Chapelle and Zien, 2005)

The LDS algorithm is implemented in two steps:

1. Training a graph-distance derived kernel.

2. Training TSVM by gradient descent with the graph-distance derived kernel.

A.2. Standard support vector machines and transductive support vector machines

Denote a training data point by x_n and associated class label by y_n ∈ {−1, 1}. The task is to learn a linear classifier (possibly in a high-dimensional kernel space) described by the weight vector w perpendicular to hyperplane separating the two classes and the bias b so that the sign of the discriminant function d(x) = w^Tx + b determines the class label for data point x. The standard SVM aims at maximizing the margin around decision boundary by solving the following optimization problem

$$\begin{array}{l}\underset{\mathit{w},\mathit{\xi },b}{\text{min}}\left\{\frac{1}{2}{\Vert \mathit{w}\Vert }^2+C{\displaystyle \sum _{n=1}^N{\mathbf{\xi }}_n}\right\}\\ s.t.y_n\left(\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right)+{\mathbf{\xi }}_n\ge 1,n=1,\dots ,N\end{array}$$ (1)

where N is the number of labeled data points. This is the soft-margin SVM allowing some degree of misclassification (in the training set) to prevent overfitting by introducing positive slack variables ξ_n, n = 1,…, N which measure the degree of misclassification of data x_n. The idea with adding the slack variable is to maximize the margin while finding a tradeoff between a large margin and a small error penalty. Here, C is the penalty parameter that controls the tradeoff between a large margin and a small error penalty.

In the transductive SVM, the idea is to maximize the margin around decision boundary by using labeled data while simultaneously driving the hyperplane as far away as possible from unlabeled points. Therefore, the optimization problem in TSVM becomes

$$\begin{array}{l}\underset{\mathit{w},\mathbf{\xi },b}{\text{min}}\left\{\frac{1}{2}{\Vert \mathit{w}\Vert }^2+C{\displaystyle \sum _{n=1}^N{\mathbf{\xi }}_n+C^{\ast }{\displaystyle \sum _{n=N+1}^{N+M}{\mathbf{\xi }}_n}}\right\}\\ s.t.y_n\left(\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right)+{\mathbf{\xi }}_n\ge 1,n=1,\dots N\\ \left|\mathit{w}·{}_{\mathit{n}}-b\right|+{\mathbf{\xi }}_n\ge 1,n=N+1,\dots ,M\end{array}$$ (2)

where N is the number of labeled data samples and M is the number of unlabeled data samples, assuming that samples 1,…, N are labeled and N + 1,…, M are unlabeled. This can be rewritten as minimizing

$$\frac{1}{2}{\mathit{w}}^2+C{\displaystyle \sum _{n=1}^{N}L\left(y_n\left(\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right)\right)}+C^{\ast }{\displaystyle \sum _{n+N+1}^{N+M}L\left|\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right|}$$ (3)

where the function L(t) = max(0, 1 − t) is the classical Hinge Loss. The implementation of TSVM was introduced first by Joachims (1999), which assigned a Hinge Loss function L(t) on the labeled samples and Symmetric Hinge Loss function L(|t|) on the unlabeled samples.

However, because the cost function defined in Eq. (3) is not differentiable, it is replaced by

$$\frac{1}{2}{\mathit{w}}^2+C{\displaystyle \sum _{n=1}^N{L}^2\left(y_n\left(\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right)\right)}+C^{\ast }{\displaystyle \sum _{n=N+1}^{N+M}{L}^{\ast }\left(\left|\mathit{w}·{\mathit{x}}_{\mathit{n}}-b\right|\right)}.$$ (4)

Here the function L^* = exp(−3t²) is the Symmetric Sigmoid function, a smooth version of the Hinge Loss function. In LDS, Eq. (4) is minimized by performing the standard conjugate gradient descent on the primal formulation for optimization.

A.3. Graph based similarities

Graph-based methods for semi-supervised learning use a graph representation G = (V, E) of the data. The graph consists of a node for each labeled and unlabeled sample V = {x_i: i = 1, …, N + M} and edges placed between nodes E = {(i, j)}, which model the similarities of the samples. The node set V is divided into labeled points V_l of size N and unlabeled points V_u of size M.

Here, the graph is constructed by using pairwise similarities between samples by squeezing the distances in high density regions. The cluster assumption states that points are probably in the same class if they are connected by a path through high density regions. As the idea here is to construct a graph which captures the true distribution of the observations, edges must be weighted based on some distance measure such as the Euclidean distance denoted here by d(i,j) := ║x_i - x_j║ However, in many problems the Euclidean distance cannot capture the true distribution in clustering (Lan et al., 2011). Therefore, a nonlinear weight is assigned to each edge e_ij = exp(ρd(i, j)) − 1 where ρ is the stretching factor to be selected by cross-validation. After creating the 10-nearest neighbors graph with weights e_ij, the distances between two points are calculated as a distance along shortest paths between the points based on Euclidean distance from all labeled and unlabeled data points. The distance matrix D^ρ according to the density distance measure is calculated from all labeled points to all data (labeled and unlabeled points) according to

$${\mathit{D}}_{i,j}^{\rho }=\frac{1}{{\rho }^2}\log {\left(1+\underset{p\in P_{i,j}}{\text{min}}{\displaystyle \sum _{k=1}^{\left|p\right|-1}\left(e_{p\left(k\right)p\left(k+1\right)}\right)}\right)}^2$$ (5)

where ρ is the stretching factor and P_i,_j is the set of all paths (p) connecting x_i and x_j. As described in Chapelle and Zien (2005), p ∈ V^l is a path of length l := |p| on G = (V, E), in case (p(k), p(k + 1)) ∈ E for 1 ≤ k < |p|, which connects the nodes p₁ and p_|p|. The kernel defined by D^ρ is not necessarily positive-definite, and, therefore, before applying SVM, we perform the eigenanalysis of D^ρ and retain only eigenvectors corresponding to the highest (and positive) eigenvalues. In more detail, let λ₁, λ₂, …, λ_N be the decreasing eigenvalues of H^ND^ρH^{(N + M)}, where H^p is the p × p centering matrix and let the U = (u_ik) be the matrix of the corresponding eigenvectors. Then, kernelized representation of x is

$${\mathit{x}}^{\ast }=\phi \left(\mathit{x}\right):x_k^{\ast }=u_{\mathit{ik}}\sqrt{{\mathrm{\lambda }}_k}\text{for}\mathrm{k}=1,\dots \mathrm{p},$$

where p is selected as described in Chapelle and Zien (2005).

Appendix B

Denote the data from the pre-processed MRI of subject i (i = 1, …, N) by x_i = [x_i1, …, x_iM]^T, where M is the number of brain voxels, let l_i ∈ {AD, MCI, NC } be the diagnosis of the subject i, and a_i the age of the subject i.

B.1. Age removal

Denote the vector of intensity values of the NC (MCI) subjects at the voxel j by ${\mathit{x}}_j^{\mathit{NC}}\left({\mathit{x}}_j^{\mathit{MCI}}\right)$ and the vector of ages of the NC (MCI) subjects by a a^NC (a^MCI).

1. Estimate the effect of age to data at each voxel separately by a fitting a linear model ${\mathit{x}}_j^{\mathit{NC}}={\alpha }_j{\mathit{a}}^{\mathit{NC}}+{\alpha }_{j0}$. Solve this model in the least squares sense resulting in estimates ${\widehat{\alpha }}_j$, ${\widehat{\alpha }}_{j0}$.

2. Apply the model from the Step 1 to remove the age effects of each voxel separately from MCI data: ${\mathit{x}}_j^{\mathit{MCIar}}={\mathit{x}}_j^{\mathit{MCI}}-{\widehat{\alpha }}_j{\mathit{a}}^{\mathit{MCI}}+{\widehat{\alpha }}_{j0}$.

B.2. Feature selection

The goal of this feature selection is to select all the features (voxels) among M that are useful in linear separation of the AD class from the NC class. The feature selection consists of the following steps:

1. Train a sparse logistic regression classifier using elastic-net penalty, i.e., a combination of l₁ and l₂ norms of the coefficient vector β, separating the class AD from the class NC for various λ_t, t = 1, …, 100 using the full data (all MRI voxels), by maximizing the elastic-net penalized log-likelihood

   $${\displaystyle \sum _{l_i=AD}\log LC\left({\beta }_0+\beta {\mathit{x}}_i\right)}+{\displaystyle \sum _{l_i=AC}\log \left(1-LC\left({\beta }_0+\beta {\mathit{x}}_i\right)\right)}-{\mathrm{\lambda }}_t\left(\alpha {\Vert \beta \Vert }_1+\left(1-\alpha \right){\Vert \beta \Vert }_2^2\right)$$ (7)

   where y_i = 1 if l_i = AD and y_i = 0 if l_i = NC and LC(z) = 1/(1 + exp(z)) is the logistic function and we set α = 0.5. Note that the algorithm used here estimates the classifiers along the whole regularization path λ_t, t = 1, …, 100 at once.

2. To select the best among λ_t, run 100 10-fold CV runs to yield ${\lambda }_{\mathit{CV}}^{\left(i\right)}$ in each run that minimize the CV error and select the smallest of these as λ*.

3. Select all the features that have a non-zero coefficient value β_j(λ) (in the trained logistic regression model) for any λ ≥ λ* the along the regularization path up to λ*. This ensures that we select all the features (voxels) that can be considered to be useful for linearly separating the AD and NC classes.

Appendix C. Supplementary data

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2014.10.002.