Quantifying effects of biodiversity on ecosystem functioning across times and places

Abstract

Biodiversity loss decreases ecosystem functioning at the local scales at which species interact, but it remains unclear how biodiversity loss affects ecosystem functioning at the larger scales of space and time that are most relevant to biodiversity conservation and policy. Theory predicts that additional insurance effects of biodiversity on ecosystem functioning could emerge across time and space if species respond asynchronously to environmental variation and if species become increasingly dominant when and where they are most productive. Even if only a few dominant species maintain ecosystem functioning within a particular time and place, ecosystem functioning may be enhanced by many different species across many times and places (β-diversity). Here, we develop and apply a new approach to estimate these previously unquantified insurance effects of biodiversity on ecosystem functioning that arise due to species turnover across times and places. In a long-term (18-year) grassland plant diversity experiment, we find that total insurance effects are positive in sign and substantial in magnitude, amounting to 19% of the net biodiversity effect, mostly due to temporal insurance effects. Species loss can therefore reduce ecosystem functioning both locally and by eliminating species that would otherwise enhance ecosystem functioning across temporally fluctuating and spatially heterogeneous environments.

Introduction

There remains a mismatch between the large scales of space and time at which the planet is losing species (Pimm et al. 2014; Ceballos et al. 2017), and the smaller scales at which biodiversity experiments have found that species loss decreases ecosystem functioning (Cardinale et al. 2011; Tilman et al. 2014; O’Connor et al. 2017). Furthermore, there is now some debate regarding whether local biodiversity has been systematically lost (Vellend et al. 2013; Dornelas et al. 2014; Murphy & Romanuk 2014; Newbold et al. 2015; Gonzalez et al. 2016), prompting questions about whether global extinctions are altering ecosystem functioning (Vellend et al. 2013). This mismatch in the scales at which biodiversity loss and its consequences for ecosystem functioning are best understood creates challenges for determining the extent to which human-driven biodiversity loss will influence nature’s benefits to people (Isbell et al. 2017). Reconciling this scale mismatch will require a greater understanding of how changes in biodiversity influence ecosystem functioning at large scales, across many times and places in temporally fluctuating and spatially heterogeneous environments.

Within a particular time and place, at the local scales over which species interact, increasing the number of species can increase ecosystem functioning because of local complementarity effects (which include niche partitioning and facilitation) and local selection effects (in which the most productive species in monoculture overyield most in species mixtures) (Tilman et al. 1997; Loreau & Hector 2001) (see Box 1 for definitions). The relative magnitudes of these effects have important implications for biodiversity conservation because they imply that different numbers of species are needed to maintain high levels of ecosystem functioning. Complementarity effects can be large when many species coexist and contribute substantially to ecosystem functioning, whereas selection effects are largest when the single most productive species in monoculture outcompetes all others in mixture (Tilman et al. 1997; Loreau & Hector 2001; Turnbull et al. 2016).

Box 1. Relationship to previous approaches for quantifying local biodiversity effects.

Our approach builds on previous studies of overyielding and previous additive partitions of the net biodiversity effect. A mixture overyields (or underyields) when it exhibits greater (or lesser) biomass production than the average of its constituent species in monocultures (Trenbath 1974; Harper 1977; Vandermeer 1981; Loreau 2004; Schmid et al. 2008). Mixture overyielding is common (O’Connor et al. 2017) and the conditions for mixture overyielding are equivalent to those for stable coexistence in the Lotka-Volterra competition model (Vandermeer 1981; Loreau 2004). An individual species overyields (or underyields) when it produces more (or less) biomass in mixture than would be expected based on its monoculture biomass production and its proportion in mixture. Overyielding has been quantified based on species’ initial, previous, or current proportions in mixture (Harper 1977). The net biodiversity effect (Loreau & Hector 2001) is a measure of mixture yielding behaviour that is positive when a mixture overyields and negative when it underyields.

The first additive partition of the net biodiversity effect was developed to address an early debate regarding whether positive biodiversity effects were mainly due to the sampling and dominance of a few highly productive species or instead to niche partitioning and facilitation among many species (Loreau & Hector 2001). It termed the former type of biodiversity effects ‘selection effects’ and the latter ‘complementarity effects’ and provided a way to quantify the relative magnitudes of each (Loreau & Hector 2001). Subsequent empirical results have shown that both types of biodiversity effects can be positive in sign and substantial in magnitude (Cardinale et al. 2007), though several of the longest-running experiments have found that complementarity effects become increasingly positive while selection effects become increasingly negative over time (Fargione et al. 2007; Marquard et al. 2009; van Ruijven & Berendse 2009; Reich et al. 2012). This implies that, in many long-term studies, biodiversity loss decreases ecosystem productivity mostly by reducing niche partitioning and/or facilitation.

A second additive partition was later developed to extract an additional component of complementarity from the selection effect (Fox 2005). As originally quantified, the selection effect did not necessarily indicate natural selection for highly productive species. Although natural selection operates as a zero-sum game, the selection effect did not. Specifically, overyielding by one species did not require underyielding by another species. Instead, each species could overyield or underyield to any extent. The second partition split the selection effect into two components. First, it isolated a ‘dominance effect’ that operated as a zero-sum game by dividing each species’ relative yield, which are ratios of mixture to monoculture yields, by the relative yield total, which is the sum of relative yields across all species in the mixture. Thus, an increase in a particular species’ contribution to the relative yield total necessarily came at the expense of another species’ contribution to it. By quantifying the covariance between monoculture yield and the proportion of mixture relative yield, the dominance effect quantifies the extent to which species that are highly productive in monoculture exhibit overyielding at the expense of other species underyielding in mixtures. The second, residual part of the selection effect was termed ‘trait-dependent complementarity’ and is less relevant to the present discussion.

Our partition builds on this progress made by previous partitions and provides two novel extensions. First, our new partition further isolates a term directly analogous to natural selection. Our total insurance effect term is equivalent to Price’s (1970, 1972) selection effect in evolutionary genetics. Note that Loreau & Hector’s (2001) selection effect and Fox’s (2005) dominance effect were both inspired by, but not equivalent to, Price’s selection effect. Both these previous partitions considered the covariance between monoculture yields and species’ overyielding or underyielding behaviour, rather than species’ dominance, in mixtures. Species can overyield by having high yields in mixture or by having low yields in monoculture. Thus, species can overyield without dominating mixtures. In contrast, our new partition more fully isolates the covariance between monoculture yields and mixture dominance than previous partitions by including a covariance term, the total insurance effect, which quantifies the covariance between monoculture yields and a variable that depends on mixture relative abundance or biomass and that does not depend on monoculture yields. Second, and most importantly, our new partition provides the first approach for quantifying additional effects of biodiversity on ecosystem functioning that arise across multiple times and places, namely temporal and spatial insurance effects.

Even when local biodiversity effects are explained by selection for a few highly productive and dominant species, many species may still be needed to maintain ecosystem functioning at larger scales if the identities of the most productive (high monoculture yield) and dominant (high relative abundance/biomass) species change across time and space. Indeed, theory predicts that positive insurance effects of biodiversity on average levels of ecosystem functioning can arise at larger scales in temporally fluctuating (Yachi & Loreau 1999) and spatially heterogeneous (Loreau et al. 2003) environments if species respond asynchronously to environmental variation and species become increasingly dominant when and where they are most productive. Although the stabilising properties of insurance effects (i.e. reduced variance in ecosystem functioning) have been further investigated (e.g. de Mazancourt et al. 2013), these unique performance-enhancing properties of insurance effects (i.e. increased average levels of ecosystem functioning) remain understudied and have yet to be quantified. Ecosystem functioning may therefore depend on both local diversity (α-diversity), if there are positive local complementarity effects, and turnover in species composition and dominance across times and places (β-diversity), if there are positive insurance effects of biodiversity on ecosystem functioning.

Although the magnitudes of temporal and spatial insurance effects of biodiversity on ecosystem functioning have yet to be quantified, empirical results from several previous studies are consistent with theoretical predictions for positive, rather than neutral or negative, insurance effects. For example, in local competition studies, dominant species tend to be more productive in monoculture than the species they outcompete (Gaudet & Keddy 1988). Furthermore, different species can promote ecosystem functioning during different years and at different places (Isbell et al. 2011); and turnover in species presence or dominance across years (Allan et al. 2011) or places (Mori et al. 2016; Hautier et al. 2018) can be associated with high levels of ecosystem functioning.

Alternatively, such turnover in species composition or dominance may have no effect on ecosystem functioning, or even decrease it. Average levels of ecosystem functioning might not be systematically affected by changes from one dominant species to another in cases where dominance is uncoupled from species’ performance in monoculture, such as if species fluctuations are purely stochastic (Yachi & Loreau 1999) or if species (MacArthur & Wilson 1967) or individuals (Hubbell 2001) are equivalent to one another, or for ecosystem functions that are not associated with yield or dominance (Hector & Bagchi 2007). If dominant species instead tend to be systematically less productive than rare species, such as if environmental conditions shift and species that become dominant are less productive than those they replace, then such temporal turnover in species composition or dominance could decrease ecosystem productivity, leading to negative insurance effects of biodiversity on mean levels of ecosystem functioning at large scales of time or space. Determining whether few or many species are needed to maintain ecosystem functioning at large scales, across many times and places, will therefore require quantifying the direction and magnitude of insurance effects of biodiversity on mean levels of ecosystem functioning.

Here, we first show how complementarity effects and selection effects can shift in relative magnitudes when they are quantified either within each time and place or across multiple times and places. We then develop a new approach for quantifying insurance effects of biodiversity on ecosystem functioning that can arise across multiple times and places. For simplicity, we describe the new approach in terms of the monoculture and mixture yields of plant species; however, as with previous related approaches (Box 1), it could also be applied to any other species and to any other ecosystem functions that are measurable or estimable on a species-specific basis (see Discussion). Although the approach could be applied to data collected at any nested scales of time or space, the upper and lower bounds on the scales of interest will depend on the species under investigation. We define the local scale as the temporal duration and spatial extent of each individual time and place at which data have been collected. We assume measurements have been made at scales relevant to the organisms under investigation. For example, the local scale of interest may be much smaller for rapidly reproducing and small-bodied species, such as algae, than for longer lived and larger species, such as trees. Here, we define the larger scale as the total temporal duration and spatial extent observed across multiple (any number of) times and places. The number of times and places that would need to be considered to sufficiently understand or predict across the full range of temporal or spatial variation remains unclear (see Discussion). We then demonstrate the new approach for contrasting hypothetical cases to isolate and explain each type of biodiversity effect on ecosystem functioning. We then apply this new approach to experimental data to empirically determine the magnitudes of biodiversity effects that can emerge across years and between two contrasting environmental conditions (fertilised or not). Finally, we discuss challenges and opportunities for extending this approach to large scales in naturally assembled communities.

Scaling-Up Local Complementarity Effects and Selection Effects

To quantify effects of biodiversity on ecosystem functioning at larger scales (i.e. across many times and places), we begin by building on a previous additive partition of the local net biodiversity effect into its local complementarity effect and selection effect components (Boxes 1, 2). We find that local complementarity effects can become total selection effects at a larger scale, across times and places, or vice versa (Box 2). Therefore, the relative magnitudes of complementarity and selection effects can shift when means and covariances are quantified either at a local scale (i.e. across species within times and places) or at a larger scale (i.e. across species and across times and places). These shifts from complementarity to selection or vice versa are partly due to mathematical relationships between means and covariances that can result from data aggregation (E3 in Box 2), but, as we show in the following examples, can also result from biological processes, such as selection effects arising at local or larger scales.

Box 2. Scaling-up local biodiversity effects and quantifying insurance effects.

To quantify biodiversity effects at larger scales, across multiple times and places, we build on a previous additive partition of the local net biodiversity effect (NBE_α) into its local complementarity effect (CE_α) and selection effect (SE_α) components (Loreau & Hector 2001):

$$NB{E}_{\alpha }={\displaystyle {\sum }_i^N\Delta R{Y}_i{M}_i=N\overline{\Delta RY}\overline{M}+\mathit{\text{Ncov}}\left(\Delta R{Y}_i,M_i\right)}$$ (E1)

where i indexes one of N species in the community, $C{E}_{\alpha }=N\overline{\Delta RY}\overline{M}$ is the local complementarity effect, SE_α = Ncov(ΔRY_i, M_i) is the local selection effect, ΔRY_i = RY_O,i – RY_E,i and RY_O,i = Y_O,i/M_i and RY_O,i is the relative yield observed in mixture, Y_i and M_i are, respectively, the observed yield in mixture and monoculture, and RY_E,i is the expected relative yield (initial proportion) for species i, and the subscript α denotes that the biodiversity effect was calculated at the local scale, within times and places.

To quantify total complementarity and total selection effects across multiple times and places, equation E1 can be generalised as:

$$NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\Delta R{Y}_{ijk}{M}_{ijk}=\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}}\overline{\overline{\overline{M}}}+\mathit{\text{PTNcov}}\left(\Delta R{Y}_{ijk},M_{ijk}\right)}}$$ (E2)

where j indexes one of T times (e.g. years), k indexes one of P places, $\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}\overline{\overline{\overline{M}}}$ is the total complementarity effect (CE_γ), averaged across all species, times, and places, and PTNcov(ΔRY_ijk, M_ijk) is the total selection effect (SE_γ), quantified across all species, times and places, and the subscript γ denotes that the biodiversity effect is quantified at a scale that is larger (i.e. more times and/or places) than that at which local biodiversity effects were quantified. Note that the net biodiversity effect is equivalent regardless of whether it is quantified at local scales using E1 and then summed across times and places, or quantified at larger scales using E2: $NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}NB{E}_{\alpha }}}.$ In contrast, local complementarity effects and selection effects cannot simply be summed across all times and places to quantify their total effects because the sum of products does not necessarily equal the product of sums (means). Given Equations E1 and E2 above, and that $NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}NB{E}_{\alpha }}},$ it can be seen that $C{E}_{\gamma }+S{E}_{\gamma }=NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}NB{E}_{\alpha }}}={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}C{E}_{\alpha }+{\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}S{E}_{\alpha }}}}}.$ Therefore, the extent to which the sum of local complementarity effects deviates from the total complementarity effect is exactly counter-balanced by the extent to which the total selection effect deviates from the sum of local selection effects:

$$C{E}_{\gamma }-{\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}C{E}_{\alpha }}}={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^{T}S{E}_{\alpha }-S{E}_{\gamma }}}$$ (E3)

Consequently, the sum of local biodiversity effects will either underestimate total complementarity and overestimate total selection effects, or vice versa. See Table 1 for examples in which biodiversity effects are explained by complementarity effects at a local scale, but selection effects at a larger scale, or vice versa.

To quantify temporal and spatial insurance effects that emerge across times and places, we further partition the total selection effect. We begin by rewriting the change in relative yield as the difference between the observed and expected relative yield:

$$NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(R{Y}_{O,ijk}-R{Y}_{E,ijk}\right)M_{ijk}}}}$$ (E4)

and then partition this difference into the sum of two differences:

$$NB{E}_{\gamma }={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(R{Y}_{O,ijk}-p_{O,ijk}\right)M_{ijk}+\left(p_{O,ijk}-R{Y}_{E,ijk}\right)}{M}_{ijk}}}$$ (E5)

where p_O,ijk is the observed relative biomass of species i at time j and place k. We define RY_O,ijk – p_O,ijk = ΔRY_O,ijk as the change in observed relative yield, with the O subscript serving as a reminder that this difference is with respect to the observed, rather than expected, proportion and p_O,ijk – RY_E,ijk = Δp_ijk as the change in dominance for species i at time j and place k. These two sums of products can then be partitioned into their respective mean and covariance components as follows:

$$NB{E}_{\gamma }=\mathit{\text{PTN}}\overline{\overline{\overline{\Delta R{Y}_O}}}\overline{\overline{\overline{M}}}+\mathit{\text{PTNcov}}\left(\Delta R{Y}_{O,ijk},M_{ijk}\right)+\mathit{\text{PTN}}\overline{\overline{\overline{\Delta p}}}\overline{\overline{\overline{M}}}+\mathit{\text{PTNcov}}\left(\Delta p_{ijk},M_{ijk}\right)$$ (E6)

which, given that $\overline{\overline{\overline{\Delta p}}}=0,$ can be simplified to:

$$NB{E}_{\gamma }=\mathit{\text{PTN}}\overline{\overline{\overline{\Delta R{Y}_O}}}\overline{\overline{\overline{M}}}+\mathit{\text{PTNcov}}\left(\Delta R{Y}_{O,ijk},M_{ijk}\right)+\mathit{\text{PTNcov}}\left(\Delta p_{ijk},M_{ijk}\right)$$ (E7)

The first two terms on the RHS of Equation E7 appear similar to the total complementarity effects and total selection effects in Equation E2. In fact, $\overline{\overline{\overline{\Delta RY}}}=\overline{\overline{\overline{\Delta R{Y}_0}}},$ and thus the first terms on the RHS of Equations E2 and E7 are equivalent and can both be interpreted as the total complementarity effect (although ΔRY_ijk ≠ ΔRY_O,ijk). Given this, the second and third terms on the RHS of E7 sum to the total selection effect.

Next, to quantify temporal and spatial insurance effects, we further partition the second covariance term on the RHS of E7. We rewrite this covariance as a sum of cross products:

$$\mathit{\text{PTNcov}}\left(\Delta p_{ijk},M_{ijk}\right)={\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(\Delta p_{ijk}-\overline{\overline{\overline{\Delta p}}}\right)\left(M_{ijk}-\overline{\overline{\overline{M}}}\right)}}}$$ (E8)

and then use standard statistical methods to partition this sum of cross products into what would be analogous to main effect and interaction terms in an analysis of variance (note that the variance is simply the special case of the covariance where both terms are identical) as follows:

Source of covariance	Sum of cross products
Total	${\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(\Delta p_{ijk}-\overline{\overline{\overline{\Delta p}}}\right)}}}\left(M_{ijk}-\overline{\overline{\overline{M}}}\right)=$                    (E9)
Average selection effect	$PT{\displaystyle {\sum }_i^N\left(\overline{\overline{\Delta p_i}}-\overline{\overline{\overline{\Delta p}}}\right)}\left(\overline{\overline{M_i}}-\overline{\overline{\overline{M}}}\right)+$
Temporal insurance effect	$P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(\overline{\Delta p_{ij}}-\overline{\overline{\Delta p_i}}\right)}}\left(\overline{M_{ij}}-\overline{\overline{M_i}}\right)+$
Spatial insurance effect	$T{\displaystyle {\sum }_k^P{\displaystyle {\sum }_i^N\left(\overline{\Delta p_{ik}}-\overline{\overline{\Delta p_i}}\right)}}\left(\overline{M_{ik}}-\overline{\overline{M_i}}\right)+$
Spatiotemporal insurance effect	${\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\left(\Delta p_{ijk}-\overline{\Delta p_{ij}}-\overline{\Delta p_{ik}}+\overline{\overline{\Delta p_i}}+\overline{\overline{\overline{\Delta p}}}\right)}}}\left(M_{ijk}-\overline{M_{ij}}-\overline{M_{ik}}+\overline{\overline{M_i}}+\overline{\overline{\overline{M}}}\right)$

Local complementarity effects can become selection effects at larger scales

Positive net biodiversity effects can be explained by complementarity effects at local scales, but by selection effects at larger scales of space or time. For example, consider the case where two species have equivalent monoculture yields at both of two different places, but are more productive in monoculture at one place than at another, and overyield most where they are most productive. In this case (Table 1A), there is no selection effect if biodiversity effects are quantified at a local scale within places, because the equivalence of monoculture yields for both species precludes any covariation between their yields in monoculture and their overyielding or underyielding in mixture. In contrast, at a larger scale, across both places, there is a positive selection effect because species overyield most where they are also most productive in monoculture (Table 1A). Biologically, this positive net biodiversity effect can be interpreted as due to a local complementarity effect, or to a larger scale selection effect driven by species occupying places where they are most productive.

Local selection effects can become complementarity effects at larger scales

Alternatively, local selection effects can become complementarity effects at larger scales of space or time. For example, consider the case where, in monoculture, one species is more productive than another at both of two places, the most productive species overyields most at the more productive place, and the least productive species overyields most at the less productive place. In this case (Table 1B), there is no complementarity effect if biodiversity effects are quantified at a local scale, within places, because a small positive complementarity effect at one place is nullified by a small negative complementarity effect at the other place. In contrast, at a larger scale, across both places, the total selection effect becomes zero due to the fact that overyielding is greatest for the least productive species at the least productive place (i.e. for species one at place two in Table 1B). Biologically, the positive total complementarity effect can be interpreted as spatial niche partitioning at a larger scale, between sites, in which only the less productive species has a realised niche (i.e. positive mixture yield) that includes the unproductive environment (place two). In this example, a positive net biodiversity effect can be interpreted as due to a local selection effect or to a larger scale complementarity effect.

Quantifying Temporal and Spatial Insurance Effects

Next, we develop a new approach for quantifying several types of biodiversity effects on ecosystem functioning across multiple times and places, including previously unquantified insurance effects. To quantify temporal and spatial insurance effects, we further partition the total selection effect (Box 2). By splitting the total selection effect into two components (Equation E7 in Box 2), we gain a term that we call the total insurance effect, PTNcov(Δp_ijk, M_ijk), which quantifies the extent to which the most productive species in monocultures tend to dominate mixtures. This term is predicted by theory to be positive when the best competitor for a single limiting resource outcompetes all other species in a constant and homogeneous environment (Tilman et al. 1997) and in temporally fluctuating and spatially heterogeneous environments if species tend to dominate mixtures at the times (Yachi & Loreau 1999) or places (Loreau et al. 2003) when and where they are most productive in monoculture.

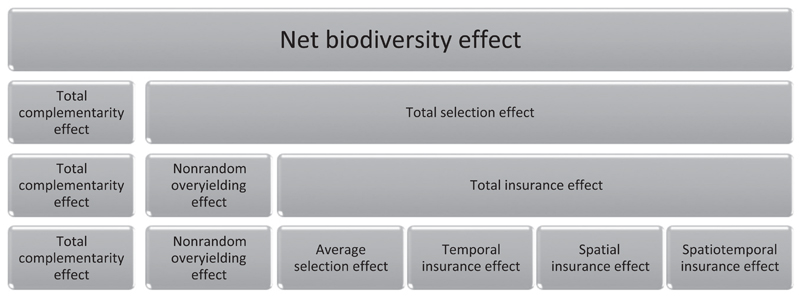
Our additive partition of the net biodiversity effect produces six types of biodiversity effects (Box 3; Fig. 1). The total complementarity effect has the same interpretation as previously given (Loreau & Hector 2001; Loreau et al. 2012) and quantifies the extent to which niche partitioning or facilitation outweigh chemical (e.g. plant allelopathy) or physical (e.g. animal fighting) interference competition. Note that the complementarity effect does not directly measure resource partitioning, but rather is a net measure of whether interspecific interactions are less detrimental or more favourable (i.e. weaker competition or stronger facilitation) than intraspecific interactions and includes other forms of niche partitioning, such as when interspecific apparent competition is weaker than intraspecific apparent competition due to specialised natural enemies (Loreau & Hector 2001; Loreau et al. 2012). The non-random overyielding effect quantifies the extent to which the most productive species in monoculture tend to overyield the most in mixtures; overyielding is measured against an expectation based on monoculture yield and observed, rather than initial, relative abundance in mixture (Box 1). The average selection effect quantifies the extent to which the species that are most productive in monoculture also tend to be the same species that are most dominant in mixtures, averaged across all times and places. The insurance effects quantify the extent to which each species dominates mixtures to a greater extent during the times and places in which it is most productive in monoculture. The spatiotemporal insurance effect quantifies non-additive temporal and spatial insurance effects, and will be positive or negative when temporal insurance effects are, respectively, stronger or weaker when multiple places are considered. Note that this decomposition follows the standard approach for partitioning main effects (temporal and spatial insurance effects) and their interaction (spatiotemporal insurance effect) for sums of squares in an analysis of variance.

Box 3. A spatial and temporal partition of the net biodiversity effect.

To present a full spatial and temporal partition of the net biodiversity effect, we consolidate results from E7 and E9 (Box 2), simplify $\overline{\overline{\overline{\Delta p}}}=0$, define nonlinear terms $\Delta p_n=\Delta p_{ijk}-\overline{\Delta p_{ij}}-\overline{\Delta p_{ik}}+\overline{\overline{\Delta p_i}}$ and $M_n=M_{ijk}-\overline{M_{ij}}-\overline{M_{ik}}+\overline{\overline{M_i}}+\overline{\overline{\overline{M}}},$ and rewrite sums of cross products as covariances to obtain the following:

Biodiversity effect	Abbreviation
Net biodiversity	NBE	${\displaystyle {\sum }_k^P{\displaystyle {\sum }_j^T{\displaystyle {\sum }_i^N\Delta R{Y}_{ijk}{M}_{ijk}}=}}$                              (E10)
Total complementarity	TC	$\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}\overline{\overline{\overline{M}}}+$
Non-random overyielding	NO	$\mathit{\text{PTNcov}}\left(\Delta R{Y}_{0,ijk},M_{ijk}\right)+$
Average selection	AS	$\mathit{\text{PTNcov}}\left(\overline{\overline{\Delta p_i}},\overline{\overline{M_i}}\right)+$
Temporal insurance	TI	$\mathit{\text{PTNcov}}\left(\overline{\Delta p_{ij}},\overline{M_{ij}}\right)+$
Spatial insurance	SI	$\mathit{\text{PTNcov}}\left(\overline{\Delta p_{ik}},\overline{M_{ik}}\right)+$
Spatiotemporal insurance	ST	$\mathit{\text{PTNcov}}\left(\Delta p_n,M_n\right)$

Each of these terms could be positive or negative. A description of each term is provided in the main text. Figure 1 shows the nested relationship between biodiversity effects. Table 2 shows examples where each term is isolated in turn.

Figure 1.

The net biodiversity effect can be partitioned into component types of biodiversity effects on ecosystem functioning. The sum of all biodiversity effects shown in each row equals the net biodiversity effect (see Boxes 2 and 3 for corresponding equations).

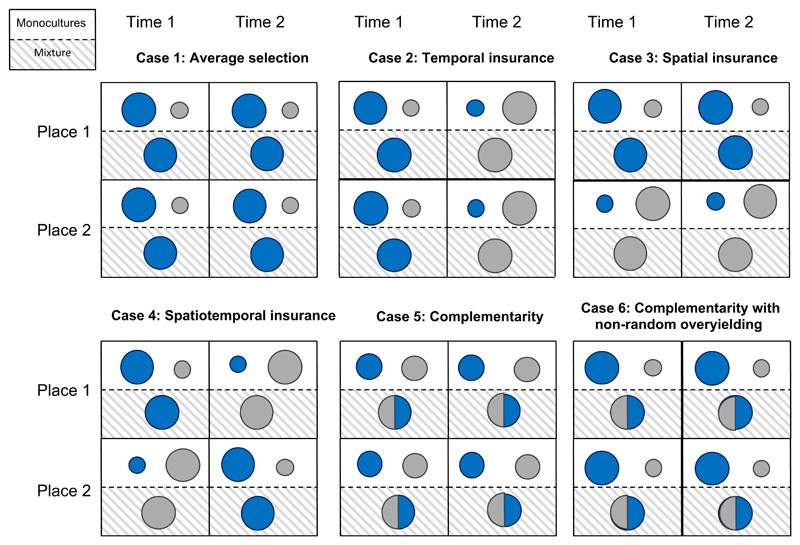
Next, we show how biodiversity effects are partitioned by this new approach for contrasting cases that isolate, in turn, each type of biodiversity effect (Table 2; Fig. 2). Where possible, we relate these cases to those considered by previous theoretical studies. We also provide an R script that demonstrates the additive partition for the examples shown in Tables 1 and 2 (Supporting Information). Although we use these contrasting cases to isolate each type of biodiversity effect in turn, real ecological systems are likely somewhere between these extreme cases. For example, rather than having identical yields at all times and places (Case 1, Table 2 and Fig. 2) or having species dominance in mixture perfectly track changes in monoculture yields over time (Case 2, Table 2 and Fig. 2) or across space (Case 3, Table 2 and Fig. 2), species in natural ecosystems may partly track such temporal fluctuations and spatial heterogeneity in environmental conditions. Note that each type of biodiversity effect could be positive or negative. Given that local biodiversity loss often decreases, rather than increases, ecosystem functioning in experiments (O’Connor et al. 2017) and naturally assembled communities (Duffy et al. 2017), here we show mostly examples of positive biodiversity effects (but see Case 6 below). Also, although we provide some examples based on resource competition theory, analogous examples could easily be considered for apparent competition (Holt et al. 1994; Leibold 1996; Chesson & Kuang 2008).

Table 2.

Example levels of ecosystem functioning (arbitrary units) in monoculture (M_ijk) and mixture (Y_ijk) for species i at time j and place k that would produce each of the six types of biodiversity effects. Biodiversity effects are quantified using E10 in Box 3, assuming equal initial proportions RY_E,ijk = 0.5 for all i, j and k. In all cases shown, total complementarity effects and total selection effects are simply the sum of local effects: $C{E}_{\gamma }={\sum }_k^P{\sum }_j^{T}C{E}_{\alpha }$ and $S{E}_{\gamma }={\sum }_k^P{\sum }_j^{T}S{E}_{\alpha }.$

			Case 1		Case 2		Case 3		Case 4		Case 5		Case 6
Time (j)	Place (k)	Species (i)	Mijk	Yijk	Mijk	Yijk	Mijk	Yijk	Mijk	Yijk	Mijk	Yijk	Mijk	Yijk
1	1	1	100	100	100	100	100	100	100	100	75	50	100	50
1	1	2	50	0	50	0	50	0	50	0	75	50	50	50
1	2	1	100	100	100	100	50	0	50	0	75	50	100	50
1	2	2	50	0	50	0	100	100	100	100	75	50	50	50
2	1	1	100	100	50	0	100	100	50	0	75	50	100	50
2	1	2	50	0	100	100	50	0	100	100	75	50	50	50
2	2	1	100	100	50	0	50	0	100	100	75	50	100	50
2	2	2	50	0	100	100	100	100	50	0	75	50	50	50
Net biodiversity effect			100		100		100		100		100		100
Total complementarity effects: CEγ			0		0		0		0		100		150
Total selection effects: SEγ			100		100		100		100		0		−50
-Non-random overyielding			0		0		0		0		0		−50
-Total insurance			100		100		100		100		0		0
•  Average selection			100		0		0		0		0		0
•  Temporal insurance			0		100		0		0		0		0
•  Spatial insurance			0		0		100		0		0		0
•  Spatiotemporal insurance			0		0		0		100		0		0

Figure 2.

Visual representation of the six contrasting types of biodiversity effects on ecosystem functioning. Larger circles indicate greater yields. Blue and grey colours correspond to two different species. Within each case, two different times (columns) are shown for each of two different places (rows). In case 1, the effect of biodiversity on ecosystem functioning depends on only one species that is highly productive in monoculture at all times and places. In cases 2–4, the effect of biodiversity on ecosystem functioning depends on different species at different times and places, due to temporal and spatial insurance effects. In cases 5 and 6, the effect of biodiversity on ecosystem functioning depends on both species at each and every time and place, due to complementarity effects. See Table 2 for the values associated with each case.

Table 1.

Shifts in whether a positive net biodiversity effect is explained by (A) complementarity effects at a local scale, but selection effects at a larger scale $\left(NB{E}_{\gamma }={\displaystyle {\sum }_k^{P}C{E}_{\alpha }=S{E}_{\gamma }}\right)$ or (B) selection effects at a local scale, but complementarity effects at a larger scale $\left(NB{E}_{\gamma }={\displaystyle {\sum }_k^{P}S{E}_{\alpha }=C{E}_{\gamma }}\right).$ Example levels of ecosystem functioning (arbitrary units) in monoculture (M_ik) and mixture (Y_ik) for species i at place k. Biodiversity effects are quantified by Equations E1 and E2 in Box 2, assuming equal initial proportions RY_E,ik = 0.5 for all i and k. For simplicity, only one time is considered. Values shown in B are approximate.

		A		B
Place (k)	Species (i)	Mik	Yik	Mik	Yik
1	1	200	200	50	8.15
1	2	200	200	350	291.7
2	1	100	0	0.44	0.88
2	2	100	0	1	0
Net Biodiversity Effect: $NB{E}_{\gamma }={\displaystyle {\sum }_k^{P}NB{E}_{\alpha }}$		100		100
Local complementarity effects: ${\displaystyle {\sum }_k^{P}C{E}_{\alpha }}$		100		0
Local selection effects: ${\displaystyle {\sum }_k^{P}S{E}_{\alpha }}$		0		100
Total complementarity effects: CEγ		0		100
Total selection effects: SEγ		100		0

Case 1: average selection effect

First, consider the simple case of competition for a single limiting resource in a homogeneous and constant environment (Tilman et al. 1997). In this case, the superior competitor outcompetes all other species by drawing down resource concentrations to levels below those at which any other species can replace itself. The superior resource competitor exhibits the highest yield in monoculture because it converts the greatest amount of resource into biomass. Mixtures of species eventually become monocultures of the most productive species that they originally included. For example, if two species, respectively, have monoculture yields of 100 and 50 g m⁻² year⁻¹, then, after transient dynamics, their mixture yields will, respectively, be 100 and 0 g m⁻² year⁻¹ at all times and places in a temporally constant and spatially homogeneous environment. There will be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}}}$ across both years and places. None of this effect of biodiversity on productivity is a total complementarity effect because $\overline{\overline{\overline{\Delta RY}}}=0\text{g}{\text{m}}^{-2}{\text{year}}^{-1}$ and thus $\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}\overline{\overline{\overline{M}}}=0\text{g}{\text{m}}^{-2}{\text{year}}^{-1}.$ Therefore, all of the net biodiversity effect is due to a total selection effect, and indeed PTNcov(ΔRY_ijk, M_ijk) = 100 g m⁻² year⁻¹. None of the total selection effect is due to non-random overyielding effects because all ΔRY_0,ijk = 0 g m⁻² year⁻¹ and therefore PTNcov(ΔRY_o,ijk, M_ijk) = 0 g m⁻² year⁻¹. Similarly, it is easy to see that there is no variation in Δp_ijk or M_ijk over time or space, and therefore none of the biodiversity effect is due to temporal, spatial or spatiotemporal insurance effects: $\mathit{\text{PTNcov}}\left(\overline{\Delta p_{ij}},\overline{M_{ij}}\right)=\mathit{\text{PTNcov}}\left(\overline{\Delta p_{ik}},\overline{M_{ik}}\right)=\mathit{\text{PTNcov}}\left(p_n,M_n\right)=0\text{g}{\text{m}}^{-2}{\text{year}}^{-1}.$ Therefore, in the simple case of competition for a single limiting resource in a constant and homogeneous environment, all of the net biodiversity effect is due to an average selection effect, $\mathit{\text{PTNcov}}(\overline{\overline{\Delta p_i}},\overline{\overline{M_l}})=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1},$ and all other components of the net biodiversity effect equal zero (Case 1, Table 2 and Fig. 2). Note that this is the only case where ecosystem functioning depends on only one of the two species across all times and places (Fig. 2).

Case 2: temporal insurance effect

Next, consider the case where species exhibit asynchronous responses to environmental fluctuations, and are able to completely dominate at the times in which conditions are most favourable for them (i.e. when they exhibit the highest monoculture yield) (Yachi & Loreau 1999). Mixtures of species again become monocultures of their most productive species, however, in this case, the identity of the most productive species changes over time. This could occur, for instance, if the resource competition described in Case 1 was rapid relative to the duration over which environmental fluctuations were experienced, such that species quickly outcompete one another and dominate as long as conditions that favour their monoculture productivity prevail. For example, if two species, respectively, have monoculture yields of 100 and 50 g m⁻² year⁻¹ at time one and 50 and 100 g m⁻² year⁻¹ at time two, then their mixture yields would, respectively, be 100 and 0 g m⁻² year⁻¹ at time one and 0 and 100 g m⁻² year⁻¹ at time two. There would again be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}}}$ across both years at two places. This net biodiversity effect would not be due to an average selection effect; however, because, averaged over time, there would be no difference between the two species in monoculture yield or mixture relative biomass (i.e. a species’ mixture yield divided by the total mixture yield), and thus $\mathit{\text{PTNcov}}(\overline{\overline{\Delta p_i}},\overline{\overline{M_i}})=0\text{g}{\text{m}}^{-2}{\text{year}}^{-1}.$ In this simple case of selection for the most productive species in a temporally fluctuating and spatially homogeneous environment, all of the net biodiversity effect is due to a temporal insurance effect, $\mathit{\text{PTNcov}}(\overline{\overline{\Delta p_{lj}}},\overline{\overline{M_{lj}}})=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1},$ and all other components of the net biodiversity effect equal zero (Case 2, Table 2 and Fig. 2). In this case, ecosystem functioning depends on only one of the two species within each time and place, but it depends on both species across both times (Case 2 in Fig. 2). Note that this case assumes that a species can vanish temporarily, and then fully recover when conditions favour it, such as by recolonising from a third, unobserved location. If, alternatively, the species goes extinct globally (i.e. not only at the places shown in Table 1, but also at all other unobserved places), then there would be a loss of ecosystem functioning because this species could no longer recover and dominate under the conditions that favoured it.

Case 3: spatial insurance effect

Next, consider the case where species exhibit asynchronous responses to environmental heterogeneity and are able to completely dominate at the places at which conditions are most favourable for them (i.e. where they exhibit the highest monoculture yield) (Loreau et al. 2003). Mixtures of species again become monocultures of their most productive species; however, in this case, the identity of the most productive species changes from one place to another. This could occur, for instance, due to tradeoffs in species’ abilities to compete for different limiting resources and spatial heterogeneity in the ratios of these resources (Tilman et al. 1997), or simply due to species having fundamental niches that do not completely overlap in space. For example, if two species, respectively, have monoculture yields of 100 and 50 g m⁻² year⁻¹ at place one and 50 and 100 g m⁻² year⁻¹ at place two, then their mixture yields would, respectively, be 100 and 0 g m⁻² year⁻¹ at place one and 0 and 100 g m⁻² year⁻¹ at place two. There would again be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}}}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}$ across both places over 2 years. In this simple case of selection for the most productive species in a temporally constant and spatially heterogeneous environment, all of the net biodiversity effect is due to a spatial insurance effect, $\mathit{\text{PTNcov}}\left(\overline{{\Delta }_{pik}},\overline{M_{ik}}\right)=100$ g m⁻² year⁻¹, and all other components of the net biodiversity effect equal zero (Case 3, Table 2 and Fig. 2). In this case, ecosystem functioning depends on only one of the two species within each time and place, but it depends on both species across both places (Case 3 in Fig. 2).

Case 4: spatiotemporal insurance effect

Next, consider the case where species exhibit asynchronous responses to environmental fluctuations and heterogeneity and are able to completely dominate at the times and places at which conditions are most favourable for them (i.e. when and where they exhibit the highest monoculture yield) (Loreau et al. 2003). This case is simply the combination of Cases 2 and 3. Spatiotemporal insurance effects are the statistical interaction between temporal and spatial insurance effects. They quantify the covariation between monoculture yields and mixture relative biomass that is shared between time and space, and that cannot be attributed exclusively to either time or space. For example, if two species, respectively, have monoculture yields of 100 and 50 g m⁻² year⁻¹ at time one and 50 and 100 g m⁻² year⁻¹ at time two when at place one, but the opposite values when at place two, and if their mixture yields track these monoculture yields as in all three cases above, then the temporal insurance effect would depend on the place (or, equivalently, the spatial insurance effect would depend on the time). There would again be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}}}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}$ across both places over both years. In this simple case of selection for the most productive species in a temporally fluctuating and spatially heterogeneous environment, all of the net biodiversity effect is due to a spatiotemporal insurance effect, PTNcov(Δp_n, M_n), = 100 g m⁻² year⁻¹, and all other components of the net biodiversity effect equal zero (Case 4, Table 2 and Fig. 2). In this case, ecosystem functioning depends on only one of the two species within each time and place, but it depends on both species across both times and places (Case 4 in Fig. 2).

Case 5: complementarity effect

Next, consider the case where species exhibit local complementarity in a constant, homogeneous environment. For example, even if the environment was constant from one year to the next and homogeneous from one place to the next, plant species may still consume somewhat different forms of limiting nutrients, exhibit phenological niche partitioning within a year, or partition rooting zones belowground (McKane et al. 2002). Complementarity effects could also arise if species facilitate one another’s growth, such as by ameliorating stressful abiotic conditions (Mulder et al. 2001; Wright et al. 2017), or if they partly escape specialised natural enemies, such as Janzen-Connell effects (Petermann et al. 2008). If two species both have monoculture yields of 75 g m⁻² year⁻¹ and mixture yields of 50 g m⁻² year⁻¹ at two times and two places, then there would again be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}}}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}$ across both places over both years. In this simple case of complementarity in a temporally constant and spatially homogeneous environment, all of the net biodiversity effect is due to a complementarity effect, $\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}\overline{\overline{\overline{M}}}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1},$ and all other components of the net biodiversity effect equal zero (Case 5, Table 2 and Fig. 2). In this case, unlike those above, ecosystem functioning depends on both species within each and every time and place (Case 5 in Fig. 2).

Case 6: complementarity with non-random overyielding

Next, consider the case where species exhibit local complementarity and non-random overyielding in a constant, homogeneous environment. The non-random overyielding effect quantifies the extent to which the most productive species in monoculture tend to overyield the most in mixtures. This is somewhat of a residual biodiversity effect, capturing all the remaining variation after complementarity effects and insurance effects are isolated, and thus has no clear biological interpretation that corresponds to previous theory. Unlike other biodiversity effects, we suspect that non-random overyielding effects will often be negative, which occurs when the least productive species in monoculture overyield the most in mixture, for the following two reasons. First, note that overyielding is assessed against a shifting baseline that is partly determined by monoculture yield. In order to overyield, species that are unproductive in monoculture need only to produce more biomass in mixture than the small amount that would be expected based on their low yields in monoculture. In contrast, species that are highly productive in monoculture would need to produce much more biomass in mixture in order to overyield, given their high yields in monocultures. In other words, the bar for overyielding is lower for unproductive than for highly productive species. Likewise, underyielding is easier for species that are highly productive than for species that are unproductive in monoculture. Second, note that overyielding is also assessed against a shifting baseline that is partly determined by dominance in mixture (when quantified based on observed, rather than initial, relative abundance or biomass; Boxes 1 and 2). As a species increasingly, and eventually completely, dominates a mixture, we would expect the mixture yield to converge on its monoculture yield. Thus, we would not expect as much overyielding (deviation of a species’ mixture yield from its monoculture yield, weighted by its current relative biomass in mixture) for highly productive or dominant species as we would for unproductive and rare species. For example, if two species have monoculture yields of 100 and 50 g m⁻² year⁻¹ and mixture yields of 50 g m⁻² year⁻¹ at two times and two places, then there would again be a positive net biodiversity effect of ${\displaystyle \sum _k^P{\displaystyle \sum _j^T{\displaystyle \sum _i^N\Delta R{Y}_{ijk}{M}_{ijk}}}=100\text{g}{\text{m}}^{-2}{\text{year}}^{-1}}$ across both places over both years. In this case, the net biodiversity effect is due to a complementarity effect, $\mathit{\text{PTN}}\overline{\overline{\overline{\Delta RY}}}\overline{\overline{\overline{M}}}=150\text{g}{\text{m}}^{-2}{\text{year}}^{-1},$ that is counter-balanced to some extent by a negative nonrandom overyielding effect PTNcov(ΔRY_o,ijk, M_ijk) = −50 g m⁻² year⁻¹, and all other components of the net biodiversity effect equal zero (Case 6, Table 2 and Fig. 2). In this case, ecosystem functioning again depends on both species within each time and place, due to the total complementarity effect (Case 6 in Fig. 2).

Applying the New Approach to Experimental Data

Next, we apply this new partition to experimental data to quantify how much of the net biodiversity effect arises across times and environmental conditions, due to insurance effects.

Experimental design

The BioCON experiment (e141) at Cedar Creek Ecosystem Science Reserve, Minnesota, USA was established by planting 296 field plots (each 2 by 2 m) containing different numbers and combinations of perennial grassland species under ambient and elevated atmospheric CO₂ and with either ambient or enriched soil N supply (Reich et al. 2001, 2012; Reich & Hobbie 2013). Plots were arranged in six circular 20-m-diameter rings, to which CO₂ treatments were randomised and applied. The treatments were fully crossed in a complete factorial combination of two levels of atmospheric CO₂ (ambient and elevated by c. 180 μmol mol⁻¹), four levels of plant species diversity (1, 4, 9 and 16 species) and two levels of N (ambient and enriched with 40 kg N ha⁻¹ y⁻¹). Here, we analysed data from a subset of these plots (n = 88 plots, including 64 monocultures and 24 mixtures that were planted with all 16 species). Specifically, to offer a simple empirical demonstration of this new method, we did not consider the elevated CO₂ treatment, given its complex interaction with the N treatment (Reich & Hobbie 2013), and we did not consider the intermediate levels of species diversity (4- or 9-species mixtures), given that some species compositions were not replicated across both N treatments. The 16 study species include four C₄ grasses (Andropogon gerardii, Bouteloua gracilis, Schizachyrium scoparium, Sorghastrum nutans), four C₃ grasses (Agropyron repens, Bromus inermis, Koeleria cristata, Poa pratensis), four N-fixing legumes (Amorpha canescens, Lespedeza capitata, Lupinus perennis, Petalostemum villosum) and four non-N-fixing herbaceous species (Achillea millefolium, Anemone cylindrica, Asclepias tuberosa, Solidago rigida). Each year in every plot aboveground biomass was harvested by clipping a 10 cm by 100 cm strip just above the soil surface in June and August. Here, we present only the August data because these peak biomass samples approximate aboveground annual net primary productivity (all aboveground biomass dies during winter). Including both June and August data would have double-counted some biomass production because these samples were not collected in exactly the same location. The data used in this study are available at the Cedar Creek Ecosystem Science Reserve website (www.cbs.umn.edu/cedarcreek/research/data). We apply the additive partition presented above, treating the two N treatments as two different places and the first 18 years of the study (1998–2015) as different times. See previous publications for additional experimental design details (Reich et al. 2001, 2012; Reich & Hobbie 2013).

Here, we use the two N treatments as two different places to illustrate the approach, and how it can be used to assess spatial insurance. Note that the two N treatments are randomised to plots within the same location and thus are two different environmental conditions, but not two different places. Using these experimental treatments as surrogates of different places likely causes us to underestimate the magnitude of spatial insurance effects in natural systems because truly different places would differ in multiple ways, rather than only in N supply. On the other hand, using these experimental treatments has the advantage of allowing us to causally attribute observed differences in species’ monoculture yield and mixture relative biomass to a single underlying component of environmental variability: N supply.

Experimental results

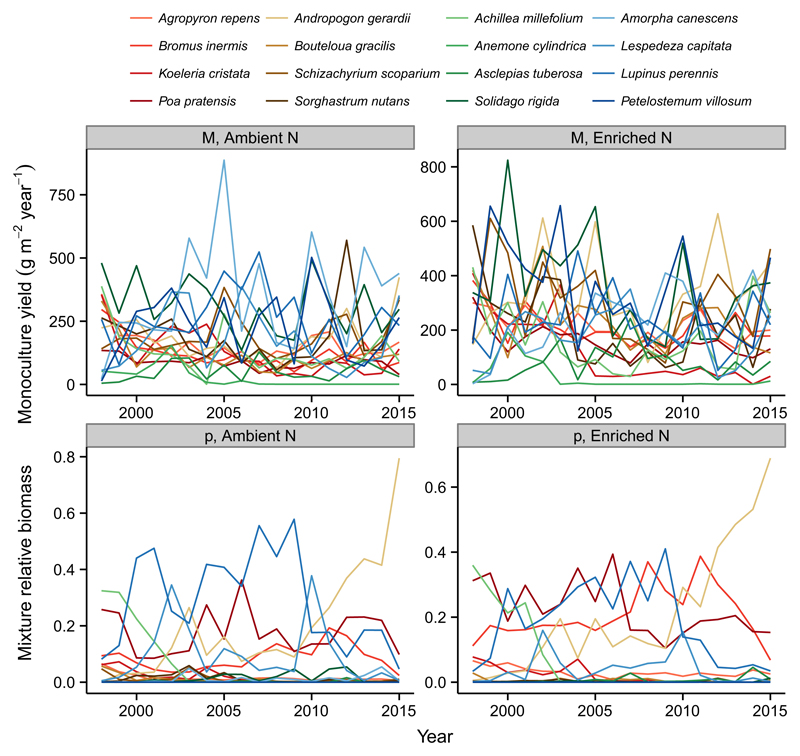
We find considerable variability in monoculture yields and mixture relative biomasses across years and nitrogen treatments (Fig. 3). Note that without this variation, there could be no temporal or spatial insurance effects, which are quantified as the covariation between monoculture yields and mixture relative biomasses. For example, during the first year of the experiment, under both ambient and enriched N conditions, a non-leguminous forb, Achillea millefolium, was the most dominant species in mixture and was the second most productive species in monoculture (lightest green line in Fig. 3). During the most recent year, under both ambient and enriched N conditions, a C₄ grass, Andropogon gerardii, was among the most productive species in monoculture and was by far the most dominant species in mixture (lightest brown line in Fig. 3). This shows that species tended to dominate mixtures during the years in which they were most productive, consistent with theoretical predictions of the temporal insurance hypothesis.

Figure 3.

Variation over time in monoculture yields (top) and mixture relative biomasses (bottom) for ambient (left) and enriched (right) rates of N supply for the BioCON experiment. Different species become highly productive in monoculture during different years and under different rates of N supply. The rank order of species’ mixture relative biomasses also changes substantially over time and between N treatments. Without these changes in the identities of highly productive and dominant species over time and between environmental conditions, there could be no covariance between them and thus no insurance effects of biodiversity on ecosystem productivity. Line colours correspond to plant functional groups: reds = C₃ grasses, browns = C₄ grasses, greens = non-N-fixing forbs, blues = N-fixing forbs.

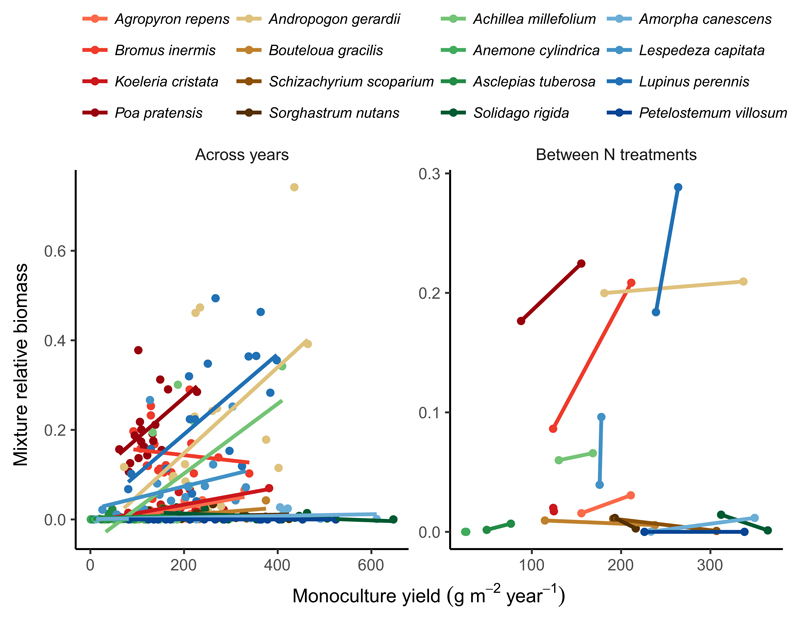
Next, to more systematically visualise these covariances, we plotted relative biomasses in mixture against monoculture yields by species for each year or N treatment. When considering covariation over time, the slopes of these lines tended to be positive, indicating that species tended to increasingly dominate mixtures during the years in which they were most productive in monoculture (Fig. 4). This appears to be particularly true for the species that were dominant during at least some years (Fig. 4). Other species remained at a low relative biomass in mixture, despite exhibiting considerable variation in monoculture yield from one year to the next (wide horizontal lines with near-zero mixture relative biomass in Fig. 4). When considering covariation between N treatments, the slopes of these lines were positive for a few species, again especially for species that averaged higher mixture relative biomass. However, most species did not increasingly dominate mixtures under the nutrient conditions in which they were most productive in monoculture (Fig. 4).

Figure 4.

Covariation between monoculture yields and mixture relative biomasses over time (left) and between ambient and enriched rates of N supply (right) for the BioCON experiment. Positive sloping lines indicate that species increasingly dominated mixtures during the years (left) or under the rates of N supply (right) in which they were most productive in monoculture. These positive covariances partly explain why increasing plant species richness increases ecosystem productivity across multiple years and environmental conditions (i.e. N supply rates). Symbol and line colours correspond to plant functional groups: reds = C₃ grasses, browns = C₄ grasses, greens = non-N-fixing forbs, blues = N-fixing forbs.

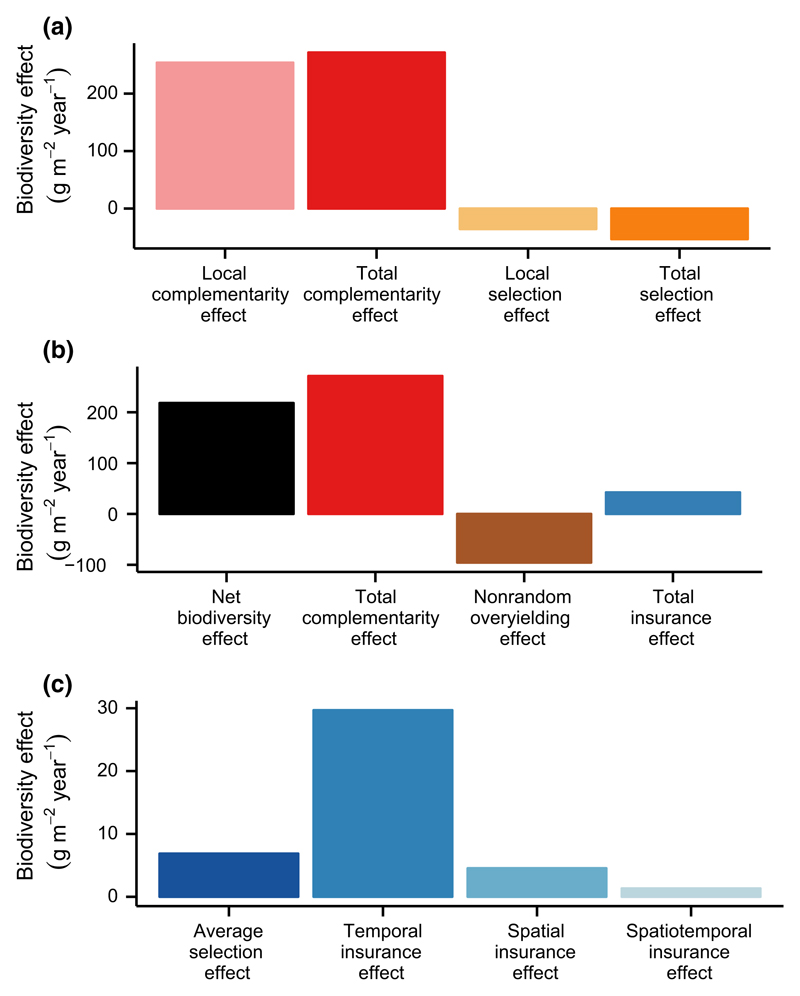
Next, we quantified complementarity effects and selection effects at both local and larger scales using Equations E1 and E2 in Box 2, finding that positive biodiversity effects were explained by positive complementarity effects at both local and larger scales (Fig. 5a). The net biodiversity effect was, however, explained by complementarity effects to a slightly greater extent at the larger scale (Fig. 5a). Specifically, across all years and both N treatments, the complementarity effect was approximately 7% larger than when it was quantified within years and N treatments (Fig. 5a). Inevitably, given Equation E3 in Box 2, the total selection effect was correspondingly smaller (i.e. a stronger negative selection effect) than the local selection effect (Fig. 5a).

Figure 5.

Magnitudes of local and larger scale biodiversity effects on ecosystem functioning for the BioCON experiment. (a) Complementarity effects were much larger than selection effects, regardless of whether they were quantified at local or larger scales. (b) The positive net biodiversity effect was due primarily to a positive total complementarity effect and secondarily to a positive total insurance effect, both of which were counter-balanced by a negative non-random overyielding effect. (c) Total insurance effects were mostly explained by temporal insurance effects.

Finally, we partitioned the total net biodiversity effect into its components using Equation E10 in Box 3, finding that it is mostly composed of total complementarity effects. Total insurance effects are also positive in sign and substantial in magnitude. The net biodiversity effect was 218.1 g m⁻² year⁻¹ on average, across all 18 years and both N treatments (Fig. 5b). This is a substantial magnitude given that the mean monoculture productivity at our site, averaged across all 16 species, all 18 years and both N treatments, was 191.5 g m⁻² year⁻¹. In other words, changing from 1 to 16 species more than doubled biomass production, on average. Much of this was due to complementarity effects (271.3 g m⁻² year⁻¹), though total insurance effects were also positive in sign and substantial in magnitude (42.4 g m⁻² year⁻¹), amounting to 19% of the magnitude of the net biodiversity effect (Fig. 5b). Further partitioning these total insurance effects reveals that they were mostly due to a positive temporal insurance effect, though the average selection effect, spatial insurance and spatiotemporal insurance were also positive in sign (Fig. 5c). Spatial insurance effects were relatively small in magnitude in our study, only 2% of the net biodiversity effect, likely because we considered experimental plots that differed in only one way: fertilised or not.

Discussion

The approach developed herein can help determine whether relatively few or many species contribute to ecosystem functioning both within and across times and places. As illustrated in the cases above, ecosystem functioning will depend on only a few dominant species when biodiversity effects are explained exclusively by the average selection effect. Alternatively, if complementarity effects are substantial in magnitude, then ecosystem functioning will also depend on α-diversity. Furthermore, if temporal or spatial insurance effects are substantial in magnitude, then ecosystem functioning will also depend on temporal or spatial β-diversity respectively. In the experimental example we considered, average selection effects were negligible, local complementarity effects were large and insurance effects were intermediate in magnitude. Thus, biodiversity effects on ecosystem functioning were explained primarily by α-diversity, secondarily by β-diversity (especially temporal β-diversity, but see further discussion of this point below) and least by the dominance of a few species that were highly productive across all years and both environmental conditions.

The absolute and relative strengths of insurance effects will likely depend on the amount of environmental variation experienced across times and places, as well as the variation in the functional traits of species in the community. In the experiment we considered, spatial insurance was quantified between two sets of plots that were located in the same place, and that differed in only one way: the rate of N supply, which limits plant growth at our site (Tilman 1987). In contrast, temporal insurance effects were quantified across nearly two decades of years that differed from one another in many ways, such as their temperature, precipitation and abundances of plant nutrients and enemies. Thus, given the data considered in this particular experiment, it is unsurprising that the magnitudes of spatial insurance effects were small in absolute magnitude and much smaller than those of temporal insurance effects. If we had considered many different places that differed in many ways, spanning large environmental gradients, we suspect that spatial insurance effects would have been considerably larger. The magnitudes of insurance effects will likely also strongly depend on the variation in the functional traits of species included in the community (Walker et al. 1999; Mori et al. 2013), and our approach could also be applied at the functional group level. Environmental variation that is beyond the fundamental niches of all species in the community would not, however, be expected to contribute to insurance effects.

To better estimate insurance effects across scales, future studies could apply our approach to data from biodiversity experiments that were replicated at two different spatial scales (Roscher et al. 2005), or replicated across different sites (Hector et al. 1999; Kirwan et al. 2007), across heterogeneous environments within a site (Losure et al. 2007; Griffin et al. 2009; Tuck et al. 2016), or across years (Losure et al. 2007). Replication across years (i.e. planting the entire experiment repeatedly) isolates effects of interannual variability from those of successional dynamics. To better estimate temporal insurance effects, future studies will also need to consider the wider range of environmental variability that species have experienced throughout their evolutionary history, and that they will experience in the future as novel conditions emerge from combinations of global environmental changes. Given that different species can promote ecosystem functioning under different global change scenarios (Isbell et al. 2011), accounting for global change insurance might also be important for future biodiversity conservation and policy decisions (Isbell et al. 2017).

While our approach can tease apart patterns resulting from biological mechanisms, as shown in the cases above, it cannot identify specific mechanisms, such as distinguishing between resource and apparent competition. Just as local complementarity effects are the net result of all positive and negative interactions between individuals in a community (Loreau et al. 2012), so, too, are total complementarity effects. A positive total complementarity effect does not indicate resource partitioning, but instead simply indicates that net interactions between individuals of different species are more favourable than intraspecific interactions, due to reduced competition (including both resource and apparent competition) and/or increased facilitation between species. Furthermore, our approach cannot predict the dependence of ecosystem functioning on biodiversity at scales larger than those over which data have been collected, for instance at the planetary scale, from measurements taken within a few experimental plots. However, our approach extends knowledge of biodiversity and ecosystem functioning relationships from one to multiple times and places and future work can determine how many times and places must be considered to make robust predictions at much larger scales.

The approach developed herein can be applied at any nested smaller and larger scales of space or time, just as α-, β- and γ-diversity can be quantified between nested scales of any magnitudes (but see Loreau 2000). Our approach does, however, require two pieces of information, species-specific levels of ecosystem functioning in both mixture and monoculture, the latter of which is exceedingly difficult to estimate experimentally at large spatial scales. How then might we scale-up from considering a few experimental monocultures at a few times and places to the planet? Although we cannot yet fully answer this question, we offer a few suggestions for extending this approach to larger scales in naturally assembled ecosystems.

First, we acknowledge that there is currently no substitute for monoculture information and that obtaining this information can be very difficult. One challenge to collecting this information reliably is that a species may be present and abundant because a site is productive, or a site may be productive because a species is present and abundant. Thus, species that appear highly productive may instead be those that tend to occupy more productive (e.g. resource-rich or enemy-free) environments (Reich et al. 1997). Determining whether dominant species tend to be more or less productive than other species that may replace them is essential for predicting whether and how species losses or gains will influence ecosystem functioning. Common garden and reciprocal transplant studies can help disentangle species’ effects on ecosystem functioning from their responses to it. Indeed, the need to isolate species’ effects on ecosystem functioning was part of the motivation for moving from early observational studies towards establishing biodiversity experiments (Tilman et al. 2014). Surprisingly, after a quarter century of progress in this field, it remains largely unclear whether the most productive species in monocultures tend to dominate species mixtures, even within biodiversity experiments. This is challenging partly because the rank order of species’ productivities in monoculture dramatically change from year to year and between environmental conditions (Fig. 3). Therefore, it is impossible to determine which species are more or less productive than others in any general sense, unless species’ monoculture yields have been observed across many years and environmental conditions. In one experiment, we found that species’ dominance in mixture partly tracks species’ monoculture productivity from one year to the next, between N treatments, and across all years and both N treatments. Thus, the ebb and flow of species’ dominance tended to ratchet up productivity across years and environmental conditions. Species loss would therefore reduce ecosystem functioning partly by reducing these opportunities for different species to make up for the productivity lost when and where a particularly dominant species is less productive, as hypothesised by previous studies (Walker et al. 1999; Yachi & Loreau 1999; Loreau et al. 2003; Allan et al. 2011; Isbell et al. 2011; Mori et al. 2013). To determine the strength of insurance effects more generally, our approach could be applied to the hundreds of other biodiversity experiments conducted in all major ecosystem types (O’Connor et al. 2017). Although we found that total complementarity effects were only slightly larger than local complementarity effects in the experiment we considered (Fig. 5a), we encourage future studies to determine whether complementarity effects often increase with scale, as this could imply that previous local biodiversity experiments have overestimated the extent to which a few dominant species could maintain high levels of ecosystem functioning.

In addition to revisiting data from biodiversity experiments, there is considerable interest in returning to observational studies in naturally assembled communities. Indeed, recent observational studies have found substantial local biodiversity effects in many ecosystems worldwide (Maestre et al. 2012; Hautier et al. 2014; Duffy et al. 2016, 2017; Grace et al. 2016; Liang et al. 2016). Although these studies primarily consider responses of ecosystem functioning to loss of local species diversity (α-diversity), a few other studies have considered responses of ecosystem functioning to spatial homogenization (loss of spatial β-diversity) (Mori et al. 2016; Hautier et al. 2018), or to changes in biodiversity at larger spatial extents (γ-diversity) (Dee et al. 2016; Oehri et al. 2017). Together these observational studies are expanding knowledge about natural ecosystems beyond that obtainable from local experiments.

In order to apply our approach to many ecosystem functions in natural ecosystems, at scales larger than those considered by experiments, two major advances are needed. First, it would be necessary to estimate species-specific levels of ecosystem functioning in monoculture (M_ijk) without actually having large monocultures. Second, it would be necessary to estimate species-specific levels of ecosystem functioning in mixtures (Y_ijk) for additional ecosystem functions, other than productivity, that are difficult to measure at the species level. One promising way to overcome both challenges would be to extend diversity interaction models (Kirwan et al. 2009; Connolly et al. 2013; Dooley et al. 2015), which estimate species identity effects (i.e. levels of ecosystem functioning in monocultures) and species interaction effects using only plot-level ecosystem function values and species’ relative abundances. For example, diversity interaction models could be fit to the data collected in experimental or nearby naturally assembled species mixtures, and the predicted values for species’ yields in monoculture and mixture could be compared to their observed values. Diversity interaction models do not solve the problem of inferring causation from observational data, but they may provide a useful bridge between experimental and observational studies, given that, after being experimentally validated as described above, they could be applied in natural ecosystems at larger scales.

Here, we extended knowledge of biodiversity effects on ecosystem functioning from single to multiple times and places. There are, however, many other ways in which relationships between biodiversity and ecosystem functioning could shift across scales. For example, the nonlinear accumulation of species and the linear accumulation of biomass production may in combination change the shape of the relationship between biodiversity and ecosystem functioning as one scales-up from a small to a large spatial extent, such as might be done in remote sensing studies (Oehri et al. 2017). Additionally, dispersal drives levels of both biodiversity and ecosystem functioning and shifts the relative strengths of complementarity effects and selection effects across scales (Loreau et al. 2003; Thompson & Gonzalez 2016; Leibold et al. 2017). The relative strengths of these biodiversity effects can also shift along environmental gradients, such as when local complementarity effects are stronger in harsher environments (Mori 2018), as predicted by the stress-gradient hypothesis (Callaway et al. 2002; Maestre et al. 2009). Further study will be needed to integrate knowledge from these and other approaches before it will be possible to scale-up to relationships between biodiversity and ecosystem services at the planetary scale (Isbell et al. 2017). Open questions include determining the scales at which: (1) ecosystem functioning is most or least sensitive to changes in biodiversity; (2) many or few species are needed to maintain ecosystem functioning; and (3) humans are having the greatest influence on biodiversity.

Supplementary Material

Additional Supporting Information may be found online in the supporting information tab for this article.