Comparison of joint modeling and landmarking for dynamic prediction under an illness-death model

Abstract

Dynamic prediction incorporates time-dependent marker information accrued during follow-up to improve personalized survival prediction probabilities. At any follow-up, or “landmark”, time, the residual time distribution for an individual, conditional on their updated marker values, can be used to produce a dynamic prediction. To satisfy a consistency condition that links dynamic predictions at different time points, the residual time distribution must follow from a prediction function that models the joint distribution of the marker process and time to failure, such as a joint model. To circumvent the assumptions and computational burden associated with a joint model, approximate methods for dynamic prediction have been proposed. One such method is landmarking, which fits a Cox model at a sequence of landmark times, and thus is not a comprehensive probability model of the marker process and the event time. Considering an illness-death model, we derive the residual time distribution and demonstrate that the structure of the Cox model baseline hazard and covariate effects under the landmarking approach do not have simple form. We suggest some extensions of the landmark Cox model that should provide a better approximation. We compare the performance of the landmark models with joint models using simulation studies and cognitive aging data from the PAQUID study. We examine the predicted probabilities produced under both methods using data from a prostate cancer study, where metastatic clinical failure is a time-dependent covariate for predicting death following radiation therapy.

1 Introduction

As survival outcomes for patients improve, there is additional follow-up information available and increased interest in predicting conditional survival for patients at a time beyond diagnosis or treatment. To achieve the most accuracy, prediction models should incorporate patient information that evolves over time and was collected during follow-up. The statistical task is to develop a technique that can quantify survival probability predictions at baseline, and produce updated risk predictions at future time points for patients who are still alive by including their new marker information.

Recent literature has explored obtaining dynamic predictions with the use of joint models for longitudinally measured markers and time-to-event outcomes (Taylor et al., 2005; Rizopoulos, 2011; Taylor et al., 2013; Rizopoulos et al., 2013). Joint modeling requires the specification of a model for the marker process, a model for the survival outcome, and a method by which to link the two models (Henderson et al., 2000). This is sufficient to obtain the joint distribution of the marker process and failure time, from which the residual time distribution can be easily derived at any landmark time of interest. Computing conditional survival probabilities from this distribution may involve numerical integration and require substantial computation. Joint models require correct specification of the joint distribution of the marker process and the event time and can require computationally intensive techniques for estimation. To avoid making distributional assumptions about the marker process and to reduce the computational burden, approximate approaches for dynamic prediction have been developed that specify a model for only a component of the joint distribution of the marker and failure time processes.

One such approach to dynamic prediction is called “landmarking”. This approach was first introduced in the context of clinical oncology by Anderson et al. (1983) as an alternative to a Cox model with a time-dependent covariate. In van Houwelingen (2007), the landmarking approach applies a simple Cox proportional hazards model to the data of individuals still alive at τ, and the resulting estimates are used to predict the probability of surviving up to a fixed horizon, τ + s. To link the landmark models, the estimated effects are allowed to change with landmark time in a smooth way. Since this method can be implemented using the Cox model, and since time is always measured from the original time origin, estimation can be conducted based on a partial log-likelihood method. Zheng and Heagerty (2005) proposed a similar approach called “partly conditional survival modeling”, which describes landmarking in the context of resetting the clock at the landmark time.

The appeal of landmarking is that it avoids specifying the distribution of the stochastic marker process in time. However, as demonstrated by Jewell and Nielsen (1993), approximate approaches fail to produce predictions that are consistent (i.e. have a defined relationship) with predictions at other landmark times. Valid prediction functions require the definition of a model for the stochastic marker process and the functional relationship between the marker and the hazard at any given time. The residual time distribution, upon which predictions are based, is determined by the hazard at w = τ + s, s > 0 conditional on event time T > τ and marker process Z(τ). The consistency condition proposed by Jewell and Nielsen (1993) states that if the hazard function is determined by Z(t) and denoted h(t, Z(t)), the hazard at all times w > τ cannot be arbitrarily chosen but must be computed from h(w|τ, Z(τ)) = E[h(w, Z(w))|T > τ, Z(τ)], where the expectation is with respect to the distribution of Z between τ and w. Thus, specification of the marker process distribution is necessary to link the hazards over time to produce consistent predictions. Under the landmarking approach, the model for h(w|τ, Z(τ)) is chosen to have the form of a Cox regression, which can be easily fit using standard software. Thus, landmarking produces a sequence of best-fitting Cox models at each landmark time and there is no restriction on the predictions from each Cox model being consistent with those at earlier time points. Based on this violation of the consistency rule, an approach for prediction models that is based on modeling only the residual time may result in theoretically incorrect models.

It is well known that the residual time distribution based on a time-varying marker will depend on the stochastic process of the marker (Kalbfleisch and Prentice, 2011). Jewell and Kalbfleisch (1996) provided some specific examples of residual time distributions for additive models. Shi et al. (1996) showed that if the marker is following a Brownian motion then a reasonable approximation to the residual time distribution is based on the linear transformation model (T − τ)^1/3 = g(Z(τ)) + ε, where g is a monotonic function and ε has a constant variance distribution. In discussing differences between a time-dependent Cox model and a landmarking approach, Putter and van Houwelingen (2016) showed that a proportional hazards assumption will not in general be valid for the landmarking model. Whether the lack of theoretical justification for the landmarking approach is a practical concern may depend on what landmarking models are used. Extensions in the landmark framework that increase flexibility may provide a sufficiently good approximation to the true residual time distribution.

The comparison of predictive performance between joint models and landmarking approaches has been recently explored in the statistical literature. Cortese et al. (2013) compared predictions of cumulative incidence between amultistate model and landmark approaches under competing risks, and found that the two modeling strategies had nearly identical predictive accuracy. Rizopoulos et al. (2013) demonstrated the superiority of the survival prediction accuracy of a joint model over landmarking under various functional forms of the association structure between a continuous longitudinal marker and failure time processes. Maziarz et al. (2016) proposed two models in the partly conditional modeling framework and compared them to a joint model by simulating data from a shared random-effects model. They showed that predictions obtained from partly conditional survival models are comparable to those from a joint model, but that partly conditional models have better computational efficiency.

We aim to contribute to this literature by contrasting landmark and joint models for dynamic prediction in the context of a binary longitudinal marker, represented by an illness-death model. In Section 2, we introduce notation for landmark and joint models and derive their predicted probabilities in the context of the illness-death model. Section 3 demonstrates that the landmark approach with a standard Cox model does not satisfy the consistency condition of Jewell and Nielsen (1993), and suggests extensions to provide a better approximation. Section 4 compares the performance of landmark and joint models using a simulation study. In Section 5, we apply these methods to cognitive aging data from the PAQUID study and metastatic clinical failure data from a prostate cancer study, and conclude with a discussion in Section 6.

2 Approaches for dynamic individualized predictions

Let ${𝒟}_n=\{T_i^{\ast },{\delta }_i,{\mathbf{X}}_i,{\mathbf{Z}}_i;i=1,\dots ,n\}$ denote the observed data, where T_i is the true event time, C_i is the censoring time, $T_i^{\ast }=\text{min}(T_i,C_i)$ is the observed event time, δ_i = 1(T_i ≤ C_i) is the censoring indicator, X_i is the baseline covariate vector, and Z_i is the longitudinal marker vector, with z_il = Z_i(t_il) denoting the marker value at time t_il, l = 1,…, n_i, for subject i.

The aim is to obtain a prediction probability for a new subject, j, from the same population, who has current marker and baseline covariate data available. Specifically, we are interested in obtaining a prediction probability of surviving up to time τ + s, s > 0, given that subject j has survived up to time τ, that is

$$p_j(\tau +s|\tau )=\text{Pr}(T_j\ge \tau +s|T_j>\tau ,{𝒟}_n,{\mathbf{X}}_j,Z_j(\tau ))$$ (1)

where Z_j(τ) denotes the subject’s marker value at time τ. In this probability statement, τ is called the landmark time and s is the prediction window. The dynamic nature of this prediction probability lies in its ability to be updated as new information for patient j becomes available at time τ^* > τ, to produce the new prediction p_j (τ^* + s|τ^*). Implicit in Eq. (1) is that the value of Z is known for subject j at time τ. In practice this may not be the case. An alternative target of interest is to change Eq. (1) to condition on the known history of Z up to time τ for subject j.

2.1 Joint modeling

Joint modeling requires the full specification of the joint distribution of the longitudinal marker process and the survival data. The joint density is often factored into a product of the densities of Z and T|Z, which requires specifying the model for the longitudinal marker process and a model for the event times with dependence on the defined marker process. As shown in Jewell and Kalbfleisch (1992) and Shi et al. (1996), once these distributions are specified the residual time distribution can be derived.

If Z is a discrete random variable, joint modeling consists of formulating a process for the transitions between the states of Z and defining the relationship between the covariate process and survival using a hazard function for T. This is sufficient to derive the joint distribution of Z and T, from which the residual time distribution is then determined.

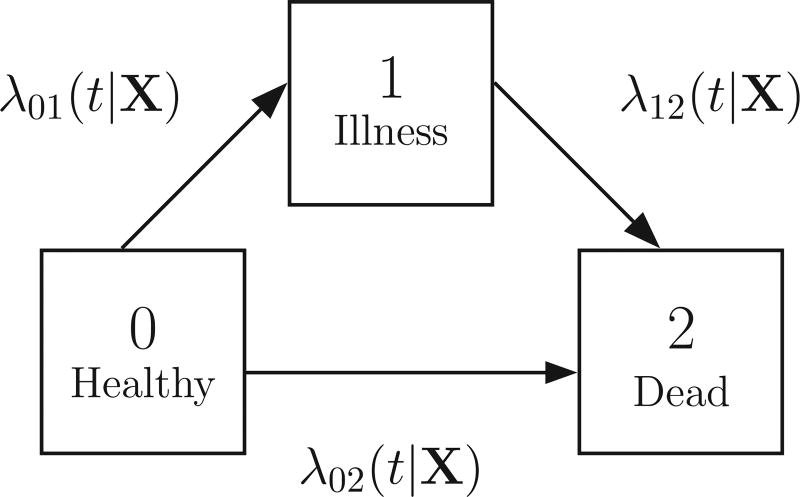
The irreversible illness-death model is the simplest example of discrete Z. In this model, Z is binary with only two states {0,1}, all subjects start in state 0, and transitions from state 1 to state 0 are not allowed. Let T be the time to death, which is a terminal state. Then the joint distribution of Z and T can be described as a simple three-state illness-death model (0: Healthy, 1: Illness, 2: Dead), as shown in Fig. 1. We then define the time-varying covariate process Z(t) ∈ {0, 1} as an indicator of whether an individual has progressed from the “healthy” state to the “illness” state by time t. In this model, λ_jk(t|X) describes the hazard of transitioning from state j to state k at time t conditional on the baseline covariate vector X, which can have a different effect on each transition. We assume that the clock does not reset once an individual has transitioned into the illness state, and thus t is time since baseline. As well, we can model the rate of transition to be dependent on the duration in the current state for those in the ill state. Under the illness-death model, the residual time distribution conditional on Z(τ) is:

$$\text{Pr}(T\ge \tau +s|T>\tau ,\mathbf{X},Z(\tau )=0)=\text{exp}\{-{\int }_{\tau }^{\tau +s}[{\lambda }_{02}(u|\mathbf{X})+{\lambda }_{01}(u|\mathbf{X})]\mathrm{d}u\}+{\int }_{\tau }^{\tau +s}\text{exp}\{-{\int }_{\tau }^{\nu }[{\lambda }_{02}(u|\mathbf{X})+{\lambda }_{01}(u|\mathbf{X})]\mathrm{d}u\}{\lambda }_{01}(\nu |\mathbf{X})\text{ exp}\{{\int }_{\nu }^{\tau +s}{\lambda }_{12}(u|\mathbf{X})\mathrm{d}u\}\mathrm{d}\nu$$ (2)

$$\text{Pr}(T\ge \tau +s|T>\tau ,\mathbf{X},Z(\tau )=1)=\text{exp}\{-{\int }_{\tau }^{\tau +s}{\lambda }_{12}(u|\mathbf{X})\mathrm{d}u\}$$ (3)

In Eq. (2) the first term represents the probability that the individual remained in state 0 from time τ to τ + s, and the second term is the probability the individual transitioned from state 0 to 1 at time ν ∈ (τ, τ + s) and then remained in state 1 from time ν to τ + s.

Figure 1.

An irreversible illness-death model depicting three states, 0 (Healthy), 1 (Illness), and 2 (Dead), and the transition intensities between state j and state k (λ_jk(t|X)), where X is a vector of baseline covariates that can have transition-specific effects.

The observed data is given as ${𝒟}_n=\{T_i^{\ast },{\delta }_i,{\mathbf{X}}_i,{\mathbf{Z}}_i,V_i;i=1,\dots ,n\}$, where in addition to the previously described notation, V_i is the known, exact transition time from state 0 to state 1 for the ith individual if they have transitioned. Thus, using a joint model approach, the full likelihood can be written as

$$L=\prod _i\text{exp }[-\{1-Z_i(T_i^{\ast })\}\{{\mathrm{\Lambda }}_{01}(T_i^{\ast }|{\mathbf{X}}_i)+{\mathrm{\Lambda }}_{02}(T_i^{\ast }|{\mathbf{X}}_i)\}]{\lambda }_{02}{(T_i^{\ast }|{\mathbf{X}}_i)}^{{\delta }_i(1-Z_i(T_i^{\ast }))}\times \text{exp }[-Z_i(T_i^{\ast })\{{\mathrm{\Lambda }}_{01}(V_i|{\mathbf{X}}_i)+{\mathrm{\Lambda }}_{02}(V_i|{\mathbf{X}}_i)\}]{\lambda }_{01}{(V_i|{\mathbf{X}}_i)}^{Z_i(T_i^{\ast })}\times \text{exp }[-Z_i(T_i^{\ast })\{{\mathrm{\Lambda }}_{12}(T_i^{\ast }|{\mathbf{X}}_i)-{\mathrm{\Lambda }}_{12}(V_i|{\mathbf{X}}_i)\}]{\lambda }_{12}{(T_i^{\ast }|{\mathbf{X}}_i)}^{{\delta }_i{Z}_i(T_i^{\ast })}$$

where ${\mathrm{\Lambda }}_{\mathit{\text{ij}}}(t|\mathbf{X})={\int }_0^t{\lambda }_{\mathit{\text{ij}}}(u|\mathbf{X})\mathrm{d}u$ is the cumulative hazard. Using the likelihood, parameter estimates of the joint model can be obtained, from which the desired residual time distribution in Eqs. (2) and (3) are computed. Since it is unlikely that the exact transition times are observed in practice, this likelihood can be adjusted to accommodate interval-censored observation times (Commenges, 2002). Alternatively, a semi-Markov model, for which the transition to death from the illness state depends on the duration in the illness state, can be fit (Foucher et al., 2010).

2.2 Landmarking

Landmarking describes the approach in which models are proposed and estimation is conducted at a set of prediction times of interest, defined as landmark times. There are several models and estimation methods that exist within the landmarking framework. After a model is selected and fit, the required residual time distribution given by Eq. (1) can be calculated.

The idea behind landmarking is to preselect a landmark time, τ, at which there is interest in making a prediction. Given access to a database of patient information, if we were interested in predicting survival up to time τ + s for patients still alive at τ, we could select all the patients in the database alive at τ and estimate the probability of survival at τ + s using a survival model (e.g. Cox proportional hazards model). We may also be interested in considering many landmark times, τ₁, τ₂, …, τ_L, and developing a prediction model for each. To do this, we construct a prediction dataset for each landmark time, τ_l, which consists of individuals still alive at ${\tau }_l^{-}$, with administrative censoring at a prespecified horizon, t_hor = τ_l + s. These landmark data sets are then stacked to create a “super prediction data set” to which the landmark models are applied. We note that with the selection of multiple landmark times, the same patient contributes to the estimation of many of the predicted residual time distributions. It is also necessary that every subject have a value of Z at every landmark time. In practice this may not be the case, and Z must be imputed from a model for Z, or more commonly by using the last-observation-carried-forward (LOCF) approximation, which will be the method used in this paper.

In the most basic application of landmarking, we fit a separate model to each landmark dataset and estimate a landmark-specific effect of the marker for predicting survival between τ and a fixed horizon t_hor = τ + s. The basic landmark model is given as

$$h(t|\tau ,Z(\tau ),\mathbf{X})=h_0(t|\tau )\text{ exp}\{{\beta }_{\tau }Z(\tau )+\mathit{\zeta }\prime \mathbf{X}\}\text{ for }\tau \le t\le t_{\text{hor}}$$

where, the dependence of the baseline hazard on τ can be modeled by estimating a different baseline hazard for each τ, that is h₀(t|τ) = h_0τ (t).

As an alternative, we can apply a “super prediction model” to the stacked super dataset and allow the regression coefficients to depend on landmark time in a smooth, parametric way, such as with a linear or a quadratic function. This super model is defined as

$$h(t|\tau ,Z(\tau ),\mathbf{X})=h_0(t|\tau )\text{ exp}\{\beta (\tau )Z(\tau )+\mathit{\zeta }\prime \mathbf{X}\}\text{ for }\tau \le t\le t_{\text{hor}}$$ (4)

where β(τ) = Σ_j γ_jf_j(τ), with basis functions f_j(τ) and parameters γ_j. This model can be fit to the stacked super dataset using a Cox model with stratification on τ and interaction terms Z(τ)f_j(τ). For estimation we maximize a pseudo-partial log-likelihood, which is the sum over the partial loglikelihoods corresponding to the Cox models fit to each of the landmark datasets.

Instead of assuming a different baseline hazard for each τ, we can further extend this model to allow the baseline hazard to change smoothly with landmark time. Thus, the extended super model is given by

$$h(t|\tau ,Z(\tau ),\mathbf{X})=h_0(t)\text{ exp}\{\theta (\tau )+\beta (\tau )Z(\tau )+\mathit{\zeta }\prime \mathbf{X}\}\text{ for }\tau \le t\le t_{\text{hor}}$$ (5)

where θ(τ) = Σ_jη_jg_j(τ), with basis functions g_j(τ) and parameters η_j. In this model, g_j(τ) are now covariates. The pseudo partial log-likelihood for this model differs slightly from the one for the model in Eq. (4). Details are given in van Houwelingen (2007).

This landmark super model can be generalized further. In Eq. (5), the effect of Z depends on τ but it does not depend on t; thus, it still has a proportional hazards structure. For some applications it may be more appropriate to assume that the effect of Z depends on the time t − τ and to include a term Z(τ)ω(t − τ), where ω(s) is a smooth function of s. Thus, we can use the nonproportional hazards extended super model given by

$$h(t|\tau ,Z(\tau ),\mathbf{X})=h_0(t)\text{ exp}\{\theta (\tau )+\beta (\tau )Z(\tau )+\omega (t-\tau )Z(\tau )+\mathit{\zeta }\prime \mathbf{X}\}\text{ for }\tau \le t\le t_{\text{hor}}$$ (6)

3 Landmark Cox model construction corresponding to the illness-death model

We now consider landmarking when Z is a binary covariate process. Under the landmark approach, when making a prediction for a new subject at landmark time τ, we use all available information at that landmark time. This method does not directly incorporate possible future transitions to illness. Since landmarking uses the LOCF approximation, if the marker process covariate, Z_i, is 0 at the time of the individual’s last observation t_il before τ, then we set Z(τ) = 0. Thus, it is implicitly assumed the individual does not transition to the illness state between t_il and τ. Under the joint modeling approach, when predicting for a new individual we integrate over all possible paths of an individual through the illness-death model, including the individual possibly progressing to illness state after their last inspection but before τ. Thus, for individuals with Z(t_il) = 0, if there is interest in predicting for landmark times far later than t_il, joint modeling can be expected to provide a better prediction than landmarking.

We can also demonstrate that the standard landmark approach uses a model that is not compatible with the illness-death model. To model the residual time distribution in a landmarking framework with binary Z, we consider the super landmark model in Eq. (4). If the proportional hazards assumption in the landmark Cox model is to hold then it is necessary that β(·) in Eq. (4) does not depend on t. We will investigate whether it is possible under the illness-death model to achieve a form for β(·) that is independent of t. If not, then we will examine how β(τ) can be generalized to better approximate the correct residual time distribution.

For the purposes of our derivation, we reparameterize the hazard in Eq. (4) as follows:

$$h(t|\tau ,Z(\tau ),\mathbf{X})=h_0(t|\tau )\text{ exp }\{\beta (\tau )(1-Z(\tau ))+\mathit{\zeta }\prime \mathbf{X}\}$$ (7)

We can then define the residual time distribution for the Cox-type landmark model as surviving to time τ + s, s > 0, given the individual was alive at landmark time τ with an illness indicator Z(τ). From Eq. (7), this can be written as

$$\text{Pr}(T\ge \tau +s|T>\tau ,\mathbf{X},Z(\tau ))=\text{exp }[-{\int }_{\tau }^{\tau +s}{h}_0(u|\tau )\text{ exp }\{\beta (\tau )(1-Z(\tau ))+\mathit{\zeta }\prime \mathbf{X}\}\mathrm{d}u]$$ (8)

3.1 Equating residual time distribution

To determine the form for β(τ) and h₀(t|τ) in Eq. (7) that corresponds to the illness-death model, we equate the appropriate residual time distributions for the two models. Starting with the situation where the individual transitioned to the illness state by time τ, it is required that Eq. (8) for Z(τ) = 1 and Eq. (3) are equal, hence

$$\text{exp }\{-{\int }_{\tau }^{\tau +s}{h}_0(u|\tau )\text{ exp}(\mathit{\zeta }\prime \mathbf{X})\mathrm{d}u\}=\text{exp }\{-{\int }_{\tau }^{\tau +s}{\lambda }_{12}(u|\mathbf{X})\mathrm{d}u\}\Rightarrow h_0(u|\tau )\text{ exp}(\mathit{\zeta }\prime \mathbf{X})={\lambda }_{12}(u|\mathbf{X})\text{ for all }\tau$$ (9)

Thus, the hazard for the Cox-type model in the landmark approach conditional on being in the illness state is equivalent to the transition intensity from illness to death. Notice that it has the same form for all landmark times.

For the situation where the individual has not yet transitioned to illness, we require that Eq. (8) for Z(τ) = 0 and Eq. (2) are equal, thus

$$\text{exp }\{-{\int }_{\tau }^{\tau +s}{h}_0(u|\tau )\text{ exp}(\beta (\tau )+\mathit{\zeta }\prime \mathbf{X})\mathrm{d}u\}=\text{Eq}.(2)\Rightarrow \beta (\tau )+\mathit{\zeta }\prime \mathbf{X}=\text{log }[-\frac{\text{log}\{\text{Eq}.(2)\}}{{\int }_{\tau }^{\tau +s}{h}_0(u|\tau )\mathrm{d}u}]$$

Substituting in the value for h₀(u|τ) from Eq. (9):

$$\Rightarrow \beta (\tau )+\mathit{\zeta }\prime \mathbf{X}=\text{log}[-\text{log}\{\text{Eq}.(2)\}]-\text{log}\{{\int }_{\tau }^{\tau +s}{\lambda }_{12}(u|\mathbf{X})\mathrm{d}u\}$$ (10)

which is the form for the covariate effects from the landmark Cox regression model that corresponds to an illness-death model. Notice that the required form for β(τ) given on the right-hand side of Eq. (10) is quite complicated since it involves Eq. (2), which is composed of two additive terms. Also, notice that it is dependent on both s and τ, which violates the form of the simple Cox regression model desired for the landmark setting, that is β(·) dependent only on τ. Thus, a landmark approach with a proportional hazards assumption is not the correct method when the true data generative model is an illness-death model.

If ${\lambda }_{12}(u|\mathbf{X})={\lambda }_{12,0}(u)\text{ exp}\{{\mathit{\alpha }}_{12}^{\prime }\mathbf{X}\}$, then ζ = α₁₂. The form of X on the right-hand side of Eq. (10) is not linear in X and furthermore, it depends on three separate linear combinations, ${\mathit{\alpha }}_{01}^{\prime }\mathbf{X},{\mathit{\alpha }}_{02}^{\prime }\mathbf{X}$, and ${\mathit{\alpha }}_{12}^{\prime }\mathbf{X}$, rather than one. If there are several baseline covariates, the covariate vector can be different for each transition, which will also not be captured by the linear form of X in the Cox model. This suggests that the landmark Cox models should include more flexible forms for X, such as ζ(τ)′X, or an interaction, such as ϕ′XZ(τ).

We now consider special cases for the transition intensities to identify situations in which the derived forms for the landmark Cox baseline hazard and covariate effects provide good approximations of the residual time distribution under the illness-death model.

3.1.1 Constant and equal baseline transition intensities

Under the simplest situation of constant and equal baseline transition intensities, ${\lambda }_{\mathit{\text{jk}}}(t|\mathbf{X})=\psi \text{ exp}\{{\mathbf{\alpha }}_{\mathit{\text{jk}}}^{\prime }\mathbf{X}\}$, we obtain the following form for the baseline hazard and covariate effects under the Cox landmark model from Eqs. (9) and (10),

$$h_0(t|\tau ,\mathbf{X})\text{ exp}(\mathit{\zeta }\prime \mathbf{X})=\psi \text{ exp}({\mathit{\alpha }}_{12}^{\prime }\mathbf{X})$$

$$\beta (\tau )+\mathit{\zeta }\prime \mathbf{X}=\text{log }[-\text{log}(\text{exp }\{-\psi s(e^{{\mathit{\alpha }}_{02}^{\prime }\mathbf{X}}+e^{{\mathit{\alpha }}_{01}^{\prime }\mathbf{X}})\}+\frac{\text{exp }({\mathit{\alpha }}_{01}^{\prime }\mathbf{X}-\psi {\mathit{\text{se}}}^{{\mathit{\alpha }}_{12}^{\prime }\mathbf{X}})\{1-\text{exp }\{-\psi s(e^{{\mathit{\alpha }}_{02}^{\prime }\mathbf{X}}+e^{{\mathit{\alpha }}_{01}^{\prime }\mathbf{X}}-e^{{\mathit{\alpha }}_{12}^{\prime }\mathbf{X}})\}\}}{e^{{\mathit{\alpha }}_{02}^{\prime }\mathbf{X}}+e^{{\mathit{\alpha }}_{01}^{\prime }\mathbf{X}}-e^{{\mathit{\alpha }}_{12}^{\prime }\mathbf{X}}}\left)\right]-\text{log}[\psi {\mathit{\text{se}}}^{{\mathit{\alpha }}_{12}^{\prime }\mathbf{X}}]$$

The form for the covariate effects does not resemble a structure that is implementable within a standard Cox regression in the landmark approach. Also, β(τ) is dependent on s and violates the form of a simple Cox regression model in the landmark setting, which assumes that β depends only on τ.

3.1.2 Proportional hazards transition intensities

For the situation with proportional hazards transition intensities, we define the transition intensity for j → k as λ_jk(t|X) = λ_jk,0(t) exp{α′X}, where λ_jk,0(t) is the baseline transition intensity for the j → k transition, such that λ_02,0(t) = λ(t), λ_01,0(t) = γλ(t), λ_12,0(t) = ηλ(t). We denote the cumulative hazard $\mathrm{\Lambda }(t)={\int }_0^1\lambda (u)\mathrm{d}u$. Then from Eqs. (9) and (10), we derive

$$h_0(t|\tau ,\mathbf{X})\text{ exp}(\mathit{\zeta }\prime \mathbf{X})=\eta \lambda (t)\text{ exp}(\mathit{\alpha }\prime \mathbf{X})$$

$$\beta (\tau )+\mathit{\zeta }\prime \mathbf{X}=\text{log }[-\text{log }(\frac{1-\eta }{1+\gamma -\eta }\text{exp }\{-(1+\gamma )e^{\mathit{\alpha }\prime \mathbf{X}}[\mathrm{\Lambda }(\tau +s)-\mathrm{\Lambda }(\tau )]\}+\frac{\gamma }{1+\gamma -\eta }\text{exp }\{-\eta e^{\mathit{\alpha }\prime \mathbf{X}}[\mathrm{\Lambda }(\tau +s)-\mathrm{\Lambda }(\mathrm{\tau })]\}\left)\right]-\text{log }[\eta e^{\mathit{\alpha }\prime \mathbf{X}}\{\mathrm{\Lambda }(\tau +s)-\mathrm{\Lambda }(\tau )\}]$$

In this scenario, the form of the covariate effects also does not have a Cox proportional hazards structure. Here, β(τ) is dependent on both τ and s, unless λ(t) is a constant. As the flexibility of the transition hazards in the illness-death model is increased, we find that the corresponding form of the covariate effects under the landmark approach is not consistent with a Cox regression model and depend on both τ and s. Allowing the effect of the baseline covariates to vary with transition, the forms of the baseline hazard and covariate effects are even more complicated.

3.1.3 Short prediction horizon

Since we are typically most interested in short-term predictions, we also consider whether the Cox model in the landmark framework approximately satisfies a proportional hazards assumption for small time horizons of interest. Thus, we explored obtaining a simpler form of the derived residual time distribution using the Taylor approximation. Taking the second-order Taylor expansion of log(Eq. (2)) and log(Eq. (3)) about s = 0, we get the following approximation of the residual time distribution for small s

$$\text{Pr}(T\ge \tau +s|T>\tau ,\mathbf{X},Z(\tau )=0)\approx \text{exp }\{-{\lambda }_{02}(\tau |\mathbf{X})s-\frac{1}{2}[{\lambda }_{02}^{\prime }(\tau |\mathbf{X})-{\lambda }_{02}(\tau |\mathbf{X}){\lambda }_{01}(\tau |\mathbf{X})+{\lambda }_{01}(\tau |\mathbf{X}){\lambda }_{12}(\tau |\mathbf{X})]s^2\}$$

$$\text{Pr}(T\ge \tau +s|T>\tau ,\mathbf{X},Z(\tau )=1)\approx \text{exp }\{-{\lambda }_{12}(\tau |\mathbf{X})s-\frac{1}{2}{\lambda }_{12}^{\prime }(\tau |\mathbf{X})s^2\}$$

Taking the derivative of the negative log of these equations, and denoting t = τ + s, gives us the hazard functions

$$h(t|T\ge \tau ,\mathbf{X},Z(\tau )=0)={\lambda }_{02}(\tau |\mathbf{X})-[{\lambda }_{01}^{\prime }(\tau )-{\lambda }_{02}(\tau |\mathbf{X}){\lambda }_{01}(\tau |\mathbf{X})+{\lambda }_{01}(\tau |\mathbf{X}){\lambda }_{12}(\tau |\mathbf{X})](t-\tau )$$

$$h(t|T\ge \tau ,\mathbf{X},Z(\tau )=1)={\lambda }_{12}(\tau |\mathbf{X})+{\lambda }_{12}^{\prime }(\tau |\mathbf{X})(t-\tau )$$

These hazards do not have the form of proportional hazards. Thus, to achieve consistency between the illness-death model and the landmark approach we need a broader class of landmark models that accommodates the derived form of the hazards and contains the Cox proportional hazards model as a special case.

Based on the derivations in this section, we conclude that Cox proportional hazards within the landmark framework is not an appropriate model for the residual time distribution arising from an illness-death model. We have shown that in plausible scenarios the covariate effects are a function of both τ and s = t − τ and that the effect of baseline covariates is unlikely to be well described by a simple, single linear combination. For the more likely, but complicated, scenario of an illness-death model with transition-specific baseline intensities and covariate effects, the associated h₀(t|τ, X) and β(τ) are nonstandard and the super landmark model does not provide a good theoretical approximation of the residual time distribution. Thus, we use a simulation study to explore the performance of extensions within the landmark framework that accommodate nonproportional hazards, coefficient effects of Z as a function of τ and s, more complex forms for the baseline covariate effects X, and interactions between Z and X.

4 Simulation study

The aims of our simulation study were to compare the predictive performance of joint and landmarking models in the context of illness-death data, and to evaluate whether increased landmark model flexibility provides a better approximation to the true model.

4.1 Data generation and structuring

Five hundred simulations of n = 500 subjects were run for each scenario. Defining the states as {0: Healthy, 1: Ill, 2: Dead}, the ages at illness onset and death without illness were generated from

$${\lambda }_{\mathit{\text{jk}}}(t_i|{\mathbf{X}}_i)=(\frac{{\rho }_{\mathit{\text{jk}}}}{{\kappa }_{\mathit{\text{jk}}}}\left){\left(\frac{t_i}{{\kappa }_{\mathit{\text{jk}}}}\right)}^{{\rho }_{\mathit{\text{jk}}}-1}\text{ exp }\right\{{\mathit{\alpha }}_{\mathit{\text{jk}}}^{\prime }{\mathbf{X}}_i\}\text{ for }j=0,k=1,2$$ (11)

For the transition intensity from illness to death (1 → 2), we generate data under two different models: (1) Markov, where the transition intensity depends only on current time and (2) semi-Markov (“clockreset”), where the transition depends on duration in the illness state. Under the Markov model, λ₁₂(t|X) is given as in Eq. (11). Under the semi-Markov model, given the known transition time V, the transition intensity from illness to death is specified as ${\lambda }_{12}^{\mathit{\text{SM}}}(t|\mathbf{X},V)={\lambda }_{12}(t-V|\mathbf{X})$.

We choose the transition intensity shape and scale parameters such that λ₁₂(t) > λ₀₂(t) > λ₀₁(t) [ρ_jk = 1.15 for all j → k; κ₀₁ = 20; κ₀₂ = 12.5; κ₁₂ = 10]. We simulate a binary baseline covariate, X, that has a stronger effect on death in ill subjects, with α₀₁ = 0.5, α₀₂ = 0.5, α₁₂ = 2. We explored simulating the exposure prevalence of X from 5% to 50%, but present only the results for 40% due to the similarity of results under other percentages. We simulate right-censoring from an exponential distribution with mean 80 and apply administrative censoring at time 20 to achieve a 15% censoring rate. We simulate marker measurement under two patterns of observation: (1) the marker process is continuously observed (then the exact transition time from “healthy” to “ill” is observed) and (2) the value of the marker is observed at random inspection times. Under the scenarios where the marker, Z, is measured at inspection times, inter-inspection times are exponentially distributed with rate 0.5.

We assume that there is interest in dynamic prediction for the first five years following baseline. Thus, we use an equally spaced grid of landmark times from time 0 to time 5, every 0.2 years. The endpoint of interest is death within a prediction window of s = 1, 3, 5 years from the prediction time. To structure the data as a super dataset, we create a landmark dataset for each τ, with administrative censoring at τ + s, and stack the landmark data sets. We also structure the data as a longitudinal dataset for the setting with simulated inspection times. In this dataset, each patient contributes a row for each of their inspection times (t_il, l = 1,…, n_i), with administrative censoring of their event times at t_il + s.

4.2 Joint models

Under the joint modeling approach, we fit both Markov and semi-Markov models. Defining ${\lambda }_{\mathit{\text{ij}},0}^W(t)$ and ${\lambda }_{\mathit{\text{jk}},0}^{\mathit{\text{Cox}}}(t)$ as the baseline hazards of a Weibull model and Cox proportional hazards model, respectively, we fit the parametric and semi-parametric joint models (MM), (MMCox), (MSM), (MSMCox), and (SMM) shown in Table 1.

Table 1.

Joint models fit in simulation study.

Model	Baseline hazard	Transition intensity ∀ j → k	Label
Markov λjk(t|X	Parametric	${\lambda }_{\mathit{\text{jk}},0}^W(t)\text{exp}\{{\alpha }_{\mathit{\text{jk}}}X\}$	(MM)
	Semi-parametric	${\lambda }_{\mathit{\text{jk}},0}^{\mathit{\text{Cox}}}(t)\text{exp}\{{\alpha }_{\mathit{\text{jk}}}X\}$	(MMCox)
Markov, V*λjk(t|X,V*)	Parametric	${\lambda }_{\mathit{\text{jk}},0}^W(t)\text{exp}\{{\alpha }_{\mathit{\text{jk}}}X+\gamma V^{\ast }\mathbf{1}(j=1,k=2)\}$	(MSM)
	Semi-parametric	${\lambda }_{\mathit{\text{jk}},0}^{\mathit{\text{Cox}}}(t)\text{ exp}\{{\alpha }_{\mathit{\text{jk}}}X+\gamma V^{\ast }\mathbf{1}(j=1,k=2)\}$	(MSMCox)
Semi-Markov λjk(t|X,V*)	Parametric	${\lambda }_{\mathit{\text{jk}},0}^W(t)(t-V^{\ast }\mathbf{1}(j=1,k=2))\text{ exp}\{{\alpha }_{\mathit{\text{jk}}}X\}$	(SMM)

For (MM) we fit a Markov illness-death model with Weibull hazard transition intensities. (MMCox) fits the model with semi-parametric transition intensities using a Cox proportional hazards model. These models are extended to (MSM) and (MSMCox) to account for the effect of the observed transition time, V^*, by including it as a covariate. For (SMM) we fit a semi-Markov illness-death model.

Estimation is conducted using methods described in Section 2.1 with the R packages SmoothHazard for (MM) (Touraine et al., 2014), mstate for (MMCox) and (MSMCox) (de Wreede et al., 2011), and the function optim for the optimization of the likelihood for (MSM) and (SMM) using the quasi-Newtonian algorithm, the code for which is available in the Supporting Information materials. We plug in the resulting estimates (λ̂_jk) into 1–Eq. (2) and 1–Eq. (3) to produce dynamic predictions of death within s years for landmark time τ_l. Note that for the models that are conditional on V^*, we replace λ₁₂(u|X) with λ₁₂(u|X, ν) in Eq. (2) and λ₁₂(u|X) with λ₁₂(u|X,V) in Eq. (3).

4.3 Landmark models

Motivated by the derivations in Section 3 and based on the equations in Section 2.2, we fit the landmark models (LM1), (LM2), (LM3), and (LM4) given in Table 2 to the simulated data, where β(τ) = β₀ + β₁τ + β₂τ², θ(τ) = θ₁τ + θ₂τ², ω(s) = ω₁s + ω₂s².

Table 2.

Landmark models fit in simulation study.

Model	Hazard	Label2
LM1	h0τ (t)exp{β(τ)Z(τ) + ζX}	(LM1)
h(t|τ,Z(τ), X)	h0(t) exp{θ(τ) + β(τ)Z(τ) + ζX}	(LM2)
	h0(t) exp{θ(τ) + β0Z(τ) + ω(t − τ)Z(τ) + ζX}	(LM3)
	h0(t) exp{θ(τ) + β(τ)Z(τ) + ω(t − τ)Z(τ) + ζX}	(LM4)
LM, V*	h0τ(t) exp{β(τ)Z(τ) + γV*Z(τ) + ζX}	(LSM1)
h(t|τ, Z(τ), X,V*	h0(t) exp{θ(τ) + β(τ)Z(τ) + γV*Z(τ) + ζX}	(LSM2)
	h0(t) exp{θ(τ) + β0Z(τ) + ω(t − τ)Z(τ) + γV*Z(τ) + ζX}	(LSM3)
	h0(t) exp{θ(τ) + β(τ)Z(τ) + ω(t − τ)Z(τ) + γV*Z(τ) + ζX}	(LSM4)
LM, Interaction	h0(t) exp{θ(τ) + β(τ)Z(τ) + ζ′X + ϕ′XZ(τ)}	(LMInt2)
h(t|τ, Z(τ), X)	h0(t) exp{θ(τ) + β0Z(τ) + ω(t − τ)Z(τ) + ζ′X + ϕ′XZ(τ)}	(LMInt3)
	h0(t) exp{θ(τ) + β(τ)Z(τ) + ω(t − τ)Z(τ) + ζ′X + ϕ′XZ(τ)}	(LMInt4)

¹LM: landmark model;

²(*1): Super model; (*2): Extended super model; (*3): Extended super model, nonproportional hazards; (*4): Extended super model, non-proportional hazards, covariate effects are a function of landmark time

For estimation, under the super dataset structuring, the τ’s in (LM1–LM4) correspond to the chosen grid of landmark (prediction) times. Under the longitudinal data structuring, only (LM2), (LM3), and (LM4) apply, and the τ’s represent the inspection times. The landmark datasets are created using the dynpred package in R (Putter, 2015). In (LM1) we fit a simple Cox model with a different baseline hazard for each τ. Thus, this approach can only be applied when we prespecify the landmark times and construct the super dataset based on these landmark times. In (LM2), we still fit a simple Cox model, but parameterize the baseline hazard to depend smoothly on τ, resulting in decreased model flexibility but allowing us to fit the model to our longitudinal dataset. In (LM3), we propose a model that allows for non-proportional hazards by including the covariates ω(s)Z(τ) that are a function of s = t − τ, to accommodate time-varying effects of our covariate process. In (LM4), we extend the Cox model to include both β(τ) and ω(t − τ), since in Section 3 we showed that under the illness-death model the form for the covariate effects for the Cox regression model in the landmark framework was a function of both s and τ.

Under the semi-Markov model for generating data, modeling complications arise due to the change in time scale between the transitions. Thus, for simplicity, we can incorporate the dependency of transition on the observed illness time, V^*, by including it as a covariate in the landmark models. Thus, we modify the models (LM1–LM4) to be conditional on V^* with parameter γ, and fit the models (LSM1), (LSM2), (LSM3), and (LSM4) given in Table 2.

After obtaining the estimates from these parameterizations (β̂, θ̂, ζ̂, ω̂, γ̂), we compute the dynamic predictions of death within a window of s years at the prespecified landmark times, τ_l, using the following equation

$$\text{Pr}(T\le {\tau }_l+s|T>{\tau }_l,Z({\tau }_l),X,V)=1-\text{exp }\{-{\int }_{{\tau }_l}^{{\tau }_l+s}h(u|Z({\tau }_l),X,V,\hat{\beta },\hat{\theta },\hat{\omega },\hat{\zeta },\hat{\gamma })\mathrm{d}u\}$$

In addition to the basic scenario of a single baseline covariate, we also evaluated the performance of landmark models when the baseline covariate vector varies by transition. We generate data with two binary baseline covariates, X₁ that has a stronger effect on death in ill subjects [α_01,1 = α_02,1 = 0.5, α_12,1 = 2] and X₂, which has no effect on death [α_01,2 = 1, α_02,2 = α_12,2 = 0]. We fit the joint models (MM) and (MMCox) with the covariates X₁ and X₂. We modify ζX in models (LM1–LM4) to ζ′X where ζ = (ζ₁, ζ₂) and X = (X₁,X₂) are the parameter and baseline covariate vectors, respectively. We also fit the additional models (LMInt2), (LMInt3), and (LMInt4), given in Table 2, that include an interaction term with illness status and parameter vector ϕ = (ϕ₁, ϕ₂).

4.4 Performance comparison metrics

The dynamic predictions produced at the sequence of landmark times are compared to the true death probabilities. These are obtained by using the true shape and scale parameters to get the true transition intensities and then using numerical integration to compute the true death probability within window s from Eqs. (2) and (3), replacing λ₁₂(u|X) with λ₁₂(u|V^*, X) when generating under the semi-Markov model. For each landmark time, we compute the bias and variance of the dynamic predictions under the landmark approaches and joint model.

To assess the discrimination and calibration of these dynamic predictions, we use the dynamic analogues of weighted area under the curve (AUC) and Brier score that account for censored data, denoted AUC(τ, s) and BS(τ, s), respectively, for landmark time τ and fixed prediction window s (Blanche et al., 2015). Since BS depends on the cumulative incidence of death in (τ, τ + s], we used a standardized version that results in an R²-type measure that compares how well the predictions perform compared to a null model that assumes that all subjects have the same predicted risk of death regardless of subject-specific information, BS₀(τ, s). We denote this scaled measure R²(τ, s) = 1 − BS(τ, s)/BS₀(τ, s).

To make comparisons between the different models, we compute AUC and R² using the prediction probabilities from the true models, denoted AUC_True and $R_{\text{True}}^2$, respectively. We then report the relative measures ΔAUC = AUC_True − AUC and $\mathrm{\Delta }{R}^2=R_{\text{True}}^2-R^2$ for each of the models, with a higher value indicating better performance.

For cross-validation, in each simulation all of the described models were fit to a training dataset, created by randomly selecting 4/5 of the simulated individuals. The remaining 1/5 individuals were treated as the validation dataset, from which predicted conditional death probabilities within the window (τ, τ + s] were obtained for those still alive at time τ.

4.5 Simulation results

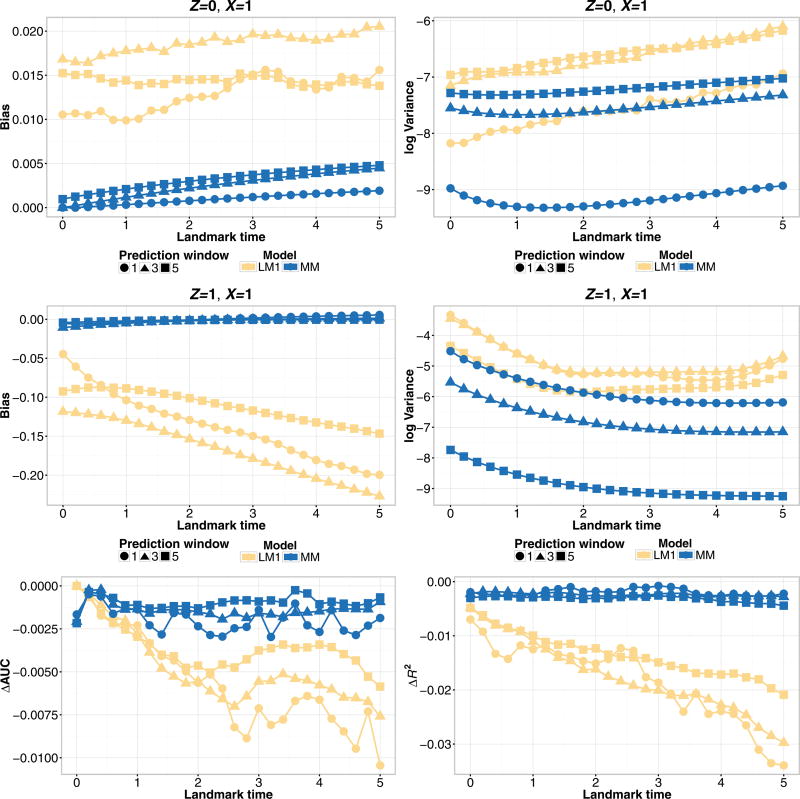
Figure 2 compares the performance of the landmark model (LM1) and the joint model (MM) under a Markov assumption with a single baseline covariate for the various prediction windows, s = 1, 3, 5. The joint model performs better than the landmark model across all of the prediction windows in terms of all of the considered metrics. For Z = 0, as the prediction window increases, the bias and variance of the joint model increases, with the reverse effect for Z = 1. There is no pattern of performance for the landmark model (LM1) across s. However, within each prediction window, the relationship between the performance of the different landmark models was consistent. Thus, we present the remaining simulation results for a single prediction window, s = 3. As well, we will focus on Z = 1 for reporting the bias and variance since the absolute bias of the models is higher than for Z = 0.

Figure 2.

Simulation estimates for bias (upper-left), variance (upper-right), ΔAUC (bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + s|T > τ,Z(τ),X) for s = 1, 3, 5-year prediction windows from joint model (MM) and landmark model (LM1), under a Markov illness-death model with a single baseline covariate and continuously observed marker measurement.

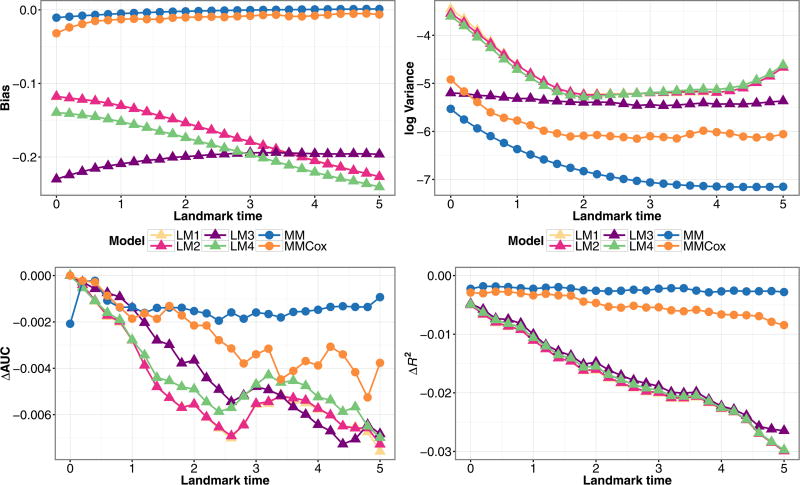
We compare the landmark and joint models in Fig. 3, which depicts the performance of the models for Z = 1, X = 1, s = 3 for a continuously observed marker. Across all the landmark times, the joint models perform the best in terms of bias, variance, ΔAUC and ΔR², and thus give more accurate predictions than the landmark models. Within the joint models, the semi-parametric model (MMCox) performs almost as well as the parametric model under which the data was generated, (MM), and both outperform the landmark models, which can have high absolute bias. In comparing the landmark models, model (LM3), which includes time-varying effects, has the lowest variance, but has the highest bias for early landmark times. The bias for model (LM3) decreases with increasing landmark time, while it increases for the other landmark models. Model (LM4), which incorporates both landmark and residual time, performed similarly to the simpler landmark models (LM1) and (LM2). All the landmark models had similar ΔAUC and ΔR². Thus, incorporating additional flexibility into the landmark models did not translate into less deviation from the true predicted probabilities or substantially better predictive performance. Due to their similar performance to (LM4), for the remaining figures we omit the results of (LM1) and (LM2).

Figure 3.

Simulation estimates for bias (upper-left) and variance (upper-right) for Z(τ) = 1, X = 1, ΔAUC(bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + 3|T > τ,Z(τ),X) from the joint models (MM), (MMCox), and landmark models (LM1–LM4), under a Markov illness-death model with a single baseline covariate and continuously observed marker measurement.

In Fig. 4, we compare the different methods of data structuring. When the marker is continuously observed there is more information available than when the process is observed at inspection times, and thus performance is better across all the metrics. Within the inspection times simulations, with the exception of the bias for the landmark model with nonproportional hazards, the longitudinal dataset outperformed the super dataset across all four performance metrics for all the landmark models. Since this relationship persisted in our simulation results, and it is unlikely that markers are observed continuously in practice, we will only present the results from the “longitudinal dataset, inspection times marker measurement” scenarios in the rest of our comparisons.

Figure 4.

Simulation estimates for bias (upper-left) and variance (upper-right) for Z(τ) = 1, X = 1, ΔAUC(bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + 3|T > τ,Z(τ),X) from the joint model (MM) and landmark models (LM3), (LM4) fit to data structured as a super or longitudinal dataset, under a Markov illness-death model with a single baseline covariate and continuously observed (CO) or inspection time (IT) marker measurement.

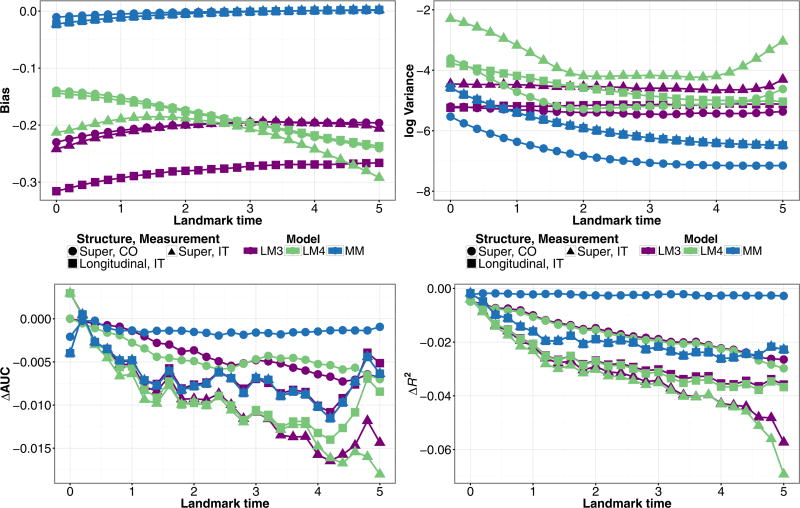
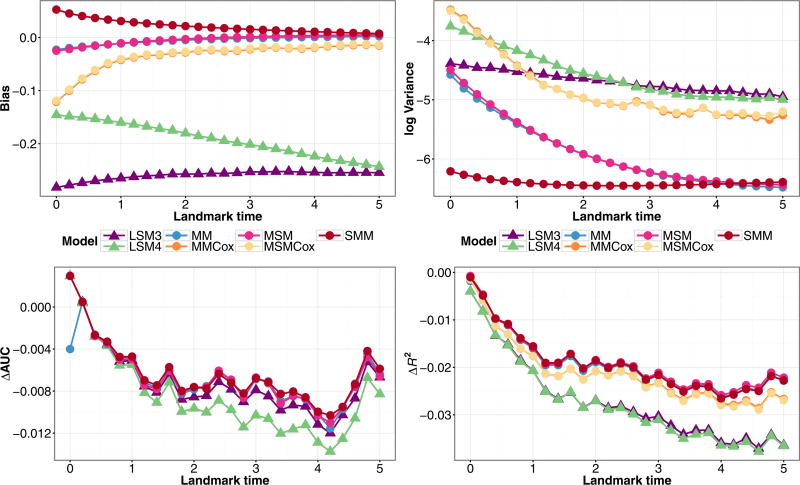
Figure 5 shows the results from models that condition on observed illness time applied to data generated from a Markov illness-death model. Among the joint models, parametric Markov model (MM) and semi-parametric (MMCox) had similar performance. The joint models that condition on V^*, (MSM) and (MSMCox), had nearly identical performance to their corresponding Markov models, and still have better performance metrics than the landmark models. The semi-Markov model (SMM) had almost identical predictive performance to (MM), and had similar bias to the other joint models and the lowest variance for early landmark times. The performance of the landmark models (LSM3) and (LSM4) did not significantly change by conditioning on V^*. Thus, when simulating under a Markov assumption, conditioning on observed illness does not affect model performance.

Figure 5.

Simulation estimates for bias (upper-left) and variance (upper-right) for Z(τ) = 1,X = 1, ΔAUC(bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + 3|T > τ,Z(τ),X) from joint models (MM), (MMCox), (MSM), (MSMCox), (SMM), and landmark models (LSM3), (LSM4) fit to data structured as a longitudinal dataset, under a Markov illness-death model with a single baseline covariate and inspection time marker measurement.

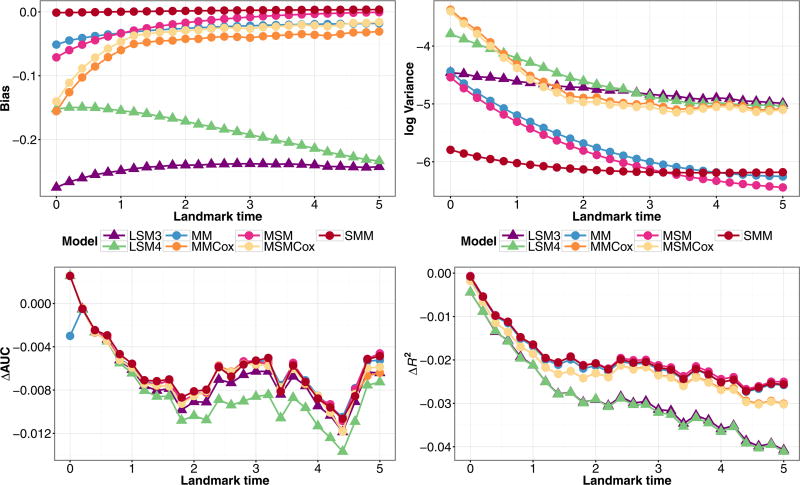
In Fig. 6, we fit these same models to data generated under a semi-Markov illness-death model. The predicted probabilities for determining the bias and variance were computed given V = 2τ/3, for landmark time τ. The results were very similar to those in Fig. 5. The (SMM) model performed the best, with the models that account for transition time performing marginally better than their counterparts, but with a greater distinction than in Fig. 5. Since the gains are minimal, but existent, when conditioning on the observed illness time in our particular situation, there is an indication that these models will outperform the Markov models in other simulation scenarios.

Figure 6.

Simulation estimates for bias (upper-left) and variance (upper-right) for Z(τ) = 1,X = 1, ΔAUC(bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + 3|T > τ,Z(τ),X) from joint models (MM), (MMCox), (MSM), (MSMCox), (SMM), and landmark models (LSM3), (LSM4) fit to data structured as a longitudinal dataset, under a semi-Markov illness-death model with a single baseline covariate and inspection time marker measurement.

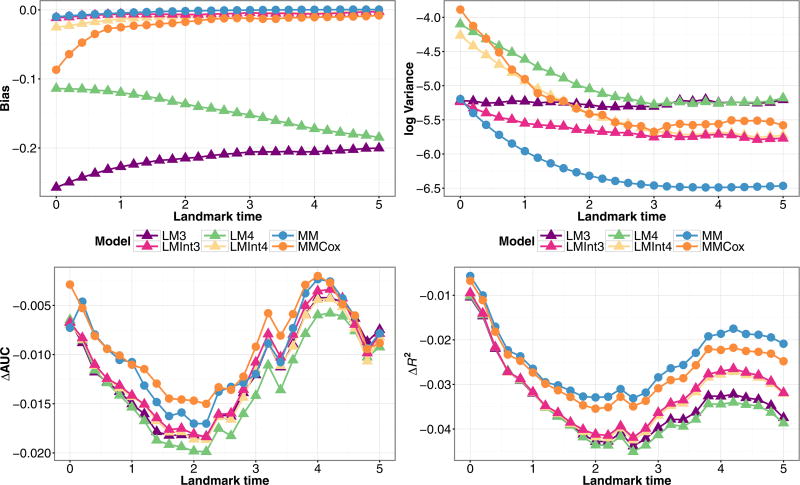
Finally, we consider the situation where we simulate two baseline covariates with different effects on each transition. From Fig. 7, we see that by including the interaction term XZ(τ), the performance of the landmark models is on par with the joint models in terms of bias. The landmark models with the interaction term have lower variance, better ΔR², and similar ΔAUC than those without the interaction. Thus, including an interaction term in the landmark Cox model captures the effect of baseline covariate vectors that differ by transition better than a linear function of X and provides a much better approximation to a joint model.

Figure 7.

Simulation estimates for bias (upper-left) and variance (upper-right) for Z(τ) = 1,X₁ = 1,X₂ = 1, ΔAUC (bottom-left), and ΔR² (bottom-right) for predicted probability P(T ≤ τ + 3|T > τ,Z(τ),X) from joint models (MM), (MMCox), and landmark models (LM3), (LM4), (LMInt3), (LMInt4) fit to data structured as a longitudinal dataset, under a Markov illness-death model with two baseline covariates and inspection time marker measurement.

Overall, based on the set of scenarios considered, the simulation results show that joint modeling gives better performance than landmarking. The difference is generally quite small, with the exception of bias for which the landmarking approach can have high absolute bias. The results suggest that more general landmark models than the simplest (LM1) can improve performance and that given inspection time data, using a longitudinal structure for the landmark dataset produces better predictions than a super dataset. The results also indicate that misspecification of the joint model did not affect predictive performance.

5 Applications to real data

In this section, we apply landmarking and joint models to data from two different studies that can be modeled with an illness-death model and have information collected beyond baseline on a binary time-dependent covariate. The large PAQUID study on cognitive aging provides interval-censored inspection time data for transition time to the illness state and allows us to use cross-validation to compare the predictive performance of the methods under longitudinal and super data structures. We also apply the models to data from a prostate cancer study with continuously observed time to clinical failure to compare the coefficient interpretations and dynamic predictions produced under the two approaches.

5.1 PAQUID study of cognitive aging

We evaluate the predictive abilities of landmark and joint models using data collected by the PAQUID study. The Personnes Agées QUID (PAQUID) Study is a large, prospective cohort study of cognitive and physical aging (Dartigues et al., 1992). We use data from the R package SmoothHazard (Touraine et al., 2014) on a random subset of 1000 subjects from the original study, which consisted of 3777 individuals aged 65 years and older living in southwestern France. Subjects had 10 visits over 20 years at which they were assessed for dementia. The longitudinal dataset was created using interval-censored observations and the approximate visit times 1, 3, 5, 8, 10, 13, 15, 17, 20 years from the initial visit.

There were 186 subjects that were diagnosed with dementia. Of the 724 deaths, 597 died without a dementia diagnosis and 127 died after diagnosis. We model the data as an illness-death model with the states, “alive without dementia”, “alive with dementia”, and “dead”. The baseline covariates are age at study entry (median 74; IQR 69–79), gender (female: 58%, male: 42%), and primary school diploma status (with diploma: 76%, without diploma: 24%).

This data represents the typical dataset for which there is interest in determining the probability of death at a given landmark time beyond baseline of study enrollment. It involves a high-risk group of individuals for which there is future information, that is dementia diagnosis, that can affect their risk of death and thus must be incorporated into prediction models to produce accurate and updated prediction probabilities. This study also involves diagnosis updates at inspection times, which allows us to evaluate the landmark models by structuring the data as both a super dataset and a longitudinal dataset. The large size of the dataset allows us to perform cross-validation to prevent overfitting when assessing model performance.

We fit both landmark and joint models as in the simulation study. The subject-specific predictions were computed at the landmark times τ = 0, 1, 3, 5, 8, 10 years for a prediction window of s = 3, 5, 7 years. The estimates for assessing predictive accuracy were obtained by performing cross-validation based on repeated random subsampling. The data were split into 2/3 training data, to which the models were fit, and AUC and R² were computed for predictions from the remaining 1/3 validation data. This procedure was repeated 500 times. We present the averaged dynamic AUC and R² values under the super and longitudinal data structure for s = 5, since the other prediction windows showed similar patterns.

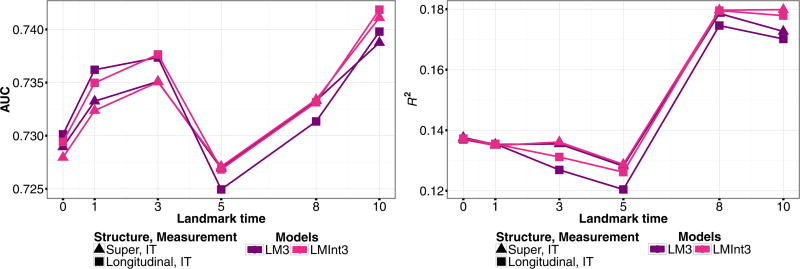
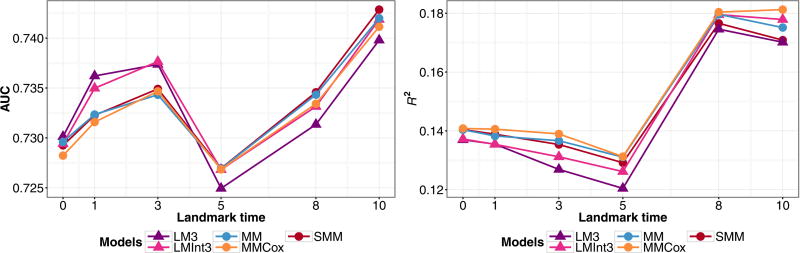
Fitting the model (MM) to the full data, we find that the baseline covariates of diploma status and gender have different effects for each of the transitions. Having a diploma has a significant effect on reducing risk of developing illness (0 → 1), and males have increased risk of death (1 → 2, 0 → 2). Thus, we consider landmark models with an interaction term. The landmark models performed similarly so we only present the results for models (LM3) and (LMInt3). In Fig. 8, we evaluate the inclusion of an interaction and compare the different data structures. The model with the interaction has better predictive performance under both structures, with the longitudinal dataset having higher AUC at earlier time points. We investigate the performance of joint Markov and semi-Markov models under the longitudinal data structuring in Fig. 9 and notice that the landmarking models have higher AUCat earlier landmark times, but that joint models (MM) and (MMCox) perform consistently better in terms of R². The joint semi-Markov model, (SMM), performs similarly to the other joint models in terms of both AUC and R².

Figure 8.

PAQUID data estimates for the cross-validated prediction accuracy measure AUC (left) and R² (right) for predicted probability P(T ≤ τ + 5|T > τ,Z(τ),X) from landmark models (LM3), (LMInt3), fit to inspection time (IT) marker measurement data structured as a longitudinal or super data set.

Figure 9.

PAQUID data estimates for the cross-validated prediction accuracy measure AUC(left) and R² (right) for predicted probability P(T ≤ τ + 5|T > τ,Z(τ),X) for joint models (MM), (MMCox), (SMM), and landmark models (LM3), (LMInt3), fit to data structured as a longitudinal dataset.

Based on this real data analysis, the predictions had similar accuracy under the different data structures. Extensions to the landmark models that incorporate s and τ as covariates did not increase flexibility enough to produce significant improvement in model performance. However, the inclusion of an interaction between baseline covariates and Z(τ) produces more accurate predictions. The joint models had marginally better or equivalent performance at the landmark times than the landmark models. The models that conditioned on transition time as a covariate did not provide a better fit; however, the semi-Markov model (SMM) performed similarly to the Markov models, and may outperform these models in a situation where the Markov assumption does not hold.

5.2 Prostate cancer study

We present the analysis results and dynamic predictions obtained from fitting the landmark and joint models to data from a prostate cancer study conducted at the University of Michigan. The dataset is composed of 745 patients with clinically localized prostate cancer who were treated with radiation therapy. We measure time from start of treatment, considering metastatic clinical failure (CF) as a time-dependent binary covariate. The states of our illness-death model are “alive without clinical failure”, “alive with clinical failure”, and “dead”. The median follow-up time was 9 years, and 52 patients experienced clinical failure. Out of 188 deaths, 154 died before and 34 died after experiencing clinical failure. The pretreatment prognostic factors measured at baseline are age (median 69; IQR 63–74), log(PSA + 1) (PSA ng/ml; median 8; IQR 5–12), Gleason score treated as a continuous covariate with a score of 7=“3+4” and 7.5=“4+3” (median 7; IQR 6–7.5), prostate cancer stage (T1: 57%, T2–T3: 43%), and comorbidities (0: 55%, 1–2: 37%, ≥3: 8%).

We use landmark and joint models to obtain predicted probabilities of death within 5 years for landmark times τ = 0, 1,…, 8 years. We assume that the marker is continuously observed, and structure the data as a super data set. The coefficient estimates from fitting the joint models are given in Table 3. The parametric and semi-parametric Markov models (MM) and (MMCox), respectively, have similar estimates for the different transitions. The (MSM) model incorporates clinical failure time as a covariate for the 1 → 2 transition, for which the estimate is not significantly different than 0 and thus the Markov assumption does not appear to be violated. This is further demonstrated by the estimates for the 1 → 2 transition in (SMM), which are very similar to the estimates from the (MM) model. The effects of the baseline covariates vary across the different transitions. Increased age significantly increases risk of death (0 → 1, 0 → 2), higher PSA, Gleason score, and Stage T2–T3 indicate increased risk of developing clinical failure (0 → 1), and among those with clinical failure, higher Gleason score increases risk of death and those with 1–2 comorbidities have decreased risk of death (1 → 2).

Table 3.

Coefficient estimates for joint models applied to prostate cancer data.

		MM		MMCox		MSM		SMM
Transition	Covariate	Coef.	SE	Coef.	SE	Coef.	SE	Coef.	SE
0 → 1	Age	0.013	0.019	0.014	0.019	0.012	0.018	0.012	0.018
	log(PSA + 1)	0.424	0.173	0.431	0.172	0.422	0.173	0.422	0.173
	Gleason score	0.740	0.156	0.753	0.159	0.740	0.156	0.741	0.156
	Stage T2–T3	0.798	0.349	0.767	0.349	0.799	0.349	0.796	0.349
	Comorbidities 1–2	0.053	0.302	0.061	0.302	0.054	0.302	0.054	0.301
	Comorbidities ≥3	0.263	0.497	0.271	0.497	0.264	0.496	0.263	0.496
0 → 2	Age	0.077	0.013	0.080	0.013	0.076	0.013	0.076	0.013
	log(PSA + 1)	0.204	0.126	0.193	0.127	0.205	0.125	0.205	0.125
	Gleason score	0.135	0.093	0.174	0.095	0.136	0.093	0.136	0.093
	Stage T2–T3	0.051	0.169	−0.030	0.172	0.051	0.169	0.051	0.169
	Comorbidities 1–2	0.678	0.181	0.700	0.182	0.679	0.181	0.678	0.181
	Comorbidities ≥3	1.426	0.236	1.491	0.238	1.425	0.236	1.425	0.236
1 → 2	Age	0.049	0.024	0.043	0.025	0.050	0.024	0.048	0.023
	log(PSA + 1)	−0.238	0.260	−0.183	0.319	−0.263	0.270	−0.293	0.271
	Gleason score	0.574	0.206	0.612	0.229	0.584	0.209	0.580	0.202
	Stage T2–T3	0.059	0.475	0.207	0.508	0.105	0.488	0.078	0.478
	Comorbidities 1–2	−0.927	0.421	−1.005	0.451	−0.942	0.424	−0.873	0.400
	Comorbidities ≥3	−0.507	0.646	−0.555	0.708	−0.453	0.659	−0.330	0.596
	Time of CF (V)					−0.036	0.089
Log-likelihood			−966.4		−1182		−966.4		−966.1
AIC			1969		2399		1971		1968

We present the results from fitting the landmark models in Table 4. In (LM3) we accommodate nonproportional hazards by considering clinical failure as a time-varying covariate. The effect of clinical failure decreases as the landmark time at which the prediction is made increases. (LM4), which (LM2) and (LM3) are nested within, has the highest log-likelihood of the models and the lowest AIC, indicating better fit. Since the joint models show that the baseline covariates have differential effects on risk of death before or after clinical failure, we present the results from (LMInt4), a model with interaction terms between clinical failure and the baseline covariates. The log-likelihood for (LMInt4) is higher than model (LM4) and it has a lower AIC even with the penalization for including six more covariates. Increased age, PSA, Gleason score, and number of comorbidities were all significantly associated with increased risk of death. The only significant interaction was with comorbidities, where those with clinical failure had a significantly decreased risk of death if they had 1–2 comborbidities compared to no comorbidities, as was seen in the joint models. The coefficients for the baseline covariates for the landmark models do not always properly capture the effect of the baseline covariates on risk. For example, the coefficient for Gleason score in (LM4) is averaged over those with and without clinical failure and thus, is much lower than the effect on the 1 → 2 transition but much higher than the effect for the 0 → 2 transition in the joint models. As well, the effect of stage, which is significant for the 0 → 1 transition in the joint models but has a small effect on the transitions to death, is not properly reflected by (LMInt4), where the effect of stage on risk of death is quite high for those who experience clinical failure.

Table 4.

Coefficient estimates for landmark models applied to prostate cancer data.

		LM2		LM3		LM4		LMInt4
	Covariate	Coef.	SE	Coef.	SE	Coef.	SE	Coef.	SE
β(τ)	CF	3.317	1.204	2.065	0.279	3.921	1.210	3.406	2.972
	CF*τ	−0.439	0.427			−0.460	0.409	−0.220	0.374
	CF*τ2	0.020	0.034			0.021	0.033	0.006	0.031
ω(τ)	CF*(t − τ)			−0.513	0.190	−0.562	0.175	−0.341	0.188
	CF*(t − τ)2			0.082	0.051	0.093	0.045	0.062	0.049
θ(τ)	τ	−0.056	0.018	−0.043	0.019	−0.069	0.023	−0.073	0.022
	τ2	0.004	0.001	0.001	0.002	0.004	0.002	0.004	0.002
ζ	Age	0.080	0.012	0.080	0.012	0.080	0.012	0.082	0.013
	log(PSA + 1)	0.227	0.111	0.234	0.110	0.227	0.111	0.246	0.112
	Gleason score	0.292	0.091	0.288	0.091	0.289	0.091	0.269	0.094
	Stage T2–T3	0.040	0.168	0.054	0.168	0.042	0.167	0.057	0.171
	Comorbidities 1–2	0.414	0.171	0.395	0.171	0.420	0.170	0.474	0.174
	Comorbidities ≥3	1.214	0.248	1.207	0.247	1.214	0.247	1.230	0.252
ζZ(τ)	CF*Age							−0.015	0.024
	CF*log(PSA + 1)							−0.577	0.366
	CF*Gleason score							0.336	0.252
	CF*Stage T2–T3							0.372	0.655
	CF*Comorbidities 1–2							−1.116	0.457
	CF*Comorbidities ≥3							−0.148	0.708
Log-likelihood			−11,135		−11,143		−11,132		−11,118
AIC			22,292		22,308		22,289		22,273

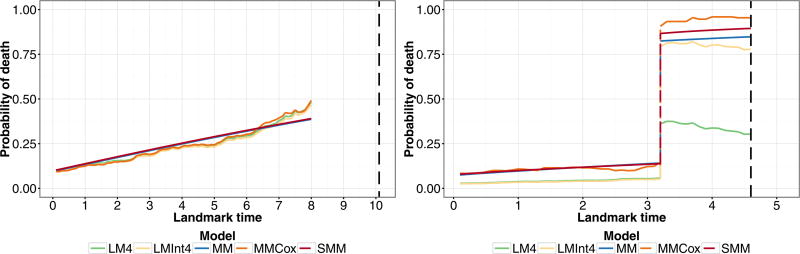
In Fig. 10, we present the predicted probabilities from the landmark and joint models, some of which have been omitted due to similar results, for two individuals in the dataset. The pattern of the predictive probabilities for these specific patients is similar to that of the other patients in the dataset with the same final clinical failure status and who experience death. Individual A has increased risk of death due to his high PSA and number of comorbidities, thus his predicted probability of death becomes quite high as landmark time increases and he dies before experiencing clinical failure. We see that for this patient, the predicted probabilities from the landmark models and the semi-parametric Markov model (MMCox) track together and the predicted probabilities for all the models are similar. Individual B is young, but has other baseline variables that characterize him as high risk. Their effect is particularly seen after the patient experiences clinical failure, after which his predicted probability of death greatly increases and he dies within 2 years. The predictions from the joint models (MM) and (SMM) are very similar both before and after clinical failure. Prior to clinical failure, the prediction probabilities from the landmark models are lower than those from the joint models by an amount that is not insignificant. After clinical failure, the landmark model without interactions (LM4) does not perform well for predicting death. Thus, the landmark models require interactions between the time-dependent binary covariate and the baseline covariates to capture the differential effects of the covariates on the different transitions.

Figure 10.

Predicted probability of death within 5 years, P(T ≤ τ + 5|T > τ,Z(τ),X) for two individuals in the prostate cancer dataset. Individual A (left) is 60 years old at baseline, with PSA 19.7 ng/mL, Gleason score 7.5 (“4+3”), T1 Stage, 6 comorbidities, and does not experience clinical failure but dies 10 years from baseline. Individual B (right) is 54 years old at baseline, with PSA 16 ng/mL, Gleason score 9, T2 Stage, zero comorbidities, and experiences clinical failure at time 3 before dying at time 4.6 years from baseline. Black dashed line indicates time of death.

6 Discussion

Models that can incorporate updated time-dependent marker information to revise survival predictions are vital for identifying high-risk subjects and making timely clinical decisions. In this paper, we have compared the theoretical justification and predictive capabilities of two such dynamic prediction approaches: joint modeling and landmarking.

We contribute to the existing literature that compares these two approaches by investigating them under an illness-death model. We focused on a survival model with a binary time-dependent covariate, which is the simplest example of a joint model, to demonstrate that even in this basic situation a Cox model in the landmark framework is not theoretically valid. With more complicated forms of the marker process, we can expect that the discrepancies between the performance of joint models and landmarking will be even greater, and that the inclusion of flexible forms in landmark models, as were suggested in this paper, and better informed imputations of the marker value at landmark times, will be even more important. In our simulation study, we demonstrate that joint modeling produces more accurate predictions than landmarking. We simulate data under a joint model since the landmark model provides an approach to describe the data, but is not a data-generating model. Thus, to provide a fair comparison we also consider misspecified models within the joint modeling framework, particularly a semi-Markov model and a Markov model with a nonsmooth baseline hazard. In addition, we compared the performance of the approaches to real data from the PAQUID study and concluded that the joint models performed marginally better than the simple landmark models.

Joint modeling and landmarking have different approaches to predicting the future for a subject. Joint modeling achieves this by directly modeling the longitudinal variable and integrating over the possible paths the variable might take, and thus uses the possibly strong relationship between the longitudinal variable and the event of interest to make the prediction. Landmarking is an approach which, in essence, obtains the empirical distribution of future event times among people similar to the person of interest. Estimation of this empirical distribution is achieved through a descriptive model of the residual times based on a finite number of parameters. Since the residual time distribution is determined by the stochastic process for the longitudinal variable, landmarking does depend implicitly on the stochastic process. The data provides information about the stochastic process of the longitudinal variable, which is exploited in the joint modeling approach but ignored in the landmarking approach. Using data from the prostate cancer study, we demonstrated that the simple landmark models do not properly capture the effects of the baseline covariates, averaging their effect on predictive probability over both individuals who have experienced “illness” and those who have not. The joint models compute the predicted probability by considering all possible paths through the illness-death model, allowing the effect of the baseline covariates to vary depending on the state in the process. The use of more flexible landmark models and interactions between the baseline covariates and the time-dependent “illness” indicator helps to mitigate this issue.

While the landmarking approach is appealing because it does not require specification of a longitudinal model, the derivations in this paper suggest that simple forms for the landmark models are unlikely to fit well, and that landmark models may need to include nonproportional hazards and interactions. Thus, just as with joint models, considerable effort may be needed to obtain a good fitting model. One difference between joint models and landmarking is in setting up the data. For joint models, the likelihood is derived from the observed data and there are no choices to make. With landmarking there are choices to make that will change the predictions, which include the number and values of the landmark times, what time horizon to use when administratively censoring the data in the super dataset, and how to impute Z(τ). To avoid using LOCF, we proposed a longitudinal data structure based on inspection times and demonstrated that in our situation it performed better than, or as well as, the super dataset proposed by van Houwelingen and Putter (2011). Alternatively, we can specify a longitudinal model for Z and impute a sensible value for Z(τ) for each subject, as was done by Maziarz et al. (2016). This approach has some similarity to the two-stage procedure of fitting a joint model in Bycott and Taylor (1998), which is known to have small bias and be more computationally convenient than a full joint model likelihood approach. They accomplish this by specifying the longitudinal marker process as a random effects model plus stochastic process and using the fit of this model to obtain less variable imputes of Z(τ) for each subject, which are then used as covariates in a time-varying Cox model.

In our opinion, joint modeling provides a more unified and principled approach that also satisfies the consistency criteria. It could even be enhanced by the incorporation of external information. If the stochastic process can be well characterized, then we might expect the predictions to be more accurate, including for longer prediction windows. In situations where the stochastic process can be well estimated from the available data, joint modeling is likely to perform better. In situations where it is harder to estimate, for example, sparse longitudinal data or many longitudinal variables, then the empirical performance of landmarking might provide a good enough approximation.