The Mouse Cortical Connectome Characterized by an Ultra Dense Cortical Graph Maintains Specificity by Distinct Connectivity Profiles

Summary

The inter-areal wiring pattern of the mouse cerebral cortex was analyzed in relation to a refined parcellation of cortical areas. Twenty-seven retrograde tracer injections were made in 19 areas of a 47-area parcellation of the mouse neocortex. Flat mounts of the cortex and multiple histological markers enabled detailed counts of labeled neurons in individual areas. The observed lognormal distribution of connection weights to each cortical area spans 5 orders of magnitude and reveals a distinct connectivity profile for each area, analogous to that observed in macaque. The cortical network has a density of 97%, considerably higher than the 66% density reported in macaque. A weighted graph analysis reveals similar global efficiency but weaker spatial clustering to that reported in macaque. The consistency, precision of the connectivity profile, density and weighted graph analysis of the present data differ significantly from those obtained in earlier studies in the mouse.

eTOC Blurb

Gămănuţ et al. investigation of anatomical cortico-cortical connections in mouse at the meso-scale level shows that almost all possible connections exist. Efficiency of the network and specificity of the connections is ensured by the existence of weighted connectivity profiles.

Introduction

The concept of the cortical area is rooted in the notion of localization of function in the cortex, where individual areas are posited to have a distinct architecture, connectivity, function, and/or topographic organization (Felleman and Van Essen, 1991; Van Essen, 2003). The mouse is increasingly used as a model system for investigating the cortex, where complex sensory (Ferezou et al., 2007), motor (Li et al., 2016) and cognitive (Carandini and Churchland, 2013; Kim et al., 2016; Manita et al., 2015) functions have been shown to depend on interactions among cortical areas via inter-areal connections, as well as on dynamic control involving higher-order thalamic nuclei (Mease et al., 2016; Sherman, 2016). The highly interactive nature of cortical processing motivates efforts to investigate the statistical properties of inter-areal networks (Wang and Kennedy, 2016), and the development of large-scale models of the cortex that may provide insights into brain function in health and disease (Bullmore and Sporns, 2012).

Early evidence for distributed hierarchical processing within the cortex (Felleman and Van Essen, 1991) drew on collated tract tracing data from numerous studies using diverse methods of generally low sensitivity. This limited the reliability of inferences about statistical features of large-scale cortical networks (Kennedy et al., 2013), and notably led to underestimating the density of the cortical graph (i.e., the fraction of connections that can exist which do exist). This in turn leads to a failure to appropriately constrain the range of plausible models of cortical networks (Markov et al., 2013b). These considerations motivate the development and use of sensitive tract-tracing methods along with accurate areal parcellation (Bassett and Bullmore, 2016). The high density and wide range of connection strengths of the cortical graph (Markov et al., 2014a; Markov et al., 2011) point to the importance of quantifying the weights of the connections linking different cortical areas (Ercsey-Ravasz et al., 2013; Oh et al., 2014; Song et al., 2014; Ypma and Bullmore, 2016).

Recent quantitative retrograde tracer studies in the macaque (Markov et al., 2014a; Markov et al., 2011) demonstrated that compared to previous studies there were (i) many more inputs to each cortical area; (ii) a wider 5-order magnitude range of connection strengths to each area; and (iii) a much narrower range of variability in the strength of individual pathways tested with repeat injections. These findings support the concept of each area having a distinctive fingerprint or connectivity profile defining its functional specificity (Bressler and Menon, 2010; Markov et al., 2011; Passingham et al., 2002); they contrast with earlier reports suggested that connection weights in cortical pathways are highly variable across individuals (MacNeil et al., 1997; Musil and Olson, 1988a, b; Olson and Musil, 1992; Scannell et al., 2000). Hence, it is important that the mouse database be investigated for its statistical variability of connection weights in order to estimate the validity of the connectivity profiles.

The weight-distance relations observed in macaque cortical connectivity data lead to a one parameter predictive model that captures multiple features of the cortical network including its spatial embedding, wire minimization, frequency distribution of motifs, global and local efficiencies and a core-periphery architecture (Ercsey-Ravasz et al., 2013). Spatial embedding constrains numerous geometrical features in a similar fashion in mouse as well as macaque cortex (Horvat et al., 2016b).

A recent systematic connectivity study obtained brain-wide weighted data (Oh et al., 2014) using anterograde tracer injections on a fixed grid of injection sites. Because most of the reported injection sites (>70%) spanned multiple areas, connectivity at the level of individual areas was inferred using a computational model involving several theoretical assumptions. Their probabilistic model of connectivity yielded an estimated density for the inter-areal cortical graph of 35–53%, much lower than the 66% reported for the macaque cortical graph (Markov et al., 2014a). The lower density reported in the mouse and also in the rat (Bota et al., 2015) is surprising given that one might anticipate increased graph density with decreasing brain size (Horvat et al., 2016b; Ringo, 1991). Furthermore, an earlier tracer study of mouse visual cortex (Wang et al., 2012) reported a considerably higher subgraph density (99%) than the 77% reported for visual areas by Oh et al., (2014). These findings suggest that the computational procedure used in the Oh et al., 2014 study to infer the connectivity of single areas from injections involving multiple areas might have resulted in significant numbers of false negatives. A re-analysis of the Oh et al., (2014) dataset estimated a whole-cortex graph density of 73% (Ypma and Bullmore, 2016). Hence, in the present study we focused on an empirical approach that is deterministic insofar as it depends on direct anatomical observations.

Here we investigate the mouse cortico-cortical connectivity and address two key issues: the density of the mouse cortical graph and the consistency of connectivity profiles across individuals. We minimized experimental variability by targeting injections of a retrograde tracer in post-hoc identified areas rather than a fixed grid of anterograde injections (Oh et al., 2014). Our choice of retrograde tracer provides several advantages for quantifying connection strengths (see Suitability of DY tracing in STAR Methods for a detailed discussion). We coupled retrograde tracing with flatmounting the cortex, which is particularly advantageous when combined with multiple histological stains used for cortical parcellation (Qi and Kaas, 2004; Sincich et al., 2003; Wang and Burkhalter, 2007; Wang et al., 2011; Wang et al., 2012). Our experimental approach allows a positive identification of both injected cortical areas and of 41 areas and 7 sub-areas where the retrogradely labeled neurons are located.

Our results show that the mouse cortex is ultra-dense, with a graph density of 97%, significantly higher than the probabilistically-based range of 35–73% (Oh et al., 2014; Ypma and Bullmore, 2016). The high density of the mouse cortical graph suggests that the activity pattern of a given area is interrelated via its connectivity profile to a widespread pattern of influences across the cortex. It seems implausible that smaller brains would be associated with greater variability of connection weights (as reported in Oh et al., 2014), as this in conjunction with a high graph density would entail lower specificity of the structure and function of the mouse cortical network compared to the macaque. Our analysis of the present retrograde labeling revealed variability of connectivity and connectivity profiles in the mouse comparable to those observed in macaque (Markov et al., 2014a). Likewise, our deterministic approach leads to a weight-distance relationship that is quantitatively similar in mouse and macaque (Horvat et al., 2016b), in contrast to the modeled data from the Oh, et al., (2014) study. Our results demonstrate that the densely-interconnected network of mouse cortex contains highly selective area-to-area connectivity profiles, which in primates underlie distributed hierarchical cortical processing (Markov et al., 2011).

Results

High-resolution cortical parcellation

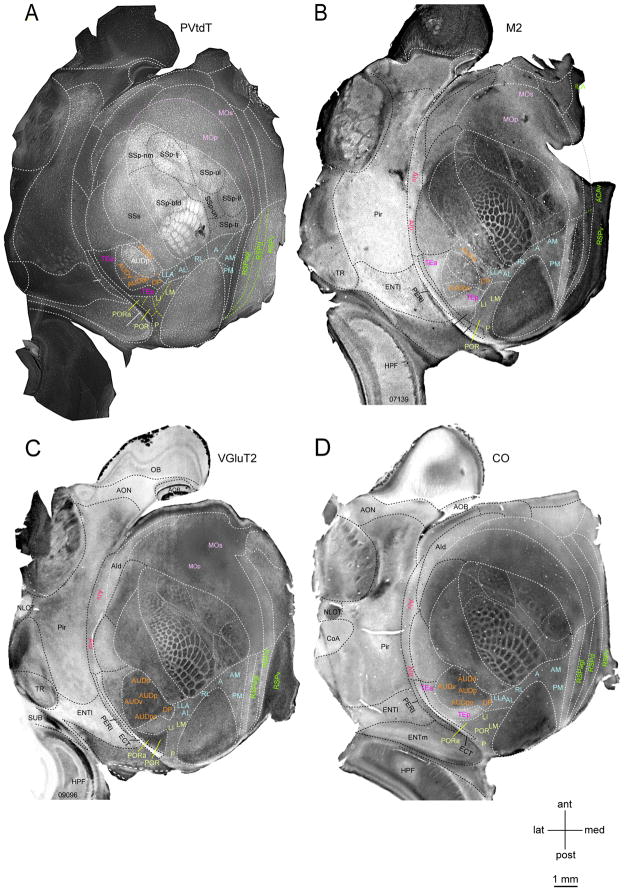
The spatial precision of the alignment of DY labeling with the areal map is a critical experimental issue given the small size of the mouse cortex. PVtdT mice allowed parcellation of cortex into 25 parcels excluding entorhinal, hippocampal and piriform cortex (Figure 1A) and provided reliable landmarks for aligning matching/complementary expression patterns of M2, VGluT2, CO (Figure 1, S1C–D) and visuotopically mapped borders (Wang and Burkhalter, 2007). In each brain this procedure allowed positive identification of 115 of the 133 borders (86.5%), the remaining borders were inferred from the known patterns of CO, M2 and VGlutT2 (Figure S1B). Importantly, because the brain map is created for each tangentially sectioned individual brain it avoids assigning labeled cells to a standard template and obviates aligning large numbers of adjacent sections. Our approach largely takes into account the individual differences in parcellation across subjects (Krubitzer and Seelke, 2012) and significantly differs from that employed in two recent studies (Oh et al., 2014; Zingg et al., 2014), which mapped corticocortical projections onto a standard Allen Reference Atlas (ARA, (Dong, 2008), generated by averaging variations of background fluorescence across hundreds of cortices. This Common Coordinate Framework (CCF, Allen Institute, brain-map.org) has become a widely used parcellation of mouse cerebral cortex (Figure S1A).

Figure 1. Expression of M2, VGluT2 and CO with respect to PVtdT in layer 3/4 of flatmounted left mouse cerebral cortex.

(A) Tangential section showing tdTomato fluorescence in PV-containing interneurons (bright white labeling). Parcels outlined by white dashed lines and labeled by black and white letters were positively identified by PVtdT expression. Black dashed lines indicate subdivisions within primary somatosensory (SSp) cortex representing different body parts. Colored letters denote known areas contained within distinct compound parcels (orange, yellow, blue, green, pink, purple) in which PVtdT-expression exhibits similar intensity and reveals no detectable subdivisions. Colored dashed lines indicate presumptive borders between these areas. (B) Bright field image of tangential section stained with an antibody against the M2 muscarinic acetylcholine receptor (dark staining). Areas outlined with white and black dashed lines and denoted with white and black letters were positively identified as distinct parcels. Areas denoted in orange, yellow, blue, green, pink, red and purple letters indicate known areas contained within distinct, but uniformly M2-labeled parcels. (C) Bright field image of tangential section stained with an antibody against VGluT2 (dark staining). Areas outlined with white and black dashed lines and denoted in white and black letters were positively identified as distinct parcels. Areas denoted in orange yellow, blue, green pink and red letters indicate known areas contained within distinct, but uniformly VGluT2-labeled parcels. (D) Bright field image of tangential section reacted for cytochrome oxidase (CO) activity (dark staining). Areas outlined with white and black dashed lines and denoted in white and black letters were positively identified as distinct parcels. Areas denoted in orange, yellow, blue, green, red and purple letters indicate known areas contained within distinct, but uniformly CO-labeled parcels. See also Figure S1 and Figure S5

Within the 25 parcels, additional areas were identified by comparing PVtdT with the patterns of M2, VGluT2 and CO expression (Figure S1C–F). These included: POR, PORa [previously referred to as 36p, (Wang et al., 2011)], AUDv, AUDpo, AUDv, DP, MOp, MOs, RSPagl, RSPd, RSPv, TEa and TEp). The borders of the visuotopically mapped areas (P, LI, LLA, RL, A, AM, PM; (Garrett et al., 2014; Wang and Burkhalter, 2007; Zhuang et al., 2017) were only partially outlined by any of the molecular markers. Here, the missing borders could be filled in by registering PVtdT maps to instructions based on the stereotypical size, shape and relative position of areas derived by previous visuotopic mapping (Wang and Burkhalter, 2007). Where this procedure differs from template matching is that areal boundaries are derived from the PVdtT map of each individual case. The grand total was 41 areas, of which SSp was subdivided into 7 subareas (Figure S1B). The variance of areal border assignments was estimated to be < 150 μm (for details see Parcellation of the cortex in STAR Methods).

Retrograde tracing with DY

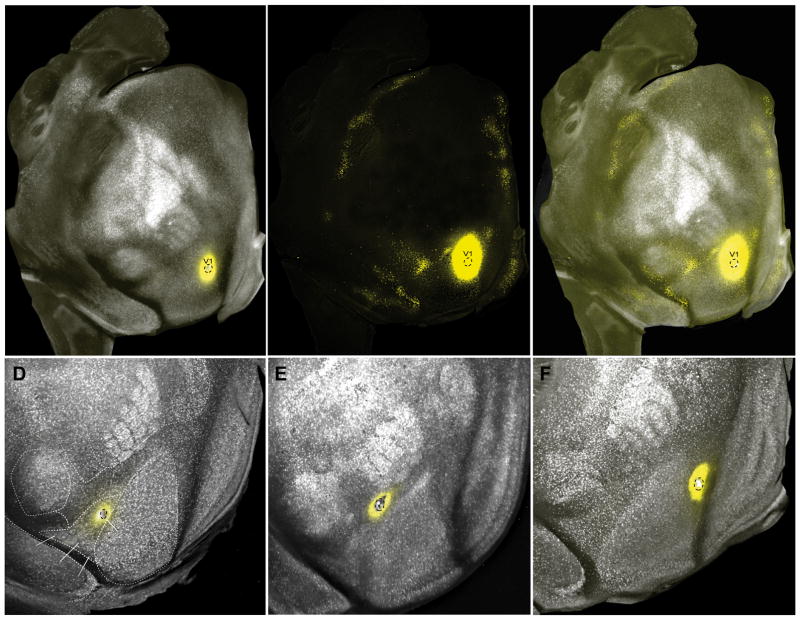
For details about DY see Suitability of DY tracing in STAR Methods. Representative examples of the DY labeling at low power are shown Figures 2A–F (note, cell counts were acquired using higher magnification). The area V1 injection shown in Figure 2A–C was confined to the lower peripheral visual field representation near the tip of V1 (Marshel et al., 2011). As expected from previous axonal tracing and topographic mapping experiments (Garrett et al., 2014; Marshel et al., 2011; Wang et al., 2007), retrogradely DY labeled neurons were clustered at the junction of areas LM, AL, LI and LLA. Additional clusters of labeled neurons were found at retinotopically corresponding locations within RL, A, AM, PM, MM, P, POR, PORa. In temporal cortex, DY labeling was contained in most areas of auditory cortex (AUDp, AUDPo, AUDd and DP) and the ventral portion of the posterior temporal area (TEp). On the medial wall, labeled neurons were clustered in dorsal retrosplenial cortex (RSPd), the secondary motor cortex (MOs), the dorsal and ventral anterior cingulate areas (ACAd, ACAv) and in the prelimbic (PL) and infralimbic (ILA) cortex. At the rostral end of cortex, labeling in orbitofrontal cortex was confined to ORBl. A complete map of neurons projecting to V1 is shown in Figure S2. The densest inputs originate from the occipital, temporal, parahippocampal, retrosplenial, cingulate, orbitofrontal, prefrontal cortex, whereas inputs from parietal somatosensory, gustatory, visceral and insular cortex are sparse or absent.

Figure 2. Retrograde DY labeling in PVtdT mice.

(A) Tangential section (slightly tilted to the lateral side away from the tangential plane) through layers 3–5 of flatmounted cortex showing the distribution of PVtdT-expressing neurons (false colored white). Parcel boundaries were assigned based on PVtdT expression densities. False colored yellow spot marks the DY injection site. Black dashed outlines indicate the border of the crystalline DY deposit, which is confined to lower peripheral visual field representation of V1. Note that the injections site appears larger due to overexposure of the fluorescence image to visualize the labeled neurons. (B) Same section as in (A) showing the distribution of retrogradely DY-labeled neurons (false colored yellow dots). Note that due to the long exposure time required to reveal DY-labeled neurons at low magnification, the injection appears larger than the site outlined (black dashed outlines) in (A). Importantly DY labeled neurons are tightly clustered at sites that match the topographic location of the injection site (Garrett et al., 2014; Marshel et al., 2011; Wang and Burkhalter, 2007). (C) Overlay of images shown in (A) and (B). (D–F) Tangential sections through layer 4 of poster half of cortex in PVtdT expressing mice, showing DY deposits (outlined by dashed black lines) in areas LM (D), AL (E) and PM (F). Although under fluorescence illumination the injection sites appear larger than the DY deposit, it is important to note that they are confined to individual areas. See also Figure S2 and Figure S7

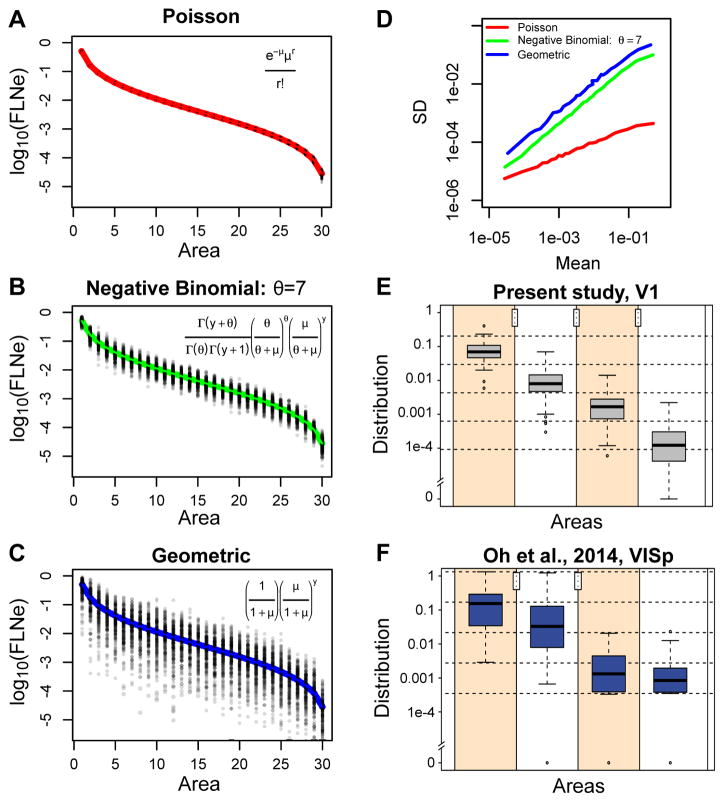
Statistical consideration of overdispersion

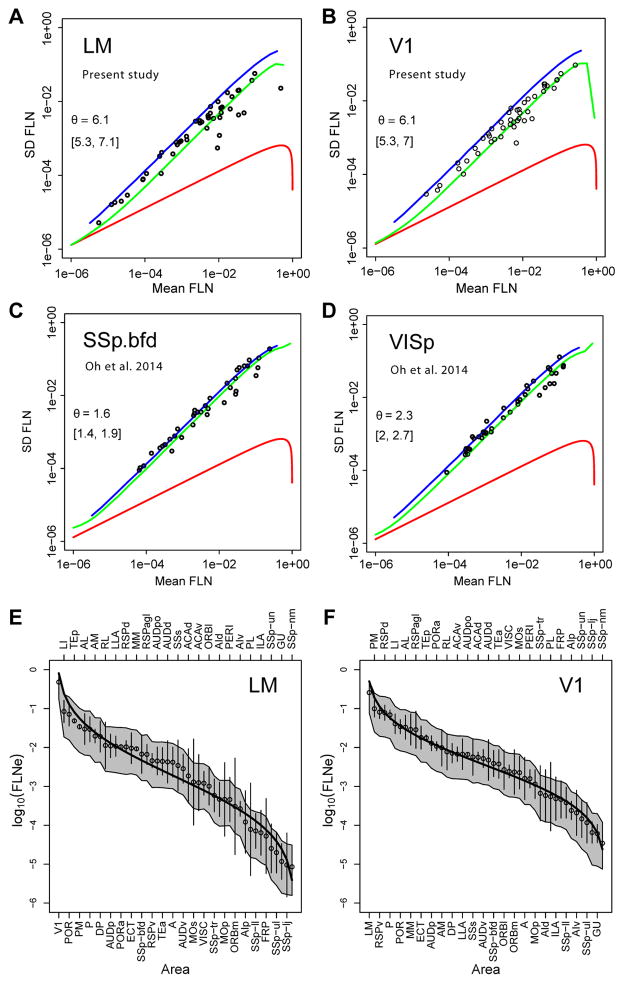
Variability in the retrograde tracer data from the present study was modeled by analyzing the statistical properties of connections resulting from repeat injections of tracers across individuals. Scatter plots of the standard deviation vs the mean (see Overdispersion in STAR Methods) are shown in Figure 3A, B with indicated dispersion values. Overall, the results indicate a negative binomial distribution with dispersion values of 6, which provides a reasonable estimate of the expected variability for neural counts obtained with retrograde tracing data in mouse. The θ estimate of 6.1 for V1 and LM is somewhat smaller than that obtained in the macaque, 7.9 (Markov et al., 2011), suggesting marginally greater levels of overdispersion across animals in the mouse data sets. These findings demonstrate that overdispersion is a systematic phenomenon of neural retrograde count data in both macaque and mouse. Thus, overdispersion needs to be considered in statistical evaluation of such data since ignoring it would lead to anti-conservative estimates of the probabilities of significant differences in connection strengths, i.e., erroneously assigning significance to small differences.

Figure 3. Variance and lognormal distribution of FLNe.

A–D Repeat injections SD as a function of the mean; θ, dispersion parameter, Red curves, Poisson distribution; blue, geometrical distribution; green, negative binomial; brackets, 95% confidence interval. (A–B) retrograde DY tracer injections of (A) LM (n=3) and (B) V1 (n=4) (present study) of DY-labeled neurons. (C–D) Anterogradely projections described by Oh et al., (2014) after injections of viral tracer into mouse (C) somatosensory barrel cortex SSp.bfd (n=5) and (D) primary visual cortex VISp (n=8). Note difference in θ values for A, B versus C, D. In order to have the same normalization as in AB, for each injection we divided the strengths of cortico-cortical projections by the sum of cortico-cortical projections from the injection (E–F) Lognormal distribution of retrograde tracing data in present study, observed means (white dots) ordered by magnitude, SEMs (error bars) of logarithms of the FLNe for the cortical areas projecting on the injected area. V1 (n=4), LM (n=3). Black curves, the expected lognormal distribution for an ordered set of projections of size n, equal to the number of source areas. The grey envelopes around each curve indicate the 95% confidence intervals obtained by simulating 10000 sets of count experiments drawn from a negative binomial distribution, with means of counts and dispersion parameter as the data.

Repeat injections make it possible to examine variability in the raw data of Oh et al., (2014) (Figure 3C, D). Although not based directly on counts, we applied the same framework to examine the variability in relation to the mean. In contrast to the retrograde tracer data, the anterograde data of Oh et al., (2014) show a dispersion of 1.6 for the somatosensory barrel field and 2.3 for area V1 and therefore in both cases indicates a more overdispersed data set compared to the retrograde tracing data in the present study; the higher incidence in overdispersion in the anterograde data may be related to the difficulties in estimating projection strength from measurements of fluorescence intensity (see Effect of template matching on the weight distribution of connections).

Lognormal distribution of weights

An intriguing aspect of cortical organization is that many physiological and anatomical features are distributed according to a lognormal distribution (Buzsaki and Mizuseki, 2014). This is a skewed, heavy-tailed distribution, typically characterized by relatively few very strong and very weak values, with many intermediate ones. A lognormal distribution was first reported for synaptic weights (Song et al., 2005), and subsequently as a characteristic of the distribution of input strengths to a cortical area in macaque (Markov et al., 2011) and mouse (Oh et al., 2014; Wang et al., 2012).

Figure 3E, F shows that, for areas LM and V1, the areas analyzed in Figure 3A, B, the ordered means of log (FLNe) values follow lognormal distributions. The range of values spans 4 to 5 orders of magnitude. The fitted curves (solid lines) do not fall outside the expected variability represented by the grey envelopes, indicating that the differences from the lognormal prediction are not significant (see Accordance with the negative binomial model in STAR methods).

Variability of deterministic connectivity maps in mouse and monkey and the consistency of weak connections

The repeatability of connections to a given area across individuals makes it possible to evaluate the variability in terms of consistency of individual pathways. By consistency, we refer specifically to whether a connection is systematically present across injections (see Variability and consistency in STAR Methods).

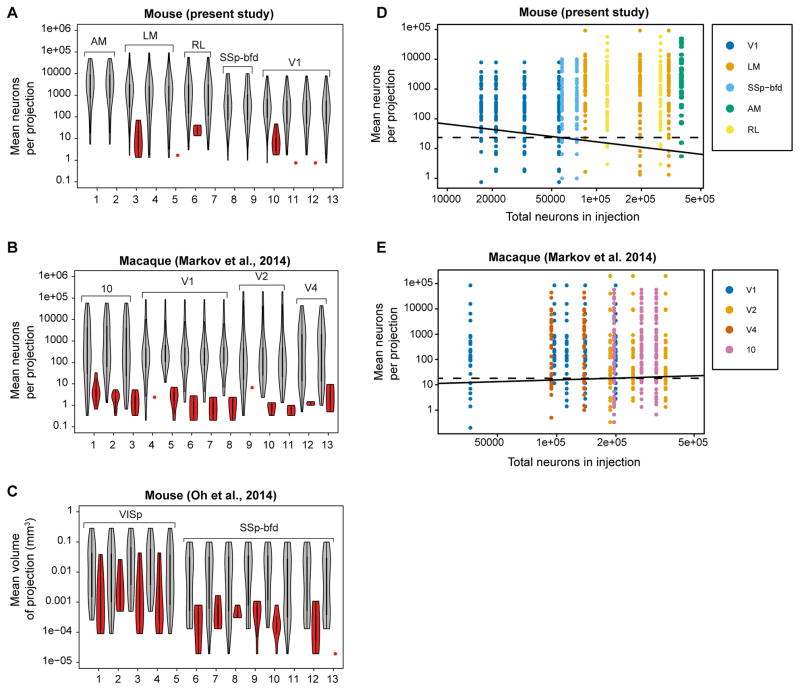
Figure 4A–C shows violin plots of means of projections for repeat injections and explores the variability of the set of inputs to a given cortical area across individuals. In this figure, connected areas that are found for all repeat injections in an area are shown in gray and those that are absent from a given injection in red. The present study shows low variability across injections. Medium to strongly connected areas were found systematically after each injection (Figure 4A). Similar findings were obtained in macaque (Figure 4B). The macaque data (Markov et al., 2014a) differed from the present observations in mouse in that similar levels of inconsistent projections were found in ten of the 13 repeats compared to only three out of the 13 in the mouse (Figure 4B). The higher variability in macaque could be related to the partial sampling in the macaque study. The relatively low level of variability in the retrograde tracer studies of mouse and macaque differs from the high variability observed in the raw data in the Oh et al., (2014) anterograde data where inconsistent projections were found across nearly all injections and at much larger weight values (Figure 4C).

Figure 4. Consistency in mouse and macaque as a function of mean weight and size of injection for repeat injections across individuals.

In A–C, violin plots of means of projections consistent across repetitions (gray), and of inconsistent projections (red). (A) Mouse retrograde tracing data from present study representing repeat injections in areas AM, LM, RL, SSp-bfd and V1; (B) Macaque retrograde tracing data from repeat injections in areas V1, V2, V4 and 10 (Markov et al., 2014a). (C) Mouse anterograde raw data, where repeat injections were restricted to single areas (VISp, SSp-bfd) (Oh et al., 2014). In order to have non-normalized data as in A and B we multiplied each strength of cortico-cortical connections with the volume of the respective injection taken from Supplementary data of Oh et al., 2014. In D, E, colored dots represent projections which are present; white dots absent. On the vertical axis are represented mean numbers of neurons per projection, on the horizontal axis injection size in terms of total number of labeled neurons per injection. The solid lines correspond to a linear classifier from a logistic regression with the variables of both axes used as features for a probability of the presence of the projection at 95%. The dashed lines correspond to a similar criterion for which only the ordinate variable was used as a classification feature. (D) Repeat injections retrograde tracer DY in mouse area V1 (n=4); LM (3), RL (2) SSp-bfd (2), AM (2); (E) Repeats in macaque area 10 (3), V1 (5), V2 (3), V4 (2).

In Figure 4D, of the 598 possible connections from repeat injections, 581 (97.2%) were present and 17 (2.81%) were absent. Absent connections are concentrated in the lower half of the diagram where low mean number of neurons per projection are found. The continuous line in Figure 4D indicates the estimated linear classifier for which the probability of a connection being present is 0.95 for this model. Its negative slope suggests a dependence of connectivity on both features such that small injections would lead to higher probabilities of absence at high mean connection strengths. However, only the mean of projection was found to contribute significantly to the linear classifier, (log(Mean): z = 5.57, p = 2.56*10⁻⁸; log(Total): z = 1.7; p = 9.6 10⁻²), thereby demonstrating no support for this hypothesis. The 95% classifier based only on the log(Mean) is indicated by the dashed line and corresponds to a value of 24 neurons. This indicates that projections containing more than 24 neurons on average, will be highly consistently identified (but not always perfectly) across individuals.

In Figure 4E, we performed a similar analysis on the macaque data reported by Markov et al (Markov et al., 2014a) from repeat injections in areas V1, V2, V4 and 10. The solid and dashed lines correspond to the same models as in Figure 4D but fitted to the macaque data. Again, the influence of the total size of the injection was not found to contribute significantly to the classifier. The dashed line corresponds to a mean of 18 neurons, slightly lower than the value found for the mouse data and close to the value of 10 estimated more informally in Markov et al. (Markov et al., 2014a).

Verification of the model of data variability, estimation of dispersion and consistency as well as the generality of the lognormal distribution of weights and consistency justified the use of a single cortical injection of retrograde tracer in macaque to characterize the projection profile of an area (Markov et al., 2014a). The present results show that this also holds for the retrograde labeling of cortical pathways in mouse.

The mouse cortical connectome exhibits distinct connectivity profiles

Armed with a description of the distribution of the data, we tested whether there are signatures in the sets of projections to each area, as is the case in macaque (Markov et al., 2011). Alternatively, every individual might present its own sets of connections and weights. Specifically, we examined each set of multiply injected areas to determine the minimum number of factors accounting for the systematic effects on the data (see Evaluating Akaike Information Criterion in STAR Methods).

For areas LM and V1, the model without interaction between explanatory variables AREA and BRAIN led to a decrease in AIC (LM: dAIC =23.8; VI: dAIC = 71.4). Thus, for both areas, this model yields a better or equivalent balance between complexity and goodness of fit than the more complex model. The optimal models were those for which individual differences appeared as unsystematic variability, i.e. without an interaction between the areas and the individual animals. The presence of such an interaction would have signified the presence of individual differences in connectivity profiles beyond the variability among animals. Its absence implies that quantitative connectivity profiles do not differ sufficiently across cases and therefore that a robust signature (connectivity profile) exists for each area.

Is it possible to observe a connectivity profile when there is overdispersion? In the hypothetical case of a Poisson distribution (Figure 5A, see Overdispersion and connectivity profiles in STAR Methods), the tight distribution of points about the ordered log normal curve indicates that such Poisson data would show a clear example of a connectivity profile or signature and an individual injection would be likely to closely reflect the average behavior indicated by the red curve. At the other extreme is the geometric distribution (Figure 5C), where the high variability (2–3 orders of magnitude range of variation for each projection) obscures the systematic trend of the expected curve (blue). As shown in simulations by Scannell (Scannell et al., 2000), data distributed in this fashion would require an inordinate number of repeat injections to establish the average behavior of the curve with sufficient precision. Note that individual injections could follow any arbitrary path through the point cloud, so their value in establishing an areal profile would be of limited informativeness. In this case, statistical analysis of a small number of injections would likely lead to the conclusion of individual differences in the profile for a single injection site, that is the presence of a statistically significant interaction between area and brain injected. The simulated results from a Negative Binomial distribution (Figure 5B) with a dispersion parameter similar to that found in retrograde labeling in macaque and mouse, falls in between the Poisson and geometric distributions. However, with the variation of individual injections being only 1 order of magnitude, far less than the span of the ordered log normal curve, single injections are much more representative of the average curve than for geometrically distributed data. As shown in our data, the variation among animals is not sufficient to reject the proposition that projection profiles from different animals are the same.

Figure 5. Relations of discrete probability distributions on log-normal FLNe distribution variabilities and connectivity profiles.

In A, B, C, the hypothetical results of 1000 injections were simulated according to a Poisson, Negative Binomial (dispersion parameter θ = 7) and Geometric distributions (θ = 1). (D) The standard deviation is plotted as a function of the means calculated for the simulated injections from A, B and C with the colors indicating the distribution from which the calculations were made. (E, F) Example of the effect of overdispersion on the reliability of projections in present data (E) and in Oh et al. 2014 (F). In both plots a single injection in V1 (VISp, respectively) was taken and the areas were ordered according to their strengths. The difference between the log of the maximum and of the nonzero minimum was then divided into four intervals (delimited by dashed horizontal lines), and assigned the log of the FLNe to the corresponding intervals, forming four groups. Next, the strengths of the corresponding areas from the other repeats were used to obtain the boxplots. The stars represent the significance levels attained of the p values of one-sided permutation tests for each pair of consecutive groups, with the null hypothesis that the mean of the group on the left is larger than the mean of the group on the right. Notice that the present data are all restricted to the initial intervals (within the limits of the dashed horizontal lines), while the data from Oh et al. 2014 in all but one case cross these limits.

In order to illustrate the effects of a geometric distribution (Figure 5C) of the anterograde data and negative binomial distributions (Figure 5B) for the retrograde data on connectivity profiles, we show a box plot analysis for area V1 for the present data (Figure 5E) and for the Oh et al., 2014 data (Figure 5F). This shows that the negative binomial distribution corresponds to a significantly more demarcated connectivity profile compared to the data with a geometric distribution in Figure 5F from Oh et al., 2014.

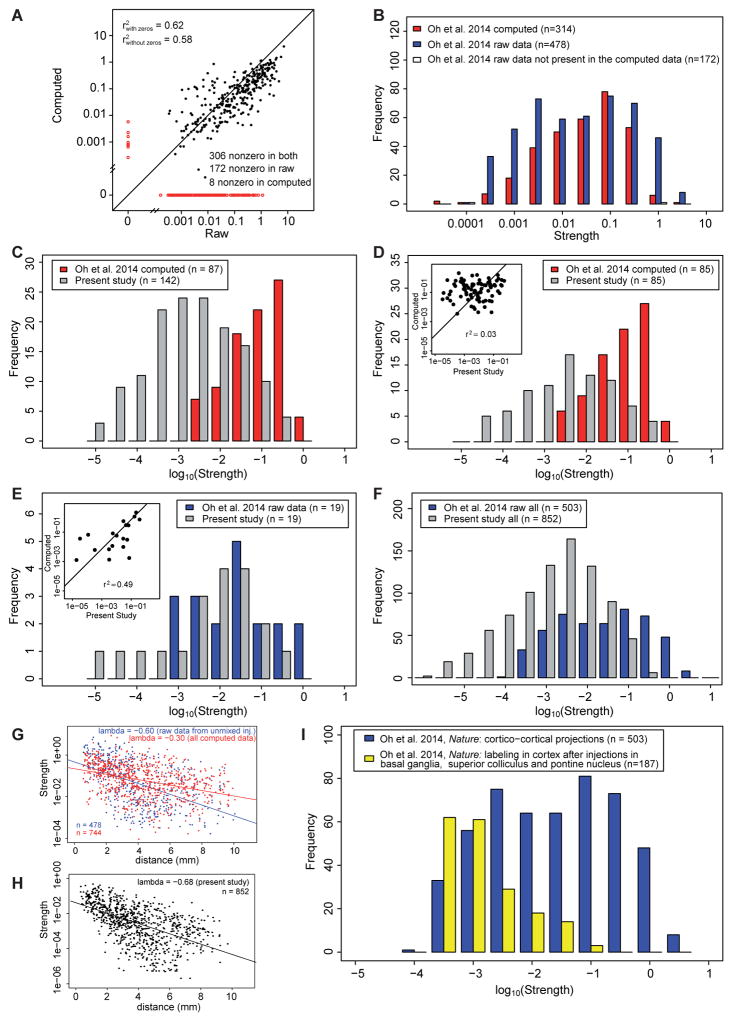
Effect of template matching on the weight distribution of connections

Comparison of raw connection strengths with those obtained from the computational model in Oh et al., 2014 allows appraisal of the modeling assumptions used in that study (see ProcessingOh et al., 2014data in STAR Methods). Figure 6A shows the agreement between the raw and the computed connections, with only 65% of them being true positives or true negatives, whereas 33% are false negatives (found in raw but not in computed) and 2% false positives (found in computed but not in raw). Moreover, the squared correlation between the true positives is modest, at only 0.58. Comparison of the weight distribution of the raw and computed data gives further insight into how the computational algorithm of the Oh et al., (2014) transforms the raw data Figure 6B. Here the blue bars are the connections that result from the raw non-mixed injections, and red bars the computed set of connections corresponding to the raw connections. The computed data equivalent to the 14 injected areas returns 314 connections, significantly less than the 478 connections observed in the raw data. The 164 connections that are present in the raw data but are absent in the computed (white bars), while predominantly weak are nevertheless found throughout the full range of weights. Figure 6B using a log scale for connection strength suggests that the Oh et al., 2014 raw data does not follow the same lognormal distribution as the computed data.

Figure 6. The data in the present study shows some similarity to the raw data in Oh et al. 2014, but not to the computed data.

(A) Correlation between the raw and computed data in Oh et al., 2014, zero values shown in red. (B) Distributions of the raw data and the corresponding connections in the computed data for the 14 areas which received unmixed injections in Oh et al., 2014; red bars, computed data, blue bars, raw data, white bars, non-zero connections in the raw data, but zero in the computed. (C) Distribution of strengths of connections for areas which are homologous in Oh et al. 2014, computed data (red) and present study (grey). Source areas: ACAd, ACAv, AId, AIp, AIv, ECT, GU, ILA, MOp, MOs, ORBl, ORBm, ORBvl, PERI, PL, RSPd, RSPv, SSp-bfd, V1; target areas, ACAd, GU, ILA, MOp, MOs, RSPd, SSp-bfd, V1. (D) Same as in C, but considering only projections that are nonzero in both sets. Insert, correlation diagram. (E) Distribution of strengths of connections for areas which are homologous and nonzero both in Oh et al. 2014, raw data (blue, the 14 areas which received unmixed injections) and present study (grey). Insert, correlation diagram. Source areas: MOp, SSp-bfd, V1; target areas: ACAd, GU, ILA, MOp, MOs, RSPd, SSp-bfd, V1. (F) Distribution of connection strengths for the full data set in present study (gray bars) compared to raw data in Oh et al., 2014 shown in panel B. (G) Distribution of projection lengths in Oh et al., 2014, raw data (blue) and computed data (red). (H) Distribution of projection lengths in present study. Notice that the spatial constant is close to the one in raw data in G. (I) Comparison of cortical labeling in Oh et al., 2014 follow anterograde tracer injections in the superior colliculus, pontine nucleus and basal ganglia with label obtained following cortical injections. See also Figure S3 and Table S1

In Figure S3, nineteen of the 41 cortical areas in an adapted atlas from the present study correspond to areas listed in the Figure 6C legend in the atlas used by Oh et al. (2014), allowing some direct comparison between the two studies. The present study found 142 connections in this set of common areas, which contrasts with the 87 connections computed for these areas by Oh et al., (2014). Figure 6C shows the set of connections shared by the two studies (same source area and same target area). This shows that the computed data from Oh et al., (2014) exhibits a lognormal distribution tightly restricted to the top three orders of magnitude compared to the broad lognormal distribution in the present study. Figure 6D provides a more direct comparison, by contrasting only those connections that are non-zero in both studies. They differ significantly in their weight range, and more importantly show no correlation (insert Figure 6D). These findings confirm that the algorithm used by Oh et al., (2014) to disentangle connections evidently led to significant transformations by reducing the number of connections and affecting their distribution of connection strengths. This is further supported by comparing those connections in the Oh et al., 2014 raw data with the 19 homologous connections in the present data (Figure 6E). Although the comparison is limited, this suggests that compared to the computed data, the raw data in the Oh et al., (2014) show an improved overlap in the weights and have a modest correlation with data from the present study (see Figure 6E insert). However, Figure 6F shows that the raw data of the Oh et al., (2014) possess a narrower range of weights compared to the present study.

Elsewhere we have shown that the weight-distance relationship is a cardinal feature of the connectome in both mouse and monkey, and it accounts for statistical aspects of many network features such as the motifs distribution, similarity and core-periphery (Ercsey-Ravasz et al., 2013; Horvat et al., 2016). In Figure 6G we compare the decline of weight with distance in the computed and raw cortico-cortical connections from Oh et al., (2014). This shows only a very modest slope for the computed data, by contrast, the slope in the raw data is comparable to that found in the present study (Figure 6H). The slope of −0.68 mm⁻¹ obtained in the present study is similar to that obtained in Horvat et al., (2016). Finally, in the Oh et al., (2014) study, our analysis of their raw data from the 26 unmixed injections in 14 isocortical areas yields a density of 92%, which is consistent with the density of 97% observed from our injections (see Partial coverage and global claims in STAR Methods).

In anterograde tracing it is challenging to distinguish between pre-terminal axons and boutons and to exclude labeled fibers of passage from the analysis. Further, there is an important difference in scale explored by the two tracers; anterograde is subcellular as it reveals individual boutons with hundreds to thousands per axon (Binzegger et al., 2004). In contrast, retrograde tracing is at the single cell level. These differences are compounded by the challenge of distinguishing boutons from interbouton axons when quantifying projection strength by measuring optical density (Wang et al., 2012), a difficulty that may contribute to the greater overdispersion in the anterograde data compared to the retrograde data (see Figure 3). Further, anterograde tracers occasionally label neurons retrogradely, and with them their collaterals both in the injected area and other areas to which the collaterals project (Reiner et al., 2000). Estimates of terminal densities from anterograde tracers using optical density measurements where axons of passage can introduce a significant bias may be less accurate than counts of labeled neurons following retrograde tracers. Since the observations of LeVay and Sherk (LeVay and Sherk, 1983), anterograde tracers have been shown to lead to retrograde labeling, and this includes the viral tracers used in the Oh et al., 2014 study (Wang et al., 2014). This can lead to labeling of local collaterals of the retrogradely labeled cells and could explain the secondary anterograde labeling observed in the Oh et al., 2014 study, where anterograde injections in the pontine nucleus and superior colliculus led to levels of labeling in cortex comparable to those reported for cortico-cortical projections (see Figure 6I, and Table S1). However, for measuring projection weights, anterograde and retrograde techniques are in principle complementary; retrograde labeling for revealing the diversity of source neurons, anterograde for informing about target specificity.

The ultra-high density of the cortical graph

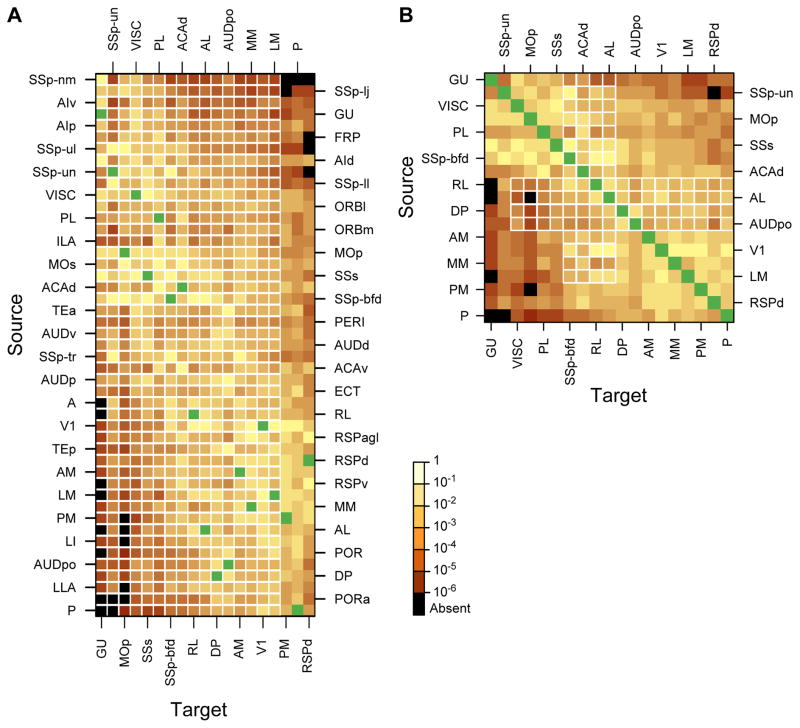
Figures 7A, B show the weighted connectivity 19 × 47 and 19 × 19 matrices in which the color of each entry represents the log₁₀ (FLNe) value for that pathway. Each column provides the FLNe profile of inputs observed for a given area and each row its outputs. The rows and columns were ordered so as to maximize the overall similarity between neighbors. Source areas of the occipital, posterior temporal and retrosplenial cortex are concentrated in the lower third of the matrix. Somatosensory, gustatory, visceral, insular, orbitofrontal and prefrontal source areas are clustered in the upper third. Motor, cingulate, auditory and parahippocampal source areas are mainly in the middle portion. Much to our surprise we found connections between nearly all injected areas. Figure 7A, B shows that the connection weights vary over five orders of magnitude, revealing two dissimilar but highly interconnected subnetworks. One exhibited strong connections between visual areas, strong inputs to occipital cortex from posterior parietal, auditory and retrosplenial cortex, moderate inputs from somatosensory, motor and orbital cortex, whereas projections from visceral, gustatory and prefrontal cortex were sparse. The other subnetwork (Figure 7A, B) exhibited strong inputs to somatosensory cortex from motor, visceral, gustatory, and insular areas, moderate input from posterior parietal and orbital cortex, and weak input from retrosplenial and prefrontal areas. Inputs to both subnetworks from cingulate parahippocampal and higher auditory cortex were similarly strong.

Figure 7. Weighted connectivity matrix.

Strengths of the projections (FLN) are color coded; black, absent connections; green, intrinsic projections where FLN is not indicated. (A) Rows, one of the 47 source areas; column, one of the 19 injected target areas. Note that the SSp-bfd and SSp-un subfields are listed as separate areas. The row and column ordering was determined by a clustering algorithm based on input and output profile similarity. (B) A weighted connectivity matrix for the 19×19 subgraph. See also Figure S4, Figure S6, Figure S8 and Table S6

In the edge-complete 19 × 19 matrix (Figure 7B) (meaning that the connectivity status of all node pairs are known), most connections between pairs were reciprocal, except for 2% (8/342 which were unidirectional showing no detectable inputs from P, LM, AL and RL to GU (Figure 7B), and from AL and PM to MOp. Note that in Figure 7B the distribution of colors is not perfectly symmetrical across the diagonal, indicating that the connection weights between pairs tended to be asymmetrical. For example area MOp received only weak inputs from visual auditory and posterior parietal areas but projected back strongly to these areas. Overall, inputs from gustatory, visceral, motor, somatosensory and prefrontal cortex to visual and auditory areas were stronger than the ascending inputs from these sensory areas.

The G_19×19 graph has M = 334 (binary) directed links from the maximum possible of N(N-1) = 342, and therefore it is strongly interconnected, with a very high graph density of ρ=0.97 (97%)(see Network density in STAR Methods). Because it is an edge complete subgraph of FIN, the density of G_19×19 is expected to be comparable to that of the FIN.

The in-degrees of the G_19×47 graph (i.e., the number of source areas projecting to each of 19 target areas), range from 38 to 46 with a mean of <k>_in = 44.8 (Figure S4A); their distribution is asymmetrical and not concentrated around the mean, but instead strikingly close to the maximum (Figure S4A, top right). To estimate the density of the FIN, the expected number of connections M_FIN ~ <k>_in N_FIN = 2107 for the FIN (G_47×47) leads to the prediction that ρ_FIN = M_FIN/[N_FIN (N_FIN − 1)] ~ <k>_in/(N_FIN − 1) ~ 0.97) (see Network density in STAR Methods).

A dominating set analysis (Markov et al., 2014a) shows that for all sets of 2 target area combinations from the 19 target parcels (171 pairs), 92% of them dominate 100% of the 47 parcels (Table S2) (see Network density in STAR Methods). Thirteen parcels out of 19 (68%) are fully connected.

Since the present study sampled only 19 areas, we may ask whether it is legitimate to infer the high-density of the full network from this data. To answer this question, in a first instance, we have examined the coverage of the injected areas across the cortex (Figure S5). This shows that injected areas are reasonably well distributed. Nevertheless, could we, by chance, have injected a subset of areas in the mouse that exhibit unusually high in-degrees? Our evidence indicates this is not the case (see Partial coverage and global claims of the STAR Methods); the necessary equivalence of in- and out-degrees coupled with graph theoretic analysis of the different data sets and parcellation schemes supports the conclusion that the mouse cortical connectome is indeed ultra-dense.

Communication efficiency in the weighted cortical network

Increasingly, the investigations of weighted networks are providing deeper insights into large-scale brain networks (Alstott et al., 2014; Bassett and Bullmore, 2016; Ercsey-Ravasz et al., 2013; Markov et al., 2013b; Muldoon et al., 2016; Song et al., 2014). Continued refinement of such approaches will be important for understanding the consequences of the ultra-high density network of the mouse brain relative to the sparser networks of larger brains (see Network communication efficiency in STAR Methods).

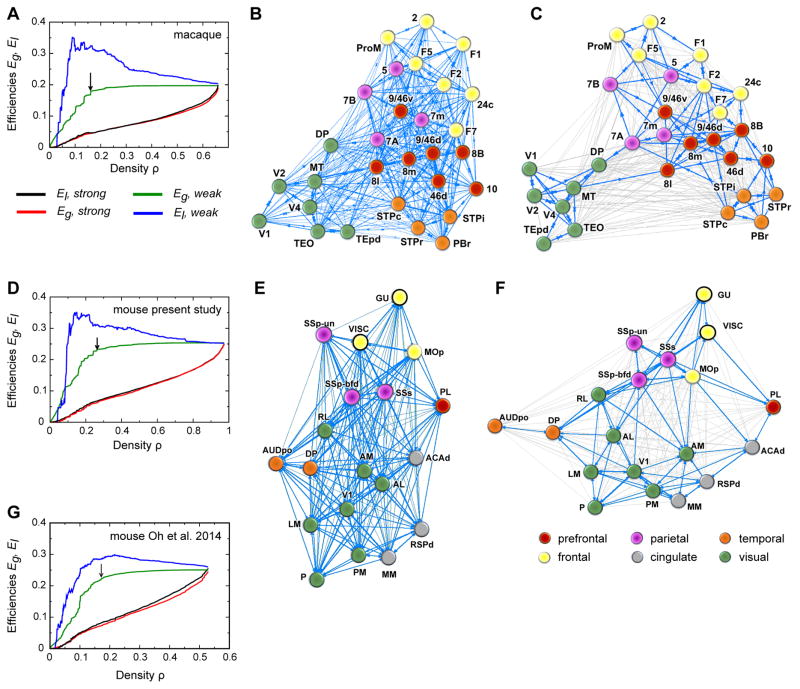
When sequentially removing from the macaque network the weakest (smallest FLNe) links, the global efficiency E_g stays nearly constant (see Figure 8A, green line) until more than 76% of the links are removed, indicating the existence of a high bandwidth, global efficiency backbone embedded within the network. This ensures a stable, baseline, high bandwidth average information transfer rate across the cortex, independent of the activity along the weak, long-range connections. The local efficiency E_l, however, shows a fast increase with the sequential removal of the weak links (see Figure 8A, blue line). This happens because, as explained in (Ercsey-Ravasz et al., 2013) and (Markov et al., 2013b), pruning the interregional shortcuts makes the network more localized, modular, and decreases interactions between the diverse functional modalities. As the weak links are removed, the local pathways between neighbors of a node through the rest of the network are mostly made of high bandwidth (large FLNe) projections, resulting in higher conductance values. The picture that emerged from this analysis for the macaque was that the cortical network has a structure which is well adapted to high-volume local information processing via high-conductance local pathways and also to a stable, nearly constant efficiency level of global information processing. It also revealed the relationship between network modularity and long-distance functional interactions, illustrated by the distribution of network communities that form when weak long-range links are present or absent (see Figure 8B, C).

Figure 8. Local and Global Communication Efficiency.

(A–C) Macaque data (taken from Ercsey-Ravasz et al., 2013). (A) Effects of graph density, via sequentially deleting weak (blue, green) and strong (red, black) links, on global efficiency (E_g) and local efficiency (E_l). Black arrow shows when the graph exhibits onset of unreachability (16% density), indicating the high efficiency backbone shown in C. (B) Weight-based layout, macaque full density (all 536 links). The Kamada-Kawai force-based algorithm for graph-drawing reveals optimal layout, with edges representing springs proportional to the link weights. (C) High-capacity backbone, blue edges are the 130 strongest connections (16% density) after weak link removal (thin gray edges), indicated by black arrow in A. (D–F) Same analysis as (A–C), for present mouse data. (D) The mouse graph exhibits onset of unreachability at 26% density. (E) Weight-based layout, mouse full density (all 334 links). (F) High-capacity backbone, blue edges are the 90 strongest connections (26% density) after weak link removal (thin gray edges), indicated by black arrow in B. (G) same analysis as in A for mouse computed data from Oh et al., 2014.

How does the mouse network compare with the macaque? Figures 8D, E, F show the results of the same analysis for the mouse data. Interestingly, the overall behavior of transmission efficiency is similar between the two mammals, suggesting that these features are strongly constraining for the mammalian brain. As E_g and E_l are both captured by the EDR in the macaque (Ercsey-Ravasz et al., 2013) and as EDR holds in the mouse as well (Horvat et al., 2016), this reflects EDR as an organizational principle. In mouse, as in macaque, the areas also cluster into functional regions (compare Figure 8E with 8B). Further, the high-bandwidth backbone (Figure 8F) presents stronger clustering than the full network (Figure 8E), just like in macaque (compare Figure 8C vs Figure 8B). However, there are significant differences between the two species. From a network point of view, the clusters in the macaque are stronger, with more high-bandwidth intra-cluster connections than high-bandwidth inter-cluster connections, especially for primary areas, whereas in the mouse the clusters are weaker with significant inter-cluster high-bandwidth connections. Moreover, while there are no strong connections between primary areas in the macaque, those do appear in the mouse, notably with a projection from V1 to SSp-bfd. When the same analysis is repeated on the Oh et al., 2014 data (see Figure 8G), the local efficiency has a weaker increase relative to the global efficiency when compared to present mouse data (Figure 8D) and macaque (Figure 8A). This happens presumably because of the inconsistencies discussed in the rest of the article.

Discussion

We find that mouse interareal connectivity is comparable to macaque in showing relatively high consistency and well-defined connectivity profiles but differs in possessing a much higher graph density. Our findings using a deterministic methodology give significantly different results from the computational data reported by Oh et al., 2014, and we explored the impact of these differences via an analysis of the high efficiency backbone. Finally, this weighted graph analysis reveals marked differences in the cortical connectomes of the mouse and macaque.

Technical considerations

PVtdT-expressing mice allowed accurate areal parcellation in each brain used for tracer injections, as reflected in the spatial map of labeled projection neurons shown in Figure S2. The utilization of quantitative retrograde tracing in these flat maps was an important part of our experimental design aimed at minimizing inter-animal sampling errors. The experimental design of the present study made it possible to verify that the uptake zone of the injection site (see Suitability of DY tracing in STAR Methods) was entirely confined to the intended area for the 27 cases fully analyzed (out of 102 injections). Modeling of FLNe variance in repeat injections across animals allowed exclusion of a geometric distribution in favor of a negative binomial distribution (Figure 3). Ranking FLNe values revealed lognormal distributions spanning five orders of magnitude with estimated 95% confidence intervals that satisfactorily contained the mean values (Figure 3). In addition, the consistency analysis of repeat injections showed that means in excess of twenty-four labeled neurons showed high consistency across injections (Figure 4). Finally, the dominating set analysis of the cortical subgraph studied here suggests that the full matrix may indeed have a density of 97% (Figure 7).

This density is considerably higher than the maximum 53% reported in the probabilistic mouse connectivity matrix (Oh et al., 2014) and in a meta-analysis of rat intracortical connections (Bota et al., 2015). High connection density might be caused by spillage of DY beyond the borders of areas or grey matter, and/or uptake by fibers of passage and damaged axons (Keizer et al., 1983). While such concerns are difficult to rule out entirely, examination of image stacks (Figure 2) revealed the location and 3D extent of the injection sites, allowing us to eliminate cases with spillage across areal and grey/white matter borders. Another potential concern involves labeling of area-to area-projecting neurons via tracer uptake by inadvertently injured axons running through layers 5 and 6 (Coogan and Burkhalter, 1993). Control experiments (not reported here) indicate that injuring callosal fibers is necessary for retrograde DY-labeling of interhemispheric projecting neurons, whereas application of DY to uninjured fibers of passage is ineffective. Thus, judged by the tight and topographically precise distribution of DY labeled cells (Figures 2, S2) we consider labeling via interareal deep layer axons likely to be negligible.

Our experimental design involved implementing a procedure to parcellate the mouse cortex that was applicable in each experimental case and therefore avoided registration to a template as was done in the study of Oh et al. (2014). By using PVtdT mice we were able to generate such an areal map for each mouse (Figure S1C). Although the parcellation by Oh et al., (2014) relied on different, presumably structural features in background fluorescence, the overall layout of the CCF and the parcellation used in the present study are notably similar (Figures S1A, B). Nevertheless, because we found a different connection density than Oh et al., (2014), it is important to consider whether this may be attributable to differences in parcellation schemes. Comparing the density observed in the two parcellation schemes gives an estimation of the relative accuracy of the density measure and its sensitivity to small changes in parcellation. Analysis of the present data using the parcellation of Oh et al., (2014) yielded a density of 95.7%, nearly identical to that of the present study (97.4%) (see Figure S6). Further, our analysis of the raw anterograde data generated by Oh et al., (2014) revealed an ultra-dense network of 90.1% (see Partial coverage and global claims of the STAR Methods). Hence, the minor parcellation differences did not have a significant impact on connection density, regardless whether it was derived by anterograde studies (Oh et al., 2014) or retrograde tracing (this study). Nevertheless, referencing connections to the individually derived map rather than a template may account for the higher consistency of connectivity profiles in the present study.

A second aim of our study was to compare the cortical graph density of mouse and macaque. Given the large differences in brain size, one possible concern is that the mouse injections might occupy a larger fraction of each area thereby encompassing local connectional heterogeneities (Falchier et al., 2002; Malach, 1989) and hence labeling a larger proportion of the total afferents to the injected area. We consider this unlikely to be a major factor, however, as measurements of injection sites showed that relative to brain size the volumes of DY injections in mouse and macaque were similar (Figure S7). Another concern is that the longer distances in the larger macaque brain may lead to suboptimal labeling of widely separated areas. Elsewhere, we have argued that this is unlikely, given that survival times exceed the active retrograde transport times required and that the intensity of individual cell labeling does not decline discernibly with increases in distance (Markov et al., 2014a).

Functional implications of the present results

Graph density is an important measure of the level of connectivity in a network. While many networks are sparse (e.g., social networks, technological/IT networks, infrastructure networks, gene regulatory networks, metabolic networks, protein interaction networks), cortical interareal networks, surprisingly, form high-density graphs. A graph is considered sparse when the number of links is of the same order as the number of nodes: for example, a network of 19 nodes would be sparse if it had 20 ~ 50 directed links, not the 334 reported here. The high-density character of the cortical network was first reported in the macaque, with a graph density of 66% (Markov et al., 2011). The current data, obtained with the same deterministic approach reveals an ultra-desnse mouse interareal network (97% density, nearly a complete graph). It is consistent with a predicted decrease in density with increasing brain size (Ringo, 1991). The much-expanded human cortex has a reported 180 areas per hemisphere (Glasser et al., 2016), about four-fold greater than the 41 reported here for the mouse and more than the ~130 areas reported for the macaque (Van Essen et al., 2012). An intriguing but unresolved question is whether human cortex might exhibit network sparsity resulting in specific structural and functional consequences as well as an increased susceptibility to disconnection syndromes (Bullmore and Sporns, 2012; Friston and Frith, 1995; Horvat et al., 2016b).

The high cortical density implies that almost all area pairs in the mouse have direct connectivity, both ways, suggesting high integration of information across the entire cortical network. While at such high densities specificity is lacking for the purely binary graph, it is restored once we take into account the weights of the connections. Inspection of the weighted connectivity matrix in Figure 7B demonstrates striking asymmetries in many bidirectional connectivity strengths, showing that the G_19×19 is a directed graph with strong weight specificity. This is also evident from comparison of individual tracer injections, for example, V1 injections show sparse labeling of somatosensory sub-areas, whereas somatosensory injections show much stronger labeling in V1. To decipher processing and information flow in such networks one must use methods that exploit the weighted nature of connections (Barrat et al., 2004; Newman, 2004), and the geometrical and morphological features of the areas within the cortical plate.

Despite its small size (<8 mm in length), the mouse brain has become an increasingly important model for investigating higher functions of the cortex using sophisticated methods that enable unprecedented progress in neuroscience. The fact that the mouse cortex has a graph density of 97% strongly impacts on how we understand the relationship between the structure and function of the cortex. The mouse cortical graph can achieve a high functional specificity despite its high density because each area has distinct connectivity profiles (Bressler and Menon, 2010; Markov et al., 2013a; Passingham et al., 2002). Comparison of the present results with findings in macaque (Markov et al., 2011; Markov et al., 2014) show specificity of the connectivity profiles, reflecting similar levels of variability in both species.

There are multiple origins of variability of cortical connectivity. The number of cortical areas in an ancestral mammal common to rodents and primates is not known, but evolution evidently led to an increase in the number of cortical areas in the primate lineage (especially humans) compared to the rodent/mouse lineage (Kaas, 2000; Striedter, 2005). Evolutionary changes include a relative increase in the extent of the cortical mantle that is referred to as association cortex in primates (i.e. cortex outside of the early sensory/motor areas). Cortical development is known to be under both intrinsic and extrinsic factors. Environmental factors that are known to influence the development of the cortex (Kennedy and Dehay, 1993; O’Leary et al., 2007) could potentially have a differential impact on arealization and variability in cortical connectivity in mouse and macaque (Buckner and Krienen, 2013). Further, the laboratory mouse is a highly-inbred strain that may exhibit less phenotypic variability than the macaque.

Many of the connections linking cortical areas show very low weights. Nevertheless, weak projections show good consistency both in mouse (present study) and macaque (Markov et al., 2013a; Markov et al., 2013b; Markov et al., 2011)). While the role of weak connections in brain networks is unknown, in social and ageing biological networks, the loss of weak connections may render the system unstable (Csermely, 2006; Granovetter, 1973). A similar hypothesis was used in theoretical analysis of the macaque cortical connectome (Goulas et al., 2015) and in recent imaging data in human (Bassett and Bullmore, 2016). Our confirmation that weak connections are consistent in the mouse highlights the importance of considering them in large-scale models of brain networks.

What does all this tell us about neural function? The combination of a high-density and marked connectivity profiles affirms the specificity of the mouse cortical graph but nevertheless suggests a comparatively high redundancy in the mouse cortex compared to larger brains, which are predicted to be sparse (Horvat et al., 2016). Future analysis of the weighted features of high and low density cortical graphs may suggest which features are invariant and which have adaptive value. These lines of research, exploring the network properties of the small and large brain and informed by differences in scaling rules across rodents and primates (Ventura-Antunes et al., 2013), are part of the emerging field of comparative connectomics (Horvat et al., 2016; van den Heuvel et al., 2016; Wang and Kennedy, 2016). The present study provides a weighted, edge-complete subgraph of the mouse cortex that will facilitate the development of comparative models across species. To the extent that such graphs are based on a uniform coverage of the cortex, the results computed on them should be representative of the expected values for the full connectome. They also serve as templates on which models of the cortex can be implemented and the results compared among them and with those from the data (Ercsey-Ravasz et al., 2013; Horvat et al., 2016; Noori et al., 2017; Song et al., 2014). This will be important for assessing the limitations of the rodent model for understanding the human brain. For example, the dense network linking the primary sensory areas in the mouse have only a limited anatomical counterpart in primates and might dictate a rodent-specific multimodal sensory integration process (Lee and Whitt, 2015; Olcese et al., 2013; Teichert and Bolz, 2017). Finally, this data will also facilitate the application of network control frameworks to help predict the neural function of diverse network modules (Yan et al., 2017).

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for reagents and resource may be directed to the Lead Contact, Henry Kennedy (henry.kennedy@inserm.fr).

Experimental Model and Subject Details

Animals

Retrograde tracing experiments with Diamidino Yellow (DY), immunostaining for M2 muscarinic acetylcholine receptor (M2), vesicular glutamate transporter 2 (VGluT2) and cytochrome oxidase (CO) histochemistry were performed in 141 male and female mice. 33 C57BL/6J (Jackon Lab) (of which 14 injected with DY, 3 of which successful for this study; 19 used for immunostaining and histochemistry). 88 PV-Cre (B6.129P2-Pvalb^tm1(cre)Arbr/J, Jackson Lab) × Ai9 (B6;129S6-Gt(ROSA)26Sor^{tm9(CAG-tdTomatoHze}/J, Jackson Lab) of which 24 successful for DY labeling in this study; 8 for fluorescence imaging of VGluT2 (Slc17a6^tm2(cre)Lowl/J, Jackson Lab); and 12 for fluorescence imaging of M2 (B6;Cg-Chrm2^tm1.Hze/J, Jackson Lab). All experimental procedures were approved by the institutional Animal Care and Use Committee at Washington University.

For the 27 mice which were successfully injected, the age span is 8–30 weeks, and sex is known for only 2 cases, both females (see Table S6). The others are mostly males, for technical reasons – females being retained for breeding. Sex wasn’t registered because there are no known sex differences in cortical connectivity.

Method Details

Tracer injections

Prior to tracer injection, mice were anesthetized with a mixture of Ketamine (86 mg · kg -1) and Xylazine (13 mg · kg −1, i.p) and secured in a headholder. Body temperature was maintained at 37°C. Left-hemisphere tracer injections were made by inserting a glass pipette (20 μm tip diameter) through the dura into the brain and injecting DY (50 nl, 2% in H₂O; EMS-Chemie, Gross-Umstadt, Germany) by pressure (Picospritzer, Parker-Hannafin). Injections were aimed stereotaxically 0.35 mm below the pial surface and often required pulling back the pipette to correct proportionally for dimpling of the dura and confining potential injury to layers 1–4. Cases in which injected DY spilled into the white matter or across areal borders were excluded from the study. From a total of 102 DY injections, 27 were successfully confined to 17 distinct areas and two subareas of SSp (Figures 2A–F). The origin of the coordinate system was the intersection between the midline and a perpendicular line drawn from the anterior border of the transverse sinus at the posterior pole of the occipital cortex. The injection sites identified as 120–280 μm-wide crystalline deposits of DY (Figure 2A, D, E, F) of occipital, temporal, insular, parietal, restrosplenial, motor, cingulate and prefrontal cortex. Their details are the following, specifying the injected area, the anterior/lateral position in mm, and the number of successfully injected animals: ACAd (6/0.1, n = 1), AL (2.4/3.7, n = 1) (Figure 2E), AM (3/1.7, n = 2), AUDpo (2.3/5, n = 1), DP (4.5/2, n = 1), GU (6/4, n = 1), LM (1.4/4.2, n = 3) (Figure 2D), MM (1.9/1.6, n = 1), MOp (6.45/2, n = 1), P (0.7/4.1, n = 1), PL (6.8/0.1, n = 1), PM (1.9/1.6, n = 1) (Figure 2F), RL (2.8/3.3, n = 2), RSPd (2.1/0.4, n = 1), SSp-bfd (3.4/3.25, n = 2), SSp-un (3.4/2.4, n = 1), SSs (3.75/3.25, n = 1), V1 (1.1/2.4–2.9, n = 4) (Figure 2A–C), VISC (4.2/4.5, n = 1). Note that under fluorescence illumination, injection sites appeared larger, but nevertheless showed no apparent spread to neighboring areas. In all cases, retrograde DY labeling was very bright and labeled large numbers of neurons in multiple areas distributed across the cortex.

Suitability of DY Tracing

The choice of a highly sensitive retrograde tracer was crucial. In contrast to tracers such as FluoroGold and Cholera Toxin B, DY is predominantly a nuclear stain, which means that labeling is dense and spot-like (Figure S2B) and lacks the ambiguities introduced by the often fragmented appearance of cytoplasmically labeled neurons. Hence, high-density labeling, such as found in the present project, can be accurately mapped out and the full range of labeling density successfully captured (Figure S2B).

How reliable is DY tracing with respect to sensitivity, restriction of pick-up zone and minimization of false positives?

Firstly, the reason for using DY was to enable direct comparison of cortical connectivity in mouse and monkey. The identification of projections that were previously unknown (Markov et al., 2014b) has shown that DY is a non-selective tracer which preferentially labels nuclei of projection neurons (Conde, 1987) with superior efficiency.

Secondly, importantly, DY has a highly restricted and identifiable pick-up zone making it possible to identify the area effectively injected with great precision. DY was taken up from a crystalline bolus deposited in the cortex, which in the present study was 120–280 μm in diameter (Figure 2). Such injections were small enough to be confined to the tiny areas of the mouse cortex, but sufficiently large to overcome possible connectional heterogeneities within an area that may cause between-injection variability (MacNeil et al., 1997; Scannell et al., 2000). Because experiments in monkey have shown that the bolus diameter roughly corresponds to the DY-uptake zone (Bullier et al., 1984a; Conde, 1987; Kennedy and Bullier, 1985; Perkel et al., 1986), we are confident that in all the reported cases here DY was captured from within a given area. To exclude DY-uptake through injured fibers we have further confined injections to layer 1–4 and thus, minimized labeling through damaged fibers of passage between different cortical areas (Yamashita et al., 2003), but allowing uptake of spreading tracer by terminals projecting to layers 5 and 6. Uptake by intact fibers of passage is rare and inefficient (Payne, 1987).

Thirdly, the problem of false positives is well defined with DY. Leakage of DY from backlabeled neurons in vivo is negligible (Keizer et al., 1983) and we have argued elsewhere with respect to published results that there is no evidence that secondary pick-up leads to false positives with this tracer (Markov et al., 2014a; Markov et al., 2011). For instance the lack of secondary uptake in cortex (Bullier et al., 1990; Bullier et al., 1984, 1984a; Markov et al., 2014b) was most convincingly shown by the failure of labeling transcallosal projection neurons in monkey V1 after injection of DY in contralateral V2, which failed to label cells in the unconnected region of V1, away from the heavily connected strip along the V1/V2 border (Dehay et al., 1986; Dehay et al., 1988). Release and secondary pick-up is rare for fixed, floating sections, but as a precaution of secondary labeling sections were immediately mounted on glass slides, air dried and stored at −20° C until analysis under fluorescence optics. Taken together it seems highly unlikely that, following retrograde transport to the source area, DY was released and picked up by neurons in quantities sufficient to produce secondary labeling.

Fourthly, for comparison, anterograde labeling with viral (Oh et al., 2014) and non-viral tracers (Zingg et al., 2014) can lead to a category of false positives that do not occur in retrograde DY tracing and complicate the interpretation of results. These include retrograde labeling of neurons and their local axon collaterals in the projection target (LeVay and Sherk, 1983; Wang et al., 2014). Such contamination may explain false positive cortical inputs from the superior colliculus and pontine nucleus observed by Oh et al. (2014).

Histology

Four days after tracer injection, mice were euthanized with Ketamine/Xylazine and perfused through the heart with phosphate buffered saline, followed by 1% paraformaldehyde (PFA) in 0.1M phosphate buffer (PB, pH 7.4). The cortex was immediately separated from the rest of the brain. To unfold and flatten the cortex, the tissue was placed on a glass surface, pial surface down. Using microsurgical knives, the hippocampus was disconnected from neocortex along the seam between alveus and cingulate bundle, and flipped outwards while still attached to the entorhinal cortex. A small incision was made to separate medial from lateral orbital cortex. Proceeding in a posterior direction the white matter was split between the corpus callosum and the cingulate bundle, enabling the unfolding of the medial wall containing medial orbital, prefrontal, cingulate, and retrosplenial cortex. The tissue was then transferred white matter down onto a filter paper covering a sponge and weighed down by a glass slide placed on top. The assembly was postfixed in a petri dish filled with 4% PFA and stored overnight at 4°C. After postfixation the tissue was cryoprotected in 30% sucrose and 40 μm thick sections were cut on a freezing microtome in the tangential plane.

In order to assign in each mouse the injection site and DY labeled neurons to individual cortical areas, we developed a parcellation scheme based on the distinctive distribution of PVtdT expression (see Parcellation of the cortex below). This eliminated counterstaining for additional areal markers, thereby avoiding loss of signal and the associated risk of secondary labeling by leakage from retrogradely DY labeled cells (see Suitability of DY Tracing above). To determine the reliability of PVtdT in distinguishing distinct parcels, we compared PVtdT borders to borders observed with M2, VGluT2 and CO reactivity, all of which have been employed previously to parcellate rodent cortex (Ichinohe et al., 2003; Wang et al, 2011; Wang et al, 2012). In order to compare all four patterns we used flatmounted PVtdT-expressing sections reacted against M2 (MAB367, Millipore) or VGluT2 (AB2251, Millipore) using fluorescent secondary antibodies for visualization. Alternatively, we used tdT fluorescence or non-fluorescent immunohistochemical ABC staining methods to visualize M2 or VGluT2 expression, with histochemistry to reveal CO reactivity. In each case, alternate sections were stained for Nissl substance to reveal the cytoarchitectonic landmarks annotated in the Allen Brain Atlas. The expression patterns were imaged under a microscope equipped for brightfield and fluorescence illumination.

Processing of labelled neurons

Sections were mounted onto glass slides and DY labeling was analyzed under UV fluorescence (excitation: 355–425 nm, emission: 470 nm) at 20×, with a microscope controlled through a computer using the Mercator software package, running on ExploraNova technology. This software enables the observer to manually tag individual neurons at high magnification levels, extensively using the Z-axis to focus on individual labeled cells (Figure S2B). High-fidelity digital charts of the co-ordinates of labeled neurons were made for all 12–24 sections per hemisphere and digitally stored (Figure S2A). Once charting was complete, sections were imaged for PVtdT (excitation 520–600 nm, emission 570–720 nm) (Figure 2), stained for Nissl substance with cresyl violet, and imaged under bright field illumination. The images of the sections were acquired using MorphoStrider software (ExploraNova). We have extensive experience with DY as a retrograde tracer (see Suitability of DY Tracing above). The manual charting of neurons as described above (see Figure S2B) minimizes false positives.

The digitized charts of labeled neurons and the images of the corresponding sections were aligned in Adobe Illustrator. The sets of images from each brain were parcellated using the regional patterns in PVtdT expression and Nissl stained cell bodies. This allowed the creation of an individual template at layer 4 for each brain, which was then aligned via adjacent section to superficial and deep layers by matching blood vessels.

Parcellation of the cortex

Our choice of PVtdT expression for areal identification was inspired by the work of Saleem and Logothetis (Saleem, 2012), who successfully used PV immunostaining to delineate cortical areas in rhesus monkey. However, there is no a priori reason to assume that the expression pattern of PVtdT outlines areal boundaries in the mouse. As this is of course true for any individual architectonic marker, we compared the pattern of PVtdT expression with those of immunolabeling for M2, VGluT2, histochemical reactivity for CO, and Nissl staining. Based on previous observations (Wang et al., 2011), our expectation was that comparing different markers would reveal overlapping or complementary spatial expression gradients reflecting areal borders across individuals. The excellent alignment of markers in for example layer 4 of V1 and SSp (Figure 1) affirms the utility of the PVtdT borders for delimiting areas.

What follows explains how, in tangential sections through layer 2–5, overlapping or complementary patterns of M2, VGluT2 and CO labeling, and overlaying visuotopically mapped areas (Wang and Burkhalter, 2007) to stained landmarks were used to further subdivide the 25 parcels identified by PVtdT expression (Figure 1A, white dashed outlines). Although the PVtdT map was less detailed than the 36 areas annotated in the CCF (Figure S1A, C), the overall layout, shapes and sizes of multiple parcels of our atlas is notably similar (Figure S1B). Moreover 19 of the parcels shown in the PVtdT map were simple (i.e. showed no additional subdivisions except for subfields of body parts in SSp) (Figure 1A, black dashed lines), and closely matched those marked positively or negatively by M2, VGluT2 and CO (Figure 1B–D; Figure S1C–F). These included: V1, SSp, SSs, AUDp, GU (Chen et al., 2011; previously annotated as the tooth/tongue representation of SSp; (Remple et al., 2003; Wang et al., 2012)), VISC (previously referred to as posteroventral area; (Fabri and Burton, 1991; Wang et al., 2012); also known as insular auditory field or insular somatosensory field; (Rodgers et al., 2008; Sawatari et al., 2011). Further, areas identified by PVtdT-expression alone included the posterior (AIp), ventral (AIv) and dorsal (AId) agranular insular areas (Van De Werd et al., 2010), ACAd, ACAv (Tanahira et al., 2009; Van De Werd et al., 2010), PL and ILA (Van De Werd et al., 2010), FRP (ARA), ORBm and ORBl (Van De Werd et al., 2010), as well as MM (Wang et al., 2012), ECT and PERI (Beaudin et al., 2013).

For the 6 remaining PVtdT-expressing parcels, at least one of M2, VGluT2 and CO markers revealed additional subdivisions, indicated by colored labels and dashed lines in Figure 1A, while 7 borders had to be inferred from stereotypical position relative to PVtdT-labeled landmarks. Such compound parcels were found in retrosplenial (RSPagl, RSPd, RSPv), motor (MOp, MOs), temporal (TEa, TEp), auditory (AUDv, AUDpo, DP, AUDd) and visual extrastriate (one parcel containing AL, LLA, RL, A, AM and PM, and another with LM, LI, P, POR and PORa) cortex, denoted in Figure S1C by red and pink shading. These compound parcels were sub-divided as follows:

Retrosplenial cortex, here we observed intensive expression of M2 in its 0.5 mm wide agranular part (RSPagl) and moderate VGluT2 and M2 expression in its ~0.25 mm dorsal part (RSPd).

Motor cortex, showed intense, uniform PVtdT expression without an obvious boundary between MOp and MOs (Tanahira et al., 2009) (Figure 1A, Figure S1C). However, a clear border between both motor areas was apparent in the transition from strong to weak CO reactivity (Figure 1D, Figure S1F). On PVtdT maps we therefore marked MOp as 1–2mm-wide curved strip along the medial border of SSp and MOs as a 1mm-wide strip adjoining MOp on the medial side.

Temporal cortex, TE, was identified as a U-shaped belt of weak and uniform PVtdT expression at the ventral border of auditory cortex (Figure 1A, Figure S1C), which was further subdivided by VGluT2 into a more darkly labeled anterior half (TEa) and a weakly expressing posterior portion (TEp) (Figure 1C, Figure S1E).

In auditory cortex, the primary area (AUDp) was surrounded by a weakly labeled, uniform belt (Figure 1A, orange labels; Figure S1C; pink shading). On the M2 map, the belt was further subdivided into the more darkly labeled AUDv, AUDpo and AUDd and the intensely labeled posterior dorsal auditory area, DP (Kimura et al., 2004) (Figure 1B, orange labels Figure S1D). On the PVtdT map AUDv and AUDpo were identified as the anterior and posterior half of the weakly-expressing parcel lateral to AUDp (Figure 1A, Figure S1C). DP was identified in the M2 map as a separate rectangular parcel anterior to TEp, lateral to LI, posterior to SSs and posterior to AUDd (Figure 1B, Figure S1D). In the VGluT2 and CO maps DP stood out as a medially-facing nose of a uniformly labeled auditory cortex (Figure 1C, D, Figure S1E, F, dark red shading). The overall partitioning of auditory cortex closely resembled the five separate tonotopic maps (Issa et al., 2014; Tsukano et al., 2016).

In extrastriate cortex, PVtdT expression was more intense in a boot-shaped compound parcel (Figure S1C, red shading) at the lateralposterior side of V1 (Figure 1A, yellow labels), surrounded by ECT, TEp, DP and AL. PVtdT expression in the parcel continuing forward and around the tip to the medial side of V1 (Figure S1C, pink shading) was weaker (Figure 1A, blue labels). Both of these extrastriate PVtdT parcels overlapped with similar parcels found in M2 and CO maps (Figure 1B, D, Figures S1D, F). Although bipartite by all of these markers, previous topographic mapping of extrastriate visual cortex has shown that the anteromedial parcel contained AL, RL, A, AM and PM, whereas the lateralposterior comprised LM, LI, P, POR and PORa (previously denoted 36p) (Wang and Burkhalter, 2007; Wang et al., 2011). Of all these areas only POR and PORa stood out as a VGluT2-expressing sub-parcel located at the foot of the lateral PVtdT-expressing boot (Figure 1C; Figure S1E; red shading). Furthermore, the toe was more darkly stained with M2 and marked area PORa (Figure 1B, Figure S1D, dark red shading), which was previously known as 36p and identified by its low abundance of the non-phosphorylated intermediate filament protein, SMI32 (Wang et al., 2011). Although PVtdT revealed few details of this organization, labeling in layer 4 provided readily identifiable landmarks (V1, SSp, RSP, AUDp) and unambiguous reference points (tip of V1, barrels of SSp, rhinal fissure, TEp) for accurately positioning all of the extrastriate areas and complete their borders based on the size and shape determined previously by mapping visuotopic connections (Wang and Burkhalter, 2007; Wang et al., 2011). For example in the lateral parcel, POR was centered on the foot of the PVtdT expressing boot lateral to V1 (> 0.75/< 1.5 mm lateral/medial of V1 and 0.75 mm anterior to the rhinal fissure [rf]), PORa occupied the toe (> 1.5mm lateral of V1) and P the heel (< 0.75 mm lateral of V1, < 0.6 mm anterior to the rf) (Figure S1C). LM and LI occupied medial and lateral parts of the boot shaft, respectively (LM: < 0.8 mm lateral of V1, > 1.25 mm anterior to POR/P; LI: > 0.8/< 1.1 mm lateral of V1, < 1.2 mm anterior to POR).

In the weakly PVtdT-expressing parcel around the tip and the medial side of V1, M2- and CO-expression was distinctly sparser (Figure 1A, B, D, blue labels; Figure S1C, D, F, pink shading). Although uniform by these markers, topographic and callosal mapping has identified six areas, AL, LLA, RL, A, AM and PM within this belt (Garrett et al., 2014; Wang and Burkhalter, 2007), which were not revealed by PVtdT, M2, VGluT2 or CO. Nevertheless, we have annotated these areas based on their stereotypical position relative to PVtdT-labeled landmarks. Specifically, AL was a triangular area with its vertex at the lateral posterior corner of SSp, its base at the border with LM (2 mm anterior to the rf) marked by a sharp decrease in PVtdT expression (Figure 1A, (Wang et al., 2011)). Of the two remaining sides one was parallel to V1 (1mm lateral of V1) and the other ran parallel to the lateral border of SSp from its posterolateral corner to intersect V1 at an approximately right angle (Wang and Burkhalter, 2007). LLA was the rectangle enclosed by DP, SSs and AL and a line parallel to the V1 border, intersecting the lateral posterior corner of SSs. RL occupied a 0.7 × 1.2 mm wide rectangle between AL, V1 and SSp with the medial border aligned with the E-row of the barrel field (Figure 1A). Area A was a 0.65 × 0.75 mm wide rhomboid between the tip of V1 and SSp, bordering RL and AM (Figure 1A). AM extended between the tip of V1 to the medial corner of SSp and was bordered laterally by A (Figure 1A). Its medial border was a narrow longitudinal strip of low PVtdT-, M2-, VGluT2- and CO-expression in MM (Figure 1A). The posterior border of AM was a line through the tip of V1 angled backwards by 35° from the coronal axis. PM was the triangle behind AM between MM and V1 (Figure 1A). MM was a narrow strip with sparse PVtdT, M2, VGluT2 and CO expressions, which separates PM/AM from the strongly VGluT2-expressing agranular retrosplenial area (RSPagl) (Figure 1A–D, Figure S1C–F).

The accuracy of parcellation was estimated by comparing maps drawn independently by 3 investigators. This involved a zeroing procedure by which stacks of sections were aligned to the pattern of PVtdT expression in layer 4 of V1 and SSp, the borders of 25 uniformly PVtdT-expressing parcels were outlined (Figure 1A), and the parcels were further subdivided into 41 areas based on position relative to readily identifiable PVtdT-positive or -negative landmarks (i.e. tip of V1, SSp, RSP, AUDp, TE, rhinal fissure), shape, and size revealed by previous mapping of connections, expression patterns of M2, VGluT2 and CO (Wang and Burkhalter, 2007; Wang et al., 2011, Wang et al., 2012). The spread in the location of areal borders between visual areas (LM/LI, LM/AL, LM/P, LM/POR, AL/RL, A/AM) measured in 5 animals was 87–142 μm. Our estimate of a < 150 μm-wide transition zone between neighboring areas differs from the sharp borders annotated in the Allen Brain Atlas (ARA; Zingg et al., 2014) and the crisp boundaries derived from averaging of background fluorescence in sections from 1231 mice (Oh et al., 2014). It is important to note that this large sample size reduced the variance over that seen in single cases, suggesting that our maps are not only highly accurate but as shown in Figure S1A, B, remarkably similar to those of the Common Coordinate Framework. Thus the important difference to Oh et al. (2014) and Zingg et al. (2014) is not the parcellation per se but the precise registration of DY injection sites and labeled neurons with parcellations derived in each individual case.

Quantification and Statistical Analysis

Computation of FLN

The assignment of the labeled neurons to their respective cortical areas resulting from the parcellation was done with in-house software, written in Python 2.7. The fraction of labeled neurons per area (FLNe) was computed by dividing the number of labeled neurons expressed within the area by the total number of labeled neurons, extrinsic to the injected area, from the ipsilateral cortical hemisphere.

FLN data is available in Table S6.

Overdispersion

Quantifying variance of weights (FLNe) allows accurate statistical inferences based on the data and estimation of the uncertainties associated with observed weight values. This allows evaluation of connectivity profiles and provides useful constraints on how well single injections can be used to estimate connectivity profiles (Markov et al., 2014a; Markov et al., 2011).

Count data are intrinsically heteroscedastic, meaning that their variability depends on the mean (Hilbe, 2007). The simplest case occurs when counts are well-described by a Poisson distribution, and the variance equals the mean. It is usually easier to reason in terms of the standard deviation, the square root of the variance, rather than the variance. The standard deviation (SD) of Poisson distributed data, increases as the square root of the mean. This implies that the coefficient of determination, defined as the ratio of the SD to the mean, decreases rapidly with increase in the mean. Hence for counts of 100, 1000, 10000, and 100000 neurons, the expected SDs would correspond to 10%, 3%, 1% and 0.3%, respectively, of the means. For the large counts involved in neural projections, such low variability is unlikely. Previous retrograde labeling data have, in fact, demonstrated that cortical connectivity data sets display significant overdispersion (Markov et al., 2011; Markov et al., 2014b; Scannell et al., 2000).

Overdispersion occurs in count data when the variance increases faster than the mean and is displayed in many data sets (Hilbe, 2007). If overdispersion is ignored, then variance is underestimated and statistical tests become anti-conservative, i.e., significance is attributed to differences that are within the normal variation of the data set. This underlines the importance of characterizing the mean-variance relations in the data and using appropriate statistical models that incorporate terms that correctly characterize the dispersion of the data.

Overdispersion can be characterized in a variety of ways. Previous retrograde labeling studies in macaque indicate that a negative binomial distribution provides a reasonable description of the data. The negative binomial distribution can be derived as a mixture of a Poisson and a Gamma distribution. In effect, the Poisson mean is no longer considered to be a fixed parameter, but instead follows a Gamma distribution. This yields a 2-parameter distribution that is specified by its mean and a dispersion parameter, θ (Hilbe, 2007). The variance of the negative binomial distribution is given by σ² = μ + μ²/θ. As θ becomes large, the mean-variance relation approaches that of a Poisson distribution. Thus, the Poisson distribution can be seen as a special case of the negative binomial. For θ = 1, the distribution becomes a geometric distribution that is quite overdispersed. Higher values of this parameter signal less overdispersion. Studies in macaque found an overdispersion parameter of about 7–8 (Markov et al., 2011; Markov et al., 2014b). Importantly, while this reflects considerable variation in counts across injections for a given area, the variability was not sufficient to obscure the 5 orders of magnitude range in the projection strengths obtained from a given injection.

Transformation of the raw counts to FLNe changes their statistical distribution. For example, in the case of the Poisson distribution, normalization of counts results in a variable distributed according to binomial law (Chung, 2006). The relation of the SD to the mean of a binomial distribution is given by: $\sigma =\sqrt{\mu (1-\mu )/n}$, where the mean is now constrained to be a value in the interval (0, 1) and n is the size of the count. Note that this is an inverted U-shaped function of the mean, but on a double-logarithmic plot, the rising portion continues to follow a square-root law and would be expected to have a slope of 0.5. In Figure 3 this is shown by the red curve in each graph. The curve turns down for values greater than 0.5, but no FLNe values this large are observed, so that the initial portion of the curve can be compared with the data. Importantly, the curve provides a poor description of the data, rising less steeply and predicting values of SD that are systematically below those in the data. This leads to rejecting a simple Poisson model of the variability of the data, as is the case in the macaque (Markov et al., 2011; Markov et al., 2014b) and demonstrates evidence of substantial overdispersion.

How much overdispersion is required to model the data was assessed informally by plotting curves for different values of the dispersion parameter and evaluating what value describes the data best. There is no simple expression for relating the normalized counts, i.e., FLNe, to the SD for a negative binomial distribution. We estimated such a curve, however, by simulating samples from a negative binomial distribution with a fixed dispersion and a range of mean values spanning those obtained in the data and then normalizing the counts as if we were computing FLNe. We repeated this simulation many times and obtained an average curve with which to compare the data. For example, the blue curve in each of the plots of Figure 3 is obtained for simulations with the dispersion equal to 1, generating the prediction for a geometric distribution. Importantly, the data points tend to fall systematically below this curve, providing evidence that the data are not as dispersed as a geometric distribution would predict. We rejected the geometric case more formally by fitting a negative binomial model to the data by maximum likelihood under the constraint that the dispersion was equal to 1 and by letting the dispersion be a free parameter. Nested likelihood ratio tests rejected the geometric distribution for the 2 injection sites shown in Figure 3 A, B in our mouse data (LM: χ² (90) = 57.3, p = 3.8 10⁻¹⁴; V1: χ² ( (180) = 76.8, p = 1.9 10⁻¹⁸).

Given that the geometric distribution could be rejected, we repeated the simulations as described above for a wide range of dispersion values to estimate the expected relation between SD and mean FLNe as a function of the dispersion. We then compared these curves with the values in Figure 3 and estimated a dispersion value that minimized the error between the simulation and the data, which constitutes the green curves for each plot with the dispersion parameter and the 95% confidence interval (indicated in brackets).

Accordance with the negative binomial model

In Figure 3E, F the error bars are twice the standard errors of the means from repeat injections.

The solid curves are the predicted values for ordered Gaussian variables with the same mean and SD as the data set. Specifically, we took the means of log (FLNe) represented by white dots and we computed the parameters of the Gaussian that would best fit these points.

To evaluate whether differences between the predicted values and the data were significant, we simulated 10000 count data sets from a negative binomial distribution with the same means as the data and with the dispersion parameters obtained from the analyses displayed in Figure 3A, B. For each data set, we normalized the counts by the total to obtain simulated FLNe values. From these distributions, we estimated the 2.5% and 97.5% quantiles to obtain a confidence interval (the grey envelopes in Figure 3E, F).

Variability and consistency

In Figure 4D, E we addressed specifically if it is possible in the retrograde studies in mouse and macaque to define a threshold above which all projections can be expected to be consistent. For discrete distributions, it is expected that there is a non-zero probability of observing no neurons, even if the projection exists, simply based on sampling variability. The probability of observing such cases would be expected to increase as the mean size of the projection decreased. In fact, the probability distributions predict the expected incidence of such missing connections. For Poisson distributed data, the probability of observing zero neurons is e^−μ, where μ is the mean number of neurons in the projection. For a negative binomial distribution, the probability of observing zero neurons is ${\left(\frac{\theta }{\theta +\mu }\right)}^{\theta }$. Deviations from such predictions in the direction of too many observations of zero labeled neurons (leading to zero-inflation) or too few (leading to zero-deflation) constitute evidence against the statistical model used for the data. An alternative is to explain such deviations as evidence that the connections are actually absent in some animals, providing evidence of individual differences in the connectivity pattern. The overdispersion of the count data might be taken as evidence of individual differences in connectivity strength, which could be due to genetic or environmental influences. However, without detailed knowledge of what factor(s) are responsible for the overdispersion, such a hypothesis cannot be confirmed.

Figure 4D displays mouse data from 13 repeat injections in target areas, where the mean number of neurons for a given projection across the multiple injections is plotted as a function of the total number of neurons counted for each injection. Thus, points are individual projections. Those resulting from different injections but for the same target areas are at identical ordinate values, as they all have the same mean and different abscissa values as injections differ only in the total number of neurons labeled in the brain. When no neurons from a given source area were observed in an injection but were observed in at least one other repeat injection, the point is plotted as a white disk but is otherwise colored. We analyzed the distribution of inconsistent projections by determining whether the features log(Mean) and log(Total) could be used to linearly classify the presence and absence of connections. This can be implemented as a logistic regression in which the expected value of the binary variable (Presence/Absence) is predicted by the two features.

Figure 4E displays the same analysis for the 13 repeat injections in macaque.

Evaluating Akaike Information Criterion

For every group of repeat injections in V1 and LM (Figure 3A, B), we modeled the number of labeled cells in the source areas as a function of two explanatory variables: AREA (a factor with a level for each source area) and BRAIN (the individual from which the counts were obtained). We fitted the data with generalized linear models (McCullagh and Nelder, 1989), with a negative binomial family. We chose the link function to be logarithmic and we used the log of the total number of cells counted from each injection as an offset or constant component, added to the model, so that in fact the FLNe was modeled.

The selection of the factors and interactions that best described the data was based on Akaike’s Information Criterion (AIC) that evaluates what terms lead to a model with the best predictive power for new data (Akaike, 1974). AIC is defined as minus twice the log likelihood for the best fitting model plus twice the number of parameters estimated in the model. The second term is a penalty for complexity. Including more factors and interactions will improve the fit to the data. The AIC introduces a penalty for additional parameters, so that in comparing several models, lower AIC values correspond to better models in the sense of balancing a tradeoff between model complexity (number of parameters) and goodness of fit. We report the difference in AIC (dAIC) between the models with and without the interaction between factors, so a positive value supports the model without an interaction. For example, when AREA is considered as an explanatory variable then it is treated as a factor with as many levels as source areas that contain retrogradely labeled cells from the injections in the target areas. A model fit to the data containing only this factor provides estimates of the average FLNe and its variability for each level of AREA. If, on the other hand, the best model fit to the data requires that the FLNe values be described by the interaction of explanatory variables AREA and BRAIN, i.e., that the values for a particular area vary significantly across individuals, then there is no basis for describing an average profile of connectivity as a signature.

Overdispersion and connectivity profiles

In Figure 5A, C, to illustrate the relationship between the different levels of the statistical modeling, we performed a simulation of the expected experimental results under three different scenarios for the sampling distribution of the data: Poisson, Negative Binomial with θ = 7, and Geometric (i.e., Negative Binomial with θ = 1). In each case, we first simulated a log normal distribution of FLNe with mean and standard deviation based on the average mean and standard deviation of the log FLNe values from all of our mouse injections (red, green and blue curves in Figure 5A–C). Then we simulated 1000 repeats with dispersion specified according to each of the models. The results of these repeats are plotted as grey, semi-transparent points in Figure 5 A–C. Figure 5D shows the SDs of the FLNe in the source areas plotted against the mean FLNe values, from the 1000 simulations, replicating the relation that we observed in Figure 3A, B.

We considered 30 hypothetical source areas with fixed mean FLNe spanning 5 orders of magnitude and evenly distributed along an average log-normal curve with the same mean and SD as one of our injections (red, green and blue, respectively, for the three distributions). Each mean FLNe was multiplied by 10⁶ to give the expected mean numbers of neurons in the source areas. These values were used for generating random counts from each of the distributions (Poisson, Negative Binomial and Geometric), as indicated in the insets of A–C. The set of random counts from every simulation were then normalized by their sum to transform them to simulated values of FLNe. This procedure was repeated 1000 times, thus revealing the expected spread of results from 1000 injections under each of the hypotheses.

Processing Oh et al., 2014 data

The Oh et al., 2014 study reports densities from data derived computationally from mixed injections involving multiple areas, which we call “computed data”, but the Supplementary Information from that study provides results obtained from a small number of unmixed injections, which we refer to as “raw data”. We calculate the density of the network that we derived from those unmixed injections and show that it differs markedly from that reported by Oh et al., 2014 for the computed data and that they are much closer to our results in the present study (see Partial coverage and global claims below).

In the study by Oh et al. (2014), the location of injection sites was inferred from a template. With this computational approach 86% of the 469 injection sites in the brain were reported to involve 2–18 different structures. There were 105 injections restricted to isocortex, of which 76% involved 2–9 different structures. The connections labeled by mixed injections were disentangled, and the strengths of connections between individual areas estimated algorithmically using both mixed and injections restricted to single structures (non-mixed injections). For the computed data, the authors derived from 452 out of 469 experiments across the whole brain a full matrix of interareal connections, from which we extracted the ipsilateral cortico-cortical connections. In contrast, the raw data contains connections from 26 injections confined to 14 single areas (non-mixed injections) in the isocortex.

Network density

The density of a directed graph is given by the ratio ρ =M/[N(N−1)] between the number of directed edges (links) M of the graph and the maximum possible number of directed links, N(N−1), where N is the number of nodes in the graph.

The graph density of the full interareal network (FIN, which contains the whole information about the connections between areas) is a fundamental measure of the graph’s overall connectedness, extensively used in network science and also in earlier analyses of cortical connectivity (Markov et al., 2013b; Markov et al., 2014a; Sporns and Zwi, 2004). Referring to the weighted connectivity matrix in Figure 7A (for the full FLN weights data see Table S6), but employing the corresponding binary connectivity matrix, we can infer the density of the FIN (Janson et al., 2000; Markov et al., 2014a; Newman, 2010). Consequently, M_FIN will be the product between the average indegrees <k>_in and the number of areas N_FIN. The density of FIN will be the ratio between this number and the total possible connections N_FIN (N_FIN − 1).

Based on an atlas of 47 areas (41 areas with SSp divided into 7 subareas, Figure S1B), the mouse FIN contains N_FIN = 47 cortical areas that represent the nodes of the G_47×47 graph. The directed edges of the FIN correspond to directed connections between nodes, with weights given by the fraction of labeled neurons. Our analysis of the FIN makes use of the G_19×47 directed subgraph of projections within FIN, which reveals all the in-degrees of the injected 19 nodes. It also makes use of the G_19×19 edge-complete subgraph of FIN, corresponding to the connections among just the 19 injected areas. Both G_19×47 and G_19×19 subgraphs contain complete information about the status of their edges and their statistical properties would not be expected to be influenced by injections into additional areas elsewhere in the cortex (see Partial coverage and global claims below). Given that the 19 injected areas are widely distributed across the cortex (see Figures S1B, S5), the G_19×19 subgraph is likely to reflect major characteristics of the FIN.

We performed a dominating set analysis on G_19×47 (Table S2) for further evidence that the FIN is indeed dense (Figure S4B). In graph theory, a subset D of nodes of a graph G with node set V is said to be dominating G, if all elements of V have a link to at least one node in D (Kulli and Sigarkanti, 1991). Here we modify this definition slightly by saying that D dominates x% of the nodes of G, if an x% of all nodes in V are linked to one or more nodes in D. The x%=100% corresponds to “full” domination. This definition includes also nodes from D. The Minimum Dominating Set (MDS) D_min is defined as the one that fully dominates G and it has the smallest size (number of nodes).

Partial coverage and global claims

For the following analysis, for simplification, we’ll name ABI the data from Oh et al., 2014 and SBRI the data obtained in the present study.

Density calculation: The density of square 1–0 matrices NxN is calculated the standard way by dividing the number of 1-entries with the number of matrix elements minus the number of intrinsic connections (A→A type entries), i.e., by N(N−1). The density of rectangular 1–0 matrices NxM with N denoting the number of injected areas and N < M, is calculated by dividing the number of 1-entries by the number of matrix elements less the number of intrinsic connections, i.e., by NM-N.

• Dataset #1: The ABI anterograde (Oh et al. 2014) raw data is based on anterograde injections in 14 areas and identifies labels in a 40-area atlas. Accordingly, the 14×14 edge-complete square matrix/graph has a density of 90.11% and the 14×40 matrix has a density of 92.12%.

• Dataset #2, ABI parcellation: For our retrograde data with the Oh et al 2014 (ABI) parcellation, the matrix is 21×45 (Figure S6A), with a density of 95.71% for the 21×21 edge-complete (injected) subgraph (Figure S6B), and a density of 96.1% for the 21×45 matrix.

• Dataset #3, present parcellation: For our retrograde SBRI data with our present parcellation, the matrix is 19×47 (Figure 7A), with a density of 97.37% for the edge-complete 19×19 matrix (Figure 7A) and the same density of 97.37% for the full 19×47 matrix.

This shows that across different parcellations and different datasets from different experiments, and different methods (anterograde vs retrograde), the mouse matrix connectivity density is consistently above 90%.

The connectome is not uniform; as shown previously, both in the macaque and mouse, the connectome is organized into a core-periphery structure with the cortical network core (primarily of high degree nodes) mostly comprised of associative areas. Selecting target areas only from the core, would, indeed generate an edge-complete subgraph that is very dense. However, all datasets include both primary and associative injected areas. In particular, ABI injected 6 primary areas, representing 43% of the 14 injected areas. SBRI with ABI parcellation has 5 primary areas injected, representing 24% of the 21 areas injected, while SBRI with present parcellation has the same 5 primary areas injected, which forms 26% of all injected areas. Additionally, the choices of the locations of injections between the two sets of experiments (ABI and SBRI) differ considerably. As we have shown above, all densities are consistently above 90%.

Next, we investigate the possibility that the non-injected areas contribute only with a low connectivity so that the full graph would have a lower final density. Recall that retrograde tract tracing reveals all the incoming connections to the injected node, from both injected and non-injected nodes. If the non-injected nodes contributed a lower connectivity to the connectome, then we should observe lower out-degrees from the non-injected nodes to the injected set, when compared to the out-degrees of the injected nodes to injected set. Table S4 shows the values of the out degrees for nodes separated into the injected and non-injected groups respectively. To be able to compare similar quantities, we normalize by the number of injected nodes. For example, for our data with the ABI parcellation, there are 21 injected nodes, but an injected node can send out-links only to 20 other nodes from the injected set (no outlinks to self), whereas a non-injected node can send outlinks in principle to all the 21 injected. Thus, if we divide the outdegree of an injected node by their number minus one (20) and the outdegree of a non-injected node by 21, we get the fraction of injected nodes towards which a specific node has an outlink to. We then repeat this with the SBRI data and present parcellation (with 19 injected nodes), shown in Table S5. For the ABI parcellation (Table S4), the outlink average fraction for an injected node is 95.7%, with a standard deviation of 5.7%, whereas for a non-injected node the same quantity is 96.4% with a standard deviation of 7.3%. Thus, from an out-degree point of view, towards the same set of nodes, there is virtually no difference between an injected node or a non-injected node. For the SBRI dataset with the present parcellation (Table S5), the average out-degree fraction of an injected node is 97.4% with a standard deviation of 3.9%, whereas the same quantity for non-injected nodes is an average of 97.4% and standard deviation of 4.4%.

For anterograde tract tracing, the roles of out-links and in-links are reversed, as in this case all the outlinks are revealed for an injected area. Repeating the same analysis as above with the anterograde ABI (raw) data, we find a similar pattern, as shown in Table S3. The average in-degree fraction of an injected node is 90.1% with a standard deviation of 8.8%, whereas the same quantity for non-injected nodes is an average of 93.1% and standard deviation of 8.7%. Here as well, from an in-degree point of view, we see no significant difference between an injected node or a non-injected node.

The above data all show very similar numbers with small deviations and they indicate that there is nothing special in terms of out-degrees between injected and non-injected nodes, and across different parcellations.

In-degree analysis for retrograde data

Since retrograde injection in an area reveals all its incoming connections, the in-degrees into the injected areas will not change with additional injections, they are final. Figures S8A, B show the in-degree distribution for the SBRI dataset for both parcellations (ABI and present). In both cases the in-degrees are very high, near the maximum. For the Oh et al parcellation (21×45 matrix), among the 21 injected areas, 10 receive in-links from all the rest (45–1 = 44), five from 43, two from 42 and the lowest is one area receiving in-links from 33 others. More than 85% of the nodes, each, receive at least 93% of all possible incoming connections. For the present parcellation (19×47 matrix), among the 19 areas 13 receive from maximum possible (46) one from 45, two from 44 and the lowest receives 38 in-links. More than 84% of the nodes, each, receive at least 95% of all possible incoming connections! Clearly, other injections would bring new edges into the network. Assuming that the average in-degree of the non-injected nodes is the lowest value found among the injected nodes (although the previous analysis shows that it should be higher than this assumption), even this brings the full network density down to only (33×24+888)/(45×44) = 85% for the ABI parcellation and to (38×28+851)/(47×46) = 89% for the SBRI parcellation, both still very high.

Network communication efficiency

The five order of magnitude variability in the interareal projection weights indicates strong specificity, and has important consequences, in particular on the capacity, or bandwidth of information transfer between cortical areas. This is best illustrated via network communication efficiency measures, first introduced in network science applications by Latora and Marchiori (Latora and Marchiori, 2003) and expanded upon by Vragovic et al (Vragovic et al., 2005). There are two such measures, the global efficiency measure E_g (Latora and Marchiori, 2003) and the local efficiency E_l (Vragovic et al., 2005). E_g is the average conductance between all source-target pairs in the network, whereas E_l measures the conductance between the neighbors of an area X through the network that does not include X, averaged over all neighbor pairs and for all X. Conductance from a source node to a target node is a weighted measure and it’s given by the conductance of the path of minimal total resistance through the network from source to target. As explained in (Markov et al., 2013b), resistance for information transfer along a projection can be modeled as the negative logarithm of the FLN edge weight of that projection and therefore resistances are additive along paths. Accordingly, a directed path from source to target that contains only high FLN edges will have a very low resistance and thus high conductance, or high information transfer bandwidth and vice-versa. In (Ercsey-Ravasz et al., 2013) and (Markov et al., 2013b), both the global and local efficiency measures revealed an optimal organization for information transfer in macaque cortex. The same studies showed that this optimal organization was well captured by the exponential distance rule (EDR) model, which describes the negative exponential dependence of weights on distance.

The clustering analysis and plotting from Figure 8D-G was done with Pajek, and it uses the Kamada-Kawai force-based algorithm (Kamada and Kawai, 1989), which draws areas that share stronger connections closer to one another than otherwise.

Data and Software Availability

The FLNe data is available at www.core-nets.org

Supplementary Material

2

Table S6. FLNe data from the present study (Related to Figure 7)

Highlights.

• Retrograde tracer injections are restricted to single areas in mouse cortex

• Individual areal maps for each brain are used for location of labeled neurons

• 97% of all possible cortico-cortical connections exist

• Areas are characterized by weight-specific connectivity profiles

Glossary

Abbreviations

A

Anterior area

ACAd, ACAv

Anterior cingulate area dorsal part, ventral part

AId, AIv, AIp

Agranular insular area dorsal part, ventral part, posterior part

AM

Anteromedial area

AMY

Amygdala

AOB

Accessory olfactory bulb

AON

Anterior olfactory nucleus

AUDp, AUDpo, AUDv

Auditory cortex primary area, posterior area, ventral area

CoA

Cortical amygdala

DP

Dorsal posterior area

ECT

Ectorhinal area (also referred to as area 36, (Beaudin et al., 2013))

ENTl, ENTm

Entorhinal area lateral part, medial part

FRP

Frontal pole

GU

Gustatory area

HPF

Hippocampal formation

ILA

Infralimbic area

LM

Lateromedial area

LLA

Laterolateral anterior area

LI

Laterointermediate area

MM

Mediomedial area

MOp, MO

Motor cortex primary, secondary

NLOT

Nucleus lateral olfactory tract

OB

Olfactory bulb

OT

Olfactory tubercle

ORBl, ORBm

Orbitofrontal area lateral part, medial part

PERI

Perirhinal area (also referred to as area 35; (Beaudin et al., 2013))

P

Posterior area

Pir

Piriform cortex

PL

Prelimbic area

PM

Posteromedial area

POR

Postrhinal area

PORa

Postrhinal anterior (previously annotated as 36p, (Wang et al., 2011))

RSPagl, RSPd, RSPv

Retrosplenial area agranular part, dorsal part, ventral part

ParS

Parasubiculum

PreS

Presubiculum

RL

Rostrolateral area

SSp

Somatosensory cortex primary (barrel field [SSp-bfd], lower jaw [SSplj], lower limb [SSp ll], upper limb [SSp-ul], trunk [SSpt], nose and mouth [SSnm])

SSs

Somatosensory cortex secondary

SUB

Subiculum

TEa

Temporal area anterior part posterior part (TEp)

TEp

Temporal area posterior part

TR

Postpiriform transition area

VISC

Visceral area

VISa

Visual anterior

VISal

Visual anterolateral

VISam

Visual anteromedial

VISli

Visual intermediolateral

VISlm

Visual lateromedial

V1, VISp

Visual primary

VISpl

Visual posterolateral

VISpm

Visual posteromedial

VISpost

Visual postrhinal