Unified approach for extrapolation and bridging of adult information in early-phase dose-finding paediatric studies

Abstract

The number of trials conducted and the number of patients per trial are typically small in paediatric clinical studies. This is due to ethical constraints and the complexity of the medical process for treating children. While incorporating prior knowledge from adults may be extremely valuable, this must be done carefully. In this paper, we propose a unified method for designing and analysing dose-finding trials in paediatrics, while bridging information from adults. The dose-range is calculated under three extrapolation options, linear, allometry and maturation adjustment, using adult pharmacokinetic data. To do this, it is assumed that target exposures are the same in both populations. The working model and prior distribution parameters of the dose–toxicity and dose–efficacy relationships are obtained using early-phase adult toxicity and efficacy data at several dose levels. Priors are integrated into the dose-finding process through Bayesian model selection or adaptive priors. This calibrates the model to adjust for misspecification, if the adult and pediatric data are very different. We performed a simulation study which indicates that incorporating prior adult information in this way may improve dose selection in children.

1 Introduction

Phase I dose-finding studies represent the first transition from laboratory work to a clinical setting and aim to obtain reliable information on the pharmacokinetics (PK), safety and tolerability of a drug. Typically, these trials are performed on healthy subjects, unless the drug is intended for the treatment of malignancies (i.e. oncology).

In paediatric clinical trials, invasive procedures are avoided or at least minimised for ethical reasons and the usefulness of clinical trials in children has been widely debated over the last decades,¹ as highlighted by two papers recently published in the journal of the American Academy for Paediatrics.^2,3 Several authors and specialists have reported a critical need for more clinical studies in paediatrics combined with an improvement in the methodologies used in practice. Some authors have argued that incorporating prior knowledge from adults should help to attain a better understanding of the paediatric population. However, other studies have shown that children should not be considered small adults but rather a specific population with a different metabolism that is not necessarily linearly related to growth.^1,4

For dose-finding paediatric studies, guidelines have been suggested for the choice of starting subset doses⁵ (e.g. the starting dose should equal 80% of the adult recommended dose, and these doses should then be increased by 30% to obtain the subset doses). However, these recommendations are arbitrary and do not rely on any scientific justifications. As a result, to improve the selection of the dose-range that should be used in a paediatric study based on the use of adult information, this information should be investigated through (1) the choice of the dose-range for a paediatric trial, (2) the dose-finding model and (3) its parameterisation.

Motivating example: Erlotinib is an oral inhibitor of the epidermal growth factor receptor tyrosine kinase that blocks cell cycle progression and can slow down tumour progression. This anticancer agent was approved by the Food and Drug Administration for the treatment of glioblastoma in adults. Several early-phase trials were conducted in adults to study the toxicity and PK of this drug at different dose levels,^6–12 and two phase I paediatric studies were conducted after the publication of the results in adults. However, only a small amount of the knowledge obtained from the adult trials was used in the design and planning of the paediatric trials. Geoerger et al.¹³ used 80% of the dose recommended for adults as the starting dose and incremented this dose by steps of 25 mg/m² to obtain the subset dose levels; however, these researchers provided no scientific justifications for these choices. Neither the available adult information nor the expert opinions were used to parametrise the model-based dose-finding design. Jakacki et al.¹⁴ also conducted a phase I dose-finding trial for erlotinib in paediatric subjects and selected the starting dose level according to the bioavailability of the solution for injection. The authors did not describe the method used for the selection of the subset dose levels, and information from studies on the adult population was not used to build a more appropriate trial for the paediatric population. This motivating example highlights the need for the development of proper extrapolation or bridging methods that should be used when prior knowledge from the adult population is available.

In the development of a dose-finding model for the paediatric population, difficulties regarding the evaluation of toxicity alone (except in oncology) have led to the use of a joint model for both toxicity and efficacy instead of a model that evaluates toxicity prior to efficacy. Several statistical methods are available for the design of early stage phase I/II clinical trials. Among them, Bayesian methods, such as the EFFTOX design and the bivariate Continual Reassessment Method (bCRM), have been proposed.^15,16 Although initially used in oncology settings, these methods have also been used for studies of the paediatric population.¹⁷ Additionally, Broglio et al.¹⁸ proposed a method in which adult and paediatric trials are performed simultaneously with dose-finding models for each population that share an identical slope but a different intercept. Doussau et al.⁵ reviewed the methods that could also be used in paediatrics, such as ‘3+3’, CRM with its modifications and Dose-finding with Escalation with Overdose Control (EWOC).

The use of an adaptive dose-finding method requires that three components be fixed prior to initiation of the trial:

1. Dose-range: Misspecification of the dose-range in a clinical trial can lead to inappropriate dose selection and invalidation of the trial. Because children have a specific metabolism, we proposed the establishment of a dose-range that is more suitable to the paediatric metabolism.¹⁹ For that purpose, we proposed the estimation of paediatric PK parameters from adult PK data, which are often available long before data for the paediatric population are available, using extrapolation techniques, such as allometry and maturation.

2. Working model (WM) or initial guess of dose–toxicity and dose–efficacy relationships: WMs are usually selected based on information from experts. In some cases, a unique choice of WM can be misleading and results in the selection of an inappropriate dose. One approach for overcoming this issue is to use several WMs for toxicity and efficacy using the bCRM^20,21 and to select the best model with based on the Watanabe-Akaike information criteria (WAIC) developed by Watanabe.^22,23

3. Prior distribution of the model parameter(s) to be estimated: although using standard non-informative priors is often advised, it is difficult to assess to what degree this choice is informative or non-informative. Moreover, it may be interesting to include information in the priors while controlling the informativeness in cases with a small effective sample size, particularly in paediatrics. Regarding the selection of priors, we considered a method developed by Morita,^24,25 which consists of evaluating the informativeness of a prior in terms of the effective sample size. The more informative a prior is, the more patients are needed to compensate for it. In a paediatric setting, where the sample size is small, this scale is a strong asset for evaluating a chosen prior. However, if the chosen prior is too informative or misspecified compared with the paediatric reality, a non-informative alternative should be available. In this case, we have modified a method proposed by Lee and Cheung²⁶ and Zhang et al.²⁷ that introduced the concept of ‘adaptive-prior’ into dose-finding studies. The idea is to be able to switch during the trial to a less informative prior if a misspecification in the prior choice is detected.

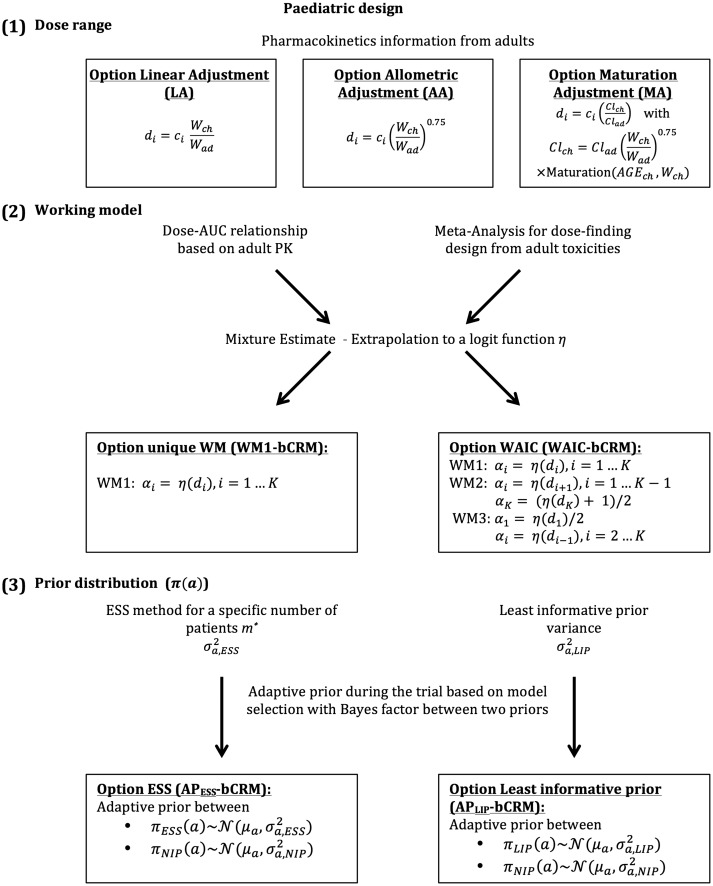
The aim of this paper is to propose a unified approach for the design of a paediatric dose-finding clinical trial through the extrapolation and bridging of information gleamed from the adult population. We have gathered and modified various methods that have been developed in different fields to propose a unified approach. The novelty of our work consists of the proposal of extrapolation with maturation from adult PK into the definition of the dose-range (1) and of the use of adult information from several sources to better parameterise the dose-finding designs (2) to (3) instead of leaving these decisions to arbitrary choices. In this work, several options are proposed for the selection of the dose-range, the WM and/or the parametrisation of the dose-finding design (Figure 1). Section 2 details the dose-finding model, illustrates the options for specifying the dose-range and describes the parametrisation of the design using adult information. The simulation settings and results are given in Sections 3 and 4. Finally, the guidelines are proposed in Section 5 and a discussion is provided in Section 6.

Figure 1.

General framework describing the different proposed steps in the planification of paediatric dose-finding clinical trials. It is composed of (1) the choice of the dose-range with three different possible options, linear adjustment (LA), allometric adjustment (AA) and maturation adjustment (MA). They are built using extrapolation from adults to children, with d_i the paediatric dose, c_i the adult dose and W_ch and W_ad, respectively, the children and adult weight; (2) the working model (WM) specification, where adult PK and toxicities can be used to built a toxicity function η. It allows to calculate the WMs (α_i, $i\in 1,\dots ,K$) for each dose i and (3) the specification of the prior density parameter a, $\pi (a)$, of the dose–response relationship.

2 Model and methods

We considered the design of a phase I/II clinical trial in the paediatric population using the Bayesian bCRM as the dose allocation method. Section 2.1 presents the bCRM method and the dose allocation algorithm. The first step (1) consists of defining the doses to evaluate. We proposed three options for the selection of the dose-range using adult to paediatric extrapolation methods, which use different adjustments of the paediatric dose from the adult’s recommended dose: linear, related to weight with allometry and related to physiological processes with maturation functions to account for maturation differences between adults and children. These three options are described in Section 2.2.1. Once the doses are defined, step (2) consists of associating each dose with a given initial guess of the toxicity and efficacy probability, and these relationships are called ‘working models’ (WMs). The selected doses are supposed to be within a desirable toxicity, and efficacy interval to ensure that patients are not overtreated or undertreated. The WMs are constructed by gathering several prior sources of information from the adult population, such as PK, phase I trials, phase II trials, toxicity and clinical response. We proposed two options for the WMs: using only one WM, or using several WMs and selecting the optimal WM using automatic criteria. A description of the methods used to elaborate the WMs is given in Section 2.2.2. Finally, step (3) involves the selection of the dose–response parameter density of the priors used in the bCRM. We proposed two options for these priors: considering adult information or considering the case with the least information. These are described in Section 2.2.3, and a summary of this general framework is presented in Figure 1.

2.1 Bivariate continual reassessment method (bCRM)

In this general framework, we used the bCRM as phase I/II dose-finding methods. This design proposes a joint model for both toxicity and efficacy.^16,28 The aim of this method is to identify the safe most successful dose (sMSD), which is the most successful dose under toxicity restriction. Let $d_1<d_2<\dots <d_K$ be the paediatric doses to be evaluated in the study, with K the number of discrete dose levels and n the total number of patients to be recruited. Choice of doses is discussed in Section 2.2.1. Toxicity and efficacy are random binary variables (0,1) where $Y_j=1$ denotes a toxicity for patient j ($j\in 1,\dots ,n$) and V _j = 1 denotes a positive response. The dose level X_j is a random variable taking discrete values x_j, where $x_j\in \{d_1,\dots ,d_K\}$. The probability of toxicity at dose level X_j = x_j is given by $R(x_j)=\text{Pr}(Y_j=1|X_j=x_j)$, the probability of efficacy with no toxicity at dose level X_j = x_j is given by $Q(x_j)=\text{Pr}(V_j=1|X_j=x_j,Y_j=0)$ and the overall success is obtained by $P(d_i)=Q(d_i)\{1-R(d_i)\}.$

Following the under-parametrised model approximation proposed by O’Quigley et al.,²⁸ we have $R(d_i)=\psi (d_i,a)={\alpha }_i^{\text{exp}(a)}$ and $Q(d_i)=\phi (d_i,b)={\beta }_i^{\text{exp}(b)}$, where $R(d_i)$ and $Q(d_i)$ are monotonic and increasing with dose, $a\in ℝ$ (resp. $b\in ℝ$). Parameters $0<{\alpha }_1<\dots <{\alpha }_K<1$ (resp. $0<{\beta }_1<\dots <{\beta }_K<1$) correspond to the WM to be chosen by the user (see Section 2.2.2). The joint probability density function is defined by

$$\begin{array}{c}\multicolumn{1}{c}{f(y,v;d_i,a,b)=\psi (d_i,a{)}^y(1-\psi (d_i,a){)}^{(1-y)}\phi (d_i,b{)}^v(1-\phi (d_i,b){)}^{(1-v)}}\end{array}$$ (1)

Under Bayesian inference, the prior distributions for a and b are respectively denoted by $\pi (a)$ and $\pi (b)$. Choice of the priors is discussed in Section 2.2.3.

The dose allocation rule is the following. Let us denote $\hat{a}$ and $\hat{b}$ the estimated means of the posterior distribution of a given WM for the current available data of toxicity and efficacy already observed with the included patients. The estimated probability of toxicity is $\hat{R}(d_i)\cong \psi (d_i,\hat{a})$ and the efficacy $\hat{Q}(d_i)\cong \phi (d_i,\hat{b})$. Finally, the overall probability of success is given by $\hat{P}(d_i)=(1-\hat{R}(d_i))\hat{Q}(d_i)$. The recommended dose for the new next cohort of patients is the sMSD $d^{*}$, that is, the dose maximising $\hat{P}(d_1),\hat{P}(d_2),\dots ,\hat{P}(d_K)$ under a constraint of toxicity target, defined with parameter τ, such that $\hat{R}(d^{*})\le \tau$.

In practice: For escalation, dose skipping was allowed only on doses already tested. A start-up phase was implemented to gather data before estimating the model parameters. The first cohort of three patients was treated at a specified dose x₀. If no toxicity was observed, a new cohort of three patients would be included at the direct higher dose. This process was repeated until at least a toxicity was observed or all doses were tested. We then moved to the dose-finding algorithm using bCRM. For safety reason, a stopping-rule was added to our algorithm, that is, if $\text{Pr}(\psi (d_1,a)>\tau )>0.9$, the trial was terminated. At the opposite, a second stopping rule was defined in case of non-efficacy. For a threshold of minimum efficacy $\tau \text{'}$, if $\text{Pr}(\phi (d_K,b)<\tau \text{'})>0.9$, the trial was terminated.

2.2 Extrapolation from adult data to paediatrics

Similarly to any model-based phase I/II dose-finding method, the design can be sensitive to three settings: (1) the choice of dose-range, (2) the WMs and (3) the prior distributions. In our proposed method, we suggest that these settings be based on extrapolations from the adult to paediatric population.

2.2.1 Specification of a dose-range

Paediatric data are often rare, and paediatric doses are usually selected based on existing recommendations for adult doses. We proposed three options for the selection of paediatric doses: linear and allometric extrapolation from adult doses, which are the current practices, and use of maturation, which is a novel approach in this context.

Option linear adjustment. Using the adult dose $d_{\mathit{ad},i}$ ($i=1,\dots ,K)$, weight W_ch of children and average weight W_ad of adults, the linear adjustment (LA) option consists of defining the paediatric dose d_i as

$$\begin{array}{c}\multicolumn{1}{c}{d_i=d_{\mathit{ad},i}\times \frac{W_{\mathit{ch}}}{W_{\mathit{ad}}}}\end{array}$$ (2)

Option allometry adjustment. This option introduces a scale parameter describing the rate at which the weight increases, which is usually equal to 0.75^4,40,41

$$\begin{array}{c}\multicolumn{1}{c}{d_i=d_{\mathit{ad},i}\times (\frac{W_{\mathit{ch}}}{W_{\mathit{ad}}}{)}^{0.75}}\end{array}$$ (3)

Option maturation adjustment. The use of maturation functions allows the adjustments to better reflect the paediatric physiology.⁴ We took advantage of this allometry–maturation approach²⁹ to propose a paediatric dose-range calculation, denoted maturation adjustment (MA). Our method is based on the available adult PK knowledge. For a given adult dose $d_{\mathit{ad},i}$, the corresponding children’s dose d_i was defined such that the same exposure to the dose was achieved. This exposure can be quantified by the AUC or C_max, which depends on PK parameters (typically clearance). Let Cl_ch (resp. Cl_ad) be the paediatric (resp. adult) clearance and $\mathit{AUC}(\text{d},\mathit{Cl})=d/\mathit{Cl}$ be the corresponding AUC. The goal of achieving equal exposure in adults and children leads to the following definition for the paediatric dose $d_i=d_{\mathit{ad},i}\times \frac{{\mathit{Cl}}_{\mathit{ch}}}{{\mathit{Cl}}_{\mathit{ad}}}$. If the adult PK clearance is available from previously published PK studies, the paediatric clearance is generally unknown but might be extrapolated through allometry and maturation functions. The resulting general equation defining the evolution of clearance in children according to age and weight for a specific drug is

$$\begin{array}{c}\multicolumn{1}{c}{\frac{{\mathit{Cl}}_{\mathit{ch}}}{F_{\mathit{ch}}}={\mathit{Cl}}_{\mathit{ad}}\times \underset{\text{Clearancematuration}}{\underbrace{\sum _h\%{\text{CYP}}_h{\mathit{MAT}}_{{\text{CYP}}_h}(\mathit{AGE})}}\times \underset{\text{Bioavailabilitymaturation}}{\underbrace{\frac{F}{F_{\mathit{ch}}}}}\times \underset{\text{Allometry}}{\underbrace{(\frac{W_{\mathit{ch}}}{W_{\mathit{ad}}}{)}^{0.75}}}}\end{array}$$ (4)

Using allometry to account for size, the bioavailability and clearance sections of the equation account for the maturation process in the paediatric population.^4,29 The maturation of clearance depends on cytochromes (CYPs), which are responsible for the hepatic elimination process. In equation (4), $\%{\text{CYP}}_h$ is the proportion of the hepatic metabolism for hepatic CYP and ${\mathit{MAT}}_{{\text{CYP}}_h}$, which is the maturation function related to age. The maturation functions for each CYP can be developed empirically or obtained from the literature (in particular, see Johnson¹⁹). Bioavailability is defined as the fraction of the dose (bioavailable fraction) that reaches the systemic circulation after oral administration. Indeed, only a fraction of the dose is absorbed at the gut level and this fraction is defined as f_abs. Before reaching the systemic circulation, the drug undergoes a first-pass effect in the gut and subsequently a second-pass effect in the liver due to the presence of CYPs. These pass effects are characterised by the gut extraction coefficient E_G and the hepatic extraction coefficient E_H, respectively. The bioavailability in adults equals $F=f_{\mathit{abs}}(1-E_G)(1-E_H)$. In the paediatric population, the amount of CYPs in the gut and liver might not have reached the adult amount, and this process depends on age. Therefore, the bioavailability in children F_ch can be expressed as

$$\begin{array}{c}\multicolumn{1}{c}{F_{\mathit{ch}}=f_{\mathit{abs}}(1-E_G\times \sum _g\%{\text{CYP}}_g{\mathit{MAT}}_{{\text{CYP}}_g}(\mathit{AGE}))(1-E_H\sum _h\%{\text{CYP}}_h{\mathit{MAT}}_{{\text{CYP}}_h}(\mathit{AGE}))}\end{array}$$ (5)

where $\%{\text{CYP}}_g$ and ${\mathit{MAT}}_{{\text{CYP}}_g}$ are similar to the above-described functions but applied to the gut. Using $\frac{{\mathit{Cl}}_{\mathit{ch}}}{{\mathit{Cl}}_{\mathit{ad}}}$, this approach yields the following paediatric dose

$$\begin{array}{c}\multicolumn{1}{c}{d_i=d_{\mathit{ad},i}\times \sum _h\%{\text{CYP}}_h{\mathit{MAT}}_{{\text{CYP}}_h}(\mathit{AGE})\times \frac{F}{F_{\mathit{ch}}}\times (\frac{W_{\mathit{ch}}}{W_{\mathit{ad}}}{)}^{0.75}}\end{array}$$ (6)

The three above-described options were compared by building a dose-range for LA, allometric adjustment (AA) and MA. The adult average weight W_ad was considered to equal 70 kg, and the average paediatric weight is not properly defined. A population of N = 100,000 patients aged 0 to 21 years was then simulated using P³M software^30,31 and for each simulated subject, the individual clearance ${\mathit{Cl}}_{\mathit{ch},j}$ ($j=1,\dots ,N$) was calculated. In addition, for each option (LA, AA and MA) and for all individuals $j=1,\dots ,N$, a set of doses $d_{i,j},i=1,\dots ,K$, expressed in mg/kg, were computed. For a given age group, the ith dose was obtained by averaging the mean across all patients belonging to that age group and rounding up to the closest multiple of 5 (due to practice constraints).

2.2.2 Choice of WMs using adult information

After selecting the dose-range for the study, the next step is to parametrise the model-based dose-finding method, i.e. the bCRM. In this method, the WMs α_i and ${\beta }_i,i=1,\dots ,K$ have to be chosen carefully. We proposed two options: defining a unique WM (WM1-bCRM) and defining several WMs (WAIC-bCRM) and selecting the best one using an automatic criteria. The methodology used to build a WM for both options follows three stages. First, the toxicity probabilities are calculated based on adult PK information. We denoted ${\gamma }_{\ell }^{(1)}$ as the corresponding probability of toxicity for the adult doses $d_{\mathit{ad},\ell },\ell =1,\dots ,L$ tested in clinical trials. Assuming equal exposure in adults and children, this approach yielded estimated toxicities ${\gamma }_{\ell }^{(1)}$ for the children’s doses $d_{\ell },\ell =1,\dots ,L$. Note that these doses are not necessarily concordant with the dose-range in the paediatric population. Indeed, the doses tested in clinical trials $d_{\mathit{ad},\ell }$ may be different from the adult doses selected to establish the paediatric dose-range. Second, information from toxicity studies (phase I and I/II clinical trials) is gathered using a retrospective design of pooled data.³² Details on this method can be found in Appendix 1. Through simulation and a power model with re-estimated parameters, the results were pooled using a down-weighting method, yielding a second estimate ${\gamma }_{\ell }^{(2)}$ of the probabilities of toxicities for the adult doses $d_{\mathit{ad},\ell }$, or the equivalent children’s doses $d_{\ell }$ was available. The third step consists of defining a mixture estimator of the toxicity probabilities ${\gamma }_{\ell }^{(T)}={\lambda }_{\ell }{\gamma }_{\ell }^{(1)}+(1-{\lambda }_{\ell }){\gamma }_{\ell }^{(2)}$, where ${\lambda }_{\ell }$ is a weight selected through a data-driven approach as defined by Liu et al.²⁰ using data collected from adult clinical trials. The weights were defined as ${\lambda }_{\ell }={\mathit{LR}}_{\ell }/({\mathit{LR}}_{\ell }+1)$, where ${\mathit{LR}}_{\ell }$ is the estimated likelihood ratio between the two estimated models for a dose level ℓ

$$\begin{array}{c}\multicolumn{1}{c}{{\mathit{LR}}_{\ell }=\frac{{\gamma }^{(1)n_{\ell ,\mathit{tox}}}(1-{\gamma }^{(1)}{)}^{(n_{\ell }-n_{\ell ,\mathit{tox}})}}{{\gamma }^{(2)n_{\ell ,\mathit{tox}}}(1-{\gamma }^{(2)}{)}^{(n_{\ell }-n_{\ell ,\mathit{tox}})}}}\end{array}$$

where $n_{\ell ,\mathit{tox}}$ is the overall number of toxicities and $n_{\ell }$ is the number of patients given dose ℓ. Finally, if the doses $d_{\ell },\ell =1,\dots ,L$ obtained through adult information did not match the paediatric dose-range $\{d_1,\dots ,d_K\}$ found as described in the previous section, a logit curve is fit to $(d_{\ell },{\gamma }_{\ell }^{(T)})$ to obtain a curve $\eta (d)$ of the probability of toxicity, which allows the calculation of the probability of toxicity for the paediatric doses d_i.

We now describe in detail the two proposed options.

Option unique WM (WM1-bCRM). We proposed the use of a unique WM extracted from the available adult information

$$\begin{array}{c}\multicolumn{1}{c}{\text{WM}1:{\alpha }_i=\eta (d_i)\text{ for }i=1,\dots ,K}\end{array}$$ (7)

Option WAIC (WAIC-bCRM). To reduce the arbitrariness of a unique choice of WM α_i, $i=1,\dots ,K$, we proposed the definition of several WMs followed by model selection. Following Liu et al., two additional WMs were built from the above-mentioned WM obtained as follows

$$\begin{array}{c}\multicolumn{1}{c}{\text{WM}2:\hspace{1em}{\alpha }_i=\eta (d_{i+1})\text{ for }i=1,\dots ,K-1\text{ and }{\alpha }_K=\frac{\eta (d_K)+1}{2}}\\ \multicolumn{1}{c}{\text{WM}3:\hspace{1em}{\alpha }_1=\frac{\eta (d_1)}{2}\text{ and }{\alpha }_i=\eta (d_{i-1})\text{ for }i=2,\dots ,K}\end{array}$$ (8)

The bCRM was performed for the three WMs, and the model selection was based on the WAIC^22,23 was applied. This approach selected the WM that best fit the data and returned an estimate of parameters a and b for each dose i.

2.2.3 Specification of prior density

In addition to the WMs, when using Bayesian model-based methods, the prior density of the dose–response model needs to be specified. In our framework, the prior distributions of the dose–toxicity model parameters were selected using two different parametrisations based on either (i) the adult information (option ESS, AP_ESS-bCRM) or (ii) least information (option least informative prior, AP_LIP-bCRM). In the first option, due to the sparsity of the data, it appears appropriate to attempt to incorporate observations into the prior. However, the information introduced by the prior distributions to the posterior should not overtake the information introduced by the likelihood distribution.

Option ESS (AP_ESS-bCRM). Let ${\pi }_{\mathit{ESS}}(a)$ be the prior normal distribution $\mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)$. The variance ${\sigma }_{a,\mathit{ESS}}^2$ was fixed such that the information introduced by the prior would be equivalent to the information introduced by a fixed number of patients, which was calibrated to control the amount of information.²⁴ This approach is based on the effective sample size (ESS): the higher the ESS, the more informative the prior. The variable m was set to a fixed hypothetical number of patients, and ${\mathbf{Y}}_m=(Y_1,\dots ,Y_m)$ is the associated pseudo-data vector. The likelihood of ${\mathbf{Y}}_m$ is $f_m({\mathbf{Y}}_m|a)=\underset{i=1}{\overset{m}{\Pi }}f(Y_i;a)$, where $f(Y_i;a)$ is the marginal likelihood obtained after integrating the likelihood of equation (1) with respect to the efficacy and the dose. Then, a non-informative prior $q_0(a)$ is introduced with the same expectation μ_a and a very large variance. The ESS is defined as the sample size m such that the posterior $q_m(a)\propto q_0(a)\times f_m({\mathbf{Y}}_m|a)$ is very close to ${\pi }_{\mathit{ESS}}(a)$. The proximity between q_m and ${\pi }_{\mathit{ESS}}(a)$ is evaluated by the distance between the second derivatives of ${\pi }_{\mathit{ESS}}(a)$ and q_m with respect to a, $I_{\pi }(a,{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)=\frac{{\partial }^2}{\partial a^2}\text{log}{\pi }_{\mathit{ESS}}(a)$ and $I_{q_m}(a,m,{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)=\int \frac{{\partial }^2}{\partial a^2}\text{log}{q}_m(a)\text{d}{f}_m({\mathbf{Y}}_m|a)$

$$\begin{array}{c}\multicolumn{1}{c}{\delta (m,{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)=|I_{\pi }(\overline{a},{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)-I_{q_m}(\overline{a},m,{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)|}\end{array}$$ (9)

where $\overline{a}$ is the empirical mean of a, which is fixed using the pooling method³² previously introduced in the specification of the WMs. For an ESS $m^{*}$, parameters $({\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)$ were chosen such that $\underset{m}{min}\delta (m,{\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)=m^{*}$. Details of the δ expression can be found in Appendix 2.

Option Least informative prior (AP_LIP-bCRM). Another method proposed by Zhang et al.²⁷ considers only information from the dose–toxicity model. Let ${\pi }_{\mathit{LIP}}(a)$ follow $\mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{LIP}}^2)$. The variance ${\sigma }_{a,\mathit{LIP}}^2$ was defined such that all doses had the same probability of being the maximum tolerated dose (MTD). The parameter space of a was divided into K intervals ${\mathcal{I}}_1=[a_0,a_1],{\mathcal{I}}_2=[a_1,a_2],\dots ,{\mathcal{I}}_i=[a_{i-1},a_i],\dots ,{\mathcal{I}}_K=[a_{K-1},a_K]$, where a₀ and a_K were the minimal and maximal possible values of a (resp. defined with $\psi (d_1,a_0)=\tau +0.05$ and $\psi (d_K,a_K)=\tau -0.05$) and $a_1,\dots ,a_{K-1}$ were the solutions of $\psi (d_i,a_i)+\psi (d_{i+1},a_i)=2\tau$ (value such that dose i was the MTD). The method theoretically verifies that parameter a had the same chances of belonging to the K intervals ${\mathcal{I}}_1,{\mathcal{I}}_2,\dots ,{\mathcal{I}}_K$. Therefore, ${\sigma }_a^2$ is calculated such that the empirical variance of the K probabilities of toxicity matches the variance of a discrete uniform distribution $(K^2-1)/12$.²⁷

However, the resulting variances ${\sigma }_{a,\mathit{ESS}}^2$ and ${\sigma }_{a,\mathit{LIP}}^2$ may be too narrow, leading to difficulties in reaching the extremes in the dose-range (minimum and/or maximum doses). Both options were combined with the adaptive prior method, which was introduced by Lee and Cheung²⁶ and Zhang et al.²⁷ and was used when the probability of the MTD being the smallest or the highest dose was high. A second prior ${\pi }_{\mathit{NIP}}(a)\hspace{1em}\sim \mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{NIP}}^2$), which is considered a non-informative prior, was associated with a higher variance ${\sigma }_{a,\mathit{NIP}}^2$ defined from the former intervals ${\mathcal{I}}_1,{\mathcal{I}}_2,\dots ,{\mathcal{I}}_K$ such that ${\sigma }_{a,\mathit{NIP}}^2$ verified $\text{Pr}(a\in {\mathcal{I}}_1\cup {\mathcal{I}}_K)=0.80$.

The decision to switch from ${\pi }_{\mathit{ESS}}(a)$ to ${\pi }_{\mathit{NIP}}(a)$ (option ESS; AP_ESS-bCRM) or from ${\pi }_{\mathit{LIP}}(a)$ to ${\pi }_{\mathit{NIP}}(a)$ (option least informative prior; AP_LIP-bCRM) was performed using the Bayes factor model selection criterion. Three models were defined, each with a uniform distribution: $M_1:a\in {\mathcal{I}}_1;M_2:a\in {\mathcal{I}}_2\cup \dots \cup {\mathcal{I}}_{K-1}$ and $M_3:a\in {\mathcal{I}}_K$ with a uniform distribution within each model. This gave

$$\begin{array}{c}\multicolumn{1}{c}{\text{Pr}({\mathbf{Y}}_m|M_1)={\int }_{a_0}^{a_1}\underset{i=1}{\overset{K}{\Pi }}\psi (d_i,a{)}^{y_i}(1-\psi (d_i,a){)}^{1-y_i}\frac{1}{a_1-a_0}\mathit{da}}\end{array}$$

for model M₁ and similar equations can be derived for $\text{Pr}({\mathbf{Y}}_m|M_2)$ and $\text{Pr}({\mathbf{Y}}_m|M_3)$. The Bayes factor was calculated as follows

$$\begin{array}{c}\multicolumn{1}{c}{\text{Pr}(M_1|{\mathbf{Y}}_m)=\frac{\text{Pr}(M_1)\text{Pr}({\mathbf{Y}}_m|M_1)}{\text{Pr}(M_1)\text{Pr}({\mathbf{Y}}_m|M_1)+\text{Pr}(M_2)\text{Pr}({\mathbf{Y}}_m|M_2)+\text{Pr}(M_3)\text{Pr}({\mathbf{Y}}_m|M_3)}}\end{array}$$

where $\text{Pr}(M_1)=\text{Pr}(M_2)=\text{Pr}(M_3)=1/3$, and similar equations can be obtained for $\text{Pr}(M_2|{\mathbf{Y}}_m)$ and $\text{Pr}(M_3|{\mathbf{Y}}_m)$. Using the rule proposed by Zhang et al.,²⁷ the following criteria was used: If $\text{Pr}(M_3|{\mathbf{Y}}_m)>0.61$ (Jeffrey’s rule), there was substantial evidence that model M₃ was more likely to be true, and a change from prior ${\pi }_{\mathit{ESS}}(a)$ or ${\pi }_{\mathit{LIP}}(a)$ to ${\pi }_{\mathit{NIP}}(a)$ was thus made.

In practice, a comparison was performed between AP_ESS-bCRM, which used the bCRM with the adaptive prior from ${\pi }_{\mathit{ESS}}(a)$ to ${\pi }_{\mathit{NIP}}(a)$, and the AP_LIP-bCRM, which used the bCRM adaptive prior from ${\pi }_{\mathit{LIP}}(a)$ to ${\pi }_{\mathit{NIP}}(a)$, respectively.

3 Simulations

The aim of the simulation study was to evaluate and compare the performances of each dose-range and model setting proposition, in terms of selected dose. Based on the motivating illustration, we proposed to plan, conduct and analyse a hypothetical phase I/II dose-finding clinical trial for erlotinib in the paediatric population. We used PK parameters as well as dose-finding toxicity and efficacy clinical trial data for erlotinib obtained from the adult population for extrapolation and bridging.

1. Specification of the dose-range: We hypothesised that the observed AUC in adults was similar in the paediatric population for the three dose-range adjustments LA, AA and MA (linear, allometric and MAs). In previous adult dose-finding studies, the doses ranged from 100 mg to 300 mg, and the MTD was 150 mg.^6,7 Based on these publications, the adult doses 100 mg, 150 mg, 200 mg, 250 mg and 300 mg were chosen as references for the calculation of paediatric doses. The corresponding doses for children were extrapolated using the adult PK data published by Lu et al.,³³ which describe the erlotinib PK as a one-compartment model with a clearance of 3.95 L/h. The maturation functions for erlotinib used in the MA option can be found in Appendix 3. The dose-ranges associated with each option (LA, AA and MA) for patients aged 2 to 5 years were generated according to equations (2), (3) and (6), respectively. The resulting dose-range for each option, which was rounded up to the nearest 5 mg/kg, is given in Table 1.

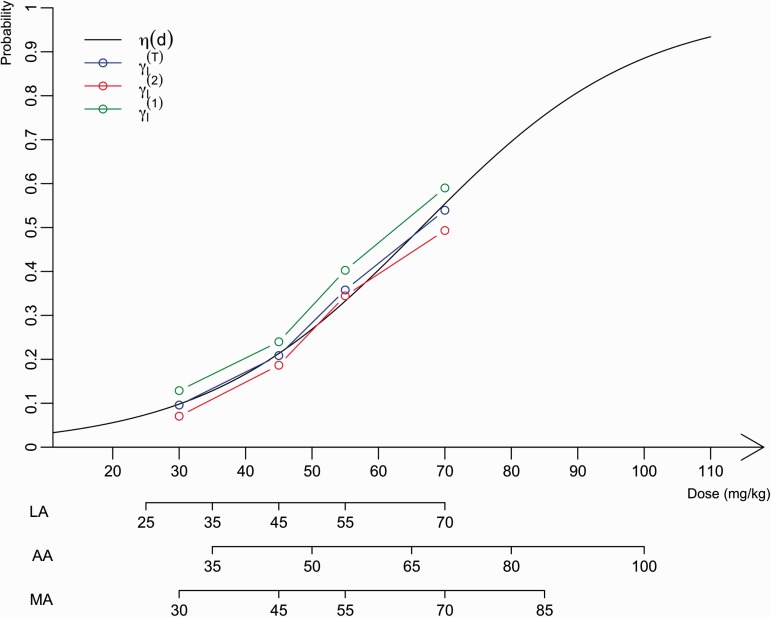
2. Choice of WMs using adult information: A WM needed to be specified for the initial dose–toxicity relationships associated with each dose-range adjustment. These WMs were elaborated as described in the Methods section with a mixture of PK, toxicity and efficacy data from adults. In the erlotinib setting, the mixture was constructed using toxicity data and PK data from early-phase clinical trials in adults (Figure 2). First, the toxicities associated with doses for children ${\gamma }_{\ell }^{(1)},\ell =1,\dots ,4$ were extrapolated using PK data published by Thomas et al.³⁴ under the assumption that the same exposure was achieved in the adult and paediatric populations (AUC relationship with dose and clearance; Table 2). Second, using the pooled data analysis proposed by Zohar et al.³² and based on adult toxicity data from seven clinical trial studies on erlotinib, the second estimate ${\gamma }_{\ell }^{(2)}$ was computed for each dose ℓ (computation details are given in the Appendix 1). These clinical studies have reported that different dose levels of erlotinib induce toxicity, defined as skin rash of grade 3 or more in adults. This information and the estimates of ${\gamma }_{\ell }^{(2)},\ell =1,\dots ,4$ are summarized in Table 2. The resulting estimated mixture ${\gamma }_{\ell }^{(T)}$ associated with each dose ℓ can also be found in Table 2. Because the dose-range obtained with the different approaches (LA, AA or MA) overlap and might correspond to different doses within the adult range, a logistic function was fit to the mixture. The resulting logit function is given by $\eta (d)={\text{logit}}^{-1}(-3.78+0.06\frac{d}{{\mathit{Cl}}_{\mathit{ch}}})$, where Cl_ch is the average clearance across in 2- to 5-year-old children. Given the dose-ranges generated as described in the previous section and $\eta (d)$, the first WM (WM1), computed with equation (7) was obtained by reading the toxicities associated with each dose from the curve (Table 1). Then, WM2 and WM3 were computed using equation (8).

Table 1.

Model settings for simulations.

	Linear adjustment					Allometry adjustment					Maturation adjustment
Doses (mg/kg)	25	35	45	55	70	35	50	65	80	100	30	45	55	70	85
WMs for toxicity
WM1	0.07	0.13	0.21	0.33	0.55	0.13	0.27	0.48	0.70	0.88	0.10	0.21	0.33	0.55	0.76
WM2	0.13	0.21	0.33	0.55	0.78	0.27	0.48	0.70	0.88	0.94	0.21	0.33	0.55	0.76	0.88
WM3	0.04	0.07	0.13	0.21	0.33	0.06	0.13	0.27	0.48	0.70	0.05	0.10	0.21	0.33	0.55
WM for efficacy	0.05	0.20	0.43	0.64	0.79	0.05	0.20	0.43	0.64	0.79	0.05	0.20	0.43	0.64	0.79
Option ESS
${\pi }_{\mathit{ESS}}(a)$	$\mathcal{N}(-0.31,0.36)$					$\mathcal{N}(-0.38,0.50)$					$\mathcal{N}(-0.34,0.42)$
Option least informative prior
${\pi }_{\mathit{LIP}}(a)$	$\mathcal{N}(-0.31,0.46)$					$\mathcal{N}(-0.38,3.13)$					$\mathcal{N}(-0.34,1.46)$
${\pi }_{\mathit{NIP}}(a)$	$\mathcal{N}(-0.31,4.33)$					$\mathcal{N}(-0.38,15.24)$					$\mathcal{N}(-0.34,8.88)$
$\pi (b)$	$\mathcal{N}(0,1.34)$					$\mathcal{N}(0,1.34)$					$\mathcal{N}(0,1.34)$

AP_ESS-bCMR uses adaptive prior from ${\pi }_{\mathit{ESS}}(a)\sim \mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{ESS}}^2)$ to ${\pi }_{\mathit{NIP}}(a)\sim \mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{NIP}}^2)$ and AP_LIP-bCRM uses adaptive prior from ${\pi }_{\mathit{LIP}}(a)\sim \mathcal{N}({\mu }_a,{\sigma }_{a,\mathit{LIP}}^2)$ to ${\pi }_{\mathit{NIP}}(a)$.

Figure 2.

Representation of the estimated probabilities of toxicity used to build WMs for paediatrics according to dose (mg/kg). The logit function $\eta (d)$ in black fits the estimated dose–toxicity relationship, ${\gamma }_{\ell }^{(T)}$ $(\ell =1,2,3,4)$, in blue, which is the mixture of both estimated dose–toxicity curves, ${\gamma }_{\ell }^{(1)}$, based on adult PK information, in green, and ${\gamma }_{\ell }^{(2)}$, based on adult phase I observations, in red. The different dose-ranges for the LA, AA and MA options are represented below the graph.

Table 2.

Toxicity, efficacy outcomes and the number of treated patients of erlotinib treatment.

	Response/toxicity (number of patients)
Publications	100 mg	150 mg	200 mg	250 mg
Toxicity
Prados et al.6	0 (3)	1 (3)	0 (3)	3 (6)
Raizer et al.9	–	11 (99)	–	–
Thepot et al.7	0 (5)	3 (25)	–	–
Calvo et al.8	–	1 (25)	–	–
Van den Bent et al.10	–	–	6 (54)	–
Sheikh and Chambers11	–	167 (307)	–	–
Clinical trial ROCHE NTC0053193412	–	11 (59)	–	–
${\gamma }_{\ell }^{(1)}$	0.13	0.24	0.40	0.59
${\gamma }_{\ell }^{(2)}$	0.07	0.19	0.34	0.49
${\gamma }_{\ell }^{(T)}$	0.09	0.21	0.36	0.54
Efficacy for glioblastoma at dose 150 mg
Prados et al.6		1 (16)
Prados et al.6 (EIAED)		5 (44)
Raizer et al.9		7 (53)
Yung et al.13		20 (48)

Note: Toxicities are skin rash of grade 3 or more and efficacy, defined as stable disease and above (RECIST), was limited to glioblastoma. The distributions for calculating the mixture ${\gamma }_{\ell }^{(T)}$ are given for each dose ℓ with the value of ${\gamma }_{\ell }^{(1)}$ based on adult PK information and the value of ${\gamma }_{\ell }^{(2)}$ built with adult toxicities.

For efficacy, the data from adults treated for glioblastoma were considered because efficacy is strongly related to the specific disease. In this setting, efficacy was defined as remission or stability regarding tumour size according to RECIST criteria. Because most of the data were associated with one dose, a method developed by Cheung et al.³⁵ was used to obtain the WM. The percentage of efficacy over all available published data (Table 2) was 20%. We obtained the WM for efficacy reported in Table 1 using the function getprior(halfwidth $=$ 0.05, target $=$ 0.2, nu $=$2, nblevels = 5) available in the dfcrm package in R.

1. Specification of prior densities: The prior densities for dose–toxicity and dose–efficacy parameters ${\pi }_{\mathit{ESS}}(a),{\pi }_{\mathit{LIP}}(a),{\pi }_{\mathit{NIP}}(a)$ and $\pi (b)$ are given in Table 1.

With the ESS option, μ_a and ${\sigma }_{a,\mathit{ESS}}^2$, the pooling method employed for the WM specification³² with a power model, resulting in an estimate of the empirical mean $\overline{a}=\text{log}(0.88)$, thus $\text{E}[\text{exp}(a)]=e^{{\mu }_a+{\sigma }_{a,\mathit{ESS}}^2/2}$. The expected chosen sample size was $m^{*}=5$ patients and ${\sigma }_{a,\mathit{ESS}}^2$ was then computed with equation (9).

Then, ${\sigma }_{a,\mathit{LIP}}^2$ was calculated with the least informative prior option, and ${\sigma }_{a,\mathit{NIP}}^2$ was calculated using K = 5 intervals by minimising $\text{Pr}(a\in {\mathcal{I}}_1\cup {\mathcal{I}}_K)-0.80=0$.

For efficacy, prior $\pi (b)$ was selected as a non-informative normal distribution $\mathcal{N}(0,1.34)$.

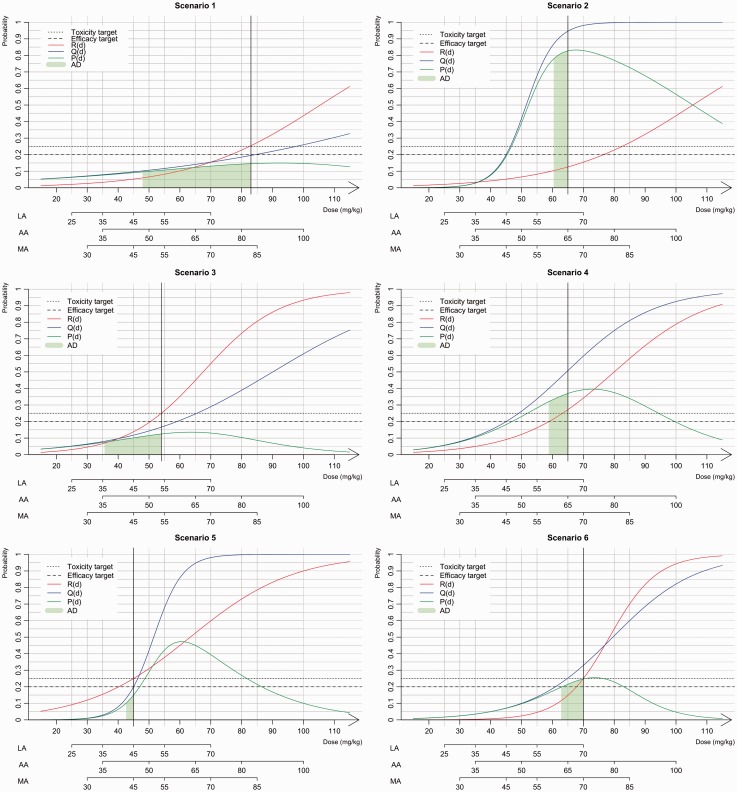
The performances of our unified approach were investigated through a simulation study under several scenarios presented in Figure 3 for the three dose-ranges options (LA, AA and MA). Extrapolation from adults yielded an initial estimate of 48 mg/kg for the MTD associated with a toxicity target of 0.25. We aimed to evaluate how this choice influences the performance of our proposed methods by selecting scenarios in which the MTD and sMSD were different. Scenarios 1, 2 and 3 were based on the results of two real paediatric trials conducted by Geoerger et al.¹⁴ and Jakacki et al.¹⁵ For all three scenarios, we considered the same MTD that was found in each trial, and the efficacy was simulated. In scenarios 1 and 2, the MTD (83 mg/kg) is equal to that reported by Geoerger et al. and is far from the efficacy extrapolated from adult information (48 mg/kg). In scenario 1, the sMSD was similar to the MTD, whereas in scenario 2, the sMSD was 65 mg/kg. In scenario 3, the MTD and the sMSD are equal to those reported by Jakacki et al. (55 mg/kg) and close to the value extrapolated from adult information. Finally, we added three scenarios: in scenario 4, the MTD (65 mg/kg) was equivalent to the MSD; in scenario 5, the MSD was higher than the MTD (45 mg/kg) and in scenario 6, the sMSD is similar to the MTD (70 mg/kg).

Figure 3.

Presentation of the six scenarios used in the simulation study. The dose–toxicity, R(d), curve is in red, the dose–efficacy, Q(d), curve is in blue and the dose-success, P(d), curve is in green. The sMSD is represented by black vertical line, the toxicity and efficacy targets are given with dashed lines. The admissible doses (AD) are given by the green area under the success P(d) curve.

For each scenario, we performed 1000 simulated phase I/II trials with a maximal sample size of N = 50 patients. Because maturation is known to differ among different paediatric age subgroups, we selected a paediatric population with an age range of 2 to 5 years. We also chose a toxicity target of $\tau =0.25$ and a minimum efficacy target of $\tau \text{'}=0.20$ (a realistic target for glioblastoma).

For each approach, the percentage of correct dose selection (PCS) of the sMSD was computed. We also evaluated the percentage of acceptable doses (ADs) that includes the closest dose to the sMSD for each approach; if this dose existed, we evaluated the next lower dose for which the probability of success P was included in $[P(\text{sMSD})-0.05;P(\text{sMSD})]$. For the three dose-range options (LA, AA and MA), we evaluated the methods as follows: (i) option unique WM (WM1-bCRM) compared with WAIC (WAIC-bCRM) using a non-informative prior ($\mathcal{N}(0,1.34)$) for parameter a of the dose–toxicity relationship and (ii) adaptive prior under option ESS (AP_ESS-bCRM) compared with adaptive prior under option least informative prior (AP_LIP-bCRM).

4 Results

Based on the toxicity results reported by Geoerger et al.,¹³ scenarios 1 and 2 shared the same MTD of 83 mg/kg. However, the sMSDs differed depending on the efficacy differed with 83 mg/kg for scenario 1 and 65 mg/kg for scenario 2 (Figure 3).

The LA, for a dose of 83 mg/kg, dose was out of range; thus, for scenario 1, the last dose (70 mg/kg) was the only option for the recommended dose. The obtained PCSs for all options were greater than 70%, and in approximately 10% of cases, the trials were stopped due to inefficiency (Table 3). In scenario 2, the exact dose of 65 mg/kg dose was not within the dose-range, and the closest dose was 70 mg/kg. As a result, the model hesitated between doses of 55 mg/kg and 70 mg/kg. In this case, the adaptive prior and WAIC options recommended doses between these two values for approximately half of the trials. Using the AA option, the closest corresponding dose to the sMSD was 80 mg/kg in scenario 1, and the PCS ranged from 45.2% to 59.1% for all methods. However, because the probability of success for the doses 65 mg/kg and 80 mg/kg doses in scenario 1 (the green area under the curve of P(d)) were very close, both doses were considered admissible. In this case, the percentage of AD was greater than 94%. In scenario 2, the sMSD was 65 mg/kg, and the PCS was greater than 90% for all options. With the MA, the sMSD was not within the dose-range; thus, the model hesitated between two doses with average percentages of AD equal to 90% for scenario 1 and 50% for scenario 2.

Table 3.

Simulation study results for the three dose-range methods, linear, allometry and maturation adjustment (LA, AA, MA) under several scenarios.

Method	Linear adjustment							Allometry adjustment							Maturation adjustment
Dose (mg/kg)	25	35	45	55	70	SR	AD	35	50	65	80	100	SR	AD	30	45	55	70	85	SR	AD
Scenario 1
WM1-bCRM	0	0	0.3	7.8	81.8	10.1	89.6	0	1.4	39.6	56.8	2.1	0.1	96.4	0	0.1	8.2	60.4	30	1.3	90.4
WAIC-bCRM	0	0	0.2	8.1	81.7	10	89.8	0	1.2	37.2	59.1	2.3	0.2	96.3	0	0.3	6.3	53.4	38.3	1.7	91.7
AP ESS-bCRM	0	0	0	14.4	77.9	6.2	92.2	0	1.4	50.9	45.2	2.2	0.2	96.1	0	0.2	12.2	59.5	26.8	1	86.2
AP LIP-bCRM	0	0	0.1	13.9	77.1	7.1	91	0	1.1	35.1	59.8	3.9	0.1	94.9	0	0.1	7.3	58.3	32.3	2	90.6
Scenario 2
WM1-bCRM	0	0	0.2	51.8	48	0	48	0	6.9	92.7	0.4	0	0	92.7	0	0	53	47	0	0	47
WAIC-bCRM	0	0	0.2	44.9	54.8	0.1	54.8	0	7.9	91.7	0.3	0	0.1	91.7	0	0.1	41.7	58.1	0	0.1	58.1
AP ESS-bCRM	0	0	0	53	47	0	47	0	8	91.8	0.2	0	0	91.8	0	0.1	62.6	37.1	0.1	0	37.1
AP LIP-bCRM	0	0	0	51	49	0	49	0	7.8	91.6	0.6	0	0	91.6	0	0	52.6	47.4	0	0	47.4
Scenario 3
WM1-bCRM	0	0.2	18.7	80.1	0.9	0.1	98.8	1	86.6	12	0	0	0.4	86.6	0	18.7	79.6	1.5	0	0.2	98.3
WAIC-bCRM	0	0.2	26.2	72	1.6	0	98.2	1.3	88.1	10.2	0	0	0.4	88.1	0	25.4	73.5	1.1	0	0	98.9
AP ESS-bCRM	0	0.4	26.1	73	0.5	0	99.1	1.2	89	9.5	0	0	0.2	89	0.1	27	71.9	1	0	0	98.9
AP LIP-bCRM	0	0.1	24.9	74.2	0.8	0	99.1	0.6	83.6	14.6	0	0	0.9	83.6	0.4	22	77.1	0.4	0	0.1	99.1
Scenario 4
WM1-bCRM	0	0	1.3	61.8	36.9	0	61.8	0.1	23.5	75.2	1.2	0	0	75.2	0	1.2	56.3	42.4	0	0.1	56.3
WAIC-bCRM	0	0	4.3	64.7	31	0	64.7	0.2	28.5	70.5	0.7	0	0.1	70.5	0	3.4	63.5	33	0	0.1	63.5
APESS-bCRM	0	0	3.2	73.4	23.4	0	73.4	0	35.4	63.9	0.4	0	0.3	63.9	0	2.8	69.8	27.4	0	0.1	69.8
APLIP-bCRM	0	0	2.5	68.2	29.2	0	68.2	0	25.1	73.6	0.6	0	0.5	73.6	0	1.1	61.1	37.5	0.1	0.1	61.1
Scenario 5
WM1-bCRM	0.9	20.7	61.5	15.9	0	1	61.5	32.5	59.7	0.4	0	0	7.4	59.7	10.9	72.2	14.5	0	0	2.4	72.2
WAIC-bCRM	0.1	18.2	68	13	0	0.7	68	36.4	56.7	0.6	0	0	6.3	56.7	13	70.9	13.7	0	0	2.4	70.9
APESS-bCRM	0.7	21.9	65.3	11.7	0	0.4	65.3	40.2	53.8	0.2	0	0	5.8	53.8	13.4	72.7	12.5	0	0	1.4	72.7
APLIP-bCRM	0.4	22.5	62.2	14.8	0	0.1	62.2	33.2	57.7	0.4	0	0	8.7	57.7	11.7	72.1	13.1	0	0	3.1	72.1
Scenario 6
WM1-bCRM	0	0	0	2.8	96	1.2	96	0	0	90.4	9.6	0	0	90.4	0	0	3.7	96.2	0.1	0	96.2
WAIC-bCRM	0	0	0	6	93.2	0.8	93.2	0	0	94.6	5.4	0	0	94.6	0	0	5.5	93.7	0.8	0	93.7
APESS-bCRM	0	0	0	7.9	90.1	2	90.1	0	0.1	92.4	7.5	0	0	92.4	0	0	5.7	94.3	0	0	94.3
APLIP-bCRM	0	0	0	5.6	93.4	1	93.4	0	0	87.8	12.2	0	0	87.8	0	0	4	95.6	0.4	0	95.6

Note: The percentage of correct selection (PCS) are represented in italic, that is, the sMSD. The percentage of acceptable dose (underlined) are summed up in bold. The simulation setting for each approach are given in Table 1.

In scenario 3, the sMSD was equal to the MTD (i.e. the 54 mg/kg dose). In the case of AA, the closest dose to the MTD was 50 mg/kg, and the PCSs for all options were greater than 71%.

In scenario 4, the sMSD and MTD were similar (the 65 mg/kg dose). In the case of AA, the dose was within the dose-range, and the PCSs of WAIC-bCRM and WM1-bCRM were 70.5% and 75.2%, respectively. However, the AP_ESS-bCRM gave a lower PCS (63.9%) compared with that obtained with the AP_LIP-bCRM (73.6%). In scenario 5, the recommended dose was 45 mg/kg, which is within the dose-range obtained with LA and MA. In this case, all options gave high PCS values greater than 60%. If the dose was not within the range, as was the case with AA, the PCS decreased an average of 10%. In scenario 6, the recommended dose was 70 mg/kg. Even if the dose was only in the ranges obtained with the LA and MA options, high PCS values (above 90%) were obtained for all dose-range options.

The comparison of the performances of AP_ESS-CRM and AP_LIP-CRM, revealed similar performances over all dose-range options and scenarios. However, WM1-bCRM and WAIC-bCRM generally provided better recommendations in terms of the admissible dose.

In the case of a too-toxic scenario (sMSD of 20 mg/kg, data not shown), the stopping rules allowed the trial to be stopped, if a toxic reaction was observed in 90% of the cases, regardless of the method.

In general, if the sMSD was within the dose-range, the PCS and AD percentages were high, whereas if the dose was close but not within the range, a lower PCS percentage and a rather high AD percentage were obtained.

5 Guidelines

Based on the results of our simulations, we suggest the following settings for the proposed approach:

1. For dose-range selection: use either options AA or MA.

2. For the WM choice: use option WAIC-bCRM because our results indicate that it is better to use several WMs in the model selection process than a unique WM.

3. For prior distribution: if the quantity and quality of the adult information is high, use the AP_ESS-bCRM option; however, if there is some doubt regarding the available adult information, use the AP_LIP-bCRM option.

6 Discussion

In this work, we present a unified approach for planning, conducting and analysing paediatric dose-finding clinical trials. This unified approach is based on several possible methods that aim to improve the choices made in the design of paediatric trials. For the analysis of the paediatric population, for which only a small number of clinical trials have been conducted and which typically includes a small number of patients, the bridging of information from the adult population (when possible) to the paediatric population, particularly using PK extrapolation tools such as allometry and maturation functions, is highly relevant.

We based our unified method on the bCRM, which jointly models toxicity and efficacy with a dose-finding allocation rule because in paediatric populations, safety takes priority over efficacy. Our unified approach includes all stages in the dose-finding process, ranging from dose-range selection to the choice of prior distributions for dose responses.

The first step of our work proposed three different dose-range adjustments (i.e. LA, AA or MA). The resulting dose-ranges overlapped, and a wider range was obtained with AA. In this study, we used the specific context of erlotinib, a drug that has been investigated in both adult and paediatric populations for cancer treatment. Both dose-finding and PK studies in adults and children are available. We thus used the available adult information to plan a paediatric trial using the proposed extrapolation and bridging methods and used the children’s dose-finding data to build scenarios for the simulation study, which allowed us to evaluate our design choices.

Our extrapolation and bridging approach used data from more than 580 adult observations. We based three of our scenarios for the simulation study on the toxicity observations reported by Geoerger et al.¹³ and Jakacki et al.,¹⁴ who performed trials that evaluated 16 and 19 children, respectively. Thus, the estimation of the MTD or recommended dose in each trial was associated with high variability due to the small sample size. In this case, it is difficult to assess how far from reality is our model from the true paediatric population. In general, our results show that in cases in which the MTD and sMSD are far from our initial guess (as in scenarios 1 and 2), our proposed dose-finding designs based on either model selection criteria or adaptive priors performed well. A similar finding was obtained for scenario 3, in which the MTD and the sMSD were not far from our initial guess. These results are in favour of the implemented methods because misspecified initial choices do not impact the performance of our proposition.

To date, there is no clear recommendation for the selection of the dose-range that should be used in paediatric dose-finding clinical trials. Allometric scaling was initially introduced by West et al.³⁶ for identifying measurements that work across and within species. Several studies have suggested that the allometric coefficient may be different in early childhood.^36,37 The discrepancy between size-based scaling and effective changes in paediatric patients, particularly neonates and infants, can also be explained by differences in physiological processes due to maturation.

The second step of our work was to propose dose-finding design choices for the dose allocation process using adult clinical trial observations. Because not all of the calculated doses were used for adults, we needed to build a logit function based on mixture estimates in adults. For this purpose, we assumed that the exposure was similar in both adults and children. Adult PK combined with maturation served as the first source of information for the toxicity probability, which was defined in terms of PK (AUC or C_max). A direct curve was reported by Thomas et al.³⁴ The second source of information was toxicity from early-phase clinical trials in adults. This method allowed us to propose tools for the establishment of the WMs and for the prior distributions of dose–toxicity parameters.

For simplicity reasons, we maintained the same scenarios for all dose-ranges, which led to different sMSDs. In cases in which the model hesitated between two doses, a lower PCS was obtained primarily because the real dose was not exactly within the dose-range. Other scenario choices could have favoured one adjustment method over the other, although this situation occurred due to arbitrary choices. Other methods that jointly model toxicity and efficacy for dose-finding, such as EFFTOX, can also benefit from our proposed approach, although some may only need to use part of our model.¹⁶ In our case, power function modelling of the dose–toxicity or dose–efficacy curves was selected for simplicity. However, several other models, such as the logit model, could easily be used in our setting.

In conclusion, the bridging and extrapolation of adult data for the design of paediatric dose-finding clinical trials appeared to improve the results of these studies. Our proposition may prove helpful for physicians and statisticians who wish to plan and conduct early-phase trials in this population. We attempted to unify and modify existing methods to obtain a clear stream of decision making regarding several crucial choices that need to be made prior to initiation of a trial. We believe that this approach will improve and allow better use of the available information sources for the planning of new trials.

Appendix 1

Pooling method

The retrospective pooled data method evaluates retrospectively data from several clinical trials. It aims at estimating the parameter of a toxicity model from several models. Let $n_i(j)=\sum _{l=1}^{j}11(x_l=d_i)$ be the number of observations at dose level d_i after j patients and $t_i(j)=\sum _{l=1}^j{y}_{l}11(x_l=d_i)$ the number of toxicities observed at dose level d_i among the first j patients. The following approach allows to compute an estimate of the parameter a

1. First, gather the number of observed DLTs at each dose level t_i ($i=1,\dots ,k$) and the number of patients included at each dose level, n_i, from all available clinical trials.

2. Then, compute the empirical probability of toxicity associated with each dose level by dividing t_i by n_i.

3. For each dose i, after n patients, define a weight $w_n(d_i)$. It is calculated by a simulation study based on a model of interest and marginal frequencies provided by observations. To calculate these weights, we simulate CRM studies of size n under the scenario generated by the empirical probability of toxicities. The weights $w_n(d_i)$ are the percentages of the total allocation for each dose level d_i.

4. Estimate $\hat{a}$, the estimate of parameter a, by solving

   $$\begin{array}{c}\multicolumn{1}{c}{W_n(a)=\sum _{i=1}^k{w}_n(d_i)U_{\mathit{in}}(a)=0}\end{array}$$

   and

   $$\begin{array}{c}\multicolumn{1}{c}{U_{\mathit{in}}(a)=H\{n_i(n)\}[\frac{t_i(n)}{n_i(n)}\frac{\psi \text{'}}{\psi }(d_i,a)+\{1-\frac{t_i(n)}{n_i(n)}\}\times \frac{-\psi \text{'}}{1-\psi }(d_i,a)]i=1,\dots ,k}\end{array}$$

where the coefficient $H(s)=11(s\ne 0)$, i.e. a function taking the value 1 when s is not equal to 0, and zero otherwise, and, in order to cover all cases, we use the convention that 0/0 is equal to 1. $U_{\mathit{in}}(a)$ can be interpreted as a score representing the weighted average across the dose level. This is the average of some function of the dose–toxicity working model for the patients experiencing toxicity and an average of a similar function of the dose–toxicity working model for the non-toxicities.

1. An estimate for the probability of toxicity at each of the available dose levels i can be computed with $\psi (d_i,\hat{a})$.

In the present paper, for the adult doses of $(d_1,d_2,d_3,d_4)=$ (100 mg, 150 mg, 200 mg and 250 mg) with a power model $\psi (d_i,a)={\alpha }_i^a$, we obtained the observed toxicity probabilities $t_i/n_i$ of $(0,0.37,0.11,0.50)$ respectively, the weights w_i $(0.02,0.31,0.31,0.36)$, which lead to the resulting estimate of $\hat{a}=0.88$ and the following estimates of the probability of toxicity $(0.07,0.19,0.35,0.49)$.

Appendix 2

Prior specification

We defined $q_0(a)$ as a normal $\mathcal{N}({\mu }_a,c{\sigma }_a^2)$ where c = 10,000. We first calculated $I_{q_m}$

$$\begin{array}{c}\multicolumn{1}{c}{q_m(a)\propto \frac{1}{\sqrt{2\pi c{\sigma }_a^2}}{e}^{-\frac{1}{2c{\sigma }_a^2}(a-{\mu }_a{)}^2}\times \underset{j=1}{\overset{m}{\Pi }}\psi (a,x_j{)}^{Y_j}(1-\psi (a,x_j){)}^{(1-Y_j)}}\end{array}$$

For the jth patient receiving dose x_j, let $[x_j]=1,\dots ,K$, the number giving the corresponding dose subscript. We have the derivative and second derivative

$$\begin{array}{c}\multicolumn{1}{c}{\frac{\partial \text{log}{q}_m}{\partial a}(a)=-\frac{(a-{\mu }_a)}{c{\sigma }_a^2}+\text{log}({\alpha }_{[x_j]})\sum _{j=1}^m(Y_j\text{exp}(a)-(1-Y_j)\frac{\text{exp}(a){\alpha }_{[x_j]}^{\text{exp}(a)}}{1-{\alpha }_{[x_j]}^{\text{exp}(a)}})}\\ \multicolumn{1}{c}{\frac{{\partial }^2\text{log}{q}_m}{\partial a^2}(a)=-\frac{1}{c{\sigma }_a^2}+\text{log}({\alpha }_{[x_j]})\text{exp}(a)\sum _{j=1}^m(Y_j-(1-Y_j)\frac{{\alpha }_{[x_j]}^{\text{exp}(a)}(1+\text{exp}(a)\text{log}({\alpha }_{[x_j]})-{\alpha }_{[x_j]}^{\text{exp}(a)})}{(1-{\alpha }_{[x_j]}^{\text{exp}(a)}{)}^2})}\end{array}$$

Therefore, we had

$$\begin{array}{c}\multicolumn{1}{c}{I_{q_m}(a,m,{\mu }_a,{\sigma }_a^2)=-\frac{1}{c{\sigma }_a^2}+{\int }_{Y_m}{\int }_{X_m}\sum _{j=1}^m\text{log}({\alpha }_{[x_j]})\text{exp}(a)(Y_j-(1-Y_j)\frac{{\alpha }_{[x_j]}^{\text{exp}(a)}(1+\text{exp}(a)\text{log}({\alpha }_{[x_j]})-{\alpha }_{[x_j]}^{\text{exp}(a)})}{(1-{\alpha }_{[x_j]}^{\text{exp}(a)}{)}^2})}\\ \multicolumn{1}{c}{\times f(Y_m|X_m)g(X_m)\text{d}{Y}_m\text{d}{X}_m}\end{array}$$

where f is the marginal distribution of $Y_m|X_m$ and g the distribution of X_m. We calculated $I_{\pi }(a)=-\frac{1}{{\sigma }_a^2}$ and obtained $\delta (m,{\mu }_a,{\sigma }_a^2)=|I_{\pi }(\overline{a},{\mu }_a,{\sigma }_a^2)-I_{q_m}(\overline{a},m,{\mu }_a,{\sigma }_a^2)|$.

Since δ was non-computable, due to the dependency of Y_m and X_m, the criterion δ was calculated using Monte-Carlo simulations. In order to calculate $({\mu }_a,{\sigma }_a^2)$, we computed the ESS for several value of $({\mu }_a,{\sigma }_a^2)$ and we chose $({\mu }_a,{\sigma }_a^2)$ such that $\underset{m}{min}(\delta (m,{\mu }_a,{\sigma }_a^2)=m^{*})$.

Appendix 3

Specification of clearance for erlotinib in children

Erlotinib is administered as tablets. It is partly absorbed by the enterocyte cells. Before reaching the portal vein, a part of erlotinib is metabolised by the cytochrome CYP3A4 through the gut wall and the hepatic barrier. The bioavailability F in adults is 60% with no food intake and 100% otherwise. However, due to ingestion problems, erlotinib is often given with no food intake. We therefore considered a 60% bioavailability. Once in the blood stream, erlotinib bounds to albumin very strongly. The unbound fraction of drug in plasma f_u is 0.05. Erlotinib elimination is mainly hepatic, with a very small renal elimination (about 9%). We neglected that proportion for the maturation process. The cytochrome CYP3A4 is responsible for about 70% of erlotinib elimination while CYP1A2 is responsible for the other 30%.³⁸ The adult apparent clearance Cl/F is 3.95 L/h. We assimilated the global clearance to the hepatic clearance Cl_H. Therefore, we can deduce the hepatic extraction ratio with the hepatic plasmatic flow Q_hep. The hepatic blood flow is 90 L/h. Correcting by the haematocrit, we obtained Q = 40.5 L/h, as reported in Table 4 and we had $E_H=\frac{{\mathit{Cl}}_H}{Q_{\mathit{hep}}}=\frac{\mathit{Cl}/F\times F}{Q_{\mathit{hep}}}=0.058$. Considering the hepatic extraction ratio and the fact that CYP1A2, responsible for 30% of the clearance, are not present in the gut wall, we considered a gut wall extraction ration null E_g = 0. We then calculated the fraction absorbed $f_{\mathit{abs}}=\frac{F}{1-E_H}=0.64$. Adult information gathered in Table 4 were used in the computation of paediatric individual clearance. Based on equation (5), we have

$$F_{\mathit{ch}}=f_{\mathit{abs}}(1-E_G\times {\mathit{MAT}}_{\mathit{CYP}3A4}(\mathit{AGE}))(1-E_H\times (0.70{\mathit{MAT}}_{\mathit{CYP}3A4}(\mathit{AGE})+0.30{\mathit{MAT}}_{\mathit{CYP}1A2}(\mathit{AGE})))$$

with the maturation function characterised by Johnson et al.³⁹ given by MAT${\mathit{CYP}3A4}_{(}\mathit{AGE})=\frac{{\text{AGE}}^{0.83}}{0.31+{\text{AGE}}^{0.83}}$ and MAT${\mathit{CYP}1A2}_{(}\mathit{AGE})=\frac{{\text{AGE}}^{1.41}}{1.13+{\text{AGE}}^{1.41}}$. The hepatic clearance Cl_ch is related to CYP3A4 and CYP1A2, which vary with age up to the adults values. As a results, equation (4) of the paediatric clearance becomes for erlotinib

$$\frac{{\mathit{Cl}}_{\mathit{ch}}}{F_{\mathit{ch}}}=\mathit{Cl}\times (0.70{\mathit{MAT}}_{\mathit{CYP}3A4}+0.30{\mathit{MAT}}_{\mathit{CYP}1A2})\frac{F}{F_{\mathit{ch}}}\times (\frac{W_{\mathit{ch}}}{W_{\mathit{ad}}}{)}^{0.75}$$

Table 4.

Pharmacokinetic parameters used for paediatric extrapolation.

Parameters	Value	Source
ka (h–1)	0.949	Lu et al.33
Cl/F (L.h–1)	3.95	Lu et al.33
V/F (L)	233	Lu et al.33
Q (L.h–1)	40.5	–
Clu (L.h–1)	47.4	–
fabs	0.64	–
fu	0.05	–
EG	0	–
EH	0.058	–

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Caroline Petit was supported during this work by a grant IDEX from the Université Sorbonne Paris Cité (2013, project 24). Sarah Zohar, Emmanuelle Comets and Moreno Ursino were funded by the InSPiRe (Innovative Methodology for Small Populations Research) Project of the European Union Seventh Framework Programme for Research, Technological Development, and Demonstration under grant agreement FP HEALTH 2013-602144. During this work, Adeline Samson was partially supported by the LabEx PERSYVAL-Lab (ANR-11-LABX-0025-01) funded by the French program Investissement d’avenir.