Abstract
Female meiotic drive, in which chromosomal variants preferentially segregate to the egg pole during asymmetric female meiosis, is a theoretically pervasive but still mysterious form of selfish evolution. Like other selfish genetic elements, driving chromosomes may be maintained as balanced polymorphisms by pleiotropic or linked fitness costs. A centromere-associated driver (D) with a ~58:42 female-specific transmission advantage occurs at intermediate frequency (32–40%) in the Iron Mountain population of the yellow monkeyflower, Mimulus guttatus. Previously determined male fertility costs are sufficient to prevent the fixation of D, but predict a higher equilibrium frequency. To better understand the dynamics and effects of D, we developed a new population genetic model and measured genotype-specific lifetime female fitness in the wild. In three of four years, and across all years, D imposed significant recessive seedset costs, most likely due to hitchhiking by deleterious mutations. With both male and female costs as measured, and 58:42 drive, our model predicts an equilibrium frequency of D (38%) very close to the observed value. Thus, D represents a rare selfish genetic element whose local population genetic dynamics have been fully parameterized, and the observation of equilibrium sets the stage for investigations of coevolution with suppressors.
Keywords: Balancing selection, centromere, genetic conflict, polymorphism, seedset, selfish genetic element, standing variation
Selfish genetic elements spread in populations by gaining excess transmission (driving) without increasing individual fitness. Selfish genetic elements are incredibly common and diverse, as the complex reproductive biology of eukaryotes create myriad opportunities for competition among subindividual elements (Lyttle 1991; Burt and Trivers 2008). When such competition occurs, individual fitness costs are often a direct effect (as in spore-killer systems in Neurospora; Turner and Perkins 1979) or a consequence of linked deleterious alleles hitchhiking on a driving element (Chevin and Hospital 2006). Depending on their strength and nature, such costs can merely slow the inevitable fixation of selfish elements or can result in balanced polymorphism within populations (Hartl 1970; Crow 1991; Lyttle 1991). In the latter case, the balance between drive and individual costs can maintain levels of genetic variation in fitness greatly exceeding that expected under mutation–selection balance (Crow and Kimura 1970). In addition, costs will select for unlinked suppressors of drive (reviewed in Crow 1991), leading to coevolutionary dynamics (arms races) with potentially far-reaching effects on organismal biology (Hurst and Werren 2001). Thus, understanding the interplay of drive and associated costs in nature is important to understanding both the short-term maintenance of population variation and long-term evolutionary patterns.
Centromere-associated female meiotic drive is a potentially common form of selfish evolution (Henikoff et al. 2001; Pardo-Manuel de Villena and Sapienza 2001b). Female meiosis is asymmetric, in that only one of the four division products goes on to become an egg (animals) or megagametophyte (plants). This asymmetry creates an arena for natural selection among homologous chromosomes, as any chromosomal element that can preferentially segregate to the egg-to-be gains a transmission advantage. The centromere of each chromosome, as the site of kinetochore formation and attachment to the spindle assembly, mediates meiotic (and mitotic) segregation. Thus, centromeres have the greatest potential for female meiotic drive, although neocentromeric elements (such as heterochromatic knobs in maize; reviewed in Dawe and Hiatt 2004) have also been shown to take advantage of the asymmetry of female meiosis. Drive by centromeric DNA arrays, and antagonistic coevolution by kinetochore proteins, has been proposed to explain the “centromere paradox,” the unexpectedly rapid evolution of these essential mediators of cell division (Henikoff et al. 2001). Under the selfish centromere model, expansion or other changes in a centromeric DNA array that cause preferential segregation to the egg pole (relative to homologs) confer a transmission advantage in heterozygotes, but also entail costs that favor the evolution of drive-suppressing variants of key kinetochore proteins (Malik and Henikoff 2002). The resulting DNA-protein arms race is posited to explain the rapid turnover of centromeres, drive large-scale patterns of karyotypic evolution (Pardo-Manuel de Villena and Sapienza 2001a), and contribute to hybrid incompatibilities (Henikoff et al. 2001; Johnson 2010).
The selfish centromere model has the potential to explain fundamental aspects of eukaryotic biology. Yet we still know little about the incidence, nature, and consequences of costs associated with centromere-associated drive. Because the other three products of female meiosis degrade anyway, centromeric meiotic drive is potentially cost-free to females. Costs (either pleiotropic or linked) may nonetheless be a key part of its dynamics. The original (verbal) centromeric drive model incorporated pleiotropic costs of drive expressed in heterozygotes (Henikoff et al. 2001; Malik and Henikoff 2002). Specifically, the same asymmetry of kinetochore function causing preferential segregation in female meiosis was proposed to also cause chromosomal mis-segregation (nondisjunction) in male meiosis, resulting in partial male sterility. However, heterozygous costs are unlikely to result in antagonistic coevolution. If these costs are greater than the transmission advantage, they prevent spread of the driving centromere. If smaller, they slow its spread, but do not prevent inevitable fixation (see Appendix). In contrast, homozygous costs associated with driving centromeres have the potential to generate and fix significant population genetic load and, because they can prevent the fixation of drivers but cannot remove them from a population, may provide time and impetus for suppressors to arise and spread (Crow 1991).
Here, we investigate female fitness costs of centromere-associated meiotic drive in Mimulus guttatus (yellow monkeyflower). This drive system was first identified in hybrids between the outcrossing M. guttatus (IM62 inbred line) and M. nasutus, a closely related selfing species. A region of Linkage Group 11 (LG11) exhibited near-perfect preferential transmission of M. guttatus alleles (D haplotype at LG11 Drive Locus) over M. nasutus (d haplotype) in female gametes of F1 hybrids and heterozygous nearly isogenic lines, consistent with drive by the M. guttatus LG11 centromere at Meiosis I (Fishman and Willis 2005; Fishman and Saunders 2008). Subsequent experiments revealed that the Drive Locus was polymorphic within the Iron Mountain (IM), Oregon population from which IM62 was derived, and that D was cytogenetically and genetically coincident with unusually large arrays of the centromeric satellite repeat Cent728 (Fishman and Saunders 2008). Furthermore, driving D haplotypes experienced a ~58:42 female-specific transmission advantage over nondriving (D−) genotypes from IM, indicating that centromere-associated drive was not a byproduct of hybrid dysfunction. Finally, inter-specific crossing experiments and wild IM collections found that individuals with two copies of the driving D haplotype (DD homozygotes) suffered a strong and significant (~20%) pollen fertility cost, whereas heterozygotes (both DD− and Dd) were just as fertile as either non-D homozygote (Fishman and Saunders 2008). Given the female-specific transmission advantage experienced by D in intraspecific heterozygotes, these male-specific recessive costs are (just barely) sufficient to prevent the fixation of the driving D haplotype at IM. Male fitness costs alone predict an equilibrium frequency of D > 70% (Fishman and Saunders 2008); however, multiple collections from the IM population indicate that the frequency of D (as indicated by diagnostic markers) has been 30–40% over a period of at least 20 years (Sweigart et al. 1999; Fishman and Saunders 2008; Scoville et al. 2009). This raises the possibility that additional costs contribute to the low-to-intermediate frequency of D and, conversely, that D maintains additional deleterious variation within the IM population.
Here, we characterize female fitness costs associated with the M. guttatus LG11 Drive Locus and compare the frequency of the driving D haplotype to expectations at evolutionary equilibrium. We first develop a population genetic model of centromere-associated drive with distinct male and female fitness costs, incorporating the mating system variation common in plants. We then present lifetime seedset data for ~1300 wild individuals from the polymorphic IM population of M. guttatus, collected over a four-year period (2010–2013). We collected and counted all fruits and seeds (and, in 2012 and 2013, total flowers) of plants surviving to produce at least one fruit, and genotyped them at a marker diagnostic of Drive Locus genotype. We ask: Does D have female fitness as well as male fitness costs? Are female costs consistent across years? Given male and female reproductive costs, does D appear to be near the predicted equilibrium frequency?
Theory
We here generalize the model of Hartl (1970) allowing sex-specific effects on zygotic fitness and self-fertilization to occur at an arbitrary rate within the population. Meiotic drive occurs during production of female gametes. If a plant is a DD− heterozygote, a fraction δ of gametes are D and 1 − δ are D−. Here, we expect δ > 0.5. The drive allele can reduce both male (production of viable pollen) and female (production of seed) reproductive capacity. Zygotic fitness effects are characterized by sex-specific selection coefficients (sM and sF) and dominance coefficients (hM and hF) as follows: D−D− has male and female fitness = 1, DD− has male fitness = 1 – hMsM and female fitness = 1 – hFsF, and DD has male fitness = 1 – sM and female fitness = 1 – sF. We assume that adult plants produce seed via outcrossing at rate t and by selfing at rate 1 − t, where 0 < t ≤ 1. Female fitness costs affect both sorts of reproduction, but male costs (other than complete sterility) only affect outcrossing; that is, we assume that adults of all genotypes are not pollen limited for self-fertilization.
Let x0 and x1 be the frequencies of the DD and DD− genotypes in zygotes (D−D− frequency is 1 − x0 − x1). Recursions for x0 and x1 can be found by first calculating the genotype frequencies within seeds produced by surviving plants (x0F and x1F) and among outcross sires (x0M and x1M):
| (1) |
| (2) |
Genotype frequencies in the next generation of zygotes, x0′ and x1′, are obtained by summing over mate pairs for outcrossed progeny and maternal plants for selfed progeny, noting the effect of meiotic drive when the female parent is DD−. Letting x2M = 1 − x0M − x1M and x2F = 1 − x0F − x1F, we find that
| (3) |
| (4) |
Equations (3)–(4) are sufficient to iteratively investigate the model, projecting genotype frequencies through time from any starting point (initial values for x0 and x1). They cannot be reduced to a single exact recursion for q (the frequency of the D allele) because self-fertilization and meiotic drive generate sustained deviations from Hardy–Weinberg equilibrium.
A boundary analysis (Appendix) yields conditions for protected polymorphism, that is, when either D or D− will increase when rare. The drive allele D will increase when rare if:
| (5) |
The nondrive allele D− will increase when rare if:
| (6) |
where G1 = 1 − t − 3hFt + hFt2 − sM(1 + t − 2hFt − hMt − hMt2) and G2 = 2(1 − sM) − t(1 − hMsM) − hF(1 − sM + 2t − sMt − t2). These equations simplify considerably for special cases. For example, if zygotic costs are fully recessive (hF = 0 and hM = 0) and the population is fully outcrossing (t = 1), then balanced polymorphism requires that
| (7) |
This implies that D will always increase when rare. This is no longer true if either cost exhibits some heterozygous effect or if there is some degree of self-fertilization. If δ satisfies both (1) and (2), the frequency of D approaches a stable equilibrium. There is an interesting region of the parameter space where zygotic costs of D are dominant or partially dominant, and as a consequence, δ can simultaneously violate (1) and (2). We have confirmed numerically that this corresponds to an unstable internal equilibrium (see Prout 2000 for a similar case). D will go to fixation if very common but cannot increase when rare. However, because fitness costs of centromere-associated meiotic drive polymorphism in M. guttatus are recessive (or nearly so), the balance of gametic and zygotic selection tends to maintain polymorphism.
Although the exact equilibrium frequency of D must be solved numerically via equations (3)–(4), we can derive an approximate equation for the equilibrium by assuming weak selection and that genotype frequencies (at equilibrium) deviate from Hardy–Weinberg proportions as predicted strictly from the rate of selfing: F = (1 − t)/(1 + t), where F is the inbreeding coefficient. The latter allows us to reduce equations (3)–(4) into a single recursion for q. The recursion for q is a high-order polynomial, but with weak selection (sM and sF → 0), Δq ≈ q(1 − q)G[q], where G[q] is quadratic in q. The relevant root is:
| (8) |
where a = 4(2hF − 1)sFt2(2δ − 1),
and c = −(1 + t)[δ4t(1 − hFsF) + sF (t − 1)(2 + (2hF − 1)t) −t(2+sM(1 − t) + 2hMsMt)].
Equation (8) assumes that sF > 0 and that dominance coefficients (hF and hM) are low enough to allow protected polymorphism (eqs. (5) and (6)). If sF = 0,
| (9) |
Methods
SYSTEM
Mimulus guttatus (yellow monkeyflower; Phrymaceae) is a wildflower common in wet-soil habitats across Western North America. The self-compatible but primarily outcrossing M. guttatus is the central member of a diverse species complex (Wu et al. 2007), and also encompasses multiple ecotypes divergent in edaphic and life-history traits (Lowry et al. 2008; Lekberg et al. 2012). We focus our analyses on the IM population in the Oregon Cascades; this high-elevation snowfield population is obligately annual, with all plants flowering and fruiting in the brief (four to eight weeks) window between melt-out and dry-down. Generally, this population consists of >100,000 densely packed flowering plants, and there is no evidence of spatial genetic structure within the ~30 m × 15 m site (Kelly and Willis 2002). Quantitative genetic analyses reveal high heritable variation for floral traits and male fertility at IM, consistent with some form of balancing selection (Kelly and Willis 2001; Kelly 2003; Scoville et al. 2009; Bodbyl Roels and Kelly 2011; Scoville et al. 2011). In the case of pollen viability, high levels of deleterious variation are explained, in large part, by the high frequency (~35%) and homozygous costs of the driving D haplotype, as well as a second, lower frequency, structural variant (Scoville et al. 2009). Floral size traits are positively associated with seedset (Fishman and Willis 2008), but experience temporally varying selection mediated by a trade-off with survival to reproduction (Mojica and Kelly 2010; Mojica et al. 2012). Numerous inbred lines and outbred experimental populations have been derived from the IM population, including IM62, which was used in constructing the M. guttatus reference genome (http://phytozome.jgi.doe.gov/) and in identifying D through genetic and cytogenetic tests.
GENOTYPING AND PHENOTYPING
Previously, we established that several polymerase chain reaction (PCR)-based markers, including the simple sequence repeats LB5a and aat356, were diagnostic of Drive Locus genotype in the IM population. In each case, a single allele is associated with D, whereas numerous alternative alleles are found in D− individuals. Previously, we reported near-perfect linkage disequilibrium (LD) and a single D haplotype across markers spanning >450 kb in the drive region, indicating a recent selective sweep and/or local suppression of recombination (Fishman and Saunders 2008). Patterns of LD in re-sequence data from 10 inbred lines derived from IM (Flagel et al. 2014), three of which are D, suggest that the D haplotype block extends a minimum of 10 Mb (F. Finseth and L. Fishman, unpubl. data).
To associate Drive Locus genotype with female fitness in the field, we collected entire plants immediately after dry-down each summer for four years (2010–2013). Mimulus guttatus plants at this site are annual; they die from drought stress and continue to ripen seeds even as the rest of the plant senesces. Because plants are small (each was collected into a 3 inch coin envelope) and the vase-like calyx retains seeds even after they dehisce from the ovary, we could thus capture all or most of the lifetime seed output of each individual. We recorded the total number of fruits (inflated calyxes around ovaries that had a chance to set seed) and, in 2012–2013, the total number of flowers (fruits + uninflated calyxes). The viable seeds were then separated from other tissue and counted in bulk to estimate total seed number (female fitness) for each plant, and total seed counts were divided by the number of fruits to obtain mean seeds per fruit (seedset/fruit).
Genomic DNA was extracted from the remaining tissue (generally the entire plant, which was stored at −80°C between seed separation and extraction) using a CTAB-chloroform protocol modified for use in 96-well format. The diagnostic marker LB5a (with a fluorescently-labeled forward primer) was amplified using a standard touchdown PCR protocol with the addition of bovine serum albumin (5 μg/μl final concentration). The PCR products, along with an in-lane size standard, were run through ABI 3700 or 3130 automated sequencers (ThermoFisher, Waltham, MA) for separation and visualization of size-variable DNA fragments. Genotypes were called automatically and verified by eye using ABI Genemapper software (ThermoFisher); as previously, a 276 basepair allele at LB5a was assigned as D and all others as D−.
STATISTICAL ANALYSES
We analyzed female fitness and seedset/fruit in generalized linear models (GLMs) including Year, Drive Locus genotype, and Year × Drive Locus genotype interaction. Initially, we included all three genotypic classes; however, because there were never significant differences between the D−D− and DD− classes, we re-coded the genotypes to reflect recessivity of D effects (DD vs. non-DD). Seedset per fruit was analyzed with a bias- and overdispersion-adjusted Poisson error distribution (log link). Total seeds had an extremely skewed distribution (most plants made <50 seeds, some made >>2000), so we log-transformed the values prior to analysis in GLM (normal distribution, identity link). Because we only had four years of sampling, and one of those years was extraordinarily fecund on the basis of previous field work in the population (Willis 1993; Fishman and Willis 2008), we did not treat year as a random factor in the models. We also used GLMs (Poisson distribution, log link) to examine possible effects of Year and Drive Locus genotype on fruit and flower (2012, 2013 only) number. All statistical analyses were performed in JMP Pro 11 (SAS Institute, Cary, NC).
Results
FIELD MEASURES OF FEMALE FITNESS
We found significant effects of Drive Locus genotype (DD vs. non-DD) on seedset per fruit (P < 0.004) and total seeds (P = 0.021), indicating recessive female fitness costs of drive (Table 1). This effect was detectable in three of the four years when analyzed individually (DD vs. non-DD effect, P < 0.05 in GLM), but there was no effect of Drive Locus genotype on either trait in 2012 (although the Year × Drive Locus interaction was not significant in either whole model). Except in 2012, DD homozygotes set 14–23% fewer seeds per fruit and 14–52% fewer total seeds than alternative genotypes (Fig. 1). Total seed production varied strongly among years (P < 0.0001, Table 1) with a nearly twofold difference between the mean number of flowers per plant in 2012 versus 2013 (2.69 vs. 4.89) and a >threefold difference in mean fruit number (1.07 vs. 3.67) between the worst (2010) and best (2013) years (Fig. 1). However, there was no evidence for Drive Locus effects on flower or fruit number (both P > 0.40).
Table 1.
Effect of Year and Drive Locus genotype (DD vs. non-DD), plus their interaction, on components of female fitness in the Iron Mountain population of Mimulus guttatus.
| Trait | Effect | df | χ2 | P |
|---|---|---|---|---|
| Flowers | Year | 1 | 128.85 | <0.0001 |
| (N = 880) | DD | 1 | 0.06 | 0.80 |
| Year × DD | 1 | 0.02 | 0.88 | |
| Fruits | Year | 3 | 295.62 | <0.0001 |
| (N = 1284) | DD | 1 | 0.63 | 0.43 |
| Year × DD | 3 | 2.61 | 0.46 | |
| Seeds/fruit | Year | 3 | 64.63 | <0.0001 |
| (N = 1284) | DD | 1 | 8.43 | 0.004 |
| Year × DD | 3 | 5.40 | 0.14 | |
| Log (seeds) | Year | 3 | 247.94 | <.0001 |
| (N = 1286) | DD | 1 | 5.37 | 0.02 |
| Year × DD | 3 | 5.11 | 0.16 |
Flower number, fruit number, and seedset/fruit were analyzed with GLM (Poison distribution, log link) and total seed number was log-transformed before analysis with GLM (normal distribution, identity link). The χ2 column gives the likelihood ratio χ2 value for a given effect in each full GLM. Significant P values are indicated in bold.
Figure 1.
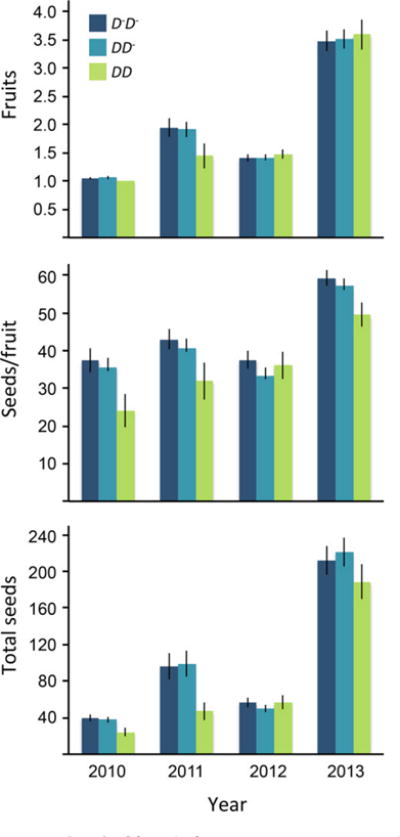
Mean (±SE) of female fitness components in each Drive Locus genotype over four years in the Iron Mountain population of Mimulus guttatus.
OBSERVED AND PREDICTED POPULATION FREQUENCY OF D
The frequency of the three Drive Locus genotypes varied significantly (P = 0.018, Pearson χ2, N = 1284), across the four-year study period (Fig. 2). Specifically, the frequency of D rose significantly between 2011 and 2012 (Pearson χ2, P < 0.01), from 0.34 in the first two years to 0.40 in the last two, with an associated increase in the frequency of DD homozygotes from 0.10 to 0.17. Previously, we estimated the strength of within-population drive by D against D− as ~58:42 (δ = 0.58), and recessive male fitness costs (pollen sterility) as 0.19 (Fishman and Saunders 2008). In the absence of female fitness or survival costs, these values predict an equilibrium frequency of D > 0.70 (eqs. (1)–(4)) and are barely sufficient to prevent its fixation (eq. (6)). Recessive female fitness costs varied from year to year, but averaged ~0.21 across the four years (DD mean = 79 seeds, non-DD mean = 100 seeds). When female fitness costs are added to the model, combined with reasonable outcrossing rates for the IM population (Willis 1993; t = 0.8–1.0; Sweigart et al. 1999), the equilibrium frequency of D is predicted to be 0.25–0.40 (Fig. 3). This range is very similar to the 0.30–0.42 frequencies observed in the field.
Figure 2.
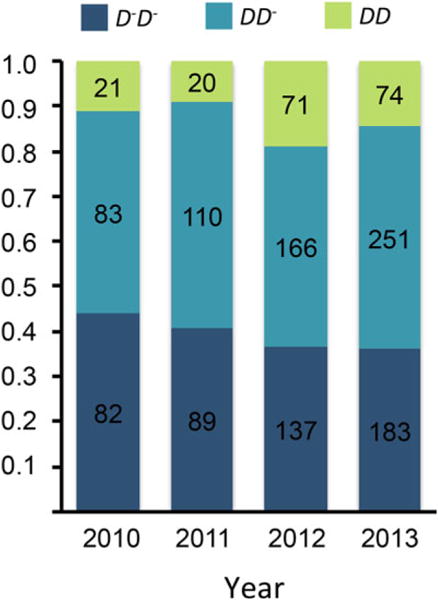
Frequency of Drive Locus genotypes in Iron Mountain M. guttatus sampled over the four-year study period. Numbers on bars show sample numbers in each category.
Figure 3.
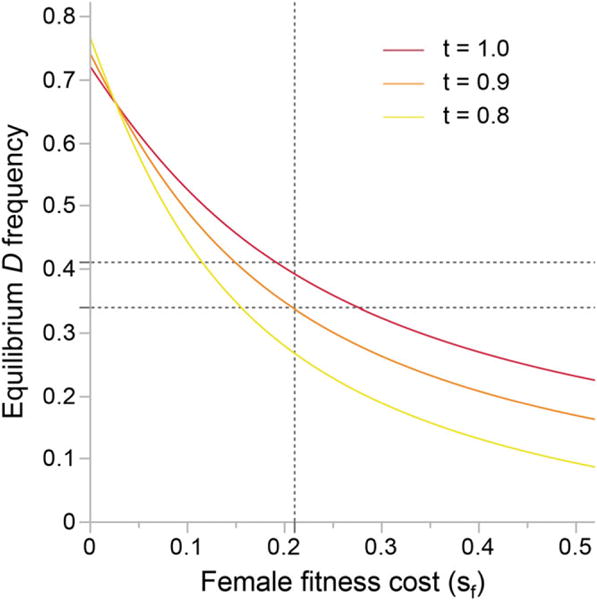
Equilibrium frequency of D is predicted as a function of the recessive female fitness cost for three outcrossing rates. Previous estimates for the strength of drive and the male fitness cost were assumed (sM = 0.20, δ = 0.58, hM = hF = 0; Fishman and Saunders 2008). The vertical line indicates the mean female cost across our four-year study period and the horizontal lines bracket field estimates of D frequency.
The trajectories of Figure 3 were determined numerically from equations (1)–(4), and not from the weak selection approximation of equations (8)–(9). With strong selection, equations (8)–(9) tend to overestimate the frequency of D (Tables S1–S2). However, they provide useful insight on the system, particularly the differing ways that male and female fitness costs affect the equilibrium. Note that with substantial male costs (sM = 0.2), selfing has a positive effect on the frequency of D if sF is small, but a negative effect if sF is large (note crossing of trajectories in Fig. 3). The approximation indicates that if female costs are held to 0.2 and sM allowed to vary, no such effect occurs and selfing uniformly reduces the frequency of D (Fig. S1). This difference results from our assumption that male fitness costs do not affect selfed seedset (self-fertilization is not pollen limited), but female costs reduce seedset generally (i.e., are equally costly whether a plant self-fertilizes or outcrosses). If self-fertilization is instead pollen-limited, such that male sterility is costly to selfers, then this interaction between male versus female costs and mating system would likely disappear. This effect of partial pollen sterility on male and female fitness in selfers is worthy of further theoretical and empirical consideration; however, because M. guttatus is largely outcrossing, and our estimates of male and female fitness costs are both substantial, assuming no cost does not affect our conclusions about the population genetics of drive.
Discussion
Female meiotic drive, competition among homologous chromosomes for inclusion in egg, may be a ubiquitous process driving the coevolutionary turnover of centromeric DNA and proteins (Henikoff et al. 2001; Malik and Henikoff 2002). In M. guttatus, we have a rare opportunity to investigate the short-term evolutionary dynamics of a centromere-associated driver (D) in a natural population. Models based on the strength of conspecific drive and male fitness costs alone had suggested protected polymorphism at the Drive Locus (both D and D− increase when rare), but together predicted a frequency of D much higher than the observed 1/3 (Fishman and Saunders 2008). Our new field-based measures of seedset suggest of female fitness costs are also very important in restricting the spread of D, and are necessary (and sufficient) to maintain the balanced polymorphism at an equilibrium near the observed frequencies (Fig. 3). Thus, D is a rare case in which population genetic theory has been directly confirmed by estimating evolutionary parameters and comparing observed to expected frequencies.
In addition to explaining why D is not more common, female costs add substantially to the load that female meiotic drive imposes on the population. Because both male and female costs are recessive, selection cannot eliminate D from the population when outcrossing rates are high. Interestingly, the predicted dynamics of D change substantially with partial selfing, but only when recessive female costs (rather than male costs alone) are included. Thus, the dynamics of driving centromeres, which differ fundamentally from well-known male meiotic drive (sperm-killer) systems, depend on the particulars of fitness costs and the mating system. In the largely outcrossing M. guttatus population at IM, the synthesis of data and theory indicate that driving centromeres persist at intermediate frequency despite (and actually because of) substantial impacts on individual reproductive fitness, setting the stage for antagonistic coevolution with suppressors of drive.
THE MAGNITUDE AND MECHANISM OF FEMALE FITNESS COSTS
Female fitness effect of D were always recessive, and always negative when present, but varied in strength among years (Fig. 1). They were most detectable and consistent when measured as seeds/fruit (vs. fruits or total seeds), suggesting that they are primarily mediated through processes intrinsic to the fruit (e.g., ovule number, seed development) rather than the whole-plant (e.g., resource acquisition, flowering time). The 2011 season, in which DD homozygotes produced fewer fruits, as well as fewer seeds per fruit, was an exception. This additional effect, as well as the lack of any seedset effects in 2012, suggests that female fitness costs of D may involve multiple traits and underlying loci.
Our finding of recessive female fitness costs is somewhat unexpected based on previous theoretical arguments that fitness costs of centromeric drive should be (1) primarily male-specific and (2) caused by centromeric competition per se and thus strongest in heterozygotes (Henikoff et al. 2001). Because all products of male meiosis become gametes (gametophytes in plants), deleterious duplications and deletions of chromosomes caused by nondisjunction should be most evident in males. Furthermore, elevated rates of chromosomal nondisjunction in hybrids between taxa divergent in heterochromatin have been observed (McKee et al. 1998; but see Gilliland et al. 2015). Thus, under a model in which all costs of female meiotic drive are pleiotropic effects of divergence in centromeric heterochromatin, recessive female costs are not predicted. Any kind of female costs also run counter to the prediction that female meiotic drive elements should accumulate dominant or overdominant mutations that increase the relative female fitness of heterozygotes, where drive occurs and can gain most from increased seedset (Burt and Trivers 2008; Patten 2014). However, our results are entirely consistent with population genetic theory in which even severely deleterious mutations, if strictly recessive, are tolerated as hitchhikers on meiotic drive elements (Hartl 1970; Crow 1991; and Appendix).
Given the large nonrecombining region associated with the D haplotype (>10 Mb with >450 genes; F. Finseth and L. Fishman, unpubl. data), hitchhiking of deleterious recessive alleles seems the most likely basis for female costs. This would be similar to the sheltered load associated with self-incompatibility loci (S-loci), at which many alleles are maintained by rare-allele advantage (Stone 2004; Llaurens et al. 2009); however, enforced heterozygosity (as well as suppressed recombination and balancing selection) may contribute to the sheltering of deleterious recessive mutations in that case. On the other hand, it is also theoretically possible that seedset costs are instead a pleiotropic effect of DD homozygosity per se. Pairing of two driving D centromeres might disrupt meiosis (e.g., through failure of LG11 sister chromatids to separate properly) and thus generate both male and female fitness costs. The similar magnitude of pollen inviability (0.19; Fishman and Saunders 2008) and seedset reduction (0.14–0.23, excepting 2012) makes this a plausible option, but the lack of any effect in 2012 and the additional fruit number costs in 2011 suggest that pleiotropy cannot be a complete explanation. Limited recombination between D and D− haplotypes (F. Finseth and L. Fishman, unpubl. data) and little variation among IM D haplotypes make demonstrating (or ruling out) a functional relationship between drive and costs difficult. However, we have identified sequence-divergent D haplotypes in other populations (L. Fishman, unpubl. data), and crosses of these lines with IM62 may allow genetic dissection of the region. In addition, developmental studies of the timing of reproductive disruption in DD plants (e.g., meiosis vs. gametogenesis vs. post fertilization in the case of seeds) could help determine whether either male or female costs are plausibly structural in origin.
It is also possible that the partial pollen sterility of DD plants could secondarily produce the observed female fitness effects, as bees can discriminate among M. guttatus flowers on the basis of pollen viability (Robertson et al. 1999; Carr et al. 2014). However, this mechanism seems unlikely given the dynamics of D during the experimental evolution of increased selfing for reproductive assurance in M. guttatus (Bodbyl Roels and Kelly 2011). In that experiment, a population was synthesized from IM genotypes such that the initial D frequency was 0.5. Replicated populations were maintained in a greenhouse either with bees (outcrossing) or without pollinators (selfing) for >five generations. The frequency of D decreased dramatically in both replicates of the selfing regime, but only slightly (on average, toward the predicted equilibrium frequency) in the outcrossing populations (Bodbyl Roels and Kelly 2011). A rapid decline of D is predicted with selfing, but only if there are female fitness costs. Because partial male sterility should be relatively inconsequential when t = 0 (see next section), and there was no indication that D was associated with floral traits under direct selection, this decrease most likely reflects pollinator-independent female fitness costs or as–yet-undetected survival costs. In addition, that experiment was conducted under relatively benign greenhouse conditions compared to our field surveys, further supporting the inference that DD seedset costs (when they occur) reflect breakdowns in female gamete and/or seed development.
IS D AT STABLE EQUILIBRIUM?
Together, the male and female fitness costs we have identified (Fishman and Saunders 2008, this study) are both necessary and sufficient to explain the current frequency of D given 58:42 conspecific drive. Across our four-year study and previously D was at 30–40% at IM, very close to predicted values for the high (t = 0.75–1.0) outcrossing rates in this population (Willis 1993; Sweigart et al. 1999). This suggests that D is at or near its equilibrium frequency, and that we have fully characterized the primary selective factors (drive and costs) important for its dynamics. This sets D apart from the best known selfish element polymorphisms (e.g., Segregation Distorter [SD] in Drosophila melanogaster, t-haplotype in mice, Ab10 in maize) where there remains a large gap between population genetic predictions and empirical estimates of costs and benefits (Burt and Trivers 2008). Much more work will be necessary to understand the dynamics and history of D across M. guttatus, as well as its mechanism of action, but its local population genetics appear largely predictable.
Of course, despite the match between our model and data, there may be other factors that influence the dynamics of centromere-associated drive in IM M. guttatus. The equilibrium frequency of D is very sensitive to its transmission advantage (eqs. (A1)–A4). For example, holding other parameters constant, if one changes δ from 0.58 to 0.60, the equilibrium frequency increases from 0.4 to 0.5. Distinguishing a transmission advantage of 0.58 from one of 0.60 statistically is extremely challenging, even if there were a single true value for δ. In addition, circumstantial evidence suggests that D− plants vary in their resistance to drive, due either to variation among D− alleles or to background genetic effects (Fishman and Saunders 2008; Scoville et al. 2009). Also, we cannot explain the significant increase in D frequency following 2011, the year in which the proportional female costs of drive were highest. Because overall seed numbers were lowest in 2011, it is also worth considering whether there may be additional fitness effects of D (positive or negative) that we have not yet characterized.
Most notably, it is possible that D could also harbor deleterious mutations affecting nonreproductive traits, as we did not estimate survival to flowering in our four-year field study. Two lines of evidence suggest, however, that we are not missing such major fitness effects. First, in the experimental evolution study of Bodbyl Roels and Kelly (2011), the frequency of D declined from 0.50 to 0.17–0.28 (mean = 0.21) over six generations of obligate selfing. Given initial conditions and t = 0.0, the model predicts a decline to 0.28 for this interval, comparable to but slightly less change than observed. In contrast, D declined in only one of the replicate outcrossing (t ~ 1) treatment populations and very slightly on average: observed mean = 0.47 which is exactly the value predicted by equations (A1)–(A4). This difference in the experimental evolution of D between selfing and outcrossing populations is consistent with our inference that female fitness costs (as opposed to unmeasured viability effects) are important determinants of its frequency in the wild, especially as it also did not appear to be linked to major floral QTLs under selection. Second, as part of a different study, we have conducted whole genome sequencing of two pooled population samples from IM. The pools consist of wild-collected seedlings (N = 200 per pool) germinating in either Fall 2012 or Spring 2013, respectively. Across a set of D-diagnostic SNPs (n = 15, spanning 15 Mb of LG11; sequencing coverage/site = 38–120X), the mean (±SD) frequency of D does not differ between cohorts: 0.36 (±0.06) and 0.36 (±0.05) for Spring and Fall, respectively, values well within the range expected from the frequencies in fruiting adults in the flanking seasons. This consistency suggests no strong negative effects of D on germination. More field and greenhouse work will be necessary to identify all effects of D on fitness, and the role of environmental conditions in shaping female fitness effects, but all evidence suggests that D is near an intermediate equilibrium defined by moderate female meiotic drive and exclusively reproductive costs.
COMPARISON WITH OTHER DRIVE SYSTEMS
Despite its substantial effects on individual fitness and population genetic load, D is at high frequency compared to other well-studied drivers. The classic male meiotic drive “alleles” in animals (e.g., t-haplotype in mice, SD in Drosophila) gain their dramatic (>90:10) transmission advantages by killing sperm carrying alternative haplotypes (reviewed in Burt and Trivers 2008). Thus, these drivers, as well as sex ratio distorters of similar mechanism, entail intrinsic heterozygous costs whenever sperm number is important for fitness (Wedell 2013). In addition, t-haplotype can cause lethality and/or complete male sterility when homozygous, and heterozygous females have reduced fitness; these costs are necessary to explain its generally low (~5%) frequency in wild populations (Ardlie 1998; Carroll et al. 2004; Manser et al. 2011). Similarly, SD causes substantial heterozygous male costs, as well as homozygous lethality or sterility; both are necessary to explain its low population frequency (reviewed in Larracuente and Presgraves 2012). Both of these drivers are widespread across species, multilayered, and associated with multiple inversions that suppress recombination. This complexity, and the age that it implies, suggests that the costs of male meiotic drivers probably derive from a mix of pleiotropy and the accumulation of deleterious alleles on a driving haplotype with suppressed recombination (Crow 1991). Because the strength of drive in these classic systems is so extreme, however, only strong, intrinsic, heterozygous costs could have prevented initial rapid fixation (and have allowed their detection as polymorphisms).
Chromosomal drive, because it takes advantage of an existing asymmetry in meiotic cell fate in females, need not impose such heterozygous costs. Furthermore, there is little empirical evidence of underdominant fertility effects of centromeric or neo-centromeric drive. In Mimulus centromere-associated female meiotic drive, all costs of D appear to be highly recessive, even in heterospecific crosses where drive is extremely strong (Fishman and Saunders 2008). Similarly, the neo-centromeric Ab10 chromosomal variant in maize, which drives at Meiosis II to gain up to a 75:25 transmission advantage (Dawe and Cande 1996; Birchler et al. 2003; Dawe and Hiatt 2004), shows no evidence of intrinsic seedset or pollen viability costs in heterozygotes. Ab10 is widespread across wild teosinte (Zea mays) subspecies, but occurs at low (0–20%) frequency per population (Buckler et al. 1999; Kanizay et al. 2013). This implies either substantial homozygous costs (greater than those in Mimulus) or heterozygous costs (Buckler et al. 1999). There are few data on the fitness effects of Ab10 and associated knobs, however, other than a post meiotic transmission disadvantage to Ab10 pollen in heterozygotes (Rhoades 1942), Unlike D, which appears to contain many functional (expressed) genes but is not yet known to have a genic component, the AB10 region contains only a few functional genes beyond several enhancer loci with functional effects on drive (Dawe and Cande 1996; Hiatt and Dawe 2003). Once we have a better sense of the species-wide distribution and abundance of D, and now that estimates of the fitness consequences of Ab10 genotype in the wild are feasible, modeling and explicit comparison of the dynamics of these two selfish chromosomal systems should be in reach.
EVOLUTIONARY IMPLICATIONS
These data provide an unusually complete picture of the selective forces acting on a natural polymorphism. We find (1) that the centromere-associated driver D is near its predicted equilibrium frequency at IM and (2) that it can shelter very high genetic load as long as the associated deleterious variation is recessive and the population is largely outcrossing. These findings have important implications for understanding how the selfish spread of D acts to shape variation at both linked and unlinked loci. The very low level of nucleotide variation within the D haplotype (L. Fishman and F. Finseth, unpubl. data) suggests that D entered the IM population as a single variant and spread rapidly and recently. Consistent with this inference, our parameterized model (with t = 1) predicts that it would take only 100 generations for D to increase from 1% to near the equilibrium of 38%.
Given that D appears to have recently increased to equilibrium at IM, we can now ask about its fate in time and space. Looking forward within IM, D is a common target for diverse deleterious mutations. Furthermore, with only a 0.58 transmission advantage, complete outcrossing and the observed moderate male costs, D could persist at 13% even if it caused complete female sterility in DD homozygotes. This is also true for male sterility (without the restriction on outcrossing rate), if female sterility is held constant at our mean estimate. Thus, D can continue to accumulate additional recessive fitness costs, increasing its individual fitness consequences but ratcheting down its predicted population frequency over time. In a very large outcrossing population such as IM (census N of reproductive plants estimated to be >>100,000), however, selection and recombination among D variants carrying different amounts of recessive load should be somewhat effective at limiting the spread of new major deleterious alleles linked to the driver. On the other hand, such highly deleterious D haplotypes cannot be completely purged from the population and, if sampled during the founding of a new population, would sweep to a new local equilibrium. Preliminary cytogenetic screens suggest that D is present at low-intermediate frequency in other Oregon populations of M. guttatus (L. Fishman and Y. Dong, unpubl. data), providing the opportunity to test the equilibrium model developed here in ecologically distinct populations.
When a costly driver is at equilibrium, theory predicts that unlinked suppressors (and linked enhancers) will be favored (Crow 1991). Thus, given substantial costs and intermediate equilibrium frequency of D in IM, but an apparently recent sweep to that frequency, we might expect evidence recent or ongoing selection on loci that affect the strength of drive. For centromere-associated drive, the most obvious suppressor (or enhancer if linked; Fishman 2013) is the centromere-specific histone (CENP-A or CenH3), which epigenetically marks the site of kinetochore formation (Henikoff et al. 2001). The model and empirical data on fitness costs presented here, in addition to explaining the current population genetics of D, provide a strong foundation for both genome-wide and CenH3-targeted investigations of coevolution between D and genic modifiers.
Supplementary Material
Figure S1. The equilibrium frequency of the drive allele ( ) from equations (8)–(9) is depicted on the y-axis as a function of (top) the selection coefficient through female function (sF) and (bottom) the selection coefficient through female function (sM).
Table S1. For a collection of parameter sets with weak selection, we determined the exact equilibrium frequency of the drive allele ( ) and compared it to the approximation of equations (8)–(9).
Table S2. For a collection of parameter sets with selection through male function and meiotic drive held to empirical estimates (hF = hM = 0, sM = 0.2, δ = 0.58), we determined the exact equilibrium frequency of the drive allele ( ) and compared it to the approximation of equations (8)–(9).
Acknowledgments
We thank D. Crowser, R. Fletcher, G. Hoffman, J. Mason, M. McIntosh, J. Van Noppen, A. Stathos, and K. Zarn for assistance with field collections, seed counting, and genotyping. This project was funded by National Science Foundation grant DEB-0846089 to LF and National Institutes of Health grant R01 GM073990 to JKK, and was also supported in part by the Montana Integrative Learning Experience for Students (MILES) program, through a grant to The University of Montana from the Howard Hughes Medical Institute—Undergraduate Science Education Program; Grant No. 52005905.
Appendix
A boundary analysis produces the conditions for protected polymorphism. When the D allele is rare, the recursions for x0 and x1 simplify approximately to linear equations:
| (A1) |
The dominant eigenvalue, λ1, for the matrix of A1 is a lengthy version of the quadratic equation. However, we can simplify the equation λ1 > 0 nicely for a minimum δ allowing the drive allele to increase when rare (eq. (5) in main text). Considering the other boundary, we now assumed that sF and sM are less than 1 (a population fixed for D would not exist if sF = 1 or sM = 1). The linearized genotype frequency recursions when D− is rare then become:
| (A2) |
where
As previously, the dominant eigenvalue for A2, λ2, is complicated, but the equation λ2 > 0 simplifies to provide a maximum δ allowing D− to increase when rare (eq. (6) in main text).
Footnotes
Supporting Information
Additional Supporting Information may be found in the online version of this article at the publisher’s website:
DATA ARCHIVING
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.dj6p6.
LITERATURE CITED
- Ardlie KG. Putting the brake on drive: meiotic drive of t haplotypes in natural populations of mice. Trends Genet. 1998;14:189–193. doi: 10.1016/s0168-9525(98)01455-3. [DOI] [PubMed] [Google Scholar]
- Birchler JA, Dawe RK, Doebley JF. Marcus Rhoades, preferential segregation and meiotic drive. Genetics. 2003;164:835–841. doi: 10.1093/genetics/164.3.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodbyl Roels SA, Kelly JK. Rapid evolution caused by pollinator loss in. Mimulus guttatus Evolution. 2011;65:2541–2552. doi: 10.1111/j.1558-5646.2011.01326.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckler ESI, Phelps-Durr TL, Buckler CSK, Dawe RK, Doebley JF, Holtsford TP. Meiotic drive of chromosomal knobs reshaped the maize genome. Genetics. 1999;153:415–426. doi: 10.1093/genetics/153.1.415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burt A, Trivers R. Genes in conflict. Belknap Press; Cambridge, MA: 2008. [Google Scholar]
- Carr DE, Roulston TH, Hart H. Inbreeding in Mimulus guttatus reduces visitation by bumble bee pollinators. PLoS One. 2014;9:e101463. doi: 10.1371/journal.pone.0101463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll LS, Meagher S, Morrison L, Penn DJ, Potts WK. Fitness effects of a selfish gene the Mus t complex are revealed in an ecological context. Evolution. 2004;58:1318–1328. doi: 10.1111/j.0014-3820.2004.tb01710.x. [DOI] [PubMed] [Google Scholar]
- Chevin LM, Hospital F. The hitchhiking effect of an autosomal meiotic drive gene. Genetics. 2006;173:1829–1832. doi: 10.1534/genetics.105.052977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF. Why is Mendelian segregation so exact? Bioessays. 1991;13:305–312. doi: 10.1002/bies.950130609. [DOI] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetics theory. Harper & Row; New York: 1970. [Google Scholar]
- Dawe RK, Cande WZ. Induction of centromeric activity in maize by suppressor of meiotic drive 1. Proc Natl Acad Sci USA. 1996;93:8512–8517. doi: 10.1073/pnas.93.16.8512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawe RK, Hiatt EN. Plant neocentromeres: fast, focused, and driven. Chromosome Res. 2004;12:655–669. doi: 10.1023/B:CHRO.0000036607.74671.db. [DOI] [PubMed] [Google Scholar]
- Fishman L. Female meiotic drive in monkeyflowers: insight into the population genetics of selfish centromeres. In: Jiang J, Birchler JA, editors. Plant centromere biology. Wiley-Blackwell; Oxford, UK: 2013. pp. 129–145. [Google Scholar]
- Fishman L, Saunders A. Centromere-associated female meiotic drive entails male fitness costs in monkeyflowers. Science. 2008;322:1559–1562. doi: 10.1126/science.1161406. [DOI] [PubMed] [Google Scholar]
- Fishman L, Willis JH. A novel meiotic drive locus almost completely distorts segregation in Mimulus monkeyflower hybrids. Genetics. 2005;169:347–353. doi: 10.1534/genetics.104.032789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman L, Willis JH. Pollen limitation and natural selection on floral characters in the yellow monkeyflower, Mimulus guttatus. New Phytol. 2008;177:802–810. doi: 10.1111/j.1469-8137.2007.02265.x. [DOI] [PubMed] [Google Scholar]
- Flagel LE, Willis JH, Vision TJ. The standing pool of genomic structural variation in a natural population of Mimulus guttatus. Genome Biol Evol. 2014;6:53–64. doi: 10.1093/gbe/evt199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilliland WD, Colwell EM, Osiecki DM, Park S, Lin D, Rathnam C, Barbash DA. Normal segregation of a foreign-species chromosome during Drosophila female meiosis despite extensive heterochromatin divergence. Genetics. 2015;199:73–83. doi: 10.1534/genetics.114.172072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl DL. Analysis of a general population genetic model of meiotic drive. Evolution. 1970;24:538–545. doi: 10.1111/j.1558-5646.1970.tb01789.x. [DOI] [PubMed] [Google Scholar]
- Henikoff S, Ahmad K, Malik HS. The centromere paradox: stable inheritance with rapidly evolving DNA. Science. 2001;293:1098–1102. doi: 10.1126/science.1062939. [DOI] [PubMed] [Google Scholar]
- Hiatt EN, Dawe RK. Four loci on abnormal chromosome 10 contribute to meiotic drive in maize. Genetics. 2003;164:699–709. doi: 10.1093/genetics/164.2.699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst GD, Werren JH. The role of selfish genetic elements in eukaryotic evolution. Nature Rev Genet. 2001;2:597–606. doi: 10.1038/35084545. [DOI] [PubMed] [Google Scholar]
- Johnson NA. Hybrid incompatibility genes: remnants of a genomic battlefield? Trends Genet. 2010;26:317–325. doi: 10.1016/j.tig.2010.04.005. [DOI] [PubMed] [Google Scholar]
- Kanizay LB, Pyhajarvi T, Lowry EG, Hufford MB, Peterson DG, Ross-Ibarra J, Dawe RK. Diversity and abundance of the abnormal chromosome 10 meiotic drive complex in Zea mays. Heredity. 2013;110:570–577. doi: 10.1038/hdy.2013.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly JK. Deleterious mutations and the genetic variance of male fitness components in Mimulus guttatus. Genetics. 2003;164:1071–1085. doi: 10.1093/genetics/164.3.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly JK, Willis J. Deleterious mutations and genetic variation for flower size in Mimulus guttatus. Evolution. 2001;55:937–942. doi: 10.1554/0014-3820(2001)055[0937:dmagvf]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Kelly JK, Willis JH. A manipulative experiment to estimate biparental inbreeding in monkeyflowers. Int J Plant Sci. 2002;163:575–579. [Google Scholar]
- Larracuente AM, Presgraves DC. The selfish Segregation Distorter gene complex of Drosophila melanogaster. Genetics. 2012;192:33–53. doi: 10.1534/genetics.112.141390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lekberg Y, Roskilly B, Hendrick MF, Zabinski CA, Barr CM, Fishman L. Phenotypic and genetic differentiation among yellow monkeyflower populations from thermal and non-thermal soils in Yellowstone National Park. Oecologia. 2012;170:111–122. doi: 10.1007/s00442-012-2297-9. [DOI] [PubMed] [Google Scholar]
- Llaurens V, Gonthier L, Billiard S. The sheltered genetic load linked to the S locus in plants: new insights From theoretical and empirical approaches in sporophytic self-incompatibility. Genetics. 2009;183:1105–1118. doi: 10.1534/genetics.109.102707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowry DB, Rockwood RC, Willis JH. Ecological reproductive isolation of coast and inland races of Mimulus guttatus. Evolution. 2008;62:2196–2214. doi: 10.1111/j.1558-5646.2008.00457.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyttle TW. Segregation distorters. Annu Rev Genet. 1991;25:511–557. doi: 10.1146/annurev.ge.25.120191.002455. [DOI] [PubMed] [Google Scholar]
- Malik HS, Henikoff S. Conflict begets complexity: the evolution of centromeres. Curr Opin Genet Devel. 2002;12:711–718. doi: 10.1016/s0959-437x(02)00351-9. [DOI] [PubMed] [Google Scholar]
- Manser A, Lindholm AK, König B, Bagheri HC. Polyandry and the decrease of a selfish genetic element in a wild house mouse population. Evolution. 2011;65:2435–2447. doi: 10.1111/j.1558-5646.2011.01336.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKee BD, Wilhelm K, Merrill C, Ren X. Male sterility and meiotic drive associated with sex chromosome rearrangements in Drosophila. Genetics. 1998;149:143–155. doi: 10.1093/genetics/149.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mojica JP, Kelly JK. Viability selection prior to trait expression is an essential component of natural selection. Proc R Soc Lond B. 2010;277:2945–2950. doi: 10.1098/rspb.2010.0568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mojica JP, Lee YW, Willis JH, Kelly JK. Spatially and temporally varying selection on intrapopulation quantitative trait loci for a life history trade-off in Mimulus guttatus. Mol Ecol. 2012;21:3718–3728. doi: 10.1111/j.1365-294X.2012.05662.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo-Manuel de Villena F, Sapienza C. Female meiosis drives karyotypic evolution in mammals. Genetics. 2001a;159:1179–1189. doi: 10.1093/genetics/159.3.1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo-Manuel de Villena F, Sapienza C. Nonrandom segregation during meiosis: the unfairness of females. Mamm Genome. 2001b;12:331–339. doi: 10.1007/s003350040003. [DOI] [PubMed] [Google Scholar]
- Patten MM. Meiotic drive influences the outcome of sexually antagonistic selection at a linked locus. J Evol Biol. 2014;27:2360–2370. doi: 10.1111/jeb.12493. [DOI] [PubMed] [Google Scholar]
- Prout T. How well does opposing selection maintain variation? In: Singh R, Krimbas CB, editors. Evolutionary genetics: from molecules to morphology. Cambridge Univ. Press; Cambridge, UK: 2000. pp. 157–181. [Google Scholar]
- Rhoades MM. Preferential segregation in maize. Genetics. 1942;27:395–407. doi: 10.1093/genetics/27.4.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson AW, Mountjoy C, Faulkner BE, Roberts MV, Macnair MR. Bumble bee selection of Mimulus guttatus flowers: the effects of pollen quality and reward depletion. Ecology. 1999;80:2594–2606. [Google Scholar]
- Scoville A, Lee YW, Willis JH, Kelly JK. Contribution of chromosomal polymorphisms to the G-matrix of Mimulus guttatus. New Phytol. 2009;183:803–815. doi: 10.1111/j.1469-8137.2009.02947.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scoville AG, Lee YW, Willis JH, Kelly JK. Explaining the heritability of an ecologically significant trait in terms of individual quantitative trait loci. Biol Lett. 2011;7:896–898. doi: 10.1098/rsbl.2011.0409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone JL. Sheltered load associated with S-alleles in Solanum carolinense. Heredity. 2004;92:335–342. doi: 10.1038/sj.hdy.6800425. [DOI] [PubMed] [Google Scholar]
- Sweigart A, Karoly K, Jones A, Willis JH. The distribution of individual inbreeding coefficients and pairwise relatedness in a population of Mimulus guttatus. Heredity. 1999;83:625–632. doi: 10.1038/sj.hdy.6886020. [DOI] [PubMed] [Google Scholar]
- Turner BC, Perkins DD. Spore killer, a chromosomal factor in Neurospora that kills meiotic products not containing it. Genetics. 1979;93:587–606. doi: 10.1093/genetics/93.3.587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedell N. The dynamic relationship between polyandry and selfish genetic elements. Phil Trans Roy Soc B. 2013;368:1–10. doi: 10.1098/rstb.2012.0049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willis JH. Partial self-fertilization and inbreeding depression in two populations of Mimulus guttatus. Heredity. 1993;71:145–154. [Google Scholar]
- Wu CA, Lowry DB, Cooley AM, Wright KM, Lee YW, Willis JH. Mimulus is an emerging model system for the integration of ecological and genomic studies. Heredity. 2007;100:220–230. doi: 10.1038/sj.hdy.6801018. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. The equilibrium frequency of the drive allele ( ) from equations (8)–(9) is depicted on the y-axis as a function of (top) the selection coefficient through female function (sF) and (bottom) the selection coefficient through female function (sM).
Table S1. For a collection of parameter sets with weak selection, we determined the exact equilibrium frequency of the drive allele ( ) and compared it to the approximation of equations (8)–(9).
Table S2. For a collection of parameter sets with selection through male function and meiotic drive held to empirical estimates (hF = hM = 0, sM = 0.2, δ = 0.58), we determined the exact equilibrium frequency of the drive allele ( ) and compared it to the approximation of equations (8)–(9).


