Abstract
Chemotherapy for non-small cell lung cancer (NSCLC) typically involves a doublet regimen for a number of cycles. For any particular patient, a course of treatment is usually chosen from a large number of combinational protocols with drugs in concomitant or sequential administration. In spite of newer drugs and protocols, half of patients with early disease will live less than five years and 95% of those with advanced disease survive for less than one year. Here, we apply mathematical modeling to simulate tumor response to multiple drug regimens, with the capability to assess maximum tolerated dose (MTD) as well as metronomic drug administration. We couple pharmacokinetic-pharmacodynamic intracellular multi-compartment models with a model of vascularized tumor growth, setting input parameters from in vitro data, and using the models to project potential response in vivo. This represents an initial step towards the development of a comprehensive virtual system to evaluate tumor response to combinatorial drug regimens, with the goal to more efficiently identify optimal course of treatment with patient tumor-specific data. We evaluate cisplatin and gemcitabine with clinically-relevant dosages, and simulate four treatment NSCLC scenarios combining MTD and metronomic therapy. This work thus establishes a framework for systematic evaluation of tumor response to combination chemotherapy. The results with the chosen parameter set indicate that although a metronomic regimen may provide advantage over MTD, the combination of these regimens may not necessarily offer improved response. Future model evaluation of chemotherapy possibilities may help to assess their potential value to obtain sustained NSCLC regression for particular patients, with the ultimate goal of optimizing multiple-drug chemotherapy regimens in clinical practice.
Keywords: Combination chemotherapy, lung cancer, mathematical modeling and computational simulation, gemcitabine and cisplatin, pharmacokinetics and pharmacodynamics
Graphical Abstract
1. Introduction
Non-small cell lung cancer (NSCLC) is a worldwide leading cause of death. About 85% of patients present with advanced (Stage IIIB or IV) disease, thus precluding curative surgery, while one-third of patients treated at early stages progress to unresectable advanced disease (Correale et al., 2006). Prognosis overall is poor, with 5-year survival rates being <50% for early and <5% for advanced disease, respectively (Non-Small Cell Lung Cancer Survival Rates, 2017). The recommendation for first-line chemotherapy for treating patients with advanced NSCLC is typically a two-drug (doublet) regimen, with cisplatin and gemcitabine being an established combination (Azzoli et al., 2009; Azzoli et al., 2011) that has shown significant reduction in overall mortality (Le Chevalier et al., 2005). Table 1 shows a sample of 21-day cycle regimens that have been evaluated for advanced disease, with response assessment after 1–2 cycles and then every 2–4 cycles. Cisplatin-based drug combinations are also employed as adjuvant chemotherapy for early (stage II/III) NSCLC following surgical resection, although the longer-term benefit is still debated (Artal Cortes et al., 2015; Tibaldi et al., 2009).
Table 1.
Sample 21-day course drug combination regimens for treating patients with advanced (Stage IIIB/IV) non-small cell lung cancer (NSCLC).
| Cisplatin | Gemcitabine | Reference |
|---|---|---|
| 75 mg/m2 (day 1) | 1250 mg/m2 (days 1 and 8) | (Lee et al., 2004; Network, 2013; Scagliotti et al., 2008; Vergnenegre et al., 2009) |
| 80 mg/m2 (day 1) | 1250 mg/m2 (days 1 and 8) | (Brodowicz et al., 2006; Perol et al., 2012) |
| 100 mg/m2 (day 1) | 1250 mg/m2 (days 1 and 8) | (Cardenal et al., 1999) |
| 75 mg/m2 (day 8) | 1250 mg/m2 (days 1 and 8) | (Akcali et al., 2008) |
The molecular pharmacology of gemcitabine (2′,2;-difluoro 2′-deoxycytidine, dFdC) is complex. Deoxycytidine kinase intracellularly phosphorylates gemcitabine to gemcitabine monophosphate (dFdCMP), which is converted to the active metabolites gemcitabine diphosphate (dFdCDP) and triphosphate (dFdCTP) (Heinemann et al., 1988). Cytotoxic mechanisms include incorporation of dFdCTP into DNA, which terminates chain elongation (Huang et al., 1991), as well as inhibition of DNA polymerase (Gandhi and Plunkett, 1990). Drug activity is enhanced by dFdCDP hindering the synthesis of deoxyribonucleotides competing with dFdCTP as substrates for DNA incorporation (Baker et al., 1991; Heinemann et al., 1990). The metabolites inhibit cytidine triphosphate synthetase (CTP synthetase) (Heinemann et al, 1995) and deoxycytidylate deaminase (dCMP deaminase) (Heinemann et al, 1992) while enhancing gemcitabine phosphorylation by decreasing inhibition of deoxycytidine kinase (Xu and Plunkett, 1990). Consequently, the active metabolites self-potentiate their intracellular accumulation for extended availability to impair DNA synthesis and its repair (Heinemann et al., 1992). The drug is inactivated mainly by deoxycytidine deaminase (Heinemann et al., 1992), and the resulting deaminated metabolite (2′,2′-difluorodeoxyuridine, dFdU) in turn may modulate the rate of gemcitabine transport and intracellular phosphorylation via deoxycytidine kinase (Hodge et al., 2011). In the case of cisplatin (cis-diamminedichloroplatinum(II), CDDP), its chloride atoms are displaced by water molecules in the cell cytosol. The hydrolyzed product reacts with nucleophiles, such as nucleic acid nitrogen donor atoms and protein sulfhydryl groups. The product binds to the N7 reactive center on purine residues, which induces DNA damage including 1,2-intrastrand cross-links such as 1,2-intrastrand d(GpG) and 1,2-intrastrand d(ApG) adducts (Sinek et al., 2009). The high mobility group (HMG)-domain proteins HMG1 and human mitochondrial transcription factor can then specifically inhibit the DNA adduct repair by human excision nuclease (Huang et al., 1994).
Traditional chemotherapy targets single cancer cell populations with drug doses and administration frequencies determined by the maximum tolerated dose (MTD) (as illustrated by Table 1) to avoid lethal patient toxicity. However, a single-target MTD approach may be unable to target other components within the tumor system. A lung tumor is a complex multicellular tissue, and interactions between different cell types and their environment may become even more complex upon treatment. Components contributing to the tumor growth and treatment response include cancer and vascular endothelial cells, immune system and stromal cells, extracellular matrix, and the cellular microenvironment. Interactions within the tissue occur across a wide range of physical scales, from the molecular (nanometer) to the tissue (centimeter) scale. These components and their interactions can significantly affect cancer cell survival and eventually lead to the emergence of drug resistance.
Previous work has shown that a regimen of drugs that under an MTD approach would typically trigger resistance in lung cancer may actually be therapeutically effective when administered metronomically (Francia et al., 2012; Pratt et al., 2013). Metronomic chemotherapy was originally developed to affect vascular endothelial cells through doses lower than MTD (Klement et al., 2000). The combination of low-dose metronomic chemotherapies simultaneously targeted to multiple cancer tissue components, such as tumor cells and vascular endothelial cells, has been shown to deliver treatment with lower systemic toxicity while avoiding the emergence of drug resistance (Bertolini et al., 2003; Stolting et al., 2004). In addition to anti-angiogenesis, metronomic chemotherapy for certain drugs has been shown to stimulate immune-suppressive immunity (Lutsiak et al., 2005), induce cancer dormancy (Bahl and Bakhshi, 2012), and promote cancer cell senescence (Ewald et al., 2010).
The large number of combinational protocols specifying the targeting of multiple tumor cell populations and their microenvironment by chemotherapeutic agents in concomitant or sequential administration may preclude determination of potential clinical options solely through empirical determination. This assessment would benefit from methods and principles typically used in systems analysis. In (Traina et al., 2010), a mathematical method was derived from the Gompertz equation (Gompertz, 1825) to define a drug dosing schedule in xenograft models based upon maximal efficacy instead of maximal tolerable toxicity. The method, inspired by Norton-Simon modeling (Norton et al., 1976), was applied to the design and analysis of preclinical data to forecast the dosing schedule. In (Hadjiandreou and Mitsis, 2014) the effects of drugs on tumor progression in mice were modeled using a Gompertz-type growth law, and optimal therapeutic patterns were explored. The in vivo response of pancreatic tumors treated with gemcitabine was simulated in (Lee et al., 2013) and of Non-Hodgkin’s lymphoma treated with doxorubicin in.(Frieboes et al., 2015). The combination of gemcitabine with non-invasive radio frequency radiation to treat pancreatic cancer has also been modeled (Ware et al., 2017). MTD and metronomic regimens were compared in (André et al., 2013) with a theoretical tumor model evaluated in a radially-symmetric configuration, while chemotherapy protocols obtained with the methods of optimal control were reviewed in (Ledzewicz and Schättler, 2014). Recently, the usefulness of mathematical modeling in designing drug regimens was reviewed in (Barbolosi et al., 2016), and modeling results specific to metronomic chemotherapy were evaluated in (Ledzewicz and Schattler, 2017). Mathematical modeling has also lent support to the concept of designing different chemotherapeutic schedules for tumors with different growth rates (West and Newton, 2017). In particular, low-dose, high-density metronomic strategies were predicted to outperform MTD therapy, especially for fast growing tumors. The modeling work to date highlights the critical need to further elucidate the relative performance of single and multi-drug regimens, metronomic and MTD strategies, and their combinations. In this study, we integrate mathematical modeling of vascularized tumor tissue with drug-specific pharmacokinetic components to evaluate response to multiple drug regimens, providing the capability to assess MTD as well as metronomic drug administration. Thus, this work represents an initial step towards the development of a comprehensive virtual system to more efficiently evaluate patient tumor-specific pharmacokinetics (PK) and pharmacodynamics (PD).
Previous work by Sinek et al. (Sinek et al., 2009) computationally evaluated intracellular pharmacokinetics and pharmacodynamics of two common chemotherapeutic drugs, cisplatin and doxorubicin in a vascularized tumor model incorporating morphological and vascular structural heterogeneity along with PK determinants simulating P-glycoprotein (Pgp) efflux and tumor tissue density. This work established a multi-compartment PK-PD model rigorously calibrated from published experimental data to simulate systemic drug bolus administration in heterogeneous tumor tissue, showing that the associated intratumoral nutrient and drug distribution may significantly hinder therapeutic efficacy. Battaglia et al. (Battaglia Jr. and Parker, 2011) developed a detailed intracellular mathematical model describing the pharmacokinetics of gemcitabine and linked it to a systemic plasma gemcitabine PK model. A simplified cell-cycle model was used for pharmacodynamic effect, with predictions based on PK parameter values calibrated from clinical data. The kinetic properties of gemcitabine triphosphate were estimated from previously published in vitro data. The detailed intracellular model coupled with the systemic PK model and the cell-cycle model was simulated to predict gemcitabine triphosphate concentrations in the plasma and intracellular compartments.
We build upon these PK models to simulate multiple chemotherapy for lung cancer, coupling PK-PD intracellular multi-compartment models with a vascularized tumor growth model (Macklin et al., 2009; van de Ven et al., 2012; Wu et al., 2013). Based on dosages used clinically, we illustrate the system’s capability by simulating four hypothetical treatment scenarios combining MTD and metronomic approaches as described in Table 2. The drugs are administered to a representative lesion ~750μm in diameter, and the effects are measured for 15 days post treatment initiation.
Table 2.
Treatment scenarios simulated in this study with a system that integrates PK-PD intracellular multi-compartment models with a vascularized tumor growth model.
| Scenario | Chemotherapy Description |
|---|---|
| Case 1 | MTD for both cisplatin and gemcitabine |
| Case 2 | Metronomic cisplatin and gemcitabine at MTD |
| Case 3 | Cisplatin at MTD and metronomic gemcitabine |
| Case 4 | Metronomic for both cisplatin and gemcitabine |
2. Materials and Methods
The vascularized tumor model builds upon (van de Ven et al., 2012; Wu et al., 2013; Wu et al., 2014) to simulate viable, hypoxic and necrotic tumor tissue in a 2D coordinate system. Initially, the tumor is small (~25 μm radius) seeded in the middle of a pre-existing grid representing regularly-spaced blood vessel capillaries. The grid in the vicinity of the growing tumor is remodeled in time via angiogenesis into a more random distribution of vessels, which in turn makes the tumor progression heterogeneous. Tissue growth, i.e., proliferation as a function of cells cycling, and tissue death, i.e., necrosis as a function of low oxygen, are described via conservation of mass equations. Diffusion of small molecules, such as oxygen, cell nutrients, and drug are combined with the conservation of mass equations to a reaction-diffusion equation. The proliferation and death rate constants are a function of the availability of oxygen, nutrients, and drug, and their values vary heterogeneously in time and through the space occupied by the tumor and the surrounding tissue.
2.1 Tumor Growth
The tumor component denotes the tumor tissue by Ω and its boundary by Σ, as described in (Macklin et al., 2009). In regions ΩP of sufficient oxygen and nutrients, the tumor tissue is proliferating, while in regions ΩH, in which oxygen and nutrients are sufficient for survival but not for proliferation, the tissue becomes hypoxic. In regions ΩN, where oxygen and nutrients are insufficient for survival, the tissue turns necrotic. A generalized Darcy’s law implements the non-dimensionalized tumor growth velocity (Macklin et al., 2009):
| (1) |
where the net effects of cell-cell and cell-matrix adhesion are represented by the cell mobility μ, the oncotic pressure is P, cell haptotaxis is χE, and ECM density is E. Definitions for χE and E are in (Macklin et al., 2009). The tumor growth can be associated with the rate of volume change by assuming that the cell density in the proliferating region is constant:
| (2) |
where the non-dimensional net proliferation rate is λp (see below).
2.2 Angiogenesis
The angiogenesis component simulates the model by (McDougall et al., 2006) and is based on (Macklin et al., 2009; Wu et al., 2013). Coupled with the tumor component, the growing tumor tissue within the vascularized microenvironment is subject to heterogeneous access to oxygen, nutrients, and drugs diffusing from the vasculature. The heterogeneity is influenced by the oncotic pressure and the distance from the nearest vascular source.
Non-small cell lung tumors can be characterized by heterogeneous vascularization, as shown previously for specific clinical samples (Schor et al., 1998), with highest microvascular density at the tumor periphery and lower density towards the core. Accordingly, the vascular model here (as developed by (Wu et al., 2013)) represents the microvasculature surrounding the tumor as a grid-like network from which angiogenesis-stimulated vessels sprout and fuse with each other as they grow towards the tumor (Bartha and Rieger, 2006; Lee et al., 2006; Welter and Rieger, 2010; Welter et al., 2008; Welter et al., 2009), generating higher vascular density at the tumor periphery than in the interior. The resulting capillary pattern has been shown to adequately represent the typical heterogeneous vascularization resulting from tumor progression (Welter et al., 2009).
The angiogenesis process is driven by tumor angiogenic factors (TAF) released by the hypoxic tissue regions (Macklin et al., 2009; Wu et al., 2013):
| (3) |
The TAF T diffuse through the tissue with coefficient DT, are produced in the tumor hypoxic region with a rate , bind to the surrounding capillary vessels with a rate , are taken up by the ECM (with density E) with a rate , and decay with a rate . The characteristic function for the host tissue is 1ΩH, and for the vasculature it is 1vessel, which equals 1 at host or vessel locations, respectively, and 0 otherwise.
2.3 Transport of Oxygen and Nutrients
The transport of oxygen and nutrients σ through the tissue with a diffusive coefficient Dσ is simulated upon extravasation from the neo- and pre-existing vasculature with rates and , respectively. Oxygen and nutrients are taken up by host and proliferating tumor cells with respective rates and , with rate λσ = qs in the hypoxic region, and decay with rate in the necrotic region. The formulation for the transport assuming steady-state conditions is as follows (Macklin et al., 2009; van de Ven et al., 2012; Wu et al., 2013; Wu et al., 2014):
| (4) |
Here, spatial position of the oxygen and nutrients is x, time is t, the interstitial pressure is pi, and the hematocrit in the vascular network is h. Extravasation is modulated by the extravascular interstitial pressure pi scaled by the effective pressure pe, with kpi as the weight of convective transport for small molecules (van de Ven et al., 2012):
| (5) |
Minimum and normal blood hematocrit required for oxygen extravasation are represented by constants h̄min and H̄D, respectively, while is the constant transfer rate from pre-existing and tumor-induced vessels.
The boundary condition for all the diffusion equations is (zero Neumann condition), where C is the diffusing element.
2.4 Tumor Parameter Values
The tumor model proliferation, necrosis, hypoxic, and oxygen parameters are first tuned so that the growth rate in avascular conditions matches an experimentally observed rate for tumor spheroids in vitro (see below). The vascularized growth is then simulated with these calibrated parameters. The main tumor model parameters and their associated values are shown in Table 3. The numerical implementation for the tumor and angiogenesis models is described in detail in (Wu et al., 2013) and references therein.
Table 3.
Main tumor model parameters and their associated values. All other tumor-related parameters are as in (Wu et al., 2013).
| Parameter | Value | Reference |
|---|---|---|
| Tumor proliferation rate | 1 day−1 | (Curtis et al., 2016) |
| Tumor necrosis threshold | 0.5700 | (van de Ven et al., 2012) |
| Tumor hypoxic threshold | 0.5750 | (van de Ven et al., 2012) |
| Oxygen diffusivity | 1 (a) | (Wu et al., 2013) |
| Oxygen transfer rate from vasculature | 5 (a) | (Wu et al., 2013) |
| Oxygen uptake rate by proliferating tumor cells | 1.5 (a) | (Wu et al., 2013) |
| Oxygen uptake rate by hypoxic tumor cells | 1.3 (a) | (Wu et al., 2013) |
| Oxygen uptake rate by tumor microenvironment | 0.12 (a) | (Wu et al., 2013) |
| Oxygen decay rate | 0.35 (a) | (Wu et al., 2013) |
| CDDP drug effect | 2.7E5 | Calibrated to data in (Curtis et al., 2016) |
| CDDP decay rate | 0.5hr half-life | (Leighl, 2012) |
| CDDP in vitro IC50 (48 hrs.) for A549 cells (spheroid) | 26.6 μM | (Curtis et al., 2016) |
| CDDP diffusivity | 0.5 (a) | (Sinek et al., 2009) |
| dFdC drug effect | 1.6E4 | Calibrated to data in (Chougule et al., 2011) and (Godugu et al., 2013) |
| dFdC decay rate | 1.0hr half-life (average) for short (<70 min) infusion | (Eli Lilly, 2017) |
| dFdC in vitro IC50 (72 hrs.) for A549 cells (spheroid) | 77.5 μM | (Chougule et al., 2011) and (Godugu et al., 2013) |
| dFdC diffusivity | 0.5 (a) | (b) |
Value is rescaled by the square of the simulation system characteristic length (1 cm) and divided by the system characteristic time (1 sec) multiplied by the oxygen diffusivity (Nugent and Jain, 1984) (1 × 10−5 cm2 s−1). CDDP: cisplatin; dFdC: gemcitabine.
Assumed as a first approximation due to molecular weight and hydrophilicity to be comparable to CDDP.
2.5 Pharmacokinetic Modeling
The PK models for specific drugs are applied to the above-described tumor growth model coupled with angiogenesis in order to evaluate the varying kinetics. The PK model for cisplatin was adapted from Sinek et al. 2009 (Sinek et al., 2009) and the PK model for gemcitabine was adapted from Battaglia et al. 2010 (Battaglia Jr. and Parker, 2011). The corresponding equations are as follows.
For cisplatin (CDDP):
| (6) |
| (7) |
| (8) |
| (9) |
For gemcitabine (dFdC):
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
The drug concentration in each compartment is represented by s, where s1 is the extracellular compartment, s2 is the intracellular compartment, s2a is an activated intracellular state (specific to dFdC), s3 is the DNA-bound state, s4 is the intracellular organelle compartment, and sm is the drug-DNA capacity. Rate kij represents a transfer from compartment i to j, and ki represents a rate of permanent removal from compartment i and the system, while K12 and K2a are scaling values specific to dFdC. Vc is the volume of a cell, F is the extracellular fraction of whole tissue, D(t) represents the bolus injection of drug into the vessels, and Ds is drug diffusivity. The dFdC uptake is V12 and the activation rate is V2a. Units for the extracellular concentration of drug (μM) are converted to fmoles/cell for the compartments that use VC (Sinek et al., 2009).
2.6 Pharmacodynamic Modeling
Following (Wu et al., 2014), it is assumed that the net tumor proliferation rate λp is proportional to the local level of oxygen and nutrients present. This rate is modulated by the rate of drug-induced death, λ̄CDDP for CDDP and λ̄dFdC for dFdC, which may be administered together (Azzoli et al., 2009; Azzoli et al., 2011). The values for these parameters were determined by simulating an avascular tumor spheroid exposed to concentrations of each respective drug (see Results), and as previously reported (Curtis et al., 2016). Only drug that reaches the DNA-bound compartment (s3,CDDP & s3,dFdC) is assumed to exert a cytotoxic effect. Accordingly, the PD model is as follows:
| (15) |
In order to simulate the cell-cycle dependent effects of CDDP and dFdC, the drugs are assumed to only affect proliferating cells. The term λM is the mitosis rate, λA is the apoptosis rate, and λN is the rate of volume loss in the necrotic regions assuming that cellular debris is constantly degraded and the resulting fluid is removed. In the equation, we include the effect of accumulated DNA-bound drug by summing the local drug concentrations during the time td that the drug is exerting its effect. When this effect is less than or equal to 1, the net proliferation is reduced, and when it exceeds 1, cell death is introduced and contributes to tumor regression. The time step of the summation is the time step of the simulation. For simplicity, it is assumed that there is no interaction between the two drug effects. The time of effect td is assumed to be 24 hours, matching typical cell-cycle duration. Finally, to incorporate the potential anti-angiogenic effect of the chemotherapy regimens, the angiogenesis process is halted during the simulated treatment phase.
2.7 Coupling of the Models
The drug is injected into the tumor system at the lower left corner of the vascular grid and flows towards the upper right (see Results). The PK and PD model equations are solved at all time at each spatial grid point corresponding to the tumor tissue, with the net proliferation rate λp in Equation 15 driving the tumor velocity in Equation 2. As the tumor boundary updates during growth, the drug distribution is updated to eliminate drug no longer contained within viable tumor regions. If the tissue turns necrotic, all intracellular and DNA-bound drugs in these regions are eliminated. Current system implementation presents limitations in terms of numerical calculations when the tumor size approaches that of the spatial boundary, and thus for all cases the simulations were run through day 15 post treatment initiation.
2.8 Sensitivity Analysis
The parameter values for the vascularized tumor model were first set consistent with the previous modeling work (as indicated by the references listed in Table 3) to enable simulation of a vascularized tumor lesion with realistic growth and vascularization patterns (Curtis et al., 2016; Macklin et al., 2009; McDougall et al., 2006; van de Ven et al., 2012; Wu et al., 2013). A parametric sensitivity analysis was then performed to evaluate which pharmacokinetic parameters contribute to output variability in this vascularized system. Each pharmacokinetic parameter was varied by 10-fold of its unperturbed value while holding the other parameters constant (parameters representing cell volume, interstitial fraction, drug diffusivity, and drug-DNA capacity were not varied). The resulting change in the net tumor proliferation rate, λp, was measured as a percent change from its value based on unperturbed parameters. Using Case 1 for this analysis (MTD for both CDDP and dFdC), the pharmacokinetic equations were solved iteratively at the end of infusion for each drug, i.e., CDDP at 120 min and dFdC at 30 min.
3. Results
3.1 Initial Tumor Growth
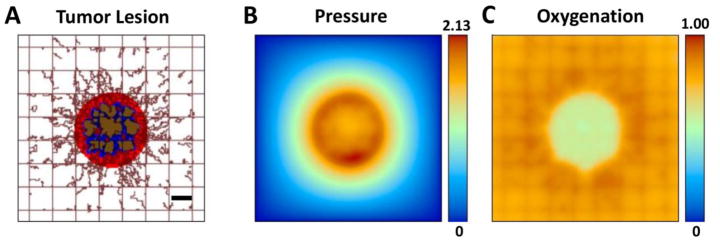
The simulated tumor begins as an avascular nodule within the capillary grid. As the tumor expands, three identifiable tissue regions are developed within: proliferating tissue in well-vascularized areas; necrotic tissue located away from vasculature; hypoxic tissue located between the necrotic and viable regions based on distance from the oxygen-releasing vasculature. Figure 1 shows a simulated tumor lesion right before treatment at day 18 after inception. Pre-existing vessels are in a regular grid with vessels located every 250 μm along each dimension, establishing normoxic conditions to the surrounding tissue, as previously simulated (Curtis et al., 2016; van de Ven et al., 2012; Wu et al., 2013; Wu et al., 2014). Irregular vessels sprout from the pre-existing vasculature in response to angiogenic stimuli released by the hypoxic regions. The tumor pressure and oxygen profiles corresponding to this stage of growth are also shown in Figure 1.
Figure 1.
Simulated NSCLC tumor prior to treatment. (A) Lesion (center) is shown with surrounding capillaries (brown lines). Red: Viable (proliferating) tissue; blue: hypoxic (quiescent) tissue; brown: necrotic (dead) tissue. Existing capillary grid is denoted by regularly spaced lines, with vessels induced by angiogenesis, irregularly growing towards the tumor, attracted by angiogenic stimuli diffusing from the hypoxic regions. Host tissue (not shown) surrounds the lesion. (B) Pressure profile (non-dimensional values) corresponding to the growing tumor lesion, with highest values (red) in the proliferating ring and lowest values (blue) in the host. (C) Oxygen concentration profile (maximum value normalized by the concentration in vasculature) is determined by diffusion from the vasculature into the hypoxic and necrotic tumor regions. Bar, 250 μm. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2 Pharmacokinetic Model Calibration
The values for the parameters of the PK models of CDDP and dFdC are taken from the pioneering work by Sinek et al. 2009 (Sinek et al., 2009) and Battaglia et al. 2010 (Battaglia Jr. and Parker, 2011), respectively, which calculated a comprehensive set of values grounded in experimental measurements with these drugs. The parameters with their corresponding values as used in this study are described in Tables 4 and 5.
Table 4.
Pharmacokinetic parameters for CDDP (from (Sinek et al., 2009) and associated references).
| Parameter | Description | Value |
|---|---|---|
| VC | Cell volume (fL cell−1) | 520 |
| F | Interstitial Fraction | 0.48 |
| DS | Drug diffusivity (μm2 min−1) | 30E3 |
| k1 | Plasma elimination rate (min−1) | 2.77E-2 |
| k12 | Drug uptake (min−1) | 0.054 |
| k21 | Drug efflux (min−1) | 1.56E-3 |
| k23 | Drug-DNA binding (min−1) | 3.82E-4 |
| k32 | Drug-DNA release (min−1) | 0 |
| k3 | Drug-DNA repair (min−1) | 0.015 |
| k24 | Lysosomal sequestration (min−1) | 0 |
| k42 | Lysosomal release (min−1) | 0 |
| sm | Drug-DNA capacity (fmole) | ∞ |
Table 5.
Pharmacokinetic parameters for dFdC (from (Battaglia Jr. and Parker, 2011) and associated references).
| Parameter | Description | Value |
|---|---|---|
| VC | Cell volume (fL cell−1) (a) | 520 |
| F | Interstitial Fraction (a) | 0.48 |
| DS | Drug diffusivity (μm2 min−1) (a) | 30E3 |
| k1 | Plasma elimination rate (min−1) | 1.16E-2 |
| V12 | Drug uptake (μM min−1) | 55.7 |
| K12 | Half-maximum transport conc. (μM) | 5.2 |
| k21 | Drug efflux (min−1) | 0 |
| k2 | Inactivation rate (min−1) | 1.7 |
| V2a | Activation rate (μM min−1) | 7.7 |
| K2a | Half maximum activation conc. (μM) | 2.5 |
| k2a3 | Drug-DNA binding (min−1) | 5.7E-3 |
| k32 | Drug-DNA release (min−1) | 0 |
| k3 | Drug-DNA repair (min−1) | 0 |
| k24 | Lysosomal sequestration (min−1) | 0 |
| k42 | Lysosomal release (min−1) | 0 |
| sm | Drug-DNA capacity (fmole) | ∞ |
Assumed consistent with cisplatin (from (Sinek et al., 2009)).
3.3 Pharmacodynamic Model Calibration
To calibrate the parameters of the PD model, we first grow a simulated in vitro avascular tumor to ~500 μm diameter with no vessels penetrating the tumor and with higher oxygen and nutrient diffusivity in the surrounding environment to mimic cell culture conditions in which spheroids are grown surrounded with plentiful medium, as in a liquid overlay suspension. The simulated spheroid develops a proliferating region of thickness ~200 μm enclosing a hypoxic region ~50 μm and a necrotic core about ~200 μm in diameter, matching typical experimental observations with these 3D cell cultures (e.g., as in our previous work ). The rates of drug-induced death λ̄CDDP for CDDP and λ̄dFdC for dFdC are tuned so that the respective drug concentration applied to the simulated spheroid reduces its size to match experimental measurements with each one of these drugs. This allows approximating the drug strength when modeling treatment administered systemically to vascularized tumors simulating in vivo conditions (Curtis et al., 2016).
We exposed the simulated avascular tumor to an inhibitory concentration of CDDP (26.6+/−3.0 μM) previously measured experimentally to achieve a 50% tumor reduction (the “IC50”) over 48 h for A549 lung adenocarcinoma spheroids (Curtis et al., 2016), obtaining a value of 2.7E5 for λ̄CDDP. For dFdC, it was previously experimentally observed that a concentration of 0.6+/− 0.2 ug/mL (2.28 uM) achieved the IC50 over 72 h for A549 cells in monolayer culture (Chougule et al., 2011). It has been further observed that the IC50 for A549 cells could be as much as 34x higher for spheroids exposed to dFdC over 72 h than in monolayer (Godugu et al., 2013), which we translate as 77.5 uM representing an upper bound value of drug concentration. The corresponding λ̄dFdC value for simulated 72 h avascular tumor exposure was 1.6E4.
3.4 Simulation of Chemotherapy
Four treatment regimens as specified in Table 6 were simulated with the combined model. Case 1 represents a conventional combinational therapy of CDDP 75 mg/m2 on day 1 and dFdC 1250 mg/m2 on days 1 and 8 (Lee et al., 2004; Network, 2013; Scagliotti et al., 2008; Vergnenegre et al., 2009) (first case in Table 1). Case 2 is standard dFdC with metronomic CDDP therapy (30 mg/m2 on days 1, 8, and 14) (Correale et al., 2006). Case 3 is standard CDDP with metronomic dFdC therapy (250 mg/m2 daily) (Francia et al., 2012). Finally, case 4 is metronomic dosing of both CDDP and dFdC. Table 6 summarizes the treatment regimens.
Table 6.
Specification of the four simulated chemotherapy regimens for a typical adult combining CDDP and dFdC following established clinical protocols for a 21-day treatment cycle.
| Day 1 | Days 2–7 | Day 8 | Days 9–13 | Day 14 | Days 15–21 | ||||
|---|---|---|---|---|---|---|---|---|---|
| (mg/m2) | CDDP | dFdC | dFdC | CDDP | dFdC | dFdC | CDDP | dFdC | dFdC |
| Case 1 | 75 | 1250 | 1250 | ||||||
| Case 2 | 30 | 1250 | 30 | 1250 | 30 | ||||
| Case 3 | 75 | 250 | 250 | 250 | 250 | 250 | 250 | ||
| Case 4 | 30 | 250 | 250 | 30 | 250 | 250 | 30 | 250 | 250 |
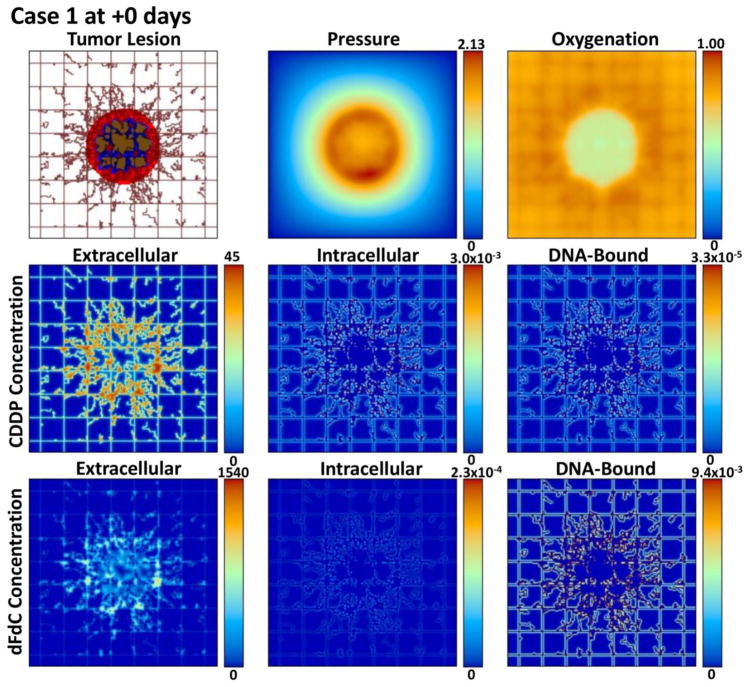
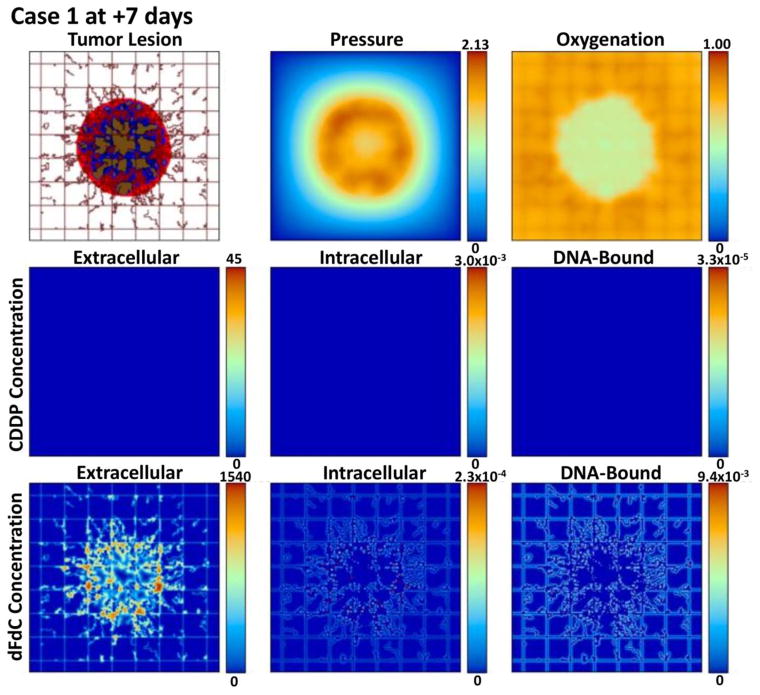
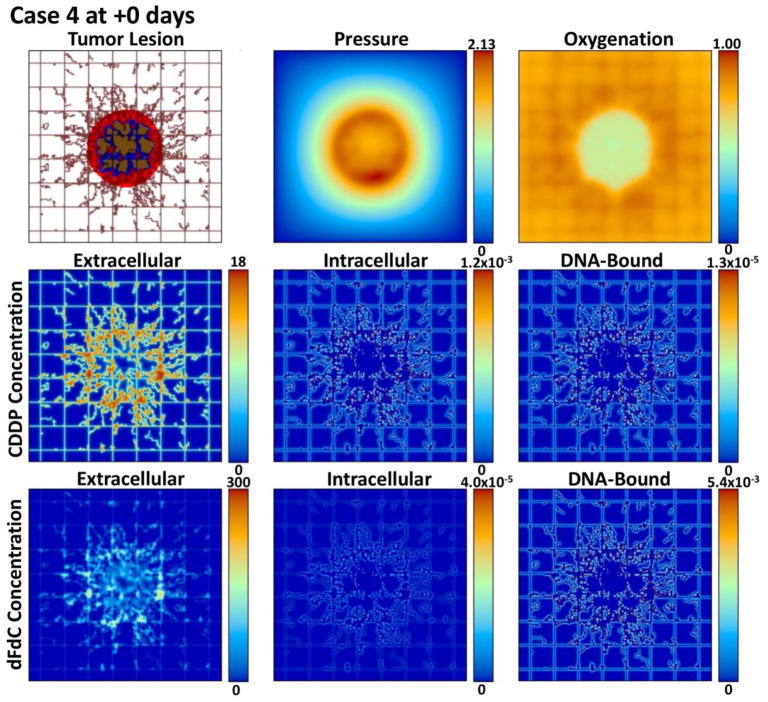
Figures 2, 3, 4, and 5 provide a qualitative assessment of the tumor and the associated CDDP and dFdC drug concentrations in the extracellular, intracellular, and DNA-bound compartments immediately after the start of treatment and after 7 days for cases 1 and 4. As expected, the extracellular drug peaks in the vicinity of the blood vasculature, while the intracellular and DNA-bound values are highest for the tissue surrounding the vasculature. The dFdC extracellular concentration is comparable between the two cases on days 1 and 8 due to the second weekly dosing with this drug. On the other hand, while the extracellular CDDP has completely washed out for case 1 by day 8 since there is no weekly bolus, case 4 reflects the next CDDP bolus of the lower-dose metronomic regimen. Cases 2 and 3 reveal the same observations as cases 1 and 4 for the respective drug dosages (not shown).
Figure 2.
Case 1 (standard CDDP and dFdC) on day 1 of treatment immediately after drug injection. The drug concentrations are shown for the extracellular (μM), intracellular (fMoles/cell), and DNA-bound (fMoles/cell) compartments as defined at this timepoint by the corresponding pharmacokinetic equations.
Figure 3.
Case 1 (standard CDDP and dFdC) after 7 days post treatment initiation. The drug concentrations are shown for the extracellular (μM), intracellular (fMoles/cell), and DNA-bound (fMoles/cell) compartments as defined at this timepoint by the corresponding pharmacokinetic equations. While the proliferation region has shrunk compared to day 1, the overall tumor is larger. The dFdC extracellular concentration reflects the second dose at this timepoint.
Figure 4.
Case 4 (metronomic CDDP and dFdC) on day 1 of treatment immediately after drug injection. The drug concentrations are shown for the extracellular (μM), intracellular (fMoles/cell), and DNA-bound (fMoles/cell) compartments as defined at this timepoint by the corresponding pharmacokinetic equations.
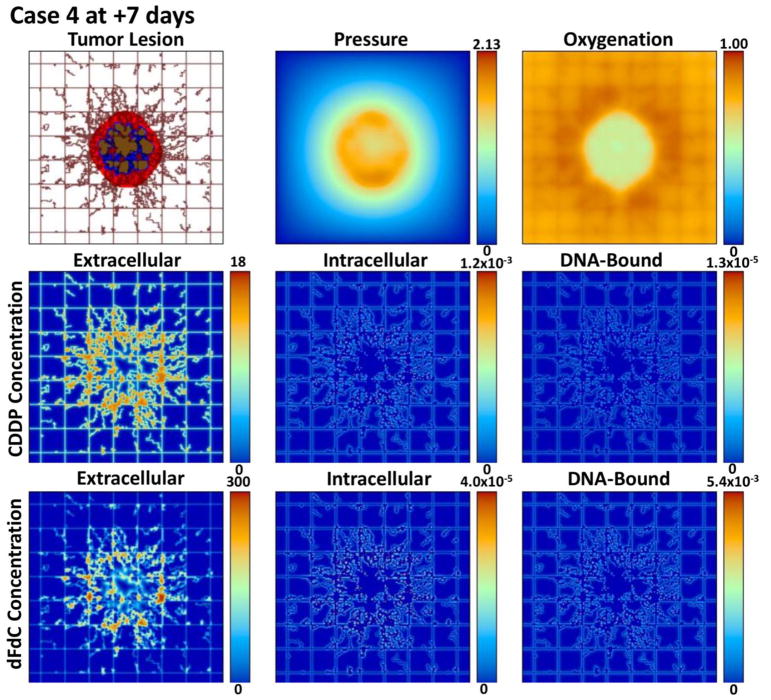
Figure 5.
Case 4 (metronomic CDDP and dFdC) after 7 days post treatment initiation. The drug concentrations are shown for the extracellular (μM), intracellular (fMoles/cell), and DNA-bound (fMoles/cell) compartments as defined at this timepoint by the corresponding pharmacokinetic equations. While the proliferation region is comparable to day 1, the overall tumor is smaller. The dFdC extracellular concentration reflects the second dose at this timepoint.
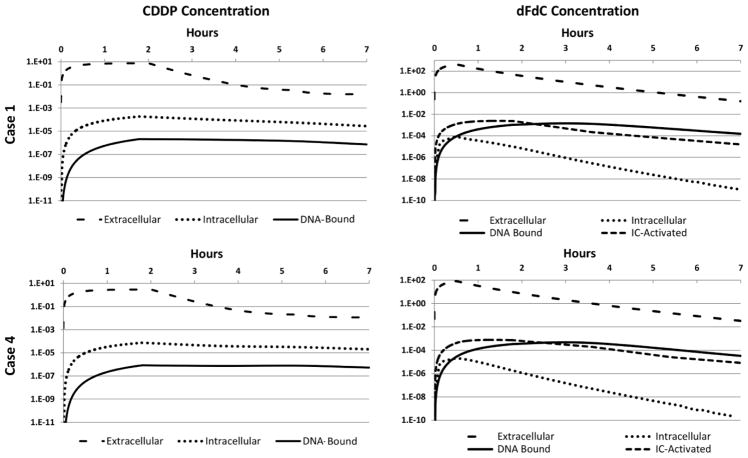
Figure 6 shows the average concentration of drug in each pharmacokinetic compartment over the course of 7 hours following treatment for cases 1 and 4, reflecting the four possible drug dosage combinations specified in Table 6. As expected for CDDP due to its pharmacokinetics, the extracellular concentrations consistently exceed the intracellular levels by at least one order of magnitude, which in turn exceed the DNA-bound drug by about one-half order of magnitude. The dFdC case, in contrast, displays higher DNA-bound than intracellular concentration starting 0.5 h post treatment initiation. This is due to longer term high dFdC availability for DNA binding through its rapid intracellular conversion to the active metabolites dFdCDP and dFdCTP by deoxycytidine kinase (Mini et al., 2006). The DNA-bound concentration also becomes higher than the intracellularly-activated value by 2.5 h after treatment. The peak average concentrations in each compartment after treatment initiation are summarized for each case in Table 7.
Figure 6.
Average concentrations of CDDP (left column) and dFdC (right column) over 7 hours following treatment initiation for Cases 1 (top row) and 4 (bottom row). Values are shown for the extracellular (μM), intracellular (fMoles/cell), DNA-Bound (fMoles/cell), and intracellularly-activated (IC-Activated, specific to dFdC) (fMoles/cell) compartments. Note that Cases 2 and 3 combine these same concentrations, as specified in Table 6.
Table 7.
Peak average drug concentration in each compartment for each regimen after treatment initiation. All CDDP concentrations peaked at 1.8 hr post injection, while for dFdC, the peaks were at 0.5 hr for the extracellular and intracellular compartments, and at 1.3 hr and 2.7 hr for the intracellularly-activated (IC-Activated) and DNA-Bound compartments, respectively.
| Peak Average Drug Concentration | |||||||
|---|---|---|---|---|---|---|---|
| CDDP | dFdC | ||||||
| Extracellular (μM) |
Intracellular (fMoles/cell) |
DNA-Bound (fMoles/cell) |
Extracellular (μM) |
Intracellular (fMoles/cell) |
IC-Activated (fMoles/cell) |
DNA-Bound (fMoles/cell) |
|
| Case 1 | 7.44 | 1.84×10−4 | 2.08×10−6 | 429 | 1.34×10−4 | 2.43×10−3 | 1.28×10−3 |
|
| |||||||
| Case 2 | 2.97 | 0.73×10−4 | 0.83×10−6 | 429 | 1.34×10−4 | 2.43×10−3 | 1.28×10−3 |
|
| |||||||
| Case 3 | 7.44 | 1.84×10−4 | 2.08×10−6 | 84 | 0.32×10−4 | 0.77×10−3 | 0.41×10−3 |
|
| |||||||
| Case 4 | 2.97 | 0.73×10−4 | 0.83×10−6 | 84 | 0.32×10−4 | 0.77×10−3 | 0.41×10−3 |
3.5 Evaluation of Tumor Response
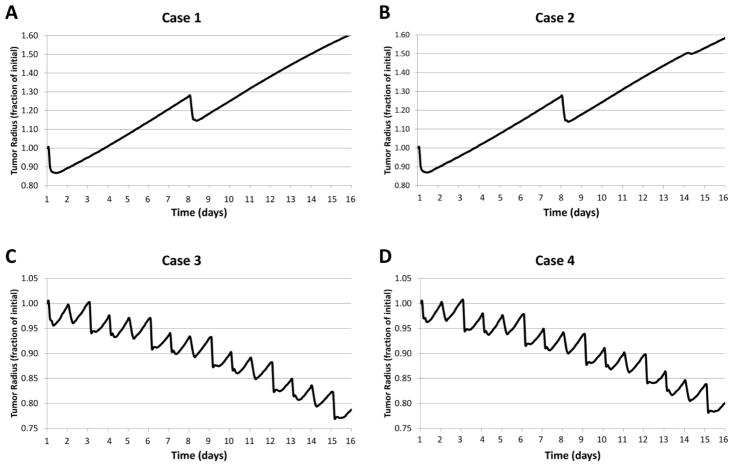
The simulated outcome for the four treatment regimens is shown in Figure 7. Over the course of 15 days, cases 3 and 4 are more effective at reducing the tumor as a fraction of the initial size than cases 1 and 2. The higher dFdC standard dosing on days 1 and 8 for cases 1 and 2 leads to a transient reduction in tumor burden, while the overall tumor growth resumes minimally affected by the CDDP standard or metronomic dosing. In contrast, the dFdC metronomic dosing for cases 3 and 4 leads to a sustained reduction in tumor burden, and with minimal contribution by either the CDDP standard or metronomic dosing. The difference between the MTD and metronomic regimens with dFdC highlights the trade-off between dosage and dose frequency, with the more frequent lower dosage being more effective.
Figure 7.
Time evolution of the tumor radius as a fraction of initial size for each treatment scenario.
To further compare the effect of the various regimens, we examined their effects on the tumor size as a fraction of a simulated untreated control (Figure 8). Although cases 1 and 2 have similar effects due to the standard dFdC dosing driving the overall response, achieving 27.8% and 29.0% reductions in tumor radius by day 16, respectively, the metronomic CDDP dosing of case 2 seems to confer a slight advantage compared to case 1. Cases 3 and 4 with metronomic dFdC are much more effective, however, attaining 64.7% and 64.1% reductions in tumor radius by day 16. Interestingly, case 4 with metronomic CDDP seems to be on a slightly less effective trajectory than case 3 with the standard dosing.
Figure 8.
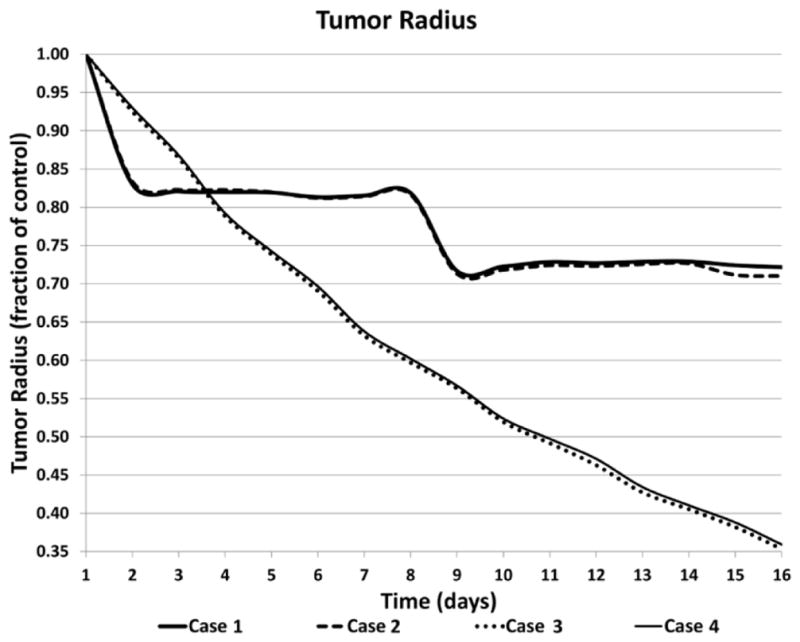
Tumor radius as a fraction of untreated control for Cases 1 through 4.
3.6 Sensitivity Analysis
A sensitivity analysis was performed to evaluate how variation in the PK parameters would affect the tumor net proliferation rate λp (Equation 15), which drives the overall tumor growth (Equation 2). Tables 8 and 9 show that for both drugs this rate is sensitive to the parameter controlling the rate of binding to DNA (k23 or k2a3, respectively), reflecting the dependency of this rate on the DNA-bound state s3 (Equations 8 and 13). However, the sensitivity due to CDDP is minimized, as the overall tumor response for the cases evaluated here is driven mainly by dFdC. Additionally for dFdC, the rate λp is also sensitive to the activation rate parameter V2a, which determines the activated drug intracellular state s2a (Equation 12).
Table 8.
Sensitivity of the tumor net proliferation rate λp on the CDDP pharmacokinetic parameters.
| Parameter | Description | λp perturbed /λp unperturbed | |
|---|---|---|---|
| Parameter x 10 | Parameter / 10 | ||
| k1 | Plasma elimination rate (min−1) | 0.93 | 1.02 |
| k12 | Drug uptake (min−1) | 1.04 | 0.92 |
| k21 | Drug efflux (min−1) | 0.98 | 1.00 |
| k23 | Drug-DNA binding (min−1) | 1.87 | 0.90 |
| k32 | Drug-DNA release (min−1) | (*) | (*) |
| k3 | Drug-DNA repair (min−1) | 0.91 | 1.06 |
| k24 | Lysosomal sequestration (min−1) | (*) | (*) |
| k42 | Lysosomal release (min−1) | (*) | (*) |
(*) Parameter unperturbed value was 0 (Table 4).
Table 9.
Sensitivity of the tumor net proliferation rate λp on the dFdC pharmacokinetic parameters.
| Parameter | Description | λp perturbed /λp unperturbed | |
|---|---|---|---|
| Parameter x 10 | Parameter / 10 | ||
| k1 | Plasma elimination rate (min−1) | 1.00 | 1.00 |
| V12 | Drug uptake (μM min−1) | 1.01 | 0.44 |
| K12 | Half-maximum transport conc. (μM) | 0.97 | 1.01 |
| k21 | Drug efflux (min−1) | (*) | (*) |
| k2 | Inactivation rate (min−1) | 0.58 | 1.08 |
| V2a | Activation rate (μM min−1) | 5.86 | 0.14 |
| K2a | Half maximum activation conc. (μM) | 0.57 | 1.10 |
| k2a3 | Drug-DNA binding (min−1) | 6.25 | 0.14 |
| k32 | Drug-DNA release (min−1) | (*) | (*) |
| k3 | Drug-DNA repair (min−1) | (*) | (*) |
| k24 | Lysosomal sequestration (min−1) | (*) | (*) |
| k42 | Lysosomal release (min−1) | (*) | (*) |
(*) Parameter unperturbed value was 0 (Table 5).
4. Discussion
This study implemented pharmacokinetic (PK) and pharmacodynamics (PD) intracellular models coupled with an established model of vascularized tumor growth (Macklin et al., 2009; van de Ven et al., 2012; Wu et al., 2013) to simulate the response of non-small cell lung cancer (NSCLC) lesions to multiple drug regimens. The focus of this work has been to integrate the modeling systems and to evaluate them with a biologically-relevant set of parameters, as a first step towards clinical utility. The actions of gemcitabine and cisplatin were simulated, assessing two widely used drugs to treat NSCLC in four different dosages combining maximum-tolerated dose (MTD) and metronomic regimens. The PK parameters were set from previous work modeling cisplatin (Sinek et al., 2009) and gemcitabine (Battaglia Jr. and Parker, 2011) treatments. The PD parameter values were calibrated to in vitro data reported in the literature for cisplatin (Curtis et al., 2016) and gemcitabine (Chougule et al., 2011; Godugu et al., 2013). The computational results obtained, although not particularly enlightening with the given set of parameter values, indicate that the coupling of the models has potential as an in silico framework to systematically assess solid tumor response to combination therapy.
Even though cisplatin had an order of magnitude larger drug effect than gemcitabine in the simulations (Table 3), the overall tumor response was mainly driven by gemcitabine (Figure 8). This is likely due to the ~15x higher dosing of gemcitabine for MTD chemotherapy (Table 6) as well as the drug’s faster kinetics enabling accumulation into the DNA compartment in higher concentrations (Figure 6). The model results suggest that this higher effect may not be realistic. For instance, the cisplatin PK model incorporated simplifying assumptions from previous experiments to derive the parameters (Sinek et al., 2009), and an underestimation of their values could lead to inadequate drug accumulation and thus a diminished effect. A sensitivity analysis shows that variation in the drug-DNA binding rate of each drug, as well as the activation rate for gemcitabine, could have a nontrivial effect on the tumor net proliferation rate. Further, the PD values were based on in vitro IC50 data (Table 3), which do not necessarily correspond to clinical dosages constrained by MTD toxicity (Table 1). An alternative choice of PD parameter values would be expected to modulate the modeled response differently, as specified in Equation 15, and would reflect variation in experimental measurements specific to cell line and culture conditions, and, ultimately, variation in patient tumor-specific parameters. For example, the IC50 for A549 cells in monolayer exposed to gemcitabine has been reported in a wide range of values, including 9 nM after 24 hr exposure (Pauwels et al., 2006), 10.4 nM after 72 hr exposure (Li et al., 2013), and 500 nM at 72 hr after 1 hr exposure (Giovannetti et al., 2005), spanning 216 to 750 nM.hr in area-under-the-curve (AUC) values.
Although cytotoxicity data obtained from in vitro monolayer culture has been reported for various lung cancer cell types, information about effects in 3D cell culture (tumor spheroids) is scarce. This is in spite of the fact that cytotoxicity is profoundly affected when cells are in a 3D environment in which cell-cell contact and diffusion gradients are promoted, more closely resembling in vivo tumor conditions. Typically, IC50 values are increased when comparing 3D cell culture to in vitro monolayer drug exposure (Curtis et al., 2016; Frieboes et al., 2009), as cells in 3D can better resist drug action via enhancement of intrinsic survival mechanisms, cell quiescence due to hypoxia in the spheroid interior, and lower exposure to drug diffusing into the spheroid. Future work will need to explore different IC50 values for cisplatin and gemcitabine, as well as for other drugs, to simulate the combination of their effects on the response of NSCLC tumors.
Cisplatin toxic effects include dose-dependent myelosuppression, nephrotoxicity, ototoxicity, and polyneuropathy (PLATINOL, 2010). A metronomic regimen administering a cumulative 90 mg/m2 over a 21-day cycle vs. 75 mg/m2 with MTD may lead to exacerbation of these effects and to possibly negating the anti-neoplastic benefit of metronomic over MTD regimens. Although gemcitabine is well tolerated, the main dose-limiting consideration in MTD regimens is myelosuppression (Eli Lilly, 2017). An additional potentially severe side effect is pulmonary toxicity, which may lead to respiratory failure weeks (Eli Lilly, 2017) or even months after administration (Sherrod et al., 2011). Nevertheless, a long standing observation is that dyspnea js usually transient and in many cases disease related (Nelson and Tarasoff, 1995). The toxicity of gemcitabine would be a concern with metronomic regimens offering daily or weekly drug exposure, although pre-clinical studies seem to indicate no increased toxicity due to metronomic administration when compared to MTD (Francia et al., 2012; Tran Cao et al., 2010). Thus, Case 3 in this study may provide the most benefit to treat the cancer without unduly increasing toxic effects, while Case 2 may represent the worst option when considering both toxicity and therapeutic effect.
The workflow envisioned for clinical application is that data from in vitro cytotoxicity assays using patient biopsy samples coupled with specific drug information and particular tumor lesion characteristics (size, extent of vascularization) would be used to calibrate model parameters and simulate potential response in vivo. Key parameters are outlined in Table 10, with the drug-specific parameters considered to be mostly patient-independent, while in vitro drug-induced death rate and cell proliferation rate, and tumor size and extent of angiogenesis would be critical patient-specific inputs.
Table 10.
Key parameters to be measured to assess potential in vivo response of multiple-drug combination chemotherapy using proposed modeling system.
| Parameter | Description | |
|---|---|---|
| Drug PK (drug-specific) | DS | Drug diffusivity |
| k1 | Plasma elimination rate | |
| V12 | Drug uptake | |
| K12 | Half-maximum transport conc. | |
| k21 | Drug efflux | |
| k2 | Inactivation rate | |
| V2a | Activation rate | |
| K2a | Half maximum activation conc. | |
| k2a3 | Drug-DNA binding | |
| k32 | Drug-DNA release | |
| k3 | Drug-DNA repair | |
| k24 | Lysosomal sequestration | |
| k42 | Lysosomal release | |
| sm | Drug-DNA capacity | |
| Drug PD (patient-specific) | λ̄ | Drug-induced death rate (e.g., λ̄CDDP), based on in vitro IC50 |
| Tumor (patient-specific) | λM | Cell proliferation rate (in vitro measurement, or from histology as in (Frieboes et al., 2013; Frieboes et al., 2015)) |
| Hypoxic and necrotic thresholds | (from histology, e.g., as in (Frieboes et al., 2013; Frieboes et al., 2015)) | |
| Size | (from imaging) | |
| Vascularity/Angiogenesis | Extent of vascularization (from imaging, or from histology as in (Frieboes et al., 2013; Frieboes et al., 2015)) |
NSCLC chemotherapy for advanced disease usually involves a doublet regimen, with cisplatin being one of the drugs. Cisplatin might be substituted with carboplatin, which has been shown to have fewer side effects. Although no survival difference has been shown between the two drugs, cisplatin-based regimens have been associated with slightly higher response rates (Ardizzoni et al., 2007; Hotta et al., 2004; Jiang et al., 2007). Instead of gemcitabine, a taxane anti-microtubule agent such as docetaxel, paclitaxel (or its albumin-bound version, nab-paclitaxel) may be combined with cisplatin. Another option for advanced disease has been the camptothecan analog irinotecan, a topoisomerase inhibitor (Yang et al., 2015). For early disease, adjuvant chemotherapy following surgical resection is also typically cisplatin-based (Arriagada et al., 2010) in combination with gemcitabine, vinorelbine, vinblastine, etoposide, docetaxel, or pemetrexed (Society). Finally, some patients might receive an anti-angiogenic drug such as bevacizumab along with a doublet regimen targeting cancerous cells.
In addition to such various combinations of drugs and their possible dosages, further modeling work will need to explore variations in periods and cycles of treatment. Chemotherapy cycles at MTD generally last three to four weeks, allowing the body to recover between drug administrations, while metronomic administration at lower dosages may be daily or weekly. Treatment cycles are repeated for several times to aim for disease remission, usually four to six cycles for advanced disease. Some patients may be given chemotherapy after completing these cycles as “maintenance therapy” to prevent recurrence (Coate and Shepherd, 2011). If all this drug administration fails to cure the patient, second-line therapies with a single drug such as pemetrexed or docetaxel, or with a targeted therapy (e.g., erlotinib) or with immunotherapy (e.g., pembrolizumab) may be attempted (Society). Further model evaluation of these as well as other therapy possibilities, in conjunction with model parameters informed with patient tumor-specific information, may help to assess their potential value to achieve sustained lesion regression. Lastly, the inclusion of additional measurable biological details, such as tumor invasiveness, intrinsic drug resistance, and immune system interactions, may further enhance the modeling, with the ultimate goal to optimize NSCLC multiple-drug chemotherapy regimens.
Highlights.
Establishes a framework for evaluation of tumor response to combination chemotherapy
Couples PK-PD multi-compartment models with a model of vascularized tumor growth
Simulates tumor response to multiple drug regimens for non-small cell lung cancer
Combination of MTD and metronomic drug regimens may not offer improved response
Acknowledgments
This work was partially supported by the National Institutes of Health – National Cancer Institute (grant number R15CA203605). The authors declare no competing financial interest.
Abbreviations
- 2D
Two-dimensional
- AUC
Area-under-the-curve
- CDDP
Cisplatin (cis-diamminedichloroplatinum(II))
- dFdC
Gemcitabine ((2′,2;-difluoro 2′-deoxycytidine)
- DNA
Deoxyribonucleic acid
- MTD
Maximum tolerated dose
- NSCLC
Non-small cell lung cancer
Footnotes
Author Contributions: LTC implemented the pharmacokinetic and pharmacodynamics models, and created the simulations. HBF conceived the study and wrote the initial manuscript. LTC and HBF analyzed the results. LTC, VvB, and HF critically reviewed and approved the final manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Administration, F. a. D, editor. PLATINOL® (cisplatin for injection, USP) Bristol-Myers Squibb Company; 2010. [Google Scholar]
- 2.Society, A. C, editor. Non-Small Cell Lung Cancer Survival Rates, by Stage. 2017 [Google Scholar]
- 3.Akcali Z, Calikusu Z, Sakalli H, Ozyilkan O. Gemcitabine and cisplatin treatment of advanced-stage non-small-cell lung cancer in patients given cisplatin on day 8. Tumori. 2008;94:474–80. doi: 10.1177/030089160809400406. [DOI] [PubMed] [Google Scholar]
- 4.André N, Barbolosi D, Billy F, Cahpuisat G, Hubert F, Grenier E, Rovini A. Mathematical model of cancer growth controled by metronomic chemotherapies. ESAIM: PROCEEDINGS. 2013;41:77–94. [Google Scholar]
- 5.Ardizzoni A, Boni L, Tiseo M, Fossella FV, Schiller JH, Paesmans M, Radosavljevic D, Paccagnella A, Zatloukal P, Mazzanti P, Bisset D, Rosell R Group CM-a. Cisplatin-versus carboplatin-based chemotherapy in first-line treatment of advanced non-small-cell lung cancer: an individual patient data meta-analysis. J Natl Cancer Inst. 2007;99:847–57. doi: 10.1093/jnci/djk196. [DOI] [PubMed] [Google Scholar]
- 6.Arriagada R, Dunant A, Pignon JP, Bergman B, Chabowski M, Grunenwald D, Kozlowski M, Le Pechoux C, Pirker R, Pinel MI, Tarayre M, Le Chevalier T. Long-term results of the international adjuvant lung cancer trial evaluating adjuvant Cisplatin-based chemotherapy in resected lung cancer. J Clin Oncol. 2010;28:35–42. doi: 10.1200/JCO.2009.23.2272. [DOI] [PubMed] [Google Scholar]
- 7.Artal Cortes A, Calera Urquizu L, Hernando Cubero J. Adjuvant chemotherapy in non-small cell lung cancer: state-of-the-art. Transl Lung Cancer Res. 2015;4:191–7. doi: 10.3978/j.issn.2218-6751.2014.06.01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Azzoli CG, Baker S, Jr, Temin S, Pao W, Aliff T, Brahmer J, Johnson DH, Laskin JL, Masters G, Milton D, Nordquist L, Pfister DG, Piantadosi S, Schiller JH, Smith R, Smith TJ, Strawn JR, Trent D, Giaccone G American Society of Clinical O. American Society of Clinical Oncology Clinical Practice Guideline update on chemotherapy for stage IV non-small-cell lung cancer. J Clin Oncol. 2009;27:6251–66. doi: 10.1200/JCO.2009.23.5622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Azzoli CG, Temin S, Aliff T, Baker S, Jr, Brahmer J, Johnson DH, Laskin JL, Masters G, Milton D, Nordquist L, Pao W, Pfister DG, Piantadosi S, Schiller JH, Smith R, Smith TJ, Strawn JR, Trent D, Giaccone G American Society of Clinical O. 2011 Focused Update of 2009 American Society of Clinical Oncology Clinical Practice Guideline Update on Chemotherapy for Stage IV Non-Small-Cell Lung Cancer. J Clin Oncol. 2011;29:3825–31. doi: 10.1200/JCO.2010.34.2774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bahl A, Bakhshi S. Metronomic chemotherapy in progressive pediatric malignancies: old drugs in new package. Indian J Pediatr. 2012;79:1617–22. doi: 10.1007/s12098-012-0759-z. [DOI] [PubMed] [Google Scholar]
- 11.Baker CH, Banzon J, Bollinger JM, Stubbe J, Samano V, Robins MJ, Lippert B, Jarvi E, Resvick R. 2′-Deoxy-2′-methylenecytidine and 2′-deoxy-2′,2′-difluorocytidine 5′-diphosphates: potent mechanism-based inhibitors of ribonucleotide reductase. J Med Chem. 1991;34:1879–84. doi: 10.1021/jm00110a019. [DOI] [PubMed] [Google Scholar]
- 12.Barbolosi D, Ciccolini J, Lacarelle B, Barlesi F, Andre N. Computational oncology--mathematical modelling of drug regimens for precision medicine. Nat Rev Clin Oncol. 2016;13:242–54. doi: 10.1038/nrclinonc.2015.204. [DOI] [PubMed] [Google Scholar]
- 13.Bartha K, Rieger H. Vascular network remodeling via vessel cooption, regression and growth in tumors. J Theor Biol. 2006;241:903–18. doi: 10.1016/j.jtbi.2006.01.022. [DOI] [PubMed] [Google Scholar]
- 14.Battaglia MA, Jr, Parker RS. Pharmacokinetic/pharmacodynamic modelling of intracellular gemcitabine triphosphate accumulation: translating in vitro to in vivo. IET Syst Biol. 2011;5:34–43. doi: 10.1049/iet-syb.2009.0073. [DOI] [PubMed] [Google Scholar]
- 15.Bertolini F, Paul S, Mancuso P, Monestiroli S, Gobbi A, Shaked Y, Kerbel RS. Maximum tolerable dose and low-dose metronomic chemotherapy have opposite effects on the mobilization and viability of circulating endothelial progenitor cells. Cancer Res. 2003;63:4342–6. [PubMed] [Google Scholar]
- 16.Brodowicz T, Krzakowski M, Zwitter M, Tzekova V, Ramlau R, Ghilezan N, Ciuleanu T, Cucevic B, Gyurkovits K, Ulsperger E, Jassem J, Grgic M, Saip P, Szilasi M, Wiltschke C, Wagnerova M, Oskina N, Soldatenkova V, Zielinski C, Wenczl M Central European Cooperative Oncology Group C. Cisplatin and gemcitabine first-line chemotherapy followed by maintenance gemcitabine or best supportive care in advanced non-small cell lung cancer: a phase III trial. Lung Cancer. 2006;52:155–63. doi: 10.1016/j.lungcan.2006.01.006. [DOI] [PubMed] [Google Scholar]
- 17.Cardenal F, Lopez-Cabrerizo MP, Anton A, Alberola V, Massuti B, Carrato A, Barneto I, Lomas M, Garcia M, Lianes P, Montalar J, Vadell C, Gonzalez-Larriba JL, Nguyen B, Artal A, Rosell R. Randomized phase III study of gemcitabine-cisplatin versus etoposide-cisplatin in the treatment of locally advanced or metastatic non-small-cell lung cancer. J Clin Oncol. 1999;17:12–8. doi: 10.1200/jco.1999.17.1.12. [DOI] [PubMed] [Google Scholar]
- 18.Chougule MB, Patel A, Sachdeva P, Jackson T, Singh M. Enhanced anticancer activity of gemcitabine in combination with noscapine via antiangiogenic and apoptotic pathway against non-small cell lung cancer. PLoS One. 2011;6:e27394. doi: 10.1371/journal.pone.0027394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Coate LE, Shepherd FA. Maintenance therapy in advanced non-small cell lung cancer: evolution, tolerability and outcomes. Ther Adv Med Oncol. 2011;3:139–57. doi: 10.1177/1758834011399306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Correale P, Cerretani D, Remondo C, Martellucci I, Marsili S, La Placa M, Sciandivasci A, Paolelli L, Pascucci A, Rossi M, Di Bisceglie M, Giorgi G, Gotti G, Francini G. A novel metronomic chemotherapy regimen of weekly platinum and daily oral etoposide in high-risk non-small cell lung cancer patients. Oncol Rep. 2006;16:133–40. doi: 10.3892/or.16.1.133. [DOI] [PubMed] [Google Scholar]
- 21.Curtis LT, England CG, Wu M, Lowengrub J, Frieboes HB. An interdisciplinary computational/experimental approach to evaluate drug-loaded gold nanoparticle tumor cytotoxicity. Nanomedicine (Lond) 2016;11:197–216. doi: 10.2217/nnm.15.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Eli Lilly. Gemzar FDA prescribing information, side effects and uses. Vol. 2017. Eli Lilly and Company; 2017. [Google Scholar]
- 23.Ewald JA, Desotelle JA, Wilding G, Jarrard DF. Therapy-induced senescence in cancer. J Natl Cancer Inst. 2010;102:1536–46. doi: 10.1093/jnci/djq364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Francia G, Shaked Y, Hashimoto K, Sun J, Yin M, Cesta C, Xu P, Man S, Hackl C, Stewart J, Uhlik M, Dantzig AH, Foster FS, Kerbel RS. Low-dose metronomic oral dosing of a prodrug of gemcitabine (LY2334737) causes antitumor effects in the absence of inhibition of systemic vasculogenesis. Mol Cancer Ther. 2012;11:680–9. doi: 10.1158/1535-7163.MCT-11-0659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Frieboes HB, Smith BR, Chuang YL, Ito K, Roettgers AM, Gambhir SS, Cristini V. An integrated computational/experimental model of lymphoma growth. PLoS Comput Biol. 2013;9:e1003008. doi: 10.1371/journal.pcbi.1003008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Frieboes HB, Edgerton ME, Fruehauf JP, Rose FR, Worrall LK, Gatenby RA, Ferrari M, Cristini V. Prediction of drug response in breast cancer using integrative experimental/computational modeling. Cancer Res. 2009;69:4484–92. doi: 10.1158/0008-5472.CAN-08-3740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Frieboes HB, Smith BR, Wang Z, Kotsuma M, Ito K, Day A, Cahill B, Flinders C, Mumenthaler SM, Mallick P, Simbawa E, Al-Fhaid AS, Mahmoud SR, Gambhir SS, Cristini V. Predictive Modeling of Drug Response in Non-Hodgkin’s Lymphoma. PLoS One. 2015;10:e0129433. doi: 10.1371/journal.pone.0129433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gandhi V, Plunkett W. Modulatory activity of 2′,2′-difluorodeoxycytidine on the phosphorylation and cytotoxicity of arabinosyl nucleosides. Cancer Res. 1990;50:3675–80. [PubMed] [Google Scholar]
- 29.Giovannetti E, Mey V, Danesi R, Basolo F, Barachini S, Deri M, Del Tacca M. Interaction between gemcitabine and topotecan in human non-small-cell lung cancer cells: effects on cell survival, cell cycle and pharmacogenetic profile. Br J Cancer. 2005;92:681–9. doi: 10.1038/sj.bjc.6602382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Godugu C, Patel AR, Desai U, Andey T, Sams A, Singh M. AlgiMatrix based 3D cell culture system as an in-vitro tumor model for anticancer studies. PLoS One. 2013;8:e53708. doi: 10.1371/journal.pone.0053708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos Trans R Soc Lond. 1825;115:513–585. doi: 10.1098/rstb.2014.0379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hadjiandreou MM, Mitsis GD. Mathematical modeling of tumor growth, drug-resistance, toxicity, and optimal therapy design. IEEE Trans Biomed Eng. 2014;61:415–25. doi: 10.1109/TBME.2013.2280189. [DOI] [PubMed] [Google Scholar]
- 33.Heinemann V, Hertel LW, Grindey GB, Plunkett W. Comparison of the cellular pharmacokinetics and toxicity of 2′,2′-difluorodeoxycytidine and 1-beta-D-arabinofuranosylcytosine. Cancer Res. 1988;48:4024–31. [PubMed] [Google Scholar]
- 34.Heinemann V, Xu YZ, Chubb S, Sen A, Hertel LW, Grindey GB, Plunkett W. Inhibition of ribonucleotide reduction in CCRF-CEM cells by 2′,2′-difluorodeoxycytidine. Mol Pharmacol. 1990;38:567–72. [PubMed] [Google Scholar]
- 35.Heinemann V, Xu YZ, Chubb S, Sen A, Hertel LW, Grindey GB, Plunkett W. Cellular elimination of 2′,2′-difluorodeoxycytidine 5′-triphosphate: a mechanism of self-potentiation. Cancer Res. 1992;52:533–9. [PubMed] [Google Scholar]
- 36.Heinemann V, Schulz L, Issels RD, Plunkett W. Gemcitabine: a modulator of intracellular nucleotide and deoxynucleotide metabolism. Semin Oncol. 1995;22(Suppl 11):11–18. [PubMed] [Google Scholar]
- 37.Hodge LS, Taub ME, Tracy TS. The deaminated metabolite of gemcitabine, 2′,2′-difluorodeoxyuridine, modulates the rate of gemcitabine transport and intracellular phosphorylation via deoxycytidine kinase. Drug Metab Dispos. 2011;39:2013–6. doi: 10.1124/dmd.111.040790. [DOI] [PubMed] [Google Scholar]
- 38.Hotta K, Matsuo K, Ueoka H, Kiura K, Tabata M, Tanimoto M. Role of adjuvant chemotherapy in patients with resected non-small-cell lung cancer: reappraisal with a meta-analysis of randomized controlled trials. J Clin Oncol. 2004;22:3860–7. doi: 10.1200/JCO.2004.01.153. [DOI] [PubMed] [Google Scholar]
- 39.Huang JC, Zamble DB, Reardon JT, Lippard SJ, Sancar A. HMG-domain proteins specifically inhibit the repair of the major DNA adduct of the anticancer drug cisplatin by human excision nuclease. Proc Natl Acad Sci U S A. 1994;91:10394–8. doi: 10.1073/pnas.91.22.10394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Huang P, Chubb S, Hertel LW, Grindey GB, Plunkett W. Action of 2′,2′-difluorodeoxycytidine on DNA synthesis. Cancer Res. 1991;51:6110–7. [PubMed] [Google Scholar]
- 41.Jiang J, Liang X, Zhou X, Huang R, Chu Z. A meta-analysis of randomized controlled trials comparing carboplatin-based to cisplatin-based chemotherapy in advanced non-small cell lung cancer. Lung Cancer. 2007;57:348–58. doi: 10.1016/j.lungcan.2007.03.014. [DOI] [PubMed] [Google Scholar]
- 42.Klement G, Baruchel S, Rak J, Man S, Clark K, Hicklin DJ, Bohlen P, Kerbel RS. Continuous low-dose therapy with vinblastine and VEGF receptor-2 antibody induces sustained tumor regression without overt toxicity. J Clin Invest. 2000;105:R15–24. doi: 10.1172/JCI8829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Le Chevalier T, Scagliotti G, Natale R, Danson S, Rosell R, Stahel R, Thomas P, Rudd RM, Vansteenkiste J, Thatcher N, Manegold C, Pujol JL, van Zandwijk N, Gridelli C, van Meerbeeck JP, Crino L, Brown A, Fitzgerald P, Aristides M, Schiller JH. Efficacy of gemcitabine plus platinum chemotherapy compared with other platinum containing regimens in advanced non-small-cell lung cancer: a meta-analysis of survival outcomes. Lung Cancer. 2005;47:69–80. doi: 10.1016/j.lungcan.2004.10.014. [DOI] [PubMed] [Google Scholar]
- 44.Ledzewicz U, Schättler H. A review of optimal chemotherapy protocols: From mtd towards metronomic therapy. Math Model Nat Phenom. 2014;9:131–152. [Google Scholar]
- 45.Ledzewicz U, Schattler H. Application of mathematical models to metronomic chemotherapy: What can be inferred from minimal parameterized models? Cancer Lett. 2017 doi: 10.1016/j.canlet.2017.03.021. [DOI] [PubMed] [Google Scholar]
- 46.Lee DS, Rieger H, Bartha K. Flow correlated percolation during vascular remodeling in growing tumors. Phys Rev Lett. 2006;96:058104. doi: 10.1103/PhysRevLett.96.058104. [DOI] [PubMed] [Google Scholar]
- 47.Lee JJ, Huang J, England CG, McNally LR, Frieboes HB. Predictive modeling of in vivo response to gemcitabine in pancreatic cancer. PLoS Comput Biol. 2013;9:e1003231. doi: 10.1371/journal.pcbi.1003231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lee NS, Byun JH, Bae SB, Kim CK, Lee KT, Park SK, Won JH, Hong DS, Park HS. Combination of Gemcitabine and Cisplatin as First-Line T herapy in A dvanced N on-Small-Cell Lung Cancer. Cancer Research and Treatment. 2004;36:173–177. doi: 10.4143/crt.2004.36.3.173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Leighl NB. Treatment paradigms for patients with metastatic non-small-cell lung cancer: first-, second-, and third-line. Curr Oncol. 2012;19:S52–8. doi: 10.3747/co.19.1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li J, Pan YP, Zhang Y. Synergistic interaction between sorafenib and gemcitabine in EGFR-TKI-sensitive and EGFR-TKI-resistant human lung cancer cell lines. Oncology Letters. 2013;5:440–446. doi: 10.3892/ol.2012.1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lutsiak ME, Semnani RT, De Pascalis R, Kashmiri SV, Schlom J, Sabzevari H. Inhibition of CD4(+)25+ T regulatory cell function implicated in enhanced immune response by low-dose cyclophosphamide. Blood. 2005;105:2862–8. doi: 10.1182/blood-2004-06-2410. [DOI] [PubMed] [Google Scholar]
- 52.Macklin P, McDougall S, Anderson AR, Chaplain MA, Cristini V, Lowengrub J. Multiscale modelling and nonlinear simulation of vascular tumour growth. J Math Biol. 2009;58:765–98. doi: 10.1007/s00285-008-0216-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McDougall SR, Anderson ARA, Chaplain MAJ. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: Clinical implications and therapeutic targeting strategies. Journal of Theoretical Biology. 2006;241:564–589. doi: 10.1016/j.jtbi.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 54.Mini E, Nobili S, Caciagli B, Landini I, Mazzei T. Cellular pharmacology of gemcitabine. Ann Oncol. 2006;17(Suppl 5):v7–12. doi: 10.1093/annonc/mdj941. [DOI] [PubMed] [Google Scholar]
- 55.Nelson R, Tarasoff P. Dyspnea with Gemcitabine is commonly seen, often disease related, transient and rarely severe. European Journal of Cancer. 1995;31:197–198. [Google Scholar]
- 56.Network, N. C. C. Non-Small Cell Lung Cancer. 2013;2017 [Google Scholar]
- 57.Norton L, Simon R, Brereton HD, Bogden AE. Predicting the course of Gompertzian growth. Nature. 1976;264:542–5. doi: 10.1038/264542a0. [DOI] [PubMed] [Google Scholar]
- 58.Nugent LJ, Jain RK. Extravascular diffusion in normal and neoplastic tissues. Cancer Res. 1984;44:238–44. [PubMed] [Google Scholar]
- 59.Pauwels B, Korst AE, Pattyn GG, Lambrechts HA, Kamphuis JA, De Pooter CM, Peters GJ, Lardon F, Vermorken JB. The relation between deoxycytidine kinase activity and the radiosensitising effect of gemcitabine in eight different human tumour cell lines. BMC Cancer. 2006;6:142. doi: 10.1186/1471-2407-6-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Perol M, Chouaid C, Perol D, Barlesi F, Gervais R, Westeel V, Crequit J, Lena H, Vergnenegre A, Zalcman G, Monnet I, Le Caer H, Fournel P, Falchero L, Poudenx M, Vaylet F, Segura-Ferlay C, Devouassoux-Shisheboran M, Taron M, Milleron B. Randomized, phase III study of gemcitabine or erlotinib maintenance therapy versus observation, with predefined second-line treatment, after cisplatin-gemcitabine induction chemotherapy in advanced non-small-cell lung cancer. J Clin Oncol. 2012;30:3516–24. doi: 10.1200/JCO.2011.39.9782. [DOI] [PubMed] [Google Scholar]
- 61.Pratt SE, Durland-Busbice S, Shepard RL, Donoho GP, Starling JJ, Wickremsinhe ER, Perkins EJ, Dantzig AH. Efficacy of low-dose oral metronomic dosing of the prodrug of gemcitabine, LY2334737, in human tumor xenografts. Mol Cancer Ther. 2013;12:481–90. doi: 10.1158/1535-7163.MCT-12-0654. [DOI] [PubMed] [Google Scholar]
- 62.Scagliotti GV, Parikh P, von Pawel J, Biesma B, Vansteenkiste J, Manegold C, Serwatowski P, Gatzemeier U, Digumarti R, Zukin M, Lee JS, Mellemgaard A, Park K, Patil S, Rolski J, Goksel T, de Marinis F, Simms L, Sugarman KP, Gandara D. Phase III study comparing cisplatin plus gemcitabine with cisplatin plus pemetrexed in chemotherapy-naive patients with advanced-stage non-small-cell lung cancer. J Clin Oncol. 2008;26:3543–51. doi: 10.1200/JCO.2007.15.0375. [DOI] [PubMed] [Google Scholar]
- 63.Schor AM, Pazouki S, Morris J, Smither RL, Chandrachud LM, Pendleton N. Heterogeneity in microvascular density in lung tumours: comparison with normal bronchus. Br J Cancer. 1998;77:946–51. doi: 10.1038/bjc.1998.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sherrod AM, Brufsky A, Puhalla S. A case of late-onset gemcitabine lung toxicity. Clin Med Insights Oncol. 2011;5:171–6. doi: 10.4137/CMO.S6643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sinek JP, Sanga S, Zheng X, Frieboes HB, Ferrari M, Cristini V. Predicting drug pharmacokinetics and effect in vascularized tumors using computer simulation. J Math Biol. 2009;58:485–510. doi: 10.1007/s00285-008-0214-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Society, A. C. Chemotherapy for Non-Small Cell Lung Cancer. 2017 [Google Scholar]
- 67.Stolting S, Klink T, Bela C, Engels C, Wagner T. Metronomic scheduling of trofosfamide chemotherapy in human NSCLC xenografts highly increases therapeutic efficacy compared to conventional scheduling by inhibition of angiogenesis. Int J Clin Pharmacol Ther. 2004;42:652–3. doi: 10.5414/cpp42652. [DOI] [PubMed] [Google Scholar]
- 68.Tibaldi C, Mazzoni E, Arcabasso G, D’Incecco A, Antonuzzo A, Menconi G, Falcone A. Cisplatin plus gemcitabine as adjuvant chemotherapy for radically resected non-small-cell lung cancer: a pilot study. Clin Lung Cancer. 2009;10:53–7. doi: 10.3816/CLC.2009.n.008. [DOI] [PubMed] [Google Scholar]
- 69.Traina TA, Dugan U, Higgins B, Kolinsky K, Theodoulou M, Hudis CA, Norton L. Optimizing chemotherapy dose and schedule by Norton-Simon mathematical modeling. Breast Dis. 2010;31:7–18. doi: 10.3233/BD-2009-0290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Tran Cao HS, Bouvet M, Kaushal S, Keleman A, Romney E, Kim G, Fruehauf J, Imagawa DK, Hoffman RM, Katz MH. Metronomic gemcitabine in combination with sunitinib inhibits multisite metastasis and increases survival in an orthotopic model of pancreatic cancer. Mol Cancer Ther. 2010;9:2068–78. doi: 10.1158/1535-7163.MCT-10-0201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.van de Ven AL, Wu M, Lowengrub J, McDougall SR, Chaplain MA, Cristini V, Ferrari M, Frieboes HB. Integrated intravital microscopy and mathematical modeling to optimize nanotherapeutics delivery to tumors. AIP Adv. 2012;2:11208. doi: 10.1063/1.3699060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Vergnenegre A, Tillon J, Corre R, Barlesi F, Berard H, Vernejoux JM, Le Caer H, Fournel P, Marin B, Chouaid C. A randomized phase II trial assessing in advanced non-small cell lung cancer patients with stable disease after two courses of cisplatin-gemcitabine an early modification of chemotherapy doublet with paclitaxel-gemcitabine versus continuation of cisplatin-gemcitabine chemotherapy (GFPC 03-01 Study) J Thorac Oncol. 2009;4:364–70. doi: 10.1097/JTO.0b013e318197f4ff. [DOI] [PubMed] [Google Scholar]
- 73.Ware MJ, Curtis LT, Wu M, Ho JC, Corr SJ, Curley SA, Godin B, Frieboes HB. Pancreatic adenocarcinoma response to chemotherapy enhanced with non-invasive radio frequency evaluated via an integrated experimental/computational approach. Sci Rep. 2017;7:3437. doi: 10.1038/s41598-017-03040-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Welter M, Rieger H. Physical determinants of vascular network remodeling during tumor growth. Eur Phys J E Soft Matter. 2010;33:149–63. doi: 10.1140/epje/i2010-10611-6. [DOI] [PubMed] [Google Scholar]
- 75.Welter M, Bartha K, Rieger H. Emergent vascular network inhomogeneities and resulting blood flow patterns in a growing tumor. J Theor Biol. 2008;250:257–80. doi: 10.1016/j.jtbi.2007.09.031. [DOI] [PubMed] [Google Scholar]
- 76.Welter M, Bartha K, Rieger H. Vascular remodelling of an arterio-venous blood vessel network during solid tumour growth. J Theor Biol. 2009;259:405–22. doi: 10.1016/j.jtbi.2009.04.005. [DOI] [PubMed] [Google Scholar]
- 77.West J, Newton PK. Chemotherapeutic Dose Scheduling Based on Tumor Growth Rates Provides a Case for Low-Dose Metronomic High-Entropy Therapies. Cancer Res. 2017;77:6717–6728. doi: 10.1158/0008-5472.CAN-17-1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Wu M, Frieboes HB, McDougall SR, Chaplain MA, Cristini V, Lowengrub J. The effect of interstitial pressure on tumor growth: Coupling with the blood and lymphatic vascular systems. J Theor Biol. 2013;320:131–51. doi: 10.1016/j.jtbi.2012.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wu M, Frieboes HB, Chaplain MA, McDougall SR, Cristini V, Lowengrub J. The effect of interstitial pressure on therapeutic agent transport: Coupling with the tumor blood and lymphatic vascular systems. J Theor Biol. 2014;355:194–207. doi: 10.1016/j.jtbi.2014.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Xu YZ, Plunkett W. Regulation of dCMP deaminase in intact CCRF-CEM cells. Vol. 30. American Association for Cancer Research; 1990. p. 405. [Google Scholar]
- 81.Yang XQ, Li CY, Xu MF, Zhao H, Wang D. Comparison of first-line chemotherapy based on irinotecan or other drugs to treat non-small cell lung cancer in stage IIIB/IV: a systematic review and meta-analysis. BMC Cancer. 2015;15:949. doi: 10.1186/s12885-015-1978-2. [DOI] [PMC free article] [PubMed] [Google Scholar]