The Selective Labels Problem: Evaluating Algorithmic Predictions in the Presence of Unobservables

Abstract

Evaluating whether machines improve on human performance is one of the central questions of machine learning. However, there are many domains where the data is selectively labeled in the sense that the observed outcomes are themselves a consequence of the existing choices of the human decision-makers. For instance, in the context of judicial bail decisions, we observe the outcome of whether a defendant fails to return for their court appearance only if the human judge decides to release the defendant on bail. This selective labeling makes it harder to evaluate predictive models as the instances for which outcomes are observed do not represent a random sample of the population. Here we propose a novel framework for evaluating the performance of predictive models on selectively labeled data. We develop an approach called contraction which allows us to compare the performance of predictive models and human decision-makers without resorting to counterfactual inference. Our methodology harnesses the heterogeneity of human decision-makers and facilitates effective evaluation of predictive models even in the presence of unmeasured confounders (unobservables) which influence both human decisions and the resulting outcomes. Experimental results on real world datasets spanning diverse domains such as health care, insurance, and criminal justice demonstrate the utility of our evaluation metric in comparing human decisions and machine predictions.

1 INTRODUCTION

Machine learning models have been very effective at automating various perception and recognition tasks such as character recognition, sentiment detection, question answering, game playing, and image classification [13, 14, 27, 31]. In all these examples, when given the same set of input data and enough labeled training data, machines tend to outperform humans. There is a large set of domains, however, where evaluating whether machines improve on human performance has been much more challenging. Often, these are settings where humans have already performed the task, and where the the machine learning algorithm must be evaluated on data where the labels are themselves consequence of the existing choices of the human decision-makers.

We first dealt with issues of this form in an analysis of judicial bail decisions [17], an application which motivated the present paper. Since this is an important setting that illustrates the basic concerns, it is useful to briefly describe the underlying background of the application here. In a bail hearing, by law requires the judge to base their decision to release defendants on a prediction—if granted bail, will the defendant return for their court appearance without committing a crime in the intervening time. Given that millions of such prediction tasks are being performed each year, and the outcomes are highly consequential, it is natural to ask whether a machine learning algorithm could make these predictions better than the judge does.

In comparing the algorithm to the judge, one has to appreciate how different this type of task is from a more standard task such as image-based object recognition. First, judges’ predictions rely on many informative features that are unobservable to the algorithm because they aren’t recorded in available datasets; these may include information such as details of the defendant’s behavior in the courtroom, and related behavioral inferences. Second, the labels we are trying to predict correspond to whether a defendant returned for their court appearance without committing a crime—the label is positive if they did, negative if they did not. But if a defendant is denied bail, then there is no opportunity for them to commit a crime or fail to show up for their court appearance, so we have no way to know what would have happened had they been released. So how do we evaluate an algorithm that proposes to release someone that the judge had jailed in the dataset? This results in a problem of selective labels: the process generates only a partial labeling of the instances, and the decision-maker’s choices—the very decisions we wish to compare the algorithm to—determine which instances even have labels at all.

Judicial bail decisions represent just one of many fundamental examples of these types of questions, and the ubiquity of the phenomenon motivates our goal in the present work—to abstract the selective labels problem beyond any one application and study it as a general algorithmic question in itself, reaching across multiple domains. To begin with, here are some further basic examples of areas where the selective labels problem naturally arises. First, a common type of medical prediction question is whether a patient needs a costly treatment for a condition; not all patients need treatment, but the treatment is generally effective whenever it is prescribed. The problem is that if our training data comes from doctors who were prescribing treatment for the condition, then (i) we typically won’t know all the features the doctor was able to observe when meeting a given patient in person, and (ii) there only exist labels for the people to whom treatment wasn’t prescribed (since the people for whom treatment was prescribed had no subsequent symptoms, whether they needed the treatment or not). In a very different domain, suppose we wanted to predict which proposals for startup companies to fund, given data on early-stage investor decisions. Again, the challenge is that these investors generally obtain “soft information” from conversations with the founders that would be difficult to record as features, and we only learn the success or failure of the startup proposals that were in fact funded.

In this paper, we are interested in how to approach this class of prediction problems, which we characterize by the set of technical ingredients outlined in the examples above:

1. The data comes from the judgments of decision-makers making a yes-no decision (e.g., granting bail, investing in a startup). In doing this, the decision-makers are basing their decisions on a set of features (X, Z) while the algorithm only observes features X; the Z are unobservables.

2. The judgments of the decision-makers determines which instances have labels, leading to a selective labels problem.

There is a third aspect to these questions that is also relevant to how we think about them. A common strategy for addressing missing labels is to randomly acquire labels on hard-to-reach parts of the distribution, for example via experiments. (Consider for example the way in which one might acquire additional labels in a recommender system by showing suggestions that may not be ranked first by the underlying algorithm.) A key feature of our motivating applications, however, is that they arise in domains where such experimentation is simply infeasible. Exactly because these decisions—releasing a defendant or withholding treatments—is consequential, it is impractical and very often unethical to randomize decisions on a subset of instances simply to increase the variability in the evaluation data.¹

Evaluating machine learning algorithms in these types of domains, without taking into account the issues above, can create misleading conclusions. For example, in the setting of bail, it could be that for young defendants, the presence of a defendant’s family at the court hearing is highly predictive of a positive label (returning for their court appearance without committing a crime). If the judge accurately uses this feature, we obtain training data where young defendants have a much lower rate of negative labels. Now, suppose this feature isn’t recorded in the administrative data available to an algorithm; then the algorithm trained on this data will falsely but confidently learn that young people commit no cime; if such an algorithm is then deployed, its error rate on young defendants will much higher than we expected. Similar issues can arise if a doctor is basing treatment decisions on symptoms that he or she observes in meeting a patient, but which aren’t recorded and accessible to the algorithm.

While prior research has explored applications of machine learning to domains where human judgments are part of the data labeling process (crime [7, 21, 43], medical diagnosis [6, 22]), the selective labels problem is often overlooked, with evaluation of the models typically carried out by computing traditional metrics such as AUC or accuracy only on the data points for which ground truth labels are available [7]. This could potentially result in biased estimates of model’s performance, because the labeled data is in fact a difficult-to-interpret non-random sample of the population. There has also been some work on inferring labels using counterfactual inference techniques [9, 12, 16, 36, 38] and leveraging these estimates when computing standard evaluation metrics. However, counterfactual inference techniques explicitly assume that there are no unmeasured confounders (that is, no unobservable variables Z) that could affect the outcome Y. This assumption does not typically hold in cases where human decisions are providing data labels [7, 21]. Thus, the combination of two ingredients—selective labels and non-trivial unobservables—poses problems for these existing techniques.

The present work

Here we propose a framework for developing and evaluating prediction algorithms in the presence of the selective labels problem. Our framework makes use of the fact that many domains involving selective labels have the following features:

1. We have data on many decision-makers rather than just one;

2. These different decision-makers have a similar pool of cases, so that it is as if the instances had been randomly assigned across them; and

3. The decision-makers differ in the thresholds they use for their yes-no decisions.

If we think of a “yes” decision as producing a label for an instance (e.g. by granting bail), and a “no” instance as resulting in no label (e.g. by denying bail), then the decision-makers who have a lower threshold and say yes on more instances are labeling a larger fraction of their sample of population. The decision-maker is trying to avoid a particular bad outcome (e.g. a defendant not returning for their court appearance, or a company that receives an investment subsequently failing), and we note that the nature of task determines that only instances that receive a label can exhibit a bad outcome. Thus, for a particular decision-maker, we define their acceptance rate to be the fraction of instances on which their decision is yes, and their failure rate to be the fraction of instances on which the bad outcome occurs. This leads to a natural trade-off curve between acceptance rate and failure rate, and points (i), (ii), and (iii) mean that we can meaningfully construct such a curve over the population of decision-makers.²

To achieve this we make use of the heterogeneity among decision-makers via technique, which we call contraction. Starting with the decision-makers of high acceptance rates, we use algorithmic predictions to “contract” the set of instances they accept until it is scaled back to acceptance rates matching that of stricter decision-makers. In this way, we sweep out an algorithmic version of the curve that trades off between acceptance rate and failure rate, and in the process evaluate the algorithm only on instances drawn from the population for which we have labels. Our contraction approach thus eliminates the need for imputation of labels for all those data points for which ground truth labels are not available. This makes our contraction technique ideal for judgment-based settings where unobservables may influence the outcomes.

To illustrate the intuition behind our contraction technique, let us consider the setting of judicial bail decisions. Let j be the judge with the highest acceptance rate, say 90%, and let 𝒟_j be the set of defendants who appear before j. Now, consider another judge k with a lower acceptance rate, say 80%, who sees a set of defendants 𝒟_k. By point (ii), the sets 𝒟_j and 𝒟_k behave distributionally as if randomly assigned between j and k. Here is how we can evaluate a form of gain from algorithmic prediction relative to judge k. Suppose j and k each see 1000 defendants, and hence j grants bail to 900 while k grants bail to 800. We train a prediction algorithm on held-out labeled data, and then we apply it to 900 defendants in 𝒟_j who were granted bail. We use the algorithm to reverse the decision to grant bail on a subset of 100 of the defendants in 𝒟_j who had been granted bail by j. In this way, we now have a set of 800 defendants in 𝒟_j who have been granted bail by a hybrid human-algorithmic mechanism: judge j granted bail to 900 of the original 1000, and then the algorithm kept 800 of these for the final decision set. (This is the sense in which we “contract” judge j’s set of 900 released defendants down to 800.) The point is that we can now compare the failure rate on this set of 800—the number of defendants who commit a crime or fail to return for their court appearance—to the failure rate on the set of 800 released by judge k. The extent to which the failure rate is lower for the hybrid human-algorithmic mechanism is a concrete type of performance guarantee provided by the contraction technique.

We demonstrate the utility of our contraction framework in comparing human judgments and model predictions across three diverse domains: criminal justice, health care, and insurance. We also show that our contraction technique accurately estimates the trade-off curve between acceptance rate and failure rate on synthetic datasets. Finally, we highlight the significance of the contraction technique by simulating the effects of unmeasured confounders (unobservables) and demonstrating how other counterfactual inference methods can result in overly optimistic—and hence inaccurate—estimates of a predictive model’s performance.

2 RELATEDWORK

Below we provide an overview of related research on selective labels and missing data. We further discuss how prior research handled these problems when evaluating predictive models. We then present a detailed overview of techniques proposed for counterfactual inference in causal inference literature.

Missing data problem

Recall that the selective labels problem is a form of missing data problem [1] which commonly arises in various settings where judgments of human decision-makers determine which instances have labels. A more commonly known variant of this problem is censoring in clinical trials where outcome labels of certain subjects are not recorded due to a variety of reasons including subjects dropping out from trials [25]. This problem has been studied extensively in the context of causal inference where the goal is to determine the effect of some treatment [2, 30, 32, 37, 38]. Since it is not always feasible to carry out randomized control trials to determine treatment effects, prior research has employed a variety of imputation techniques (discussed in detail below) to infer outcomes of counterfactual scenarios. For example, Freemantle et al. studied the effects of dosage of insulin on patients with type 2 diabetes using propensity score matching [11]. Similarly, McCormick et al. studied the effect of student-teacher relationships on academic performance using matching techniques [29]. The effectiveness of these techniques relies on the absence of unobservables, an assumption, which does not hold in our case.

Prior research also categorized missing data problems based on the reasons behind the missingness [26, 28]. A variable (label or a feature) value of some data point could be: (1) missing completely at random (MCAR) (2) missing at random (MAR), where the missingness can be accounted for by variables where there is complete information. For example, men are less likely to fill out depression surveys, but this is not dependent on their level of depression once we account for the fact that they are male [39]. (3) missing not at random (MNAR) [40], where the variable value that is missing is related to the reason why it’s missing. For example, this would occur when people with high levels of depression failed to fill out the depression survey. Depending on the reason for missingness, various imputation techniques have been proposed to address the missing data problem. For instance, listwise deletion, where data points with missing values are removed from the dataset, was used when data was missing completely at random. and for regression modeling, nearest-neighbor matching, interpolation etc were adopted when the values are MAR (see Chapter 25 of [12], [18]). Note that there is a significant overlap between these methods and the techniques used for imputation in causal inference literature. These methods are not readily applicable to our setting as they assume that there are no unobservables influencing the occurrence of missing labels. MNAR problems are often addressed using approaches such as selection and pattern-mixture models [24] which require us to make assumptions about the underlying generative process of the data.

Evaluation in the presence of selective labels

There has been a lot of interest in developing accurate risk assessment models in health care [6], education [19], and criminal justice [7]. For example, Berk et al. [7] developed models to predict if a defendant is likely to commit a violent crime when released on parole. Selective labels problem arising in some of these settings makes it harder to train and evaluate predictive models. For instance, Berk et al. evaluated their model only on the set of defendants who have been granted parole. This evaluation could be potentially biased if the observed feature distribution or the conditional outcome distribution of the defendants who were released does not match that of defendants who were denied parole. This assumption is often violated in practice. There have been some attempts to work around this problem by using imputation to assign labels to those data points with missing labels [22, 43]. These imputed labels were then used in evaluating model performance. However, the imputation procedures adopted also make similar assumptions as above and are therefore not well suited to address the problem at hand ([43]). In earlier work [17] we explored techniques to overcome the presence of unobservables in one particular domain, judicial bail decisions. In contrast, here we study the issue of selective labels as a general problem in itself and explore in greater depth the performance of our proposed solution to address it across a broader set of domains.

Counterfactual inference

Counterfactual inference techniques have been used extensively to estimate treatment effects in observational studies. These techniques have found applications in a variety of fields such as machine learning, epidemiology, and sociology [3, 8–10, 30, 34]. Along the lines of Johansson et al. [16], counterfactual inference techniques can be broadly categorized as: (1) parametric methods which model the relationship between observed features, treatments, and outcomes. Examples include any type of regression model such as linear and logistic regression, random forests and regression trees [12, 33, 42]. (2) non-parametric methods such as propensity score matching, nearest-neighbor matching, which do not explicitly model the relationship between observed features, treatments, and outcomes [4, 15, 35, 36, 41]. (3) doubly robust methods which combine the two aforementioned classes of techniques typically via a propensity score weighted regression [5, 10]. The effectiveness of parametric and non-parametric methods depends on the postulated regression model and the postulated propensity score model respectively. If the postulated models are not identical to the true models, then these techniques result in biased estimates of outcomes. Doubly robust methods require only one of the postulated models to be identical to the true model in order to generate unbiased estimates. However, due to the presence of unobservables, we cannot guarantee that either of the postulated models will be identical to the true models.

3 PROBLEM FORMULATION

Here we formalize the notions of selective labels and unobservables, and formulate our problem statement.

Selective labels and unobservables

The goal of this work is to evaluate predictive models in a setting that is characterized by:

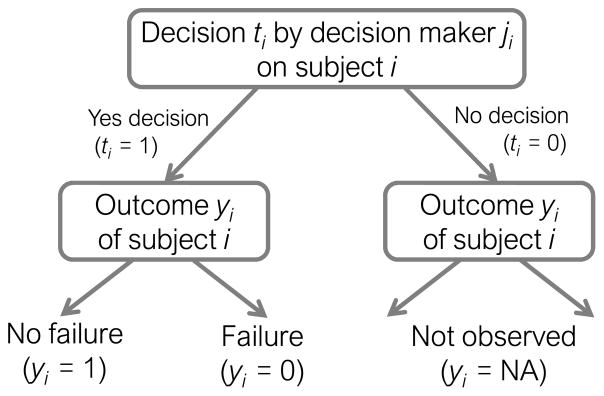
• Selective labels: The judgments of decision-makers determine which instances are labeled in the data (Figure 1).

• Unobservables: There exist unobservables (unmeasured confounders) which are available to the decision-makers when making judgments but are not recorded in the data and hence cannot be leveraged by the predictive models. Furthermore, these unobservables may influence the outcomes and are independent of the features recorded in the data.

Figure 1.

Selective labels problem.

Let x_i denote the feature values of subject i which are recorded in the data. Note that each observation i is also associated with unobservable features z_i that are not captured in the data. This means that the human decision-maker j_i who makes a yes (t_i = 1) or no decision (t_i = 0) on subject i has access to both x_i and z_i. On the other hand, only x_i (but not z_i) is available to predictive model. Let y_i ∈ {0, 1, NA} denote the resulting outcome (that is, label). The selective labels problem (Figure 1) occurs because the observation of the outcome y_i is constrained based on the decision t_i made by the judge j_i:

$$y_i=\{\begin{array}{ll}0\text{or}1,\hfill & \text{if}{t}_i=1\hfill \\ \mathit{not}\mathit{observed}(NA),\hfill & \text{otherwise}\hfill \end{array}$$

Below, we discuss the characteristics of the observational data and the black box model which are inputs to our framework:

Input data

A dataset 𝒟 = {(x_i, j_i, t_i,y_i)} consisting of N observations, each of which corresponds to a subject (individual) from an observational study where x_i, j_i, t_i, y_i are as defined above.

Black box predictive model

Another input to our framework is a black box predictive model ℬ which assigns risk scores to observations in 𝒟. More specifically, ℬ is a function which maps the characteristics (or feature values) x of an observation in 𝒟 to a probability score s ∈ [0, 1]. This score indicates how confident the model is in assigning the observation to t = 0 (e.g., denying bail).

Problem statement

Given the observational data 𝒟 and predictive model ℬ, our goal is to evaluate the performance of ℬ and benchmark it against the performance of human decisions in 𝒟, given the selective labeling of the data and the presence of unobservables.

4 OUR FRAMEWORK

In this section, we introduce contraction, a technique that allows us to address the selective labels problem in the presence of unobservables. We show how it can be used to compare the performance of a predictive model with a given human decision-maker. We then formally define the trade-off curve of failure rate versus acceptance rate, two quantities defined in the introduction: the acceptance rate is the fraction of individuals for whom the decision-maker makes a yes decision, thus providing them with a label and the failure rate is the fraction of bad outcomes in the full population of instances based on the decisions made.

Acceptance rate and failure rate

Decision making often involves optimizing for competing objectives. The goal is to not only minimize the chance of undesirable outcomes (e.g., crimes) but also to reduce the burden (physical, monetary, emotional) on the subjects and other resources (e.g., jail space). In order to quantify such competing objectives and assess the performance of a decision-maker (human or machine), we outline the following metrics:

1. The failure rate of a decision-maker is defined as the ratio of the number of undesirable outcomes (e.g., crimes) occurring due to the decisions made to the total number of subjects judged by the decision-maker. For example, if a judge makes decisions concerning the bail petitions of 100 defendants, releases 70 of them out of which 20 commit crimes, the failure rate of the judge is 0.2.

2. The acceptance rate of a decision-maker is defined as the ratio of the number of subjects assigned to yes decision (t = 1) (e.g., release) by the decision-maker to the total number of subjects judged by the decision-maker. For instance, the acceptance rate of a judge who releases 70% of defendants who appear before him is 0.7.

The goal, given these definitions, is to achieve a high acceptance rate with a low failure rate.

Contraction technique

We can compare a black box predictive model to any given human decision-maker by forcing the acceptance rate of the model to be the same as that of the judge and measuring the corresponding failure rate. If the model exhibits a lower failure rate than the judge at the same acceptance rate, then we can claim that the model is better than that judge. There is, however, an important caveat to this. It is not straightforward to evaluate the failure rate of a model because the outcome labels of some of the observations might be missing due to the selective labels problem. As discussed earlier, imputation and other counterfactual inference techniques cannot be used due to the presence of the unobservables. Here, we discuss a new technique called contraction which allows us to compare the performance of a predictive model to any human judge even in the presence of the unobservables.

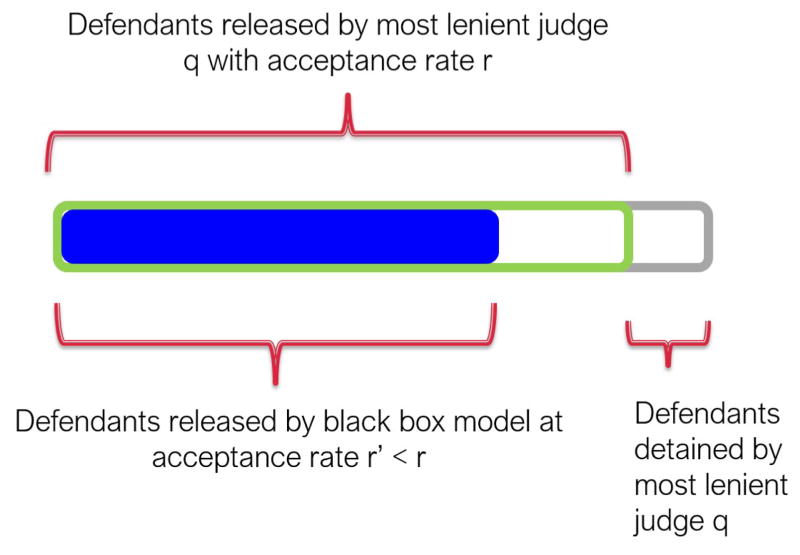
To illustrate the contraction technique(Figure 2), consider the bail setting where each judge decides on bail petitions of 100 defendants. Let us say our goal is to compare the performance of a black box model with that of some judge j′ who releases 70% of the defendants who appear before him, i.e., judge j′ releases 70 defendants and has a acceptance rate value of 0.7. In order to compare the model performance with j′, we run the black box model on the set of defendants judged by the most lenient judge q who releases, say 90%, of the defendants. We achieve this by constraining the black box model to detain the same 10 defendants who were detained by q thus avoiding the missing labels. In addition to these 10 defendants, we allow the black box model to detain another 20 defendants deemed as highest risk by the model. We then compute the failure rate on the remaining 70 defendants who are considered as released by the model. Since the outcome labels (crime/no crime) of all of these defendants are observed, the failure rate can be easily computed from the data.

Figure 2.

Pictorial representation of contraction technique.

Algorithm 1.

Contraction technique for estimating failure rate at acceptance rate r

1:	Input: Observational data 𝒟, Probability scores 𝒮, Acceptance rate r
2:	Procedure:
3:	Let q be the decision-maker with highest acceptance rate in 𝒟
4:	𝒟q = {(x, j, t, y) ∈ 𝒟|j = q}
5:	▷ 𝒟q is the set of all observations judged by q
6:
7:	ℛq = {(x, j, t, y) ∈ 𝒟q |t = 1}
8:	▷ ℛq is the set of observations in 𝒟q with observed outcome labels
9:
10:	Sort observations in ℛq in descending order of confidence scores 𝒮 and assign to ${\mathcal{R}}_q^{\mathit{sort}}$
11:	▷ Observations deemed as high risk by ℬ are at the top of this list
12:
13:	Remove the top [(1.0−r)|𝒟q|]−[|𝒟q| − |ℛq|] observations of ${\mathcal{R}}_q^{\mathit{sort}}$ and call this list ℛℬ
14:	▷ ℛℬ is the list of observations assigned to t = 1 by ℬ
15:
16:	Compute $u={\displaystyle \sum _{l=1}^{\mid {\mathcal{R}}_{\mathcal{B}}\mid }}\frac{𝟙(y_l=0)}{\mid {\mathcal{D}}_q\mid }$
17:	Return u

More generally, the idea behind the contraction technique is to simulate the black box model on the sample of observations judged by the decision-maker q with the highest acceptance rate by contracting the set of observations assigned to yes decision i.e., t = 1 by q while leveraging the risk scores (or probabilities) assigned to these observations by the model. The complete pseudo code formalizing the contraction technique discussed above is presented in Algorithm 1. The contraction technique exploits the following characteristics of the data and the problem setting:

1. Multiple decision-makers: There are many different decision-makers, rather than just one.

2. Random assignment of subjects to decision-makers: If the sample of observations on which we simulate the model is not identical to the sample seen by the judge with whom we are comparing the model, it is not possible to fairly compare the failure rate estimates of the two. We therefore require that observations/subjects are randomly assigned to decision-makers. We find that this requirement typically holds in practice in many decision making settings (more details provided in the experimental evaluation section).

3. Heterogeneity in acceptance rates: The contraction technique relies on the fact that different decision-makers can vary significantly in the thresholds they use for their decisions, resulting in different acceptance rates.

It is important to note that the quality of the failure rate estimate obtained using contraction depends on the extent of agreement between the model and the most lenient judge q with respect to the instances that went unlabeled by q. In the above bail example, if the 10 defendants denied bail by judge q were also among the top 30 highest-risk defendants as ranked by the model, then the estimate of the failure rate would be equal to the true value. If, on the other hand, none of these 10 defendants were among the top 30 high risk defendants based on the model’s confidence scores, then the estimated failure rate would not be the same as the true value.

We now describe how to provide a worst-case bound on the maximum difference between the estimate of failure rate obtained using contraction and its true value.

Proposition 4.1

Suppose the conditions (1)–(3) noted above for applying contraction are satisfied. The error in the estimate of failure rate u of ℬ computed by the contraction algorithm (Algorithm 1) at any value of acceptance rate r ≤ ψ never exceeds $\frac{(1.0-a)\mid {\mathcal{D}}_q-{\mathcal{R}}_q\mid }{\mid {\mathcal{D}}_q\mid }$. The notation is defined in Algorithm 1. In addition, a is the fraction of observations in the set 𝒟_q − ℛ_q that both ℬ and q agree on assigning to a no decision (t = 0), and ψ is the acceptance rate of q.

We now briefly sketch the argument that justifies these bounds. The error in the estimate stems mainly from the disagreements between ℬ and q about assigning defendants in the set 𝒟_q − ℛ_q to a no decision (t = 0). Given that ℬ favors assigning (1.0 − a)|𝒟_q − ℛ_q | subjects in that set to a yes decision i.e., t = 1 (e.g., release), in the worst case, all of these subjects might result in failures or undesirable outcomes. The upper bound on the failure rate is therefore $u+\frac{(1.0-a)\mid {\mathcal{D}}_q-{\mathcal{R}}_q\mid }{\mid {\mathcal{D}}_q\mid }$. Similarly in the best case, all the (1.0 − a)|𝒟_q − ℛ_q| subjects that ℬ chooses to assign to a yes decision (t = 1) result in no failures, and in addition, the same number of subjects that ℬ chooses to assign to t = 0 (e.g., deny bail) turn out to be subjects with undesirable outcomes (failures). Therefore the lower bound on the failure rate is $u-\frac{(1.0-a)\mid {\mathcal{D}}_q-{\mathcal{R}}_q\mid }{\mid {\mathcal{D}}_q\mid }$. In either case, the difference between the failure rate estimated by the contraction algorithm and its true value does not exceed $\frac{(1.0-a)\mid {\mathcal{D}}_q-{\mathcal{R}}_q\mid }{\mid {\mathcal{D}}_q\mid }$.

Machine and human evaluation curves

We can use the contraction technique discussed above to compute the failure rate of the black box model ℬ at various choices for the acceptance rate r ∈ [0, ψ] where ψ is the acceptance rate of the decision-maker q with highest acceptance rate value. We can then plot the curve of failure rate vs. acceptance rate for ℬ which we refer to as the machine evaluation curve.

Analogous to the machine evaluation curve, we can also plot the failure rate vs. acceptance rate curve for human decision-makers. This can be done by grouping decision-makers with similar values of acceptance rate into bins and treating each bin as a single hypothetical decision-maker. We can then compute the failure rate and acceptance rate values for each such bin and plot them as a curve. We refer to this curve as the human evaluation curve.

The machine and human evaluation curves together provide us with a useful way of benchmarking a given model’s performance against human judgment. If the machine evaluation curve exhibits lower failure rates at all possible values of acceptance rate compared to the human evaluation curve, this suggests that the model may be able to make better decisions than expert human decision-makers.

5 EXPERIMENTAL EVALUATION

In this section, we discuss the detailed experimental evaluation of our framework. First, we analyze the accuracy of the estimates of model failure rates obtained using our contraction technique by simulating the selective labels problem using synthetic data. We also compare the effectiveness of our contraction technique to various state-of-the-art baselines commonly used for counterfactual inference and imputation. Lastly, we analyze the utility of our framework in comparing human decisions and model predictions on real-world tasks which are all affected by the selective labels problem: judicial bail decisions, treatment recommendations in health care, and insurance application decisions.

5.1 Evaluation on Synthetic Data

Here we analyze how closely the estimates of failure rates obtained using contraction mimic the true values using synthetic data which captures the effect of selective labels.

Synthetic data

We generate a synthetic dataset with M = 100 human judges each judging 500 subjects (or observations) resulting in a total of N = 50k observations. We simulate three feature variables: X, Z, and W. X corresponds to observable information that is available to both predictive models and human decision-makers. Z represents an unobservable that is accessible only to the human decision-makers but not to the predictive models. In order to mimic real world settings, we include a variable W which represents information that is neither accessible to human decision-makers nor the predictive models but influences the outcome. We model these as independent Gaussian random variables with zero mean and unit variance.

We randomly assign subjects to decision-makers and assign an acceptance rate value r to each decision-maker by uniformly sampling from [0.1, 0.9] and rounding to the nearest tenth decimal place. The outcome variable Y is simulated by modeling its conditional probability distribution as follows: $P(Y=0\mid X,Z,W)=\frac{1}{1+exp-({\beta }_{X}X+{\beta }_{Z}Z+{\beta }_{W}W)}$ where the coefficients β_X, β_Z, and β_W are set to 1.0, 1.0, and 0.2 respectively. The outcome value of an instance for which the variables X, Z, and W take the values x, z, and w respectively is set to 0 if P(Y = 0|X = x, Z = z, W = w) ≥ 0.5, otherwise its outcome value is set to 1.

Analogously, we simulate the decision variable T by modeling its conditional probability distribution as: $P(T=0\mid X,Z)=\frac{1}{1+exp-({\beta }_{X}X+{\beta }_{Z}Z)}$ where ε ~ N(0, 0.1) represents a small amount of noise. The decision variable corresponding to an instance for which X = x, Z = z is set to 0 if the value of P(T = 0|X = x, Z = z) lies within the top (1 − r) * 100% of instances assigned to the decision-maker j, otherwise it is set to 1.

Lastly, the selective labels problem is simulated by ensuring that the outcome labels of only those instances which are assigned to a yes decision (t = 1) are available in the data for the purposes of training the predictive models and computing our evaluation curves.

Model evaluation

We split the synthetic dataset randomly into two sets of 25k instances each and use one of these sets as a training set to train the predictive model and the other as an evaluation test set to which we apply our framework. We train logistic regression model on this training set. We also experimented with other predictive models and observed similar behavior. We use only the instances for which outcome labels are available (i.e., observations assigned to a yes decision) in the training set to train the predictive model. We then evaluate the predictive performance of the model using the following techniques:

• True Evaluation represents the true performance of the model. We evaluate the failure rate on the entire evaluation set using all outcome labels (both observed by the model as well as those hidden from the model)³.

• Contraction: We apply contraction technique discussed in Section 4 to obtain this curve.

• Labeled Outcomes Only: To plot this curve, we first obtain all the subjects whose outcome labels are available in the evaluation set and rank them in ascending order based on the probability scores assigned by the predictive-model. We then simulate the model at various values of acceptance rates r by assigning the observations corresponding to the top r fraction of the sorted list to yes decisions (t = 1). We then compute the failure rate on the observations assigned to yes decisions directly from their corresponding ground truth labels.

• Imputation: We use several commonly employed imputation techniques such as gradient boosted trees, logistic regression, nearest neighbor matching based on feature similarity, propensity score matching, and doubly robust estimation to impute all the missing outcomes in the evaluation set [26, 30]. We then use these imputed outcomes wherever true outcome labels are not available to compute the failure rates of the predictive model. All of the aforementioned approaches except for nearest neighbor matching require learning a regression/imputation model. We use the observations in the evaluation set for which outcome labels are available to learn these models.

Results

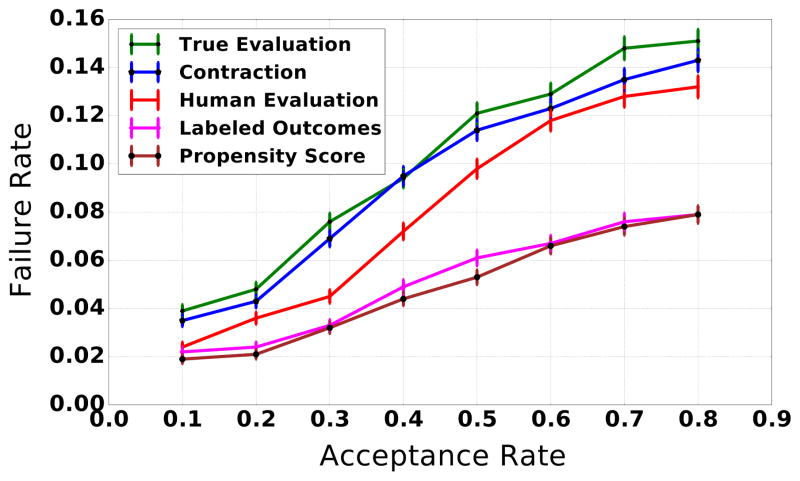
Figure 3 shows evaluation curves for the predictive model as well as the human evaluation curve (Section 4). Note that the true evaluation curve (green curve) captures the true performance of the predictive model. It can be seen that the evaluation curve plotted using contraction (blue curve) closely follows the true evaluation curve demonstrating that contraction is very effective in estimating the true performance of the predictive model.

Figure 3.

Effect of selective labels on estimation of predictive model failure rate (error bars denote standard errors): Green curve is the true failure rate of the predictive model and the machine evaluation using contraction (blue curve) follows it very closely. However, various imputation techniques heavily underestimate the failure rate. Based on the estimates of imputation, one would conclude that the predictive model outperforms human judges (red curve), while in fact its true performance is worse than that of the human judges.

Figure 3 also shows the failure rates estimated by propensity score matching. It can be seen that this technique heavily under-estimates the failure rate of the model. We also observed similar behavior in the case of other imputation techniques. This implies that the estimates of model performance obtained using imputation techniques in the presence of selective labels problem and unobservables are not reliable. Similar behavior is exhibited by the evaluation curve plotted using labeled outcomes only.

Lastly, Figure 3 also shows the failure rates of the human judges (red). Given that the judge has access both to variables X and Z we observe that the judge is making better predictions (lower failure rate) than the predictive model (which only has access to variable X). However, notice that imputation techniques so heavily overestimate the performance of the predictive model that it would lead us to wrongly conclude that the model is outperforming the human judges, while in fact its predictions are less accurate than those of the human judges.

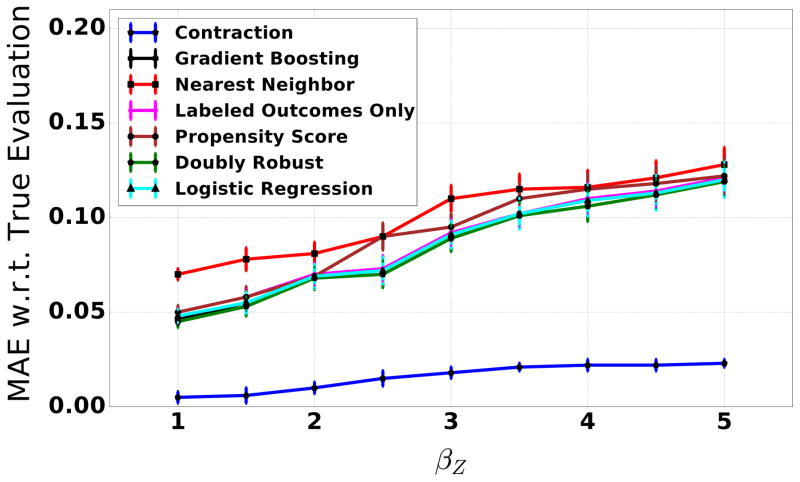
To further demonstrate the effects of selective labels and unobservables on accurately estimating the failure rates of predictive models, we plot the discrepancy, i.e., mean absolute error computed across all possible acceptance rates between the true evaluation curve and the estimated performance of the model using various techniques including contraction(Figure 4). Here we vary the weight β_Z of the unobservable variable Z when generating the outcome labels in the synthetic dataset. As β_Z increases, the effect of unobservables becomes more pronounced. Notice, however, that contraction only slightly overestimates the performance of the model regardless of how strong the problem of selective labels and unobservables is. On the other hand, imputation techniques heavily overestimate the performance of the model and the degree of overestimation steadily increases with β_Z. The mean absolute error of contraction is 6.4 times smaller (at β_Z = 1) compared to the best performing imputation technique and this gap only increases with the increase in the value of β_Z.

Figure 4.

Effect of unobservables (error bars denote standard errors): As we increase the influence of unobservable Z on the outcome Y, imputation techniques result in erroneous estimates of model performance. Contraction, on the other hand, produces reliable estimates.

Analyzing the error rate of contraction technique

Recall that the correctness of the failure rate estimates obtained using contraction technique depend on acceptance rate of the most lenient decision-maker, agreement rate of no decisions between the black box model ℬ and the most lenient decision-maker, and the total number of subjects judged by the most lenient decision-maker. More specifically, higher values of each of these parameters result in tighter error bounds (Section 4) and consequently accurate estimates of failure rates. Next we empirically analyze the effect of each of the aforementioned aspects on the correctness of failure rate estimates obtained using contraction technique.

First, we analyze the effect of the acceptance rate of the most lenient decision-maker on the failure rate estimates obtained using contraction. We generate multiple synthetic datasets by varying the upper bound on the acceptance rate values which can be assumed by decision-makers and then plot the discrepancy (mean absolute error) between true evaluation curves and the estimates obtained using contraction(Figure 5(left)) across various possible acceptance rates of the most lenient decision-maker. It can be seen that the discrepancy increases as the acceptance rate of the most lenient decision-maker decreases. This is consistent with the error bound obtained in Section 4 and can be explained by the fact that the higher the acceptance rate of the most lenient decision-maker, the larger the number of outcome labels observed in the ground truth.

Figure 5.

Analyzing the effect of acceptance rate of most lenient decision-makers (left), agreement rate between the black box model and the most lenient decision-makers (center), and number of subjects judged by the most lenient decisionmakers (right) on the failure rate estimates obtained using contraction technique. Error bars denote standard errors.

Next, we analyze the impact of the agreement rate of no decisions (e.g., who to jail) between the black box model and the most lenient decision-maker(s). In order to do so, we first generate a synthetic dataset and train a logistic regression model as described earlier. We then generate multiple instances of the logistic regression model by changing its predictions in such a way that we can obtain different values of agreement rates between this model and the most lenient decision-maker. Figure 5(center) shows the plot of the mean absolute error of the resulting estimates from contraction with respect to the true evaluation curve at various values of agreement rates. It can be seen that the mean absolute error is low when the agreement rate values are high and it increases with a decrease in the agreement rate. This is mainly because agreement rates are high when the black box model and the most lenient decision-makers make no decisions on the same set of subjects. In such a case, the failure rate estimates can be directly computed from the ground truth.

Lastly, we analyze the effect of the number of subjects judged by the most lenient decision-maker(s) on the correctness of the failure rate estimates obtained using contraction. We generate multiple synthetic datasets by varying the number of subjects judged by the most lenient decision-maker. This is achieved by generating the synthetic data using a similar process as discussed earlier but instead of setting N = 50k, we increase or decrease the value of N until the desired number of subjects are assigned to the most lenient decision-maker. Figure 5(right) shows the plot of mean absolute error of the contraction estimates with respect to the true evaluation curve at various values of the number of subjects judged by the most lenient decision-maker. It can be seen that the mean absolute error decreases steadily with an increase in the number of subjects assigned to the most lenient decision-maker.

5.2 Experiments on Real World Datasets

Next we apply our framework on real world datasets to compare the quality of human decisions and model predictions. We highlight the insights obtained using our evaluation metrics–human and machine evaluation curves on diverse domains such as criminal justice, health care, and insurance.

Dataset description

The bail dataset contains bail decisions of about 9k defendants-collected from an anonymous district court and comprises of decisions made by 18 judges. It captures information about various defendant characteristics such as demographic attributes, past criminal history for each of the 9k defendants. Further, the decisions made by judges in each of these cases (grant/deny bail) are also available. The outcome labels (if a defendant committed a crime when out on bail or not) of all the defendants who have been granted bail and released are also recorded. The selective labels problem in this case stems from the fact that the outcome labels of defendants who have been denied bail by judges cannot be observed.

The medical treatment dataset captures 60k patients suffering from coughing and/or wheezing collected by an online electronic health record company [20]. For each patient various attributes such as demographics, symptoms, past health history, test results have been recorded. Each patient in the dataset was prescribed either a milder treatment (quick relief drugs) or a stronger treatment (long term controller drugs). The outcome labels in this setting indicate if there was a relapse of patient symptoms within 15 days of treatment recommendation. If a patient experiences a relapse of symptoms within 15 days, we consider it a failure. Note that patients assigned to stronger treatment do not experience such a relapse, therefore the selective labels problem here is that we do not observe what would have happened to a patient who received the stronger treatment if he/she had been assigned to a milder treatment.

The insurance dataset comprises of decisions made by 74 managers of an insurance provider which insures large-scale corporations [21]. The dataset comprises of about 50k insurance requests filed by client companies. It captures information about various aspects of the client companies such as the domain they operate in (e.g., legal, chemical, tech etc.), losses and profits, assets owned, previous expertise etc. Each insurance request is either approved/denied by the manager in charge. The outcome labels (profit/loss to the insurance provider) of approved insurance requests are available in the data. The selective labels problem here stems from the fact that we do not observe profit/loss for insurance requests that were denied.

Experimental setup

We split each of the datasets into training and evaluation sets so that we can learn the predictive models on the training set and apply our framework to the evaluation set. In the bail decisions dataset, we use a subset of 4.8k defendants and 9 judges for evaluation. In case of asthma treatments, we use a subset of adult patients comprising of 28k instances and spanning 39 doctors as the evaluation set. Analogously, we use a set of 38k subjects and 41 deciding managers associated with chemical domain as our evaluation set in the insurance requests data and leverage the rest to train the predictive models. We train the predictive models on those instances for which outcome labels are available in the training set. We experimented with various predictive models such as gradient boosted trees, random forests, decision trees, logistic regression, and SVMs. Due to space constraints, we only present results with gradient boosted trees (number of trees = 100) in this section.

Testing for random assignment

Recall that the correctness of our contraction technique relies on the assumption that observations are randomly assigned to human decision-makers, i.e., there is no relationship between human decision-makers and characteristics of subjects. We utilized the following multiple hypothesis testing procedure [23] to validate this assumption:

1. We fit a regression model (M1) which predicts the value of outcome variable y_i for each observation characterized by x_i in the evaluation set. We achieve this by training a regression model on the subjects in the evaluation set who were assigned to yes decisions (t = 1). Let ŷ = {ŷ₁,ŷ₂ ···} denote the estimates obtained for all the observations in the evaluation set using M1.

2. We then fit another regression model (M2) to predict the estimate (ŷ) of M1 based only on the identifier information of human decision-makers.

3. We then calculate the F-test statistic assuming that the null hypothesis that there is no relationship between the decision-makers and characteristics of subjects is true and call this statistic F_s.

4. We determine the 95% confidence interval given the degrees of freedom of the regression model M2 and accept the null hypothesis if F_s falls within this interval. We reject the null hypothesis and assume that the random assignment assumption does not hold otherwise.

Based on the above test, we found that the null hypothesis holds on all our evaluation sets indicating that subjects are randomly assigned to decision-makers in our evaluation sets.

Evaluation and results

We plot human and machine evaluation curves for all the three real-world datasets (Figure 6). We plot all the machine and human evaluation curves as described in Section 5.1.

Figure 6.

Comparing the performance of human decision-makers and predictive models on bail (left), medical treatment (center), and insurance (right) datasets (error bars denote standard errors). Labeled outcomes only curve results in overoptimistic estimates. Contraction produces more accurate estimates of model performance

Figure 6 shows that both the machine evaluation curve plotted using contraction (black) as well as the one plotted only using only the labeled outcomes (blue) indicate that the predictive model is exhibiting lower failure rates than human decision-makers (red) at all possible values of acceptance rates on all the three datasets.

The estimates of model performance obtained using contraction are more reliable in practice because it turns out to be the case that the subjects assigned to no decisions (t = 0) by the decision-maker(s) with highest acceptance rate (let this decision-maker be denoted as j′ with risk tolerance r′) are often so risky that the model concurs with the decision-maker in assigning these subjects to no decision (t = 0). We found that the agreement rate (see Section 4) which is the ratio of the number of observations that both the predictive model at risk tolerance r′ and j′ agree on assigning to no decision (t = 0) to the total number of observations assigned to no decision by j′ is 0.891, 0.932, and 0.718 on bail decisions, asthma treatments, and insurance requests datasets respectively. These high agreement rates ensure that the estimates of model performance obtained using contraction are close to the true values. It can be inferred from Figure 6 that the estimates of labeled outcomes only curve are overly optimistic about the model performance across all the datasets given that our contraction estimates accurately model the true values.

6 CONCLUSIONS AND FUTUREWORK

In this paper, we addressed the problem of evaluating predictive models in settings affected by the selective labels problem. More specifically, we developed an evaluation metric, failure rate vs. acceptance rate, which can be used to effectively compare human decisions and algorithmic predictions. Furthermore, we proposed a novel technique called contraction which can be used to estimate our evaluation metric without resorting to traditional imputation/counterfactual inference procedures which are not suitable for settings with unmeasured confounders (unobservables). This work marks an initial attempt at addressing the problem of selective labels in the presence of unmeasured confounders and paves way for several interesting future research directions. For instance, our framework can be readily applied to various domains where human decision making is involved ranging from public policy to health care and education. Furthermore, it would be interesting to explore how the contraction technique proposed in this work can be leveraged to improve the process of training machine learning models on selectively labeled data.