Detection of coronary artery disease by reduced features and extreme learning machine

Abstract

Objective

Cardiovascular diseases generate the highest mortality in the globe population, mainly due to coronary artery disease (CAD) like arrhythmia, myocardial infarction and heart failure. Therefore, an early identification of CAD and diagnosis is essential. For this, we have proposed a new approach to detect the CAD patients using heart rate variability (HRV) signals. This approach is based on subspaces decomposition of HRV signals using multiscale wavelet packet (MSWP) transform and entropy features extracted from decomposed HRV signals. The detection performance was analyzed using Fisher ranking method, generalized discriminant analysis (GDA) and binary classifier as extreme learning machine (ELM). The ranking strategies designate rank to the available features extracted by entropy methods from decomposed heart rate variability (HRV) signals and organize them according to their clinical importance. The GDA diminishes the dimension of ranked features. In addition, it can enhance the classification accuracy by picking the best discerning of ranked features. The main advantage of ELM is that the hidden layer does not require tuning and it also has a fast rate of detection.

Methodology

For the detection of CAD patients, the HRV data of healthy normal sinus rhythm (NSR) and CAD patients were obtained from a standard database. Self recorded data as normal sinus rhythm (Self_NSR) of healthy subjects were also used in this work. Initially, the HRV time-series was decomposed to 4 levels using MSWP transform. Sixty two features were extracted from decomposed HRV signals by non-linear methods for HRV analysis, fuzzy entropy (FZE) and Kraskov nearest neighbour entropy (K-NNE). Out of sixty-two features, 31 entropy features were extracted by FZE and 31 entropy features were extracted by K-NNE method. These features were selected since every feature has a different physical premise and in this manner concentrates and uses HRV signals information in an assorted technique. Out of 62 features, top ten features were selected, ranked by a ranking method called as Fisher score. The top ten features were applied to the proposed model, GDA with Gaussian or RBF kernal + ELM having hidden node as sigmoid or multiquadric. The GDA method transforms top ten features to only one feature and ELM has been used for classification.

Results

Numerical experimentations were performed on the combination of datasets as NSR-CAD and Self_NSR- CAD subjects. The proposed approach has shown better performance using top ten ranked entropy features. The GDA with RBF kernel + ELM having hidden node as multiquadric method and GDA with Gaussian kernel + ELM having hidden node as sigmoid or multiquadric method achieved an approximate detection accuracy of 100% compared to ELM and linear discriminant analysis (LDA)+ELM for both datasets. The subspaces level-4 and level-3 decomposition of HRV signals by MSWP transform can be used for detection and analysis of CAD patients.

Introduction

As per the World Health Organization (WHO) reports, cardiovascular heart diseases are major cause of mortality in the total population. WHO evaluated that 30% of world population deaths result from cardiovascular heart diseases and expected 23.6 million will endure to these diseases by 2030 [1]. Death rate due to coronary artery disease (CAD) is higher than some other kind of cardiovascular coronary diseases [2]. Coronary artery disease (CAD) is portrayed by narrowing or blockage of coronary artery for the most part caused by atherosclerosis. Atherosclerosis involves plaques and cholesterol accumulates inside the coronary arteries, which impeded the flow of blood into the heart muscles [3]. Because of this, heart pumping is disturbed and may eventually prompt sporadic heartbeat pulses and hence sudden heart failure. The CAD starts in early life and increases gradually. On the off chance that it is not analyzed and treated properly, it will in the end prompt either auricular ischemia or ventricular ischemia or then myocardial infarction. In this way, the starting stage detection of CAD is of prime noticeable quality, and requires an efficient detection approach and heart rate variability (HRV) analysis techniques.

The HRV investigation has turned into a prominent non-invasive diagnostic tool in cardiology to evaluate the activities of the autonomic nervous system (ANS). The HRV is determined by computing time intervals between successive R peaks points on the QRS complex of the electrocardiogram (ECG) [4]. Morphological format impression of ECG signal is basic yet not sufficient to recognize the presence of CAD because subtle variations are challenging to identify by ECG alone in CAD patients, hence, it is a must to portray these ECG signals into HRV signals [5,6]. Over the years, various methods, like time domain, spectral domain and non-linear domain methods have been proposed for examining the variations of these interval values, the purpose of most being the credentials of HRV dissimilarities between ECGs of healthy young, elderly subjects and CAD, cardiac heart failure patients in addition to the study of the autonomic nervous system (ANS), leading to possible prognostic or diagnostic information [7,8]. In recent years, a number of investigators have analyzed the HRV by different advanced digital signal processing methods, statistical methods [9], box plot and mean and standard deviation and prominence has been given on classification to detect the normal group and diseased group with different classifiers [10–13].

Advanced digital signal processing approaches can be used in computer-aided diagnosis system to detect the CAD patients. It is a cost effective methods to improve the detection speed of cardiac disease. These systems use features derived by linear, as spectral, time [14] and nonlinear [15] signal processing methods to identify disease related information from cardiovascular signals. Nonlinear techniques are more sensitive than linear methods for recognizing and comprehending the abnormalities of HRV [16]. The explanation behind this better affectability and accuracy has been described by Acharya et al. [6], who demonstrated that the heart is a chaotic (non-linear) oscillator under normal cardiovascular activity. Using non-linear features extracted directly or indirectly from HRV signals, an effective reliable computer supported diagnosis systems can be designed which can detect cardiovascular activity with a high level of accuracy as well as positive affectability values.

The machine learning and artificial intelligence methods are extremely powerful tools for binary and multi-class classification and prediction of cardiac disease. Recently, a new learning process for single hidden layer feedforward neural networks (SLFNs) design called extreme learning machine (ELM) strategy has been widely used in many fields like bio-medical signal analysis and large data analysis [17]. The primary advantage of ELM is that the hidden layer of SLFNs does not require tuning and it also has fast rate of convergence [18]. Indeed, for the arbitrarily picked hidden layer biases and input weights, ELM will prime to a least squares elucidation of a system of non- linear signals for the unidentified output weights having the smallest norm property [18]. Nevertheless, the learning speed of ELM can be thousands of times faster than the traditional feedforward network learning algorithms [17].

In this paper, we have proposed a noninvasive efficient approach using generalized discriminant analysis (GDA) having radial basis function (RBF) or Gaussian (Gausn) kernel function + ELM that can automatically detect the CAD patients using HRV signals. Due to the non-linear nature of HRV signals [19], the multiscale wavelet packet (MSWP) transform [20] is employed to decompose the HRV signals into 4-levels sub space signals. The 64 features are extracted from decomposed sub spaces of HRV signals using fuzzy entropy (FZE) and Kraskov nearest neighbour entropy (K-NNE). Not all the features distinguish well between normal and CAD HRV signals. Therefore, we have used features ranking technique such as the Fisher score, which rank the features according to their clinical significance. The top ten ranked features (highest to lowest, which are ranked by Fisher scheme) are fed to the features reduction scheme as GDA or linear discriminant analysis (LDA). Then, the reduced dimension of features is fed to the extreme learning machine (ELM) binary classifier which differentiates between normal and CAD subjects. The sequence of steps involved in the proposed work is shown in Figure 1. The simulated results show that the proposed detection system achieved an approximate testing accuracy of 100 % for both data sets compared to LDA having regularized solution (Regul. Soln) or singularity solution (Sinty Soln) + ELM having sigmoid or multiquadric hidden nodes and ELM having sigmoid or multiquadric hidden nodes.

Figure 1.

Flow chart of proposed algorithm for detection of CAD and normal subjects.

The following section explains the HRV signal extraction and detection method. The database and pre-processing are described in Section 2. Methodology is explained in Section 3. Results and discussions are described respectively in sections 4 and 5. Finally the paper is concluded in Section 6.

Materials and pre-processing

Database

The R-R interval (HRV) data used in this work has been obtained from the ECG signals provided by the normal sinus rhythm (NSR) from MIT BIH database and the CAD data has been obtained from St. Petersburg Institute of Cardiological Technics database [21]. The databases of NSR consisted of eighteen long-term ECG recordings of subjects referred to the Arrhythmia Laboratory at Boston’s Beth Israel Hospital. Subjects involved in this database were found to have had no significant arrhythmias; they include five men, aged 26 to 45, and thirteen women, aged 20 to 50 [21]. The database of St. Petersburg Institute of cardiological technics consists of 75 annotated recordings extracted from 32 Holter records. Each record was 30 minutes long and contains standard ECG leads. Only thirteen subjects (9 men and 4 women, aged 18–80; mean age: 58) suffered from CAD [21]. The self-recorded data base consists of 13 healthy men subjects, aged between 23 and 32 years. The ECG was continuously recorded for 30 minutes of each subject in the relaxed supine and normal sinus rhythm position in a room free from any kind of disturbance with controlled temperature (22–25°C). The subjects did not suffer from diabetes and any type of heart disease. The recording of ECG using electrode placement method was done at the sampling rate of 500 Hz with BIOPAC: MP150 in combination with BIOPAC’s “Acqknowledge 4.2” software. The R peaks of the ECG signal were detected using modified Tompkins’s algorithm [22,23]. The R-R interval for each subject was then computed. All ECG measurements were taken at the National Institute of Technology, Jalandhar, India.

Pre-processing

Pre-processing of R-R interval time series data was required before analysis of HRV signals to reduce error and enhances the sensitivity of time series data. First we have done ectopic beat or interval detection and correction before HRV analysis. In this paper, the ectopic beats were detected on the premise of standard deviation filter method which marks outliers as being intervals that lie outside the overall mean R-R interval by a user defined value of standard deviation. The user defined value was used as 3 times the standard deviation [24]. A cubic spline interpolation method was used to replace ectopic intervals located during the detection process. After replacing R-R intervals, they were coded as normal to normal intervals (NN intervals). The NN intervals were sampled at 4 Hz.

Initially, we have selected 2,150 samples of NN interval for each subject of the database, the first 100 samples and last 50 samples have been excluded from each subject of epoch so that all the subjects were alleviated to the recording atmosphere. This was done in order to provide the prospect of subject evaluation under similar activity levels. To increase in training and testing data size, the remaining 2000 samples of NN interval were divided into segments of 500 NN intervals. Finally, the segments of NN intervals were used for the feature extraction by MSWP transform.

Methodology

HRV signals decomposition by MSWP transform

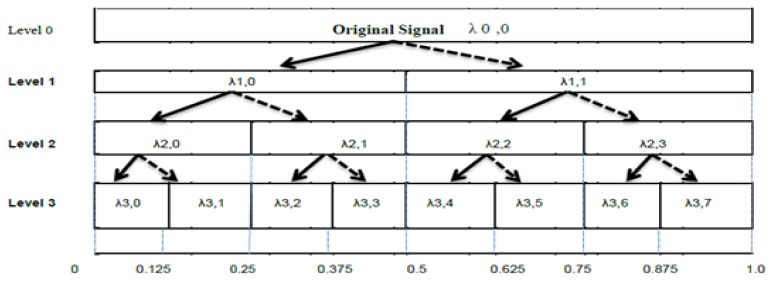
The multiscale Wavelet Packet (MSWP) transform was first described by Coifman et al. [25]. They comprehensive the link between wavelets and multiresolution approximations. The MSWP may be considered as a tree of sub-spaces, with λ_0,0 denoting the original signal space, i.e., the root node of the tree. In a general notation, the node λ_l,m, with l denoting the scale and m denoting the subband index within the scale, is decomposed into two orthogonal subspaces as an approximation space λ_l,m→ λ_l+1,2m and detail λ_l,m→ λ_l+1,2m+1 space. This is done by dividing the orthogonal basis {θ_l(t - 2^lm)}mɛZ of λl,minto two new orthogonal base {θ_l+1(t - 2^l+1m)}_mɛZ of λ_l+1,2m and {ϕ_l+1(t - 2^l+1m)}_mɛZ of λ_l+1,2m+1 [26]. Where θ_lm(t) and ϕ_lm(t) are scaling and wavelet function, respectively and are defined as θ_lm(t) = 1/✓|2^l| {θ((t-2^lm) /2^l)} and ϕ_l,m(t) = 1/✓|2^l| {ϕ((t-2^lm)) /2^l)}, where 2^l is a scalling parameter and 2^lm is translation function.

The HRV data was decomposed by the MSWP using the Haar wavelet whose mother wavelet function is simply a step function. The dilation and translating for the MSWP were built on powers of 2 or dyadic chunks, e.g., 2⁰, 2¹, 2² etc. The dilation function was repeatedly represented as a tree of high and low pass filters. The first level of the tree decomposes the HRV original data into detail (high frequency, indicated by bold line in Figure 2) and approximation (low frequency, indicated by dotted line in Figure 2) components. Both branches of the tree were split into finer components as λ0,0 into λ1,0 and λ1,1. Figure 2 shows the tree for MSWP for 4 levels of decomposition. A complete description of the method is explained in [20]. The MSWP generated 2^level features at each level of decomposition. Hence, the total no of features are 31 for the 4 level decomposition of HRV signals. For the analysis of MSWP transform, the number of samples of HRV per every window and the increments during windows were chosen as 32 and 4, respectively.

Figure 2.

Example of decomposition of MSWP for 3 levels, vertical axis and horizontal axis shows level of decomposition and frequency variety as a fraction of the Nyquist frequency. The λ1,0, λ1,1……….. λ1,1 represents detail and approximation components of HRV signals.

Non-linear feature as fuzzy entropy

Nonlinear features are broadly used to investigate the HRV signals [10,27]. These features have ability to extract the concealed nonlinear nature of HRV signals [6]. For finite HRV time series X={X₁, X₂……………X_M}, of length M. The fuzzy entropy (FZE) can be calculated as

$$\text{FZE}(\text{X},\text{m},\text{N},\text{R})=\text{ln}({\mathrm{\rho }}^{\text{m}})-\text{ln}({\mathrm{\rho }}^{\text{m}+1})$$ (1)

Where ρ^m is defined as:

$${\rho }^m(X,N,R)=\frac{1}{M-m}{\sum }_{i_1=1}^{M-m}\frac{1}{M-m-1}{\sum }_{i_2=1,i_1\ne i_2}^{M-m}{e}^{-}\frac{{(D_{i_{1,i_2}})}^N}{R}.$$

Again, ρ^m+1 calculated same manner for embedding dimension m+1. The value of similarity degree D_i1,i2 is calculated through fuzzy function as

$$e^{-}\frac{{(D_{i_{1,i_2}})}^N}{R}.$$

for HRV time series X, where N is Fuzzy power and R is tolerance [28]. In this work, the embedding dimension m, FZE of power N, and tolerance R for all of the data of decomposed HRV were respectively chosen as 4, 2, and 0.15 times the standard deviation of decomposed HRV signals.

Non-linear features as Kraskov nearest neighbour entropy

The Kraskov nearest neighbour entropy (K-NNE) estimator KNNE ( X ) of differential entropy for a HRV variable signal X of length M can be calculated as [29,30]

$$\text{KNNE\hspace{0.17em}}(X)=\vartheta (M)-\vartheta (k)+\text{log}(c_D)+\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$M$}\right.{\mathrm{\Sigma }}_{l=1}^M\text{log}\hspace{0.17em}[\varepsilon (l)]$$ (2)

Where d represents the dimension of signal X, the ɛ(l) is the distance between the l^th sample of HRV signal X and its k nearest neighbor. The ϑ(k) denotes a digamma function and calculated as [29]

$$\vartheta (Y)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Gamma }(Y)$}\right.\frac{d\mathit{\Gamma }(Y)}{dY},$$ (3)

The c_D denotes a size of D dimensional unit ball. It is calculated for Euclidean norm [30]

$$c_D=\frac{{\pi }^D}{\mathit{\Gamma }(1+\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}$$ (4)

For simulation of K-NNE, k-nearest neighbours sample was chosen as 5.

Box Plot

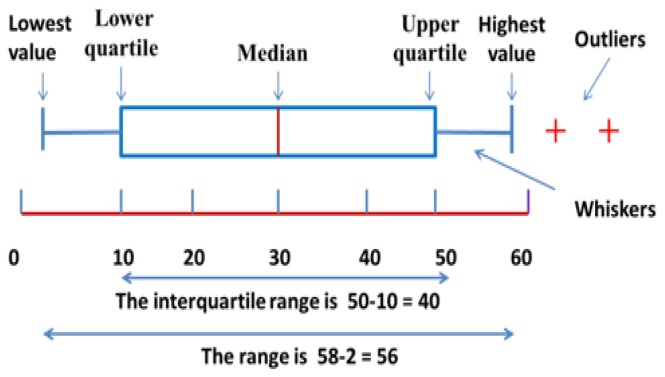
A box plot is a graphical method for representing groups of numerical data along with their quartiles values. It may also have straight lines outspreading vertically from the boxes (whiskers) indicative of erraticism separate the upper and lower quartiles with box plot [46]. Outliers are plotted as separate points or plus symbols. Box plots are non-parametric, they show variety in tests of a measurable data without making any presumptions of the underlying statistical dissemination [47].The dividing between the assorted parts of the case demonstrates the level of scattering (spread) and skewness in the information, and show outliers. Besides, the box plot allows the visual assessment of several parameters, notably the interquartile range, mid-range and median. The labeling of a box plot is shown in Figure 3.

Figure 3.

A brief descriptions with proper labeling of box plot.

Features Ranking Method

Features can be chosen using a feature ranking approach. The ranking approaches allocate ranks to the considered large number of features and array them according to their statistical significance. Further, the lower ranked features can be ignored and higher ranked features can be considered for classification [31,32]. These approaches reduce the intricacy of the features dimensions and significantly decreases the time for processing the data without affecting the binary classification enactment. In this work, we have used Fisher score method to rank the features extracted by entropy methods. It is based on filter methods, to rank the features as a pre-processing stride previous to the learning algorithm, and to choose those features having high ranking Fisher score [33].

Generalized discriminant analysis

As a result of the large changes in the HRV time series patterns of a number of cardiac disease classes, there is commonly a significant similarity between some of the cardiac disease classes like NSR and CAD subjects in the non-linear feature space. In these classes having the larger similarity with each other, it is a challenge to differentiate between the two by ranking methods [34]. In this condition, a feature dimension transformation technique like GDA will be very useful. The GDA is a non-linear extension of LDA.

In GDA, the given training data sample is mapped by a kernel function like RBF or Gaussian (Gausn) to a high-dimensional feature space of HRV, where dissimilar classes label of features are made-up to be linearly distinguishable. The LDA technique is then applied to the high-dimensional feature space, where it finds for those vectors that best differentiate among the classes label somewhat than those vectors that best define the training data [35]. Indeed, the aim of the LDA is to search for a transformation matrix that maximizes the ratio of the between-class label scatter to the within-class scatter. In addition, it provides a number of independent features spaces which to be the data [9]. If there are β classes label in the given features, the dimension of feature space of HRV can be reduced to β-1 by GDA method. In this paper, 2 numbers of classes (i.e. binary classes) are taken and the top 10 features are reduced to one feature by GDA. The mathematical expressions of GDA are explained in [35].

Extreme Learning Machine as binary classifier

Assume that {X_k,T_k}_k=1,2….,m is a data set of training samples, where for the input features X_k={X_k1, X_k2,…….,X_Kn}^tɛRⁿ are applied to the input nodes and its corresponding target vector value (class label) T_kɛR or ɛ{-1,1}, where t denotes the transpose of the vector matrix. For one of the learning machine method SLFNs, ELM arbitrarily assigned value of weights vector a_s={a_s1,a_s2,…..,a_sn}^t and the bias B_SɛR containing the input layer to s^th hidden node. The weight vector a_s connecting between input layers to the hidden nodes. The SLFNs with L number of hidden nodes approximate the input features with zero error if there exists analytically determines the output weight vector W={W₁,W₂,………..W_L}^tɛR^L connecting between hidden nodes and output nodes [36]. The target value of SLFNs or ELM is formulated as

$$T_k={\mathrm{\Sigma }}_{s=1}^L{W}_S\hspace{0.17em}\mathit{\Theta }\hspace{0.17em}(a_s,B_s,X_k)$$

for k= 1, 2, ----, m. Where Θ(.)= Θ(a_s,B_s,X_k) is activation function, which represents the output of the sth hidden nodes for the input features samples and parameters. The target vector (generated from output nodes) is linearly related with W and Θ hence, it can be formulated in the matrix form as

$$\text{H\hspace{0.17em}W}=\text{T}$$ (5)

Where

$$\text{H}={\left[\begin{array}{ccc}\mathit{\Theta }\left({\text{a}}_1,{\text{B}}_1,{\text{X}}_1\right)& \cdots & \mathit{\Theta }\left({\text{a}}_{\text{L}},{\text{B}}_{\text{L}},{\text{X}}_1\right)\\ ⋮& \dots & ⋮\\ \mathit{\Theta }\left({\text{a}}_1,{\text{B}}_1,{\text{X}}_{\text{m}}\right)& \cdots & \mathit{\Theta }\left({\text{a}}_{\text{L}},{\text{B}}_{\text{L}},{\text{X}}_{\text{m}}\right)\end{array}\right]}_{\text{m}\times \text{L}}$$ (6)

is the output matrix of hidden layer neural network and T={T₁, T₂,…….,T_m}^tɛR^m is the vector of target. To obtain a minimum norm least square solution of W for the linear system of (13), this can be explicitly achieved to be [18]. W=H^†T. Where H^† is the inverse of H matrix, this is known as name of Moore-Penrose generalized inverse [37]. Finally, by accomplishing the solution of W={W₁, W₂,………..W_L}^tɛR^L, a decision function F(.)is determined for any input of features sample X={X_k1, X_k2,….,X_Kn}^t ɛR^n. Mathematical expression of F(.) is represented as

$$\text{F}(\text{X})=(\mathrm{\Theta }({\text{a}}_1,{\text{B}}_1,\text{X}),\mathrm{....},\mathrm{\Theta }({\text{a}}_{\text{L}},{\text{B}}_{\text{L}},\text{X}))\text{W}$$ (7)

Though, intended for binary classification problem, the decision function is based on signum function, and defined as

$$\text{F}(\text{X})=\text{sign}\{(\mathrm{\Theta }({\text{a}}_1,{\text{B}}_1,\text{X}),\mathrm{....},\mathrm{\Theta }({\text{a}}_{\text{L}},{\text{B}}_{\text{L}},\text{X}))\text{W}\}$$ (8)

It is important to note that, once the values of the weights vector a_sɛRⁿ and the bias B_sɛR are arbitrarily assigned at the establishment of the learning algorithm, these values remain fixed and so the elements of matrix H remain constant.

The performance of the proposed method ELM has been tested on additive hidden nodes and RBF. For this test, the activation function Θ(a_s,B_s,X) was considered as the sigmoid function and defined as Θ(a_s,B_s,X)=1/(1+exp(-(a^tX+B)). For additive nodes, multiquadric function described by [38] as

$$\mathit{\Theta }\hspace{0.17em}(\text{a},{\text{B}}_{\text{s}},\text{X})=\sqrt{({\left|\right|X-a\left|\right|}_2^2+B^2)}$$

the function is intended for RBF hidden nodes. Intended for multiquadric and sigmoid activation functions, the hidden node parameters were picked arbitrarily with uniform distribution in [−0.4, 0.4]. The input weights of the hidden nodes and biases of hidden layer were selected arbitrarily at the starting of the learning for ELM and these values remains constant in every test of simulation. The number of hidden nodes parameter L was calculated by executing 10-fold cross-validation on the features with corresponding binary class label. In order to validate our proposed scheme, we have generated arbitrarily pre-defined subjects for training and rest subjects for testing of every data set. These processes were conducted in 20 independent trials and average of testing accuracy was calculated. The accuracy was calculated by using binary classification Gold standard scheme and defined as

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\times 100$$ (9)

Where TP, TN, FP, and FN denote number of true positives, true negatives, false positives and false negatives respectively.

Results

Table I depicts the comparative investigation of NSR-CAD dataset and Self_NSR-CAD dataset by top ten ranked features of FZE and K-NNE in the form of mean and its standard deviation (S d.), with their p value obtained from Wilcoxon rank sum test. Top ten ranked features were extracted by FZE and K-NNE entropy from 4-level decomposition of HRV signals by MSWP transform for both datasets. These ranked features are arranged in the descending order according to their Fisher score, shown in the Table I (top to bottom, 1st and 5th column) for both datasets. In case of NSR-CAD data set, the features of FZE at decomposition level-4 of HRV signals, approximate (App) and detail (Det) coefficient having higher features score than K-NNE features at decomposition level-4 of HRV signals. While, in case of Self_NSR-CAD data set the features of K-NNE at decomposition level-4 at first rank then after FZE at decomposition level-4, level-3. Results of Table I also shows that the features extracted by FZE and K-NNE at 4th level and 3rd level of decomposition as App and Det coefficient has lowest p-value (<0.00001). A lower most p-value specifies that this feature has highest discernment ability. Therefore, we can choose 4th or 3rd level of decomposition to analyze the NSR subjects and CAD patients. The mean value of FZE features at 4th and 3rd level for CAD patient is higher than NSR and Self_NSR subjects, while, the mean value of K-NNE features at this level of decomposition for NSR is higher than CAD.

Table I.

The Mean and standard deviation (S d.) and corresponding p-Value of the top ten ranked features extracted by FZE and K-NNE from 4-level decomposition of HRV signals by MSWP transform for NSR-CAD and Self_NSR-CAD data set. Top ten ranked features arrange on the basis of highest Fisher score to low score (top to bottom, 1^st and 5^th column) in the table for both data set. L indicates the level of decomposition; App. represents approximate coefficient and Det. represents detail coefficient of decomposed subspace signals. For statistical significance, if p>0.05: not significant, p≤0.05: significant and p<0.01: very significant.

Features-Level/Approximate or Detail coefficient	NSR (Mean ± S d.)	CAD (Mean ± S d.)	p-Value	Features-Level/Approximate or Detail coefficient	Self-NSR (Mean ± S d.)	CAD (Mean± S d.)	p-Value
FZE-L4-App.	0.038±0.017	0.12±0.081	1.30E-12	K-NNE-L4-App.	−2.938±0.666	−1.727±1	3.71E-08
FZE-L4-Det.	0.033±0.016	0.105±0.071	1.74E-12	FZE-L4-Det.	0.029±0.013	0.101±0.07	2.87E-07
FZE-L4-Det.	0.03±0.015	0.101±0.07	9.99E-10	FZE-L3-Det.	0.021±0.01	0.08±0.058	2.33E-07
FZE-L4-App.	0.039±0.019	0.115±0.076	1.05E-10	FZE-L2-Det.	0.016±0.008	0.062±0.047	2.15E-05
FZE-L4-App.	0.036±0.016	0.123±0.088	2.19E-10	FZE-L1-App.	0.011±0.006	0.048±0.037	1.7E-04
K-NNE-L4-App.	−2.931±0.737	−1.72±1.004	1.61E-10	K-NNE-L4-App.	−2.857±0.661	−1.72±1.004	9.6 E-07
FZE-L3-App.	0.025±0.015	0.082±0.056	2.23E-09	FZE-L4-App.	0.038±0.021	0.123±0.088	8.30E-07
FZE-L3-Det.	0.023±0.015	0.08±0.058	1.26 E-09	FZE-L3-App.	0.028±0.014	0.082±0.056	8.23 E-07
K-NNE-L4-Det.	−3.062±0.891	−1.761±1.041	3.18E-09	FZE-L4-Det.	0.037±0.018	0.105±0.071	9.38 E-06
K-NNE-L3-App.	−3.409±0.891	−2.108±1.041	3.18E-09	K-NNE-L3-Det.	−3.691±0.733	−2.293±1.343	5.86E-06

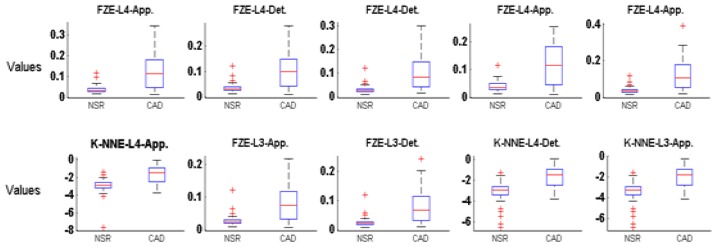
Boxplots for the top ten features of FZE and K-NNE entropy estimator are illustrated in Figure 4 for the NSR-CAD dataset. As seen the shapes of box plot related to the NSR and CAD subjects are well separated from the other classes within the same features. In each case, the median values, lower quartile, upper quartile and highest values of features for CAD subjects are higher than those of NSR subjects. However, lowest values are similar for all top ten features. In the case of NSR subjects, the outliers (indicates the dynamicity of HRV signal) are more compared to CAD subjects hence, these statistical parameters can be differentiated between NSR and CAD subjects.

Figure 4.

Box plot of top ten ranked features extracted by non-linear FZE and K-NNE method from decomposed HRV signals by MSWP for NSR-CAD data set.

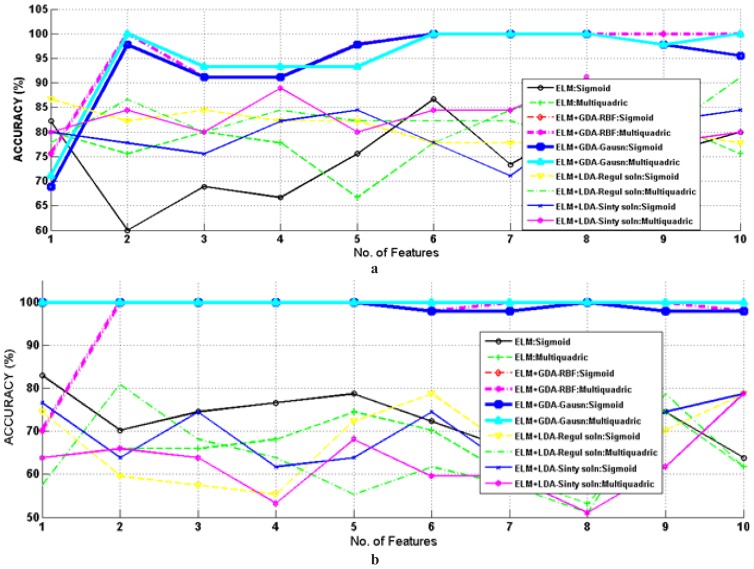
A graph of number of features versus testing accuracies for several classification methods is shown in Figure 5 (a) and (b) for NSR-CAD and Self_NSR-CAD data set. In this figure, the ELM with several dimension reduction schemes having different kernel functions were used in this work to achieve maximum accuracy of binary classification using the least number of features from the top ten features. Top ten features extracted by FZE and K-NNE from decomposed HRV are organized in the order according to their ranking by Fisher score. These ranked features were fed to the binary classifier one by one up until the highest detection accuracy was reached. In case of the NSR-CAD data set, the proposed classifier achieved approximately 100 % testing accuracy for two features, depicted in Figure 5 (a) While, in case of Self_NSR-CAD, the maximum accuracy of 100% is attained by ELM with multiquadric and sigmoid hidden node+ GDA with Gaussian kernel function for every top ten features, shown in Figure 5 (b). Their results were compared from LDA having Regul. Soln or Sinty Soln + ELM having sigmoid or multiquadric hidden nodes and ELM having sigmoid or multiquadric hidden nodes. This detection was an upsurge in the accuracy with GDA compared to without GDA, a clear result since GDA was used as a feature vector dimension transformation approach and transform to one feature vector by selecting best discriminating of top ten ranked features.

Figure 5.

Plots depicting detection accuracies for different number of top ten ranked features with GDA + ELM, LDA+ ELM having different kernel functions and hidden nodes and ELM having hidden nodes as sigmoid and multiquadric for (a) NSR- CAD (b) Self_NSR-CAD.

Discussion

In Table II, an ephemeral summary of investigation carried out by many authors for HRV signals, study the features using several techniques like discrete wavelet transform (DWT), flexible analytic wavelet transform (FAWT), wavelet packet transform (WPT) [32,39], different features dimension reduction approach namely principal component analysis (PCA), independent component analysis (ICA), LDA, GDA [35,40], and several binary classification techniques as k-nearest neighbors (KNN) algorithm, Support vector machine (SVM), artificial neuron network (ANN), ELM exploring in terms of accuracy investigated on CAD patients and healthy subjects. It shows that broad research has been completed in recent years in the study and detection of CAD patients with different methods. Babak et al. [35], Patidar et al. [41], Lee et al. [12] and Mohit et al. [32] have employed HRV study using linear and non-linear methods for features extraction and t-test, PCA, GDA as an features diminishment scheme, while classifying tried for different approaches and found SVM and least squares support vector machine (LS-SVM) as better with 95.77%, 90%, 99.72% and 100% accuracy.

Table II.

An ephemeral summary and assessment of the classification accuracy of the proposed work with the existing work.

Authors	Methods	Features	Classifier	Accuracy %
Karimi et al. [39 40]	DWT, HSS and WPT	Several statistical features	ANN	90
Lee et al. [12]	Nonlinear methods, Linear, and reduced features by t-test	5 nonlinear features and 6 Linear	SVM	90
Babak et al. [35]	Linear, non linear methods and features reduced by GDA and LDA	7 time domain, 1 frequency and 7 non-linear	SVM	95.77
Zhao and Ma [42 43]	EMD, and TEO	Several statistical features	BPNN	85
Babaoglu et al. [43 44]	GA, EST and BPSO	11 Features	SVM	81.46
Babaoglu et al. [44 45]	EST and features reduced by PCA	18 Features	SVM	79.17
Dua et al. [40 41]	Features reduced by PCA	6 Nonlinear features	MLP	89.5
Giri et al. [11]	DWT, features reduced by ICA,	10 Features	GMM	96.8
Patidar et al. [41 42]	TQWT and features reduced by PCA	2 Entropy features	LS-SVM with Morlet wavelet kernel	99.72
Nan Liu et al. [45 46]	Selective and total segments	Linear and frequency feat	ELM & SVM	68.48 & 71.20
Mohit et al. [32]	FAWT and ranking method like Entropy, ROC and Bhattacharya	FzEn and K-NN Entropy estimator	LS-SVM with RBF & Morlet wavelet kernel	100
Monappa et al. [4]	Linear and non-linear, features reduced by PCA	Various time domain, Frequency domain and non-linear domain	PNN, KNN and SVM	Without PCA: 68.33, 76.67 and 90.00 With PCA: 68.33, 85.00 and 91.67
This work	MSWP transform, Fisher ranking method and features reduced by GDA,LDA	31 features by K-NNE & 31 features by FZE method.	ELM	100

In this paper, the non-linear features extracted by FZE and K-NNE methods from 4 level decomposed HRV using MSWP transform were carried out for the HRV analysis acquired from ECG recording of NSR subjects and CAD patients. The mean value of FZE features at 4th and 3rd level for CAD patient is higher than NSR subjects since, the variability in NN interval tachogram more in the NSR group than CAD affected patients. While the mean value of K-NNE features at this level of decomposition for NSR patients was higher than for CAD patients. Further, the extracted features by non-linear methods for HRV analysis has been used with Fisher score ranking method and GDA as feature dimension transform technique as classifier modules to obtain an approximate accuracy of 100% and without GDA an accuracy of 85%. Overall there was an increase in the accuracy with GDA compared to without GDA, an obvious result since Fisher score scheme and GDA were used as top ten features ranked on the basis of Fishers score and feature space transformation technique.

Our proposed method has the following novelty

1. The proposed method uses only one feature after reduction of top ten features to attain the excellent accuracy of 100%. However, Patidar et al. [41] also achieved classification testing accuracy of 99.72% by only two features.

2. Results are robust: due to 10-fold cross-validation has been used for selection of hidden nodes and extracted features of each subjects generated randomly for training and rest subjects for testing of every data set.

3. The proposed algorithm can be employed in advanced signal processing system like a computer aided diagnostic system. As, this method only needs one feature for classification and is using ELM for detection of CAD patients, the diagnosis of CAD will be fast. Due to this, in future, online CAD detection system can be possible for clinical applications.

Limitations of our proposed method

(a) Before the application of the proposed approach in diagnosing of CAD patients, the algorithm should be trained by large data sets of HRV signals.

Conclusion

In this work, a new approach has been proposed for the detection of CAD patients based on extracted features dimension reduction technique as GDA with RBF or Gaussian kernel function and binary classifier as ELM having multiquadric RBF hidden nodes. It was concluded based on the detection accuracy graph that the proposed hybrid GDA + ELM coronary artery disease detection algorithm achieved 100% accuracy. The features extracted by FZE and K-NNE at 4th level and 3rd level of decomposition as approximate and detail coefficient had the lowest p-value (<0.00001). Therefore, 4th or 3rd level of decomposition of HRV signals by MSWP transform may be used for analysis of CAD patients. The mean value of FZE features at 4th and 3rd level for CAD patient was higher than for NSR subjects, while the mean value of K-NNE features at this level of decomposition for NSR was higher than CAD patients. Hence, our proposed approach scheme could be used as a part of medicinal facilities, polyclinics, health care and group screening to help cardiologists in their standard determination. This approach needs only one feature for binary classification using ELM, after transformation of top ten entropy, therefore the diagnosis of CAD will be fast. Due to this, in future, online cardiac heart diseases detection systems can be possible for clinical purpose.