The Impact of Providing Vision Screening and Free Eyeglasses on Academic Outcomes: Evidence from a Randomized Trial in Title I Elementary Schools in Florida

Abstract

More than 20 percent of all school-aged children in the United States have vision problems, and low-income and minority children are disproportionately likely to have unmet vision care needs. Vision screening is common in U.S. schools, but it remains an open question whether screening alone is sufficient to improve student outcomes. We implemented a multi-armed randomized controlled trial to evaluate the impact of vision screening, and of vision screening accompanied by eye exams and eyeglasses, provided by a non-profit organization to Title I elementary schools in three large central Florida school districts. We find that providing additional/enhanced screening alone is generally insufficient to improve student achievement in math and reading. In contrast, providing screening along with free eye exams and free eyeglasses to students with vision problems improved student achievement as measured by standardized test scores. We find, averaging over all students (including those without vision problems), that this more comprehensive intervention increased the probability of passing the Florida Comprehensive Achievement Tests (FCAT) in reading and math by approximately 2.0 percentage points. We also present evidence that indicates that this impact fades out over time, indicating that follow-up actions after the intervention may be necessary to sustain these estimated achievement gains.

INTRODUCTION

More than 20 percent of school-aged children in the United States have vision problems (Basch, 2011; Ethan et al., 2010; Zaba, 2011). Low-income and minority children have a greater than average risk of under-diagnosis and under-treatment of vision problems (Basch, 2011; Ganz et al., 2006, 2007). For example, Title I students are two to three times more likely than non-Title I students to have undetected or untreated vision problems (Johnson et al., 2000).ⁱ There has been little attempt, however, to quantify the impact of vision interventions on student outcomes such as test scores, attendance rates, and discipline incidents. This study attempts to fill this void.

We evaluate the impact of a multi-armed randomized controlled trial in which a non-profit organization, Florida Vision Quest (FLVQ), offered enhanced vision services to a randomly selected group of Title I elementary schools in three large central Florida school districts (counties) during the fall of the 2011/2012 school year.ⁱⁱ FLVQ provides state-of-the-art screening, comprehensive vision exams, and free eyeglasses for low-income children in central Florida. Despite a long record of partnership with area school districts, thus far FLVQ’s work has been motivated solely by compelling anecdotal evidence; this is the first independent evaluation of FLVQ and the services it offers.ⁱⁱⁱ

The results of this analysis will be useful to policymakers and practitioners in Florida and elsewhere. There is a long tradition in the United States of public schools providing basic screening for health problems such as hearing and vision impairment (Appelboom, 1985).^iv It remains, however, an open question whether such screening improves student outcomes and whether school districts can improve student outcomes by upgrading their vision screening technologies or by collaborating with local non-profits, such as FLVQ, to provide comprehensive vision exams and free eyeglasses. Vision interventions may be a very cost-effective way to improve student outcomes; if districts can identify and remedy vision problems early, they may be able to avoid more costly remediation in subsequent years.

The economic theory for such an intervention is straightforward—identifying and remedying vision problems should increase students’ acquisition of human capital. If students cannot see, they cannot read (be it their textbooks or the writing on the board at the front of the classroom), and if they cannot read they have little hope of keeping pace with the demands of school and will likely underperform relative to their full potential. By identifying and treating vision problems at an early age, students will acquire human capital at a faster rate, which will yield both private and social benefits.^v

We find that providing additional/enhanced screening alone (screen-only schools) is generally insufficient to improve student math and reading skills as measured by scores on the Florida Comprehensive Achievement Test (FCAT). Indeed, some estimates indicate possibly negative impacts of this intervention. However, averaging over all students (including those with good vision), the intervention that included not only screenings but also vision exams and free eyeglasses (full treatment schools) increased both the probability of passing the FCAT reading test and the probability of passing the FCAT math test by 2.0 percentage points, although the statistical significance of these results is strong only for the reading test. We also find suggestive evidence that sizeable positive spillovers may be accruing to students with good vision in the full treatment schools, although, as explained below, this evidence must be interpreted with caution.

Further analysis indicates that the impact of the full treatment intervention is likely stronger for low-income students (as proxied by free or reduced-price lunch status) and English language learners (who in central Florida are largely Hispanic). In addition, when the analysis excludes the district that experienced serious implementation problems, the results for the other two districts show that the full treatment intervention significantly improved student achievement on the math test as well as the reading test.

We hypothesize that the lack of an impact in one district may be attributed to problems with the implementation of the intervention. The estimates with all three districts are the most policy relevant estimates since, if the intervention is brought to scale or replicated elsewhere, it is likely that implementation problems of one type or another will occur. It may be, however, that these implementation problems will decrease over time, thus we also present estimates that focus only on the two districts where the implementation was not problematic. When the district where there was no impact is excluded, the positive impacts of the full treatment intervention on the probability of passing the reading and math tests are higher: 2.6 percentage points (p < 0.01) and 3.6 percentage points (p < 0.01), respectively. These impacts are averaged over all students; the impact on students who received glasses is almost certainly higher but is difficult to estimate with the data available.

Given that standardized test pass rates in these districts are around 50 percent, these are substantial gains. Yet we also find that the impact fades out over time, indicating that sustained follow-up to the intervention may be necessary to retain these initial gains in student learning.

LITERATURE REVIEW

This study investigates whether diagnosing and providing eyeglasses to students with poor vision enables them to acquire human capital at a faster rate than would occur in the absence of diagnosis or diagnosis plus the offer of glasses. We contribute to two strands of the existing literature.

First, as noted above, there is some evidence on the prevalence of undiagnosed and untreated vision problems among school-aged children in the U.S. (Basch, 2011; Ethan et al., 2010; Zaba, 2011). Common refractive errors such as myopia (nearsightedness), hyperopia (farsightedness) and astigmatisms can be corrected with eyeglasses, but many children either do not know that they have problems, do not have glasses, or do not wear their glasses. Research also shows that the rates of undiagnosed and untreated vision problems vary by race and ethnicity (Kleinstein et al., 2003) and socio-economic status (Ganz et al., 2006, 2007). Yet this evidence is sparse and incomplete. We contribute new data on the prevalence of undiagnosed and untreated vision problems in Title I schools in central Florida.

Second, there is some evidence linking vision problems and academic outcomes (Gomes-Neto et al., 1997; Hannum & Zhang, 2012; and Walline & Johnson Carder, 2012). This literature is largely correlational in nature and thus does not necessarily imply that treating vision problems will improve educational outcomes for students with vision problems because those students may be fundamentally different from students without vision problems in some unobserved way. If a third variable is causing both the poor vision and the low academic performance—for example, low birth weight could lead to vision problems and learning disabilities (Hack et al., 1995)—then correcting the vision impairment may do little to improve academic outcomes. Even among students whose vision problems are detected, there may be unobservable differences between those who go on to wear glasses and those who do not follow up with any treatment. For example, Hannum and Zhang (2012) find that wearing glasses is positively correlated with socio-economic status and overall academic achievement.

Sonne-Schmidt (2011) applies a regression discontinuity method to estimate the causal impact of eyeglasses on middle school and high school students in the United States and finds that wearing glasses increases test scores by approximately 0.1 standard deviations (of the distribution of test scores) and by as much as 0.3 standard deviations for students with myopia. Glewwe et al. (2016) conduct a randomized controlled trial (RCT) in China in which students in grades 4 to 6 in a randomly selected group of townships were provided vision exams and, if needed, eyeglasses. They find that wearing glasses increases average test scores for students with poor vision by 0.16 standard deviations. We contribute the first evidence from an RCT conducted in a developed country.^vi

EXPERIMENTAL DESIGN AND IMPLEMENTATION

Experimental Design

To rigorously evaluate the impact of FLVQ’s provision of vision exams and eyeglasses, we conducted a multi-armed randomized controlled trial targeting 4th- and 5th-grade students in Title I elementary schools in central Florida. The randomization was done at the school level. The benefit of the randomized design is that it provides a valid counterfactual. That is, it allows for an estimate of the impact of an intervention by comparing two groups of schools that received the two different FLVQ interventions to a third group that provides estimates of what would have happened in the absence of these interventions.

FLVQ uses a photoscreening device called the “Spot,” which is manufactured by PediaVision/WelchAllyn (Peterseim et al., 2013).^vii Photoscreening devices are essentially infrared cameras that use auto-refraction and video-retinoscopy technologies to screen for refractive errors, amblyopic precursors and pupil abnormalities. The person doing the screening stands about one meter away from the student and takes a digital photograph of the student’s eyes. The information acquired yields an automatic assessment of a student’s vision. With photoscreening, screening is very accurate, and very quick (Salcido, Bradley, & Donahue, 2005).

Using the Spot, FLVQ screened all 4th- grade and 5th-grade students in the intervention schools who were present on the day of the screening. No screening was done for 4th- and 5th-grade students in the control schools. For the first of the two groups of intervention schools, which we refer to as the screen-only schools, this was the only service provided. Students who failed the screening were sent home with a note (in English or Spanish) for parents indicating that they should follow-up with an optometrist of their choosing. For the other group of intervention schools, which we call the full treatment schools, students who failed the screening were offered comprehensive vision exams aboard the FLVQ mobile vision clinic. The mobile vision clinic is a bus that has been equipped with all the tools usually available in an optometrist’s office, and is staffed with licensed eye care professionals. If the onboard optometrist prescribed glasses, FLVQ provided two pairs of glasses to the student at no charge.

FLVQ did not have sufficient resources to screen all of the Title I elementary schools in the three school districts, nor did it have sufficient resources to provide follow-up exams and glasses to all of the schools that were screened. Rather than have FLVQ choose which schools to serve, we persuaded its staff to randomize the choice, thus using the resource constraint as an opportunity to provide a rigorous evaluation of the two levels of services provided by FLVQ.

There are two main mechanisms through which these interventions may affect student outcomes. This multi-armed study is designed to differentiate between the two. First, perhaps there is an information problem. That is, there may be students (parents) who do not know that they (their children) have vision problems. In Florida, students are routinely screened for vision problems in Kindergarten, first grade, third grade, and sixth grade. This intervention targets fourth and fifth graders, thus adding two extra screenings. Also, the Spot photoscreening may be a more effective screening tool than traditional screening (Salcido, Bradley, & Donahue, 2005). Both the fact that students are screened in grades that schools do not usually screen and the fact that the screening is done with an arguably superior technology should identify students who are missed by the district’s standard screenings. If the academic performance of the students in the screen-only schools exceeds that of the students in the control group after this intervention, this suggests that simply providing more or better information will increase student learning.

Second, if the main barrier is not identifying vision problems, but rather obtaining glasses, then the screen-only intervention will be insufficient. If the real issue is an access problem there will be no difference between students in the screen-only schools and students in the control group. Students (parents) may know about vision problems but lack the resources needed to obtain access to an optometrist or acquire eyeglasses to remedy those problems. In the full-treatment schools any student who is identified with vision problems is offered a vision exam and two pairs of eyeglasses, all free of charge. Not only are the exam and eyeglasses free, they are brought to the students at their schools. There is no need for students (parents) to invest any resources other than the time and effort needed to return a permission form, and to use and care for the glasses. The difference, if any, between the screen-only and the full-treatment schools will isolate the importance of resolving the access problem by providing onsite vision exams and free eyeglasses.^viii

Implementation

Three Florida school districts agreed to participate in the study: We refer to them as District 1, District 2, and District 3. At the request of the three districts, we do not use their names. Only the Title I elementary schools in each district were eligible to participate.

Randomization

In each school district, we ranked the Title I schools by their students’ academic proficiency. Specifically, we used the average of each school’s points over the preceding three years. The points measure, designed by the Florida Department of Education, includes pass rates as well as gains on the state-mandated Florida Comprehensive Achievement Tests (FCATs). The schools were stratified by this academic proficiency and the randomization was conducted within these strata. This provides additional assurance that the treatment and control groups will have comparable levels of academic proficiency prior to the intervention.

There were 11 strata in District 1, five in District 2, and seven in District 3. The number of strata was determined by the number of schools that FLVQ estimated their resources would cover. One full treatment school and one screen-only school were randomly selected from each strata. The remaining schools serve as the controls. Strata ranged in size from three to six schools. Because the strata contain different numbers of schools, and because schools differ in size, the sample used for our analysis has between 268 and 1,069 students in each strata. The average is 657. Fixed effects for each strata are included in the analysis.

District 1 had 37 Title I elementary schools in 2010/2011. We randomly assigned 11 to the screen-only group, 11 to the full-treatment group and 15 to the control group. After doing this, we learned that one school assigned to the full-treatment group was not part of the district but, rather, was a charter school, and that FLVQ had worked in a prior school year with two other schools assigned to the full-treatment group. All three of these schools, along with the other schools in the strata, were dropped from the final analysis, leaving us with eight full-treatment schools, eight screen-only schools, and 11 control schools. The schools that FLVQ had worked with previously were dropped because it is possible that informational spillovers carried over from previous years if parents in these two schools had already heard about the services provided by FLVQ.

In District 2 there were 16 Title I elementary schools in 2010/2011. Prior to randomization, we learned that FLVQ had worked with one school in the prior school year; this school received the full treatment but was not included in the randomization and is excluded from our analysis. The remaining 15 schools were grouped into five strata, with three schools in each stratum. Five (one from each stratum) were randomly chosen to be full-treatment schools, five (one from each stratum) were assigned to the screen-only group, and the remaining five (one from each stratum) were the control schools. After this random assignment, we discovered that one school randomly assigned to the full-treatment intervention had worked with FLVQ in a previous year. In addition, one school in the screen-only group refused to participate in the intervention. Both of these schools were from the same stratum, so all three schools in this stratum were dropped from the analysis. Thus the sample for analysis from District 2 contains four full-treatment schools, four screen-only schools and four control schools.

District 3 had 65 Title I elementary schools in 2010/2011. FLVQ had worked in 28 of them over the prior two years, so our sampling frame used only the remaining 37. These were divided into seven strata. We randomly assigned seven schools (one from each stratum) to the screen-only group, seven (one from each stratum) to the full-treatment group, and the remaining 23 to the control group. The control group was much larger than the treatment groups because funding constraints limited the number of schools that FLVQ could serve.

Table 1 provides information on the number of schools and students in the treatment and control groups, by school district. None of these schools had prior experience with FLVQ.^ix The total sample includes all students who were enrolled in the 76 schools at the start of the interventions (fall of 2011). The analytic sample includes students in the total sample whom we could match across data sets and who had a valid post-test score (spring of 2012) in one or both of the tested subjects. A few students are missing a post-test score in only one subject, so the (analytic) sample sizes are slightly lower for the math and reading analytic samples relative to the overall analytic sample.

Table 1.

Treatment and control groups by district.

Schools
	District 1	District 2	District 3	Total
Control Group	11	4	23	38
Screen Only	8	4	7	19
Full Treatment	8	4	7	19
Total	27	12	37	76

Students
	District 1	District 2	District 3	Total
Control Group	2,240	1,101	4,356	7,697
Screen Only	1,570	1,058	1,325	3,953
Full Treatment	1,158	1,245	1,369	3,772
Total sample	4,968	3,404	7,050	15,422
Analytic sample	4,968	3,050	6,554	14,572
Reading	4,959	3,040	6,527	14,526
Mathematics	4,965	3,045	6,539	14,549

Notes: The total sample includes all students in the tested school-grades. The analytic sample includes students that we could match across data sets and who had at least a valid post-test score for math or reading test. Some students are missing a post-test for only one subject so the sample sizes are slightly smaller for the math and reading test (analytic) samples.

When a student was missing one or more demographic variables, or when a student was missing a pre-test score, the value for that variable was imputed.^x There were 1,665 students who were missing a pre-test score, which primarily reflects student mobility. Table 2 compares students with pre-test scores and students for whom we had to impute a pre-test score. Mobility differs somewhat by district; we are missing pre-test scores for 11 percent, 17 percent, and 8 percent of students in Districts 1, 2, and 3, respectively. Since there are relatively more control schools in District 3, this means that, for the sample as a whole, the proportion of students for whom we imputed pre-test scores is smaller in the control schools than in the treatment schools. Students with imputed pre-test scores are slightly younger, less likely to be female, Black, or multi-race, and much more likely to be Hispanic. They are also more likely to be eligible for a free or reduced-cost lunch and to receive special education services, but are less likely to receive gifted and talented services. All of these patterns are consistent with the fact that highly mobile students are more likely to come from disadvantaged backgrounds. Students with imputed pre-test scores have fewer absences in their current district because they have been in the district for less time.

Table 2.

Summary statistics, imputation and attrition.

	No Missing Data	Imputed	Attrition
	(all pre test scores & at least one post test score N = 12,907)	(at least one post test score & no pre test score N = 1,665)	(at least one pre test score & no post test score N = 444)
District
District 1	4,413 (88.8%)	555 (11.2%)	0 (0.0%)
District 2	2,498 (78.1%)	552 (17.3%)	147 (4.6%)
District 3	5,996 (87.5%)	558 (8.2%)	297 (4.3%)
F-test (p-value)	-	0.0000	0.0000
Treatment Assignment
Full Treatment	3,102 (84.6%)	461 (12.6%)	103 (2.8%)
Screen Only	3,241 (84.6%)	467 (12.2%)	121 (3.2%)
Control	6,564 (87.3%)	737 (9.8%)	220 (2.9%)
F-test (p-value)	-	0.1172	0.9334
2011 FCAT Scores
Reading z-scores	−0.004 (0.99)	-	−0.262*** (0.97)
Math z-scores	0.015 (0.99)	-	−0.328*** (1.02)
Reading level	2.89 (1.14)	-	2.55*** (1.14)
Math level	2.98 (1.10)	-	2.63*** (1.11)
Demographics
Grade	4.51 (0.50)	4.49** (0.50)	4.50 (0.50)
Age (months)	132.70 (9.08)	132.06** (9.36)	133.72*** (9.63)
Female	0.493 (0.50)	0.467* (0.50)	0.489 (0.50)
White	0.267 (0.44)	0.238 (0.43)	0.158*** (0.36)
Asian	0.022 (0.15)	0.020 (0.14)	0.018 (0.13)
Black	0.286 (0.45)	0.255* (0.44)	0.324 (0.47)
Hispanic	0.346 (0.48)	0.447*** (0.50)	0.435*** (0.50)
Multi-race	0.035 (0.18)	0.026* (0.16)	0.027 (0.16)
Special education	0.133 (0.34)	0.167*** (0.37)	0.158 (0.37)
Gifted	0.052 (0.22)	0.013*** (0.11)	0.024** (0.15)
Free/reduced lunch	0.884 (0.32)	0.921*** (0.27)	0.901 (0.30)
ELL	0.321 (0.47)	0.344 (0.48)	0.363 (0.48)
2010–2011 Absences/Behavior
Total absences	7.64 (8.02)	1.88*** (6.00)	8.14 (8.16)
Unexcused absences	4.46 (5.52)	1.23*** (4.41)	5.28** (5.91)
Referrals	0.31 (1.12)	0.68* (2.22)	0.53* (2.02)
Suspensions	0.31 (1.45)	0.13*** (1.07)	0.64* (2.55)

Notes: Number of observations and row percentages are reported for the top two panels of the table (district and treatment assignment). The remaining panels report means and standard deviations for observations with both pre-test and post-test (1st column), observations with post-test but no pre-test (2nd column) and observations with no post-test (3rd column). For the top two panels, the F-test is for differences across districts (1st panel) or across treatment assignment groups (2nd panel). More specifically, and using attrition as an example, the F-test is of the null hypothesis H₀: β₁ = β₂ = β₃ in the regression equations: attrition = β₁×(District 1) + β₂×(District 2) + β₃×(District 3) + ε or attrition = β₁×(Full Treatment) + β₂×(Screen Only) + β₃×(Control) + ε. For all the other panels, statistical significance indicates whether columns 2 and 3 differ from column 1. More precisely, it is for a t-test of H₀: β₁ = 0 in the regression equation: variable = α + β₁×(attrition) + ε.

^***p<0.01;

^**p<0.05;

^*p<0.1.

High rates of student mobility also mean that not every student persists to the post-test. We have 444 students who attrited from the sample between the time of the screenings (fall) and the time of the post-test (spring). We do not impute post-test scores, so these students are dropped from the analytic sample. Table 2 also compares the demographics of students with a post-test score and to those of students without a post-test score.^xi The districts differed in the percentage of students missing a valid post-test score (see the top panel in the final column of Table 2) but, most importantly for our study, attrition rates are not significantly different across the full-treatment, screen-only, and control schools (see the second panel in Table 2). Students who are missing a valid post-test score are older, less likely to be white, more likely to be Hispanic, and less likely to be in a gifted and talented program. This is consistent with the fact that highly mobile students are more likely to come from disadvantaged socioeconomic backgrounds. Students who are missing a valid post-test score also have more unexcused absences and behavior problems, and they had lower pre-test scores than students who persist. Again this is consistent with patterns of student mobility.

Balance tests for the analytic sample, shown in Table 3, indicate that the randomization was successful. Any non-random attrition seems to have led to the treatment schools having a slightly lower reading (level) pre-test score and more English language learner (ELL) students than in the control schools, but these differences are small and significant only at the 10 percent level. The lower reading (level) pre-test score in the treatment schools can lead to bias against (for) finding an impact of the intervention; even though our regressions condition on the baseline scores, the lower reading pre-test score in the treatment schools could lead to slower (faster) growth in test scores over time. Regarding ELL students, if the average ELL student has slower (faster) test score growth than the average non-ELL student, the higher share of ELL students in the treatment schools will bias against (in favor of) finding a result of the intervention. A priori, either of these is possible, so there is no presumption of bias in any particular direction. Finally, there is a more significant difference in the number of multiple race students, but these students comprise a small fraction (3 to 4 percent) of the total so it is unlikely that these differences will bias the results.^xii Overall, the balance checks in Table 3 show that the three groups of schools are quite similar.

Table 3.

Balance tests.

	Full Treatment	Screen Only	Control	p-value of F-test
Reading 2011	−0.086 (1.013)	−0.009 (0.939)	0.015 (1.003)	0.1059
Math 2011	−0.045 (1.000)	0.024 (0.962)	0.015 (1.003)	0.2350
Reading 2011 (level)	2.817 (1.155)	2.881 (1.115)	2.909 (1.145)	0.0577
Math 2011 (level)	2.901 (1.103)	2.977 (1.087)	2.996 (1.101)	0.1100
Grade	4.511 (0.500)	4.511 (0.500)	4.512 (0.500)	0.9944
Age (Months)	132.75 (9.303)	132.59 (9.098)	132.66 (9.106)	0.5085
Asian	0.025 (0.155)	0.017 (0.130)	0.022 (0.145)	0.2594
Black	0.293 (0.455)	0.224 (0.417)	0.309 (0.462)	0.3931
Hispanic	0.369 (0.483)	0.406 (0.491)	0.338 (0.473)	0.3216
Multiple race	0.040 (0.195)	0.027 (0.162)	0.034 (0.182)	0.0092
Girl	0.483 (0.500)	0.488 (0.500)	0.490 (0.500)	0.5900
Special education	0.137 (0.344)	0.145 (0.352)	0.135 (0.342)	0.9099
Gifted	0.054 (0.226)	0.038 (0.191)	0.048 (0.214)	0.8208
Free or reduced lunch (FRL)	0.890 (0.313)	0.888 (0.316)	0.877 (0.328)	0.3494
ELL	0.352 (0.478)	0.364 (0.481)	0.294 (0.455)	0.0950
Total Absences in 2010–2011	7.215 (9.003)	7.187 (7.812)	7.358 (7.656)	0.2627
Unexcused Abs in 2010–2011	3.851 (5.426)	4.114 (5.505)	4.522 (5.548)	0.9845
Referrals in 2010–2011	0.281 (1.038)	0.318 (1.031)	0.338 (1.288)	0.5207
Suspensions in 2010–2011	0.337 (1.666)	0.275 (1.299)	0.300 (1.451)	0.6125

Notes: The first three columns of this table report means and standard deviations for all variables in each group. An F-test of joint significance is used to test the hypothesis that: β₁ = β₂ = β₃ for OLS regressions (with school level clustered robust standard errors) of the following form: Variable = β₁×(Full Treatment) + β₂×(Screen Only) + β₃×(Control) + Strata fixed effects + ε.

Delivery of Vision Services

FLVQ arranged screening dates with each school in the two intervention groups during the fall of 2011. Table 4 summarizes the results of the screenings and, where applicable, the follow-up exams.^xiii As seen in the top panel, in the full-treatments schools, we have screening data for 81 percent of students. This is less than 100 percent because some students were absent on the day of the screening and some observations did not match across data sets.

Table 4.

Screening and exam results by district.

Full Treatment
	District 1		District 2		District 3		All districts
	Count	Share	Count	Share	Count	Share	Count	Share
Total students	1,158	1.00	1,245	1.00	1,369	1.00	3,772	1.00
Screened	967	0.84	1,014	0.81	1,075	0.79	3,056	0.81
Failed screening	339	0.29	296	0.24	340	0.25	975	0.26
Exam given	295	0.25	145	0.12	260	0.19	700	0.19
Glasses dispensed	232	0.20	132	0.11	232	0.17	596	0.16

Screen Only
	District 1		District 2		District 3		All districts
	Count	Share	Count	Share	Count	Share	Count	Share
Total students	1,570	1.00	1,058	1.00	1,325	1.00	3,953	1.00
Screened	N/A	N/A	848	0.80	1,036	0.78	N/A	N/A
Failed screening	N/A	N/A	263	0.25	275	0.21	N/A	N/A

Notes: This table reports the number and share of students who take part in each element of the intervention. Data from the screen-only schools in District 1 are unavailable. Share is share of total students. N/A indicates that screening data are not available for District 1 screen-only schools.

In the full-treatment schools, 975 students failed the screening and thus were offered a comprehensive vision exam aboard the mobile clinic, and 72 percent of them (700 out of 975) were seen by an optometrist in the mobile clinic.^xiv This is less than 100 percent because students must complete a parent permission form to see the optometrist and they must be present on the day(s) the mobile clinic is scheduled for their school. Almost all of the students seen aboard the mobile clinic were given glasses.^xv In the end, 16 percent of students in the full-treatment schools (596 out of 3,772) were provided glasses by FLVQ. Among the students in the full-treatment schools who failed the screening, 61 percent (596 out of 975) were provided eyeglasses.

There were three major problems with the implementation in District 1, which was the first of the three districts to implement the program. First, the notices that were sent home to the parents in the screen-only group indicated that their children would be receiving the full treatment. That is, they mistakenly indicated that free eyeglasses would be provided. Parents were then informed of this error via the district’s automated phone messaging system, but this information may have failed to reach a large proportion of parents. Second, vision screening data from the screen-only group were not recorded due to human error. As indicated in Table 4, there are no data for this group on how many were screened and how many failed the screening. Third, there was a problem interpreting the output of the Spot device at most of the full-treatment schools and some of the screen-only schools. Some students were incorrectly identified as having vision problems (false positive) and some students who had vision problems were missed (false negative). FLVQ estimates that this happened to approximately 100 students. When this issue was discovered, FLVQ gave the schools where this occurred a list of the affected students. FLVQ offered to see all affected students aboard the mobile clinic. The majority of the false negatives were not seen aboard the mobile clinic because of insufficient time to collect parent permission forms, thus many students who otherwise would have been given an exam, and likely glasses, were missed in District 1.

The implementation in Districts 2 and 3 was done after that in District 1, and was much smoother. Due to this variation in implementation, all estimates are shown both aggregated over districts and separately by district.

DATA AND ESTIMATION METHOD

The data for the study come from three sources: the photoscreener, the records kept by FLVQ, and administrative records from each school district. We constructed a student-level panel that includes vision data for the intervention schools and demographic, attendance, discipline and test score records for both the intervention schools and the control schools.

When a student is screened using the photoscreener, it stores detailed readings for each of the student’s eyes. We primarily use the summary result that indicates whether a student passed or failed the screening. We also have data on the device’s preliminary diagnosis; the most common diagnoses are myopia and astigmatism. After a student is seen aboard the mobile clinic, FLVQ records whether the student is prescribed glasses as well as when the glasses were given to the student. We have no data on students’ prior vision services. For instance, we do not know whether they had previously failed vision screenings or been prescribed glasses. Regrettably, we have no vision data of any kind for all students in the control schools.

The primary outcomes used to assess the impact of the intervention are reading and math scores on the Florida Comprehensive Achievement Test (FCAT). The FCAT is given in April of each year, near the end of the academic year; for example, the 2011 FCAT occurs near the end of the 2010/2011 academic year. We obtained three years of FCAT data (one pre-intervention and two post-intervention) from Districts 1 and 3, and two years of FCAT data (one pre-intervention and one post-intervention) from District 2.^xvi

We have FCAT scale scores (a continuous measure) for each student in District 1 and District 3, but not for District 2. In 2011/2012 the state transitioned to the FCAT 2.0. As a result, the 2011 scale scores range from 100 to 500, while the 2012 scale scores range from 140 to 302 in reading and 140 to 298 in math. For all regression estimates that use scale scores, these tests are normalized to have means of 0 and standard deviations of 1 within district-grade-year-subject combinations using the means and standard deviations of the schools assigned to the control group.^xvii For all three districts we have FCAT achievement level scores (a categorical measure), which range from 1 to 5. Level 3 is defined as demonstrating a satisfactory level of success. Levels 4 and 5 are more than satisfactory, and levels 1 and 2 are less than satisfactory. To pass the FCAT, students must score a 3 or above. These achievement level scores are our primary outcome because we have this measure for all three districts.

Additional outcome data include attendance rates and discipline records (office referrals and suspensions). It may be that students with undiagnosed or untreated vision problems miss school more often than their peers, or are more likely to misbehave in class and be referred to the principal’s office, or even be suspended. All of these are likely to reduce academic achievement. Attendance and discipline variables allow us to test whether these are mechanisms through which the intervention has an impact. It is also possible that vision services improve students’ lives along non-academic dimensions. The intervention may make it easier for students to participate in leisure activities such as sports. For example, they may be able to complete homework more quickly and allocate more time to leisure activities. Unfortunately, we have no data on students’ leisure activities.

Although randomization provides a convincing counterfactual, econometric methods that control for covariates can estimate the effect of the intervention more precisely than simple comparisons of group means. The simplest regression model that one could estimate is:

$${\mathrm{Y}}_{\text{ist}}=\mathrm{\alpha }+{\mathrm{\beta }}_1{\mathrm{P}}_{1\mathrm{s}}+{\mathrm{\beta }}_2{\mathrm{P}}_{2\mathrm{s}}+\mathrm{\zeta }{\mathrm{A}}_{\mathrm{s}}+{\mathrm{u}}_{\text{ist}}$$ (1)

where Y_ist is the outcome of interest, such as student test scores, for student i in school s at time t; P_1s equals one if school s was randomly assigned to the screen-only program and zero otherwise, P_2s equals one if school s was randomly assigned to the full treatment program and zero otherwise, and schools randomly assigned to the control group serve as the omitted (comparison) group; A_s is a fixed effect for the strata used in the randomization for school s; and u_ist represents all other factors (observed or unobserved) that could affect test scores for student i in school s at time t. The main coefficients of interest, β₁ and β₂, are the impacts of the screen-only and full-treatment programs, respectively.

Given that assignment of schools to the program was random, the variables P_1s and P_2s will be uncorrelated with u_ist, so ordinary least squares estimates of β₁ and β₂ will be unbiased estimates of the impacts of the two arms of the program.^xviii However, greater statistical precision can be obtained if other variables that affect student i’s test scores are added to the regression. We have student-level demographic variables from school administrative records, including grade, age (in months), race/ethnic group, gender, free/reduced-cost lunch status, and receipt of English Language Learner (ELL), special education, or gifted services. We include controls, X_nit for n = 1…k, for these k variables for student i at time t, as well as the FCAT scores from the year prior to the intervention,^xix Y_is(t-1), to control for observable differences between students:

$${\mathrm{Y}}_{\text{ist}}=\mathrm{\alpha }+{\mathrm{\beta }}_1{\mathrm{P}}_{1\text{st}}+{\mathrm{\beta }}_2{\mathrm{P}}_{2\text{st}}+{\mathrm{\gamma }}_1{\mathrm{X}}_{1\text{it}}+{\mathrm{\gamma }}_2{\mathrm{X}}_{2\text{it}}+\dots {\mathrm{\gamma }}_{\mathrm{k}}{\mathrm{X}}_{\text{kit}}+\mathrm{\theta }{\mathrm{Y}}_{\text{is}(\mathrm{t}-1)}+\mathrm{\zeta }{\mathrm{A}}_{\mathrm{s}}+{\mathrm{u}}_{\text{ist}}$$ (2)

Note that the addition of the prior year’s FCAT scores changes the interpretation of all coefficients; they measure gains in the FCAT test. Because of this we include pre-test scores in all regressions, even those that exclude the demographic control variables.

We also allow the program impacts to vary according to student characteristics, although this must be done with caution; to avoid finding spurious “significant” results this should be done only for a few variables, those for which there is a clear reason to expect a differential effect. Let X₁ indicate a type of student who would most likely benefit from the program, for example a student with vision problems or a student from a poor family that perhaps cannot afford eyeglasses (which could be measured by the variable indicating eligibility for a free or reduced-price lunch). The following regression allows for separate impacts by X₁:

$${\mathrm{Y}}_{\text{ist}}=\mathrm{\alpha }+{\mathrm{\beta }}_1{\mathrm{P}}_{1\mathrm{s}}{\mathrm{X}}_{1\text{ist}}+{\mathrm{\beta }}_2{\mathrm{P}}_{2\mathrm{s}}{\mathrm{X}}_{1\text{ist}}+{\mathrm{\delta }}_1{\mathrm{P}}_{1s}(1-{\mathrm{X}}_{1\text{ist}})+{\mathrm{\delta }}_2{\mathrm{P}}_{2s}(1-{\mathrm{X}}_{1\text{ist}})+{\mathrm{\gamma }}_1{\mathrm{X}}_{1\text{ist}}+{\mathrm{\gamma }}_2{\mathrm{X}}_{2\text{ist}}+\dots {\mathrm{\gamma }}_{\mathrm{k}}{\mathrm{X}}_{\text{kist}}+\mathrm{\theta }{\mathrm{Y}}_{\text{is}(\mathrm{t}-1)}+\mathrm{\zeta }{\mathrm{A}}_{\mathrm{s}}+{\mathrm{u}}_{\text{ist}}$$ (3)

In this regression, β₁ and β₂ indicate the effects of the two programs for students i in school s with X₁ = 1, and δ₁ and δ₁ are the effects for students for whom X₁ = 0. Note that, for all regressions in this paper, the standard errors are clustered at the school level.^xx

RESULTS

We contribute evidence on a series of questions concerning school-based vision interventions. First, we provide new evidence on the prevalence of vision problems in Title I elementary schools in central Florida. We present summary statistics as well as disaggregated screening results by type of vision problem and by demographic subgroups. Second, we provide experimental estimates of the impacts of the vision screening and the screening plus free exams and eyeglasses interventions on (growth in) student test scores. We present both aggregate results and results that focus on demographic subgroups. The subgroups we focus on are students who qualify for free/reduced-price lunch (an indicator of low family income) and students who qualify for English Language Learner services (a marker for recent immigration). Finally, we offer evidence on the impact of the intervention on non-test score outcomes, namely attendance and behavior problems.

Prevalence of Untreated Vision Problems

We begin by documenting the prevalence of untreated vision problems in schools serving low-income students. We find that a startlingly high percentage of students in these schools need glasses but either do not have them or have them but do not wear them regularly. Recall that there was an error in District 1 that resulted in some false-positive and some false-negative screening results. Therefore, we discuss our findings with and without District 1.

As seen in the top panel of Table 4, 975 of the 3,056 students in the full-treatment schools who were screened failed the screening.^xxi This is a 32 percent failure rate. Excluding District 1 yields a 30 percent failure rate (636 out of 2,089). Of the students who failed the screening and were seen by an optometrist aboard the mobile unit, 85 percent (596 out of 700) were prescribed glasses. Excluding District 1, that figure rises to 90 percent (364 out of 405). In other words, our data show that more than one in four students in low-income schools have untreated (or undertreated) vision problems.^xxii This suggests that lack of information or lack of access to vision care, or both, are very common problems among low-income students in central Florida.

Table 5 shows statistics by demographic subgroups. We find that, among race/ethnic categories, Asian students are most likely to fail the screening and be prescribed glasses. About 42 percent of Asian students failed the screening compared to 29 to 32 percent in other race/ethnic categories; this difference is statistically significant at the 5 percent level, but given that Asian students in these districts are only 2 percent of the sample, and that Asian is a very broad category, this difference should be interpreted with care. Notably, there is little difference between students who are eligible for free/reduced-price lunch and those who are not. One possibility is that in these schools, the small number of students who are not eligible are still far from wealthy, so this may not be the best indicator of family wealth for this population.

Table 5.

Screening and exam results by demographic subgroup.

Panel A: By Race and Ethnicity
	White	Black	Hispanic	Asian	Native American	Multiple race
Failed screening	29.0%	31.6%	30.1%	41.6%	30.8%	28.5%
Myopia	22.1%	21.4%	21.9%	32.0%	21.8%	24.0%
Astigmatism	5.9%	8.9%	6.8%	8.0%	10.3%	4.5%
Other diagnosis	8.0%	11.3%	7.9%	12.0%	7.4%	5.6%
Screened students	885	1,437	1,950	125	380	179

Panel B: By Free and Reduced Lunch (FRL), English Language Learner (ELL) and Special Education Status
	FRL	Non-FRL	ELL	Non-ELL	Special education	No special education
Failed screening	29.6%	28.9%	31.2%	30.3%	29.7%	31.2%
Myopia	20.3%	20.6%	22.6%	21.8%	19.4%	23.0%
Astigmatism	7.5%	8.3%	7.5%	7.5%	9.6%	6.9%
Other diagnosis	9.0%	8.8%	8.2%	9.3%	8.3%	9.3%
Screened students	3,540	433	1,966	2,990	387	2,707

Notes: This table reports the “Spot preliminary diagnosis” by demographic groups. It includes all students who were screened, combining both the full-treatment schools and the screen-only schools for which we have data. The percent who failed the screening does not equal the sum of the percent with various preliminary diagnoses because some students were given multiple preliminary diagnoses.

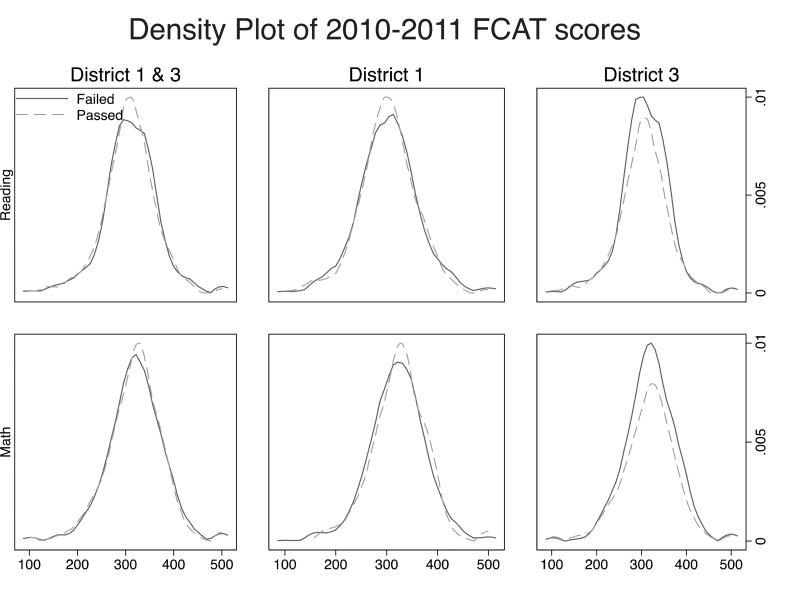
We do not find that students with vision problems tend to have lower pre-intervention test scores than students without vision problems. The mean reading (math) test score for students with normal vision is −0.06 (−0.02), and the mean for students with vision problems is −0.02 (−0.01). More generally, we see in Figure 1 that, in all three districts and for both math and reading, the distribution of scores for students who passed the screening is very similar to the distribution for students who failed the screening; students in our sample with vision problems do not have lower baseline test scores.^xxiii

Figure 1.

Experimental Estimates of the Impact of Vision Services

Although students with vision problems are not concentrated at the bottom of the achievement distribution, at virtually any point on the distribution such students may be underperforming relative to their full potential. Tables 6 through 12 provide estimates of the program impact based on the randomized controlled trial. In general, all these estimates are intent to treat (ITT) estimates, in two distinct senses. First, they are estimates of the impact of offering services, and some students did not obtain the services because they were absent on the days of the screening or did not return a permission slip to be seen on the mobile eye clinic. Second, except for Tables 11 and 12, the estimates compare all students, both those with and without vision problems; and thus the estimates are for offering vision services to the average student, not just to students who need vision services.

Table 6.

The impact of vision interventions on 2012 FCAT levels (ordered logit).

Panel A: Reading
	All Districts		Districts 2 & 3		District 1		District 2		District 3
Full Treatment	0.112** (0.049)	0.133*** (0.047)	0.156** (0.063)	0.178*** (0.060)	−0.008 (0.061)	−0.004 (0.047)	0.100** (0.044)	0.130*** (0.047)	0.153* (0.090)	0.167* (0.089)
Screen Only	−0.075 (0.047)	−0.061 (0.044)	−0.039 (0.070)	−0.039 (0.063)	−0.161*** (0.048)	−0.094** (0.048)	−0.300*** (0.069)	−0.239*** (0.072)	0.120* (0.063)	0.091 (0.062)
Grade	-	0.485*** (0.053)	-	0.482*** (0.059)	-	0.349*** (0.102)	-	0.416*** (0.119)	-	0.419*** (0.073)
Age	-	−0.028*** (0.003)	-	−0.025*** (0.004)	-	−0.024*** (0.004)	-	−0.023*** (0.006)	-	−0.019*** (0.005)
Girl	-	0.180*** (0.033)	-	0.166*** (0.040)	-	0.167*** (0.062)	-	0.032 (0.074)	-	0.189*** (0.046)
Asian	-	0.231** (0.109)	-	0.304** (0.119)	-	−0.181 (0.235)	-	0.466*** (0.165)	-	0.037 (0.158)
Black	-	−0.288*** (0.054)	-	−0.237*** (0.068)	-	−0.355*** (0.075)	-	−0.225 (0.146)	-	−0.313*** (0.080)
Hispanic	-	−0.141*** (0.051)	-	−0.117** (0.048)	-	−0.101 (0.100)	-	−0.065 (0.073)	-	−0.255*** (0.072)
Multi-race	-	−0.123 (0.079)	-	−0.111 (0.101)	-	−0.054 (0.119)	-	−0.247* (0.135)	-	−0.087 (0.158)
ELL	-	−0.207*** (0.054)	-	−0.191*** (0.065)	-	−0.272*** (0.093)	-	−0.345*** (0.099)	-	−0.068 (0.084)
FRL	-	-	-	−0.245*** (0.058)	-	-	-	−0.174** (0.080)	-	−0.274*** (0.082)
Special Education	-	-	-	-	-	−0.823*** (0.115)	-	-	-	−0.686*** (0.120)
Gifted	-	-	-	-	-	0.864*** (0.096)	-	-	-	1.170*** (0.144)
District 2	−0.042 (0.078)	0.072 (0.081)	-	-	-	-	-	-	-	-
District 3	−0.485*** (0.105)	−0.262** (0.104)	−0.449*** (0.123)	−0.338*** (0.105)	-	-	-	-	-	-
Observation	14,526	14,526	9,567	9,567	4,959	4,959	3,040	3,040	6,527	6,527
Chi-squared test Full = Screen only	13.56***	16.26***	7.48***	10.75***	6.85***	3.10*	46.92***	39.32***	0.14	0.72

Panel B: Math
	All Districts		Districts 2 & 3		District 1		District 2		District 3
Full Treatment	0.114 (0.085)	0.132 (0.081)	0.226** (0.104)	0.248** (0.100)	−0.152 (0.147)	−0.161 (0.141)	0.148 (0.117)	0.187 (0.117)	0.252* (0.144)	0.273** (0.135)
Screen Only	−0.089 (0.082)	−0.089 (0.081)	0.043 (0.113)	0.040 (0.114)	−0.333** (0.106)	−0.319*** (0.094)	−0.149 (0.164)	−0.091 (0.175)	0.149 (0.134)	0.127 (0.129)
Grade	-	0.497*** (0.095)	-	0.460*** (0.124)	-	0.451*** (0.160)	-	0.479** (0.197)	-	0.372** (0.165)
Age	-	−0.027*** (0.003)	-	−0.025*** (0.003)	-	−0.020*** (0.006)	-	−0.026*** (0.005)	-	−0.020*** (0.005)
Girl	-	−0.078*** (0.029)	-	−0.038 (0.036)	-	−0.205*** (0.050)	-	−0.093* (0.054)	-	−0.061 (0.052)
Asian	-	0.513*** (0.106)	-	0.468*** (0.119)	-	0.614*** (0.338)	-	0.499*** (0.188)	-	0.388** (0.168)
Black	-	−0.469*** (0.066)	-	−0.453*** (0.090)	-	−0.491*** (0.085)	-	−0.518*** (0.145)	-	−0.485*** (0.119)
Hispanic	-	−0.217*** (0.052)	-	−0.204*** (0.064)	-	−0.217** (0.096)	-	−0.123 (0.097)	-	−0.313*** (0.092)
Multi-race	-	−0.234*** (0.085)	-	−0.328*** (0.101)	-	−0.071 (0.167)	-	−0.256** (0.129)	-	−0.434*** (0.150)
ELL	-	−0.083 (0.044)	-	−0.103** (0.049)	-	0.025 (0.132)	-	−0.135 (0.090)	-	−0.043 (0.058)
FRL	-	-	-	−0.208*** (0.064)	-	-	-	−0.178*** (0.068)	-	−0.168* (0.096)
Special Education	-	-	-	-	-	−0.623*** (0.119)	-	-	-	−0.542*** (0.117)
Gifted	-	-	-	-	-	0.818*** (0.234)	-	-	-	1.119*** (0.179)
District 2	−0.322*** (0.120)	−0.220** (0.105)	-	-	-	-	-	-	-	-
District 3	−0.842*** (0.092)	−0.543*** (0.083)	−0.502*** (0.133)	−0.299*** (0.115)	-	-	-	-	-	-
Observation	14,549	14,549	9,584	9,584	4,965	4,965	3,045	3,045	6,539	6,539
Chi-squared test Full = Screen only	5.16**	6.46**	2.69	3.43*	1.44	1.36	3.24*	2.83*	0.52	1.14

Notes: The standard errors in parenthesis are clustered at the school level. All regressions include the 2011 FCAT scores and controls for strata.

^***p<0.01;

^**p<0.05;

^*p<0.1.

Table 11.

The impact of vision interventions on 2012 FCAT levels, by screening result (ordered logit).

	Reading			Math
	Districts 2 & 3	District 2	District 3	Districts 2 & 3	District 2	District 3
Full treatment x Failed screening	0.303*** (0.080)	0.407*** (0.047)	0.127 (0.125)	0.372*** (0.106)	0.478*** (0.089)	0.225 (0.162)
Full treatment x Passed screening	0.265*** (0.062)	0.379*** (0.057)	0.121 (0.083)	0.215* (0.113)	0.260 (0.172)	0.144 (0.126)
Screen only x Failed screening	0.176** (0.072)	0.160** (0.092)	0.184 (0.117)	0.218*** (0.073)	0.159** (0.071)	0.280** (0.121)
Screen only x Passed screening	omitted	omitted	omitted	omitted	omitted	omitted
Full treatment x No screening	−0.166 (0.133)	−0.317** (0.144)	−0.117 (0.175)	−0.178 (0.236)	−0.501*** (0.191)	0.043 (0.298)
Screen only x No screening	−0.391*** (0.144)	−0.868*** (0.205)	−0.060 (0.088)	−0.330* (0.179)	−0.788** (0.325)	0.004 (0.136)
P-value of Chi-squared tests
H0: Full x Failed - Scr x Failed = 0	0.2263	0.0044	0.7322.	0.2305	0.0093	0.7895
H0: (Full x Failed - Scr x Failed) - Full x Pass) = 0	0.1891	0.2657	0.2966	0.6367	0.7236	0.3144
Observations	4,525	2,033	2,492	4,530	2,037	2,493

Notes: The standard errors in parentheses are clustered at the school level. All regressions include controls for strata. Additional controls, not shown, are the same as in Table 6.

^***p<0.01;

^**p<0.05;

^*p<0.1.

Table 12.

Average marginal effects on 2012 FCAT levels for full-treatment school students, relative to screen-only school students (separately for students who failed the screening and students who passed the screening).

Panel A: Reading (N = 4,525)
	Level 1	Level 2	Level 3	Level 4	Level 5
Failed screening	−0.014 (0.012)	−0.006 (0.005)	0.005 (0.004)	0.010 (0.008)	0.005 (0.004)
Passed screening	−0.031*** (0.008)	−0.011*** (0.003)	0.012*** (0.003)	0.020*** (0.005)	0.010*** (0.003)

Panel B: Math (N = 4,530)
	Level 1	Level 2	Level 3	Level 4	Level 5
Failed screening	−0.019 (0.016)	−0.004 (0.003)	0.007 (0.007)	0.009 (0.008)	0.007 (0.006)
Passed screening	−0.028* (0.015)	−0.005** (0.002)	0.011* (0.006)	0.012* (0.006)	0.009** (0.004)

Notes: This table reports average marginal effects calculated from the coefficients reported in the first three rows of Table 11 for the columns that include Districts 2 and 3.

^***p<0.01;

^**p<0.05;

^*p<0.1.

Average Impacts on FCAT Scores

Table 6 presents estimates of the average impacts of both arms of the program for all the districts together, then for the two districts where implementation was not problematic, and finally for each of the three districts separately. The dependent variable is the 2012 FCAT achievement level, the only learning outcome measure that we have for all three districts. The dependent variable takes values from 1 to 5, with higher numbers representing better mastery of the content. Therefore we use an ordered logit specification.^xxiv The raw coefficients from the ordered logit can be difficult to interpret, so in Table 7 we also present average marginal effects for the model that includes demographic controls and uses data for all three districts.

Table 7.

Average marginal effects.

Panel A: All Districts, Reading (N = 14,526)
	Level 1	Level 2	Level 3	Level 4	Level 5
Full treatment	−0.014*** (0.005)	−0.006*** (0.002)	0.004*** (0.001)	0.010*** (0.003)	0.006*** (0.002)
Screen only	0.006 (0.005)	0.003 (0.002)	−0.002 (0.001)	−0.004 (0.003)	−0.003 (0.002)

Panel B: All Districts, Math (N = 14,549)
	Level 1	Level 2	Level 3	Level 4	Level 5
Full treatment	−0.016 (0.010)	−0.004* (0.002)	0.005 (0.003)	0.008 (0.005)	0.007* (0.004)
Screen only	0.010 (0.010)	0.003 (0.002)	−0.003 (0.003)	−0.005 (0.005)	−0.004 (0.004)

Panel C: Districts 2 and 3, Reading (N = 9,567)
	Level 1	Level 2	Level 3	Level 4	Level 5
Full treatment	−0.019*** (0.007)	−0.007*** (0.003)	0.006*** (0.002)	0.013*** (0.004)	0.007*** (0.002)
Screen only	0.005 (0.007)	0.002 (0.003)	−0.002 (0.002)	−0.003 (0.005)	−0.002 (0.003)

Panel D: Districts 2 and 3, Math (N = 9,584)
	Level 1	Level 2	Level 3	Level 4	Level 5
Full treatment	−0.030** (0.013)	−0.006*** (0.002)	0.010** (0.005)	0.014** (0.006)	0.011*** (0.004)
Screen only	−0.004 (0.014)	−0.001 (0.003)	0.002 (0.005)	0.002 (0.007)	0.002 (0.005)

Notes: This table reports average marginal effects calculated from the coefficients reported in the first two rows of Table 6 for the columns that include all three districts (panels A and B) or Districts 2 and 3 only (panels C and D) and use the control variables.

^***p<0.01;

^**p<0.05;

^*p<0.1.

All coefficients on the non-program variables are as expected.^xxv Demographic patterns are consistent with the literature on student achievement. Girls made greater gains in reading and smaller gains in math than boys. Black students generally made smaller gains in both subjects than White (the omitted category) and Asian students. In one of the three districts, Hispanic students made significantly smaller gains than White students on reading, and the same is true for math in two of the three districts. Students who are eligible for free or reduced-cost lunch made smaller gains than non-eligible students. English language learner students made smaller gains on the reading test (but not the math test) in two of the three districts than their peers who have English as their first language. Within grade, older students made smaller gains than younger students. This may be because students who are struggling are more likely to be held back and thus be older than their peers.^xxvi

Turning to the main coefficients of interest, the signs and magnitudes are consistent across the models with and without demographic controls. We focus on the specifications with demographic controls, which tend to be more precisely estimated. In the specification that combines all three districts, students in the full-treatment schools made larger gains on both the reading and the math tests than students in the control schools, although only the reading test estimate is statistically significant at conventional levels. Looking at the average marginal effects for reading reported in Table 7, we see that being in the full-treatment group is associated with a 0.4 percentage point higher probability of scoring at level 3, a 1.0 percentage point higher probability of scoring at level 4, and a 0.6 percentage point higher probability of scoring at level 5. Levels 3 and above are considered at or above proficiency, so taken together we see that students in full-treatment schools are 2.0 percentage points more likely to be proficient in reading than their peers in control schools (2.0 = 0.4 + 1.0 + 0.6). Similarly for math, students in the full-treatment schools are 2.0 percentage points more likely to be proficient in math than their peers in the control schools (2.0 = 0.5 + 0.8 + 0.7) but this result is not statistically significant at conventional levels.

Examining the three districts separately in Table 6, we see that the full treatment was not effective in District 1. If anything, the full treatment was associated with smaller gains than in control schools—but this difference is neither large nor statistically significant. In Districts 2 and 3, the full treatment was generally effective (all estimated effects are statistically significant except for math scores in District 2). The difference between District 1 and other districts may be due to the implementation problems in District 1. If we exclude District 1 on the assumption that the lack of impact can be traced to the implementation problems outlined above and estimate a model that combines only Districts 2 and 3, we find that the impact of the full treatment increases the probability of scoring at or above proficiency (level 3 or higher) by 2.6 percentage points in reading and 3.6 percentage points in math, as seen in panels C and D of Table 7. Both of these estimates are statistically significant at the 1 percent level. We cannot say conclusively, however, that the implementation problems are to blame for the lack of impact in District 1, so we prefer the estimates that include all three districts. One justification for this approach is that, were the program to be scaled-up, there would likely be similar issues with large scale implementation. Thus, from a policy standpoint, the estimate using all three districts is the most appropriate.

Students in the screen-only schools generally do not make larger gains than students in the control schools. In fact, in Districts 1 (reading and math) and 2 (reading only) students in the screen-only schools actually experience significantly smaller gains than the control school students. There are at least three possible explanations for this, which will be examined further below in the discussion of the results in Table 10. One possibility is that the screening supplants instructional time and students do not follow up with care. A second possibility is that students, or their parents, could have been upset that they were told about a vision problem but were not offered help to address that problem. This may make a student more inclined to give up and attribute his or her academic difficulties to the unresolved vision problem. This is consistent with evidence given below that discipline referrals and suspensions increased in the screen-only schools. This may have been particularly likely in District 1, where the screen-only schools were mistakenly told that they would be provided glasses. Even when we omit District 1 and estimate the impact of screen-only schools in Districts 2 and 3, the coefficient is negative for reading and positive for math but in both cases the estimated impacts are small and statistically insignificant, making it difficult to claim that the screen-only intervention would be successful elsewhere, even if implementation were problem-free. A final possibility is that, despite random assignment, students in the screen-only and control schools differed in unobserved ways; further research on this type of intervention is needed to distinguish between these three possibilities.

Table 10.

Average marginal effects, by subgroup.

Panel A: Reading, by Free Lunch Status, Districts 2 and 3 (N = 9,567)
	Level 1	Level 2	Level 3	Level 4	Level 5
Full treatment × FRL	−0.023*** (0.007)	−0.009*** (0.003)	0.008*** (0.003)	0.015*** (0.005)	0.009*** (0.003)
Full treatment × non-FRL	0.007 (0.015)	0.002 (0.006)	−0.002 (0.005)	−0.004 (0.010)	−0.003 (0.006)
Screen only × FRL	0.000 (0.007)	0.000 (0.003)	0.000 (0.002)	0.000 (0.005)	0.000 (0.003)
Screen only × non-FRL	0.037*** (0.012)	0.014*** (0.005)	−0.012*** (0.004)	−0.024*** (0.008)	−0.014*** (0.005)

Panel B: Math, by Free Lunch Status, Districts 2 and 3 (N = 9,584)
Full treatment × FRL	−0.034*** (0.014)	−0.006*** (0.002)	0.012** (0.005)	0.016*** (0.006)	0.012*** (0.004)
Full treatment × non-FRL	−0.007 (0.013)	−0.001 (0.002)	0.003 (0.005)	0.003 (0.006)	0.003 (0.005)
Screen only × FRL	−0.008 (0.015)	−0.002 (0.003)	0.003 (0.005)	0.004 (0.007)	0.003 (0.005)
Screen only × non-FRL	0.023 (0.023)	0.004 (0.004)	−0.008 (0.008)	−0.011 (0.011)	−0.008 (0.008)

Panel C: Reading, by English Language Learner Status, All Districts (N = 14,526)
Full treatment × ELL	−0.021** (0.009)	−0.009** (0.004)	0.006** (0.003)	0.015** (0.006)	0.010** (0.004)
Full treatment × non-ELL	−0.010* (0.006)	−0.004* (0.002)	0.003* (0.002)	0.007* (0.004)	0.005* (0.003)
Screen only × ELL	0.010 (0.010)	0.004 (0.004)	−0.003 (0.003)	−0.007 0.007	−0.005 (0.005)
Screen only × non-ELL	0.004 (0.005)	0.002 (0.002)	−0.001 (0.001)	−0.003 (0.004)	−0.002 (0.002)

Panel D: Math, by English Language Learner Status, All Districts (N = 14,549)
Full treatment × ELL	−0.033** (0.013)	−0.008*** (0.003)	0.011** (0.005)	0.016** (0.006)	0.014*** (0.005)
Full treatment × non-ELL	−0.008 (0.010)	−0.002 (0.002)	0.003 (0.003)	0.004 (0.005)	0.004 (0.004)
Screen only × ELL	−0.008 (0.016)	−0.002 (0.004)	0.003 (0.005)	0.004 (0.008)	0.003 (0.007)
Screen only × non-ELL	0.019** (0.009)	0.005* (0.002)	−0.006** (0.003)	−0.009** (0.004)	−0.008** (0.004)

Notes: This table reports average marginal effects calculated from the coefficients in Table 9 for columns with multiple districts.

^***p<0.01;

^**p<0.05;

^*p<0.1.

To further compare the two interventions, Chi-squared tests of the difference between the coefficients on the full-treatment and the screen-only interventions are shown at the bottom of each panel in Table 6. In the model that combines all three districts these tests strongly support the claim that the full-treatment intervention outperformed the screen-only intervention. Looking at the districts separately reveals this is driven by the impacts in District 2, where there was a negative impact of the screen-only intervention, especially for reading. Overall, the evidence in Tables 6 and 7 indicates that the full-treatment intervention increased test scores, while the screen-only intervention did not increase test scores, and even may have reduced those scores. Thus, we conclude that, in Title I schools in central Florida, access to treatment is a bigger barrier than lack of information to ensuring that children’s vision problems are adequately treated.

We estimated versions of Table 6 separately for 4th- and 5th-grade students (not shown but available upon request). We find that the impacts after one year are driven by the 5th-grade students. This may be because the traditional screening schedule includes a screening in the third grade, so the 4th-grade students are only one year removed from that screening. This hypothesis is supported by the fact that point estimates on the indicator for the screen-only intervention are also higher (i.e., more positive) for 5th-grade students than for 4th-grade students. Indeed, in District 3 and in the estimate that combines District 2 and District 3, we see evidence that 5th-grade students in the screen-only schools made greater gains in math scores than 5th-grade students in the control schools, but we still do not see an impact of the screen-only intervention for 4th-grade students, nor for reading in either grade (results available upon request).

The estimates in Table 6 may be somewhat imprecise because the FCAT level scores ignore variation within each of the five levels. To take advantage of this variation, Table 8 presents estimates of the average impact of the two interventions on the standardized scale scores (rather than achievement level scores) for Districts 1 and 3 (recall that District 2 did not provide scale scores). The scale scores were standardized using data from the control schools to have a mean of 0 and a standard deviation of 1 in those schools within each subject-grade-year combination. For brevity, the demographic controls are not shown, but they are the same (and have very similar effects) as in Table 6. Consistent with Table 6, when both districts are combined, the full treatment has positive impacts on both reading and math scores, approximately 0.05 standard deviations for reading and 0.03 standard deviations for math, although only the reading result is statistically significant at the 5 percent level. Also similar to Table 6, the screen-only schools have slightly lower test score gains than the control schools, but these estimates are small and statistically insignificant. The positive impact of the full-treatment schools is due to the schools in District 3, which had larger and statistically significant gains in reading and math scores in 2012 than the control schools. The magnitude of the impacts indicates about 0.080 (reading) and 0.094 (math) standard deviations more growth in test scores than in the control schools. As in Table 6, the full treatment does not appear to have had an impact in District 1.

Table 8.

The impact of vision interventions on standardized 2012 and 2013 FCAT scale scores (OLS).

Panel A: 2012 FCAT Scale Scores
	Reading Score 2012						Math Score 2012
	District 1 & 3		District 1		District 3		District 1 & 3		District 1		District 3
Full treatment	0.050** (0.022)	0.050** (0.021)	0.016 (0.025)	0.017 (0.019)	0.077** (0.035)	0.080** (0.033)	0.029 (0.034)	0.030 (0.032)	−0.056 (0.043)	−0.055 (0.040)	0.091* (0.046)	0.094** (0.043)
Screen only	−0.006 (0.016)	−0.000 (0.015)	−0.034* (0.020)	−0.018 (0.017)	0.021 (0.023)	0.012 (0.022)	−0.016 (0.028)	−0.012 (0.026)	−0.096*** (0.032)	−0.087*** (0.029)	0.055 (0.041)	0.046 (0.038)
Demographic Controls	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes
Observations	11,486	11,486	4,959	4,959	6,527	6,527	11,501	11,501	4,962	4,962	6,539	6,539
F-test (Full = Screen)	6.28**	5.83**	4.31**	3.36*	2.31	3.64*	1.83	1.87	0.76	0.59	0.68	1.42

Panel B: 2013 FCAT Scale Scores
	Reading Score 2013						Math Score 2013
	District 1 & 3		District 1		District 3		District 1 & 3		District 1		District 3
Full treatment	0.009 (0.024)	0.010 (0.022)	0.037 (0.037)	0.040 (0.030)	−0.014 (0.030)	−0.011 (0.028)	0.016 (0.031)	0.018 (0.025)	−0.016 (0.048)	−0.012 (0.038)	0.037 (0.039)	0.039 (0.032)
Screen only	−0.040* (0.022)	−0.037** (0.017)	−0.074** (0.031)	−0.065** (0.024)	0.005 (0.024)	−0.008 (0.019)	−0.017 (0.032)	−0.022 (0.024)	−0.063 (0.040)	−0.067* (0.036)	0.022 (0.050)	0.008 (0.031)
Demographic Controls	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes
Observations	10,338	10,338	4,439	4,439	5,899	5,899	10,307	10,307	4,428	4,428	5,879	5,879
F-test (Full = Screen)	3.56*	4.83**	10.08***	15.27***	0.33	0.01	0.77	1.92	0.82	1.64	0.07	0.68

Notes: The standard errors in parenthesis are clustered at the school level. All regressions include baseline (2011) test scores and controls for strata. Additional controls, not shown, are the same as in Table 6. District 2 did not provide FCAT scale scores for either year so we are unable to estimate results for that district or for all three districts combined.

^***p<0.01;

^**p<0.05;

^*p<0.1.

The 2012 tests were administered during the last two weeks of April. Students who received glasses from FLVQ had them for between 1.5 and 6.5 months before taking the 2012 tests. In District 3, the last district to receive the intervention, students had their glasses for an average of only three months prior to the tests. For students who had glasses for a relatively short period, FCAT gains may mostly be due to being more able to read the test, as opposed to increased acquisition of human capital; that is, the test became a more accurate measure of their existing human capital.^xxvii Having glasses for a longer period of time should lead to additional acquisition of human capital that is reflected in higher test scores, though it is possible that the benefit of glasses could erode over time if students break, lose, or stop using them.^xxviii

Table 8 reports the results for the 2013 tests, which were taken over one year (13.5 to 18.5 months) after the intervention. The results indicate that the positive impacts found in 2012 faded out by 2013.^xxix Further, there was no large increase in the standard errors, so we can reject the hypothesis that the 2012 results persisted into 2013 and just became harder to identify due to increased imprecision in the estimates. Fade out in education interventions—especially when the outcome measure is a test score—is common, and so may not be cause for alarm. For example, Duncan and Magnuson (2013) find that impacts from pre-school programs such as Head Start fade out rather quickly. Another example of fade out is Taylor (2014), who finds that gains from an extra math course quickly fade out for middle school students. In our case, fade out may indicate that students are losing or breaking their glasses, or not persisting in wearing them regularly. Another possible explanation for no significant impact on the 2013 tests is that the 5th-grade students, who were driving the results for the 2012 tests, were in sixth grade in 2013, and 6th-grade students are screened in all schools. Of course, both fade out and this explanation could be generating the insignificant results for the 2013 tests.

We are unable to follow up beyond 2013 with the students who were part of the randomized controlled trial. However, we have access to a supporting data set that gives us reason to believe that persistence with wearing glasses is low. In 2014, FLVQ screened over 100,000 students in a variety of central Florida districts (both Title I schools and non-Title I schools) and these data show that older students are significantly more likely to fail the screening than younger students. Further, more than 20 percent of students who had glasses and thus should have been wearing them (or other corrective lenses, such as contacts), were not wearing them at the time of screening, and this share increases as students age.^xxx Florida, as most other states, focuses its vision screening policy in the elementary grades. These data suggest that undetected or untreated vision problems remain a problem, and probably increase through middle school and high school. Thus, while our randomized controlled trial indicates that access to an initial vision exam and a first pair of glasses can increase student learning, at least in the short run, access to sustained follow-up care may be even more important.

Impacts on FCAT Scores for Subgroups of Students

Next, we examine variation in the impact of the interventions by student characteristics. A priori, one would expect that providing vision screening services and free eyeglasses should have a larger impact on children from low-income families, who presumably have limited medical care options and are less able to afford eyeglasses. On the other hand, low-income families may be better served by social safety nets such as Medicaid, leaving lower-middle-income students with fewer healthcare options and, as noted above, the students in these districts who do not qualify for a free/reduced-price lunch are likely not to be wealthy but instead to be on the margin of qualifying for the program.

The top panel of Table 9 presents estimates that allow the impact of each program to vary by whether students in the treatment schools receive a free or reduced-price lunch (FRL). The dependent variable is the categorical score that was used in Table 6. District 1 is not included because it did not provide FRL data. Focusing on the estimates that combine Districts 2 and 3,^xxxi we see that there is a larger impact in the full-treatment schools for students who qualify for FRL; the marginal effects reported in Table 10 indicate that the full treatment increases the probability of passing the FCAT reading test by 3.2 percentage points and increases the probability of passing the FCAT math test by 4.0 percentage points. The difference between the FLR and non-FRL students in the effect of the full-treatment intervention is statistically significant at the 10 percent level for both the reading and math tests. We also see in Table 9 that any negative impacts of the screen-only intervention are concentrated on the non-FRL students, although the difference between the FRL and non-FRL is significant only for the reading test.^xxxii

Table 9.

The impact of vision interventions on 2012 FCAT levels, by subgroup (ordered logit).

By free-reduced lunch (FRL) status
	Reading			Math
	Districts 2 & 3	District 2	District 3	Districts 2 & 3	District 2	District 3
Full x FRL	0.208*** (0.064)	0.151*** (0.052)	0.197** (0.088)	0.273** (0.106)	0.187 (0.123)	0.311** (0.141)
Full x Non-FRL	−0.059 (0.133)	0.016 (0.149)	−0.147 (0.202)	0.060 (0.105)	0.183 (0.139)	−0.110 (0.146)
Screen x FRL	−0.003 (0.066)	−0.235*** (0.067)	0.144** (0.066)	0.067 (0.116)	−0.106 (0.167)	0.179 (0.134)
Screen x Non-FRL	−0.337*** (0.110)	−0.228 (0.200)	−0.344*** (0.130)	−0.183 (0.182)	0.032 (0.289)	−0.321** (0.163)
P-value of Chi-square tests;
H0: Full×FRL=Full×Non-FRL	0.0637	0.4103	0.0886	0.0847	0.9782	0.0182
H0: Screen×FRL=Screen×Non-FRL	0.0048	0.9726	0.0006	0.1448	0.4519	0.0050
Observation	9,567	3,040	6,527	9,584	3,045	6,539

By English language learner (ELL) status
	Reading				Math
	All Districts	District 1	District 2	District 3	All Districts	District 1	District 2	District 3
Full x ELL	0.202** (0.084)	−0.066 (0.183)	0.288*** (0.086)	0.178 (0.129)	0.278** (0.111)	0.086 (0.285)	0.230 (0.168)	0.342** (0.164)
Full x Non-ELL	0.098* (0.054)	0.001 (0.050)	−0.027 (0.079)	0.162 (0.109)	0.072 (0.082)	−0.180 (0.128)	0.145 (0.107)	0.234* (0.141)
Screen x ELL	−0.095 (0.095)	−0.167 (0.143)	−0.200* (0.115)	0.123 (0.164)	0.068 (0.132)	0.002 (0.188)	−0.061 (0.250)	0.236 (0.151)
Screen x Non-ELL	−0.043 (0.049)	−0.084 (0.054)	−0.256*** (0.085)	0.076 (0.071)	−0.157** (0.076)	−0.366*** (0.095)	−0.120 (0.128)	0.072 (0.135)
P-value of Chi-square tests;
H0: Full×ELL=Full×Non-ELL	0.2806	0.7323	0.0177	0.9170	0.0289	0.1913	0.5808	0.4129
H0: Screen×ELL=Screen×Non-ELL	0.6335	0.6042	0.7091	0.8063	0.0583	0.0430	0.7751	0.1816
Observation	14,526	4,959	3,040	6,527	14,549	4,965	3,045	6,539

Notes: The standard errors in parenthesis are clustered at the school level. All regressions include controls for strata. Additional controls, not shown, are the same as in Table 6.

^***p<0.01;

^**p<0.05;

^*p<0.1.

The bottom panel of Table 9 shows that the full treatment generally had a larger impact on students who were receiving English Language Learner (ELL) services than it did for non-ELL students. Focusing on the results that combine districts, the difference between ELL and non-ELL students in the full-treatment schools on the math test is significant at the 5 percent level, and the same difference on the math test for the screen-only schools is significant at the 10 percent level. The marginal effects in Table 10 show that the full treatment for ELL students increased the probability of passing the FCAT reading test by 3.0 percentage points and the probability of passing the FCAT math test by 4.1 percentage points, while the respective impacts for non-ELL students were only 1.4 and 1.0 percentage points, respectively, and the latter is not statistically significant. One hypothesis to explain why ELL status matters is that in central Florida the majority of ELL students are of Hispanic descent and a sizable minority has parents who are undocumented immigrants. Nearly two thirds of undocumented immigrants are uninsured (Rodriguez et. al., 2009), and undocumented immigrants are excluded from Medicaid except under extreme emergency circumstances—which would not include vision care (Sommers, 2013). The FLVQ intervention provided free eye-glasses without regard to immigration or insurance status.

Perhaps the most obvious distinction to make among students is between those who passed the screening—and therefore were not offered glasses or any other services since they did not have any unmet vision problems—and those who failed the screening and were either notified and advised to seek treatment (screen-only schools) or offered a free eye exam and free eyeglasses (full-treatment schools). We expect most, and perhaps all, of the benefits to accrue to the students identified as having unmet vision problems. In principle, the specification should include a dummy variable indicating poor vision for students in both sets of treatment schools and in the control schools. Unfortunately, this is not possible because there are no data on vision problems for control school students. However, this can be done if the sample is limited to the screen-only and full-treatment schools, although the results require careful interpretation.

Table 11 reports regressions that allow the impact of the program to vary by whether students passed the screening, failed the screening, or were not screened at all, but the sample is limited to screen-only and full-treatment schools. In addition, since District 1 did not retain screening data for the screen-only schools, Table 11 includes only students in Districts 2 and 3. In this specification, students who pass the screening in a screen-only school serve as the comparison (omitted) group.

Our first finding is that the students who were not screened because they were absent on the day of the screening have much lower test score growth than students who were screened. This is quite plausible because students who are more likely to be absent, other things equal, will learn less due to those absences. Little else can be learned from the students who were not screened, so the following paragraphs focus on the four different groups who were screened. Note that, because none of these groups is a pure control group, the estimates are all relative within these four groups, and thus are not estimates of any impacts relative to a pure control group.

Within the four groups that were screened, random assignment to either the screen-only treatment or the full treatment enables us to obtain unbiased estimates of the impact of the full treatment relative to the screen-only treatment. This can be done separately for those who failed the screening and for those who passed the screening. While it is also tempting to estimate the impact of failing the screening (relative to passing the screening) on those assigned to either of the two treatments, these students’ vision problems are not randomly assigned and thus such estimates could be biased, so we do not draw any inferences of this type.

Consider first the students who failed the screening, who are the intended beneficiaries of both of these interventions. The estimates in Table 11 measure the marginal effect of the full treatment relative to the screen-only treatment for these students. That is, for students with vision problems it measures the additional impact of free eye exams and free eyeglasses beyond simply screening. The estimated impact is the difference between the estimates in rows 1 and 3. Focusing on the estimates that combine both districts, the point estimates for both math and reading in row 1 are larger than those in row 3, which suggests that, relative to the screen-only intervention, the full-treatment intervention benefitted students with vision problems. At the bottom of Table 11 we report p-values for chi-squared tests that compare the estimates in rows 1 and 3; they find that these positive impacts are not statistically significant when both districts are combined, although they are highly statistically significant for District 2.^xxxiii

Table 11 also provides evidence on whether the full treatment benefitted the students who passed the screenings, and thus presumably have good vision. The estimates in row 2 show that the students who passed the screening and were randomly assigned to the full-treatment schools performed better than their counterparts who were randomly assigned to the screen-only schools. This finding is significant at the 1 percent level in reading and significant at the 10 percent level in math (and driven largely by District 2). This is surprising since there is no direct mechanism for the full treatment to help students with good vision. They were not seen aboard the mobile vision lab and were not given free eyeglasses.

Even more puzzling, for most of the estimates the coefficient in row 2 exceeds the difference between rows 1 and 3, suggesting that the full treatment (relative to the screen-only treatment) benefitted students with good vision more than those with bad vision. This is also evident in Table 12, which shows that the full treatment, relative to the screen-only treatment, increased the probability of passing the 2012 FCAT reading exam (obtaining level 3 or higher) by 2.0 percentage points for students who failed the screening and by 4.2 percentage points for students who passed the screening; the analogous impacts for passing the math exams are 2.3 percentage points and 3.1 percentage points. Yet these differences between these two types of students are not statistically significant. In particular, the last row of Table 11 also reports p-values for chi-squared tests that compare the impact from being randomly assigned to a full-treatment school (relative to being randomly assigned to a screen-only school) for the students who failed the screening (i.e., row 1 minus row 3) with the same impact for the students who passed the screening (i.e., row 2). None of these differences is statistically significant, so the apparent finding that the effect of the full treatment (relative to the screen-only treatment) was stronger for students who passed the screening than it was for students who failed the screening should be interpreted with caution. Indeed, one would expect the spillover effect onto the students with good vision to be smaller than the more direct impact on students with vision problems, but the precision of our estimates is insufficient to measure precisely the relative size of these two impacts.^xxxiv

The most interesting, and most statistically significant, result from Table 11 is that the students who passed the screening benefitted from the full treatment relative to the screen-only treatment, and thus presumably relative to no treatment at all. One possible mechanism through which students with good vision could benefit from the full treatment would be through positive spillovers. Such spillovers could take a number of forms. Perhaps students who were already wearing glasses and passed the screening tended not to wear them prior to the intervention. The full-treatment schools’ provision of eyeglasses to between 10 and 20 percent of the students may have changed those schools’ glasses-wearing culture, encouraging students who already had glasses to wear them more regularly. It could also be that teachers’ classroom behavior may have shifted in response to some of their students having a learning impediment removed, and this may have benefited students without that impediment. A related potential mechanism is that students who failed the screening previously asked their peers with better vision for help, and now these peers can focus on their own assignments. It may also be that the students who received glasses improved their behavior, reducing disruptions in class, yet we find no support in the data for this last hypothesis (see the discussion below of Table 13); unfortunately, the other hypotheses cannot be tested with our data and must be left for future research.

Table 13.

Impacts of vision interventions on attendance and behavior outcomes (OLS).

	Total Absences 2012–2013		Unexcused Absences 2012– 2013		Referrals 2012– 2013	Suspensions 2012–2013
	District 1	District 3	District 1	District 3	District 3	District 3
Full treatment	0.678 (0.475)	0.009 (0.316)	0.567* (0.310)	−0.027 (0.291)	0.135 (0.137)	−0.000 (0.192)
Screen only	0.062 (0.378)	0.146 (0.294)	0.185 (0.309)	−0.276 (0.265)	0.218*** (0.077)	0.277* (0.139)
Grade	−1.549*** (0.479)	−0.405 (0.249)	−1.373*** (0.434)	−1.140*** (0.243)	0.393*** (0.107)	0.898*** (0.188)
Age (months)	0.061*** (0.020)	0.114*** (0.020)	0.061*** (0.017)	0.070*** (0.014)	0.028*** (0.006)	0.056*** (0.011)
Girl	−1.012*** (0.231)	−0.811*** (0.159)	−0.744*** (0.200)	−0.328*** (0.119)	−0.272*** (0.061)	−0.474*** (0.099)
Asian	−1.299 (1.087)	−1.669** (0.645)	−0.020 (0.787)	−1.145*** (0.376)	0.078 (0.069)	0.181 (0.134)
Black	−1.096** (0.456)	−0.709** (0.274)	−0.020 (0.414)	−0.265 (0.205)	0.567*** (0.074)	1.053*** (0.095)
Hispanic	−0.677* (0.392)	0.417 (0.267)	−0.125 (0.284)	0.773*** (0.186)	0.111** (0.054)	0.257*** (0.083)
Multiple race	0.417 (0.603)	0.119 (0.558)	0.712 (0.466)	0.170 (0.395)	−0.058 (0.102)	0.072 (0.325)
Special Education	0.412 (0.483)	−1.206*** (0.342)	0.095 (0.420)	−0.556** (0.259)	−0.149 (0.109)	−1.123*** (0.186)
Gifted	−0.793** (0.316)	−0.392 (0.412)	−0.684** (0.272)	−0.376 (0.227)	−0.109 (0.083)	0.027 (0.224)
Free lunch	-	1.066*** (0.295)	-	1.007*** (0.210)	0.248*** (0.057)	0.411*** (0.097)
ELL	−0.737* (0.363)	−1.182*** (0.255)	−0.650** (0.301)	−0.999*** (0.200)	−0.201*** (0.050)	−0.254*** (0.092)
Total absences 2010–11	0.512*** (0.030)	0.517*** (0.024)	-	-	-	-
Unexcused absences 2010–11	-	-	0.544*** (0.039)	0.425*** (0.028)	-	-
Referrals 2010–11	-	-	-	-	0.588*** (0.078)	-
Suspensions 2010–11	-	-	-	-	-	0.966*** (0.153)
2011 FCAT	Yes	Yes	Yes	Yes	Yes	Yes
Strata	Yes	Yes	Yes	Yes	Yes	Yes
Observations	4,839	6,305	4,839	6,305	6,305	7,050

Notes: The standard errors in parenthesis are clustered at the school level. All regressions include controls for strata.

^***p<0.01;

^**p<0.05;

^*p<0.1.

An alternative interpretation for the finding that students who passed the screening in the full-treatment schools had higher test score gains than their counterparts in the screen-only schools is that, by chance, the random assignment did not fully remove unobserved differences between these two groups of students. While the balance tests in Table 3 show little evidence of problems with the random assignment, the unusual findings in the previous two paragraphs could be interpreted in this way, and only future research will be able to determine the size of, and the mechanisms behind, any spillover effects from the full-treatment intervention.

A final issue regarding the impact of the full treatment on both students with and without vision problems is placebo effects; perhaps student outcomes improved simply because of the extra attention provided by the non-profit rather than the actual follow-up services provided. The mobile vison clinic bus not only has optometrist equipment but also is decorated with images of the local National Football League team (which supports FLVQ). While it seems doubtful that these images would spur large gains, it is worth noting that placebo effects could also explain both why students’ academic performance improved after only two to three months with the eyeglasses and the subsequent observed fade out.

Impacts on Non-Academic Outcomes

Finally, Table 13 shows estimated impacts of both interventions on two types of non-academic outcomes, namely attendance and behavior outcomes. District 2 provided neither attendance nor discipline data, and District 1 did not provide discipline data. We use 2012/2013 outcomes because, unlike test outcomes that are from a single day (i.e., the test day), for attendance and discipline data, 2011/2012 outcomes include both time prior to the intervention and time after the intervention. All estimates control for data from two years prior; for example, the regression for absences in 2012/2013 includes as an explanatory variable absences in 2010/2011. All estimates also control for 2011 FCAT achievement levels.

We see no evidence that the intervention reduced student absences. In fact, the only statistically significant result on absenteeism has an unexpected sign, although it is significant only at the 10 percent level: Students in the full-treatment schools in District 1 appear to have had unexcused absences more often than control school students even after conditioning on absences from two years prior. One possible explanation is that the students were absent more often because they missed school for eye appointments related to their new vision diagnosis. This seems unlikely, however, since the mobile vision unit brought the eye appointment to the school. Perhaps the best explanation is that one significant result at the 10 percent level out of eight estimates of the impacts of both interventions simply reflects random chance when there really is no effect.

There is also no evidence that either intervention reduced behavior problems. In fact, in District 3, the only district for which we have disciplinary data, students in the screen-only schools were more likely to have behavior problems than students in the control schools, even after conditioning on discipline data from two years prior. One possible explanation is that students who fail the vision screening but are not offered help obtaining glasses become fatalistic and are more likely to give up on their schooling.

More generally, using data from one year before the interventions, we find no correlation between bad vision and behavior problems. Neither do we find that students who failed the screening in the fall of 2011 had more absences or behavior referrals in the academic year prior to the intervention (2010/2011 school year) than did students who passed the screenings. Thus, it does not appear that vision interventions have their primary impact through reducing either absences or discipline problems.

CONCLUSION

This is the first study in the United States to use a randomized controlled trial to estimate the impact of offering vision services on student outcomes. We find that providing additional/enhanced screening alone is generally insufficient to improve student learning as measured by test scores. However, the full-treatment intervention, which included vision exams and free eyeglasses, improved student achievement as measured by the Florida Comprehensive Achievement Test (FCAT). Averaging over all three school districts, students in the full-treatment schools are approximately 2.0 percentage points more likely to pass the FCAT tests. Note that this average includes students who did not need glasses, students who needed but did not receive glasses, and an entire district where the program was not well implemented. When the sample is restricted to the two districts where the program was smoothly implemented, students in the full treatment schools were 2.6 percentage points more likely to pass the FCAT reading test and 3.6 percentage points more likely to pass the FCAT math test. Note that these average effects also include students in those schools who did not need eyeglasses and students who needed them but did not receive them; attempts to estimate impacts separately for those with and without vision problems are hampered by smaller sample sizes and the lack of a pure control group that distinguishes between students with and without vision problems. We also find evidence of spillover effects onto students with good vision in the full-treatment schools, yet the size of this effect relative to the impact for students with vision problems in those schools is not precisely estimated. If additional evidence supports the existence of sizeable spillover effects, it would suggest that analyses that focus only on students who received eyeglasses may underestimate the full effect of that intervention on students’ academic outcomes.

While the results of this study provide evidence that provision of free eyeglasses in schools with high proportions of disadvantaged students could be an effective education policy to increase student learning, this study alone does not provide sufficient evidence to recommend such a policy change. In particular, the estimates of large spillover effects onto students without vision problems in the full-treatment schools (relative to the screen-only schools) seem implausibly high; they are even higher than the effects on students with vision problems in these schools (again relative to that impact in screen-only schools), and while this difference is not statistically significant, these implausible results raise the possibility that the random assignment did not completely remove all unobserved differences among the students across the three types of schools (although Table 3 reveals little evidence of differences in observed characteristics). The finding that the screen-only intervention may have had some negative effects on student learning reinforces the need for caution in interpreting our results.

Future research on the impact of provision of vision services on students’ educational outcomes should address issues that could not be resolved in this study. First, further research on the possibility of spillover or placebo effects, and on the mechanisms that generate them, may have very important policy implications. Second, given the lack of impact, and perhaps even a negative impact, of the screen-only intervention, and the fact that this intervention is much less expensive than the full-treatment intervention, research on the factors that may help or hinder the effectiveness of this intervention could also be very useful for policymakers. Third, the results of the full intervention appear to fade out quickly from the first to the second year; additional research on why this happens—and what can be done to minimize it—would be very valuable. Fourth, given that secondary schools typically do not screen students for vision problems, it would be useful to conduct similar research at the secondary school level to see whether vision services programs can improve the educational outcomes of older students. Finally, the generalizability of these results may be limited to other similar contexts with high numbers of low-income and ELL (largely Hispanic) students and to the specific policy environment, particularly with regard to insurance coverage. While much remains to be learned, it appears that vision interventions have the potential to improve student learning at a relatively low cost, and thus may be a wise investment for scarce education resources in the United States, and in other countries as well.