Orientation-independent room temperature optical ¹³C hyperpolarization in powdered diamond

Shining light on diamond particles makes them MRI-“bright,” opening avenues for room temperature hyperpolarized liquids.

Abstract

Dynamic nuclear polarization via contact with electronic spins has emerged as an attractive route to enhance the sensitivity of nuclear magnetic resonance beyond the traditional limits imposed by magnetic field strength and temperature. Among the various alternative implementations, the use of nitrogen vacancy (NV) centers in diamond—a paramagnetic point defect whose spin can be optically polarized at room temperature—has attracted widespread attention, but applications have been hampered by the need to align the NV axis with the external magnetic field. We overcome this hurdle through the combined use of continuous optical illumination and a microwave sweep over a broad frequency range. As a proof of principle, we demonstrate our approach using powdered diamond with which we attain bulk ¹³C spin polarization in excess of 0.25% under ambient conditions. Remarkably, our technique acts efficiently on diamond crystals of all orientations and polarizes nuclear spins with a sign that depends exclusively on the direction of the microwave sweep. Our work paves the way toward the use of hyperpolarized diamond particles as imaging contrast agents for biosensing and, ultimately, for the hyperpolarization of nuclear spins in arbitrary liquids brought in contact with their surface.

INTRODUCTION

Nuclear magnetic resonance (NMR) is a widely used spectroscopic technique (1) and a true workhorse in a variety of fields, ranging from chemical structure analysis to medical imaging (2). Despite its versatility and broad applicability, its inherent low sensitivity has prevented some applications of the technology, for instance, in desktop spectrometers and in point-of-care medical use. Dynamic nuclear polarization (DNP)—the ability to use electron spins to enhance the polarization of, and hence, signal from, nuclear spins (3)—has emerged as an attractive solution for several applications. However, the need to perform the electronic polarization at cryogenic temperatures and high magnetic fields (4, 5) has motivated the search for simpler, low-cost hyperpolarization alternatives.

A particularly compelling idea, which has garnered much recent attention, is the use of atom-like defects in diamond as optical hyperpolarizing agents (6). Specifically, the electronic spin corresponding to the diamond nitrogen vacancy (NV) center is optically polarizable to ≈99% at room temperature (7), has remarkable coherence properties (8), and can be created close (<4 nm) to the surface so as to be hyperfine-coupled to external nuclei (9, 10). These attributes facilitate coherent transfer of polarization from the NV centers to proximate nuclei, boosting their NMR signal by orders of magnitude at room temperature. Recent studies have shown large (>0.5%) optical hyperpolarization of ¹³C nuclear spins in single-crystal diamond with a variety of DNP techniques (11–14).

Despite this encouraging progress, these methods have been limited to single crystals. DNP transfer to outside spins has remained unsuccessful due to their reduced contact surface area with the external liquid. A more viable alternative is the use of diamond in powdered form either as nanoscale particles or as microscale particles, which offers a larger contact surface area, for instance, ≳ 6700 mm²/mg for 100-nm particles, orders of magnitude greater than ~ 0.13 mm²/mg for a single crystal of equivalent mass. The goal of optically “hyperpolarized nanodiamonds” has been a long-standing one (15), yet the strong orientational dependence of the spin-1 NV centers has remained challenging to surmount (16). Unlike a single crystal with a narrow resonance, the electronic linewidth of micro- or nanodiamonds is greatly (inhomogenously) broadened to a ≳5.7-GHz powder pattern even at modest fields >0.1 T, making conventional DNP strategies ineffective.

Here, we overcome these challenges to optically hyperpolarize diamond powder, obtaining high bulk ¹³C polarization comparable to the best results in single crystals (11). Note that this is in comparison to past results wherein hyperpolarized signals were measured against Boltzmann signals under the same experimental conditions. We have developed a new, remarkably simple, low-field optical DNP technique that proves to be fully orientation-independent. Unlike conventional DNP (5), the regime in which we perform the transfer exploits the fact that the NV electrons can be polarized independent of field, and low field can be used advantageously to reduce the broadening of the electronic linewidth. Here, the bulk nuclear polarization is unambiguously detected by inductive readout subsequent to rapid shuttling of the hyperpolarized powder to high field (Fig. 1A) and is compared against the corresponding Boltzmann polarization at 7 T, similar to the studies of Fischer et al. (11) and Álvarez et al. (12), but in contrast to previous works on single NV centers or small ensembles (17–19). Figure 1B shows the DNP protocol in detail; nuclear hyperpolarization is affected by sweeping microwave irradiation across the NV center powder pattern at a low-field B_pol ≈ 1 to 30 mT under continuous laser irradiation.

Fig. 1. Experiment overview.

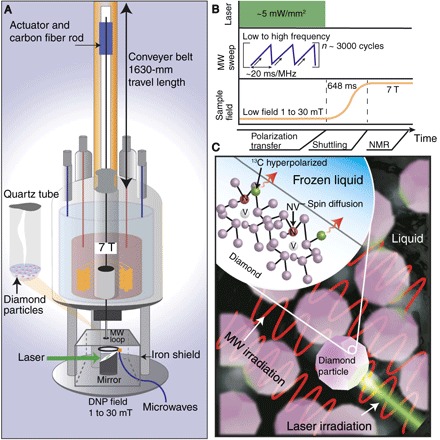
(A) Polarization transfer from optically pumped NV centers to ¹³C in diamond particles is carried out by microwave irradiation at low field (B_pol ~ 1 to 30 mT), after which the sample is shuttled rapidly for bulk inductive readout at 7 T. We quantify the polarization enhancement with respect to the thermal signal at 7 T. (B) Polarization transfer protocol: Laser light (532 nm) is continuously applied along with swept microwave (MW) irradiation across the NV center spectrum at B_pol to hyperpolarize the ¹³C nuclei. The sweep time per unit bandwidth is 20 ms/MHz. (C) Envisioned nanodiamond polarizer: Optically hyperpolarized ¹³C diamond nuclei relay polarization to ¹³C spins in a frozen liquid by spin diffusion, aided by the intrinsically large surface area of nanoparticles. Subsequent rapid thaw would allow enhanced NMR detection with chemical shift resolution.

RESULTS

Figure 2 summarizes the key features of the technique, demonstrated for a typical example of 200-μm microparticles with 1.1 % natural-abundance ¹³C containing about 1 part per million (ppm) of NV centers (see Materials and Methods). Under optimized conditions, we obtain hyperpolarization over 277 times that of the 7-T Boltzmann level (Fig. 2A)—a high polarization level comparable to the best results on single crystals (11, 12) yet achieved here on a completely randomly oriented powder. The use of optical pumping enables orders of magnitude higher ¹³C polarizations than those obtained using thermally polarized P1 centers under comparable conditions (20). The polarization builds up in under 60 s of optical pumping (Fig. 2B) and points to the efficiency of the underlying DNP mechanism. The slow rise in polarization after initial exponential growth is a direct indication of spin diffusion in our system—the ¹³C’s close to the NV centers being highly polarized and the spin diffusing their polarization to nuclei further away. Note that for clarity, the signals in Fig. 2A have their noise unit normalized, and a single-shot DNP signal has about 25 times the signal-to-noise ratio (SNR) of the 7-T thermal signal obtained after ≈7 hours of averaging—a time gain of over five orders of magnitude for identical SNR. The ¹³C signal is so greatly enhanced that it enables detection of a single 200-μm particle in a single shot with unit SNR.

Fig. 2. Optical hyperpolarization in diamond microparticles.

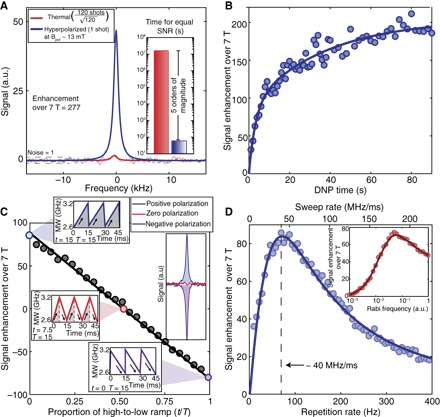
Hyperpolarization experiments were performed on dry 200-μm particles with 1.1% natural-abundance ¹³C. Solid fit lines are depicted over data points. (A) Signal gain by DNP under optimized conditions. Blue line shows the ¹³C NMR signal due to Boltzmann polarization at 7 T, averaged 120 times over 7 hours. Red line is a single-shot DNP signal obtained with 60 s of optical pumping, enhanced 277 times over the 7-T thermal signal (enhanced 149,153 times at B_pol = 13 mT). The signals have their noise unit-normalized for clarity. Hyperpolarization thus leads to more than five orders of magnitude gains in averaging time (inset). (B) Buildup curve showing rapid growth of bulk ¹³C polarization. Slow rise at longer times is due to ¹³C spin diffusion. (C) Hyperpolarization sign is controlled by MW sweep direction across the NV center powder pattern. Continuous family of sweeps demonstrating the idea, with extremal points representing low-to-high frequency MW sweeps and vice versa. Time t is the period of the high-to-low frequency component in one cycle of total period T. Inset: ¹³C signal undergoes near-perfect sign inversion upon reversal of the sweep direction. Sweeping in a symmetric fashion leads to net cancellation and no buildup of hyperpolarization. (D) Sweep rate dependence of the signal enhancement. The sweep bandwidth is 570 MHz, and the excitation laser power is ≈5 mW/mm². The solid line is the result of a fit using the expression in the main text; we find k = 18.4 MHz/ms and Λ= 30 kHz for a Rabi field Ω =0.35 MHz. Inset: Dependence of ¹³C NMR signal as a function of the MW Rabi frequency. Here, the solid line serves as a visual guide. a.u., arbitrary units.

Our technique allows simple control of the hyperpolarization direction (Fig. 2C). Sweeping the microwaves in a ramped fashion from low to high frequency leads to nuclear polarization aligned to B_pol. Accordingly, anti-alignment is possible by sweeping from high to low frequency. This allows on-demand control of the sign of polarization. As expected, a triangular sweep pattern with equal amounts of high-to-low and low-to-high frequency sweeps leads to destructive interference in alternate periods and no net polarization buildup (Fig. 2C). This feature may prove useful, for example, for common-mode noise rejection in signal-enhanced nanodiamond imaging. This room temperature hyperpolarized magnetic resonance imaging (MRI) would provide a complementary, noninvasive, three-dimensional imaging modality to high–NV density nanodiamonds presently used as nonblinking fluorescent biomarkers (21–23). Through our method, functionalized diamond microparticles in solution can be hyperpolarized with modest optical power (~1-mW/200-μm particle) and single-shot detection sensitivity. This will open up new possibilities for targeted biosensing (24, 25). The use of NV centers instead of persistent radicals as a source of electron spin in DNP will eliminate potential undesirable effects in in vivo imaging such as oxidative stress without proper filtration.

Using the notation in the energy diagram of Fig. 3A, the process of nuclear spin hyperpolarization can be better understood in the rotating frame, where resonances take the form of avoided crossings. Because one traverses the full set of m_S = 0 ↔ m_S = ±1 transitions, moderately fast sweep rates make the more weakly avoided crossings partially nonadiabatic, thus resulting in a selective population transfer between the different branches and, consequently, the generation of net nuclear spin polarization. As an illustration, consider the case of a positive hyperfine coupling (A_zz = + 0.5 MHz) shown in Fig. 3B in the subset m_S = 0 ↔ m_S = −1. Assuming that for simplicity, the NV spin is in the m_S = 0 state, nuclear spins polarize positively, as one sweeps the Landau-Zener crossing from low to high frequencies; similarly, a negative polarization arises if one starts from the right side of the crossing and the direction of the sweep is reversed. Central to this proposed polarization process are the differential Landau-Zener transition probabilities, selectively favoring, in this case, the transfer of populations between branches with different electron and nuclear spin quantum numbers. The resulting nuclear spin polarization is negligible if the population transfer throughout the Landau-Zener crossings is complete (the fully nonadiabatic limit), meaning that the optimum is attained at some intermediate sweep rate, consistent with our observations (Fig. 2D).

Fig. 3. Proposed mechanism of polarization transfer.

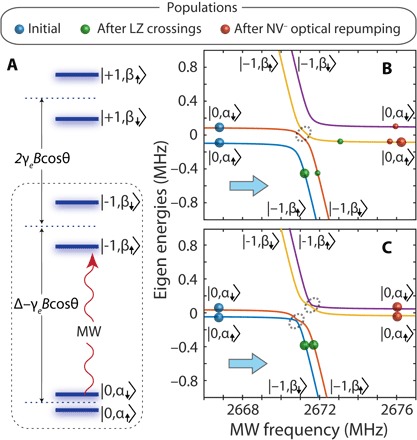
(A) Energy levels of an NV⁻ electron spin hyperfine coupled to a ¹³C nuclear spin. Δ denotes the NV zero-field splitting, γ_e is the electron gyromagnetic ratio, and B (assumed much smaller than Δ) is the external magnetic field forming an angle θ with the NV axis. The quantum numbers in all kets refer to electron and nuclear spins, in that order; the notation for the nuclear spin states highlights the manifold-dependent quantization axis, in general different from the magnetic field direction. (B) Calculated energy diagram in the rotating frame corresponding to the m_S = 0 ↔ m_S = −1 subset of transitions [dashed rectangle in (A)] assuming a hyperfine coupling A_zz = +0.5 MHz. (C) Same as in (B) but for A_zz = −0.5 MHz. In (B) and (C), we assume that B = 10 mT and θ = 45° and use a transverse hyperfine constant A_zx = 0.3|A_zz|. Colored solid circles denote populations at different stages during a sweep in the direction of the arrow, and faint dashed circles indicate the narrower avoided crossings where population transfer takes place. LZ, Landau-Zener.

The dynamics for negative hyperfine couplings are qualitatively different. The more weakly avoided crossings occur between branches within the same electron spin manifold, with the consequence that the nuclear spin polarization buildup becomes inefficient in either sweep direction (Fig. 3C). In other words, because one sweeps the set of transitions connecting the m_S = 0 and m_S = −1 manifolds, only carbon spins with positive hyperfine couplings contribute to pump nuclear spin polarization. The converse is true for the m_S = 0 ↔ m_S = +1 subset of transitions because, when |A_zz| is greater than the nuclear Larmor frequency,the physics remains unchanged if we simultaneously reverse the signs of the electron spin projection number and hyperfine coupling constant. Because the number of nuclear spins experiencing positive and negative hyperfine couplings is comparable, it follows the notion that the ¹³C signals from the m_S = 0 ↔ m_S = +1 manifold should feature similar amplitudes and the same (sweep direction–dependent) sign, as observed within the m_S = 0 ↔ m_S = −1 subset (Fig. 3, B and C), which we confirm experimentally (see below). Implicit in the above picture is the assumption that the probability of optically exciting the NV spin during the Landau-Zener crossings is sufficiently low, a condition fulfilled herein given the relatively fast sweep rates (~40 MHz/ms at the optimum; Fig. 2D) and low illumination intensities (~10 mW/mm²) used in our experiments.

As a crude approximation to the results in Fig. 2D, we write the nuclear spin polarization $\mathit{P}\propto \mathit{g}(\stackrel{.}{\mathrm{\omega }})\mathit{q}(\stackrel{.}{\mathrm{\omega }})[1-\mathit{Q}(\stackrel{.}{\mathrm{\omega }})]$, where $\mathit{Q}(\stackrel{.}{\mathrm{\omega }})= \text{exp}(-{\mathrm{\Omega }}^2/\stackrel{.}{\mathrm{\omega }})$ is the transition probability between branches differing only in the electron spin number, $\stackrel{.}{\mathrm{\omega }}$ is the frequency sweep rate, and Ω is the Rabi field amplitude. On the other hand, we express the transition probability between branches with different electron and nuclear spin numbers as $\mathit{q}(\stackrel{.}{\mathrm{\omega }})= \text{exp}(-{\mathrm{\Lambda }}^2/\stackrel{.}{\mathrm{\omega }})[1-\mathit{Q}(\stackrel{.}{\mathrm{\omega }})]$, where Λ (in general, a function of the hyperfine coupling and magnetic field orientation) captures the effect of the smaller gap size near the narrower crossing, and the last factor ensures that we regain the correct limit for fast sweeps (where Q ≫ q and the populations in each state before and after the crossing remain unchanged). Finally, $\mathit{g}(\stackrel{.}{\mathrm{\omega }})=[1-\text{exp}(-\stackrel{.}{\mathrm{\omega }}/\mathit{k})]$, with k being a fitting parameter, takes into account the cumulative effect of varying multiple sweeps within a fixed measurement time per point. The agreement we attain with the experimental data set (solid trace in the main plot of Fig. 2D) may be, in part, fortuitous because the correct response must arise from an integral over all hyperfine couplings and magnetic field orientations, a task we will carry out in subsequent work.

Our preliminary calculations suggest that weakly coupled carbons (that is, |A_zz| ≲ 2 MHz) are dominant in driving the nuclear spin polarization process because they polarize efficiently and are comparatively more numerous than those in the first or second shell around the NV. Further, the frequency mismatch with bulk carbons (arising from second-order hyperfine contributions within the m_S = 0 manifold; see the Supplementary Materials) is considerably lower for more weakly coupled carbons, thus facilitating spin diffusion to the bulk. However, we caution that the proposed polarization mechanism should not be understood as exclusive because other polarization channels involving more strongly coupled carbons (|A_zz| ≳ 10 MHz) may also play a role, particularly in ¹³C-enriched samples where the two-spin model used here breaks down.

To demonstrate more precisely how all NV center orientations contribute to the obtained hyperpolarization signal, we map the underlying electronic powder pattern via the ¹³C signal (Fig. 4). The DNP involves sweeping microwaves over a 100-MHz window, and then moving it in frequency space. While natively a convolution, the obtained signal does faithfully report on the electronic lineshape broadening, as expected with increasing field (Fig. 4, A to C). The results in Fig. 4D also exhibit another surprising aspect: Unlike in conventional DNP methods, for example, solid effects, cross effects, and thermal mixing (26), where one expects a dispersion-like frequency dependence where certain parts of the electronic spectrum contribute positively or negatively to the enhancement, here, all parts of the spectrum provide the same enhancement sign. This is also independent of whether one accesses the part of the spectrum corresponding to m_s = +1 or m_s = −1 electronic spin states. The hyperpolarization sign, as in Fig. 2C, only depends on the direction of MW sweep. Figure 4D also illustrates that only half of the full electronic spectrum is sufficient to saturate the full extent of polarization, consistent with the fact that every NV center orientation is represented on either half of the powder pattern.

Fig. 4. Contributions of different NV orientations to DNP.

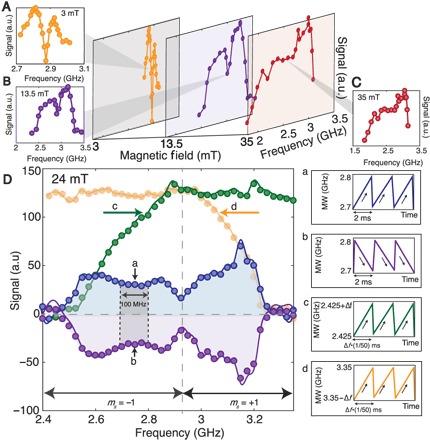
(A to C) Electronic powder pattern mapped by performing DNP in a 100-MHz window, which is swept across in frequency space. This reports on the contributions of each window to the resulting signal and different orientations’ relative contribution to DNP at different magnetic fields. Note that amplifier bandwidth limitations lead to an artificial cutoff at ≈3.2 GHz. (D) Sign contributions from different NV orientations. (a and b) Every part of the powder pattern, even if corresponding to different (m_s = ±1) electronic states, produces the same sign of hyperpolarization (shaded regions) that only depends on the direction of MW sweep. Solid lines are smoothened curves. Keeping the lower frequency (c) and upper frequency (d) of the DNP window fixed provides the cumulative contribution of different parts of the electronic spectrum to the polarization buildup. It shows that half of the powder pattern is sufficient to saturate the polarization enhancement. Note that we maintain the same differential sweep rate per unit spectral width equivalent to 40 MHz/ms in all experiments.

Finally, we measured the hyperpolarized signal from a varying number of particles (see Fig. 5) to estimate the minimum number of detectable particles. We took single-shot SNR averaged over 30 runs of the experiments. Figure 5 demonstrates that, after hyperpolarization with 40 s of laser pumping, it is possible to measure 0.994 particles (that is, one single 200-μm particle) with SNR = 1 in one shot at 7 T. This level of sensitivity has important implications in hyperpolarized imaging experiments, where the ability to detect a single particle would allow the hyperpolarized particles to act as MRI tracers. Rej et al. showed nanodiamonds to have long ¹³C T₁’s, even as large as 30 min at high fields (27), making them compelling to use as reporters in MRI.

Fig. 5. Minimum number of particles detectable.

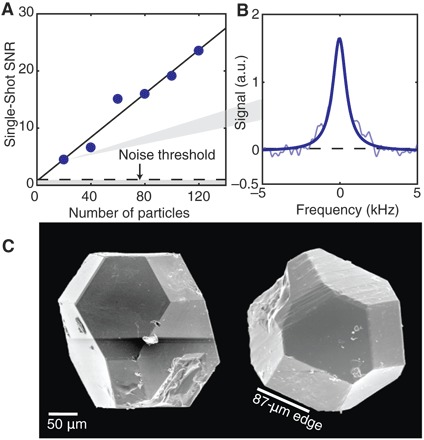
(A) Single-shot SNR scaling with the number of Element6 200-μm diamond microparticles in the sample tube. The experiments are performed by careful particle counting and averaging more than 30 single-shot measurements for each accumulated collection of particles. By extrapolation, we determine that it is possible to obtain signal from a single particle with a single-shot SNR of 0.994. (B) Average of 30 single-shot signals from 20 particles. (C) SEM micrograph (Hitachi S5000) of individual Element6 high pressure–high temperature diamond particles used in majority of the experiments. The particles have a uniform size distribution (edge length, 87 ± 3.9 μm) and a truncated octahedral shape set by particle growth conditions.

DISCUSSION

These results demonstrate that in addition to providing large signal enhancements, our technique exploits a unique low-field DNP mechanism that is qualitatively different from others in the literature. We exploit the fact that the NV electrons are optically polarized at any field, and low fields mitigate their strong orientational dependence. From a technological standpoint, our technique is relatively simple to implement: Hyperpolarization occurs at room temperature, MW amplifiers and sweep sources in the 2- to 4-GHz range are low-cost and readily available, a simple stub antenna serves for MW irradiation, the laser and MW powers used are very modest, and there is no requirement for magnetic field alignment. This opens up the possibility of constructing low-cost tabletop nanodiamond polarizers. Low field also comes with the added benefit of long target nuclear T₁’s in the external nuclei due to reduced chemical shift anisotropy, allowing the potential for higher buildup of polarization. For instance, ¹³C spins in pyruvate, an important molecule in the metabolic cycle and cancer detection, can exceed 55 s at 10 mT (28). When mildly frozen, for instance, at liquid nitrogen temperature, the resulting T₁ can be nearly an hour (29). However, one limitation is the lower nuclear T₁ times in diamond at low fields, which limits the time period for spin diffusion within each particle. There is a strong indication that the ¹³C lifetime is set by their interactions with the dominant dipole–coupled electronic spin bath consisting of nitrogen impurities (P1 centers). Recent advances in diamond growth with high (>20%) NV center conversion efficiency are a positive sign that they could be effectively mitigated (30). Moreover, there is strong evidence (31) that ¹³C lifetimes can be sufficiently long even for particles sizes down to 100 nm.

In conclusion, we have developed a new DNP technique for polarization transfer from NV centers in diamond that is completely orientation-independent and have demonstrated its application for hyperpolarizing ¹³C nuclei in diamond microparticles to attain bulk polarization in excess of 0.25%. We also found that the method worked on smaller particles (1 μm), although DNP enhancements were reduced on account of lower NV concentrations and shorter T₁. Our low-field optical DNP mechanism is unique in that the entire electronic spectrum contributes constructively to the polarization buildup with on-demand control of the hyperpolarization direction. Our work paves the way toward exploiting the large surface area intrinsic to diamond nanoparticles to optically hyperpolarize a liquid at room temperature. Given a spin diffusion constant of D = 8 × 10³Å²/s (32), one could potentially polarize ~244 μl of liquid per milligram of 100-nm hyperpolarized diamonds in 125 s. Moreover, the use of ¹³C enrichment in the diamond particles or as surface coatings will greatly enhance these spin diffusion rates to external liquids. We also envision utility of our method for signal enhancements in nanoscale MRI experiments mediated by NV sensors (33). Moreover, it presents an advance toward MRI modalities for biosensing constructed out of optically hyperpolarized, surface-functionalized diamond particles. The diamond particles are nontoxic, can be functionalized (23), and hence in an MRI modality, can potentially serve as a sensitive biosensor for disease detection (34) and noninvasively characterize fluid flow in bioreactors (35).

MATERIALS AND METHODS

Diamond particles

The experiments in this work were performed with 7.50 ± 0.25 mg (287 ± 27 particles) of 200- to 250-μm diamond microparticles from Element6, with ≈1-ppm NV center concentration. Scanning electron microscopy (SEM) images (see Fig. 5C) show that the particles have a truncated octahedral shape, although with some imperfections and irregularities. Overall, the particles in the sample measured face to face from respective opposite faces are 200 to 250 μm in size and approximately 400 μm measured diagonally edge to edge. Using the known scale of the images, all visible edge lengths were measured, and the average edge length was found to be 87 ± 3.9 μm (marked in Fig. 5C). This average edge length was used for all further calculations of surface area and volume (see the Supplementary Materials).

Experimental design

A fast field-cycling device was used to leverage rapid mechanical sample shuttling from the low-field polarizing volume (1 to 30 mT) composed of stress annealed iron (1.57 mm thick; NETIC S3-6 alloy, Magnetic Shield Corp) to a wide-bore, 7-T superconducting magnet for detection. A conveyor belt actuator stage (Parker HMRB08) carries a rigidly fastened NMR tube (8 mm) containing the diamond particles along the fringing field of the magnet to magnetic field extremes. A home-built NMR probe with a hollow opening was designed to allow rapid mechanical transfer of the sample between the low-field volume and the 7-T magnet. The sample was channeled through a series of funnel-shaped guiding stages made of soft teflon that dynamically align the sample concentric to the magnetic bore to within 1 mdeg. Shuttling a sample from 8 mT to 7 T takes 648 ± 2.5 ms with high positional precision (50 μm) at a maximum speed of 2 m/s and acceleration of 30 m/s². The motion of the actuator stage was synchronized to trigger at the end of a polarization cycle with inductive detection, coinciding with the end of shuttling. NMR measurements were performed with a custom-printed saddle coil tuned to 75.03 MHz for ¹³C detection (see the Supplementary Materials).

Hyperpolarization of diamond

Hyperpolarization was performed at the low-field volume (1 to 30 mT) for times up to a minute, after which the sample was rapidly shuttled to 7 T for bulk ¹³C measurement. Low-field DNP was implemented by continuous irradiation of laser light that polarized NV centers, accompanied by frequency sweeps over the NV center powder pattern. A Coherent Verdi laser (532 nm) delivered a continuous collimated beam that was expanded to match the diameter of the NMR tube containing the sample (8 mm). The laser power was selected to conditions that maximized DNP transfer efficient at a total laser power of 200 mW over an 8-mm beam diameter (see the Supplementary Materials). Frequency sweeps were generated via voltage controlled oscillators (VCOs) (1.9 to 3.7 GHz; Mini-Circuits ZX95-3800A+). The VCOs were regulated by programmable ramp inputs to control the direction, bandwidth, and sweep rate of frequency sweeps. The outputs were combined and amplified with a 100-W amplifier (Empower SKU-1146) before being directed to the sample via a stub-loop antenna (see the Supplementary Materials).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaar5492/DC1

section S1. Methods and materials

section S2. Indirect NV spectroscopy by ¹³C DNP

section S3. Mechanism for orientation-independent polarization transfer

section S4. Experimental design

section S5. DNP electronics setup

section S6. DNP optics setup

section S7. Shot-to-shot variation of enhancement

section S8. Polarization loss due to shuttling

section S9. Data processing

fig. S1. Enhanced ¹³C DNP for particles in solution.

fig. S2. Electron powder pattern measured via ¹³C DNP.

fig. S3. Single-crystal electronic lineshape measured via ¹³C DNP.

fig. S4. Simulations of DNP enhancement.

fig. S5. Detail of experimental setup schematically described in Fig. 1A.

fig. S6. Low-field DNP setup.

fig. S7. Schematic circuit for DNP excitation.

fig. S8. Sweep rate dependence on laser power.

fig. S9. DNP enhancement spread due to orientational shaking.

References (36–41)