Explicit ions/implicit water generalized Born model for nucleic acids

Abstract

The ion atmosphere around highly charged nucleic acid molecules plays a significant role in their dynamics, structure, and interactions. Here we utilized the implicit solvent framework to develop a model for the explicit treatment of ions interacting with nucleic acid molecules. The proposed explicit ions/implicit water model is based on a significantly modified generalized Born (GB) model and utilizes a non-standard approach to define the solute/solvent dielectric boundary. Specifically, the model includes modifications to the GB interaction terms for the case of multiple interacting solutes—disconnected dielectric boundary around the solute-ion or ion-ion pairs. A fully analytical description of all energy components for charge-charge interactions is provided. The effectiveness of the approach is demonstrated by calculating the potential of mean force for Na⁺–Cl⁻ ion pair and by carrying out a set of Monte Carlo (MC) simulations of mono- and trivalent ions interacting with DNA and RNA duplexes. The monovalent (Na⁺) and trivalent (CoHex³⁺) counterion distributions predicted by the model are in close quantitative agreement with all-atom explicit water molecular dynamics simulations used as reference. Expressed in the units of energy, the maximum deviations of local ion concentrations from the reference are within k_BT. The proposed explicit ions/implicit water GB model is able to resolve subtle features and differences of CoHex distributions around DNA and RNA duplexes. These features include preferential CoHex binding inside the major groove of the RNA duplex, in contrast to CoHex biding at the “external” surface of the sugar-phosphate backbone of the DNA duplex; these differences in the counterion binding patters were earlier shown to be responsible for the observed drastic differences in condensation propensities between short DNA and RNA duplexes. MC simulations of CoHex ions interacting with the homopolymeric poly(dA·dT) DNA duplex with modified (de-methylated) and native thymine bases are used to explore the physics behind CoHex-thymine interactions. The simulations suggest that the ion desolvation penalty due to proximity to the low dielectric volume of the methyl group can contribute significantly to CoHex-thymine interactions. Compared to the steric repulsion between the ion and the methyl group, the desolvation penalty interaction has a longer range and may be important to consider in the context of methylation effects on DNA condensation.

I. INTRODUCTION

Ions play essential roles in governing the structure, dynamics, and function of nucleic acids.^1–7 For example, they stabilize the conformations of nucleic acids and modulate their interactions with ligands and proteins. Multivalent cations are able to induce the inter-helix attraction in DNA molecules resulting in DNA aggregation.^8–10 Differences in ion binding patterns between DNA and RNA can lead to profound differences in how their mechanical properties respond to changes in the ion concentration.¹¹ Subtle differences in how tetravalent spermine polyions bind to unmethylated vs. methylated DNA may help understand how these epigenetic markers affect chromatin compaction.¹² Therefore, an accurate description of interactions of ions with DNA and RNA molecules and between themselves is of fundamental importance in our understanding of the behavior of nucleic acids and their complexes.

All-atom explicit solvent molecular dynamics (MD) simulations allow one to quantify thermodynamic properties and structural details of ion-nucleic acid interactions at atomic resolution. These simulations can reveal mechanisms underlying many biologically important, yet completely unintuitive phenomena, often not accessible experimentally. However, on microsecond time scales that may be needed for adequate sampling of large nucleic acid systems in the presence of complex multivalent ions with strong binding affinities, these simulations can be very demanding.¹³ For much larger systems such as the nucleosome, time scales beyond 1 μs¹⁴ are currently outside the reach of traditional explicit solvent atomistic simulations. Simulation of chromatin components such as nucleosome arrays is even more computationally demanding, while conformational preferences in these systems are very sensitive¹⁵ to the presence of multi-valent ions such as Mg²⁺ or CoHex³⁺. Multi-scale modeling^16–18 of chromatin that can retain the realism of the explicit treatment of multi-valent ions remains a significant challenge.

At the same time, simulations based on the implicit solvent framework^19–28 can extend the effective simulation times by one to two orders of magnitude due to enhanced conformational sampling,²⁹ with further speed-ups possible through algorithmic advances.^30,31 Within this framework, the solvent is treated as a dielectric continuum interacting with the solutes through electrostatic and dispersion forces. A widely used method of estimating the solvent electrostatic contribution to the system free energy is by solving the Poisson-Boltzmann (PB) equation. Advanced numerical algorithms for solving this equation have been developed,^32–36 and proof-of-concept MD simulations based on the numerical PB had been reported.^37–40 Specifically, an explicit ions/implicit water model based on the numerical PB approach was proposed⁴¹ and was used to simulate short DNA and RNA fragments interacting with monovalent ions. The model, however, was not tested with multivalent ions, which is our focus here. In general, it is believed that the algorithmic complexity of the numerical PB approach, conceptual difficulties associated with incorporating PB-based algorithms into Molecular Dynamics,⁴² and significant computational expense⁴³ preclude its wide adoption in dynamics.

Instead, the most widely used practical implicit solvent model in Molecular Dynamics is the generalized Born (GB) approximation, which represents a compromise between the computational efficiency and accuracy. Some of the GB models approach the accuracy of the numerical PB,⁴³ including ligand binding calculations,^44,45 which is directly relevant to our goals here. The GB can be rigorously derived from the PB for a special case of a perfectly spherical single solute;^28,46 for an arbitrary molecular shape, the GB can be considered an approximation to the PB. As such, the GB model inherits many of the approximations to reality already present in the PB model and adds several more. The effect of the associated inaccuracies on the outcomes of practical GB-based simulations is system specific: below, we review the ones most critical to highly charged nucleic acids interacting with multivalent ions.

Both classical PB and GB models suffer from inaccuracies in treating ion atmosphere around, and estimating solvation free energies of highly charged solutes.^41,47–49 This is because both models utilize a mean-field description of the ions and, therefore, do not account for ion-ion correlations or discreteness of ions near the charged solute surface. While in the case of monovalent ions, the correlation effects are small and can often be neglected, the correlations between multivalent ions can introduce significant corrections to ion distributions and electrostatic potentials around solutes.^50–54 Moreover, both classical PB and GB models, when treating ions implicitly, neglect, or at best only crudely approximate, ion desolvation effects which appear when ions approach the low dielectric solute region. We note that an approach to approximating ion desolvation penalty directly within the PB formalism has been recently proposed.⁵⁵ Nevertheless, without explicitly considering multivalent ions tightly bound to the macromolecule,^56–58 one can not expect from the “classical” PB/GB approach an accurate quantitative description of the electrostatic potentials and ion distributions around the solutes, critical for related condensation phenomena. To sum up, while the mean-field atmosphere of monovalent ions around DNA can be fairly well described by the classical PB [with an appropriate choice of the dielectric boundary (DB)], the model fails to accurately describe many important aspects of the distribution of multivalent ions around charged solutes.

Another deficiency of both the PB or GB models originates from their consideration of only the dipole polarization of the solvent. In the case of water, the higher electric multipole moments of water molecules lead to multiple effects, e.g., charge hydration asymmetry (CHA). The neglect of these effects by the GB/PB can result in a significant deviation from reality of the hydration free energies of ions,⁵⁹ and even neutral polar molecules,⁶⁰ unless the definition of the dielectric boundary (DB) is adjusted to account for these effects.^61,62

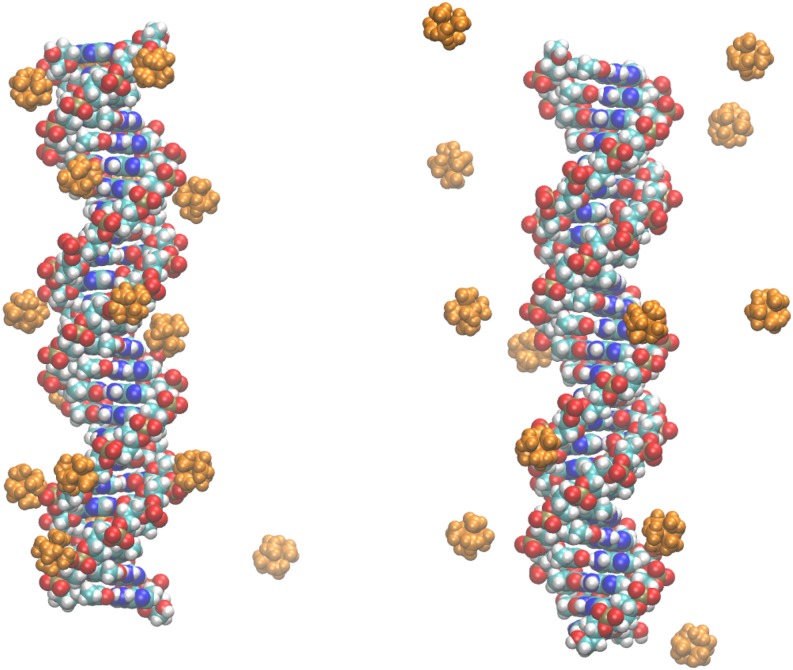
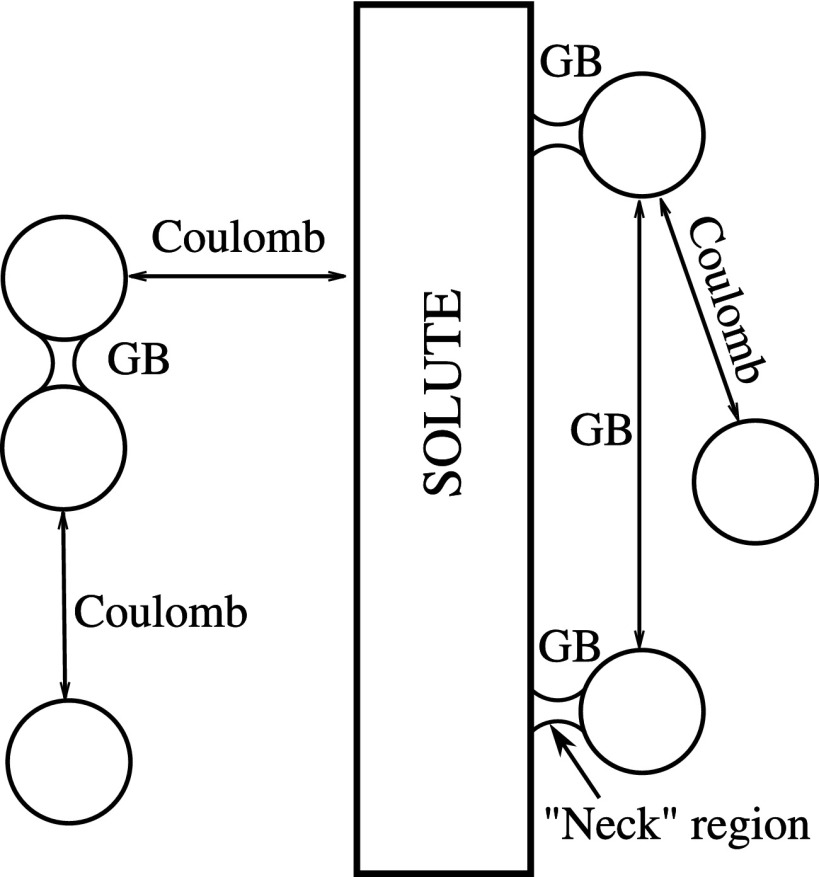
Finally, we have discovered in the course of this work that the “canonical” GB model⁶³ has a specific flaw absent at the PB level, at least in principle. Namely, the canonical GB model is not designed to handle disconnected (discontinuous) dielectric boundaries, that is, solutes which are not topologically equivalent to a sphere. For example, in the limit of infinitely high solvent dielectric, the numerical PB correctly predicts the zero interaction energy between two ions separated by a distance larger than the diameter of the water molecule, while the GB incorrectly predicts a non-zero interaction. This limitation is of little consequence in many practical simulations, e.g., of a single solute, but becomes a critical flaw in the case of multiple highly charged ions interacting, but not permanently associating, with a solute; see Fig. 1.

FIG. 1.

Qualitatively different distributions of multivalent CoHex³⁺ ions around the DNA duplex in the explicit (left) and implicit (right) water. Shown are the representative configurations from an all-atom MD simulation of explicit CoHex ions around a 25 base pair long DNA duplex. Ion distribution resulting from the standard explicit water treatment (TIP3P,⁶⁴ left) is compared to the one based on one of the latest GB models⁶⁵ available in AMBER⁶⁶ (right).

To address the above deficiencies of the PB/GB conceptual approach while retaining the advantage of the GB in dynamics applications, here we develop and test an explicit ions/implicit water GB-based model that is able to accurately describe the ion atmosphere around charged nucleic acid molecules. The model considers ions as explicit particles and directly estimates all the interactions between them and nucleic acid molecules. At the same time, the solvent effects are treated implicitly using a modified GB model for the electrostatic interactions and the effective surface tension model for the non-polar effects. Since the results of the PB and GB models are rather sensitive to the choice of the solute/solvent dielectric boundary, especially in the case of highly charged solutes, we develop here a non-standard approach to define the DB around ions and nucleic acids which preserve the geometry of the Lee-Richards⁶⁷ solvent accessible surface (SAS) within physically justified limits based on the experimentally determined atomic and ionic radii. The “disconnected boundary” defect of the GB model described above is addressed.

II. THEORY

A. Canonical generalized Born (GB) model: A brief introduction

The key component of the interaction potential between solutes in the presence of high dielectric solvent (e.g., water) is the change of the solvation free energy of the complex. The solvation energy ΔG_solv can be represented as a sum of electrostatic ΔG_el and non-polar ΔG_nonpolar contributions,²⁰

$$\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}=\mathrm{\Delta }{G}_{\mathrm{e}\mathrm{l}}+\mathrm{\Delta }{G}_{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}},$$ (1)

which are estimated independently.

The generalized Born (GB) model provides an approximate way [relative to the exact solution the Poisson equation (PE)] to calculate the electrostatic part, ΔG_el, of the solvation free energy of any singly connected solute or tightly bound complex.²⁸ The canonical GB approximation is based on the equation proposed by Still et al.,⁶³

$$\begin{array}{ccc}\hfill \mathrm{\Delta }{G}_{\mathrm{e}\mathrm{l}}=-\frac{1}{2}\left(\frac{1}{{ϵ}_{in}}-\frac{1}{{ϵ}_{out}}\right)\sum _{i,j}\frac{q_i{q}_j}{\sqrt{d_{ij}^2+R_i{R}_j\exp \left(-d_{ij}^2/(4R_i{R}_j)\right)}},& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (2)

where ϵ_in and ϵ_out are the dielectric constants of the solute and the solvent, respectively, d_ij is the distance between solute atoms i and j, and q_i are the atomic charges. The main parameters of the equation are the effective Born radii R_i, with $R_i^{-1}$ characterizing the average degree of solvent exposure of atom i.

Among the variety of methods and models to calculate R_i (see, e.g., Ref. 28 for review), we will use the so-called “R6” GB model,⁶⁸ which is theoretically well-grounded^68,69 and, at the same time, among the most accurate⁷⁰ GB models, including the calculation of binding energies.⁴⁵ The R6 model evaluates R_i through the integration of r⁻⁶ function centered on atom i over the volume V_ext, outside the solute dielectric boundary (DB),

$$R_i^{-1}={\left(\frac{3}{4\pi }\underset{V_{ext}}{\int }\frac{dV}{|\mathbf{r}-{\mathbf{r}}_i{|}^6}\right)}^{\frac{1}{3}},$$ (3)

where r_i is the radius-vector of atom i. This approach assumes that DB is a surface separating low dielectric region of a solute from the high dielectric domain of a solvent.

Equation (3) can be transformed to a more computationally convenient form,

$$R_i^{-3}={\rho }_i^{-3}-\frac{3}{4\pi }\underset{V_{int}}{\int }\frac{dV}{|\mathbf{r}-{\mathbf{r}}_i{|}^6},$$ (4)

where the region of integration V_int is now inside the solute DB but outside the sphere of radius ρ_i centered on atom i, i.e., |r − r_i| ≥ ρ_i and r ∉ V_ext. The values of ρ_i are usually set equal to the atomic (van der Waals) radii of solute atoms, which are typically used to set the dielectric surface of a solute.

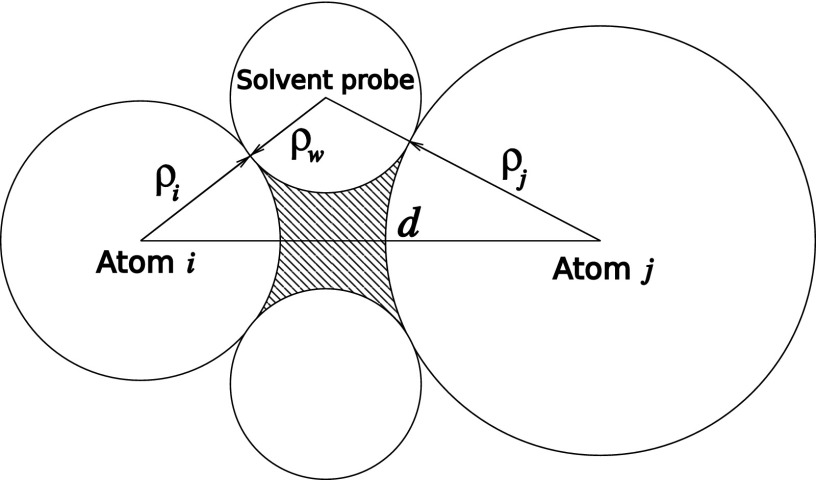
In the case of two non-bonded solute atoms i and j in a solvent (see Fig. 2), the integration volume V_int for calculating R_i consists of two parts: the sphere around atom j determined by the atomic dielectric radius ρ_j, and the region between the two atoms inaccessible for a solvent probe of radius ${\rho }_w$ (so called the “Neck” region). The formation of the “Neck” region at small atom-atom separations reflects a discrete molecular structure of the solvent and causes a partial desolvation of the two atoms (ions). This desolvation leads to a substantial deviation of the electrostatic interactions between the two atomic size charges in a solvent from the Coulomb law. This effect can be approximated within the implicit solvent approach in several distinct ways.^34,73,74 Here we follow a geometric approach introduced in Ref. 74 in the context of the GB model.

FIG. 2.

Sketch of the dielectric boundary (DB) around a pair of non-bonded solute atoms (ions) in a solvent, separated by a distance d. The DB is defined as a surface around the volume inaccessible to a solvent probe of radius ${\rho }_w$ [Richards-Connolly^71,72 molecular surface (MS)]. This volume consists of two atomic spheres determined by atomic dielectric radii ρ_i and ρ_j and a region between these spheres (depicted as dashed area) inaccessible to the solvent probe and called the “Neck” region.

The results of the r⁻⁶ integration over the two parts of V_int in Eq. (4) are called “Sphere,” $I_{ij}^{(S)}$, and “Neck,” $I_{ij}^{(N)}$, integrals, respectively, and Eq. (4) can be rewritten as

$$R_i^{-3}={\rho }_i^{-3}-\frac{3}{4\pi }\left(I_{ij}^{(N)}+I_{ij}^{(S)}\right).$$ (5)

The “Sphere” integral in Eq. (5) can be estimated analytically as^75–77

$$\begin{array}{ll}\hfill I_{ij}^{(S)}(d)& =\frac{4\pi {\rho }_j^3}{3{(d^2-{\rho }_j^2)}^3},d>{\rho }_i+{\rho }_j\hfill \\ \hfill I_{ij}^{(S)}(d)& =\frac{\pi }{12d}\left(\frac{d+3{\rho }_j}{{(d+{\rho }_j)}^3}+\frac{3({\rho }_j^2-{\rho }_i^2-{(d-{\rho }_i)}^2)+2d{\rho }_i}{{\rho }_i^4}\right),\hfill \\ \hfill & |{\rho }_j-{\rho }_i|<d<{\rho }_i+{\rho }_j.\hfill \end{array}$$ (6)

The “Neck” integral in Eq. (5) can be approximated analytically using the following equations⁷⁷

$$\begin{array}{cc}{I}_{ij}^{(N)}(d)\hfill & =0,d<{\alpha }_{ij},\hfill \\ I_{ij}^{(N)}(d)\hfill & =A_{ij}{(d-{\alpha }_{ij})}^4{({\beta }_{ij}-d)}^4,{\alpha }_{ij}<d<{\beta }_{ij},\hfill \\ I_{ij}^{(N)}(d)\hfill & =0,d>{\beta }_{ij}.\hfill \end{array}$$ (7)

Here, parameter A_ij sets the value of the maximum of $I_{ij}^{(N)}(d)$ at $d=d_{ij}^{max}$ (both quantities can be tabulated by using the corresponding numerical integration over the “Neck” region for a given pair of solute atoms), β_ij = ρ_i + ρ_j + 2${\rho }_w$ is the smallest atom-atom distance at which the solvent probe can fit between the two dielectric spheres, and ${\alpha }_{ij}=d_{ij}^{max}-({\beta }_{ij}-d_{ij}^{max})$ is the separation at which the symmetrical analytical function $I_{ij}^{(N)}(d)$ vanishes.

The non-polar term ΔG_nonpolar in Eq. (1) can be regarded as the free energy cost to create a cavity in a solvent to accommodate the solute and van der Waals interactions of the solute with water. We follow the widely used approach^20,78–82 assuming that ΔG_nonpolar is linear with the area of the Lee-Richards solvent accessible surface (SASA) of a solute,

$$\mathrm{\Delta }{G}_{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}=\gamma \text{SASA},$$ (8)

where γ is an effective microscopic surface tension parameter. In the case of an ion-ion or ion-atom pair, the SASA of each ion can change from its value ${\text{SASA}}_i=4\pi {({\rho }_i+{\rho }_w)}^2$ for the fully solvated isolated ion i (when d > ρ_i + ρ_j + 2${\rho }_w$) to a reduced value for the partially desolvated ion, when the SASs of the two ions (ion and atom) overlap,

$$\begin{array}{ccc}\hfill {\text{SASA}}_i(d)& =\hfill & 2\pi {({\rho }_i+{\rho }_w)}^2\left(1+\frac{d^2+{({\rho }_i+{\rho }_w)}^2-{({\rho }_j+{\rho }_w)}^2}{2d({\rho }_i+{\rho }_w)}\right),\hfill \\ \hfill & \hfill & d\le {\rho }_i+{\rho }_j+2{\rho }_w.\hfill \end{array}$$ (9)

B. Effective charge-charge interactions in implicit solvent

The ability to estimate ΔG_solv using the implicit solvent approach, in particular the GB model, gives us a way to estimate the interactions between solutes in a solvent. Below we present standard equations for calculating the interaction free energy between two charged atomic particles in a solvent. The equations can be easily generalized for more than two particles, i.e., for the interactions between a many-atom molecular solute and ions. The approach described below is widely used to estimate a free energy of ligand biding.⁷⁰ The assumptions involved are described in Ref. 22.

The interaction free energy W_ij(d) of two atomic charges i and j in an implicit solvent separated by a distance d can be approximated as a sum of their interaction energy in “vacuum,” E^(ij), and the change of their solvation free energy, $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(ij)}$, relative to the solvation free energy at infinite separation, $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(i)}+\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(j)}$,

$$W_{ij}(d)=E^{(ij)}(d)+\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(ij)}(d)-(\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(i)}+\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(j)}).$$ (10)

Generalized to the many-atom solute, this is the equation that governs the energetics of ion-DNA interactions in our MC simulations below.

Excluding the electronic polarization component, “vacuum” interaction energy E^(ij)(d) in Eq. (10) can be presented as a sum of Coulombic and van der Waals interactions,

$$\begin{array}{ccc}\hfill E^{(ij)}(d)=E_{el}^{(ij)}(d)+E_{vdW}^{(ij)}(d)=\frac{q_i{q}_j}{{ϵ}_{in}d}+{\epsilon }_{ij}\left({\left(\frac{{\tilde{R}}_{ij}}{d}\right)}^{12}-2{\left(\frac{{\tilde{R}}_{ij}}{d}\right)}^6\right),& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (11)

where ε_ij and ${\tilde{R}}_{ij}$ are parameters of van der Waals interaction in the form of the Lenard-Jones (LJ) potential.

III. RESULTS: MAJOR MODIFICATIONS OF THE GB MODEL IN THE PROPOSED EXPLICIT IONS/IMPLICIT WATER APPROACH

A. Solute-solvent dielectric boundary (DB)

One of the key steps in an implicit solvent approach, including the GB and PE/PB methods, is a construction of the dielectric boundary (DB)—the region that separates the low dielectric solute domain from the high dielectric (in the case of water) domain of the bulk solvent.^{21,28,32,34,83} This transition region is not an observable entity on the microscopic level and depends on the dielectric model. For example, the region can be described by a smooth dielectric function ϵ(r) derived from a Gaussian-based approach,^34,84 or it can be represented by a sharp boundary (the solute/solvent dielectric surface), which separates the solute domain with a dielectric constant ϵ_in from the solvent domain with ϵ_out. Here we use the sharp DB as the basis for our model.

In the GB method, the DB is crucial in determining the effective Born radii, Eq. (3), the main parameters in the work of Still et al. Eq. (2).^43,63,69,70 Outcomes of implicit solvent calculations are extremely sensitive to details of the DB.^83,85 An optimal DB geometry absorbs many approximations made by the specific continuum solvent model.

Two of the most widely used definitions of the solute/solvent DB in the GB approximation are the Richards-Connolly solvent excluded surface (SES)^71,72 [also called the molecular surface (MS)] and the van der Waals surface (VDWS).^85,86 To specify the geometry of DB, both definitions (SES and VDWS) commonly use atomic radii sets. In the case of water, the standard value 1.4 Å of a water molecule radius is used for as a water probe radius for SES. One of the earliest and widely used sets is the bondi van der Waals radii set determined from the experiments.⁸⁷ Its modified version, mbondi,⁸⁸ is currently standard in AMBER. Other radii sets have the values of atomic radii optimized for specific types of solutes.

For many solutes, SES and VDWS based DB surfaces produce reasonable values of the solvation free energies.^43,83,86,89 But in the case of ions or salt bridges, the substantial deviations in these energies from their experimental values were observed with the realistic sizes of the atomic and ionic radii.^47,90,91 To improve the agreement of PB based ion-ion interactions with the reference interaction site model (RISM)⁹² or the MD⁹³ results, the cationic radii in Refs. 90 and 91 had to be substantially increased compared to their values derived from the experiment.^94–96 Simultaneously, a water probe radius was decreased from its standard value 1.4 Å to 0.8 Å.⁹⁰ These optimized values of ionic and solvent probe radii are very different from their experimentally determined values and are difficult for physical interpretation.⁶² They also distort the geometry of SAS needed for estimation of the nonpolar part of the solvation energy, e.g., Eq. (8). It was suggested that the origin of this significant difference is attributed to higher order electric multipole moments of water molecules⁵⁹ and is beyond the dipole polarization approximation in the implicit solvent model.

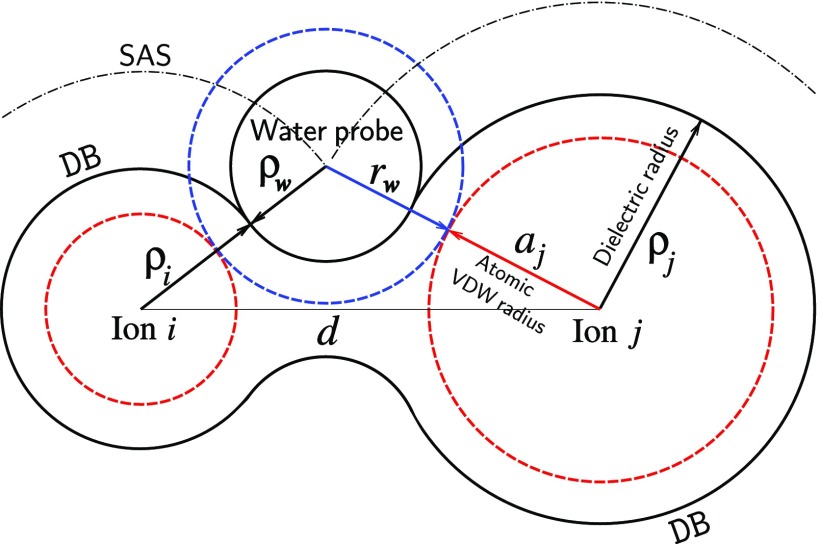
To avoid the potential difficulties in physical interpretation of the radii parameters used to determine the DB and SAS, we propose to distinguish between the two types of the solute/solvent interfaces, Fig. 3: (1) The interface described by the SES determined with the standard sets of experimental van der Waals atomic (ionic) radii a_i and standard (1.4 Å) water probe size $r_w$. This interface can be interpreted as the boundary between the solute and solvent electron densities and is used to build the SAS. (2) The DB which, in the case of a “two-dielectric” model, is treated as the surface of the localization of induced solvent polarization charges. The proposed DB is neither VDWS nor SES with the standard water probe of 1.4 Å but is the surface derived from the standard SAS geometry using an effective water probe dielectric radius ${\rho }_w$. By construction, the DB can be built as an effective SES using effective atomic (ionic) and water probe dielectric radii, ρ_i and ${\rho }_w$, which maintain the geometry of the standard SAS.

FIG. 3.

The geometry of the proposed dielectric boundary (DB) for a pair of ions (atoms) separated by a distance d < a_i + 2$r_w$ + a_j. Ions and water probe van der Waals surfaces, related to the corresponding van der Waals radii a_i, a_j, and $r_w$, are depicted by red and blue dashed lines, respectively. The DB of the ion pair is defined by the effective ionic (atomic) dielectric radii ρ_i and ρ_j, Eq. (12), and by the effective water probe dielectric radius ${\rho }_w$ which is specified by the distance from the SAS to the DB. For the solvent separated configurations (d > a_i + 2$r_w$ + a_j), the ion pair DB consists of two spheres of radii ρ_i and ρ_j.

We are going to show that by taking into account the charge distribution in water at the solute/solvent interface one can construct the DB which, being used in the standard GB model, is capable of reproducing the electrostatic part of ΔG_solv for a cation-anion pair on the level of accuracy comparable with the explicit water simulation results.

In a water molecule, the partially positively charged hydrogen atoms are located at the distance of about 1 Å from the oxygen atom center.⁹⁷ Most of explicit water models reflect this fact by having two positive partial charges placed at about the same distance from the oxygen center. A major part of the dielectric response of liquid water to a solute electric field is due to the orientational polarization of water, which changes the thermally averaged microscopic charge distribution in water layers adjacent to the solute. The most significant changes in the first hydration shell around the solute begin at about 1 Å below the SAS, in the layer of the closest approach of water hydrogen nuclei to the SES. Therefore, we suggest to place the solute/solvent DB at ${\rho }_w$ = 1.0 Å below the SAS, at the layer where the most significant changes of the averaged water charge distribution due to orientational polarization of water are expected.

Since the SAS near the solute atom is determined by the sum of atomic and water probe van der Waals radii, (a_i + $r_w$), and is an experimentally observable quantity,^94,95,98 the geometry of the proposed DB can be specified by the effective dielectric radii ρ_i of atoms (ions),

$${\rho }_i=(a_i+r_w)-{\rho }_w,$$ (12)

and the radius of the sphere ${\rho }_w$, corresponding to the proposed distance from the SAS to DB. The quantity ${\rho }_w$ can be considered as an effective dielectric radius of the water probe, ${\rho }_w$ < $r_w$, which together with the atomic (ionic) effective dielectric radii ρ_i, Eq. (12), fully determine the solute/solvent DB in the form of the Richards-Connolly surface; see Fig. 3.

In many GB models, the effective dielectric probe radius ${\rho }_w$ and the atomic dielectric radii ρ_i are somewhat arbitrary parameters. Contrary to this, some physical restrains can be applied to the atomic (a_i) and water probe ($r_w$) van der Waals radii. For example, the sums a_i + $r_w$ determine the position of the first hydration shell around the solute, which can be accessed experimentally.^94,95,98 Defining atomic (ionic) dielectric radii ρ_i through Eq. (12) retains these restrains. The proposed approach still requires the knowledge of a_i and $r_w$ or their sum but needs no optimization of the effective dielectric radii ρ_i defined via the position of SAS and the only additional parameter ${\rho }_w$, which we set to 1.0 Å.

In what follows, we use the proposed DB to calculate the effective Born radii, considering three distinct cases: (1) for the isolated DNA, which is kept fixed during our simulations, we use the DB around the DNA to numerically calculate the “ion-free” effective Born radii of all atoms in the DNA; (2) for the ion-ion interactions, we approximate the corrections to each ion’s effective Born radius (starting from ρ_j for an isolated ion) by considering the DB for each possible ion-ion pair (as depicted in Fig. 3) and then analytically calculating the corresponding “Neck” and “Sphere” integral corrections, Eq. (5); (3) for the DNA-ion interactions, all the corrections to the “ion-free” effective Born radii of the DNA atoms and the ions are approximated by considering the DB for each DNA atom-ion pair separately and analytically calculating the corresponding “Neck” and “Sphere” integrals.

B. Interaction in cation-anion pair: Water probe size and Na⁺–Cl⁻ potential of mean force (PMF)

In this section, we explore and refine the proposed above definition of the solute/solvent dielectric boundary. We apply the new methodology of defining the DB to calculate the potential of mean force W(d) for an isolated Na⁺–Cl⁻ ion pair in water and find the adjusted value of the water probe radius $r_w$. To evaluate PMF W(d) [Eq. (10)], we use the unmodified GB model [Eqs. (2) and (5)–(7)] for clarity and simplicity (see a note at the end of Sec. III C). The critical modifications needed to account for the presence of the DNA molecule and much larger trivalent CoHex ions will be discussed in Sec. III C.

The proposed DB around the ion pair is specified by the effective water probe dielectric radius ${\rho }_w$ = 1.0 Å and the dielectric radii of ions ρ_i. The latter can be determined from Eq. (12) using the intrinsic ionic radii a_i and the realistic water probe radius $r_w$.

The standard water probe size $r_w$ = 1.4 Å is typically considered complementary to the ionic radii from Refs. 94–96 used here. However, at small ion-ion separations, the electric field between the cation and anion is greater than the field around the single ion, resulting in a greater water polarization and stronger ion-water interaction. These factors lead to reduced ion-water (a_i + $r_w$) distances for water molecules between the two ions.

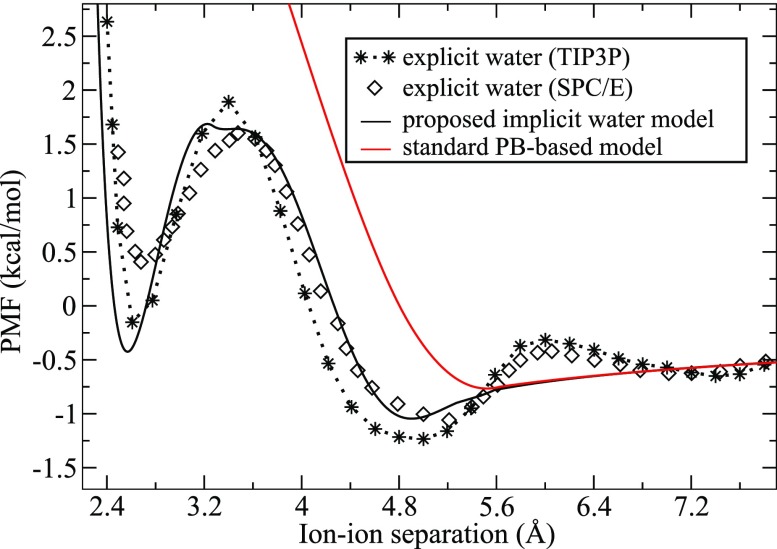
The ion-water distances are related to the position of the second minimum in the cation-anion PMF determined from the MD simulations^99,100 (see Fig. 4). This minimum reflects the beginning of a partial dehydration of the cation-anion pair due to steric displacement of water molecules from the region between the two ions and roughly corresponds to the a_i + 2$r_w$ + a_j distance. The sum of the ionic radii, 1.02 Å for Na⁺ and 1.81 Å for Cl⁻,⁹⁶ and the two standard water probe size values $r_w$ = 1.4 Å is clearly larger than the positions of the second Na⁺–Cl⁻ PMF minimum (5.0–5.2 Å) shown in Fig. 4.

FIG. 4.

Na⁺–Cl⁻ ion pair PMF W(d) [Eq. (10)] calculated using the GB approach with the analytical estimation of the “Sphere” [Eq. (6)] and “Neck” [Eq. (7)] integrals and the new dielectric boundary (DB) definition (see Fig. 3) (black solid line), numerical solution of PB equation with the “standard” solvent excluded surface (SES) based definition of the DB and water probe radius $r_w$ = 1.4 Å (solid red line), and the results from the MD simulations with explicit TIP3P (stars)⁹⁹ and SPC/E (diamonds)¹⁰⁰ water models.

Keeping the ionic radii a_i unchanged, the reduction of the ion-water distances can be taken into account by decreasing the $r_w$ compared to its standard 1.4 Å value. This reduction is important for the proper description of the shape and position of the dehydration energy barrier. With our choice of ${\rho }_w$ = 1.0 Å (distance from the SAS to the DB, an effective dielectric water probe radius), which determines the effective dielectric ionic radii ρ_i [see Eq. (12)], we found that the value $r_w$ = 1.22 Å satisfies the above requirements for the position of the second PMF minimum and reasonably reproduces the explicit solvent MD PMFs using the proposed model for the DB within the GB approach. This new value of $r_w$ results in the gap between the SES determined by a_i and $r_w$ and the DB specified by ρ_i and ${\rho }_w$ which is estimated as ($r_w$ − ${\rho }_w$) = 0.22 Å (see Fig. 3). We will use this $r_w$ = 1.22 Å value (along with ${\rho }_w$ = 1.0 Å) to determine all other effective dielectric atomic (ionic) radii for ions and solutes (DNA and RNA duplexes) described in this study.

The GB derived Na⁺–Cl⁻ PMF in Fig. 4 is calculated using the same ε_ij and ${\tilde{R}}_{ij}$ CHARMM27 LJ parameters¹⁰¹ [Eq. (11)] which were used for the MD derived PMF⁹⁹ and the parameter γ = 10 cal/(mol Ų) for the nonpolar part ΔG_nonpolar [Eq. (8)] of the ion hydration free energy.

As an additional confirmation for the proposed implicit water approach that uses unmodified, experimental ion radii (e.g., a_i = 1.02 Å for Na⁺), we have calculated distributions of Na⁺ ions around the DNA duplex within the standard non-linear PB approach, Fig. 5. As expected, the non-linear PB theory is capable of describing monovalent ion distributions around the DNA (Fig. 5), but only when the cation (Na⁺) radius is 1.02 Å, chosen based on the physical considerations presented above. The accuracy of non-linear PB theory for predicting the number of bound ions (specific or non-specific binding) to a biomolecule depends on the Stern layer thickness because its value is added to the radii of the solute atoms to determine the ion accessible regions. Typically, ionic radii values of 2 Å have been used to define the Stern layer thickness for hydrated Na⁺.^102,103 Our PB calculations of Na⁺ distribution around the DNA with this “standard” 2.0 Å Na⁺ radius did not result in a good agreement with the MD-derived distributions, Fig. 5. Similar findings were reported for predicting the number of bound ions to a lipid bilayer, where the radius of 1.4 Å gave a better agreement with MD results¹⁰⁴ than the radius of 2.0 Å. Our calculations suggest that a non-hydrated sodium radius of 1.02 Å is the appropriate value to use for calculating Na⁺ interactions with strongly charged molecules such as DNA.

FIG. 5.

Na⁺ ion cylindrical distributions around the 25 bp poly(dA·dT) DNA duplex derived from the explicit water MD simulations with the TIP3P water model (thick solid black line) and from the non-linear PB calculation using experimental Na⁺ value 1.02 Å for monovalent ion radii (dashed blue line) and “standard” 2 Å Na⁺ radius (thin solid red line).

C. Modification to the GB model to account for non-connected geometries

It is known that the “canonical” GB model⁶³ becomes essentially exact (compared to PB) in the limiting case of a spherical geometry of the solute in water. For this case, the GB Green function can be derived (in the limit ϵ_out → ∞) from the exact PE solution on a sphere.²⁸ If the solute shape is substantially non-spherical, the GB estimations of pairwise interactions between individual atomic charges of the solute may deviate substantially from the PB estimates,¹⁰⁵ although they are still correct qualitatively. However, the very physics of the canonical GB approximation can break down for solutes composed of multiple disconnected parts in close proximity to each other.

Considering explicit ions in an implicit solvent, we often encounter this non-connected geometry when the charges are completely separated by the solvent. For example, for the two ions in the bulk or for the ion near the solvent exposed solute atom, when the separation distance d_ij is greater than the sum ρ_i + 2${\rho }_w$ + ρ_j, the “Neck” region shown in Fig. 2 (dashed area) completely disappears. In this case, all the electrostatic interactions between the corresponding charges occur through the solvent, the case where the GB model may drastically deviate from the PE; see Table I. In the limiting case ϵ_out → ∞, both the PE and the Coulomb law predict vanishing of the ion-ion interactions, whereas the GB model does not. This deficiency of the canonical GB model in the case of disconnected solute geometries leads to the overestimation of the repulsive contributions between counterions around the charged solute resulting in wrong counterion distribution. The example of the consequences of these incorrect ion-ion interactions in the canonical GB approach has been presented in Fig. 1 for the case of CoHex counterions around the DNA molecule.

TABLE I.

The breakdown of the GB model for disconnected solute geometries. Comparison of the electrostatic interaction energy (kcal/mol) of two CoHex ions at the separation distance d = 9.8 Å (d > a_i + 2$r_w$ + a_i, a_i = 3.63 Å, $r_w$ = 1.22 Å), using the GB model, numerical solution of the PE, and the Coulomb law. Solvent dielectric constant ϵ_out = 80.

Evaluation model	Generalized Born	Poisson equation	Coulomb law
Interaction energy	9.9	4.3	3.8

To approximate the Coulomb like behavior for the disconnected (solvent separated) configurations of two atomic charges (see Fig. 6), predicted by the PE, we modify Eqs. (5) and (2). Namely, when the neck integral $I_{ij}^{(N)}(d)$ in Eq. (5) vanishes at the solvent separated distances, the sphere integral corrections $I_{ij}^{(S)}$ is set to zero, reducing the effective Born radius R_i in Eq. (5) to its value calculated as if there were no ion j. In addition, to cancel the electrostatic “vacuum” parts of Eqs. (2) and (11), the exponent in Eq. (2) for the cross terms (i ≠ j) is set to zero too.

FIG. 6.

Solute-ion and ion-ion interaction modes in the proposed explicit ions/implicit water model. Interactions between ions separated by a layer of the solvent (no ion-ion “Neck” formed) are estimated via the modified GB equations resulting in the Coulomb law behavior. For smaller separations (“Necks” formed), ion-ion interactions are estimated via the canonical GB equation. Interactions between two ions, both forming “Necks” with the solute, are estimated via the canonical GB equation at any ion-ion distance. Interactions between the solute atoms and ions being within ion-solute “Neck” distance are estimated via the canonical GB equation. At larger ion-solute distances, the interactions are estimated via the modified GB equations approximating the Coulomb law behavior. All the interactions within the (singly connected) solute are estimated via the canonical GB.

When the two ions are solvent separated ($I_{ij}^{(N)}=0$), but both of them are bound to the solute (create “Necks” with the nearest solute atoms), part of the charge-charge interactions between these ions can occur through the low dielectric solute region. In these cases, both ions are considered as parts of the solute, and unmodified Eqs. (2) and (5) are applied to describe the interactions between these ions (see Fig. 6).

We have found that the deviation of the new formalism from the canonical GB for a single Na⁺–Cl⁻ pair (relatively small monovalent ions) is quite small and has negligible effect on the computed ion-ion PMF; however, the deviation becomes large and very important once the DNA is added or large trivalent CoHex ions are involved. The use of the new formalism is therefore recommended in general for disconnected solute geometries.

D. Implementation details. Effective potentials for ion-DNA(RNA) and ion-ion interactions in implicit water

In Secs. III A–III C, we have formulated a new approach to define the dielectric boundary around charged solutes (see Fig. 3) and proposed modifications to the canonical GB model to account for the disconnected geometries of ion-ion and solute-ion configurations in the explicit ions/implicit water GB model. We showed that the proposed DB and the GB based analytical interaction potentials between charged particles can reasonably reproduce the cation-anion PMF calculated using explicit water models.

In this section, we extend the proposed explicit ions/implicit water GB approach to many-atomic solutes and multiple explicit ions and formulate analytical equations for corrections to the effective Born radii of solute atoms and ions.

In the Sec. IV, we will apply the derived equations to simulate ion distributions around constrained (all atom positions are fixed) short DNA and RNA duplexes.

1. Effective Born radii of solute atoms interacting with explicit ions

The effective Born radii R_k of constrained solute (DNA) atoms for a given fixed solute configuration are pre-calculated without ions in the implicit solvent using the GBNRS6 GB flavor⁷⁷ and the proposed new DB definition. In the presence of explicit ions near the solute, the magnitudes of R_k can deviate from their initial “ion-free” values $R_k^0$. Similar to Eq. (5), the corrections to R_k due to surrounding ions are calculated as sums of “Sphere” ($I_{kj}^{(S)}$) and “Neck” ($I_{kj}^{(N)}$) integrals over the corresponding dielectric volumes of neighboring ions (index j). These integrals are modified as described in Refs. 74, 77, and 106.

• (1)We follow Mongan et al.⁷⁴ and scale the “Neck” contributions $I_{kj}^{(N)}$ to R_k by factors n_j,

$$I_k^{(N)}=\sum _j{n}_j{I}_{kj}^{(N)}.$$ (13)

Factors n_j depend on the ion size and charge and, therefore, are ion type specific. They are subject to optimization; see below.

• (2)To implement the connectivity rules discussed in Sec. III C, we scale the “Sphere” contributions $I_{kj}^{(S)}$ to R_k by factors s_j,

$$I_k^{(S)}=\sum _j{s}_j{I}_{kj}^{(S)}.$$ (14)

s_j = 1 (“Sphere” integral $I_{kj}^{(S)}$ contributes to $I_k^{(S)}$) if ion j is within the “Neck” distance with at least one solute atom k′ ($d_{k^{\prime }j}<a_{k^{\prime }}+2r_w+a_j$, $I_{k^{\prime }j}^{(N)}\ne 0$). Otherwise, the contribution of $I_{kj}^{(S)}$ should be neglected by setting s_j = 0. That is, an ion separated from the solute by a continuous solvent layer does not affect Born radii of the solute atoms.

The cumulative quantities $I_k^{(N)}$ and $I_k^{(S)}$ contribute to R_k in a manner similar to Eq. (5) as follows. For reasons described in Ref. 77, the maximum value of the corrected effective Born radius R_k is capped by the electrostatic size A of the solute molecule^77,107 (in the case of the DNA duplex A = 18 Å),^77,107

$${(R_k)}^{-3}={(R_k^0)}^{-3}(1-c_k\tanh (F_k)),$$ (15)

where

$$F_k=\frac{3}{4\pi }(I_k^{(N)}+I_k^{(S)})/\left(c_k{(R_k^0)}^{-3}\right)$$ (16)

and

$$c_k=1-\frac{{(R_k^0)}^3}{A^3}.$$ (17)

2. Effective Born radii of explicit ions interacting with solute atoms and other explicit ions

In the presence of low dielectric volumes of the solute (DNA) and other ions, the effective Born radius R_j of an ion j may change. Similar to the case of solute atoms, the correction to $R_j^0$ of an isolated ion is due to the contributions of the “Sphere” ($I_j^{(S)}$) and “Neck” ($I_j^{(N)}$) integral sums.

The “Sphere” integral correction to $R_j^0$ can be split into the ion-solute ($I_j^{(S1)}$) and ion-ion ($I_j^{(S2)}$) parts,

$$I_j^{(S)}=I_j^{(S1)}+I_j^{(S2)}.$$ (18)

The ion-solute part can be evaluated as a sum of pairwise ion-atom contributions $I_{jk}^{(S)}$ [Eq. (6)],

$$I_j^{(S1)}=s_j\sum _k{I}_{jk}^{(S)},$$ (19)

where factor s_j accounts for the connectivity rules in the same way as in Eq. (14). That is, s_j = 1 when ion j is within the “Neck” distance to at least one of the solute atoms k, and s_j = 0 otherwise.

Equation (19) replaces the 1/r⁶ integration over the solute dielectric volume [Eq. (4)] by a sum of the integrals over the individual atom dielectric volumes. This procedure over-counts the solute volume due to overlapping of the spherical dielectric volumes of neighboring solute atoms.¹⁰⁸ To reduce this over-counting, we follow the practice of AMBER GB models¹⁰⁹ and scale the solute dielectric atomic radii ρ_k entering $I_{jk}^{(S)}$ [Eq. (6)] by correction coefficients fs_k (see Table II). Factors fs_k depend on the solute atom type: they are optimized to reproduce $I_j^{(S1)}$ calculated by numerical integration over the dielectric volume of DNA. Thus, they are specific for nucleic acids and the proposed strategy to build the DB around charged solutes. The optimization is done by minimizing RMSD between the analytical [Eqs. (19) and (6)] and numerical (GBNSR6 code⁷⁷) evaluations of $I_j^{(S1)}$ over a large set (75) of random bound ion positions (s_j = 1) around the DNA molecule. Initially, the original GBNSR6 code was used to build the DB surface around the solute without the explicit ions. Then, the code was modified to use the pre-build DB and to do the 1/r⁶ integration over the volume defined by the DB, external to the ion positions. The optimization of the radii scaling factors fs_k in the analytical evaluation of $I_j^{(S1)}$ was done using the MATLAB function “fminsearch.” The optimized values of fs_k specific for DNA (RNA) molecules are presented in Table II.

TABLE II.

Volume over-counting radii correction coefficients fs_k and the unscaled effective dielectric atomic radii ρ_k (in Å) [Eq. (12)] for different nucleic acid atom types.

Solute atom type	H	C	N	O	P
Dielectric radii ρk	1.44	1.92	1.77	1.72	2.07
Coefficients fsk	0.992	0.000	1.002	0.994	0.937

The ion-ion ($I_j^{(S2)}$) part of the “Sphere” integral correction to $R_j^0$ can be written as

$$I_j^{(S2)}=\sum _{j^{\prime }}{s}_{j{j}^{\prime }}{I}_{j{j}^{\prime }}^{(S)}.$$ (20)

Here, $I_{j{j}^{\prime }}^{(S)}$ is the 1/r⁶ “Sphere” integral centered on ion j over the dielectric volume of ion j′ [Eq. (6)], $s_{j{j}^{\prime }}$ the connectivity switching factors. In agreement with the connectivity rules introduced in Sec. III C, factor $s_{j{j}^{\prime }}=1$ if ions j and j^′ are within the ion-ion “Neck” distance ($d_{j{j}^{\prime }}<a_j+2r_w+a_{j^{\prime }}$). Otherwise, $s_{j{j}^{\prime }}=s_j{s}_{j^{\prime }}$ where factors s_j were introduced in Eq. (14) and correspond to the ion-solute connectivity rules. Thus, the integral $I_{j{j}^{\prime }}^{(S)}$ contributes to the $I_j^{(S2)}$ if both ions j and j′ are within the “Neck” distance to the solute (DNA) atoms or the distance between these ions is within the ion-ion “Neck” distance.

Similar to the “Sphere” integral correction [Eq. (18)], the “Neck” integral correction to the effective Born radius of ion j can be slit into two parts, ion-solute ($I_j^{(N1)}$) and ion-ion ($I_j^{(N2)}$) “Neck” integral contributions,

$$I_j^{(N)}=I_j^{(N1)}+I_j^{(N2)}.$$ (21)

As in Eq. (13), we evaluate the $I_j^{(N1)}$ as a scaled sum of the ion-atom “Neck” integrals $I_{jk}^{(N)}$,

$$I_j^{(N1)}=c_j^V{n}_j\sum _k{I}_{jk}^{(N)}.$$ (22)

Neck scaling factors n_j are the same as in Eq. (13) for the solute-ion “Neck” integrals. They are ion specific and are optimized to reproduce ion distributions around DNA molecules, see Secs. IV A and IV B. Additional variable scaling factor $c_j^V$ in Eq. (22) is applied to counteract the overestimation of the sum of “Neck” integrals in Eq. (22) due to possible overlaps of multiple ion-atom “Neck” volumes when an ion is close to multiple groups of solute atoms; for example, Na⁺ in the minor groove of DNA. Factor $c_j^V=c_j^V({\widehat{V}}_j)$ depends on the relative ion j position via the weighted relative volume ${\widehat{V}}_j$ of the solute atoms within a predefined spherical volume (radius R_s) around the ion.⁷⁷ Similar to the “measure of the volume” introduced by the FACTS model of solvation,¹¹⁰ the ${\widehat{V}}_j$ is defined as

$${\widehat{V}}_j=\frac{{\sum }_k{a}_k^3{\mathrm{\Theta }}_{kj}}{R_s^3},$$ (23)

where a_k are solute atomic radii and

$${\mathrm{\Theta }}_{kj}=\left\{\begin{array}{cc}\hfill {\left(1-{\left(d_{kj}/R_s\right)}^2\right)}^2\hfill & d_{kj}\le R_s,\hfill \\ \hfill 0\hfill & d_{kj}>R_s.\hfill \end{array}\right.$$ (24)

The parameter R_s is set to 10 Å, which is the same value used in the FACTS method¹¹⁰ and in Ref. 77. The increase of the weighted relative volume ${\widehat{V}}_j$ decreases the scaling factor $c_j^V({\widehat{V}}_j)$ as

$$c_j^V({\widehat{V}}_j)=1-f_c\tanh (f_v{\widehat{V}}_j).$$ (25)

Parameters f_c = 0.68 and $f_v$ = 8.0 have been optimized to reproduce the dependence of the solvation free energy of the 12 base pair DNA duplex (PDB ID: 2BNA) and one Na⁺ ion bound to the DNA minor groove on the ion position in the groove. We used 90 DNA-ion configurations with the equidistant ion positions 0.1 Å apart, along the midsection of the minor groove. The reference energies of the DNA-ion complex were calculated using the APBS PB solver.³² Depending on the volume ${\widehat{V}}_j$, the scaling factor $c_j^V$ varies from 1 to ∼0.3.

The ion-ion “Neck” integral term ($I_j^{(N2)}$) is represented as an unscaled sum of all ion-ion “Neck” integrals $I_{j{j}^{\prime }}^{(N)}$,

$$I_j^{(N2)}=\sum _{j^{\prime }}{I}_{j{j}^{\prime }}^{(N)}.$$ (26)

With the “Neck” ($I_j^{(N)}$) and “Sphere” ($I_j^{S)}$) integral corrections, the effective Born radius R_j of ion j can be evaluated in the same manner as the solute atom radius R_k, using Eqs. (15)–(17), where atom index k is replaced by ion index j.

All the remaining parameters of the model not shown in Table II are given in the supplementary material. A collection of in-house Fortran programs to reproduce the GB-MC results of this work is available at http://people.cs.vt.edu/∼onufriev/software.php.

IV. MONTE CARLO SIMULATION RESULTS USING PROPOSED EXPLICIT IONS/IMPLICIT WATER GB MODEL

We apply the proposed explicit ions/implicit water model to evaluate the interactions of ions with highly charged DNA and RNA molecules in water. To validate the model, we calculate ion distributions around the nucleic acid duplexes using ensembles of equilibrium ion configurations. To generate the configurations, we use an in-house implementation of the canonical Metropolis Monte Carlo (MC) method¹¹¹ with the proposed interaction potentials described in Secs. II and III. All the simulation details are described in Sec. V.

A. Distributions of monovalent Na⁺ ions around DNA duplex

We use the proposed GB based interaction potentials between a highly charged solute and explicit ions in implicit water to calculate monovalent Na⁺ ion distributions around the homopolymeric 25 base pair (bp) poly(dA·dT) DNA duplex.

The “Neck” integrals scaling parameter n_j [Eq. (13)] for the proposed GB approach is optimized by comparing the evaluated ion distributions with the results from explicit water MD simulations using TIP3P⁶⁴ and TIP4P-Ew¹¹² water models. All other parameters are described in Sec. V or presented in the Appendix.

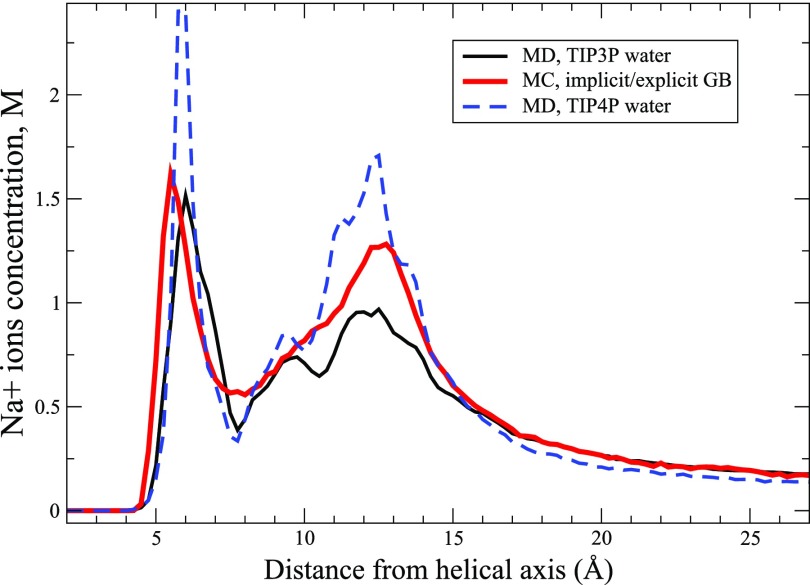
The Na⁺ ion distributions derived from the explicit ions/implicit water GB-MC simulations with the optimized “Neck” scaling parameters (n_j = 0.4) and from the MD simulations using two different explicit water models (TIP3P⁶⁴ and TIP4P-Ew¹¹²) are presented in Fig. 7. One can see that the GB derived ion distribution reproduces the MD results with a reasonable accuracy, comparable with the accuracy of explicit water simulations. The latter one can be estimated as the ratio of the Na⁺ ion concentrations at the distribution peak at 12-13 Å (the ions residing in the vicinity of the DNA phosphate groups) derived from the TIP4P-Ew vs. TIP3P water based simulations. Almost double the concentration of Na⁺ ions at this peak in TIP4P-Ew water compared to TIP3P suggests the difference in the effective Na⁺-DNA interaction potentials for these two explicit water models of the order of only k_BT. Since the GB derived distribution is roughly within the accuracy gap between the two explicit water distributions, the accuracy (k_BT) of the effective Na⁺-DNA interactions of these two explicit water models can serve as a measure of the accuracy of the proposed GB model interaction potentials in the case of monovalent ions. We note that our model reproduces the double-peak structure of Na⁺ distributions in Fig. 7 better than the previously published explicit ions/implicit water model⁴¹ that used the near “standard” 1.8 Å Na⁺ radius. This observation further emphasizes the importance of the dielectric boundary definition proposed in this work.

FIG. 7.

Na⁺ ion cylindrical distributions around the 25 bp poly(dA·dT) DNA duplex derived from the MC simulations using the proposed explicit ions/implicit water GB model (thick solid red line) and from the explicit water MD simulations with the TIP3P water model (solid black line) and with the TIP4-Ew water model (dashed blue line). The GB based result is shown for the optimized “Neck” integrals scaling parameter n_j = 0.4.

B. Distributions of trivalent CoHex ions around DNA and RNA duplexes

To test the proposed explicit ions/implicit water GB approach in the case of multivalent ions where the ion-ion correlations play a significant role in the effective ion-solute interactions, we apply the modified GB model to evaluate interactions of trivalent CoHex³⁺ counterions with DNA and RNA duplexes. A proper reproduction of the multivalent ion distributions around nucleic acid duplexes is especially interesting since some subtle features of these distributions are responsible for the aggregation propensity of the nucleic acids.¹¹³

We use the same Monte Carlo code with the proposed GB interaction potentials as in the case of monovalent ions and calculate the distributions of explicit trivalent CoHex ions around the 25 bp homopolymeric poly(dA·dT) DNA duplex, mixed sequence DNA duplex, and homopolymeric poly(rA·rU) RNA duplex, assuming fixed configurations of nucleic acid molecules. Simulation details are described in Sec. V. The only parameter which needed to be re-optimized compared to the small monovalent ion case is the “Neck” scaling factor n_j which is ion type sensitive. For this optimization, we compare the results of the GB-MC simulations of the poly(dA·dT) DNA-CoHex system with the results of all-atom MD simulation of the same DNA duplex and CoHex counterions using the explicit TIP3P water model.¹¹³ We find that the best agreement of the implicit water results to the explicit water reference corresponds to n_j = 0.9. Only the homopolymeric DNA duplex results were used for the re-optimization of this parameter. The other two test systems, the mixed sequence DNA and homopolymeric RNA, are simulated without any additional re-optimization.

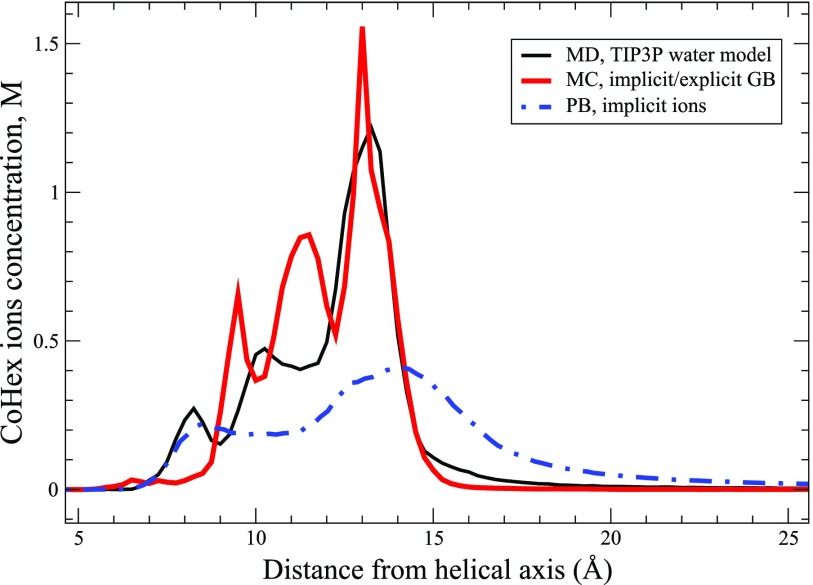
CoHex distributions around the 25 bp poly(dA·dT) DNA duplex derived from the explicit ions/implicit water GB-MC simulation with the optimized parameter n_j and from the all-atom MD simulation using the explicit TIP3P water model are presented in Fig. 8. The distribution derived from the non-linear PB calculation with implicit CoHex ions is presented in Fig. 8 as well. As expected, the mean-field PB approach does not reproduce the key qualitative feature of CoHex ion distribution around the DNA—a sharp peak at 13 Å. Instead, the PB-derived CoHex distribution is broad and diffuse. This is because ion-ion correlations important for proper condensation of trivalent ions at the DNA surface are missing in the implicit ion mean-field description. As a result, the ion-ion repulsion is overestimated, leading to a more diffuse ion distribution compared to the explicit ions/explicit solvent. When applied to explicit ions, the canonical GB also can not reproduce the correct CoHex distribution, Fig. 1. As we have discovered, charge-charge repulsion between the CoHex ions trying to condense onto the DNA surface is also overestimated in this case, resulting in a diffuse counterion cloud. However, the physical origin of the overestimation is different from that in the PB model. Specifically, the canonical GB model overestimates the repulsive desolvation contributions to the interaction between charges when applied to the discontinuous dielectric boundary¹¹⁴ around the solute-solute, solute-ion, or ion-ion pairs. Some of these overestimations cancel each other to an extent between GB self- and cross terms in the case of opposite charge interactions but not for interactions between like charges.

FIG. 8.

CoHex ion distributions around the 25 bp homopolymeric poly(dA·dT) DNA duplex derived from the MC simulations using the proposed explicit ions/implicit water GB model (thick solid red line) from the explicit water MD simulations using the TIP3P water model (thin solid black line) and from the non-linear PB calculation with explicit CoHex ions (dot-dashed blue line). The GB derived results are shown for the optimized “Neck” integrals scaling parameter n_j = 0.9.

By contrast, the CoHex distribution estimated based on the proposed implicit/explicit model, Fig. 8, reasonably reproduces the position, the height, and the width of the major peak of the CoHex density at 13 Å from the helical axis, which represents most (∼2/3) of the DNA bound CoHex ions. The ions under this peak are bound at the “external” surface of the DNA sugar-phosphate backbone and strongly interact with the DNA phosphate groups. Two smaller peaks in the ion distribution at 9.5 and 11.5 Å may correspond to the lesser peaks seen in the explicit water at 8 and 10 Å, respectively. These represent CoHex ions in the major groove but still bound to the phosphates. Even with the presence of the two “spurious” peaks, the corresponding difference in the ion concentrations seen in the implicit vs. the explicit solvent distributions (at the peak positions) is still small—expressed as the effective CoHex-DNA interaction energies; the interactions in the implicit water differ by less than k_BT from the explicit water results, which may be acceptable. A more detailed analysis will be needed to pinpoint the origin of the shift and enhancement of these two peaks relative to the explicit solvent results and to fine tune the interaction potentials of our model to obtain better agreement with the reference.

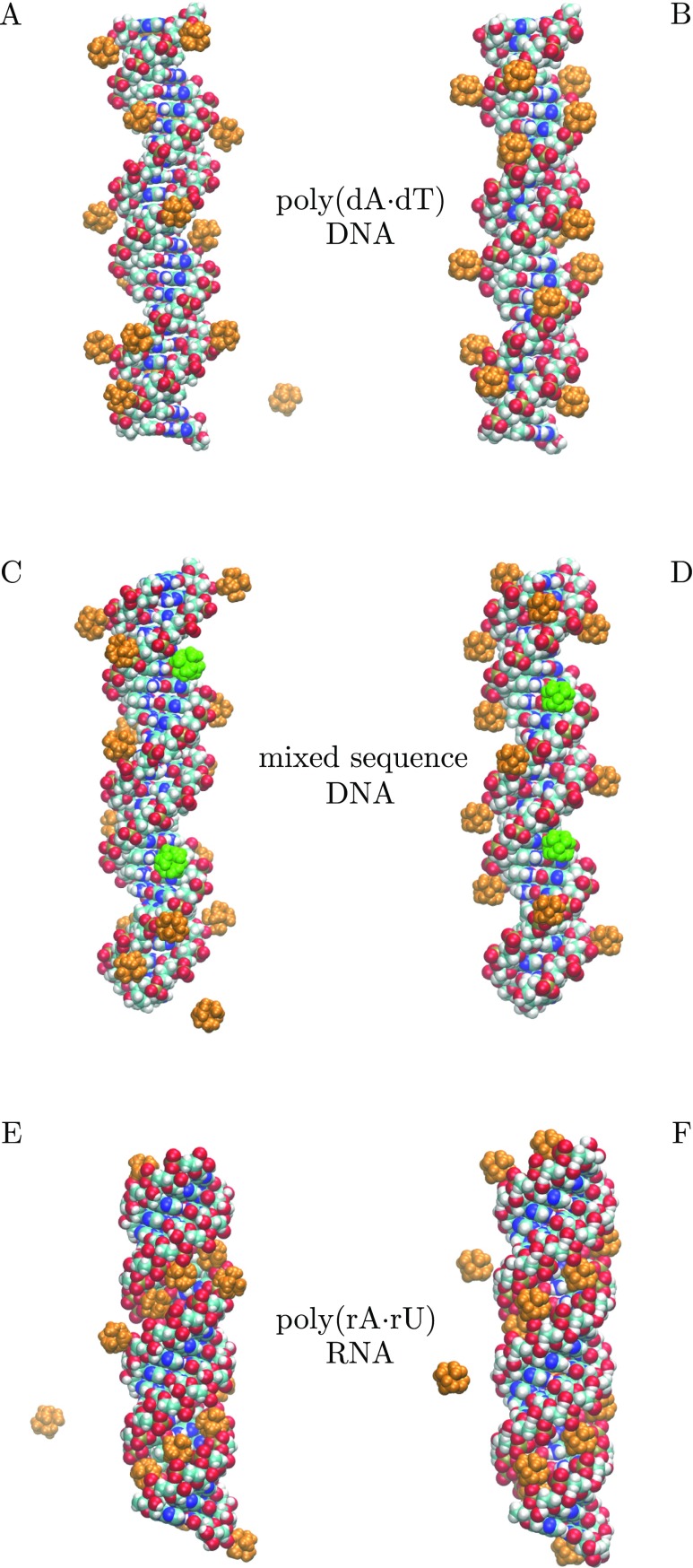
To further test the proposed explicit ions/implicit water GB model without any additional parameter re-optimization, we carried out the GB-MC simulations of the 25 bp mixed sequence DNA and homopolymeric poly(rA·rU) RNA duplexes. Representative configurations of CoHex ions bound to DNA and RNA duplexes from the MD and GB-MC simulations are shown in Fig. 9 for all three simulated systems. In all three cases, the GB-MC simulations (right panels in Fig. 9) reproduce the major features of CoHex binding to DNA and RNA molecules (left panels in Fig. 9). In the case of DNA duplexes, CoHex ions bind preferentially to the surface of the phosphate-sugar backbone exposed to the bulk, in the “external” ion biding shells of the duplexes (at 12–16 Å from the helical axis).¹¹⁴ GB-MC simulation of the mixed sequence DNA duplex reproduces the sequence specific binding of CoHex ions to the nucleotide bases at Guanine-phosphate-Cytosine (GpC) steps in the major groove of DNA,¹¹³ Fig. 9 (green ions). In the case of the A-form RNA duplex, CoHex ions bind mostly inside the RNA major groove, in the “internal” ion binding shell (within 12 Å from the helical axis), still strongly interacting with the phosphates group oxygens exposed into the RNA major groove.

FIG. 9.

Representative snapshots of CoHex ions (orange) binding to 25 bp DNA and RNA duplexes from explicit (TIP3P) water MD simulations (left) and from the proposed explicit ions/implicit water GB model used in MC simulations (right). CoHex ions bound to the GpC steps in the major grooves of the mixed sequence DNA duplexes are shown in green.

It has been suggested^113,115 that the fraction of neutralizing CoHex counterions bound in the “external” ion binding shell of nucleic acid duplexes is responsible for the condensation propensity of these duplexes. The larger this fraction, which is duplex structure and sequence dependent, the higher the condensation propensity of the nucleic acid molecules. It has been suggested that the preferential “internal” shell binding of CoHex counterions and, therefore, small fraction of CoHex counterions bound in the “external” shell of RNA duplexes are responsible for a very weak attraction between the duplexes preventing RNA condensation in solutions. All-atom MD simulations correctly reproduce the relative order of the values of this fraction for different DNA and RNA duplexes,¹¹³ which correspond to the relative order of their condensation propensities. Thus, a proper reproduction of the “internal” and “external” CoHex ion binding modes for different types of nucleic acid duplexes would be an important characteristic of the proposed explicit ions/implicit water GB model.

The estimates of the average quantities of bound CoHex ions in the “external” and “internal” ion binding shells for the three DNA and RNA duplexes in the GB-MC and explicit water MD simulations are summarized in Table III. The number of ions bound in the “internal” ion binding shells also includes ions referred to as deeply buried ions in Ref. 113, which are bound to the nucleotide bases deep inside the major groove of a nucleic acid duplex, Fig. 9 (green ions).

TABLE III.

Average numbers of bound CoHex ions in the “external” (12–16 Å from the helix axis) and “internal” (0–12 Å) ion binding shells of 25 bp DNA and RNA duplexes derived from the explicit (TIP3P) water MD and explicit ions/implicit water GB-MC simulations.

	“External” shell ions		“Internal” shells ions
		Explicit solvent		Explicit solvent
	GB-MC	MD	GB-MC	MD
Poly(dA·dT) DNA	8.7	9.4	7.0	5.2
Mixed sequence DNA	8.7	8.6	7.2	5.9
Poly(rA·rU) RNA	1.6	1.3	11.5	12.8

The results presented in Table III show a reasonable agreement between the proposed explicit ions/implicit water GB-MC approach and the fully explicit solvent reference, suggesting that the proposed model captures the main features of trivalent CoHex distributions around nucleic acid duplexes. The proposed GB model reproduces the major difference in ion binding to DNA and RNA duplexes, i.e., the much smaller number of bound CoHex ions in the “external” shell of the RNA duplex. This reduced quantity of the “externally” bound CoHex ions of RNA duplexes was suggested as the main reason of a low condensation propensity of RNA molecules.¹¹³

However, the presented results suggest that the accuracy of our GB based ion-DNA interaction potentials is not sufficient to reproduce a more subtle difference in CoHex binding in the “external” ion binding shells of the homopolymeric and mixed sequence DNA duplexes. While the MD simulations with the explicit water show about 0.8 bound ion difference, the explicit ions/implicit water GB-MC approach shows none. This can be attributed to the excessive binding of CoHex ions in the major groove of poly(dA·dT) DNA at a distance of 10-12 Å from the helical axis to the phosphates in the GB-MC simulations. On the other hand, our GB-MC approach reproduces the specific binding of two CoHex ions to the GpC steps inside the major groove of the mixed sequence DNA duplex, Fig. 9 (green ions). This specific binding was suggested¹¹³ to be one of the reasons for a reduction of the fraction of “externally” bound CoHex ions and consequently the reduced condensation propensity of the mixed sequence DNA duplexes compared to the homopolymeric DNA.

The explicit ions/implicit solvent GB-MC approach has a great advantage in the speed of generating equilibrium configurations of ions over the all-atom explicit water MD simulations. As presented above, the GB-MC CoHex ion distribution was calculated from a set of ion configurations generated during 1.6 × 10⁶ MC ion moves, which took 17 h using a single CPU core. A good convergence of the distribution was reached after 0.8 × 10⁶ MC ion moves. On the other hand, in the case of explicit water MD simulations, it was necessary to generate at least 100–300 ns trajectory to calculate the equivalent converged CoHex distribution. Using the same single CPU core with the observed simulation rate 0.8 ns/day would take 125 to 375 days to generate the required trajectory. Thus, the proposed GB-MC method has an about 200 fold advantage in speed.

C. Effect of demethylation of thymine residue in poly(dA·dT) DNA duplex

Analyzing the effect of DNA sequence on the tetravalent spermine induced interaction between DNA duplexes, Yoo et al.¹² have shown that the methylation of Cytosines in GC-rich DNA molecules results in increased counterion-mediated attraction between DNA molecules. Comparing the interactions between AT-rich and GC-rich DNA duplexes, the authors also suggested that methyl groups of thymine act as steric blocks forcing out spermine ions from the major grooves of AT-rich duplexes to the “external” shell regions, which increases the effective DNA-DNA attraction.

To test the effect of the thymine methyl groups on CoHex binding to the poly(dA·dT) DNA within our explicit ions/implicit water GB-MC approach, we “de-methylated” all of the thymine groups. Namely, in each thymine base of the homopolymeric DNA duplex, we replaced the methyl group by a hydrogen atom with a partial charge equal to the sum of all partial charges of the replaced methyl group. The resulting CoHex distribution derived from extended (1.6 × 10⁶ steps) MC simulation of the modified DNA has shown a slight decrease (0.4 ion) of the number of CoHex ions in the “external” ion binding shell and a corresponding increase (0.6 ion) of the number of ions in the “internal” shells. The changes are consistent with the idea¹² that the presence of methyl groups can shift the ion distribution toward the external shell, conducive of DNA-DNA attraction. However, in the case of CoHex ions and poly(dA·dT) DNA, the effect is rather small.

To check to what extent this small effect may be explained by the steric (van der Waals) repulsion or by a partial CoHex desolvation due to the proximity of the methyl group representing a low dielectric volume, we “methylated” the “de-methylated” DNA in a way that mimics only the desolvation, but not the steric, effect of the methyl group. Namely, we increased the size of the hydrogen atoms that replaced the methyl groups in the modified DNA duplex from 1.2 to 2.0 Å, mimicking the dielectric volume of the methyl group but kept the original van der Waals interaction parameters of the hydrogen atom. The resulting numbers of bound CoHex ions observed in a GB-MC simulation in both shells have returned approximately to their values in the original “control” duplex, constituting 8.9 and 6.8 ions, respectively.

The above results suggest that it is ion desolvation penalty due to the low dielectric volume of the thymine methyl group that is mostly responsible for the ion binding difference in the case of highly charged CoHex counterions. A simple analytical estimation of the effect of the low dielectric sphere of the methyl group size on the approaching trivalent CoHex shows that the effective range of the CoHex ion desolvation extends beyond the methyl group steric repulsion distance by roughly the size of the water molecule, which is ∼3 Å. As a result, the effective volume of the methyl group unavailable for CoHex due to the desolvation induced repulsion becomes about 10 times larger than excluded volume due to the steric repulsion alone. We conclude that desolvation effects should be taken into account in the analysis/explanation of the effects of methylation on binding of multi-valent counterions.

V. SIMULATION PROTOCOLS

A. Poisson-Boltzmann calculations

We performed nonlinear Poisson-Boltzmann calculations using APBS (v. 1.3) to compute the cation concentration profiles around the 25 bp poly(dA·dT) DNA duplex in NaCl or CoHexCl₃ salt solutions. Calculations were performed on a 200 Å cube box with 1.041 66 Å grid resolution (193 × 193 × 193 grid dimensions). The bulk salt concentration was set to 128 mM and 5 mM for the DNA-NaCl and DNA-CoHexCl₃ systems, respectively. The solvent probe radius and temperature T were 1.4 Å and 298 K, respectively. The ion accessible region was defined using the same radius for the cation and the anion: 1.02 Å or 2.0 Å for the DNA-NaCl system and 3.63 Å for the DNA-CoHexCl₃ system. The solvent and solute dielectric constants were 80 and 4, respectively. The molecular surface definition with 9-point harmonic averaging was used to define and smooth the dielectric and ion-accessibility coefficients (srfm keyword value was smol). Cubic B-spline discretization was applied to map the solute point charges onto the grid (chgm keyword value was spl2). The individual ion concentrations at each grid point were finally calculated using the formula

$$c_{ion}=c_{bulk}\times Acc\times \exp \left(-q\varphi \right),$$ (27)

where, c_bulk is the bulk ion concentration in M units, Acc is the ion accessibility map (0 ≤ Acc ≤ 1), q is the ion charge in e units, and ϕ is the electrostatic potential in k_BT/e units. To compute the 1D (cylindrical) concentration profile, the grid concentration values were interpolated onto a finer grid with a resolution of 0.104 166 Å using cubic spline interpolation and then averaged within cylindrical shells of 2 × 0.104 166 Å width at each radial distance from the DNA helical axis.

B. DNA–NaCl system. Explicit ions/implicit water GB-MC simulations

25 bp poly(dA·dT) DNA duplex was constructed in the canonical B-form using Nucleic Acid Builder (NAB).¹¹⁶ For Monte Carlo simulations with the proposed explicit ions/implicit solvent GB approach, the DNA duplex and 72 Na⁺ and 24 Cl⁻ ions are placed into a cylinder of 34 Å radius and 114 Å height with the harmonic reflective boundary potential [3 kcal/(mol Ų) force constant]. The dielectric constants of the solutes and the solvent were chosen as ϵ_in = 4 and ϵ_out = 80, respectively. The effective surface tension parameter in the nonpolar solvation term is γ = 5 cal/(mol Ų). The DNA duplex atomic partial charges and the parameters for van der Waals interactions between DNA, Na⁺, and Cl⁻ ions are taken from the AMBER ff99bsc0 force-field.⁶⁶ Ionic radii for Na⁺ and Cl⁻ are taken from Ref. 96 and are 1.02 Å and 1.81 Å, respectively. The DNA duplex was fixed in its original canonical B-form. 960 000 MC moves of ions were generated at temperature T = 300 K. The optimized “Neck” scaling factor n_j was 0.4.

For the estimation of the free energies of the DNA-ion configurations in the Monte Carlo procedure, the additive constants $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(i)}$ and $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}}^{(j)}$ in Eq. (10)—the hydration free energies of isolated ions and solute—are not calculated.

C. DNA–NaCl system. Explicit water MD simulations

All-atom MD simulations of the monovalent ion distributions around the same 25 bp poly(dA·dT) DNA duplex in canonical B-form using an explicit TIP3P water model⁶⁴ were carried out using the AMBER12⁶⁶ package and AMBER ff99bsc0 force field.^117,118 The simulated system contained 72 Na⁺ and 24 Cl⁻ ions and 16 885 TIP3P water molecules. The DNA atoms were harmonically restrained with 50 kcal/(mol Ų) force constant. Canonical NVT ensemble, periodic boundary conditions, and the particle mesh Ewald (PME) method were used to generate 320 ns trajectory utilizing 2 fs time step at T = 300 K temperature. The latter was maintained using the Langevin thermostat with the collision frequency of 1 ps⁻¹. The force filed parameter for Na⁺ and Cl⁻ ions are default AMBER parm99 force field ion parameters, adapted from Refs. 119 and 120, respectively. First 20 ns of the trajectory were excluded from calculating Na⁺ distributions. The distributions calculated using next 100 ns and larger 300 ns portions of the trajectory are practically indistinguishable, suggesting good convergence of the system with monovalent ions. Additional simulation of the same system was carried out using the TIP4P-Ew¹¹² explicit water model and Joung and Cheatham¹²¹ parameters for Na⁺ and Cl⁻ ions. The rest of the simulation details are as described above.

D. DNA(RNA)–CoHex system. Explicit ions/implicit water GB-MC simulations

The construction of the 25 bp homopolymeric poly(dA·dT) DNA duplex is described above. The 25 bp mixed sequence¹¹³ DNA duplex and the 25 bp homopolymeric poly(rA·rU) RNA duplex were constructed in canonical B- and A-form, respectively, using NAB.¹¹⁶ Each duplex (charge −48 e) was neutralized by 16 CoHex ions. No other ions were included in the simulations. All other parameters and the force-fields were the same as in the case of the DNA–NaCl system described above. For the GB based interactions, CoHex³⁺ ions are considered as spheres of 3.63 Å radius: the sum of 2.43 Å cobalt-hydrogen distance and 1.2 Å bondi hydrogen atom radius. For the van der Waals interactions, all 25 atoms of CoHex ion have been considered explicitly. 1 600 000 MC moves of ions were generated at temperature T = 300 K. The optimized “Neck” scaling factor n_j was 0.9.

In summary, to reproduce the results shown in Fig. 8 and Table III, one needs the set of parameters presented in the supplementary material.

E. DNA(RNA)–CoHex system. Explicit water MD simulations

The details of the all-atom MD simulations of DNA(RNA)–CoHex systems using the explicit TIP3P water model⁶⁴ are described elsewhere¹¹³ and are similar to the all-atom MD simulation of the DNA–NaCl system described above. For the homopolymeric and mixed sequence DNA duplexes in the canonical B-form, we use the results of MD simulations described in Ref. 113. Additional MD simulation has been performed for the homopolymeric RNA duplex in the canonical A-form using the TIP3P water model. All MD simulations were carried out using the AMBER12⁶⁶ package and AMBER ff99bsc0 force field^117,118 with CoHex parameters described in Ref. 122.

VI. CONCLUSIONS

Accurate evaluation of ionic atmosphere around hydrated nucleic acids is of great importance for understanding their structure and dynamics, but the use of traditional explicit water models for such computations may become prohibitively expensive. Implicit solvation methods eliminate solvent degrees of freedom allowing substantial reduction of computational efforts. Equally important, these methods facilitate the understanding of complex phenomena by dissecting the underlying energetics into distinct physical components. However, atomistic simulations of multi-valent ion distributions around charged polymers with an accuracy comparable to that expected from the explicit solvent MD simulations remains problematic.

Here, we have developed and tested a modification of the analytically generalized Born approach which allows one to explicitly consider ions around charged polymers and, at the same time, to treat water implicitly. The major components of the proposed model are an approach for positioning the dielectric boundary (DB) around highly charged solutes and explicit ions and a modification of the GB electrostatic interaction terms to account for the case of disconnected DB around a solute-ion or ion-ion pair. Specifically, we propose that the DB should be placed at the distance of the water O–H bond (about 1 Å) below the solvent accessible surface (SAS) around the solute. The GB interactions are modified according to solute-ion and ion-ion connectivities: low dielectric regions within a single continuous DB interact according to the canonical GB, while regions belonging to disjoint, separate pieces of the DB interact via a scaled Coulomb potential. Key parameters of the model have been optimized against the explicit solvent potential of mean force for a Na⁺–Cl⁻ ion pair, the numerical PB-derived solvation energy of explicit Na⁺ ion in the minor groove of the DNA duplex, and the ion distribution around homopolymeric poly(dA·dT) DNA obtained from the explicit water MD simulations.

We have tested the proposed explicit ions/implicit water GB model by carrying out Monte Carlo (GB-MC) simulations of monovalent (Na⁺ and Cl⁻) and trivalent [cobalt(III) hexammine (CoHex³⁺)] ions around DNA and RNA nucleic acid duplexes of various sequences. The results of these GB-MC simulations are compared with traditional explicit water all-atom MD simulations. The counterion distributions derived from the explicit ions/implicit water GB-MC simulations are found to be in reasonable agreement with the explicit water MD results: The GB-MC derived ion distributions suggest that the effective ion interaction potentials based on the modified GB are within ∼k_BT agreement with the explicit solvent interactions. The proposed approach confidently reproduces all major features of CoHex distributions around DNA and RNA duplexes, most relevant to counterion-induced condensation of nucleic acids. These include the preferential CoHex binding to the outer surface of the sugar-phosphate backbone of the B-form DNA duplex and primary CoHex binding inside the major groove of the A-form RNA duplex. Moreover, the proposed modified GB approach is able to distinguish between the specific CoHex binding inside the major groove of the mixed sequence DNA duplex and the lack of such biding in the case of homopolymeric poly(dA·dT) DNA, which is a relatively fine distinction. However, the model is not sensitive enough to resolve an even finer difference in CoHex biding to the external surface of these duplexes seen in the explicit water MD simulations. Further fine tuning of the effective interaction potentials is needed to overcome these discrepancies. When constructing the current model, we opted for the simplest functional forms consistent with the general principle; there is definite room for improvement. The use of additional characteristics of the counterion distribution as target quantities for model parameter optimization should also be considered. For example, pair correlation functions of CoHex distributions can be sensitive to the details of the interaction potential.

We have applied the new model to investigate the effect of the thymine methyl group on subtle features of CoHex distribution around DNA, following a recent suggestion that the steric effects are responsible for the difference in the ion distribution patters between methylated and unmethylated DNA, leading to differences in counterion-induced aggregation. Within our implicit water approach, we can easily separate the purely steric (methyl group–ion) repulsion from an effective repulsion induced by desolvation of the counterion coming in contact with the methyl group. We find that the desolvation induced repulsion of CoHex due to the low dielectric volume of the methyl group has a longer range and becomes appreciably sooner than the pure steric repulsion upon CoHex binding to the DNA at the thymine methyl group. A more detailed future study can easily extend the sequence space to be explored owing to the computational effectiveness of the proposed explicit/implicit model. Such a study can utilize a combination approach in which the most interesting predictions from the explicit ions/implicit water model are further refined within fully explicit, traditional simulations. DNA methylation is a class of post-translational modifications extremely important for the epigenetic control of cell function, but atomistic mechanisms behind this control are only beginning to emerge.

The proposed model is fully analytical, which should facilitate its eventual adaptation for MD simulations. An adaptation to Grand Canonical Monte Carlo simulations will be more straightforward. Incorporating more complex types of polyions, including flexible ones such as spermine, is likely within easy reach. We also envision incorporation of the model into multi-resolution approaches to the simulation of chromatin components, where the atomistic treatment of multi-valent counterions may be critical.

SUPPLEMENTARY MATERIAL

See supplementary material for the force field and solvation parameters used in our modified generalized Born model.