Measurements of neuronal color tuning: procedures, pitfalls, and alternatives

Abstract

Measuring the color tuning of visual neurons is important for understanding the neural basis of vision, but it is challenging because of the inherently three-dimensional nature of color. Color tuning cannot be represented by a one-dimensional curve, and measuring three-dimensional tuning curves is difficult. One approach to addressing this challenge is to analyze neuronal color tuning data through the lens of mathematical models that make assumptions about the shapes of tuning curves. In this paper, we discuss the linear-nonlinear cascade model as a platform for measuring neuronal color tuning. We compare fitting this model by three techniques: two using response-weighted averaging and one using numerical optimization. We highlight the advantages and disadvantages of each technique and emphasize the effects of the stimulus distribution on color tuning measurements.

Introduction

In humans, apes, and Old World monkeys, color vision is mediated by the long (L), medium (M), and short (S) wavelength-sensitive cone photoreceptors. Signals from these three cone classes are combined in the retina, sent to the brain, and propagated through a complex processing hierarchy of recurrently connected visual areas. At each stage of this hierarchy, signals from the preceding stages are mixed to create new signals. Signals in the early stages are closely related to the physical properties of light, whereas signals in the later stages are more closely related to perception (Komatsu, 1998; Gegenfurtner, 2003; Solomon and Lennie, 2007; Conway, 2009; Conway et al., 2010; Bohon et al., 2016). Neuronal color tuning measurements can help reveal how and where these transformations occur.

A Problem in Color Neurophysiology

Color tuning measurements made in different laboratories are not always comparable. Different laboratories typically use different stimuli, and comparisons are based on data summaries, such as distributions of preferred colors or cone weights. In an ideal world, these summaries would not depend on an experimenter’s choice of stimuli, but in reality they usually do. For example, differences in spatiotemporal stimulus parameters affect color tuning (Derrington et al., 1984; Thorell et al., 1984; Cottaris and DeValois, 1998; Solomon et al., 2004; Conway and Livingstone, 2006). These effects are important but beyond the scope of this article; we focus on how the spectra of lights presented in neurophysiology experiments affect measurements of color tuning.

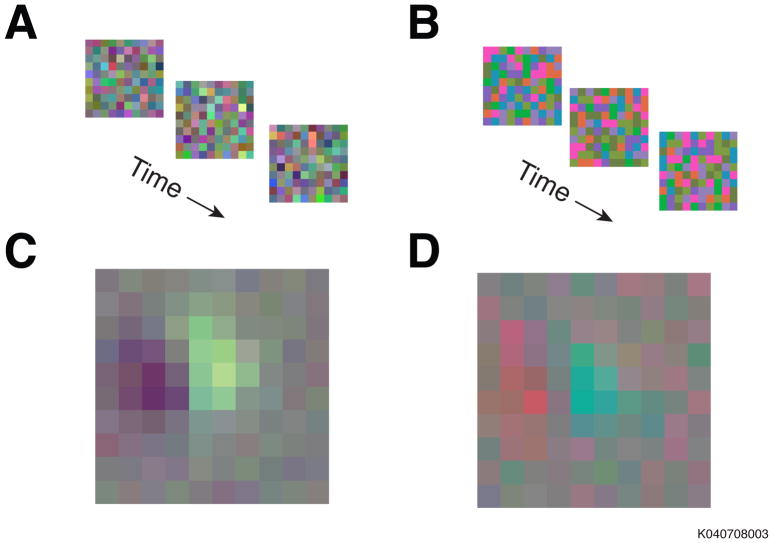
To illustrate the type of problem we are considering, we analyze an example data set. We probed individual neurons in the primary visual cortex (V1) of a macaque with two types of white noise stimuli. In the phosphor noise stimulus, the three display primaries modulated independently (Figure 1A). In the cone noise stimulus, they modulated in ratios selected to stimulate the three cone types independently (Figure 1B) (see Appendix I for methodological details of the experiment). The average phosphor noise stimulus that preceded a spike from a single example neuron (Figure 1C) appears different from the average cone noise stimulus that preceded a spike (Figure 1D); but do these two images reflect the same color tuning? We will return to this example neuron twice more as we present three techniques to estimate color tuning and discuss the transformation of estimates between color spaces. To begin, we discuss the model upon which the analysis techniques are based: the linear-nonlinear (LN) cascade.

Figure 1.

The responses of individual V1 neurons from an awake fixating monkey were probed with stimuli from two different distributions. (a) Stimuli from the phosphor noise distribution. The color of each square was determined by the independent modulation of the three phosphors in a CRT monitor. (b) Stimuli from the cone noise distribution. Each colored square modulated the activity of the three photoreceptor-types independently. (c) The average stimulus that preceded a spike during the presentation of the cone noise. (d) The average stimulus that preceded a spike from the same neuron during the presentation of the phosphor noise.

The Linear-Nonlinear Cascade Model

Models have a central role in color neurophysiology. Without them, color tuning measurements are simply a collection of numerical tables that map stimuli to responses—tables that do not predict responses to untested stimuli and that can never be sufficiently large to characterize tuning fully. In this paper, we focus specifically on cone signal combination under the LN model. This class of model has a long history in the field of color psychophysics, specifically in the areas of contrast detection (Krauskopf et al., 1982; Cole et al., 1993; Sankeralli and Mullen, 1996; D’Zmura and Knoblauch, 1998), color discrimination (Ingling and Tsou, 1977; Wandell, 1985; Krauskopf and Gegenfurtner, 1992; Eskew et al., 1999), and appearance judgments (Hurvich and Jameson, 1957; Thornton and Pugh, 1983; Poirson and Wandell, 1993). Some of the issues we discuss regarding color spaces and transformations between them can be found in Knoblauch, 1995; Sankeralli and Mullen, 2001; D’Zmura and Knoblauch, 2001; Brainard, 1996; Brainard and Stockman, 2010; Stockman and Brainard, 2010, Hansen and Gegenfurtner, 2013. Here, we distill from this body of work a few key elements that are particularly useful for color neurophysiology. We apply these techniques to neurophysiological data, compare their accuracy for measuring neuronal color tuning, and provide intuitions into their respective strengths and weaknesses.

The LN model provides a simple but powerful description of neural responses. As the name suggests, this model has both a linear and a nonlinear component. The linear component specifies how stimulus elements are weighted and summed:

$$[v_1{v}_2{v}_3]\left[\begin{array}{l}A\hfill \\ B\hfill \\ C\hfill \end{array}\right]$$ Eq. 1

where the vector [v₁ v₂ v₃] represents three stimulus elements (e.g. signals from the three cone types), and the weighting vector [A B C] describes how the elements are combined. The sign and magnitude of each element in the weighting vector indicates how the corresponding element in the stimulus vector contributes to or detracts from the neuron’s response. Input to the LN model can be represented by any number and kind of stimulus elements (e.g. cone excitations, DKL mechanism modulations, CIE chromaticity coordinates). The nonlinear component transforms the weighted sum into neural responses:

$$R=f\left([v_1{v}_2{v}_3]\left[\begin{array}{l}A\hfill \\ B\hfill \\ C\hfill \end{array}\right]\right)$$ Eq. 2

where R typically represents a spike count or spike rate. The function f captures nonlinear response features like spiking thresholds, spike-rate saturation, and rectification.

The LN model simplifies the problem of measuring color tuning, fundamentally, by reducing multiple stimulus elements to a single scalar through weighting and summing. The weighting vector describes this simplification by specifying a neuron’s sensitivity to each element. The direction of the weighting vector though color space—the neuron’s preferred direction—is a useful summary of color tuning. In contrast, the magnitude of the weighting vector is less informative. Any uniform scaling of the weights can be compensated exactly by scaling of the domain of f, so a family of LN models exists that make identical response predictions despite each having a different f and correspondingly different weights. For this reason, weighting vectors are often normalized so that their absolute values sum to one (Derrington et al., 1984; Lennie et al., 1990; Reid and Shapley, 2002; Johnson et al., 2004; Conway and Livingstone, 2006; Horwitz et al., 2007).

Technique 1: Response Weighted Averaging

Response weighted averaging is a data analysis technique that can provide valuable insight into how neurons represent visual stimuli. The response-weighted average stimulus (RWA) is described mathematically as:

$$\mathit{RWA}=\frac{1}{n}{\sum }_{i=1}^n{R}_i{[v_1{v}_2{v}_3]}_i$$ Eq. 3

where n is the total number of tested stimuli, [v₁ v₂ v₃]_i is the i^th stimulus, and R_i is the response to the i^th stimulus. The elements of the RWA, like those of the weighting vector, reflect the influence of each visual signal on the response of the neuron. The average stimuli in Figures 1C and 1D are examples of RWAs.

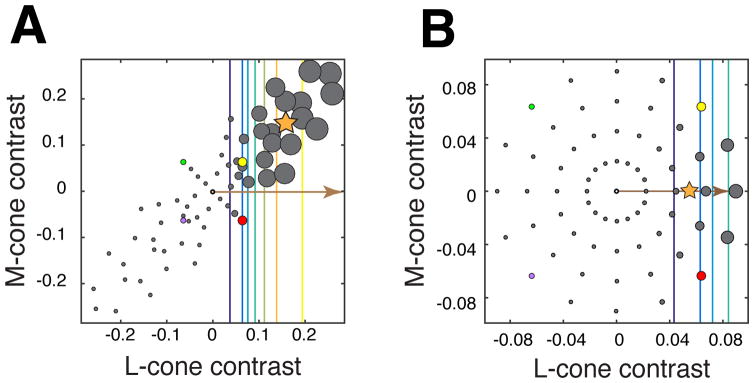
The RWA can be used to estimate a neuron’s preferred color direction (Cottaris and DeValois, 1998; Chichilnisky and Baylor, 1999; Sun et al., 2006; Horwitz et al., 2007), but its accuracy depends on the stimulus distribution. This estimate is biased if the stimulus distribution is asymmetric (e.g. distended or unequally sampled). To visualize this bias, consider a hypothetical neuron that receives exclusively L-cone input. The stimuli that evoke the largest responses from such a neuron will strongly modulate the L-cones. If such a neuron were probed with a stimulus distribution in which L- and M-cone signals are positively correlated (Figure 2A), then the stimuli that evoke the largest responses (and therefore dominate the RWA) will also strongly modulate the M-cones. The RWA (star) reflects this correlation, and, consequently, does not align to the L-cone axis, which is the neuron’s preferred color direction (arrow).

Figure 2.

Responses of a hypothetical neuron that receives only L-cone input. For simplicity, only L- and M-cone modulations are simulated in this example. The position of each gray point represents a stimulus in the LM plane. The size of each point represents the magnitude of the corresponding response. Contour lines, from cool to warm colors, represent the increasing responses of the neuron to stimuli of progressively higher contrast. The brown arrow indicates the preferred color direction of the neuron, and the orange star represents the response-weighted average stimulus (RWA). (a) A distended stimulus distribution in which L- and M-cone modulations are positively correlated. The RWA does not align with the neuron’s preferred direction. (b) A radially symmetric stimulus distribution of L- and M-cone modulations. The RWA aligns with the preferred direction. For reference, the purple, green, yellow, and red points represent identical lights in each distribution.

The RWA is an unbiased estimator of the preferred direction when the stimulus distribution is radially symmetric (RS) (Figure 2B) (Chichilnisky, 2001). Intuitively, this is because there exist whole families of stimuli that give rise to the same weighted sum, and therefore, the same response. Under the LN model, all such stimuli describe contours through color space that are straight and perpendicular to the preferred direction (colored lines). When stimuli that drive the same response are distributed symmetrically about the preferred direction (arrow), their average (star) aligns with the preferred direction. In most experiments, the preferred direction of a neuron is unknown a priori, so the stimulus distribution must be symmetric in all directions to guarantee an unbiased estimate¹.

Radial symmetry of a stimulus distribution depends on how the axes of the color space are defined. Stretching one axis of the color space distends the stimulus distribution along that axis, biasing the RWA in the direction of the stretch. This problem might appear formidable, since no single set of stimuli nor representation thereof is universally accepted as the best for measuring color tuning, and no distribution of stimuli is RS in every color space. Fortunately, an estimate of a neuron’s preferred color direction, obtained in any color space by any means, can be transformed to any linearly related color space in a straightforward way. To demonstrate this procedure and to provide a practical application, we discuss how stimuli and weights are transformed between color spaces below.

The Representation and Transformation of Lights and Weights

The preferred direction of a neuron can be estimated in one color space (e.g. where the stimulus distribution is RS) and transformed into any linearly related space (e.g. where the distribution is not RS). This transformation can be demonstrated using the two color spaces introduced in Figure 1: a phosphor space and a cone space. In both spaces, the origin [0 0 0] represents the background of the display, which is also the average of the stimulus distribution. Changes in phosphor intensity relative to this light level are represented with positive and negative values, as are changes in cone excitation. Each light is represented by a single point in each space and can be transformed between them via matrix multiplication:

$$[LMS]=[RGB]\ast M$$ Eq. 4

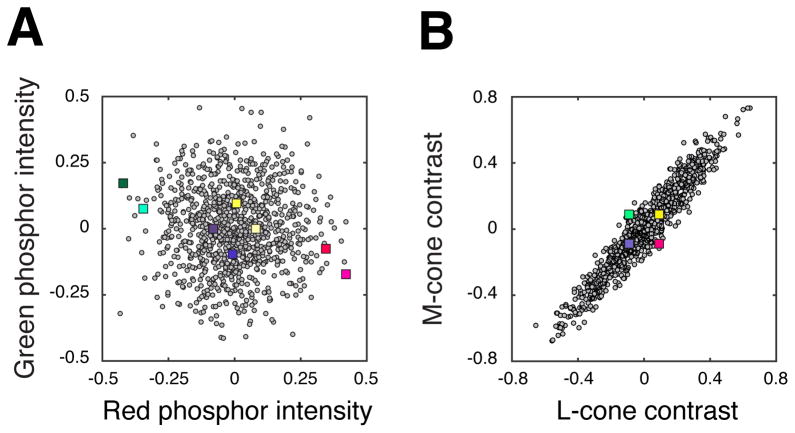
where [R G B] is an nx3 matrix of stimuli represented in phosphor space, [L M S] is this same collection of stimuli represented in cone space, and M is a 3×3 transformation matrix. Transforming the representation of lights alters their distribution. For example, a stimulus distribution that is RS in phosphor space (Figure 3A, gray points) is distended in cone space (Figure 3B, gray points) and vice versa (colored squares).

Figure 3.

Phosphor noise stimuli (gray circles) and cone noise stimuli (colored squares) represented in two color spaces. (a) Phosphor and cone noise stimulus distributions projected onto the red-green plane of phosphor space. The phosphor noise distribution is approximately radially symmetric (RS) in this space, and the cone noise distribution is distended. (b) The same two distributions projected onto the LM plane of cone space. In this color space, the cone noise distribution is approximately RS, and the phosphor noise distribution is distended. Only four colored squares are visible because +S- and −S-cone stimuli have an equal projection onto this plane.

Real neural responses do not depend on how an experimenter choses to represent visual stimuli. For the responses of an LN model neuron to have this property, the weights must be transformed between color spaces such that a given stimulus produces the same weighed sum irrespective of its representation. To achieve this, the transformation of the stimuli must be counterbalanced by the transformation of the weights. If the matrix M transforms lights from phosphor space to cone space (eq. 4), then the weights are transformed by its inverse transpose (M^−T):

$$[lms]=[rgb]\ast M^{-T}$$ Eq. 5

where [r g b] and [l m s] are the weights in phosphor and cone space, respectively, that reflect the same color tuning. Combining equations 4 and 5 clarifies the relationship:

$$R=[LMS]\ast \left[\begin{array}{c}l\\ m\\ s\end{array}\right]=[RGB]\ast M\ast M^{-1}\ast \left[\begin{array}{c}r\\ g\\ b\end{array}\right]$$ Eq. 6

where $M^{-1}\ast \left[\begin{array}{c}r\\ g\\ b\end{array}\right]$ is simply a rearrangement of terms in equation 5.

The general principle demonstrated here is that any invertible transformation of the stimuli must be accompanied by a compensatory transformation of the weights, so that weighted sums are invariant to changes in the stimulus representation. Using this principle, we can tabulate the transformations of stimuli and weights between linearly related color spaces (Table 1):

Table 1.

Transformations of stimuli and weights between linearly related color spaces.

	Space 1→Space 2 (e.g. phosphor space to cone space)	Space 2→Space 1 (e.g. cone space to phosphor space)
Stimuli [v1 v2 v3]	M	M−1
Weights [A B C]	M−T	MT

An Experimental Example

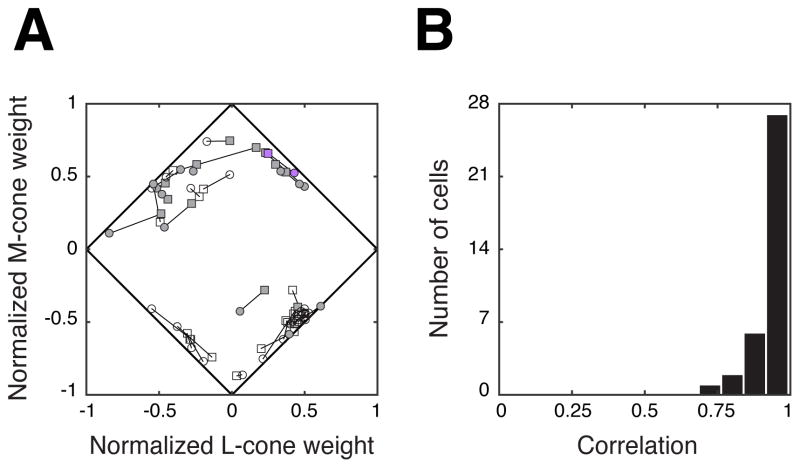
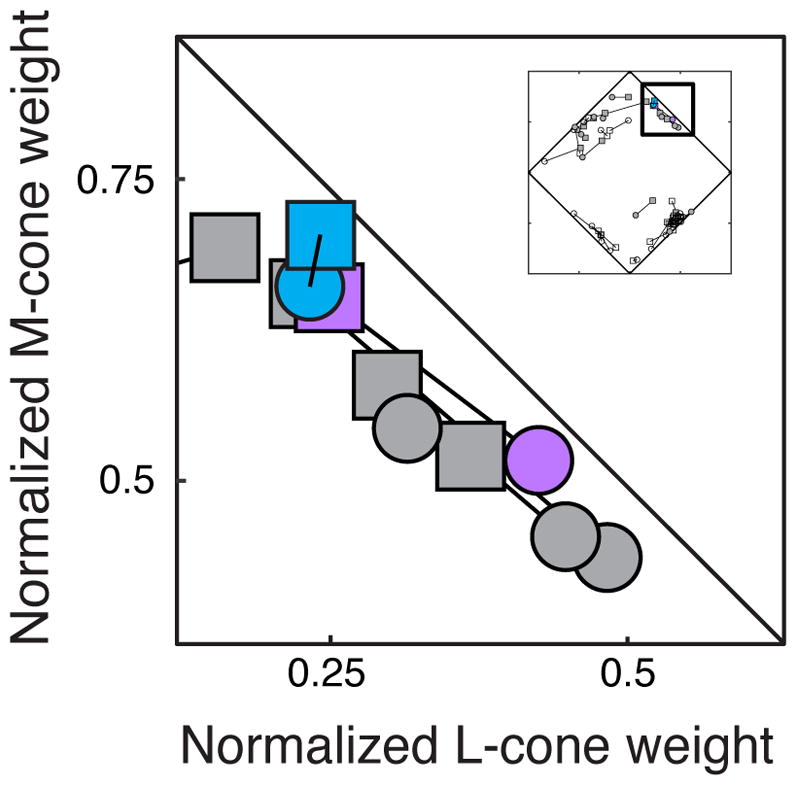
We return to the example neuron from Figure 1, which was probed with two stimulus distributions, each of which was RS in the color space in which it was constructed (Figure 3). We generate two estimates of the preferred color direction: one in phosphor space, and one in cone space. These two color spaces are linearly related, so the two estimates can be transformed from one space to the other, or into a third via equation 5. By convention, we represent both estimates in cone contrast space. Both estimates indicate similar color tuning (Figure 4A, purple symbols). Similar results were obtained for a larger population of V1 neurons, as captured by the proximity of each neuron’s normalized cone weight estimates (Figure 4A, gray symbols) and the high correlations between them (Figure 4B).

Figure 4.

(a) Normalized cone weight estimates from the population of neurons recorded in this experiment (n = 35). Two cone weight estimates (connected with black lines) were obtained from each neuron: one from the responses to the phosphor noise (circles), and one from the responses to the cone noise (squares). Shaded symbols indicate positive S-cone weights, and unshaded symbols indicate negative S-cone weights. The example neuron from Figure 1 is highlighted in purple. (b) Correlation coefficients between the normalized cone weight estimates obtained from the two distributions. Cone weight estimates derived from the phosphor noise agreed closely with those derived from the cone noise for the majority of tested neurons.

Technique 2: Linear Regression

To estimate the preferred color direction of a neuron whose responses have been probed with a non-RS stimulus distribution, the experimenter must turn to alternative techniques. One special case offers an easy solution: if the stimuli can be linearly transformed into a new color space in which their distribution is RS, the preferred color direction can be estimated in the new space using the RWA, then transformed to the original space using Table 1 (multiplication with the inverse-transpose of the stimulus transformation matrix).

This technique is not generally applicable, however, because most non-RS stimulus distributions cannot be made RS via linear transformation. Nevertheless, there is always an approximation that comes close: multiplying the stimuli with a whitening matrix. This multiplication transforms the stimuli so that they have variance of “1” in all directions (their distribution need not be the same in all directions, which is why the whitened distribution is not necessarily RS). The preferred color direction of a neuron can be estimated with the RWA of the whitened distribution, then transformed to the original color space. This solution does not necessarily provide an unbiased estimate of a neuron’s preferred color direction, but it can provide a substantial improvement over the RWA of the non-whitened stimulus distribution. This technique is identical to linear regression.

Technique 3: Numerical Optimization

An even more general approach to the problem of estimating the preferred color direction is to use numerical optimization to iteratively adjust the weights of the LN model to minimize an appropriate measure of error (e.g. the sum of squared differences between the actual and predicted responses). Numerical optimization is more computationally intensive than linear regression or calculating the RWA. Nevertheless, it can be used to accurately estimate the weighting vector, as well as any additional parameters of the model, largely irrespective of the stimulus distribution. Additional parameters may include those that govern the shape of f (the nonlinear component), or weights that represent input from non-stimulus sources (e.g. response history or the firing of other neurons; Pillow et al., 2008). Through numerical optimization, all of these parameters can be fit simultaneously, and thus potentially more accurately than if each were estimated sequentially, as when the RWA is used to estimate the preferred color direction and other procedures are used to estimate f.

Generally, the goal of this procedure is to describe the data with a model that maximizes (or alternatively minimizes) an objective function. The objective function describes the relationship between the parameters of the model (e.g. the weights) and a number that represents how well each set of parameter values describes the data. The objective function may also include penalties for parameter values that are unrealistic or are unlikely to generalize well to new data.

The objective function must be tailored to the experiment, and although many circumstances warrant a particular set of functions, there is often no best choice. One set of objective functions that is well grounded in statistical theory—likelihood functions—represent the probability of observing a set of neuronal responses across all possible choices of model parameter values. The parameter values that maximize the likelihood function identify the model under which the observed responses are most likely to occur. This maximum likelihood estimate can be written:

$$\left[\begin{array}{c}A\\ B\\ C\end{array}\right],\widehat{\theta }=\mathit{argmax}\left(\mathcal{L}\left(f\left(\left[\begin{array}{c}a\\ b\\ c\end{array}\right],\theta \right)|R\right)\right)$$ Eq. 7

where [a b c] is a weighting vector, θ is a vector of any additional parameters that f might have, R is a vector of all the observed responses, ℒ is the likelihood, or the conditional probability of responses R given the candidate weights [a b c] and parameters values θ. [A B C], θ̂ are the parameter values that maximize this likelihood.

The parameter values that maximize likelihood may not be calculable analytically, but may be found using numerical optimization. Although many strategies exist for finding local maxima of the likelihood function, no strategy is guaranteed to produce a singular set of parameter values that maximizes the function globally. Instead, the fitting algorithm must search iteratively through many combinations of parameter values. Because the number of potential parameter combinations is infinite in most scenarios, not every possible combination can be tested; therefore, the possibility usually remains that a better set exists. Despite this shortcoming, an experimenter may confidently fit the data using techniques that avoid local maxima in the likelihood function if the number of parameters is reasonably low. Under restricted conditions, the likelihood function can be proven to have only a single maximum, facilitating fitting models with many parameters (Paninski et al. 2007).

Comparing Estimation Techniques

To compare the accuracy of preferred direction estimates obtained by maximum likelihood with those obtained by response-weighted averaging, we performed two analyses. First, we used both techniques on the example neuron from Figure 1. Second, we used both techniques to estimate the preferred color directions of simulated neurons (see Appendix II for simulation details).

The example dataset consisted of spike times from a single neuron stimulated with phosphor noise and cone noise. To estimate cone weights, we represented every stimulus as cone contrasts relative to the background and fitted the data with an LN model using numerical optimization (maximum likelihood). Fitted cone weights were similar whether computed from the phosphor noise data (Figure 5, circles) or from the cone noise data (Figure 5, squares), confirming that maximum likelihood is relatively insensitive to the distribution of stimuli used in the experiment.

Figure 5.

Normalized cone weight estimates for the example neuron from Figure 1 estimated via the response-weighted average (purple) and maximum likelihood (blue). Normalized cone weight estimates derived from the phosphor noise (squares) agreed closely with those derived from the cone noise (circles) using both techniques.

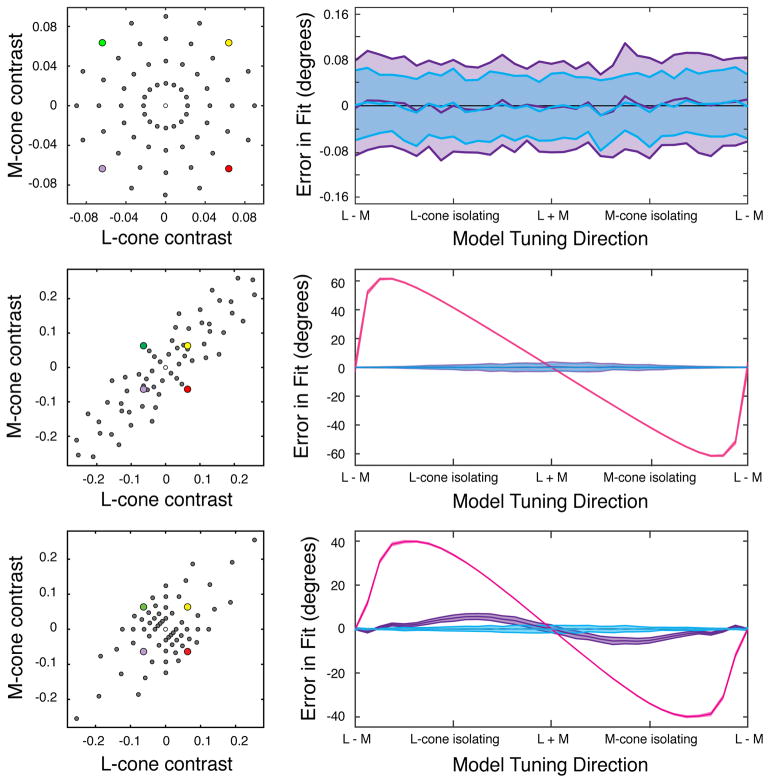
In our second analysis, we compared estimates of the preferred directions of simulated neurons using the RWA, linear regression, and maximum likelihood. Each technique was applied to three different stimulus distributions: an RS distribution (Figure 6A, left), a distended distribution that could be made RS by whitening (Figure 6B, left), and a distended distribution that could not be made RS by whitening (Figure 6C, left). For simplicity, only L- and M-cone modulations were simulated. We compared the true preferred direction with the estimated preferred direction obtained with each technique. The RWA estimate was unbiased only when the distribution was RS (Figure 6, pink curves). Linear regression was additionally unbiased when whitening the distribution produced radial symmetry (Figure 6, purple curves). Maximum likelihood was unbiased in all three cases (Figure 6, blue curves).

Figure 6.

Estimates of preferred color direction obtained from the responses of simulated neurons. Preferred color directions were estimated with three techniques and three stimulus distributions. Gray circles represent stimuli that were presented to the simulated neuron. The purple, green, yellow, and red points represent identical lights in each distribution. For simplicity, only L- and M-cone modulations were simulated. (a) Left: a radially symmetric stimulus distribution. Right: the mean and standard deviation of the error between the true and estimated preferred directions. Estimation via the response-weighted average stimulus (RWA) (purple) and maximum likelihood (blue) were both unbiased. (b) Left: a distended stimulus distribution that was RS when whitened. Right: estimation via the RWA of the non-whitened distribution (pink) was biased, but estimation via linear regression (purple) and maximum likelihood (blue) were unbiased. (c) Left: a distended stimulus distribution that could not be made RS by linear transformation. Right: estimation via the RWA (pink) and linear regression (purple) were both biased, but estimation via maximum likelihood (blue) remained unbiased.

Discussion

We described three techniques for measuring preferred color directions: two based on the RWA, and one based on numerical maximization of likelihood. Below, we summarize their advantages and disadvantages. Then, we discuss incorporating cone adaptation into the LN model. Finally, we outline a general strategy for extending the LN model.

The RWA has the advantages that it is easy to calculate and can be used to estimate a neuron’s preferred color direction without explicit specification of the parametric form of f (e.g. Naka-Rushton or exponential) or the error model (e.g. Poisson distributed spike counts). Numerical optimization methods have the advantages that they can be used with any reasonable stimulus distribution, a variety of objective functions, and are easily generalizable to models that are more complex than the LN model. The RWA and the maximum likelihood estimate converge if f is strictly monotonic and the stimulus distribution is RS.

Accounting for Adaptation with Visual Signals and Weights

The techniques we described are for estimating the parameters of the LN model. They do not guide the selection of stimulus representation. Some stimulus representations can facilitate response descriptions under a narrow range of conditions, others under a broader range. For example, the red-green detection mechanism can be modeled as LN under constant illumination conditions:

$$R=[LMS]\left[\begin{array}{c}A\\ B\\ C\end{array}\right]$$ Eq. 8

where L, M, and S represent cone excitation differences, or the changes in photoisomerizations caused by a stimulus against a static background (Boynton et al., 1964; Sperling and Harswerth, 1971; Kranda and King-Smith, 1979; Cole et al, 1993; Sankeralli and Mullen, 1996; Giulianini and Eskew, 1998), and R represents the response of the red-green detection mechanism.

If the background illumination is changed, however, the cones adapt, thresholds shift, and new weights are needed to describe them. To account for this adaptation, the background illumination must be included in the model. One possibility is to incorporate the background into the weights, yielding a dynamic weighting vector that changes with every background:

$$R=[LMS]\left[\begin{array}{c}\frac{A^{\prime }}{L_0}\\ \frac{B^{\prime }}{M_0}\\ \frac{C^{\prime }}{S_0}\end{array}\right]$$ Eq. 9

where L₀, M₀, and S₀ represent cone excitations due to the background, and A′ = A * L₀, etc. Alternatively, the background can be incorporated into the representation of the stimulus:

$$R=[LMS]\left[\begin{array}{c}\frac{A}{L_0}\\ \frac{B}{M_0}\\ \frac{C}{S_0}\end{array}\right]=\left[\frac{L}{L_0}\frac{M}{M_0}\frac{S}{S_0}\right]\left[\begin{array}{c}A\\ B\\ C\end{array}\right]$$ Eq. 10

Scaling the stimulus by the background changes the representation from cone excitation differences to cone contrasts. In this color space, a single static weighting vector describes detection thresholds under a wide array of illumination conditions (Thornton and Pugh, 1983; Stromeyer et al., 1985; Kalloniatis and Harwerth, 1991; Chaparro et al., 1994).

Cone contrast is a relatively simplistic way of modeling cone adaptation (for more complex alternatives, see Stockman and Brainard, 2010 and Angueyra and Rieke, 2013). This example is not meant to advocate for any particular color space, but to show that cone adaptation can be incorporated into the weights or into the representation of the stimulus, creating two isomorphic LN models. Both provide equivalent descriptions, but accounting for cone adaptation in the stimulus representation isolates receptoral from post-receptoral processes. This example underscores that the relationship between stimuli and responses may appear complex under one representation, but simple under another.

Beyond the LN Model

The LN model does not adequately describe neural responses under all conditions or in all color spaces. Some neurons are poorly described by the LN model (Thorell et al. 1984; Komatsu et al. 1992; Hanazawa et al. 2000; Solomon and Lennie 2005; Bushnell et al. 2011). For such neurons, weight estimates are not meaningful. However, the LN model may provide a useful skeleton on which to build richer classes of models that describe the responses of these neurons more accurately (Rust et al., 2006; Horwitz and Hass, 2012; Golden et al, 2016).

Improvements to the LN model will likely spur new advances in color neurophysiology. Finding a class of model that describes color tuning more accurately while being simple enough to work with is not trivial, but complementary approaches may provide leverage on this problem. First, patterns of residuals can be analyzed to find systematic deviations from the predictions of the LN model, and the model can be extended to eliminate these patterns. Second, known neuronal nonlinearities such as contrast gain control and contrast energy calculations can be incorporated into the model. Third, early stages of the visual system can be modeled with greater precision, thereby more accurately constraining how downstream neurons process color signals.

We described stimuli in terms of their effects on the cones, but the techniques we described generalize beyond these descriptions. Deep in the visual system, for example, neurons are poorly described by weighted sums of cone signals. One intriguing possibility is that such neurons may perform LN-like operations but on inputs that are abstract quantities (Pagan et al., 2016). Finding stimulus representations that are combined quasi-linearly by neurons but are only distantly related to cone excitations may be a fruitful approach for understanding color tuning in higher-level visual areas.

Appendix I: Electrophysiological Methods

We recorded from 35 V1 neurons in an awake fixating rhesus monkey to interleaved white noise modulation from two different stimulus distributions. All experiments were done in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the Code of Ethics of the World Medical Association (Declaration of Helsinki).

The white noise stimulus comprised a 10 × 10 grid of 0.1° squares whose color changed randomly on every screen refresh (75 Hz). The color of each square during a given trial was drawn from one of two distributions. The phosphor noise stimulus modulated each of the three display primaries independently (Fig 1A and Fig 3A), creating a Gaussian distribution of stimuli that was RS in phosphor space. The cone noise stimulus modulated each cone-type independently between a high and low value (Fig 1B and Fig 3B). Each stimulus was equidistant from the origin in proportional cone-contrast space, in which cone contrast is scaled according to the relative proportion of each cone-type in the retina, such that:

$$\mathit{Lcc}\ast \mathit{Lcp}\approx \mathit{Mcc}\ast \mathit{Mcp}\approx \mathit{Scc}\ast \mathit{Scp}$$ Eq. 1A

where Lcc, Mcc, Scc is the maximum L-, M- and S-cone contrast (0.09, 0.09, 0.4), and Lcp, Mcp, and Scp are the approximate proportions of L-, M-, and S-cones in the macaque retina (0.45, 0.45, 0.1). Both stimulus distributions had equal mean luminance and chromaticity, which was identical to the background.

For each neuron tested, two RWAs were computed: one using the responses from cone noise trials and one using the responses from phosphor noise trials. Responses in these experiments were represented as the number of spikes occurring on each stimulus frame, measured after an estimated response latency.

To estimate a single preferred color direction from each RWA, we used linear regression to find a 3-element vector that describes the consensus color tuning across stimulus pixels and time-delays (Horwitz and Albright, 2005). Thus, the preferred color direction of each neuron was represented by a pair of 3-element vectors: one describing the weights in phosphor intensity space and the other describing the weights in proportional cone-contrast space. These weight estimates were then transformed to cone-contrast space by matrix multiplication, as per Table 1.

Appendix II: Simulation Methods

Modeled responses were generated according to an LN model (eq. 2) in which the nonlinear function f was a Naka-Rushton function:

$$\lambda =U\ast \frac{{\mathit{contrast}}^N}{{c_{50}}^N+{\mathit{contrast}}^N}+bl$$ Eq. 2A

where U is the peak response (the upper asymptote), bl is the baseline response (the lower asymptote), N is an exponent, contrast is the dot product between the stimuli [L M] and a unit-length weighting vector $\left[\begin{array}{c}A\\ B\end{array}\right]$, and c₅₀ is the contrast at which the response reaches half maximum. Noise was added to these modeled responses by passing the output of the Naka-Rushton function through a Poisson random number generator:

$$R=\mathit{Pois}(\lambda )$$ Eq. 3A

Each of 33 simulated neurons was tuned to a unique direction in the LM plane and was probed with three stimulus distributions, each comprising 64 unique stimuli. Each unique stimulus was presented 5 times. The upper asymptote (U), baseline (bl), and exponent (N) were fixed across datasets (U = 50, bl = 0, N = 3), and the c₅₀ was defined for each neuron to be in the middle of the range of tested stimulus contrasts. For each simulated neuron and stimulus distribution, 100 datasets were generated and analyzed to estimate the neuron’s preferred color direction.

To estimate preferred directions using maximum likelihood, each dataset was fitted with a Naka-Rushton function in which U, c₅₀, bl, N, and the weighting vector $\left[\begin{array}{c}A\\ B\end{array}\right]$ were free to vary. The fitted values for each dataset were those that maximized the Poisson likelihood of the parameters given the responses R:

$$\widehat{\theta }=\mathit{argmax}\left(\mathcal{L}(R_1\dots R_n\mid {\lambda }_1\dots {\lambda }_n)\right)=\mathit{argmax}\left({\prod }_{i=1}^n\frac{{{\lambda }_i}^{R_i}\ast e^{-{\lambda }_i}}{R_i!}\right)$$ Eq. 4A

in which n is the total number of stimuli, R_i is the response to the i^th stimulus, λ_i is the predicted response to the i^th stimulus, and θ̂ is a vector of the best fitting parameter values (comprising U, bl, N, c₅₀, and [A B]). For practical reasons, we minimized the equivalent log-likelihood function:

$$\widehat{\theta }=\mathit{argmin}\left(-\mathcal{L}(R_1\dots R_n\mid {\lambda }_1\dots {\lambda }_n)\right)=\mathit{argmin}\left(-{\sum }_{i=1}^n{R}_i\ast (log({\lambda }_i)-{\lambda }_i)\right)$$ Eq. 5A