Pushing the Limits of Delta Bonding in Metal–Chromium Complexes with Redox Changes and Metal Swapping

Abstract

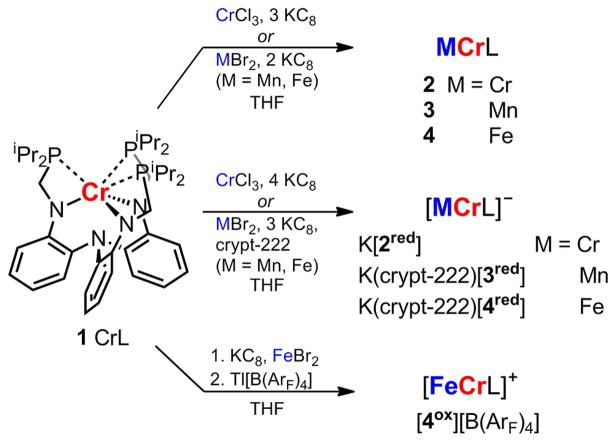
Into the metalloligand Cr[N(o-(NCH₂P(ⁱPr)₂)-C₆H₄)₃] (1, CrL) was inserted a second chromium atom to generate the dichromium complex Cr₂L (2), which is a homobimetallic analogue of the known MCrL complexes, where M is manganese (3) or iron (4). The cationic and anionic counterparts, [MCrL]⁺ and [MCrL]⁻, respectively, were targeted, and each MCr pair was isolated in at least one other redox state. The solid-state structures of the [MCrL]^+,0,− redox members are essentially the same, with ultrashort metal–metal bonds between 1.96 and 1.74 Å. The formal shortness ratios (r) of these interactions are between 0.84 and 0.74 and are interpreted as triple to quintuple metal–metal bonds with the aid of theory. The trio of (d–d)¹⁰ species [Cr₂L]⁻ (2^red), MnCrL (3), and [FeCrL]⁺ (4^ox) are S = 0 diamagnets. On the basis of M—Cr bond distances and theoretical calculations, the strength of the metal–metal bond across the (d–d)¹⁰ series increases in the order Fe < Mn < Cr. The methylene protons in the ligand are shifted downfield in the ¹H NMR spectra, and the diamagnetic anisotropy of the metal–metal bond was calculated as −3500 × 10⁻³⁶, −3900 × 10⁻³⁶, and −5800 × 10⁻³⁶ m³ molecule⁻¹ for 2^red, 3, and 4^ox respectively. The magnitude of diamagnetic anisotropy is, thus, affected more by bond polarity than by bond order. A comparative vis–NIR study of quintuply bonded 2^red and 3 revealed a large red shift in the δ⁴ → δ³δ* transition energy upon swapping from the (Cr₂)²⁺ to the (MnCr)³⁺ core. Complex 2^red was further investigated by resonance Raman spectroscopy, and a band at 434 cm⁻¹ was assigned as the Cr—Cr bond vibration. Finally, 4^ox exhibited a Mössbauer doublet with an isomer shift of 0.18 mm/s that suggests a primarily Fe-based oxidation to Fe(I).

Graphical Abstract

INTRODUCTION

The chemical bond is arguably the most fundamental yet evolving concept in chemistry.¹ Although the notation of the delta bond was developed in 1929,² the first structural evidence of the delta bond came in 1964 when a quadruple bond (σ + 2π + δ) was invoked to explain the short Re–Re distance and eclipsed conformation in [Re₂Cl₈]^2−.3 Since this seminal discovery, studies of metal–metal multiple bonds have flourished and traversed a number of disciplines. Physical chemists coupled new methodologies to generate and interrogate bare, or unligated, dinuclear metal clusters, to understand the bonding, electronic structures, and spectroscopic properties of metal–metal bonds across the periodic table.⁴ These efforts were heavily aided by theorists, who improved the accuracy of their predictions by developing new electronic structure theories to address the problems of electron correlation.⁵

In a momentous discovery, a complex with a quintuply bonded (σ + 2π + 2δ) dichromium unit was isolated using bulky terphenyl ligands.⁶ Today, the coordination chemistry of the quintuple bond comprises several dichromium, a few dimolybdenum, and a single MnCr heterobimetallic species.⁷ The reactivities of these quintuply bonded species are currently being explored, and initial studies show promise as inorganic counterparts to the wider reactivity of unsaturated carbon–carbon bonds.^7,8

Heterometallic multiple bonds involving exclusively first-row transition metals have been reported by Thomas and co-workers⁹ and by some of us.¹⁰ Starting from the monochromium complex Cr(N(o-(NCH₂PⁱPr₂)C₆H₄)₃) (abbreviated as CrL, 1), which acts as a metalloligand to bind a second transition metal, a series of MCr binuclear compounds was isolated for M = Mn, Fe, Co, and Ni. The series culminated in a quintuply bonded MnCr heterometallic species that opened the possibility of investigating metal substitution effects on delta bonding. In addition, the rich electrochemistry of the neutral MCr bimetallics gave us hope that redox counterparts with high bond multiplicity could be isolated and probed to understand the redox properties associated with delta bonding. To this end, we report four additional members of the MCr series, including the homobimetallic dichromium complex Cr₂L (2) and the MCr cationic and/or anionic counterparts [MCrL]^+,− for M = Cr, Mn, and Fe (Figure 1). In particular, the trio of (d–d)¹⁰ species comprising [Cr₂L]⁻ (2^red), MnCrL (3), and [FeCrL]⁺ (4^ox) form a unique group of isostructural and potentially isoelectronic bimetallics with multiple metal–metal bonds. These bimetallics of the mid-first-row transition metals were investigated through spectroscopic studies [nuclear magnetic resonance (NMR), electron paramagnetic resonance (EPR), resonance Raman (rR), and Mössbauer], complemented by quantum chemical calculations.

Figure 1.

Metal–chromium complexes and their (d–d)ⁿ counts, where the polarity of the M—Cr bonds increases in the order Cr < Mn < Fe. White boxes represent new compounds. Previously reported complexes are shown in light gray boxes.

EXPERIMENTAL SECTION

General Considerations

Unless otherwise stated, all manipulations were performed inside a glovebox under a N₂ atmosphere or using standard Schlenk techniques. Standard solvents were deoxygenated by sparging with N₂ and dried by passing through activated alumina columns of an SG Water solvent purification system. Deuterated solvents were purchased from Cambridge Isotope Laboratories, degassed by freeze–pump–thaw cycles, and stored over activated 4 Å molecular sieves. The ligand N(o-(NHCH₂PⁱPr₂)-C₆H₄)₃ (abbreviated as H₃L),¹¹ CrL (1),^10b MnCrL (3),^10a FeCrL (4),^10b Tl[B(3,5-(CF₃)₂C₆H₃)₄],¹² and [FeCp₂][B(3,5-(CF₃)₂C₆H₃)₄] (where FeCp₂ represents ferrocene)^13,14 were synthesized according to literature procedures. Elemental analyses were performed by Complete Analysis Laboratories (Parsippany, NJ).

Synthesis of 2, Cr₂(N(o-(NCH₂PⁱPr₂)C₆H₄)₃)

A solution of 1 (0.115 g, 0.157 mmol) in tetrahydrofuran (THF; ca. 4 mL) was mixed with a stirred slurry of CrCl₃ (0.026 g, 0.16 mmol) in THF (ca. 4 mL) for 15 min, forming a homogeneous green solution. The solution was then added to KC₈ (0.064 g, 0.47 mmol). Within minutes, the solution turned dark brown, and a precipitate formed. After removal of the solvent in vacuo, the sample was dissolved in toluene and filtered through a Celite plug. The brown solution was dried in vacuo, yielding a brown powder (0.093 g, 76%), which was used without further purification. Single crystals of 2 were grown by diffusion of n-pentane into a concentrated solution of 2 in THF. ¹H NMR (ppm, C₆D₆, 500 MHz): 34.2, 10.9, 9.1, 5.0, 4.1, 3.4, 1.4, 1.2, 1.0, −0.5, −2.4, −15.2. UV–vis–NIR (THF) λ_max (nm) (ε (M⁻¹ cm⁻¹)): 495 (sh, 2330), 600 (1480), 880 (930), 1460 (140). Anal. Calcd for 2, C₃₉H₆₀N₄P₃Cr₂: 59.91 C, 7.74 H, 7.17 N. Found: 59.79 C, 7.69 H, 7.09 N.

Synthesis of K[2^red], K[Cr₂(N(o-(NCH₂PⁱPr₂)C₆H₄)₃)]

A solution of 1 (0.11 g, 0.15 mmol) in THF (ca. 4 mL) was mixed with a stirred slurry of CrCl₃ (0.024 g, 0.15 mmol) in THF (ca. 4 mL) for 15 min, forming a homogeneous green solution. The solution was then added to KC₈ (0.084 g, 0.62 mmol), forming a dark green solution with a precipitate. The sample was filtered through a Celite plug and dried in vacuo, yielding a crude green powder (0.12 g, 98%). Single crystals of 2^red were grown by diffusion of n-pentane into a concentrated THF solution of 2^red. The ¹H NMR spectrum had extremely broad peaks at room temperature, indicative of fluxional behavior. ¹H NMR (ppm, THF-d₈, 500 MHz, −80 °C): 6.39 (t, J = 7 Hz, 1H), 6.15 (d, J = 7 Hz, 1H), 6.06(d, J = 7 Hz, 1H), 5.45 (t, J = 7 Hz, 1H), 5.28 (d, J = 12 Hz, 1H), 4.47 (d, J = 12 Hz, 1H), 2.73 (br, 1H), 2.63 (br, 1H), 1.85 (br, 3H), 1.54 (br, 3H), 1.21 (br, 3H), 0.27 (br, 3H). ¹³C NMR (ppm, THF-d₈, 126 MHz, −80 °C): 157.6, 136.5, 126.5, 124.9, 106.4, 106.1, 67 (overlapping with solvent), 34.1, 29.1, 23.5, 21.2, 21.0, 19.0. ³¹P NMR (ppm, THF-d₈, 200 MHz, −80 °C): 42.4. UV–vis–NIR (THF) λ_max (nm) (ε (M⁻¹ cm⁻¹)): 315 (18300), 675 (1880). Anal. Calcd for K(2^red), C₃₉H₆₀N₄P₃Cr₂K: 57.06 C, 7.37 H, 6.82 N. Found: 56.97 C, 7.28 H, 6.69 N.

Synthesis of K(crypt-222)[3^red], [K(crypt-222)][MnCr(N(o-(NHCH₂PⁱPr₂)C₆H₄)₃)]

A solution of 1 (0.12 g, 0.16 mmol) in THF (ca. 4 mL) was mixed with a stirred slurry of MnBr₂ (0.027 g, 0.17 mmol) in THF (ca. 4 mL) for 15 min, forming a homogeneous green solution. Solid KC₈ (0.057 g, 0.51 mmol) was then added. Within minutes, the solution turned dark red-brown, and a precipitate formed. After removal of the solvent in vacuo, the sample was washed with toluene (ca. 1 mL), reconstituted in THF (ca. 2 mL), and filtered through a Celite plug into a solution of 2.2.2-cryptand (crypt-222; 0.049 g, 0.16 mmol) in THF (ca. 2 mL). The solution was dried in vacuo and washed with Et₂O (ca. 4 mL). An alternative synthesis procedure was also employed as follows: To a solution of 3 (0.038 g, 0.048 mmol) in THF (ca. 4 mL) was added solid KC₈ (0.0065 g, 0.048 mmol). Within minutes, the initial red-brown color of the solution turned yellow-brown. After the solution had been filtered through a glass filter, the filtrate was mixed with crypt-222 (0.018 g, 0.0477 mmol) and stirred for 10 min; the solvent was then removed in vacuo to yield 54 mg of 3^red (0.045 mmol, 94% crude yield). Single crystals of 3^red (18 mg, 11% crystalline yield) were grown by diffusion of npentane into a concentrated THF solution of 3^red. ¹H NMR (ppm, THF-d₈, 500 MHz): 19.3, 17.2, 8.7, 7.8, 4.4, 3.5, 2.5, 1.1, 0.5, −6.6. UV–vis–NIR (THF) λ_max (nm) (ε (M⁻¹ cm⁻¹)): 745 (1230), 1350 (760). Anal. Calcd for K(crypt-222)[3^red], [K(C₁₈H₃₆N₂O₆)]-[C₃₉H₆₀N₄P₃CrMn]: 57.03 C, 8.06 H, 7.00 N. Found: 57.06 C, 8.14 H, 6.97 N.

Synthesis of 4^ox[B(Ar_F)₄], [FeCr(N(o-(NCH₂PⁱPr₂)C₆H₄)₃)][B(3,5- (CF₃)₂C₆H₃)₄]

A THF slurry (ca. 6 mL) of KC₈ (22.2 mg, 0.164 mmol) was added to a stirring solution of 1 (120 mg, 0.164 mmol) in 12 mL of THF at −78 °C. The mixture was warmed to room temperature, stirred for 5 min, and filtered. Solid FeBr₂ (20.8 mg, 0.164 mmol) was added to the stirring filtrate at −78 °C. The reaction mixture was warmed to room temperature and stirred until all of the FeBr₂ solid had reacted, ~20 min. The reaction mixture was filtered, and the solvent was removed in vacuo. The crude residue was taken up in 4 mL of toluene, diluted with 10 mL of pentane, cooled to −20 °C, and filtered to remove a brown solid. This was repeated two more times, and then the solution was cooled to −20 °C overnight, from which a green crystalline powder, presumably (Br)FeCr(N(o-(NCH₂PⁱPr₂)C₆H₄)₃) (33.2 mg, 23% yield), was isolated. These crystals were dissolved in 4 mL of THF, and to this stirring solution was added dropwise Tl[B(Ar_F)₄] (40.9 mg, 0.038 mmol) in 4 mL of Et₂O. After this mixture had been stirred for 20 min at room temperature, a gray solid was filtered off, and the filtrate was dried in vacuo, yielding 55 mg (0.033 mmol, 87% yield) of 4^ox[B(Ar_F)₄]. Single crystals of 4^ox were grown by diffusion of n-pentane into a concentrated THF solution of 4^ox. ¹H NMR (ppm, THF-d₈, 500 MHz, 7 °C): 7.80 (s, 8H), 7.58 (s, 4H), 7.16 (t, J = 8 Hz, 3H), 7.11 (d, J = 8 Hz, 3H), 6.63 (d, J = 8 Hz, 3H), 6.48 (t, J = 8 Hz, 3H), 6.36 (s, 6H), 3.15 (br, 3H), 2.88 (br, 3H), 1.52 (m, 9H), 1.44 (m, 9H), 1.34 (m, 9H), 0.72 (m, 9H). ¹³C NMR (ppm, THF-d₈, 126 MHz, −20 °C): 135.4 [aryl, B(Ar_F)₄], 128.6 (aryl), 126.6 (aryl), 120.9 (aryl), 118.1 [aryl, B(Ar_F)₄], 111 (aryl), 75.6 (CH₂), 32.8 (CH), 28.0 (CH), 22.4 (CH₃), 20.3 (CH₃), 19.4 (CH₃), 18.0 (CH₃) (note that quarternary carbons were not observed). ³¹P NMR (ppm, THF-d₈, 126 MHz, 17 °C): 26.6. UV–vis–NIR (THF) λ_max (nm) (ε (M⁻¹ cm⁻¹)): 463 (4860), 730 (3890), 1495 (490). Anal. Calcd for 4^ox[B(Ar_F)₄], [C₃₉H₆₀N₄P₃FeCr][C₃₂H₁₂F₂₄B]: 51.72 C, 4.40 H, 3.40 N. Found: 51.67 C, 4.40 H, 3.26 N.

Physical Methods

¹H NMR spectra were recorded on a Bruker 500 MHz spectrometer at room temperature unless otherwise stated. All ¹H and ¹³C NMR spectra are referenced to the internal solvent residual. Variable-temperature NMR experiments were performed on a Bruker 500 MHz spectrometer. The temperature of the NMR probe was calibrated against an external methanol standard. Diamagnetic anisotropy (χ_|| − χ_⊥) was calculated as¹⁵

$$\mathrm{\Delta }\delta =\left(\frac{1}{3r^2}\right)\frac{({\chi }_{\Vert }-{\chi }_{\perp })[1-3{cos}^2(\theta )]}{4\pi }$$ (1)

where Δδ is the difference in chemical shift (ppm) between the resonance in a bimetallic complex versus a reference complex, namely, the isostructural Ni–Al complex featuring a Ni → Al dative bond. The distance of the proton to the center of the metal–metal bond is r, and the acute angle between the proton and the metal–metal axis is θ [Table S2, Supporting Information (SI)]. The units are 10⁻³⁶ m³ molecule⁻¹. The barrier to inversion, ΔG^‡, was calculated as

$$\mathrm{\Delta }{G}^{‡}=R{T}_{\mathrm{c}}\left[23.760+ln\left(\frac{T_{\mathrm{c}}}{k_{\mathrm{c}}}\right)\right]$$ (2)

where the coalescence temperature T_c is in kelvin; R is the ideal gas constant; and k_c = [π(Δν₀)]/√2, where Δν₀ is the difference in frequency (Hz) between the exchanging protons (Table S1, SI).¹⁶ UV–vis–NIR spectra were collected at room temperature on a Cary-14 spectrometer. Cyclic voltammetry was conducted using a CH Instruments 600 electrochemical analyzer. The one-cell setup utilized a glassy carbon working electrode, Pt wire counter electrode, and Ag/AgNO₃ reference electrode in CH₃CN. Analyte solutions were prepared in a THF solution of 0.4 M [ⁿBu₄N][PF₆] and referenced internally to the FeCp₂^0/+ redox couple. IR spectra were collected using a Bruker Tensor-37 FTIR instrument with OPUS 6.5 software. Perpendicular-mode X-band EPR spectra were recorded at 20 K with a Bruker ESP 300 spectrometer equipped with an Oxford ESR 910 liquid-helium cryostat and an Oxford temperature controller. X-band EPR spectra were simulated using the EPR program (version W95) written by Frank Neese (MPI-CEC, Mülheim, Germany). Mössbauer data were recorded on an alternating-constant acceleration spectrometer. The minimum experimental line width was 0.24 mm s⁻¹ (full width at half-height). The sample temperature was maintained constant in an Oxford Instruments Variox or an Oxford Instruments Mössbauer-Spectromag 2000 cryostat, which is a split-pair super-conducting magnet system for applied fields (up to 8 T). The field at the sample was oriented perpendicular to the γ-beam. The ⁵⁷Co/Rh source (1.8 GBq) was positioned at room temperature inside the gap of the magnet system at a zero-field position. Isomer shifts are quoted relative to iron metal at 300 K. Resonance Raman samples were prepared in a nitrogen-filled glovebox in dry THF and were immediately frozen in quartz tubes at −196 °C. Resonance Raman spectra were recorded on an Acton 506M3 spectrometer using a Princeton Instruments ACTON PyLoN LN/CCD-1340 × 400 detector. The spectra were obtained at −196 °C using a backscattering geometry. Excitation at 647.1 nm was provided by a Spectra-Physics BeamLok 2060-KR-V Krypton ion laser. Excitation at 514.5 nm was provided by a Spectra-Physics BeamLok 2065-7S argon ion laser. Raman shifts were externally referenced to indene and internally referenced to the solvent (THF).

X-ray Crystallographic and Structure Refinement Details

Single crystals of 1 were grown by adding hexamethyldisiloxane to a concentrated solution of 1 in Et₂O and storing at −30 °C. Brown plates of 1, 2, K(crypt-222)[3^red], and 4^ox[B(Ar_F)₄] and a green plate of K[2^red] were placed on the tip of a 0.1-mm-diameter glass capillary and mounted on a Bruker APEX II CCD diffractometer for data collection at 173(2) K for 1, 2, K[2^red], and K(crypt-222)[3^red] and at 123(2) K for 4^ox[B(Ar_F)₄]. The data collection was carried out using Mo Kα radiation (graphite-monochromated). The data intensity was corrected for absorption and decay (SADABS).¹⁷ Final cell constants were obtained from least-squares fits of all measured reflections. The structure was solved using SHELXS-97 and refined using SHELXL-97.¹⁸ A direct-methods solution was calculated that provided most non-hydrogen atoms from the electron-density map (E map). Fullmatrix least-squares/difference Fourier cycles were performed to locate the remaining non-hydrogen atoms. All non-hydrogen atoms were refined with anisotropic displacement parameters. Hydrogen atoms were placed in ideal positions and refined as riding atoms with relative isotropic displacement parameters. Complex 2 was solved in the space group P321 and contained channels along the crystallographic c axis; although substantial electron density was observed, no solvent molecules could be located. The SQUEEZE function of the PLATON program was used to remove solvent molecules within the void space.¹⁹ The SQUEEZE function removed 839 electrons from a voidspace volume of 396 ų. These values are consistent with the presence of approximately 21 THF molecules within the channel. Independent crystals of 4^ox[B(Ar_F)₄] displayed substantial disorder at 173 and 123 K. At 123 K, the entire cationic component was found to be disordered over two sites with a 57:43 occupancy. The anionic component exhibited rotational disorder of the CF₃ groups, which were treated as ideal rotors. One aryl ring of the counteranion appeared to exhibit rotational disorder, precluding anisotropic refinement of the respective CF₃ group. The presumed minor component of this disorder was not located during refinement. The data for 3^red was twinned, and the appropriate twin law was applied. Crystallographic data are summarized in Table 1.

Table 1.

Crystallographic Details for Complexes of 1, 2, K[2^red], K(crypt-222)[3^red], and 4^ox[B(Ar_F)₄]

	1	2	K[2red]·THF	K(crypt-222)[3red]	4ox[B(ArF)4]
chemical formula	C39H60CrN4P3	C39H60N4P3Cr2	C39H60N4Cr2P3K·C4H8O	C39H60N4P3MnCr·C18H36N2O6K	C39H60N4P3FeCr·C32H12F24B
formula weight	729.82	781.82	893.02	1200.35	1648.90
crystal system	monoclinic	trigonal	monoclinic	trigonal	triclinic
space group	P21/n	P321	Cc	P3̄	P1̄
a (Å)	11.1248(7)	16.067(3)	12.9903(19)	11.3119(7)	10.5449(8)
b (Å)	20.166(1)	16.067(3)	27.035(4)	11.3119(7)	18.5182(14)
c (Å)	17.373(1)	11.673(2)	14.055(2)	28.5164(18)	20.4402(16)
α (deg)	90	90	90	90	71.0960(10)
β (deg)	92.293(1)	90	93.906(2)	90	78.6720(10)
γ (deg)	90	120	90	120	87.5320(10)
V (Å3)	3894.4(4)	2609.7(9)	4924.6(12)	3160.1(4)	3701.7(5)
Z	4	2	4	2	2
Dcalcd (g cm−3)	1.245	0.995	1.204	1.262	1.479
λ (Å), μ (mm−1)	0.71073, 0.449	0.71073, 0.805	0.71073, 0.853	0.71073, 0.564	0.71073, 0.512
T (K)	173(2)	173(2)	173(2)	173(2)	123(2)
θ range (deg)	2.20–27.42	2.260–24.640	2.1945–24.658	2.184–27.486	2.207–27.2555
reflns collected	33608	6896	25827	33862	43571
unique reflns	6647	2958	9412	4397	10885
data/restraint/parameters	8993/0/436	6896/0/145	11248/0/487	4850/0/226	16967/762/1030
R1, wR2 [I > 2σ(I)]	0.0418, 0.0993	0.0466, 0.0903	0.0422, 0.0873	0.0296, 0.0689	0.1116, 0.3043

Computational Methods

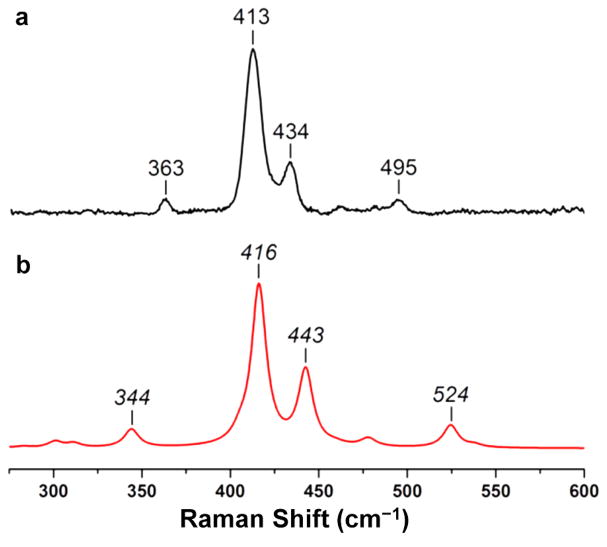
A quantum chemical study of the model complexes, 2′, 2^red′, 3^red′, and 4^ox′, was performed, where the isopropyl groups were truncated to methyl groups. Analogous studies for 3′, 4′, and 4^red′ were reported previously.¹⁰ Gas-phase geometry optimizations were performed with density functional theory (DFT) using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional as implemented in the TURBOMOLE 6.4 package.²⁰ Initial starting structures for geometry optimizations were derived from experimentally determined X-ray structures. No symmetry constraints were used. For C and H atoms, the double-ζ-quality basis set def-SV(P) was used. The triple-ζ-quality basis set def-TZVP was employed for N and P. Additional polarized functions were introduced for Fe, Mn, and Cr by using def-TZVPP.²¹ The DFT calculations were performed using an unrestricted, broken-symmetry formalism, and the resolution of the identity (RI) approximation was used for the Coulomb integrals.²² All stationary points were confirmed as minima by computing vibrational frequencies using the harmonic approximation. For 2^red′, Raman intensities were computed from polarizabilities as implemented in TURBOMOLE. To increase the accuracy of computed vibrational frequencies, a scale factor is commonly employed.²³ In the computed Raman spectra for 2^red′, the computed frequencies (391, 473, 503, 597 cm⁻¹) were scaled by a factor of 0.88 to obtain the reported frequencies (344, 416, 443, 524 cm⁻¹; Figure 10), whose intensities were plotted as a convolution of Lorentzian functions with half height widths of 10 cm⁻¹.

Figure 10.

Stack plot of (a) the resonance Raman spectrum of 2^red (10.4 mM in THF, λ_ex = 647.1 nm, 77 K) (black) and (b) the DFT-calculated Raman spectrum of 2^red′ (red).

In addition to DFT calculations, the electronic structure was further investigated using complete-active-space and restricted-active-space self-consistent field (CASSCF/RASSCF) followed by second-order perturbation theory (CASPT2/RASPT2) calculations on the DFT/PBE-optimized geometries using the MOLCAS 7.8 package.²⁴ Relativistic effects were included through the use of the scalar Douglas–Kroll–Hess (DKH) Hamiltonian.²⁵ The relativistic allelectron ANO-RCC basis sets were used for all elements.²⁶ In all of these calculations, the ANO-RCC-VTZP basis set was used for Fe, Mn, and Cr; the ANO-RCC-VDZP basis set was used for N and P; and the ANO-RCC-MB basis set was used for C and H.²⁶ Additionally, the Cholesky decomposition technique was used combined with local exchange screening to reduce significantly the computational costs involved in generating the two-electron integrals.²⁷ Atomic charges were computed at the CASSCF level for the ground state using the LoProp procedure.²⁸

Active-Space Choice

Previously, the CASSCF active space for 3′, 4′, and 4^red′ was constrained to the valence 3d electrons in 15 orbitals, including all of the 3d orbitals from the two metals and five empty correlating 4d orbitals of Mn or Fe.¹⁰ A larger active space was used here for 2′, 2^red′, 3^red′, and 4^ox′, consisting of the valence 3d electrons in 20 orbitals, including all of the 3d orbitals and empty correlating 4d orbitals of both metals. For consistency, 3′, 4′, and 4^red′ were recomputed with the larger active space, and the results were consistent with those of the earlier studies. To account for the double-shell effect, RASSCF calculations incorporating a large configuration interaction space were performed for all species and spin multiplicities, denoted by (n,20)/(n,10)/2, where n = 9, 10, and 11 for the (d–d)⁹, (d–d)¹⁰, and (d–d)¹¹ species, respectively.^5c In this notation, the numbers in the first set of parentheses correspond to the total number of electrons (n) and the total number of orbitals (20) in all of the RAS spaces. The numbers in the second set of parentheses correspond to the number of active electrons and the number of orbitals in the primary space, containing the 3d orbitals of both metals. The final value of 2 refers to the maximum number of electrons allowed into the secondary space. The natural orbital occupation numbers were used for the evaluation of effective bond orders (EBOs), which were calculated as the difference between the total occupancies of the bonding and antibonding molecular orbitals of the metal–metal bond divided by 2.^5a,b

State-averaged complete-active-space self-consistent field (SACASSCF) calculations were performed for the (d–d)¹⁰ complexes. Because of the computational cost of calculating multiple electronic states, the active spaces for SA-CASSCF calculations were truncated from the aforementioned RASSCF choices to a (10,10) active space. For each (d–d)¹⁰ complex, a six-root calculation was performed. The complete-active-space state interaction (CASSI) method was applied to compute the transition probabilities.²⁹ The CASSCF wave functions were employed together with the CASPT2 energies. CASSI results served to obtain a qualitative orbital ordering based on an analysis of the energies and natures of the orbitals involved in the electronic excitations of the various roots and to characterize the low-energy vis–NIR spectroscopic transitions.

RESULTS AND DISCUSSION

Synthesis and Cyclic Voltammetry (CV)

The neutral MCr complexes for M = Mn and Fe were generated previously by mixing the metal dibromide precursors, MBr₂, with the monometallic chromium complex (1, CrL) and 2 equiv of reductant, KC₈ (Scheme 1).^10,30 A similar procedure was used to generate the chromium homobimetallic complex. Mixing 1, chromium(III) chloride, and 3 equiv of KC₈ produced the red-brown dichromium complex (2, Cr₂L). As previously reported, neutral MCr complexes with M = Mn, Fe, Co and Ni exhibit multiple one-electron-transfer processes by cyclic voltammetry (CV). The cyclic voltammogram of 2 is shown in Figure 2, along with the cyclic voltammograms of the manganese–chromium (3, MnCrL) and iron–chromium (4, FeCrL) complexes, and the redox potentials are listed in Table 2. Complex 2 exhibits two reversible, one-electron-transfer processes: an oxidation at −1.60 V and a reduction at −2.26 V (vs FeCp₂/FeCp₂⁺). Presumably, reduction of 2 generates a {Cr₂}¹⁰ species that would be isoelectronic to diamagnetic 3. Collectively, the cyclic voltammograms suggest the possibility of characterizing several redox members (Figure 1), including an isoelectronic (d–d)¹⁰ subset that comprises [Cr₂L]⁻, MnCrL, and [FeCrL]⁺.

Scheme 1.

Syntheses from Complex 1 (Left) of Neutral Metal–Chromium Complexes 2–4 and Their One-Electron-Reduced and/or -Oxidized Counterparts

Figure 2.

Cyclic voltammograms of 2–4 with [ⁿBu₄N]PF₆ (0.1–0.4 M) in THF (vs FeCp₂ ^0/+). Scan rates and electrolyte concentrations were as follows: 2 (black), 25 mV/s, 0.4 M; 3 (blue), 250 mV/s, 0.4 M; and 4 (red), 10 mV/s, 0.1 M.

Table 2.

Redox Potentials^a (E°′, V) of 2–4

complex	reduction	oxidation
2	−2.26	−1.60
3	−2.21, −2.55b	−1.18c
4	−2.33	−1.32, −0.62

^aVersus FeCp₂^0/+.

^bQuasireversible.

^cIrreversible; E_pa reported.

The reduction of 4 to [FeCrL]⁻ (4^red) was previously achieved using 1 equiv of KC₈ in THF.^10b The monoanionic counterparts of 2 and 3, [Cr₂L]⁻ (2^red) and [MnCrL]⁻ (3^red), respectively, were generated directly from 1 using CrCl₃ and MnBr₂, respectively, and the appropriate number of equivalents of KC₈ (Scheme 1). In THF, the color of 2^red is forest-green, whereas 3^red and 4^red are red-brown. One equivalent of crypt-222 was added to solutions of 3^red and 4^red to improve the crystallinity of the salt product. Chemical oxidation of 4 to [FeCrL]⁺ (4^ox) can be performed with [FeCp₂][B(Ar_F)₄]. However, an alternative, cleaner synthesis of [4^ox][B(Ar_F)₄] avoids neutral 4 altogether. Complex 1 was stirred with 1 equiv KC₈ and then FeBr₂ to generate a green intermediate, which is presumably (Br)FeCrL. Abstraction of the halide with Tl[B(Ar_F)₄] gave [4^ox][B(Ar_F)₄] in moderate yield. The presence of the [B(Ar_F)₄] counterion renders [4^ox][B(Ar_F)₄] highly soluble even in hydrocarbon solvents such as benzene. So far, efforts to isolate the dicationic (d–d)⁹ [FeCrL]²⁺ or the dianionic (d–d)¹² [MnCrL]²⁻ have not been fruitful.

NMR and EPR Spectroscopies

The three (d–d)¹⁰ species 2^red, 3, and 4^ox are all diamagnetic, allowing for detailed comparisons by ¹H NMR spectroscopy. These complexes all display fluxional behavior, as shown in Figure 3 for 2^red (for 3 and 4^ox, see Figures S6 and S9, respectively, SI). At high temperature, each complex exhibits C_3v symmetry (total of seven unique protons) with equivalent methyl, methylene, and methine protons. As the temperature is lowered, the solution structures of the MCrL species adopt a C₃-propeller configuration (total of 12 unique protons), where the methylene protons are diastereotopic and the two methine protons and four methyl groups are also distinct.

Figure 3.

Stacked plot of variable-temperature ¹H NMR spectra for K[2^red] (THF-d₈, 500 MHz). Protons are color-matched to the inset color figure. For clarity, only one ligand arm is labeled.

The energy barrier (ΔG^‡) for the fluxional process can be estimated from the coalescence temperature of the methylene peaks for the trio of (d–d)¹⁰ complexes 2^red, 3, and 4^ox.¹⁶ For example, the coalescence of the methylene resonances of 2^red occurs at 15 °C, as shown in Figure 3. The energy barriers for 2^red, 3, and 4^ox were estimated to be 13.0, 14.6, and 16.6 kcal mol⁻¹, respectively (Table S1, SI). Two possible mechanisms could account for the observed fluxionality: (1) dissociation of one phosphine donor followed by rotation and reassociation³¹ or (2) a simple twisting of the methylene backbone while the phosphine arms remain associated. Unfortunately, the variable-temperature (VT) ³¹P NMR behavior of these species (Figures S4, S7, and S10, SI) was inconclusive. Notably, the aryl protons of the ligand backbone remained sharp and coupled throughout the VT-NMR studies of 2^red, 3, and 4^ox (up to 60 °C), which rules out the presence of a low-lying triplet state (Figures S3, S6, and S9, SI).

The ¹H NMR spectrum of 2 is paramagnetic and displays 12 resonances, suggesting that it is locked in a C₃ environment on the NMR time scale (Figure S2, SI). The S = ¹/₂ spin state was confirmed by X-band EPR spectroscopy (Figure 4a). The S = ¹/₂ EPR signal is isotropic, with g = 1.99, which is typical for a Cr-based spin.³² The spectral splitting arises from coupling to three I = ¹/₂ ³¹P nuclei with an isotropic coupling constant (A) of 10 × 10⁻⁴ cm⁻¹, suggesting that spin density resides at the Cr center in the phosphine-binding pocket. Notably, the hyperfine coupling is lower than that reported for octahedral phosphine-ligated Cr(I) carbonyls, such as [Cr-(CO)₃(PMe₃)₃]⁺, which feature hyperfine coupling constants in the range of 57–96 MHz, or (19–36) × 10⁻⁴ cm^−1.33 This might suggest some delocalization of the unpaired spin in dichromium unit. Complex 3^red is also paramagnetic, and the 10 resonances observed by ¹H NMR spectroscopy are consistent with C₃ symmetry (Figure S12, SI). The solution-state magnetic moment of 3^red is 1.87 μ_B, indicating S = ¹/₂.³⁴ The X-band EPR spectrum of 3^red (Figure 4, bottom) is rhombic, with g = (1.95, 1.88, 1.52), where g_ave is 1.79. Hyperfine coupling to the ⁵⁵Mn nucleus (I = 5/2) can be discerned in g_x where A_x = 36 × 10⁻⁴ cm⁻¹. Complex 4, with a (d–d)¹¹ electron count, was previously characterized as S = ¹/₂ by EPR spectroscopy. The reported g_ave value of 1.88 for complex 4 is consistent with a Cr-based spin.

Figure 4.

X-band EPR spectra (9.65 MHz) of (a) 2 (20 K) and (b) 3^red (34 K) in frozen THF (1 mM). Experimental spectra are shown in solid black lines, with corresponding simulations in dashed red lines. Simulation parameters were as follows: for 2, g_x = g_y = g_z = 1.99; W = (11, 16, 11 G), A(3 × ³¹P) = 10 × 10⁻⁴ cm⁻¹; for 3^red, g_ave = 1.79, g = (1.95, 1.88, 1.52), W = (30, 200, 620) G, A_x(⁵⁵Mn) = 36 × 10⁻⁴ cm⁻¹.

Solid-State Structures

Single-crystal X-ray diffraction studies of complexes 1, 2, 2^red, 3^red, and 4^ox provided the solid-state structures shown in Figure 5, with the relevant geometric parameters in Table 3. For comparison, the data for previously reported compounds 3 and 4 are also included. All of the complexes are essentially threefold-symmetric and have a highly conserved coordination geometry. As anticipated based on our previous work, 2, 2^red, 3^red, and 4^ox all have ultrashort metal–metal bonds (<2.0 Å), suggesting multiply bonded metal atoms. Dichromium complex 2^red has the shortest metal–metal bond distance in the series, at 1.7407(6) Å, as well as one of the shortest dichromium distances in the literature (Table 4).^6a,35 Among heterometallic complexes, the shortest metal–metal bonds are currently found in 3 and 3^red, followed by the (d–d)^10–12 FeCr complexes 4^ox, 4, and 4^{red 10b} and the (d–d)^{9, 10} FeV complexes V(ⁱPrNPPh₂ ) ₃FeI and V-(ⁱPrNPPh₂)₃FePMe₃.^9c

Figure 5.

Solid-state structures of 1, 2, 2^red, 3^red, and 4^ox obtained by X-ray crystallography at 123 K for 4^ox and at 173 K for the remaining compounds. Thermal ellipsoids are shown at 50% probability. Hydrogen atoms, counterions, and lattice solvent molecules have been omitted for clarity. Green, chromium; red, manganese; pink, iron; blue, nitrogen; orange, phosphorus. M—Cr bond distances are given in red, and average M—P and Cr—N bond distances are given in blue.

Table 3.

Geometrical Parameters, Including Bond Lengths (Å) and Angles (deg), for 2–4^a

	2	2red	3	3red	4	4ox
M—Cr (Å)	1.913(1)	1.7407(6)	1.8192(9)	1.8389(6)	1.944(1)	1.955(7)
rb	0.82	0.74	0.78	0.79	0.83	0.84
M—P (Å)	2.420(1)	2.3844(9) ± 0.004	2.3792(7)	2.3167(5)	2.265(2) ± 0.004	2.268(8) ± 0.014
Cr—Neq (Å)	1.997(3)	2.094(2) ± 0.014	2.010(3)	2.0472(15)	1.960(2) ± 0.019	1.889(8) ± 0.011
Cr—Nap (Å)	2.359(5)	2.499	2.370(3)	2.416(2)	2.284(3)	2.240(9)
M to P3 plane (Å)	−0.132	−0.203	−0.189	−0.174	−0.192	−0.270
Cr to N3 plane (Å)	+0.447	+0.654	+0.494	+0.558	+0.412	+0.329
Σ(P—M—P) (deg)	359.12	357.85	358.14	358.32	357.85	355.9
Σ(N—Cr—N) (deg)	345.45	332.09	342.51	338.49	347.1	351.1
M—Cr—Nap (deg)	180	179.85	180	180	177.5	178.1

^aComplexes 2^red, 4, and 4^ox crystallized with approximate threefold symmetry, so several parameters (e.g., M—P bond lengths) represent the averages of three (2^red) or six (4) distinct values. Estimated standard deviations (esd) are provided in parentheses, and standard deviations of averages are shown with ± after the average value.

^br = ratio of the M—Cr bond distance to the sum of the M and Cr single-bond metallic radii.^36a

Table 4.

Ultrashort Cr—Cr Bond Distances in Selected Cr₂ Systems

Cr2 complex	d(Cr—Cr) (Å)	r	ref(s)
Cr2(2,6-(2,6-iPr2C6H3)2C6H3)2	1.8351(4)	0.78	6a
Cr2(2,6-(2,6-iPr2C6H3)2-4-SiMe3(C6H2))2	1.8077(7)	0.77	35a
Cr2(N,N′-bis(2,6-diisopropylphenyl)-1,4-diazadiene)2	1.8028(9)	0.77	35e
K[Cr2L] (2red)	1.7407(6)	0.74	this work
Cr2(HC(N(2,4,6-(CH3)3C6H2)2)2	1.7404(8)	0.74	35f
K(crypt-222)[Cr2(HC(N(2,6-(CH3)2C6H3)2)3]	1.7397(9)	0.74	35g, 38
Cr2(Me2NC(N(2,6-iPr2C6H3)2)2	1.7293(12)	0.74	35c
Cr2((2,6-(CH3)2C5H8N)C(2,6-iPr2C6H3)2)2	1.7056(12)	0.73	35d
Cr2− a	1.705(10)b	0.73	39
Cr2a	1.68(1)b	0.72	40

^aGas phase.

^bBased on a Morse fit of the vibrational frequency or rotational analysis.

As an aside, all of the examples cited above use bridging ligand(s) to stabilize the bimetallic cores. A long-standing critique has been that the bridging ligands might ultimately be responsible for short metal–metal distances, in lieu of any true metal–metal bonding. It then follows that the diamagnetic (or low-spin) nature of the bimetallic species arises from antiferromagnetic coupling of the two metal spins. We would argue that this critique is invalid here. The present ligand is highly flexible and supports a wide range of metal–metal distances, not all of which are short. For example, the isostructural CoCrL and NiCrL complexes have longer M—Cr bond distances of 2.14 and 2.41 Å, respectively. Indeed, the M—Cr bond lengths change by 0.7 Å from [Cr₂L]⁻ (2^red) to NiCrL, which is substantially larger than any intrinsic differences in the metals’ single-bond metallic radii (Cr, 1.172 Å; Ni, 1.149 Å) or covalent radii (Cr, 1.39 Å; Ni, 1.24 Å).³⁶ Also, despite a constant ligand and supporting Cr metal, the Cr—N_apical bond length changes by 0.4 Å (2.50 Å in 2^red, 2.09 Å in NiCrL). Finally, an absence of metal–metal interaction would require the two metal-based spins to couple antiferromagnetically, either through the ligand or through space. The former cannot account for singlet–triplet splitting of more than 10–100 cm⁻¹ because the ligand backbone is saturated, where fully diamagnetic behavior at room temperature requires excited spin states to be higher than 1000 cm⁻¹ in energy. Spin–spin interactions through space are even weaker (ca. 1 cm⁻¹), even at a short distance of 1.5 Å.³⁷ Thus, the argument for through space spin–spin coupling is highly inconsistent with the fully diamagnetic behavior of 2^red, 3, and 4^ox in the VT-NMR studies described above.

A useful metric for comparing metal–metal bonding across different metals is the formal shortness ratio (r),⁴¹ which is defined as the ratio of the metal–metal bond distance to the sum of the single-bond metallic radii.^36a By accounting for the sizes of different metals, the r value allows for a more fair comparison between homo- and heterobimetallic bonds. As defined, values close to unity represent single bonds, and values significantly below unity indicate multiple bonds. The r values for all complexes here are well below unity (0.74–0.84). The isoelectronic species {Cr₂}¹⁰ 2^red and {MnCr}¹⁰ 3 have the lowest r values of 0.74 and 0.78, respectively. We propose these low r values are indicative of delta bonding, and theoretical studies support these molecules as being fomally quintuply bonded (σ + 2π + 2δ).^10a We have also shown that the δ-symmetry d orbitals at iron and chromium in {FeCr}¹¹ 4 do not interact because of their poor energy overlap, and hence, the formal bond order decreases to 3 (σ + 2π). Because 4^ox has an r value that is close to that of 4, 4^ox is also interpreted as triply bonded. Indeed, 4^ox is characterized by the largest r value in this series, 0.84, consistent with its lower bond order. According to the r values, {Cr₂}⁹ 2 and {MnCr}¹¹ 3^red are in the middle of this series, suggesting an intermediate bond order between 3 and 5. For (d–d)⁹ and (d–d)¹¹ systems, the expected dominant electronic configurations of (σ)²(π)⁴(δ)³ and (σ)²(π)⁴(δ)⁴(δ*)¹, respectively, would both predict a bond order of 4.5. However, the r value for 2 is only slightly lower than those for the Fe—Cr triply bonded complexes 4 and 4^ox. A possible explanation is that the two δ bonds are not fully formed in the case of 2, resulting in a bond order less than 4.5 (vide infra). The Cr—Cr bond distance of 1.913(1) Å in 2 is consistent with a wide range of dichromium complexes with formal quadruple bonds.⁴¹ Also, δ bonds are weak by nature, so their effects on bond lengths (and r values) are often unclear.⁴²

X-ray crystallography can sometimes be useful to reveal changes in metal oxidation states through corresponding changes in metal–ligand bond lengths. Structural comparison between various redox states might provide insight into the redox site(s), although these are preliminary assignments, as d electrons can easily delocalize across the two metals, and they should be validated with complementary spectroscopic and theoretical studies. The metal–metal bond contracts substantially between {Cr₂}⁹ 2 and {Cr₂}¹⁰ 2^red (Δ = −0.17 Å), which is about twice the change observed in the analogous redox pair [Cr₂(ArNC(H)NAr)₃]^0/− [Δ = −0.08 Å, Ar = 2,6-(CH₃)₂C₆H₃].³⁸ One possible explanation for the relatively long Cr—Cr interaction in 2 versus 2^red is the variable strength of the Cr—N_apical interaction, which lengthens appreciably upon reduction (Δ = 0.14 Å). The presence of axial donors is well-known to elongate Cr—Cr multiple bonds, and σ donors can account for changes up to 0.1 Å.^41,43 Reduction of 2 to 2^red also induces contraction of Cr—P bond distances and elongation of Cr—N_eq bond distances by 0.036 and 0.097 Å, respectively. The greater change in the Cr—N_eq bond distances might suggest a more localized reduction at the Cr residing in the amide-binding pocket.

Upon reduction of the formally quintuply bonded {MnCr}¹⁰ 3 to {MnCr}¹¹ 3^red, the metal–metal bond lengthens slightly from 1.8192(9) to 1.8389(6) Å, which is expected as the additional electron should populate an antibonding orbital. Upon reduction, the Mn—P bond distances decrease (Δ = −0.063 Å), whereas the Cr—N distances increase [Δ(Cr—N_eq) = 0.037 Å, Δ(Cr—N_ap) = 0.046 Å], which can be interpreted as stronger manganese–phosphine back-bonding and increased Cr—N_eq repulsion upon reduction of the MnCr core. In contrast, the oxidation of 4 did not produce any statistically significant changes in the Fe—Cr and Fe—P bond metrics, but alterations in the Cr—N_eq bond were statistically significant [Δ = 0.07(2) Å]. These structural changes possibly suggest oxidation at Cr, but we note that the esd values in 4^ox (up to 0.009 Å) are large enough to mask moderate changes.

Diamagnetic Anisotropy

In analogy with unsaturated organic molecules with π bonds, complexes with multiple metal–metal bonds can have large diamagnetic anisotropies, Δχ, that impact their NMR chemical shifts.⁴⁴ In axially symmetric molecules, the circulating electrons in the multiple bond can either shield (+) or deshield (−) nearby protons, depending on the proton’s position within the spatial zones demarcated by the double cone, as shown in Figure 6. Protons in the equatorial region, for example, methylene resonances, are expected to shift downfield if multiple bonds are present. Indeed, the methylene protons in all three (d–d)¹⁰ complexes (3, 2^red, and 4^ox) are significantly deshielded, appearing 2–3 ppm downfield relative to the methylene protons in the free ligand.⁴⁵ The diamagnetic anisotropy (χ_|| −χ_⊥ or Δχ) can be calculated using the equation¹⁵

Figure 6.

Spatial zones of shielded (+) and deshielded (−) chemical shifts that arise from the diamagnetic anisotropy of the multiply bonded {MCr}¹⁰ cores.

$$\mathrm{\Delta }\delta =\left(\frac{1}{3r^3}\right)\frac{({\chi }_{\Vert }-{\chi }_{\perp })[1-3{cos}^2(\theta )]}{4\pi }$$

where Δδ is the difference in ¹H NMR chemical shifts of the methylene protons in the multiply bonded bimetallic complex compared to that of a reference complex without any multiple metal–metal bonds. For the reference complex, we chose the isostructural Ni–Al bimetallic featuring a Ni → Al dative bond (Figures S14 and S15, SI).¹¹ The remaining variables were extracted from the corresponding solid-state structures: r is the distance and θ is the acute angle of the methylene protons relative to the center and axis of the metal–metal bond, respectively. By assimilating data from NMR and X-ray crystallographic studies, we implicitly assume that the solution and solid-state structures are similar. In addition, we discount an energetically low-lying triplet state as the cause of the dramatic NMR shifts. The VT-NMR profiles of 2^red, 3, and 4^ox are inconsistent with paramagnetic contributions (Figures S3, S6, and S9, SI). Moreover, in the dichromium species that have thermally accessible singlet–triplet gaps, the Cr—Cr bond distances are dramatically longer, ≥2.25 Å.⁴⁶

Whereas diamagnetic anisotropies are known for several homobimetallic species, such data are limited for heterobimetallic pairings (Table 5).^44c,d,47 Cotton and co-workers systematically studied a series of quadruply bonded complexes, M₂X₄(μ-PP)₂, where M₂ = Mo₂, MoW, and W₂.^47a,c,48 The average Δχ values were found to increase across the pairings in the order Mo₂ < MoW < W₂, where each substitution of a Mo center for W increased Δχ by approximately −640 × 10⁻³⁶ m³ molecule⁻¹ (13%). The Δχ values calculated for {Cr₂}¹⁰ 2^red, {MnCr}¹⁰ 3, and {FeCr}¹⁰ 4^ox in this work are −3500 × 10⁻³⁶, −3900 × 10⁻³⁶, and −5800 × 10⁻³⁶ m³ molecule⁻¹, respectively. The diamagnetic susceptibility should increase with the effective bond order, but polarization of the metal–metal bond can dominate. Substituting Mn for Cr results in an 11% gain in Δχ, whereas swapping Fe for Cr produces a dramatic 66% increase. This trend is well-known in organic molecules, whereby heteronuclear π bonds, such as C═O (+420) and N═O (+1300), exhibit larger diamagnetic anisotropies than their homonuclear analogues, in this case C═C (+150) and C≡C (−340), respectively.⁴⁹

Table 5.

Diamagnetic Anisotropies (Δχ) of Multiply Bonded Bimetallic Complexes

complexa	Δχ (×10−36 m3 molecule−1)	ref
2red	−3500	this work
3	−3900	this work
4ox	−5800	this work
Cr2(DFM)4	−5230	47b
Mo2(DFM)4	−5020	47bb
W2(DFM)4	−5480	47b
Re2(DFM)4	−4430	47bb
Ru2(DFM)4	−3780	47bb
Mo2X4(PP)2	−4450c	48
MoWCl4(PP)2	−5082c	47a
W2X4(PP)2	−5727c	47c

^aDFM = di-p-tolylformamidinate; PP = dppe, dppm, dmpm, dmpe.

^bAnd references therein.

^cAverage value.

Theoretical Calculations

Quantum chemical studies were conducted on the bimetallic models 2′, 2^red′, 3^red′, and 4^ox′, where the isopropyl groups were truncated to methyl groups. Computational studies of 3′ and 4′ were reported previously.¹⁰ Geometry optimizations were performed using density functional theory (DFT) for several possible spin states. For all of the complexes, the computed spin state with the lowest energy corresponded to the proposed ground state backed by experimental evidence (Tables S4–S7, SI). To address the strong correlation effects known for complexes with metal–metal bonds, we performed complete-active-space self-consistent field (CASSCF) followed by second–order perturbation theory (CASPT2) calculations. These methods give a more accurate description of bimetallic systems that are characterized by a heavy multireference character, large dynamic correlation energy, and/or significant relativistic effects.^5a,50 For many of the systems in this work, a single electronic configuration represents the majority (55–64%) of the ground-state wave function. The exception is 2′, for which the contribution of the main configuration is slightly lower at 42% (Table 6).

Table 6.

Main Electronic Configurations of Metal–Chromium Complexes and Formal versus Effective Bond Orders (FBOs vs EBOs)

MCr complex	main electronic configuration	%a	rb	FBO	EBO
(d–d)9
CrCr (2′)	σ2π4δ2(Cr dxy)1	42	0.82	4	2.71
(d–d)10
CrCr (2red′)	σ2π4δ4	60	0.74	5	3.99
MnCr (3′)	σ2π4δ4	55	0.78	5	3.85
FeCr (4ox′)	σ2π4(Fe dxy, dx2–y2)4	55	0.84	3	2.21
(d–d)11
MnCr (3red′)	σ2π4(Mn dxy, dx2–y2)4(Cr dxy)1	64	0.79	3	2.39
FeCr (4′)	σ2π4(Fe dxy, dx2–y2)4(Cr dxy)1	58	0.83	3	2.15
(d–d)12
FeCr (4red′)	σ2π4(Fe dxy, dx2–y2)4(Cr dxy)2	60	0.84	3	2.35

^aPercentage of the ground-state wave function that is described by the main configuration.

^bFormal shortness ratio (experimentally determined; see text for definition).

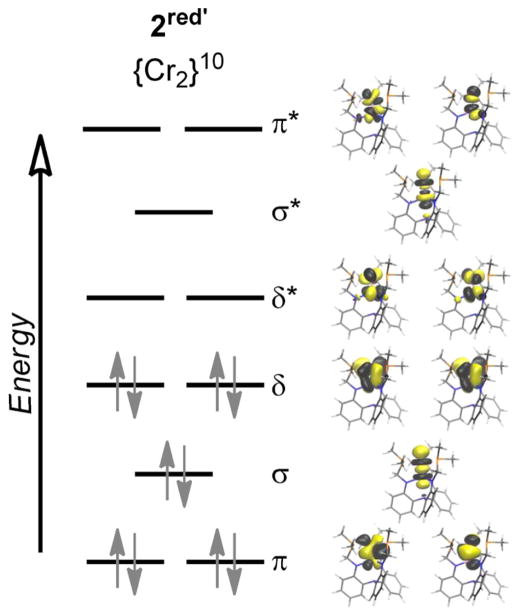
Because of the weak ligand field associated with trigonal coordination geometries, all five d orbitals in these bimetallic species have the potential to participate in metal–metal bonding. The d orbitals can combine maximally to form quintuple bonds comprising one σ (d_z²), two π (d_xz, d_yz), and two δ (d_xy, d_x²–y²) bonds. Indeed, all five of these interactions are observed in 2^red′ and 3′, where the (d–d)¹⁰ electron count fills all of the metal–metal bonding molecular orbitals (MOs), as shown in Figure 7 for 2^red′. Such a high bond order is consistent with the exceedingly low r values of 0.74 and 0.78 determined from experiment for 2^red and 3, respectively.

Figure 7.

Qualitative MO diagram of 2^red′ showing the natural bonding orbitals of σ (d_z²), π (d_xz, d_yz), and δ (d_xy, d_x²–y²) symmetry for the main configuration (60%) from RASSCF calculations.

However, this simple MO picture does not hold for the other members (Figures S23–S29, SI). In complexes where the two metal partners are increasingly different, e.g., Fe and Cr in 4^ox′, 4′, and 4^red′, the metal–metal bonds are increasingly polarized, resulting in localization of the δ-symmetric d orbitals so that only delocalized σ and π bonds remain (Table 6). Indeed, an r value of 0.84 for (d–d)¹⁰ 4^ox is more congruous with threefold rather than fivefold bonding. Fivefold interactions also break down when the electron count deviates from (d–d)¹⁰. In (d–d)⁹ 2′ and (d–d)¹¹ 3^red′ and 4′, one would predict FBOs of 4.5 based on the simple MO pictures. However, as one or both pairs of δ-symmetric d orbitals become increasingly localized (Table 7), the formal bond orders drop to 4, 3, and 3 for 2′, 3^red′, and 4′, respectively.

Table 7.

Percentages of Metal Character (%Cr, %M) in Metal–Chromium Bonding Orbitals of σ, π, and δ Symmetries from CASSCF Calculations

	σ		π		δa
MCr complex	%Cr	%M	%Cr	%M	%Cr	%M
(d–d)9
CrCr (2′)	46	54	52	48	50	50
			52	48	0	100
(d–d)10
CrCr (2red′)	45	55	48	52	39	61
			48	52	39	61
MnCr (3′)	40	60	38	62	33	67
			38	62	33	67
FeCr (4ox′)	33	67	45	54	13	87
			44	56	12	88
(d–d)11
MnCr (3red′)	44	56	47	53	14	86
			53	47	3	97
FeCr (4′)	31	69	45	55	8	92
			49	51	18	82
(d–d)12
FeCr (4red′)	36	64	27	73	0	100
			27	73	0	100

^aItalicized values are percentages below 75%/25% and represent δ-bonding MOs that are more aptly described as localized, e.g., d_xy.

Whereas the formal bond order (FBO) is based solely on a single main configuration, the effective bond order (EBO) takes into account the natural populations of bonding/antibonding orbitals summed over all contributing configurations (Table 6). The quintuply bonded species 2^red′ and 3′ have EBO values that are closer to quadruple bonds. This is not unusual, as other quintuply bonded dichromium complexes in the literature also have EBOs close to 4.^{6a,35c,d,f,g,38,50a} The triply bonded species 3^red′, 4^ox′, 4′, and 4^red′ have slightly lowered EBOs, ranging from 2.21 to 2.39. The formally quadruply bonded complex 2′ shows the steepest reduction of bond order, with an EBO of 2.71, which is a direct result of its more multiconfigurational nature and, hence, partial population of the higher-lying antibonding orbitals. Because the r value of 0.82 for 2 is on par with the values for the other triply bonded complexes, a lower bond order is reasonable.

An analysis that parses the natural population of the activespace orbitals into weighted contributions from each metal partner can provide the d-electron count at each metal center, which can be useful in contemplating oxidation states (Tables S9–S14, SI). In a first approximation of the neutral bimetallics, the asymmetric charge distribution in the ligand would favor a trivalent metal in the triamido pocket, for example, M_N(III), while stabilizing a zerovalent metal in the triphosphine site, for example, M_P(0). However, because of covalent metal–metal bonding, the electronic charges can be further distributed between the two metal centers. For neutral dichromium 2′ and MnCr 3′, the calculated oxidation states are consistent with M_P(I)M_N(II), specifically, Cr_P(1.0)Cr_N(2.0) and Mn(0.9)-Cr(2.1). Their one-electron reduced counterparts, 2^red′ and 3^red′, have core oxidation states of Cr_P(0.5)Cr_N(1.5) and Mn(0.3)Cr(1.7), respectively, where the additional electron is delocalized on the two metal partners nearly equally. The neutral FeCr complex 4′, which has core oxidation states of Fe(0.6)Cr(2.4), is halfway between the two extremes of M_P(0)M_N(III) and M_P(I)M_N(II). Its redox analogues 4^ox′, Fe(1.2)Cr(2.8), and 4^red′, Fe(0)Cr(2.0), are interpreted as containing Fe(I) and Fe(0), respectively. Thus, the computations predict that reduction of the (FeCr)ⁿ core is equally shared by the two metals, whereas oxidation is primarily localized at the iron site.

With the calculated structures in hand, we were also able to gauge the predicted structural perturbations upon change of redox state (Table S18, SI). Upon comparison of the neutral bimetallics against their charged analogues, it became clear that the predicted bond changes are all consistent with increased Cr—N repulsion (elongation) and increased M—P π-back-bonding (contraction) upon reduction. Notably, the Cr—N_eq and Cr—N_ap bonds are extremely sensitive, elongating by 0.05–0.07 and 0.03–0.09 Å, respectively, per additional electron. In contrast, the M—P bonds were fairly insensitive, decreasing by ≤0.02 Å per additional electron. For example, the differences between 4′ and 4^ox′, which were predicted to be primarily Fe-based, include a 0.05-Å change in the Cr—N_eq bond length, but as little as a 0.007-Å perturbation in the Fe—P bond.

Mössbauer Spectroscopy

To elucidate the redox changes at the iron site, 4^ox was further investigated by ⁵⁷Fe Mössbauer spectroscopy (Figure 8). The Mössbauer doublet is characterized by an isomer shift of 0.18 mm/s and a quadrupole splitting (ΔE_Q) of +5.85 mm/s. Previously, 4 and two variants of 4^red [with K(crypt-222) and K(18-c-6) counterions] were analyzed by Mössbauer spectroscopy. Akin to 4 and 4^red, 4^ox has an excessively large ΔE_Q value (>5.0 mm/s), which was attributed to large charge anisotropy in the iron valence shell that arises from the strong covalent bonds within the [FeCr]³⁺ core. Whereas 4 and 4^red showed essentially identical isomer shifts of 0.25 and 0.26–0.29 mm/s, respectively,^10b 4^ox has a notably lower isomer shift by approximately 0.1 mm/s. Differences in isomer shifts are essentially determined by the degree of 4s-electron population at the Mössbauer atom, which arises from covalent-bond formation with σ-type ligand orbitals.⁵¹ Higher oxidation states, at least for Werner-type complexes in the mid-to-high-valent regime, cause shorter iron ligand bonds and, hence, lower isomer shifts.⁵² Hence, the oxidation state of the iron nucleus remains Fe(0) in 4 and 4^red, but increases to Fe(I) in 4^ox.

Figure 8.

(a) Zero-field ⁵⁷Fe Mössbauer spectrum of 4^ox recorded at 80 K and (b) magnetic spectrum recorded at 4.2 K with a field of 7 T applied perpendicular to the γ-rays. The green line represents the best fit with δ = 0.18 mm s⁻¹, Δ E_Q = +5.85 mm s⁻¹, η = 0 (85% purity), and S = 0. There is also a high-spin Fe(II) impurity with δ = 0.83 mm s⁻¹ and Δ E_Q = 2.15 mm s⁻¹ (dotted blue line in top panel).

However, one has to note that, in the low-valent regime [e.g, Fe(0), Fe(I)], the negative correlation of the isomer shift with the oxidation state typically fades, and even the opposite scenario can be observed, namely, that lower oxidation states result in lower isomer shifts.^53,54,9c This has been explained by the onset of Fe(3d) → π-back-donation for low-valent iron,⁵⁵ which, by shortening the iron ligand bonds, leads to increased s-electron density at the Mössbauer nucleus, giving lower isomer shifts. In two representative redox series, [(SiP₃)FeN₂]ⁿ and [(SiP₃)FeCO]ⁿ,⁵³ the Fe—P bond lengths contract by ca. 0.1 Å per unit oxidation state decrease from Fe(II) to Fe(0), which lends support to increased π-back-bonding from low-valent iron. In contrast, the FeCr series does not fit with other low-valent iron complexes. The average Fe—P bond distances in 4^ox, 4, and 4^red are all similar at 2.268(8), 2.265(2), and 2.2444(8) Å, respectively, and no Fe—P back-bonding is observed. The isomer shifts of 4 and 4^ox behave as expected (for no Fe—L back-donation) and are consistent with the proposed oxidation states of Fe(0) and Fe(I), respectively.

Vis–NIR and Resonance Raman (rR) Spectroscopies

The electronic absorption spectra of the bimetallic complexes, as shown in Figure 9 and summarized in Table 8, were recorded in THF at room temperature. Except for a common UV peak at ~310 nm, which is ascribed to a ligand-based transition, the MCr bimetallics show sufficiently different vis–NIR transitions that justify substantial metal-based character. Generally, in the electronic spectra of multiply bonded bimetallic complexes, the most interesting feature is the δ → δ*-type transition.^47b,56 A seminal study of quadruply bonded M₂ ⁴⁺ cores in tetragonal M₂X₄P₄ complexes revealed dramatic red shifts in the δ² → δδ* energies upon metal substitution of W for Mo: Mo₂ ⁴⁺ (average 608 nm, 16460 cm⁻¹) > MoW⁴⁺ (658 nm, 15200 cm⁻¹) > W₂⁴⁺ (682 nm, 14660 cm⁻¹).^47c The first heavy-metal substitution, namely, Mo₂⁴⁺ to MoW⁴⁺, perturbs the δ² → δδ* excitation significantly more than the second substitution, namely, MoW⁴⁺ to W₂⁴⁺. Similar effects of metal substitution were also observed in a trio of homobimetallic M₂(mhp)₄ compounds (M₂ = Cr₂, Mo₂, W₂; mhp = deprotonated 6-methyl-2-hydroxypyridine), where the δ² → δδ* energies decrease down the group (from 22500 cm⁻¹ for M₂ = Cr₂ to 18700 cm⁻¹ for M₂ = W₂).^56a To our knowledge, electronic absorption data are limited for trigonal M₂ⁿ⁺ systems and especially so for quintuply bonded species.^{6a,35a,e,f,57} Thus, we were keen to determine the δ⁴ → δ³δ* transition energy in the isoelectronic quintuply bonded complexes 2^red and 3, which would allow a quantitative comparison between homo- and heterobimetallic quintuple bonds.

Figure 9.

Vis–NIR plots for (a) 2 and 2^red; (b) 3 and 3^red; and (c) 4^ox, 4, and 4^red in THF at room temperature. Artifacts from solvent subtraction or light-source changes appear at ~1750 nm.

Table 8.

Visible–NIR Electronic Absorbance Data for 2, 2^red, 3, 3^red, 4, 4^red, and 4^ox

complex	λmax (nm)	ε (M−1 cm−1)
2	495	2330
	600	1480
	880	930
	1460	140
2red	675 (14815)a	1880
3	400	4400
	550	1850
	1025 (9756)a	2160
3red	745	1230
	1350	760
4	448	3640
	645	1440
	1344	220
4red	680	1200
	1110	7400
4ox	463	4860
	730	3890
	1495	490

^aIn wavenumbers (cm⁻¹).

The lowest-energy band observed for 2^red has a λ_max value of 675 nm, or 14815 cm⁻¹. This band is assigned as the δ⁴ → δ³δ* excitation, and a resonance Raman (rR) study of 2^red corroborates the assignment (vide infra). For 3, the lowest-energy band is significantly shifted to lower energy by ~5000 cm⁻¹ to 1025 nm (9756 cm⁻¹). The dramatic decrease in the δ⁴ → δ³δ* transition energy upon formal substitution of Cr(I) with Mn(I) is unprecedented and might be a consequence of a smaller δ/δ* splitting and/or larger exchange stabilization of the excited state in the case of heterobimetallic 3 versus homobimetallic 2^red.

To comprehend the electronic absorption spectra of the (d–d)¹⁰ species, state-averaged CASSCF/PT2 and CASSI calculations were performed on the main configuration of 2^red′, 3′, and 4^ox′ (Tables S15–S17, SI). Because these calculations are expensive, only the first six excitations were computed. Gratifyingly, δ⁴ → δ³δ* transitions were predicted for both 2^red′ and 3′, and the transition energy for 3′ (673 nm) was correctly calculated to be lower than that for 2^red′ (545 nm). Although the absolute energies do not correspond well with the experimental values, the computed energy difference of 3500 cm⁻¹ is in good agreement. For 4^ox′, δ → δ*-type transitions were notably absent, and the two low-lying transitions at 1006 and 1021 nm, which might correspond to the experimental band at 1495 nm, were d_Fe ⁴ → d_Fe ³π* transitions. These findings validate the quintuple bonding in 2^red and 3, as well as the lower bond order in 4^ox.

Ground-state metal–metal vibrational frequencies are known for a handful of dichromium species,^56a,58 but to our knowledge, such data are lacking for any quintuply bonded complexes. To obtain MCr vibrational frequencies of quintuply bonded species, 2^red and 3 were probed by resonance Raman (rR) spectroscopy. Excitation into the δ⁴ → δ³δ* band should selectively enhance the ν_MCr vibration. Indeed, irradiating a frozen sample of 2^red at 647.1 nm afforded a series of low-frequency bands between 350 and 550 cm⁻¹ (Figure 10), specifically at 363, 413, 434, and 495 cm⁻¹. The resonance enhancement of these modes was confirmed by the resultant depletion in their intensity when using a different wavelength (λ_ex = 514.5 nm) that is off-resonance with the δ⁴ → δ³δ* transition (Figure S18, SI).

The observation of multiple vibrations by rR spectroscopy can result from coupling of the ν_MM vibration with various ligand normal modes.^58b,59 Thus, we turned to DFT to elucidate the origin of the observed peaks. The DFT-calculated Raman spectrum of 2^red′ revealed four intense vibrations in the low-frequency region, whose spectral pattern and relative intensities are in good agreement with experiment. The calculated frequencies were 8–20% higher than the experimental ones, which is reasonable at the DFT level of theory.⁶⁰ To increase the accuracy of computed vibrational frequencies, a scale factor is commonly employed (see Computational Methods).²³ Hence, a scale factor of 0.88 was applied, giving the predicted Raman spectrum shown in Figure 10. The two most intense DFT-calculated vibrations at 416 and 443 cm⁻¹ are the asymmetric Cr—Cr—N_ap stretch and a relatively pure Cr—Cr vibration, respectively (Figures S20 and S21, SI). Thus, we assign the dichromium stretching frequency ν_CrCr at 434 cm⁻¹ (corresponding to the calculated ν_CrCr value of 443 cm⁻¹). Of note, ν_CrCr values for quadruply bonded dichromium complexes are greater at 556 and 570 cm⁻¹,^58a,c despite having longer Cr—Cr bond distances (1.89, 2.11 Å vs 1.74 Å in 2^red). On the other hand, the naked dichromium molecule, which has a formal sextuple bond, also exhibits a relatively low ν_CrCr value of 481 cm^−1.53 The lack of correspondence between bond order and ν_CrCr value might be due in part to the distorted potential energy surface of Cr₂, which has a minimum at 1.68 Å as well as a flat, shelf-like region at 2.5 Å.^39,61

Finally, in contrast to 2^red, the isoelectronic manganese–chromium species 3 did not exhibit any enhanced nonsolvent features, precluding any determination of ν_MnCr (Figure S22, SI). However, the absence of ν_MnCr band(s) is reasonable considering that the δ⁴ → δ³δ* transition in 3 occurs at a longer wavelength that is currently beyond the range of our visible laser setup.

CONCLUSIONS

To better understand the nature of δ bonding, complexes with interactions between chromium and another mid-first-row transition metal (Cr, Mn, and Fe) were investigated. Specifically, bimetallics with (d–d)⁹ to (d–d)¹¹ configurations were targeted to maximize the multiplicity of their metal–metal bond. The quintuply bonded complexes, [Cr₂L]⁻ (2^red) and MnCrL (3), have ultrashort M—Cr bonds, at 1.74 (r = 0.74) and 1.82 Å (r = 0.78), respectively. Complexes 2, 4, 4^ox, and 4^red have r values of 0.82–0.84, which are in the range of triple to quadruple bonds. A (d–d)¹⁰ configuration does not necessitate the formation of delta bond(s), as the FeCr complex 4^ox lacks any. Also, deviations from the (d–d)¹⁰ count can destroy δ bonds completely. The prototype MO picture of fivefold bonding would predict a formal bond order of 4.5 for (d–d)⁹, but the experimental r value is more consistent with a lower bond order that is closer to 3. Finally, in contrast to the sensitive nature of δ bonds, σ and π bonds are quite robust in this series.

The spectroscopic characterization of this series also yielded some interesting findings. For instance, the diamagnetic anisotropy of metal–metal multiple bonds appears to be primarily affected by the polarity of the M—Cr bond, rather than its multiplicity. The δ⁴ → δ³δ* transition energy was redshifted by over 5000 cm⁻¹ by a simple metal-atom substitution, from [Cr₂L]⁻ to MnCrL. The ν_CrCr value for quintuply bonded [Cr₂L]⁻ was unexpectedly lower than those of the quadruply bonded analogues from the literature. In the [FeCrL]^+,0,− redox series, the Mössbauer isomer shifts are consistent with the process

$${[\text{Fe}(\mathrm{I})\text{Cr}(\text{III})\mathrm{L}]}^{+}\stackrel{+{\mathrm{e}}^{-}}{\to }\text{Fe}(0)\text{Cr}(\text{III})\mathrm{L}\stackrel{+{\mathrm{e}}^{-}}{\to }{[\text{Fe}(0)\text{Cr}(\text{II})\mathrm{L}]}^{-}$$

The redox change from [Fe(I)CrL]⁺ to Fe(0)CrL, however, manifests in significant bond changes not in the first coordination sphere of iron, but rather in that of chromium. Thus, assigning oxidation states based on changes in metal–ligand bond lengths, as revealed by X-ray crystallography, might be misleading in bimetallic systems with covalent metal–metal bonds and/or mixed amide–phosphine ligands.