Non-contact cohesive swimming of bacteria in two-dimensional liquid films

Abstract

Bacterial swimming in confined two-dimensional environments is ubiquitous in nature and in clinical settings. Characterizing individual interactions between swimming bacteria in 2D confinement will help to understand diverse microbial processes, such as bacterial swarming and biofilm formation. Here we report a novel form of biophysical interaction between flagellated bacteria in 2D confinement: When two nearby cells align their moving directions, they tend to engage in cohesive swimming without direct cell body contact, as a result of hydrodynamic interaction but not flagellar intertwining. We further found that cells in cohesive swimming move with higher directional persistence, which can increase the effective diffusivity of cells by ~3 times as predicted by computational modeling. As a conserved behavior for peritrichously flagellated bacteria, cohesive swimming in 2D confinement may be key to collective motion and self-organization in bacterial swarms; it may also promote bacterial dispersal in unsaturated soils and in interstitial space during infections.

Motile behavior of bacteria is of great ecological and medical significance because it is essential for bacterial dispersal, chemotaxis, and pathogenesis. A large number of bacterial species use flagellar motility to propel their motion [1]. Flagellar motility has been studied extensively in various environments, both in bulk fluids [1–6] and under quasi-2D confinement [7–15]. By contrast, flagellar motility in ‘strictly’ 2D confinement with a thickness close to cell width (~2 microns or smaller) is less well understood. Individual swimming behavior of bacteria in 2D confinement has received significant recent attention from theorists [14,16,17] but has only been qualitatively described in experiments [18–20].

Characterizing bacterial swimming behavior and interactions in 2D confinement will help to understand diverse microbial processes in natural environment and in clinical settings, such as bacterial swarming [21–26], biofilm formation [27,28], bacterial dispersal in unsaturated soils [29,30], and pathogen spreading in the interstitial fluid of animal tissues [31–34]. Moreover, the accurate characterization of individual bacterial interactions in 2D confinement is essential to the understanding of how single cell behavior lead to collective dynamics in bacterial swarms, a question of direct relevance to active matter self-organization [21,35–38] and low-Reynolds number hydrodynamics [2,39]. Steric repulsion and flagellar intertwining were believed to dominate individual interactions between swimming bacteria in proximity [19,40], and steric repulsion was suggested to be a key mechanism responsible for self-organization in quasi-2D bacterial suspensions [9,11,12,20,41]. However, it is unclear whether these conclusions are applicable to bacteria swimming in 2D confinement.

Here we report a novel form of interaction between flagellated bacteria in 2D confinement, i.e. cohesive swimming between nearby cells that involves neither steric repulsion nor flagellar intertwining. To observe this phenomenon, we developed a simple yet highly robust and reproducible method to confine low-density bacterial populations in liquid films ~2 microns in thickness (see Supplemental Methods[42]). We first allowed B. subtilis (DS1919 with wildtype flagellar motility; hereafter referred to as “wildtype” or “WT”) to swarm on an agar surface to an appropriate colony size, and then cells at swarm edge were diluted and transferred to fresh agar surface. The cells were then covered with a clean glass coverslip and observed by microscopy with careful control of humidity. We found that this method robustly produced a 2D dilute cell suspension confined between two no-slip walls, i.e. the agar surface and the glass coverslip, and the 2D suspension formed this way was maintained for ~10 min before the fluid is absorbed by agar. Cells (0.8 μm in diameter, 7.3±1.8 μm in length) moved vigorously at a speed of 52±7 μm/s (mean±s.d.) with suppressed tumbling [18] (Supplemental Text and Supplementary Fig. 1[42]). They moved in curved trajectories with a bimodal curvature distribution (Supplementary Fig. 2a[42]), suggesting that they experienced equal hydrodynamic interactions with the two solid walls [14,43–45]. Importantly, cells remained in the same focal plane under the microscope, supporting the conclusion that their motion was restricted to 2D. We managed to control bacterial density at about 9.5×10⁻⁴ cells/μm², corresponding to an average cell-cell distance of ~5 cell lengths and allowing occasional collision between cells.

Remarkably, when two cells aligned their moving directions as they approached or collided with each other, they tended to swim side-by-side cohesively without cell body contact for an extended distance up to ~200 μm (Fig. 1a; Supplementary Movie 1[42]). The duration of non-contact cohesive swimming (i.e. the trapping time) was 1.10±0.55 s (mean±SD, n=94; Fig. 2a). During such cohesive swimming, the two cells typically remained separated by a distance of 0.7±0.4 μm, with the mean distance comparable to cell width (0.8 μm) (Fig. 1b). This non-contact cohesive swimming is in stark contrast to the pair-wise swimming behavior found in earlier reports that involved direct cell body contact throughout the swimming process [19]. Multicellular clusters consisting of three or more cells also displayed non-contact cohesive swimming (Supplementary Movie 2[42]). Similar non-contact cohesive swimming behavior was found in Escherichia coli (Supplementary Movie 3[42]) and in Proteus mirabilis (Supplementary Movie 4[42]), both are gram-negative bacteria with peritrichous flagella, demonstrating that the behavior is conserved among peritrichously flagellated bacteria. Interestingly, P. mirabilis cells have a broad distribution of cell length, and those longer cells often recruit a number of shorter ones to perform non-contact cohesive swimming (Supplementary Movie 4[42]).

Figure 1.

(a) Trajectories of two cells undergoing non-contact cohesive swimming. Two wildtype B. subtilis (DS1919) cells approach each other and as soon as one of them tumbled (at ~0.5 s), they swam cohesively for ~3.7 s (from 0.5 s to 4.2 s) without direct cell body contact. The image sequence was selected from Supplementary Movie 1[42]. Dashed lines represent trajectories of the two cells. Scale bar, 20 μm. (b) Nearest distance between the two cells in panel a plotted against time. The shaded area indicates the duration of cohesive swimming. The nearest distance at any instant was defined as the minimal distance between any two points belonging to different cells; so the nearest distance is zero if two cells are in direct body contact.

Figure 2.

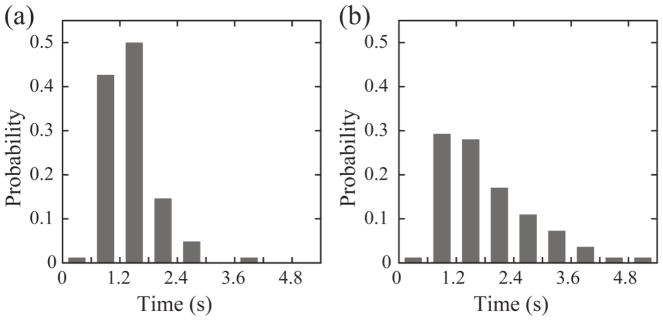
Probability distribution of trapping time for cohesively swimming cell pairs of B. subtilis. (a) wild type; (b) smooth-swimming mutant; bin size is 0.6 s . The trapping time is defined as the time duration traveled by two cohesively swimming cells before they separate spontaneously. Two cells are considered as engaging in cohesive swimming if the distance between their centers is less than their average length and if the angle between their velocity directions is less than 10°. The mean trapping time of wild-type and smooth-swimming B. subtilis is 1.10±0.55 s (mean±s.d., n=94) and 1.55±0.95 s (mean±SD, n=82), respectively.

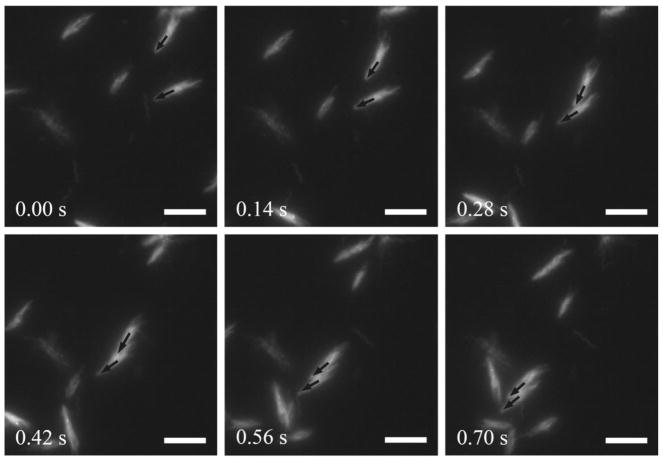
Next we sought to understand the mechanism of the observed non-contact cohesive swimming behavior. Apparently steric repulsion is not involved here. Flagellar intertwining can lead to two cells swimming cohesively through bulk fluids, and electron microscopy studies suggested that it may account for the formation of multicellular rafts or clusters during bacterial swarming [46,47]. To examine whether flagellar filaments of adjacent cells intertwined during the non-contact cohesive swimming, we intended to visualize the motion of flagellar filaments of cohesive cell pairs, which requires high-speed and high-resolution fluorescence microscopy [48]. Wildtype B. subtilis cells in 2D confinement undergo run-and-tumble motion with a mean run time of ~3.0 s (Supplementary Fig. 1[42]). Although the mean tumbling interval is longer than the mean duration of non-contact cohesive swimming, we found it difficult to capture events of cohesive swimming within the small field of view under high-resolution microscopy (~70 μm × 70 μm) as cell pairs occasionally separated due to tumbling. To overcome this difficulty we constructed a smooth-swimming B. subtilis mutant (DK2178) whose flagellar filaments are genetically modified and can be labeled with thiol-reactive fluorescent dyes (e.g. Alexa Flour 546 C₅-maleimide; Life Technologies) [49] (Supplementary Methods[42]). This smooth-swimming mutant swarms in a similar way as wild type [50] and displays non-contact cohesive swimming in 2D confinement as well, with a longer duration of cohesive swimming (1.55±0.95 s, mean±SD, n=82; see Fig. 2b and Supplementary Fig. 3[42]) that substantially increases the chance of capturing events of cohesive swimming. By fluorescence imaging, we found that flagellar intertwining (i.e. formation of flagellar co-bundle) did not occur between two cells undergoing non-contact cohesive swimming, and their flagella bundles appeared to rotate independently (Fig. 3 and Supplementary Movie 5[42]). The result showed that flagellar intertwining is not a mechanism for the non-contact cohesive swimming in 2D confinement. This is consistent with the report that swarm cells rarely engage in direct flagellar interaction [48].

Figure 3.

Flagellar dynamics of two cells undergoing non-contact cohesive swimming. Flagellar filaments of B. subtilis DK2178 cells were fluorescently labeled and appeared bright in the image sequence. The two black arrows indicate the orientations of two cells that approached each other and traveled as a cohesive pair. Scale bar, 10 μm. See Supplementary Movie 5[42].

Hydrodynamic interactions dominate over noise for two swimming bacteria within a distance of one cell length [40]. We then sought to examine the contribution of hydrodynamic interactions to the non-contact cohesive swimming. A pusher-type flagellated swimmer such as B. subtilis and E. coli can be modeled as a force dipole which pushes fluid away from the body along the long axis and draws fluid toward the sides [2]. In 2D confinement this (screened) dipolar flow field results in short-range hydrodynamic attraction between two approaching cells, and the hydrodynamic attraction is counteracted by the orientational change of cell bodies due to effective rotational diffusion. The two cells would undergo cohesive swimming for a finite duration until separation when the angle between them reaches a critical value 2θ_c, at which the effects of hydrodynamic attraction and of effective rotational diffusion are just balanced by each other. This process is analogous to bacteria swimming near solid walls, in which case cells arrive at the wall with some angle, reorient to swim parallel to it for a while and eventually leave due to rotational diffusion. Indeed, the process of bacteria-wall interaction can be modeled as a swimmer interacting with its “mirror image” [40,44]. We used a similar approach as Drescher et al. and Spagnolie et al. took [40,44] for the study of bacteria-wall interactions to derive the time taken by two cohesively swimming cells in 2D confinement to separate from each other (i.e. the trapping time) in the presence of hydrodynamic interaction (Supplemental Text[42]):

$$t\approx (\frac{{\theta }_c^2}{D_r^{\mathit{eff}}})exp[\frac{U({\theta }_c)}{D_r^{\mathit{eff}}}]$$ [1]

In Eq. [1], $D_r^{\mathit{eff}}=0.23\pm 0.02{\text{rad}}^2/\mathrm{s}$ was obtained by fitting the mean square deviation of cell orientation over time to $\langle \mathrm{\Delta }{\theta }^2\rangle =2D_r^{\mathit{eff}}t$, and U(θ_c) is the value of the following function taken at θ = θ_c:

$$U(\theta )\approx \frac{3F_{p}L{\theta }^2}{128\pi \eta H^3}$$ [2]

In Eq. [2] F_p is the propulsive force generated by rotating flagella, L is approximately cell length (~7.3 μm), η is water viscosity, and 2H is the distance between two the centers of the two cells. The derivation of Eqs. [1–2] is provided in Supplemental Text [42]. We obtained the propulsive force of rotating flagella as F_p=0.26±0.05 pN by fitting cell alignment process during cell-cell collisions (Supplementary Fig. 4 and Supplementary Text[42]), which agrees with the values measured by optical trap (~0.57 pN) [51] and predicted by resistive force theory (0.41±0.23 pN) [52]. Taking this propulsive force, we found θ_c ≈ 10° and obtained an estimate of trapping time of 6±2 s. Our estimate is consistent with the upper limit of the experimental result of the duration traveled by cohesively swimming cells (~ 4–5 s; Fig. 2). In experiment, the speed of cells often has a small variation, which causes cells to separate from each other more quickly than the ideal situation we modeled here. We conclude that the hydrodynamic interaction mediates non-contact cohesive swimming.

Next we sought to investigate the motion pattern of B. subtilis cells undergoing cohesive swimming. These cells swam at a mean speed (51±8 μm/s, mean±s.d.) similar to that of cells moving individually, but they displayed higher directional persistence as measured by the following auto-correlation function (Fig. 4a):

$$C(\mathrm{\Delta }t)=\langle cos\left({\theta }_i(t+\mathrm{\Delta }t)-{\theta }_i(t)\right)\rangle$$ [3]

Figure 4.

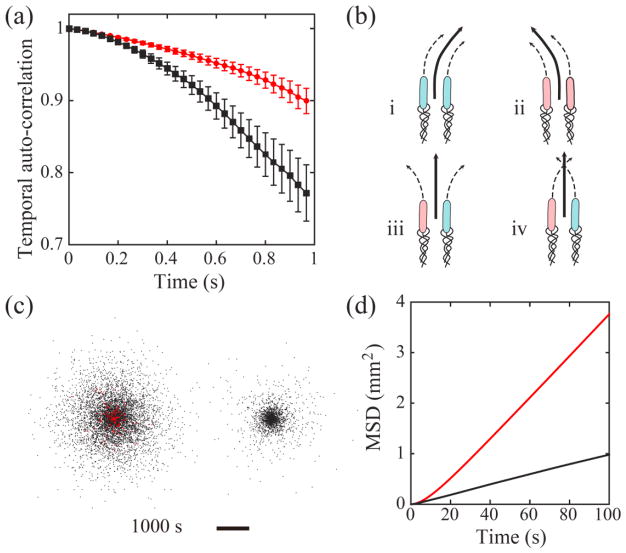
(a) Auto-correlation of cells’ velocity direction measured in experiments. Red circles correspond to cells moving as cohesive pairs (n=126 cells), and black circles correspond to individually moving cells (n=96 cells). Bars represent standard error of the mean. (b) Illustration of 4 possible scenarios of cell-wall interaction for a pair of cells undergoing cohesive swimming. Cells colored in pink (or blue) interact with the upper (or lower) wall and tend to curve to the left (or to the right). The two cells in scenarios (iii) and (iv) interact with opposite walls, so the pair has reduced directional bias. (c) Spatial distribution of modeled cells with (Left) and without (Right) cohesive swimming at the end of a typical simulation run. Red dots represent cells undergoing cohesive swimming and black dots represent cells moving individually. The duration of simulation corresponds to cell dispersal for 1000 s. Scale bar, 5 mm. See Supplementary Movie 6 [42]. (d) Mean square displacement (MSD) of cells in simulations. All modeled cells outside the “virtual inoculum” (see definition in main text) were included in the calculation. Red and black lines plot the average MSD (n= 5 independent simulation runs) for cells with and without cohesive swimming, respectively.

Here (θ_i(t +Δt) − θ_i(t)) is the angle between velocity directions of the i-th cell at time t and at time t+Δt; the angular brackets denote averaging over all tracked cells and over the time t. The higher directional persistence is also reflected in the narrower distribution of trajectory curvature for cells in cohesive swimming (Supplementary Fig. 2b[42]). Directional persistence of cells is governed by direction bias and rotational diffusion. Direction bias arises from the hydrodynamic interaction between cells and solid walls [14,43–45], which causes cells to swim in circles near boundaries, while rotational diffusion results from the combination of thermal Brownian rotation and the randomness of flagellar propulsion direction. Our measurement yielded direction bias B=0.38 rad/s and rotational diffusion constant D_r =0.035 rad²/s for cells in cohesive swimming; and B =0.72 rad/s and D_r =0.043 rad²/s for cells moving individually (Supplementary Text[42]). The direction bias of cells in cohesive swimming is only about half as much as that of cells moving individually, while the rotational diffusion constant is similar. So the higher directional persistence of cells in cohesive swimming is primarily due to reduced direction bias. To understand this result, we noticed that the flagellar bundles of two cells undergoing cohesive swimming in 2D confinement are expected to interact with the two solid walls independently and with equal probability. This is because flagellar bundles of the two cells rotate independently as suggested by flagellar visualization (Fig. 3), and because cells swimming individually interact with the two solid walls with equal probability as suggested by the nearly symmetric curvature distribution of cell trajectories (Supplementary Fig. 2a[42]). So there is 50% chance for the two cells in cohesive swimming to interact with opposite walls at any instant, in which case the cell pair will have reduced directional bias (Fig. 4b). Consequently the mean direction bias of cells in cohesive swimming is reduced, resulting in the higher directional persistence (Fig. 4b).

Based on the above results, we reasoned that bacteria may enhance population dispersal in 2D confinement by engaging in cohesive swimming. To verify this idea, we built a stochastic computational model to simulate the dispersal dynamics of wildtype cells in 2D space (Supplemental Text [42]). When two modeled cells came close enough, they interacted with each other either in the form of cohesive swimming or simple alignment, depending on their initial moving directions. Modeled cells were initially deposited at random positions within a circular area of radius 100 μm at the cell density found in our experiments (9.5×10⁻⁴ cells/μm²); this circular area was referred to as the “virtual inoculum”. To mimic the dispersal of bacteria from a source with unlimited supply of new cells, which may be relevant to the dispersal of bacteria from biofilms or from established infection sites, we kept cell density at the virtual inoculum as constant throughout simulations. Using experimentally obtained model parameters for wildtype B. subtilis, we simulated population dispersal and obtained the mean square displacement (MSD) of cells outside the virtual inoculum as a function of time (Fig. 4c,d and Supplementary Movie 6[42]). For comparison, the dispersal dynamics of cells without the ability to perform cohesive swimming was also simulated. By fitting the MSD plots in Fig. 4d with the numerical solution of 2D diffusion equation with the same boundary conditions as used in the simulations [53], we found that the effective diffusion coefficient (D) for cells with cohesive swimming (D =10.3×10³ μm²/s) is ~4 times greater than that of cells without cohesive swimming (D = 2.4×10³ μm²/s). These results show that the higher directional persistence of cells conferred by cohesive swimming can indeed facilitate population dispersal.

To summarize, we discovered that peritrichously flagellated bacteria in 2D confinement could engage in cohesive swimming in the absence of direct cell-to-cell contact. The non-contact cohesive swimming is mediated by hydrodynamic interaction but does not involve flagellar intertwining between cells. Our result demonstrates that the way flagellated bacteria interact in 2D confinement is essentially different from that in bulk fluids or in quasi-2D liquid films, and it provides new insight for understanding how single cell behavior lead to collective dynamics in 2D bacterial colonies, such as in bacterial swarms. Resembling the early stage of biofilm formation [22,27], bacterial swarms display rich dynamics of collective motion and self-organization [23,54]. These collective cellular behavior contribute to multidrug tolerance of bacterial swarms [55–57], facilitate long-range material transport [24,58], and may promote invasiveness and virulence of infectious pathogens [59]. Here our results reveal that cohesive swimming mediated by short-range hydrodynamic attraction may be another key factor that gives rise to collective motion and self-organization in bacterial swarms, in addition to steric repulsion via direct contact of rod-shaped cells [20,60].

The higher directional persistence conferred by non-contact cohesive swimming may promote bacterial dispersal in unsaturated soils and in interstitial space during infections, as these processes often occur in confined 2D environments [29,32]. For example, P. mirabilis cells migrating in multicellular rafts (similar to those seen in our experiments; see Supplementary Movie 4[42]) during catheter-associated urinary tract infections [46,59] may spread faster over catheter surface with higher directional persistence as compared to cells moving individually. A similar example is well known in spermatozoa. Sperm of polyandrous species form cohesive groups due to hydrodynamics interaction between sperm cells [61,62]; these cohesive groups swim with higher linearity than individuals, allowing them to travel faster through the female reproductive tract [63]. Taken together, our results reveal non-contact cohesive swimming as a unique form of individual interaction between flagellated bacteria that may promote bacterial collective motion, self-organization, and dispersal in 2D environments.