Local initiation conditions for water autoionization

Significance

The dissociation of water is arguably the most fundamental chemical reaction occurring in the aqueous phase. Despite that the splitting of a water molecule very seldom occurs, the reaction is of major importance in many areas of chemistry and biology. Direct experimental probing of the event is still impossible and also simulating the event via accurate computer simulations is challenging. Here, we achieved the latter via specialized rare-event algorithms estimating rates of dissociation in agreement with indirect experimental measurements. Even more interestingly, by a rigorous analysis of our results we identified anomalies in the water structure that act as initiators of the reaction, a finding that suggests paradigms for steering and catalyzing chemical reactions.

Abstract

The pH of liquid water is determined by the infrequent process in which water molecules split into short-lived hydroxide and hydronium ions. This reaction is difficult to probe experimentally and challenging to simulate. One of the open questions is whether the local water structure around a slightly stretched OH bond is actually initiating the eventual breakage of this bond or whether this event is driven by a global ordering that involves many water molecules far away from the reaction center. Here, we investigated the self-ionization of water at room temperature by rare-event ab initio molecular dynamics and obtained autoionization rates and activation energies in good agreement with experiments. Based on the analysis of thousands of molecular trajectories, we identified a couple of local order parameters and show that if a bond stretch occurs when all these parameters are around their ideal range, the chance for the first dissociation step (double-proton jump) increases from $10^{-7}$ to $0.4$. Understanding these initiation triggers might ultimately allow the steering of chemical reactions.

Among all possible chemical reactions that occur in water, the most fundamental is the water dissociation reaction (1), which is of major importance in many areas of chemistry and biology (2). Water plays an important role as a universal solvent for a wide variety of chemical processes and can act both as an acid and as a base. In aqueous solution, water will self-ionize and form hydroxide (OH⁻) and hydronium (H₃O⁺) ions which take on Eigen- or Zundel-like structures (2–6). Experiments show that the mean lifetime for an individual molecule before undergoing autoionization is about $11$ h (7, 8).

The autoionization event has not been directly probed by experiments and the dissociation rate is obtained using the water dissociation equilibrium constant and the rate for the much faster recombination reaction (7, 8). The experimental challenges make the autoionization event a pertinent target for computer simulations for which previous constrained ab initio simulations have given important information about the mechanism (9–11). However, the use of constraints leads to a loss of the spontaneous dynamics of the system and the selection of a reaction coordinate that accurately measures the progress of the reaction is challenging. These limitations can be avoided by path-sampling methods such as transition path sampling (TPS) (12) or replica exchange transition interface sampling (RETIS) (13, 14) which are specifically designed for sampling rare events without altering the dynamics while less influenced by the choice of the order parameter (15). Geissler et al. (16) applied TPS with ab initio molecular dynamics (MD) to simulate just $10$ uncorrelated autoionization events and demonstrated that the mechanism involves transfer of protons along a hydrogen bond wire with concomitant breaking of the wire. In their work, local solvent properties (e.g., ion coordination numbers and the presence of specific hydrogen bonds) were used to interpret the destabilization that leads to ionization. The absence of clear visually observable correlations led to the conclusion that the destabilization is caused by rare electric-field fluctuations which arise primarily from long-range electrostatic interactions and thus that local order parameters are not suitable to describe the event. Hassanali et al. (17) studied the reverse recombination reaction (i.e., neutralization of ionized water molecules) with standard ab initio MD and reported that this event takes place by a collective compression of the water wire bridging the ions, followed by a triple concerted proton jump. The OH⁻ ion which is neutralized remains in a hypercoordinated state and Hassanali et al. (17) hypothesized that it could serve, together with the compression of the wire, as a nucleation site for autoionization. This view opposes the statement of Geissler et al. (16) that the dissociation event is primarily triggered by nonlocal structural fluctuations. We note that concerted proton transfers and collective compression of water wires have also been observed for the recombination of a weak base in water (18).

Both of these studies give important information about the autoionization mechanism, although they do not unambiguously reveal the conditions that need to accompany a bond stretch fluctuation to initiate the reaction. In this work, we aim to tackle this ambiguity and quantitatively identify initiation conditions for water autoionization. Simulating the dissociation events may not be sufficient as the apparent initiation conditions observed in trajectories that lead to dissociation may also be present in trajectories with an initial bond stretch but still fail to dissociate. Also nonreactive or “almost reactive” trajectories contain important information as these allow for identification of effective initiation conditions that really matter: those that discriminate between reactive and nonreactive trajectories. To collect this information, we applied the RETIS method and harvested reactive and nonreactive trajectories which we analyzed using the recently developed predictive power method (19) and we built a predictive machine-learning model (20). This allowed us to quantitatively examine the importance of local order parameters and initiation conditions for water autoionization. Based on this analysis we identify important initiation triggers and calculate the full rate of dissociation.

Results and Discussion

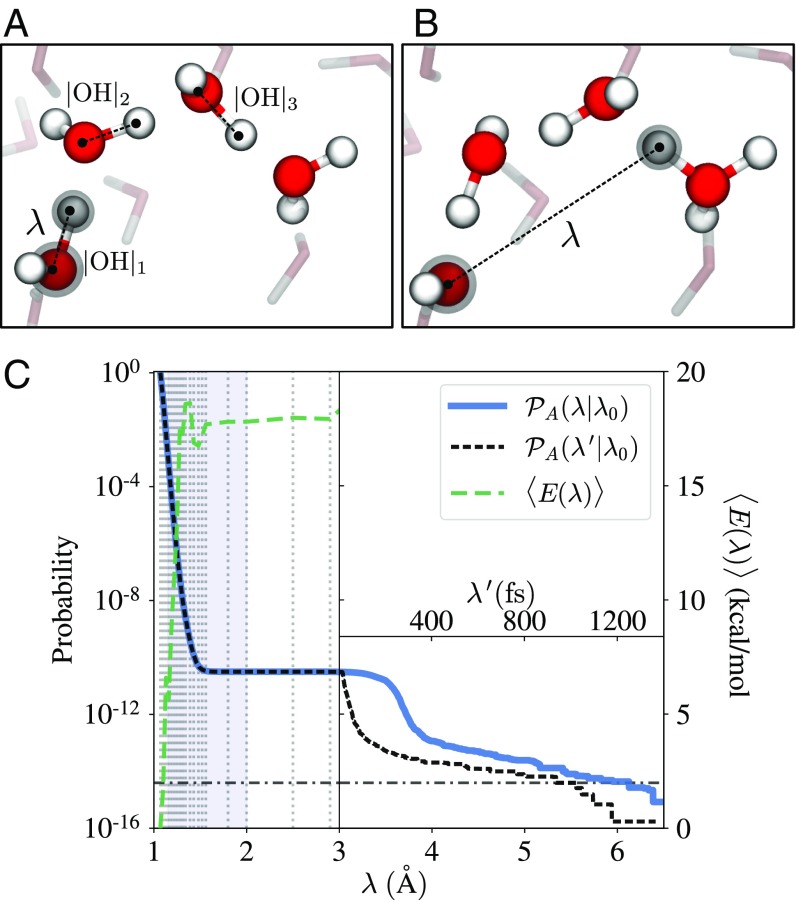
The autoionization event was investigated using ab initio RETIS simulations as described in Materials and Methods. For the RETIS simulations, we used a relatively simple geometric distance order parameter, $\lambda$, as illustrated in Fig. 1: When the system consists of only H₂O species, $\lambda$ is the largest covalent O–H bond distance, and when the system contains OH⁻ and H₃O⁺ species, $\lambda$ is taken as the shortest distance between the oxygen in OH⁻ and the hydrogen atoms in H₃O⁺. In the following, we refer to the oxygen atom used for the order parameter as O^λ. The type of species (OH⁻, H²O, or H³O⁺) was identified by allocating to each hydrogen a single bond connecting it to the closest oxygen. Note that the definition of the order parameter does not require a threshold for defining a chemical bond nor does it constrain the order parameter to specific water molecules for the duration of the simulation. This means that we compute the rate of dissociation of any water molecule in the system instead of a single targeted O–H bond or water molecule.

Fig. 1.

The order parameter and the probability for water autoionization. (A and B) Definition of the order parameter ($\lambda$, dashed line), taken as the largest covalent O–H distance in the system when no ionic species are present (A) or as the shortest distance between the OH⁻ oxygen atom and the hydrogen atoms in H³O⁺ when ionic species are present (B). A hydrogen bond wire with four members is shown with red (oxygen) and white (hydrogen) spheres and the distances $|\text{OH}{|}_1$, $|\text{OH}{|}_2$, $|\text{OH}{|}_3$ are also indicated. These distances are used to investigate the possible concerted motion of hydrogen atoms along the wire. (C) The crossing probability (${\mathcal{P}}_A$) and average energy of trajectories ($⟨E⟩$) as a function of the order parameter. The (black) dashed line is calculated using an alternative definition of the order parameter ($\lambda \prime$) where the trajectory length (in femtoseconds) defines the order parameter for $\lambda >3$ Å. The horizontal dotted-dashed line is the crossing probability ($4.0\times 10^{-15}$) obtained for long paths ($\lambda \prime \ge 1$ ps). The activation energy is equal to the plateau value of the average energy which approaches $17.8$ kcal/mol. The shaded area ($1.15<\lambda <2.0$) is the domain used for the predictive power analysis.

From our RETIS simulations, the water dissociation rate constant, $k_{\text{D}}$, can be obtained as the product of a flux, $f_A$, and a (conditional) probability, ${\mathcal{P}}_A\left({\lambda }_N|{\lambda }_0\right)$:

$$k_{\text{D}}=f_A\times {\mathcal{P}}_A\left({\lambda }_N|{\lambda }_0\right).$$ [1]

Here, ${\lambda }_0$ and ${\lambda }_N$ are interfaces defining the initial ($\lambda <{\lambda }_0$) and final ($\lambda >{\lambda }_N$) states and ${\mathcal{P}}_A\left({\lambda }_N|{\lambda }_0\right)$ is the probability of reaching the final state before (possibly) reentering the initial state, given that the initial interface ${\lambda }_0$ has been crossed. The flux, $f_A$, is a measure of the frequency of crossings with ${\lambda }_0$. Since we consider the dissociation of any water molecule in our system, we have normalized $f_A$ by the number of water molecules present. Typically, for rare events, the crossing probability is very small and in practice, ${\mathcal{P}}_A\left({\lambda }_N|{\lambda }_0\right)$ is calculated by first positioning several more interfaces ${\lambda }_0<{\lambda }_1<\dots <{\lambda }_N$ between the initial and the final state. The overall crossing probability is then obtained as a product of several (history-dependent) conditional probabilities (14). The conditional probabilities are calculated in a separate path ensemble simulation where the $\left[i^{+}\right]$ path ensemble defines the collection of paths crossing ${\lambda }_i$. The number and location of the interfaces alter the efficiency of the method, but not the results.

In the present case, we placed the final interface beyond the maximum distance obtainable in our system. All trajectories were thus propagated until the system contained only H²O species again. Separated ions may still recombine fast (within a few femtoseconds) even if the separation is large (16) and this observation was confirmed in our analysis (SI Appendix, Fig. S1). To better identify and distinguish the metastable ionized states, we used path reweighting (21) to project the crossing probability on an alternative order parameter, $\lambda \prime$, which equals the trajectory length (in femtoseconds).

In Fig. 1, we show the calculated crossing probability from our simulations as a function of the order parameter. In principle, there are two potential mechanisms which lead to an increase of the reaction coordinate $\lambda$ after the first proton jump. The ionic species can separate further by another proton jump, the so-called Grotthuss mechanism, reassigning the H₃O⁺ or OH⁻ ion to another oxygen and causing a sudden discontinuous increase in the reaction coordinate. A second possible mechanism keeps the first ionic species intact and lets them move away from each other by diffusion, yielding a more gradual increase of the reaction coordinate. Based on the completely flat intermediate plateau region between $1.5$ Å and $3.2$ Å, we can conclude that only the first mechanism is effective. For $\lambda >3$ Å, we consider $\lambda \prime$ as the order parameter and we have used a threshold of $\lambda \prime \ge 1$ ps as a criterion to identify a stable dissociation event. This choice is rather arbitrary since there is not a clear separation of timescales for the reverse recombination reaction which would result in another flat plateau region of the crossing probability. With a threshold of $1$ ps, the crossing probability is ${\mathcal{P}}_A=4.0\times 10^{-15}$. Combined with the initial flux, calculated to be $f_A=2.9\times 10^{-3}$ fs⁻¹ in our simulations, the resulting dissociation constant is $k_{\text{D}}=f_A{\times \mathcal{P}}_A=1.1\times 10^{-2}$ s⁻¹. An alternative rate constant not requiring any time threshold can be defined by counting the trajectories that undergo a hydrogen swap; i.e., in the last frame some of the water molecules have swapped their protons. The rationale behind this definition is that the proton swap must imply a significant reorganization of the hydrogen bond network so that the reverse reaction can be considered as an independent recombination reaction. Vice versa, the forward reaction has established a quasi-stable state since it is not followed up by a correlated reverse reaction. This definition yields a rate of $k_{\text{D}}=0.16$ s⁻¹.

Comparing with experimentally determined dissociation constants at 25 °C [$k_{\text{D}}=2.5\times 10^{-5}$ s⁻¹ (7) and $k_{\text{D}}=2.04\times 10^{-5}$ s⁻¹ (8)] we overestimate the rate constant by a factor $500$ (although the simulated rate will drop and gets closer to the experimental rate if a larger threshold is chosen). Considering all factors that play a role in the accuracy (statistical error, functional, small system size, purely classical treatment of protons, the time threshold value) the deviation with experiments is satisfactory and comparable to other density functional theory studies. Depending on the functionals considered in the ab initio calculation, energy barriers may be in error by $10$–$20$ kJ/mol (22) which at room temperature would already correspond to a factor $55$–$\mathrm{3,000}$ difference between experimental and theoretical rate constants. Still, density functional theory generally manages to reproduce trends and mechanistic information in reasonable agreement with experiments (23).

We also calculated the average energy of the generated trajectories as a function of the order parameter (Fig. 1). The energy is expected to converge to the activation energy as can be derived from the temperature derivative of the rate constant (24, 25). We note that this activation energy gives a more direct comparison with experiments than free energy barriers which depend on the choice of order parameter. The activation energy obtained from the average energy of the accepted paths is approximately $17.8$ kcal/mol. For comparison, an Arrhenius plot of the experimental data of Natzle and Moore (8) results in an activation energy of approximately $17.3$ kcal/mol while Eigen and Maeyer (7) reported an activation energy between $15.5$ kcal/mol and $16.5$ kcal/mol. The deviation with our result is lower than the typical error margin mentioned above and the fact that the experimental activation barriers are lower than our simulation result, despite having lower rate constants, is rather remarkable. Since experimental data on this topic are at least three decades old, we hope that our finding will encourage future experimental investigations on the dissociation reaction.

Path sampling methods generate reactive (and nonreactive) trajectories which can be used to discover possible mechanisms and initiation conditions. To characterize these conditions, we considered additional collective variables, which we label $\xi =\left({\xi }_1,{\xi }_2,\dots \right)$. In principle, these ${\xi }_i$s can be functions of all positions and momenta in the system, and they do not necessarily have simple physical interpretations. Since the ability to form hydrogen bonds is one of the characteristic features of water (26) and since previous computational studies have demonstrated the relevance of the hydrogen bond wire connecting the ionized species (16, 17), we have focused on a set of relatively simple collective variables which quantify the hydrogen bond network and the distortion from tetrahedral geometry.

The first collective variable we consider is the length of the hydrogen bond wire bridging the nascent ion species. Our aim is to predict the outcome of initiated trajectories and in particular the initiation conditions for reactive events. Thus, we cannot define the hydrogen bond wires as connecting the ionic species, since this is one of the outcomes we wish to predict. For a single trajectory, we define the hydrogen bond wire as the shortest wire containing the O^λ species and $i-1$ other water species at the first point in time when $\lambda$ is greater than a given threshold value, ${\lambda }_{\text{t}}=1.15$ Å. Typically, this threshold is reached within $3$–$6$ fs in our trajectories. This defines a wire containing $i$ water species whose length, $w_i$, is obtained as the sum of the O–O distances of consecutive members.

In addition, we have considered the following four collective variables which describe the local structure surrounding the O^λ species: (i) The number of hydrogen bonds accepted, $n_{\text{a}}$, and (ii) donated, $n_{\text{d}}$, by the water species containing O^λ; (iii) the tetrahedral order parameter, $q$, obtained using the angles defined by O^λ and its four nearest oxygen atoms (27, 28) (by the definition $q=1$ for a perfect tetrahedral structure and $q\ne 1$ otherwise); and (iv) an angle order parameter, $q_{\cos }$, defined as the smallest of the cosine of the two internal angles in the wire. We refer to Materials and Methods for additional information on these collective variables.

After defining the extra $\xi$s, we analyzed the trajectories using the predictive power method (19). This method begins by classifying the trajectories as reactive or nonreactive based on two thresholds ${\lambda }^{\text{r}}$ and ${\lambda }^{\text{c}}$ defined such that ${\lambda }^{\text{r}}>{\lambda }^{\text{c}}>{\lambda }_0$. A trajectory is considered reactive if it reaches the specified ${\lambda }^{\text{r}}$; otherwise it is considered nonreactive. At the first crossing point with ${\lambda }^{\text{c}}$, we record the $\xi$s and form two distributions using the reactive/nonreactive classification: $r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$, the fraction of ${\lambda }^c$-passing trajectories that cross ${\lambda }^c$ at a point $\xi$ and reach ${\lambda }^{\text{r}}$, and $u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$, the fraction of ${\lambda }^c$-passing trajectories that cross ${\lambda }^c$ at a point $\xi$ but fail to reach ${\lambda }^{\text{r}}$. These two distributions give information on the relation between the additional order parameters and the reactivity. For instance, if $u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)=0$, it could be that $\xi$ is inaccessible, but if we can cross ${\lambda }^{\text{c}}$ at $\xi$, the trajectory will be reactive. To quantify the importance of the different $\xi$s, we calculate the predictive ability, ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$, defined as (19)

$${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}=1-\frac{1}{{\mathcal{P}}_A\left({\lambda }^{\text{r}}|{\lambda }^{\text{c}}\right)}\int \frac{r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)}{r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)+u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)}\text{d}\xi ,$$ [2]

such that $1{\ge \mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}{\ge \mathcal{P}}_A\left({\lambda }^{\text{r}}|{\lambda }^{\text{c}}\right)$. If the collective variables do not correlate with reactivity, the lower limit is attained but if the $\xi$s are relevant for the reaction, ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}{>\mathcal{P}}_A\left({\lambda }^{\text{r}}|{\lambda }^{\text{c}}\right)$. We use the ratio ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}{/\mathcal{P}}_A\left({\lambda }^{\text{r}}|{\lambda }^{\text{c}}\right)\ge 1$ to measure how much the predictive ability is increased when considering the extra $\xi$s, compared with using the crossing probability alone. Note that the definition in Eq. 2 shows that if the overlap of the two distributions is small, then the predictive ability increases.

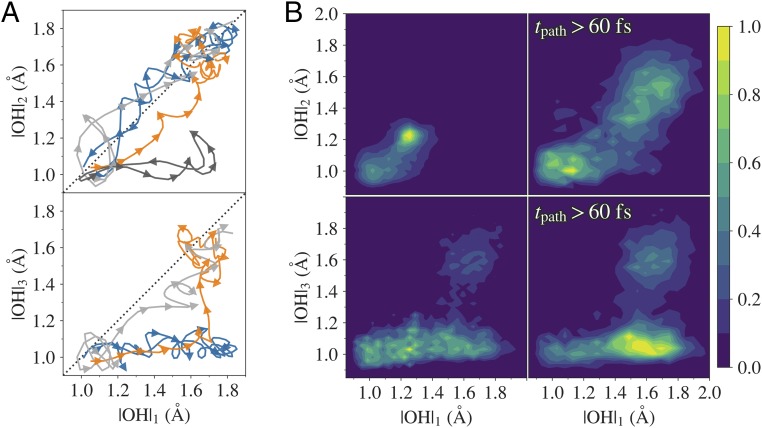
We first investigated the lengths of hydrogen bond wires containing three, four, and five water molecules. Comparing the predictive abilities for these collective variables (respectively, $w_3$, $w_4$, $w_5$) we find that $w_4$ and $w_5$ are more correlated with reactivity and that $w_4$ is more relevant for larger ${\lambda }^{\text{r}}$ (SI Appendix, Fig. S2). Thus, in the following we focus on wires containing four water molecules. For the water wires, we observe that when the ionic species are separated by at least two water molecules, the ionic state survives for a longer time compared with cases where they are separated by just one water molecule. This implies that (at least) three proton transfer events have occurred. We monitored the distances of the initially covalent O–H bonds and show these for the first ($|\text{OH}{|}_1$), the second ($|\text{OH}{|}_2$), and the third ($|\text{OH}{|}_3$) transferred proton in Fig. 2. As can be expected from the Grotthuss mechanism (29, 30), the initial autoionization event is followed by several proton transfers in which the ionic species separate along the wire. Fig. 2 shows that this can happen in both a concerted and a stepwise way: The transfer of the first and the second proton occurs almost exclusively in a concerted way, while the transfer of the third proton (if it occurs) can happen stepwise or concertedly. This is also reflected in the waiting time between these events (SI Appendix, Fig. S3): The waiting time distribution between the second and the third proton transfer is broader compared with the first and the second transfer. To investigate the stability of the wires, we also calculated the hydrogen bond wire in time-reversed trajectories (SI Appendix, Fig. S4). We find that trajectories are indeed starting and ending with a contracted wire ($w_4<7.6$ Å) as reported by Hassanali et al. (17), but at the end these wires do not necessarily contain the same oxygen atoms. This might occur due to an actual breakage of the hydrogen bond wire or by a lesser disruption (for example, by a shift of the selection of four consecutive oxygens within a five-membered wire). The majority of the longer trajectories reform via another wire, but there are still a significant number of long trajectories ($>1$ ps) for which the recombination is exactly the same as the dissociation path. This contradicts the hypothesis (16) that a breakage of the wire is a necessary condition to reach a metastable state. Also, visual inspection shows that relatively long trajectories exist in which the hydrogen bond wire remains intact except for some very short on/off fluctuations in the hydrogen bonds. We find the abovementioned hypothesis therefore difficult to defend. Conversely, we can also examine whether an actual breakage always leads to a long-lived metastable state. For this we adopt again the assumption that all trajectories with a hydrogen swap necessarily imply an indisputable breakage of the hydrogen bond wire. SI Appendix, Fig. S5, shows that trajectories with a proton swap are on average longer, but can still be relatively short ($35$ fs).

Fig. 2.

The concerted behavior of the autoionization event. (A) The distances ($|\text{OH}{|}_i$) of initially covalent O–H bonds for the first ($i=1$), the second ($i=2$), and the third ($i=3$) proton transfer in four trajectories. The arrows show the time direction and the different trajectories exemplify different types of hydrogen transfer: failed stepwise (dark-gray color, shown only for $|\text{OH}{|}_1$–$|\text{OH}{|}_2$), concerted (light-gray color), concerted only for $|\text{OH}{|}_1$–$|\text{OH}{|}_2$ (blue color), and concerted stepwise (orange color). (B) Using all trajectories in the final path ensemble, densities for $|\text{OH}{|}_1$–$|\text{OH}{|}_2$ and $|\text{OH}{|}_1$–$|\text{OH}{|}_3$ have been obtained (Left column). Right column shows the density when considering trajectories with a length $t_{\text{path}}>60$ fs. All trajectories were collected from the final path ensemble.

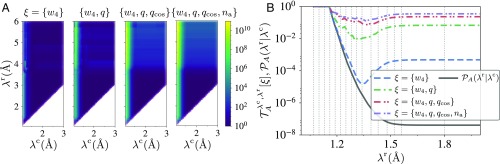
Comparing the additional collective variables (SI Appendix, Figs. S6 and S7), we find that $n_{\text{d}}$ is less relevant than the other variables and we do not consider it further. The other collective variables are more correlated with reactivity and in Fig. 3A, we show the predictive ability for some of their combinations. In Fig. 3B we show ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$ as function of ${\lambda }^{\text{r}}\le 2$ Å for ${\lambda }^{\text{c}}=1.16$ Å compared with the crossing probability using several combinations of the collective variables. Fig. 3 A and B shows that we can increase the predictive ability by a factor $10^7$ compared with the crossing probability. We note that since the crossing probability is small in this case, with a ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\sim 0.4$, we cannot perfectly predict the outcome. This indicates that there are other collective variables important for the description, possibly even nonlocal ones, as suggested by Geissler et al. (16). Also, we stress that here we are focusing only on the first concerted-jump step of the reaction in which the order parameter increases from $1.16$ Å to $2.0$ Å. As is clear from Fig. 1C the vast majority of trajectories reaching $\lambda =2.0$ Å will not lead to long-lived metastable states. Predicting this from the very first snapshot seems still a step too far since it depends on collisions between water molecules after many MD steps far away from the initially stretched OH bond.

Fig. 3.

Increasing the predictive power for water autoionization by considering additional collective variables. (A) The predictive power (${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left[\xi \right]$) relative to the crossing probability (${\mathcal{P}}_A\left({\lambda }^{\text{r}}|{\lambda }^{\text{c}}\right)$) using additional collective variables: hydrogen bond wire length ($\xi =w_4$), the orientation order parameter ($\xi =q$), the angular order parameter ($\xi =q_{\text{cos}}$), and the number of hydrogen bonds accepted ($\xi =n_{\text{a}}$) by the O^λ species. (B) The predictive power and the crossing probability as a function of ${\lambda }^{\text{r}}$ for ${\lambda }^{\text{c}}=1.16$ Å and different combinations of collective variables. Due to the threshold criterion for defining the wires (main text), the probability is shifted so that ${\mathcal{P}}_A=1$ for $\lambda <1.15$ Å.

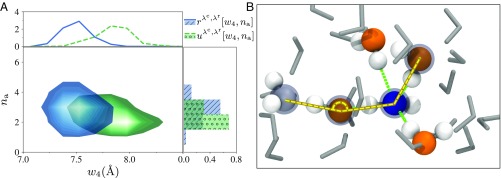
Inspecting the initiation conditions in more detail, we investigate the reactive and nonreactive distributions $r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$ and $u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$ in Fig. 4 for ${\lambda }^{\text{c}}=1.16$ Å and ${\lambda }^{\text{r}}=2.0$ Å. Here, we examine all dissociation events, even the ones that recombine quickly and show the distributions for $\xi =\left(w_4,n_{\text{a}}\right)$ in Fig. 4A [see SI Appendix, Fig. S8 for the distributions for $\xi =\left(w_4,q\right)$ and $\xi =\left(w_4,q_{\text{cos}}\right)$]. Along the $w_4$ coordinate we observe a clear separation of the two distributions which indicates that trajectories crossing ${\lambda }^{\text{c}}=1.16$ Å have a larger probability of being reactive for shorter wires (smaller $w_4$). This supports the hypothesis of a “compressed” wire as an important condition for autoionization, as first suggested by Hassanali et al. (17). Along the $n_{\text{a}}$ coordinate we observe a higher probability of reactivity for wires in which O^λ is hypercoordinated, which was also proposed by Hassanali et al. (17). Still, the chance of not being reactive is larger at any point $\left(w_4,n_{\mathrm{a}}\right)$ in Fig. 4A [$r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$ would not be visible if it had not been normalized]. For example, if (i) $7.15<w_4<7.6$ and at the same time $n_{\mathrm{a}}=3$, the probability for a reactive event is $3.6\cdot 10^{-6}$, which is small but still a factor 58 larger than the chance to be reactive from a random point at ${\lambda }^c$. In a more extreme case, if (ii) $w_4<7.3$ and simultaneously $n_{\mathrm{a}}=4$, the chance increases to $0.15$. The predictive ability ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$ provides a weighted average of these chances in which the weights are proportional to the relevance (19); since of all reactive trajectories, 45% cross ${\lambda }^{\text{c}}$ in region i and only 0.6% in region ii, the latter will have 75 times lower weight.

Fig. 4.

Initiation conditions and local collective variables. (A) Reactive ($r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$) and nonreactive ($u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$) distributions for $\xi =\left\{w_4,n_{\text{a}}\right\}$ and ${\lambda }^{\text{c}}=1.16$ Å and ${\lambda }^{\text{r}}=2.0$ Å. For visualization purposes, the depicted distributions are normalized [implying magnification of $10^7$ for $r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$]. Top and Right Insets show the one-dimensional projections of the distributions. A clear separation of the two distributions can be seen along the $w_4$ coordinate, indicating that reactive trajectories are more compressed compared with nonreactive trajectories. In addition, the oxygen atom used in the order parameter calculation (O^λ) accepts on average a larger number of hydrogen bonds in reactive trajectories, compared with nonreactive trajectories. (B) Illustrative snapshot from a reactive trajectory where O^λ is shown in blue. The four surrounding oxygen atoms which are used for the calculation of the tetrahedral order parameter $q$ are shown in orange. The water wire is highlighted with a yellow line (and gray transparent spheres) and the angle parameter $q_{\text{cos}}$ is indicated. In this snapshot, the water wire is compressed, $q$ exhibits deviation from a tetrahedral structure, $q_{\text{cos}}$ indicates that three oxygen atoms are lining up in the wire, and O^λ accepts three hydrogen bonds and donates one (shown with green lines).

If we consider the $q$ coordinate, we observe that $r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$ is shifted toward lower $q$ values compared with $u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$, which indicates that a distortion from a tetrahedral arrangement around the dissociating water species may also initiate the event. This finding is somewhat surprising as in some other aqueous phase chemical reactions the opposite effect was found (31). Similar conclusions can be drawn for the distribution of $\xi =\left(w_4,q_{\text{cos}}\right)$. Here, there is a peak along the $q_{\text{cos}}$ coordinate for the reactive distribution closer to a linear arrangement of the water molecules. In Fig. 4B we show a representative snapshot, obtained early (after $3$ fs) in a reactive trajectory. Overall the results shown in Fig. 3 report that a compression of the water wire (measured by $w_4$) and hypercoordination (measured by $n_{\text{a}}$) or distortion (measured by $q$ and $q_{\text{cos}}$) are necessary initiation conditions for autoionization. However, these are not sufficient conditions as shown by the values of ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$ in Fig. 3B: Still $60\%$ of the trajectories starting off within the ideal $\xi$ parameter range fail to establish a concerted proton jump.

Machine learning (ML) applied to path-sampling data (33, 34) is a promising approach to find important collective variables that can easily be missed by human intuition. To explore this possibility, we built ML models for predicting the outcome of trajectories given the state of the water system early in the trajectories. We focus on the same range as in the predictive power analysis and we use the state of the system, when $\lambda >1.15$ Å is first attained, to predict the outcome. We used several ML techniques in which every odd path ensemble was included in the calibration and the even path ensembles were used for the test set. An alternative split in which the data within each path ensemble were evenly divided in two gave similar results. Moreover, as heavily skewed distributions are difficult to treat with ML, we further omitted the reweighting of the datasets with the statistical weights of the corresponding path ensembles. However, we applied the ML techniques as a qualitative approach to find new parameters that could be tested quantitatively within the predictive power method (19).

In addition, to avoid a potential risk of overinterpretation we opted to restrict the complexity of the ML decision process and imposed a maximum of four order parameters when computing ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$. For instance, excellent predictive performances ($>90\%$) were obtained using the ensemble-based gradient-boosting machines (35, 36). However, the interpretation of the model is problematic since an ensemble of $100$–$150$ deep decision trees (added in a sequence) is used. Although the performance is improved, the chance of overfitting with accidental correlations increases. We have therefore restricted ourselves to the single-tree–based decision models based on classification and regression decision trees (CART) (20). The restriction to four order parameters for the ${\mathcal{T}}_A^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}$ function is based on similar reasons. Adding more parameters gives more sparse matrices representing the reactive/nonreactive distributions, and, as a result, numerical integration for computing the overlap between these distributions becomes very sensitive to the bin size and could underestimate the overlap due to bins being empty by insufficient statistics.

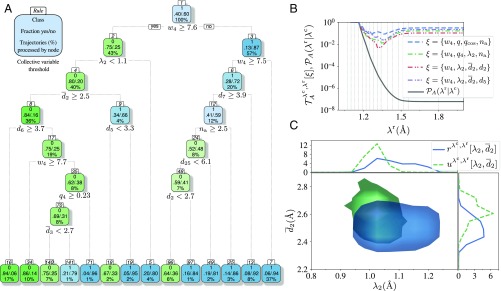
We considered $138$ collective variables consisting of oxygen–oxygen distances; oxygen–hydrogen distances for initially bound water molecules; all angles formed by O^λ and its four closest oxygen neighbors; and the Steinhardt order parameters of orders $3$, $4$, and $6$ (32) (see Materials and Methods for more details). In addition, the order parameters already considered were added. Fig. 5A shows the resulting decision tree. Remarkably, of all of the input parameters, the $w_4$ parameter is both on top of the decision tree and the most important variable as measured by the reduction in the classification error attributed to each variable at each split in the decision tree (20) (SI Appendix, Fig. S9). Also the tetrahedral ordering and the number of accepted hydrogen bonds appear in the decision tree. To describe the first effect, the ML approach prioritized the Steinhardt $q_4$ order parameter above the similar $q$ parameter previously used by us. Some distances that also appear in the decision tree like $d_{25}$, the distance between O^λ and its 25th closest oxygen, are most likely due to accidental correlations caused by the limited size of the dataset. This is verified by inspecting the importance of this variable: $d_{25}$ does not appear among the $20$ most important variables (SI Appendix, Fig. S9), and, in fact, other similar variables (e.g., $d_{24}$) are ranked higher, albeit with low importance. A more important and intuitively sound parameter that is suggested by the ML approach is ${\lambda }_2$, the OH distance between the oxygen closest to O^λ and its hydrogen with the largest intramolecular bond. Recomputing the predictive ability using parameters from the ML tree (Fig. 5B) did not yield higher performances than the combination $w_4$, $q$, $n_{\mathrm{a}}$, and $q_{\cos }$, but should be conceived as equally good, considering statistical uncertainties.

Fig. 5.

Results from the machine-learning analysis. (A) Classification and regression tree for predicting the outcome of initiated trajectories. Here, we considered several additional collective variables (description in Materials and Methods), but only a small subset is eventually needed for constructing the tree: $w_4$, $q_4$ [the Steinhardt fourth-order parameter (32)], ${\lambda }_2$ (the length of the stretched hydrogen bond in the water molecule closest to the O^λ species), $d_i$ (the distance from O^λ to the $i$th closest oxygen), and ${\overline{d}}_i$ (the average distance considering the $i$ closest oxygens). The notation for the nodes is explained with the stand-alone node in the top left corner. This tree predicts trajectories to be reactive, i.e., reaching a $\lambda \ge 2$, or nonreactive based on the collective variables obtained at the frame in the trajectories when $\lambda$ is first $\ge 1.15$. The nodes predicting reactive trajectories are colored blue (class $1$) while the nodes predicting nonreactive trajectories are colored green (class $0$). Note that the percentages at the bottom of the squares do not reflect the physically correct fractions since path ensembles were not reweighted using their statistical weights. The rules are textual representations of traversing the tree; for instance, rule $5$ (which predicts reactive trajectories) can be expressed as $w_4\ge 7.6$ and ${\lambda }_2\ge 1.1$. These rules give different initiation conditions, and they are listed in SI Appendix, Table S1, for the bottom row of nodes. (B) The predictive power and the crossing probability as a function of ${\lambda }^{\text{r}}$ for ${\lambda }^{\text{c}}=1.16$ Å and different combinations of collective variables. Here we compare the predictive power using collective variables we identified with variables marked as important by the machine-learning analysis. (C) Reactive ($r^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$) and nonreactive ($u^{{\lambda }^{\text{c}},{\lambda }^{\text{r}}}\left(\xi \right)$) distributions for $\xi =\left\{{\lambda }_2,{\overline{d}}_2\right\}$ and ${\lambda }^{\text{c}}=1.16$ Å and ${\lambda }^{\text{r}}=2.0$ Å. For visualization purposes, the depicted distributions are normalized. Top and Right Insets show the one-dimensional projections of the distributions.

Conclusions

We investigated the autoionization of water at room temperature, using an unconstrained ab initio rare-event simulation method. Our simulations sample reactive events that happen on the timescale of minutes and we demonstrated that autoionization can be initiated by the hypercoordination of a stretched OH bond and the compression of a hydrogen bond wire as suggested by Hassalani et al. (17). However, these are not sufficient conditions. Only when the wire is strongly condensed ($<7.3$ Å) and the stretched OH bond accepts four hydrogen bonds, does the reaction probability become significant (0.15), but only 0.6% of the reactive trajectories start off with such extreme conditions. The vast majority of reactive paths start with milder initial values for these two parameters. In this region of parameter space the reaction probability is largely enhanced compared with an arbitrary case, but still extremely small. Hence, the reaction takes place when additional structural parameters have values inside the right range. We identified additional structural parameters which correspond to the alignment of the hydrogen bond wire and the distortion from a tetrahedral arrangement. Hence, we showed that the local order parameters can be used to predict the self-ionization event, although it requires a combination of several conditions.

Due to the multiple correlated factors that influence the water autoionization, we combined our analysis method with ML techniques which identified additional parameters not considered before, in particular the O–H stretch of the oxygen closest to O^λ. Even though the ML result did not outperform the level of predictiveness by the human effort based on intuition, visual inspection of many molecular movies, and intensive trial-and-error approaches, the ML approach found all previously identified parameters very efficiently and, in addition, revealed some equally important parameters that were overlooked. We therefore believe that ML applied to path sampling has a great potential especially since data limitations will become less of an issue in the future due to the further expected increase of high-performance computing, a better parallelization scheme of sampling unequal trajectory-length path ensembles, and the use of more efficient Monte Carlo (MC) path-generating moves (37). It would therefore be promising to apply the same method to other aqueous-phase chemistry studies which so far have mainly been based on biased dynamics (31, 38).

The fundamental understanding of reaction triggers that can be gathered by this approach could open up avenues of practical applications. For instance, even if not all identified parameters correlating with reactivity will necessarily imply causal correlation, it is plausible that an intelligent manipulation of their equilibrium distribution via external electric fields (39) or inclusion of additives might lead to catalytic ways to steer reactions and in particular water dissociation.

Materials and Methods

Simulation Methods.

The MD simulations required by the RETIS algorithm (14) were performed with the Born–Oppenheimer MD capabilities of the CP2K program package (40). We used the Becke–Lee–Yang–Parr (BLYP) functional with a DZVP-MOLOPT (41) basis set and a plane-wave cutoff of $280$ Ry. The BLYP functional gives a reasonable description of the structure and dynamics of liquid water (42, 43) and the absence of dispersion corrections (44) is likely of minor importance for ion–water interactions where the dominant interactions are mainly electrostatic. However, we note that the BLYP functional is known to give an overstructured description of liquid water with a low diffusion coefficient (45). Previous studies on the recombination mechanism for water (17, 46) and for weak bases in water (18) have, however, found that the collective compression of the hydrogen bond wire and the motion of the protons are reproduced with different choices of the functional and basis set.

The initial system consisted of $32$ water molecules placed in a cubic simulation box of $9.85\times 9.85\times 9.85$ ų. All MD simulations were carried out under constant energy (microcanonical) dynamics, with a time step of $0.5$ fs and periodic boundaries.

The transition region was divided into $20$ path ensembles by positioning RETIS interfaces at $\lambda =$ {$1.07$, $1.10$, $1.13$, $1.16$, $1.19$, $1.22$, $1.25$, $1.28$, $1.31$, $1.34$, $1.39$ $1.43,$ $1.48$, $1.52$, $1.56$, $1.80$, $2.00$, $2.50$, $2.90$, $3.29$} Å. In addition, a final interface was placed at $\lambda =\infty$ such that all trajectories were propagated until they reached the pure water state again. After generating an initial path for each path ensemble (this was done by repeatedly modifying the momenta of the particles and evolving the system forward in time until valid paths were obtained) the RETIS algorithm attempts to either swap paths between different path ensembles or generate new trajectories by the so-called shooting or the time-reversal move. In our simulations the probability of performing a swapping move was set to $50\%$ while the probabilities of the two other moves were both set to $25\%$. New velocities for the shooting move were drawn from a Maxwell–Boltzmann distribution corresponding to an average temperature of $300$ K.

We performed $24$,$000$ MC moves for each path ensemble, using the RETIS algorithm. This generated between $\mathrm{8,000}$ and $18$,$000$ distinct trajectories in each path ensemble. The length of the trajectories ranged from $13.5$ fs to $\mathrm{1,365}$ fs and we disregarded the first $400$ trajectories in our analysis.

Analysis of Trajectories.

Crossing probabilities along the reaction coordinate $\lambda$ were computed by matching the results of the different path ensembles. Projection of the crossing probability along $\lambda \prime$ was obtained using the reweighting scheme of Rogal et al. (21) for the path ensembles in the transition interface sampling framework.

For trajectories harvested with the RETIS algorithm we calculated additional collective variables: the hydrogen bond wire length ($w_i$), the number of hydrogen bond donors ($n_{\text{d}}$) and acceptors ($n_{\text{a}}$), the orientation order parameter ($q$), and the angle formed by O^λ and its closest oxygen neighbors ($q_{\text{cos}}$). Using the first configuration in each trajectory, hydrogen atoms were assigned to the closest oxygen atom and this defined the initial H₂O molecules. Then, the hydrogen bond network was obtained for each configuration in the trajectory. Hydrogen bonds were identified using the criteria of Luzar and Chandler (47) and all (shortest) hydrogen bond connections between all pairs of water molecules were determined using the Floyd–Warshall algorithm (48). This allowed us to represent the hydrogen bond structure as a graph. Next, the oxygen atom (O^λ) used in the definition of the order parameter was identified. With no ${\text{OH}}^{-}$ present, this is the oxygen atom for which the covalent O–H distance is largest and when we have ${\text{OH}}^{-}$ present in the system, this is the ${\text{OH}}^{-}$ oxygen atom. After identifying O^λ, we obtained the number of hydrogen bonds accepted ($n_{\text{a}}$) and donated ($n_{\text{d}}$) by the water species containing it. The relevant hydrogen bond wire was obtained using the following criteria: (i) The wire should contain the oxygen atom used for the order parameter (identified as explained above) when the order parameter first crossed $1.15$ Å, (ii) the wire should contain $i$ water species, and (iii) the wire should be the shortest of the wires where two criteria i and ii are met. The length of the wire was defined as the sum of the O–O distances of consecutive molecules in the wire.

The orientation order parameter measures the distortion from a tetrahedral orientation of four water molecules around a central molecule and is defined by (27, 28)

$$q=1-\frac{3}{8}\sum _{j=1}^3\sum _{k=j+1}^4{\left(\cos {\psi }_{jk}+\frac{1}{3}\right)}^2.$$ [3]

Here, ${\psi }_{jk}$ is the angle formed by the central oxygen and its four nearest oxygen neighbors. The central oxygen is always O^λ or the oxygen with the largest OH bond for pure water or the OH⁻ oxygen if it is present. For a perfect tetrahedral orientation $q=1$ and it is $q\ne 1$ otherwise. The angle order parameter, $q_{\cos }$, was obtained directly as $q_{\cos }=min\left(\cos \alpha ,\cos \beta \right)$, where $\alpha$ and $\beta$ are the two internal angles in the wire.

After calculating these additional collective variables, we analyzed the trajectories using the methodology of van Erp et al. (19). For the analysis we used $100$ subinterfaces for both ${\lambda }^{\text{r}}$ and ${\lambda }^{\text{c}}$ for the range $0<\lambda /\text{Å}<6.4$. The histograms in the collective variable space were constructed using $20$ bins for $4.0\le w_3/\text{Å}\le 7.0$, $7.0\le w_4/\text{Å}\le 9.6$, $9.0\le w_5/\text{Å}\le 12$; $20$ bins for $0\le q\le 1$; and $25$ bins for $-1\le q_{\cos }\le 1$, while the bins (midpoints) were placed at $-0.5,0.5,1.5,\dots ,6.5$ for both $n_{\text{a}}$ and $n_{\text{d}}$.

The classification models were constructed using CARTs (20) available within the R (49) software package. The mean of sensitivity and specificity was used as the classifier performance measure (50).

For the CART models we considered several sets of collective variables and we obtained these variables at the frame in the trajectories where the order parameter first crossed $1.15$ Å. The trajectories were classified as reactive if they reached a $\lambda \ge 2$ and as nonreactive otherwise. The first set of collective variables consisted of all $\mathrm{4,560}$ atom–atom separations in the system, which gave a model in which the oxygen–oxygen distances were most important. This model did not lend itself to an easy interpretation and we next considered several models with a reduced number of collective variables.

In the best-performing model (performance measure for training $0.89$ and for testing $0.88$) we considered $138$ collective variables: all oxygen–hydrogen distances for initially bound water molecules, all oxygen–oxygen distances involving O^λ, the averaged distances between O^λ and its $i=\left\{\mathrm{2,3},\dots ,31\right\}$ oxygen neighbors, the cosine of all angles formed by O^λ and its $4$ closest oxygen neighbors, all of the collective variables considered in the predictive power analysis, and the Steinhardt order parameters of order $3$, $4$, and $6$ (32). When performing the predictive power analysis for the collective variables used by the CART analysis, we used $20$ bins in the range $\left[0.7,2.0\right]$ for oxygen–hydrogen distances and $20$ bins in the range $\left[1.0,4.2\right]$ for oxygen–oxygen distances, and for angles and the Steinhardt order parameters we used similar bins to those for $q_{\cos }$ and $q$ given above.