Significance
Ice mélange, a granular collection of broken icebergs ranging from tens of meters to hundreds of meters in size, sits in front of many of the Earth’s most active tidewater glaciers. In addition to influencing heat and mass transport in the ocean, the jam-packed mélange provides a geophysical living laboratory to test principles developed for small-scale granular materials such as sand. By characterizing both flow and mechanical stress using field measurements, laboratory experiments, and numerical modeling, we show that ice mélange is a quasi-2D, creeping granular fluid which constantly jams and unjams as it advances through the fjord. Most importantly, our results show how ice mélange can act as a “granular ice shelf” which buttresses even the largest icebergs that calve into the ocean.
Keywords: jamming, granular, glacier, mélange, calving
Abstract
Tidewater glacier fjords are often filled with a collection of calved icebergs, brash ice, and sea ice. For glaciers with high calving rates, this “mélange” of ice can be jam-packed, so that the flow of ice fragments is mostly determined by granular interactions. In the jammed state, ice mélange has been hypothesized to influence iceberg calving and capsize, dispersion and attenuation of ocean waves, injection of freshwater into fjords, and fjord circulation. However, detailed measurements of ice mélange are lacking due to difficulties in instrumenting remote, ice-choked fjords. Here we characterize the flow and associated stress in ice mélange, using a combination of terrestrial radar data, laboratory experiments, and numerical simulations. We find that, during periods of terminus quiescence, ice mélange experiences laminar flow over timescales of hours to days. The uniform flow fields are bounded by shear margins along fjord walls where force chains between granular icebergs terminate. In addition, the average force per unit width that is transmitted to the glacier terminus, which can exceed 107 N/m, increases exponentially with the mélange length-to-width ratio. These “buttressing” forces are sufficiently high to inhibit the initiation of large-scale calving events, supporting the notion that ice mélange can be viewed as a weak granular ice shelf that transmits stresses from fjord walls back to glacier termini.
Ice mélange, an agglomeration of sea ice and iceberg clasts (Fig. 1A), forms when ocean currents or surface winds fail to evacuate icebergs from a fjord. Ice mélange characteristics vary by fjord, but in general, fjords with constrictions and high iceberg production rates favor mélange retention. For some glaciers, such as those in the Uummannaq district of West Greenland (1, 2), the Wilkins Ice Shelf (3), and tidewater glaciers in Alaska, ice mélange has an ephemeral existence and forms only when air and water temperatures are low enough to permit the growth of a thick sea ice matrix. At other glaciers, such as Jakobshavn Isbræ and Helheim Glacier in Greenland, ice mélange has a perennial existence and is held together by iceberg–iceberg and iceberg–bedrock contact forces (4–6), although winter sea ice growth likely bolsters ice mélange rigidity (7, 8).
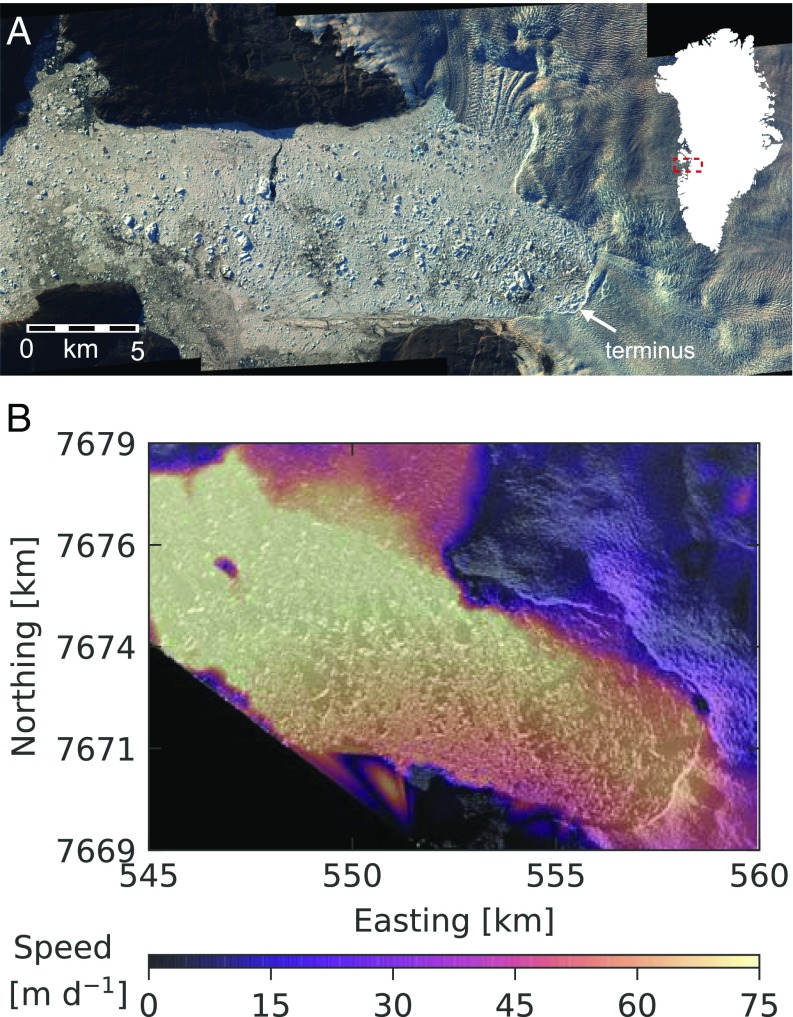
Fig. 1.
(A) July 6, 2010 map view of Jakobshavn Isbræ from WorldView-2 imagery (copyright 2018 Digital Globe, Inc.). Ice mélange extends more than 20 km from the glacier terminus. (B) Velocity field derived from terrestrial radar images acquired 2 d apart (August 6–8, 2012).
The presence of ice mélange has several implications for fjord dynamics. Ice mélange is a source of freshwater to fjords (9, 10) and suppresses ocean waves (11), thus affecting fjord circulation patterns (12–14). Ice mélange also exerts stress on glacier termini, which may inhibit calving and indirectly affect glacier dynamics (6, 15–17). Time-lapse and remote-sensing observations show that weakening and dispersion of ice mélange in spring precedes seasonal terminus retreat (1, 2, 5–7, 18, 19). Some numerical modeling experiments have arrived at similar conclusions (15–17), although there is disagreement regarding the magnitude of the stress that must be exerted on a glacier terminus to impact glacier dynamics (20). These numerical simulations involved applying a temporally varying stress to a well-defined terminus in viscous glacier flow models. However, the glacier–ice mélange boundary is not always clearly delineated [especially in winter (6)] and the glacier itself can be highly fractured near the terminus. Thus, current numerical models may not accurately characterize the terminus force balance.
Following granular modeling studies of sea ice and river ice (21–26), recent studies have taken a granular mechanics approach to characterizing the dynamics of ice mélange. Peters et al. (27) showed in observations of mélange at Jakobshavn Isbræ that dynamic jamming occurs during transient events associated with iceberg calving, thus suggesting that ice mélange behaves fundamentally like simple granular materials explored in laboratory settings (27, 28). Robel (8) used a discrete-element model to show that ice mélange resistance is strongly affected by sea ice growth in the interstitial spaces and also successfully reproduced the jamming phenomena observed in Peters et al. (27). The icebergs in the mélange are among the world’s largest granular clasts (10–1,000 m) and thus provide a geophysical laboratory to test concepts in granular physics that are often experimentally tested with millimeter-sized grains (28–35).
Here we use field data, laboratory experiments, and numerical models to investigate flow profiles, mechanical stresses, and jamming behavior of ice mélange. The laboratory experiments and numerical simulations provide direct measurement of processes that are difficult or impossible to observe in the field. We find that as ice mélange is steadily pushed down-fjord by a glacier’s terminus, it undergoes a nearly uniform flow in the central region, with strong shear at the boundaries of the fjord where the icebergs are locked by fjord geometry. The roughness of the fjord walls also provides an anchor for granular force chains, in analogy to the Janssen effect in grain silos (36). The resulting shear stress at the walls serves as the primary resistive stress inhibiting the flow of mélange. Our results indicate that ice mélange can exert more than 107 N/m average load across the terminus, which is sufficient to prevent kilometer-scale icebergs from calving (6, 15).
Field Data
In 2012 we conducted a terrestrial radar survey of Jakobshavn Isbræ, Greenland (Fig. 1A), with a Gamma Remote-Sensing ground portable radar interferometer (GPRI) (37, 38). The radar scanned the terminus and proglacial ice mélange every 3 min during a 2-wk study period. The GPRI is a Ku-band ( = 1.74 cm) real aperture imaging radar with a maximum range of 16 km, a range resolution of 0.75 m, and azimuth resolution that is proportional to range. For this study, we used radar backscatter images with an azimuth resolution of 16 m in the near field and 92 m in the far field. We reprojected the images to 15-m Cartesian space and georectified them to Universal Transverse Mercator coordinates. Two images acquired 48 h apart during a period of terminus quiescence were used to produce a velocity field with the Lucas–Kanade optical flow method (39) in OpenCV. The Lucas–Kanade method tracks individual features with high accuracy and produces a sparse array of velocity vectors. In this application the algorithm tracked 2,430 features, which we then interpolated to a grid using cubic interpolation. For comparison, we used the same algorithm to generate velocity fields of the laboratory experiments and numerical simulations.
Fig. 1B shows the resultant velocity field. During this time the terminus was moving at m/d. The mélange velocity was quite uniform, except near the fjord walls where the velocity was nearly zero due to friction, leading to shear flow in this region. The velocity of the mélange also gradually increased in the flow direction (toward the top left corner of the map in Fig. 1B). This is most likely due to three effects. First, subglacial discharge creates a net outflow of water from the fjord, which will tend to stretch and expand the mélange. Second, wind and tides have an asymmetric influence. The mélange maintains rigidity during rising tides or on-shore winds (compression), but can expand freely during falling tides or off-shore winds. This asymmetry has a larger effect on icebergs down-fjord where the mélange can expand freely into open waters. Third, the mélange is inherently 3D. Icebergs will move vertically and/or rotate if they are out of hydrostatic equilibrium and thus locally expand the mélange in regions of lower stress.
Laboratory Experiments
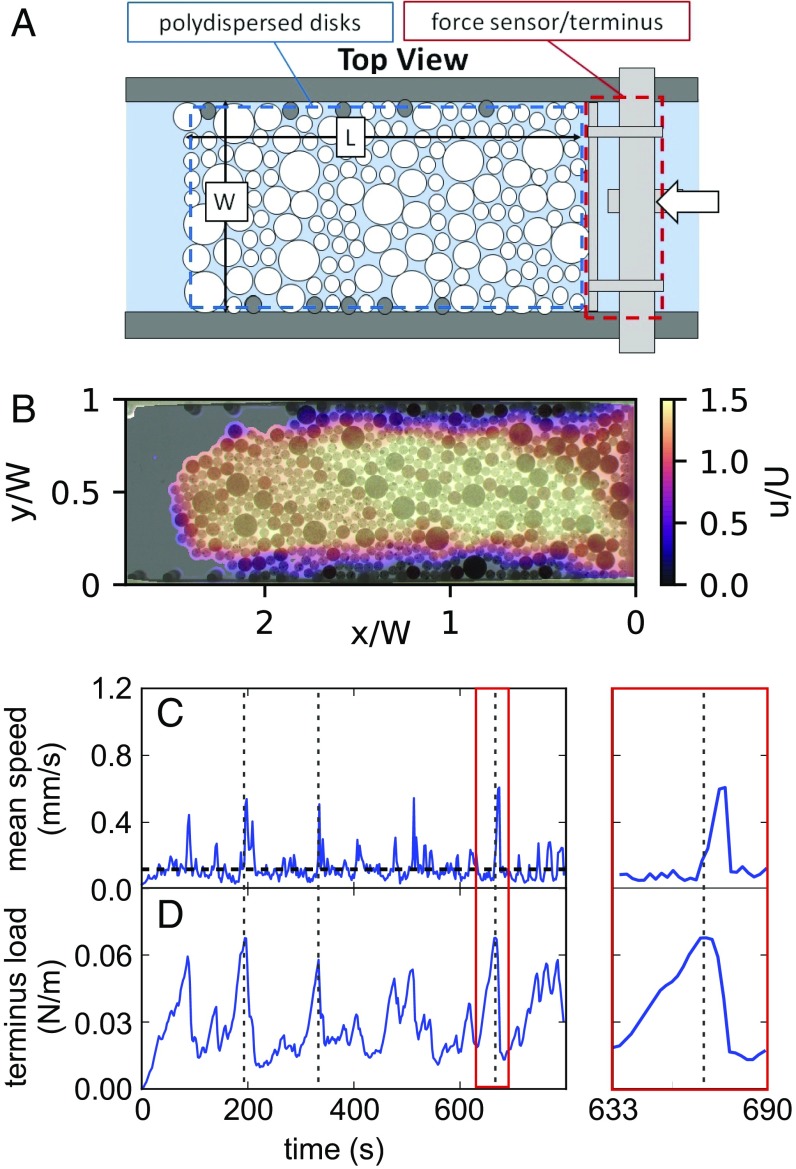
Fig. 2 A and B shows a schematic of the experimental setup and a typical image of the laboratory-analog mélange. The mélange was modeled as a 2D, floating collection of centimeter-scale cylindrical particles which were slowly pushed through the channel by the “terminus” while the net pushing force was monitored. The speed of the terminus was 0.12 mm/s. The dimension of the synthetic mélange was defined by the width () and length () as indicated in Fig. 2A. The walls of the channel were adhered with fixed particles to simulate pinning points analogous to the complex geometry of rocky fjord walls (Fig. 1A). The channel was attached to an aluminum frame from above and submerged into soapy water. The soap was added to minimize surface tension forces which can cause floating particles to aggregate. The channel was 1 m long and the width was varied from 0.12 m to 0.3 m. All particles were composed of low-density polyethylene (LDPE) plastic (density = 920 kg/m3). The smallest particles used in the experiment were 6.8 mm in diameter and mm in height. For most experiments, we used a polydisperse collection of particles of four different sizes based on iceberg size distributions observed in field data (9). The terminus was composed of stainless steel balls embedded into LDPE plastic and hung from two strings on each end so that it acted as a pendulum. The deflection of the pendulum was measured by a displacement sensor (LD701; OMEGA Engineering, Inc.) and then converted to a net force using the weight of the partially submerged pendulum.
Fig. 2.
(A) Experimental setup. White particles are mobile, and gray particles are fixed to the wall. (B) Velocity field derived from optical flow analysis of the experiment, normalized by the terminus velocity . The data were boxcar averaged over 100 frames (200 s), which corresponds to 24 mm of terminus motion. (C and D) Average speed (C) and terminus force (D) in the mélange during a typical experiment. The peaks in the force correspond to the initiation of movement in the mélange, indicated by the dashed vertical lines. An expanded view of one jamming event is highlighted in red. The terminus speed was = 0.12 mm/s, and the channel width was = 0.12 m.
The slow advance of the mélange was characterized by jamming and unjamming events: periods of compression, followed by particle rearrangements (Movie S1). A temporally averaged velocity profile (averaged over 200 s) from a typical experiment is shown in Fig. 2B. The velocity was calculated using the same optical flow method as with the field data, which produced 3,733 discrete tracks. The experiment showed the same shear margins near the walls of the fjord as the field data, but lacked the increasing velocity down-fjord, which is most likely due to the 2D nature of the experiment and the lack of wind, ocean currents, and tides. During a jamming event, the lateral load on the terminus, measured by the total force on the terminus divided by its width, increased steadily until a rearrangement of particles occurred (40). At this point the force on the terminus suddenly dropped, the local velocity increased, and the stress in the mélange increased again until the next unjamming event (Fig. 2D). Unjamming events preceded a sharp spike in the velocity of the particles (Fig. 2C). An important distinction between the experiments and ice mélange is that during jamming events, the pendulum terminus deformed, while real icebergs break and deform in ice mélange. This became an issue when scaling the experimental terminus force to compare with field and numerical data. To address this, we directly simulated the experimental conditions and computed the necessary conversion factor (Fig. S1).
Numerical Simulations
For the 2D numerical simulations, icebergs were modeled as either a single disk of radius (monomers) or two disks of radius and 1.4 that were “glued” together (dimers) to mimic the noncircular nature of real granular icebergs. When two single disks overlapped by a distance , they experienced a normal, repulsive force based on a spring–dashpot viscoelastic model where the spring force is derived from the Hertzian contact theory for two spheres (41, 42):
| [1] |
The second term in the parentheses is essentially the time derivative of the first term. The effective radius of particle and particle is . The constant , where is the Young’s modulus of the material and is Poisson’s ratio. We denote the minimum-sized disk used in the simulations as and the density of ice as , so that units of length, mass, and time are measured in , , and , respectively. The coefficient is the crossover timescale between viscous and elastic behavior and was set to 1.0 in simulation units. In the event that was ever attractive (i.e., a rapid decrease in ), the force was set to zero. In addition to the normal force, a tangential frictional force was modeled in the following way (41):
| [2] |
Here is the relative tangential velocity between the particle surfaces, is the kinetic friction coefficient, and is a viscosity that determines the saturating frictional force, which was also set equal to 1.0 in simulation units. This form continuously interpolates between a velocity-independent Coulomb friction at high velocities and zero friction at low velocities and small contacts, thus avoiding numerical instabilities associated with a jump in the friction at zero velocity. Since kinetic friction mostly served to dissipate energy during the brief duration of unjamming events, the results were fairly insensitive to the specific choice of and . The material properties used when comparing the simulations to typical ice mélange were = 9 GPa, = 0.33, and = 910 kg/m3, and we set the value of = 40 m.
Initially, 500–4,000 iceberg particles were randomly placed in the model fjord. The system was then relaxed using the Fast Inertial Relaxation Engine algorithm (43) until the particles no longer touched each other. The walls of the fjord were composed of immobile particles with radius = . Extra, immobile particles covered 20% of the walls to simulate “roughness” that kept the adjacent icebergs from slipping. The terminus was composed of a single line of particles with radius that advanced quasi-statically with constant velocity . The velocity was chosen so that the magnitude of the granular forces did not depend on . The particles also experienced a small viscous drag force and torque that were proportional to the iceberg velocity and angular velocity, respectively, and were not meant to accurately model hydrodynamic drag from the surrounding ocean water. Since most of the stress in the ice mélange was produced by jamming forces, these viscous forces simply served to dissipate energy from icebergs on a rapid timescale, especially during unjamming events and near the front of the mélange. Iceberg sizes were chosen from recently measured distributions in ice mélange (9). Finally, the equations of motion for the icebergs were time integrated using a second-order velocity-Verlet algorithm with a time step of 0.11.5 ms. More details can be found in Supporting Information.
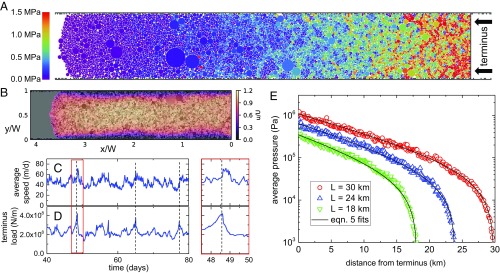
In Fig. 3A, we show the stress distribution in the mélange during a typical simulation. Each particle is colored according to the sum of the contact forces divided by the perimeter of the particle. Since this quantity is technically a force per length due to the 2D nature of the simulations, we relate this to a typical stress by assuming an average thickness of the mélange of 200 m. Force chains composed of similarly colored particles can be observed emanating from the fjord wall to the interior of the mélange and are typically inclined at 45° to the fjord walls. The force chains keep the system in a jammed state, even though the end of the mélange is stress-free.
Fig. 3.
(A) Stress distribution in the mélange during a typical simulation with W = 4.8 km and L km. To calculate the stress, the mélange is assumed to be 200 m thick. (B) Velocity field derived from optical flow analysis of images from a typical simulation, normalized by the terminus velocity. The data were boxcar averaged over 100 frames, corresponding to 1,000 m of terminus motion (20 d). (C and D) Average speed (C) and terminus force (D) in the mélange during a portion of the simulation. The black dashed lines indicate peaks in the load and the subsequent speedup in the mélange. An expanded view of one jamming event is highlighted in red. (E) Mean stress vs. distance from the terminus for three simulations with = 4.8 km. The solid lines show fits to the data using Eq. 5 with = 10.2 kPa, 12.2 kPa, 12.9 kPa and = 0.34, 0.29, 0.26 for = 18 km, 24 km, 30 km, respectively.
Fig. 3B shows a typical velocity field in a simulation. To compare with both the field and laboratory data, we again used the same optical flow analysis on a series of images generated from the simulation, resulting in 2,430 tracks. Although the flow is mostly uniform across the width of the mélange, the same shear margins can be seen near the fjord walls where the particles cannot slip due to the immobile particles that simulate wall roughness. In a similar fashion to the experiments, we plot the total force on the terminus and the mean speed of the particles in Fig. 3 C and D. To reduce simulation time, the terminus moved much faster than a typical glacier terminus. To ease the comparison between the simulation data and field data, we have scaled the time axis to correspond to a terminus speed of 40 m/d, which is characteristic of Jakobshavn Isbræ (6), and also verified that a slower terminus speed produced the same stress in the mélange. As in the experiment (Fig. 2 C and D), jamming events are evident as peaks in the force per width on the terminus, followed by unjamming events indicated by motion in the mélange.
The average pressure, due to contact forces in the mélange as a function of distance from the terminus, is plotted in Fig. 3E for three different simulations with constant and different values of . There is a rapid decay in the pressure away from the terminus. If hydrodynamic drag forces are negligible, then the width-averaged pressure in the mélange is balanced by the shear stress at the fjord walls. If we assume that is the horizontal distance from the terminus, the total force on a volume element of width , height , and length is
| [3] |
where is the pressure and is the shear stress at the boundaries, both of which depend on . A universal feature of granular materials is that the stress required to initiate flow increases with pressure (32). For ice mélange, let us assume the relationship
| [4] |
where is the effective coefficient of friction, which depends on the material friction coefficient and the geometry of the fjord walls, i.e., wall roughness (44, 45). The constant is the minimum shear stress required to produce flow through the rearrangement of particles. Since the mélange is in a state of quasi-static flow, the fact that when is consistent with well-known effects such as granular dilatancy (30), but also accounts for 3D ridging of icebergs that can facilitate rearrangements in floating granular systems (21).
Combining Eqs. 3 and 4 and assuming the open boundary of the mélange is stress-free (), we arrive at the following expression for :
| [5] |
The quantity is the length scale over which the applied terminus load is screened by the friction at the side walls. The exponential dependence is analogous to the increase in pressure with depth in a grain silo (36, 44). The solid black lines in Fig. 3E are fits to Eq. 5, illustrating excellent agreement.
Data Synthesis and Discussion
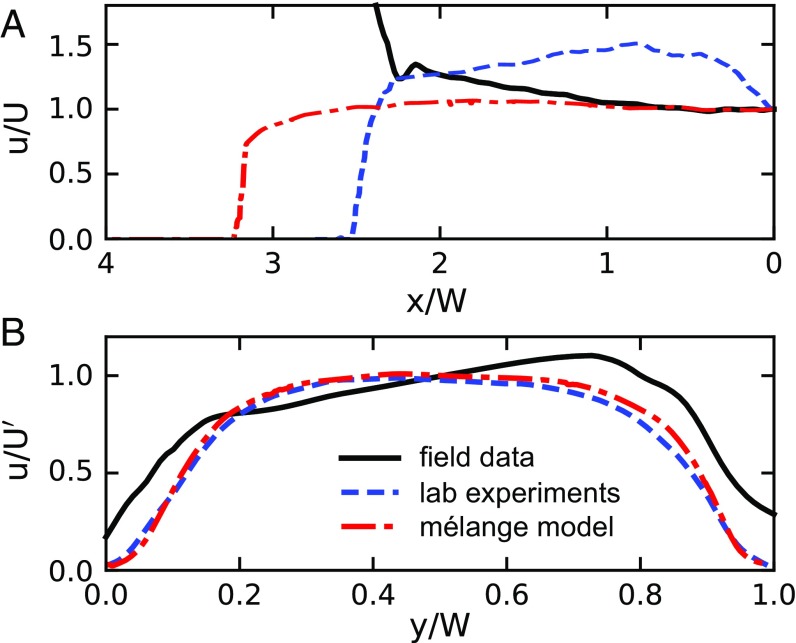
The velocity fields from all three datasets exhibit uniform flow over the majority of the fjord, except near the fjord margins where icebergs are pinned by the geometry of the walls and cannot move. The nearly uniform flow profile also indicates that the mélange is jammed over a very large spatial extent, up to tens of kilometers from the terminus. To more quantitatively compare the velocities from the three sets of data, we plot averaged longitudinal (along-fjord) and transverse (across-fjord) velocity profiles in Fig. 4. The longitudinal profiles’ spatial extent has been normalized by the fjord width and the velocity by the terminus velocity . For the transverse profiles, we normalize the velocities by the local velocity along the centerline, . This allows us to compare data where the mean velocity varies along the length of the fjord, as in Fig. 1B. The laboratory data show an increase in velocity near the terminus (Fig. 4A), which is due to the granular convection occurring at the corners between the fjord walls and the terminus (Fig. 2B). This is essentially a finite-size effect that also exists in the mélange model, yet is less evident because there are approximately three times more particles across the width of the fjord in the simulations.
Fig. 4.
(A) Time-averaged longitudinal velocity profiles taken along the middle of the fjord (). The velocity is normalized by the terminus velocity at . (B) Time-averaged transverse velocity profiles across the fjord. There is no slip along the walls of the fjord at and .
Fig. 4B shows the averaged transverse velocity profiles, which are remarkably similar between the laboratory data and the model. The middle 60% of the fjord width shows uniform flow, whereas the shear margins compose the remaining 20% on each side. Discrepancies between the field data, experiment, and theoretical results are at least partly attributable to the complex geometry of the fjord: The fjord width is not perfectly uniform and has an additional inflow of ice from the ice sheet on the north end of the transect, resulting in nonzero velocities there (Fig. 1A). In Fig. S2, we compare the velocity profiles from different mélange simulations with various fjord widths, scaled by the width of the fjord and alternatively by the smallest particle radius, . Although it seems the width of the shear margin more closely follows the particle size, narrow channels deviate significantly from this scaling. One distinguishing feature of ice mélange as a granular material is that the constitutive icebergs are very polydisperse, as opposed to most studies of granular flows which use monodisperse or nearly monodisperse samples.
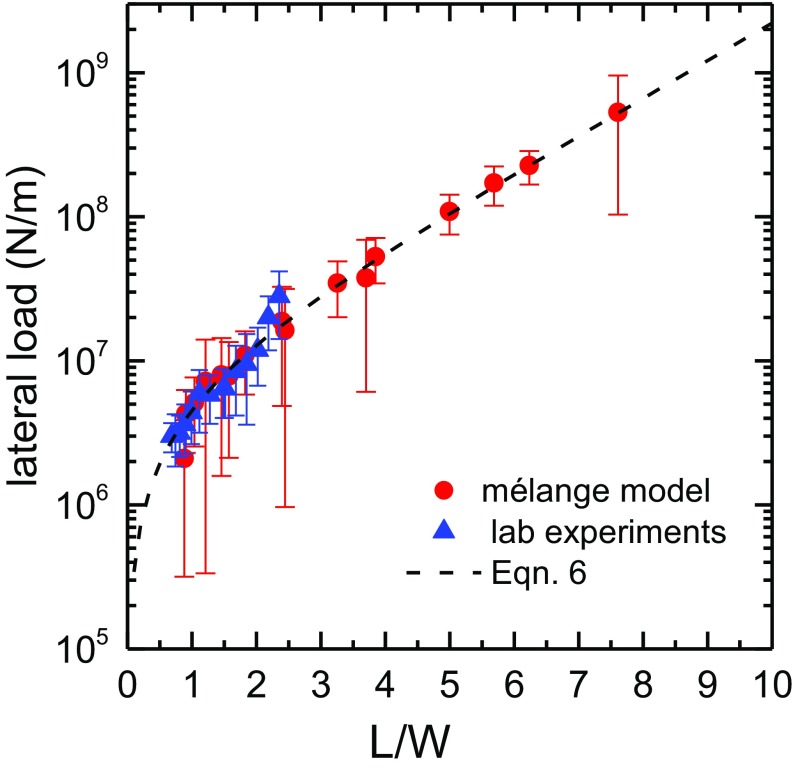
To assess the potential for ice mélange to affect calving by exerting a buttressing force on the glacier terminus, we compare the net force per unit width () on the terminus for both the model and experiment as a function of in Fig. 5. All laboratory data have been scaled by calibrating them to the simulations (Fig. S1). The data show that increases with mélange length, but decreases with mélange width. A simple dependence on the ratio may be expected by evaluating Eq. 5 at and multiplying by the thickness of the mélange:
| [6] |
Fig. 5 shows good agreement between Eq. 6 and both the laboratory experiments and the mélange model. In addition, Fig. 5 also demonstrates that the lateral load can easily exceed 107 N/m. This value is sufficient to inhibit two distinct aspects of calving: the propagation of fractures which initiate calving (15, 16) and the postfracture rotation of cubic-kilometer–sized icebergs (6).
Fig. 5.
Lateral load (force per unit width) on the glacier terminus as a function of the ratio . The laboratory data were calibrated to the model parameters, as shown in Fig. S1. The dashed line represents Eq. 6 with = 8.25 kPa, = 200 m, and = 0.3.
One limitation to 2D models and experiments is that for the loads shown in Fig. 5 and the stress shown in Fig. 3, both breakage of ice and rafting/overturning of icebergs become important. The lateral load required to buckle a floating ice field during compression is , where is the density of the water, and is a constant that depends on the iceberg geometry, density, and contact friction (21, 26). For smaller icebergs where 40 m, the buckling threshold is N/m, assuming . Thus, the load on the terminus should be quantitatively related to the local ice rubble thickness. Since the stress in the mélange decreases down-fjord (Fig. 3E), this may be important to quantitatively explain recent measurements of mélange thickness which show thicker regions near the terminus (9).
In summary, the field data, laboratory experiments, and simulations all paint a picture of a jammed, quasi-2D granular material that slowly advects through a channel. The agreement between the velocity fields shown in Fig. 4 suggests that simplified 2D models and laboratory experiments capture the salient features of ice mélange flow, despite the known variations in thickness of ice mélange within fjords. The buttressing force shown in Fig. 5 suggests that ice mélange may be thought of as a “granular ice shelf” in the jammed state characterized by a simple relationship (Eq. 6). However, this relationship may overestimate the effects of mélange during the summer when the end of the fjord may not be jammed and underestimate its effects in the winter due to the presence of binding sea ice (8).
It remains to be seen whether the flow of ice mélange (i.e., open channel, quasi-static flow) can be modeled using recent continuum rheologies of granular materials, such as the (46) or nonlocal rheology (47). A simplified rheology would help to assess the role of ice mélange along the ice–ocean boundaries of ice sheet models, which are used to project future changes in the cryosphere. Often these models assume a depth-averaged stress on the boundary, which can be computed from Fig. 5 by dividing by the glacier thickness. For example, using a glacier terminus thickness of 1,000 m, a lateral load of 107 N/m would be equivalent to 10 kPa, which is comparable to the variations in stresses on a terminus due to tides (48), although the net effect of ice mélange on calving should be enhanced by focusing the stress near the water line (15).
Supplementary Material
Acknowledgments
Radar images were made possible with an instrument loan from Mark Fahnestock and Martin Truffer at the University of Alaska Fairbanks. We gratefully acknowledge financial support from the National Science Foundation, Grants DMR-1506446 (to J.C.B.), DMR-1506991 (to C.-C.K. and M.D.), and DMR-1506307 (to J.M.A. and R.C.), and NASA Earth and Space Fellowship NNX14AL29H (to R.C.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. D.R.M. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1715136115/-/DCSupplemental.
References
- 1.Howat IM, Box JE, Ahn Y, Herrington A, McFadden EM. Seasonal variability in the dynamics of marine-terminating outlet glaciers in Greenland. J Glaciol. 2010;56:601–613. [Google Scholar]
- 2.Walter JI, et al. Oceanic mechanical forcing of a marine-terminating Greenland glacier. Ann Glaciol. 2012;53:181–192. [Google Scholar]
- 3.Humbert A, Braun MH. The Wilkins ice shelf, Antarctica: Break-up along failure zones. J Glaciol. 2008;54:943–944. [Google Scholar]
- 4.Geirsdóttir A, Miller GH, Wattrus NJ, Björnsson H, Thors K. Stabilization of glaciers terminating in closed water bodies: Evidence and broader implications. Geophys Res Lett. 2008;35:L17502. [Google Scholar]
- 5.Joughin I, et al. Continued evolution of Jakobshavn Isbræ following its rapid speedup. J Geophys Res. 2008;113:F04006. [Google Scholar]
- 6.Amundson JM, et al. Ice mélange dynamics and implications for terminus stability, Jakobshavn Isbræ, Greenland. J Geophys Res Earth Surf. 2010;115:F01005. [Google Scholar]
- 7.Cassotto R, Fahnestock M, Amundson JM, Truffer M, Joughin I. Seasonal and interannual variations in ice mélange and its impact on terminus stability, Jakobshavn Isbræ, Greenland. J Glaciol. 2015;61:76–88. [Google Scholar]
- 8.Robel AA. Thinning sea ice weakens buttressing force of iceberg mélange and promotes calving. Nat Comm. 2017;8:14596. doi: 10.1038/ncomms14596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Enderlin EM, Hamilton GS, Straneo F, Sutherland DA. Iceberg meltwater fluxes dominate the freshwater budget in Greenland’s iceberg-congested glacial fjords. Geophys Res Lett. 2016;43:11287–11294. [Google Scholar]
- 10.Moon T, et al. Subsurface iceberg melt key to Greenland fjord freshwater budget. Nat Geosci. 2017;11:49–54. [Google Scholar]
- 11.MacAyeal DR, Freed-Brown J, Zhang WW, Amundson JM. The influence of ice mélange on fjord seiches. Ann Glaciol. 2012;53:45–49. [Google Scholar]
- 12.Walters RA, Josberger EG, Driedger CL. Columbia Bay, Alaska: An ‘upside down’ estuary. Estuarine Coastal Shelf Sci. 1988;26:607–617. [Google Scholar]
- 13.Mortensen J, et al. On the seasonal freshwater stratification in the proximity of fast-flowing tidewater outlet glaciers in a sub-arctic sill fjord. J Geophys Res Oceans. 2013;118:1382–1395. [Google Scholar]
- 14.Mortensen J, Bendtsen J, Rysgaard KLS. Seasonal variability of the circulation system in a west Greenland tidewater outlet glacier fjord, Godthåbsfjord (64°N) J Geophys Res Earth Surf. 2014;119:2591–2603. [Google Scholar]
- 15.Krug J, Durand G, Gagliardini O, Weiss J. Modelling the impact of submarine frontal melting and ice mélange on glacier dynamics. Cryosphere. 2015;9:989–1003. [Google Scholar]
- 16.Todd J, Christoffersen P. Are seasonal calving dynamics forced by buttressing from ice mélange or undercutting by melting? Outcomes from full-Stokes simulations of Store Glacier, West Greenland. Cryosphere. 2014;8:2353–2365. [Google Scholar]
- 17.Vieli A, Nick FM. Understanding and modelling rapid dynamic changes of tidewater outlet glaciers: Issues and implications. Surv Geophys. 2011;32:437–458. [Google Scholar]
- 18.Reeh N, Thomas H, Higgins A, Weidick A. Sea ice and the stability of north and 5 northeast Greenland floating glaciers. Ann Glaciol. 2001;33:474–480. [Google Scholar]
- 19.Sundal AV, et al. Controls on short-term variations in Greenland glacier dynamics. J Glaciol. 2013;59:883–892. [Google Scholar]
- 20.Cook S, et al. Modelling environmental influences on calving at Helheim glacier in eastern Greenland. Cryosphere. 2014;8:827–841. [Google Scholar]
- 21.Hopkins MA, Tuhkuri J. Compression of floating ice fields. J Geophys Res. 1999;104:15815–15825. [Google Scholar]
- 22.Herman A. Molecular-dynamics simulation of clustering processes in sea-ice floes. Phys Rev E. 2011;84:056104. doi: 10.1103/PhysRevE.84.056104. [DOI] [PubMed] [Google Scholar]
- 23.Tremblay LB, Mysak LA. Modeling sea ice as a granular material, including the dilatancy effect. J Phys Oceanogr. 1997;27:2342–2360. [Google Scholar]
- 24.Løset S. Discrete element modelling of a broken ice field–Part I: Model development. Cold Reg Sci Technol. 1994;22:339–347. [Google Scholar]
- 25.Shen HH, Hibler WD, III, Leppäranta M. The role of floe collisions in sea ice rheology. J Geophys Res. 1987;92:7085–7096. [Google Scholar]
- 26.Uzuner MS, Kennedy JF. Theoretical model of river ice jams. J Hydrol Div. 1976;102:1365–1383. [Google Scholar]
- 27.Peters IR, et al. Dynamic jamming of iceberg-choked fjords. Geophys Res Lett. 2015;42:1122–1129. [Google Scholar]
- 28.Waitukaitis SR, Roth LK, Vitelli V, Jaeger HM. Dynamic jamming fronts. Europhys Lett. 2013;102:44001. [Google Scholar]
- 29.Kadanoff LP. Built upon sand: Theoretical ideas inspired by granular flows. Rev Mod Phys. 1999;71:435–444. [Google Scholar]
- 30.Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases. Rev Mod Phys. 1996;68:1259–1273. [Google Scholar]
- 31.Cates ME, Wittmer JP, Bouchaud JP, Claudin P. Jamming, force chains, and fragile matter. Phys Rev Lett. 1998;81:1841–1844. [Google Scholar]
- 32.Forterre Y, Pouliquen O. Flows of dense granular media. Ann Rev Fluid Mech. 2008;40:1–24. [Google Scholar]
- 33.van Hecke M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J Phys Condens Matter. 2010;22:033101. doi: 10.1088/0953-8984/22/3/033101. [DOI] [PubMed] [Google Scholar]
- 34.Liu AJ, Nagel SR. The jamming transition and the marginally jammed solid. Annu Rev Condens Matter Phys. 2010;1:347–369. [Google Scholar]
- 35.Kunatunga S, Kamrin K. Continuum modelling and simulation of granular flows through their many phases. J Fluid Mech. 2015;779:483–513. [Google Scholar]
- 36.Janssen HA. Versuche über getreidedruck in silozellen [Experiments on corn pressure in silo cells] Z D Ver Dtsch Ing. 1895;39:1045–1049. [Google Scholar]
- 37.Werner C, et al. 2012 The GPRI multi-mode differential interferometric radar for ground-based observations. Ninth European Conference on Synthetic Aperture Radar: EUSAR 2012. Available at https://ieeexplore.ieee.org/document/6217065/. Accessed April 17, 2018.
- 38.Dixon TH, et al. Emerging technology monitors ice-sea interface at outlet glaciers. Eos Trans AGU. 2012;93:497–498. [Google Scholar]
- 39.Lucas B, Kanade T. An iterative image registration technique with an application to stereo vision. In: Hayes PJ, editor. Proceedings of the Seventh International Joint Conference on Artificial Intelligence. William Kaufmann; Los Altos, CA: 1981. pp. 674–679. [Google Scholar]
- 40.Kuo CC, Dennin M. Buckling-induced jamming in channel flow of particle rafts. Phys Rev E. 2013;87:030201(R). [Google Scholar]
- 41.Burton JC, Lu PY, Nagel SR. Collision dynamics of particle clusters in a two-dimensional granular gas. Phys Rev E. 2013;88:062204. doi: 10.1103/PhysRevE.88.062204. [DOI] [PubMed] [Google Scholar]
- 42.Pöschel T, Schwager T. Computational Granular Dynamics: Models and Algorithms. Springer; Berlin: 2005. [Google Scholar]
- 43.Bitzek E, Koskinen P, Gähler F, Moseler M, Gumbsch P. Structural relaxation made simple. Phys Rev Lett. 2006;97:170201. doi: 10.1103/PhysRevLett.97.170201. [DOI] [PubMed] [Google Scholar]
- 44.Ovarlez G, Kolb E, Clément E. Rheology of a confined granular material. Phys Rev E. 2001;64:060302. doi: 10.1103/PhysRevE.64.060302. [DOI] [PubMed] [Google Scholar]
- 45.Karim MY, Corwin EI. Eliminating friction with friction: 2D Janssen effect in a friction-driven system. Phys Rev Lett. 2014;112:188001. doi: 10.1103/PhysRevLett.112.188001. [DOI] [PubMed] [Google Scholar]
- 46.Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature. 2006;441:727–730. doi: 10.1038/nature04801. [DOI] [PubMed] [Google Scholar]
- 47.Kamrin K, Koval G. Nonlocal constitutive relation for steady granular flow. Phys Rev Lett. 2012;108:178301. doi: 10.1103/PhysRevLett.108.178301. [DOI] [PubMed] [Google Scholar]
- 48.Walter JI, et al. Oceanic mechanical forcing of a marine-terminating Greenland glacier. Ann Glaciol. 2012;53:181–192. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.