Gravisensors in plant cells behave like an active granular liquid

Significance

The sensor of gravity in plants consists of tiny starch-rich grains called statoliths that sediment and form miniature granular piles at the bottom of the gravisensing cells. How such a sensor could be a reliable clinometer is unclear, as granular materials are known to display jamming and finite avalanche angles. Here we address this issue by comparing statolith avalanches in plant cells to microfluidic avalanches of Brownian particles in biomimetic cells. We reveal that statoliths behave like a liquid, not a granular material, due to the cell activity that strongly agitates statoliths. Our study elucidates the physical grounds of the high sensitivity of plants to gravity and bridges the active microrheology of statoliths to the macroscopic response of the plant.

Abstract

Plants are able to sense and respond to minute tilt from the vertical direction of the gravity, which is key to maintain their upright posture during development. However, gravisensing in plants relies on a peculiar sensor made of microsize starch-filled grains (statoliths) that sediment and form tiny granular piles at the bottom of the cell. How such a sensor can detect inclination is unclear, as granular materials like sand are known to display flow threshold and finite avalanche angle due to friction and interparticle jamming. Here, we address this issue by combining direct visualization of statolith avalanches in plant cells and experiments in biomimetic cells made of microfluidic cavities filled with a suspension of heavy Brownian particles. We show that, despite their granular nature, statoliths move and respond to the weakest angle, as a liquid clinometer would do. Comparison between the biological and biomimetic systems reveals that this liquid-like behavior comes from the cell activity, which agitates statoliths with an apparent temperature one order of magnitude larger than actual temperature. Our results shed light on the key role of active fluctuations of statoliths for explaining the remarkable sensitivity of plants to inclination. Our study also provides support to a recent scenario of gravity perception in plants, by bridging the active granular rheology of statoliths at the microscopic level to the macroscopic gravitropic response of the plant.

Biological sensors display a wide range of strategies that combine sensitivity and robustness to cope with a fluctuating and noisy environment. In this respect, the gravity sensor of plants is unique (1, 2). It is found in specific cells, called statocytes, in which tiny assemblies of starch-rich particles, called statoliths, sediment at the bottom of the cell and give the direction of gravity. When a shoot or a root is tilted, the detection of statoliths in statocytes triggers a complex signaling pathway involving the redistribution of growth hormones within the tissue. This leads to differential growth between the two sides of the plant organ and the bending of the organ toward the vertical direction. A remarkable feature of this gravitropic response is that it does not exhibit any threshold at low inclination (3, 4). Plant aerial organs respond to the weakest tilt, an ability that is key to maintaining their vertical posture during life under the terrestrial gravity field (5).

It has long been assumed that statocytes behaved as a force sensor, where gravity was detected by sensing statoliths’ weight on the cell edges (6) or through interaction with the cytoskeleton network (7–9). Recently, this force-sensor hypothesis has been falsified by experiments revealing that shoot gravitropism is actually insensitive to the intensity of gravity within the 0.1 to 3 g range and only depends on the inclination of the organ (4). The gravity sensor of plants thus functions as an inclination sensor rather than a force or acceleration sensor. This suggests that the position of the statoliths in statocytes, not their weight, is the relevant gravitropic stimulus (2).

The position-sensor hypothesis implies that statoliths have to move and change position to trigger the gravitropic response, even at a very small inclination. However, from a physics standpoint, such a flowing behavior of a granular assembly is challenging. A pile of grains is known to remain static as long as the pile inclination is below a critical angle known as the avalanche angle, due to friction and geometrical interlocking between particles (10). The avalanche angle lies between 5 and 30° depending on particle shape and interparticle friction (11) and also depends on the flow history through hysteresis effects. A clinometer based on these properties should thus appear poorly sensitive and unreliable. Understanding how plants overcome this constraint requires questioning the actual motion of statoliths in response to gravistimulation. Few studies have performed live cell imaging visualization of statoliths. Collective sedimentation dynamics (6, 7, 12) and individual fluctuating motion (6, 13, 14) have been reported, which are both strongly influenced by the cytoskeleton properties (14–18). The flowing behavior of statoliths could thus be more complex than that of simple passive grains. However, to date, investigations of statolith dynamics were performed only for very large inclination (90°) or after reversing the direction of the cell with respect to gravity (180°). While essential to explain the remarkable sensitivity of plant to gravity, the way statoliths move and respond to weak inclination remains unknown.

In this article, we address this issue by investigating in situ the flow response of statolith assemblies to a wide range of cell inclinations and over long time scales. We reveal a peculiar flowing behavior not observed in classical granular material, where statoliths first flow in bulk like a granular avalanche but then creep and recover a flat free surface under gravity like a liquid. To understand this behavior, we perform similar experiments using inert microsize particles in biomimetic cells. The comparison between the biological and artificial systems shows that the high fluidity of statoliths comes from their large random agitation, whose origin is not thermal but biological.

Results

In Situ Observation of Statolith Piles in Wheat Coleoptile Cuts.

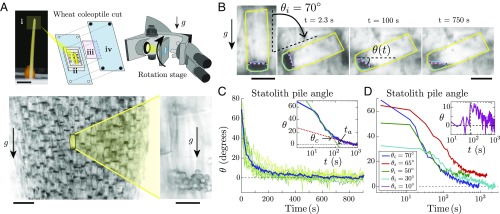
To visualize the statolith dynamics in response to plant inclination, we focus on the statocytes of wheat coleoptiles, a classical model organ in plant gravitropism studies (3, 4, 12). Those cells are mostly found along the conducting vessels or at the apex of the coleoptiles. Thin longitudinal coleoptile cuts are placed vertically in an inclined microscope, so that the observation plane contains the gravity vector (Fig. 1 A, Top and Materials and Methods). A rotation stage then orients the cells at a given angle from the gravity direction. When cells are placed vertically at rest, statoliths sediment at the bottom of the cells after several minutes. Brightfield illumination over a wide field of view shows a large number of statocytes where all dark spots are groups of statoliths (Fig. 1 A, Bottom Left). Observation with a higher magnification reveals that statocytes typically contain a few tens of statoliths that form a pile at the bottom of the cell (Fig. 1A). Theses piles are analogous to tiny granular packings made of a few layers of grains (typically 2 to 3) and composed of nearly spherical grains of diameter $d=4.5\pm 0.5$ $\mathrm{\mu }$m.

Fig. 1.

Statolith avalanches in gravisensing cells of wheat coleoptiles. (A, Top) Experimental setup: (i) wheat coleoptile and part close to the apex from which the cut is taken. (Scale bar, 5 mm.) (ii) PDMS chamber with pillars. (iii) Glass coverslip. (iv) PMMA vise. (Bottom Left) Visualization of statolith piles (dark areas) sedimented at the bottom of the cells under gravity. (Scale bar, 100 $\mathrm{\mu }$m.) (Bottom Right) Close-up on a gravisensing cell showing the individual statoliths of diameter $d$ about 4.5 $\mathrm{\mu }$m. (Scale bar, 20 $\mathrm{\mu }$m.) (B) Time-lapse pictures of the avalanche of statoliths after tilting the rotation stage by ${\theta }_i=70^{°}$. The statolith pile angle $\theta \left(t\right)$ is defined as the angle made by the free surface of the statoliths obtained from image analysis (purple line) with the horizontal (see Materials and Methods). (Scale bar, 25 $\mathrm{\mu }$m.) (C) Statolith pile angle vs. time for $n$ different cells (green lines, $n=13$) from the same cut initially inclined at $70^{°}$. The blue line corresponds to the averaged value. (Inset) Averaged time evolution in semilogx representation, showing a first fast avalanching regime (linear fit in green) followed by a slow creeping regime (linear fit in red). The transition between the two regimes occurs at a critical angle ${\theta }_c\simeq 10^{°}$. The typical characteristic time $t_a$ is defined by extending the avalanche regime to $\theta =0$. (D) Averaged statolith pile angle vs. time for different initial inclination above the critical angle ${\theta }_c$ and different cuts ($n$ is between 8 and 13). (Inset) Statolith pile angle vs. time for an initial inclination ${\theta }_i=10^{°}\simeq {\theta }_c$ ($n=6$). The vertical dashed line corresponds to the time when the cut was tilted.

Statolith Avalanches Reveal Liquid-Like Behavior.

To trigger the motion of statoliths, a large tilt angle (${\theta }_i=70^{°}$) is applied to the cells by rotating the stage (Fig. 1B and Movie S1). Time-lapse video shows that statoliths move collectively like a miniature submarine avalanche of grains (11, 19), reaching their new rest position in a few minutes. To quantify these avalanche dynamics, we developed a dedicated image processing tool that tracks the free surface of the statolith pile during the avalanche (Fig. 1B, Movie S2, and Materials and Methods). This technique enables us to measure the angle $\theta \left(t\right)$ made by the free surface of the pile with the horizontal over several cells, simultaneously (Fig. 1 B and C). While $\theta \left(t\right)$ for a single pile exhibits large fluctuations due to the small number of statoliths per pile, the averaged value of the pile angle over several cells is well-defined. Fig. 1C shows that the free surface of statolith piles relaxes to horizontal, as a liquid would do. Plotting data using a time-logarithm scale reveals that the avalanche dynamics are actually composed of two different regimes (Fig. 1 C, Inset; see Methodology to Define and Fit the “Avalanche” and “Creep” Regimes and Fig. S1 for the procedure to fit the two regimes). First, the pile angle rapidly decays in a characteristic time $t_a\simeq 2$ min from the initial inclination ${\theta }_i$ to a critical angle ${\theta }_c\simeq 10^{°}$. This regime is similar to a granular flow above the avalanche angle (11, 19). After this rapid avalanche, the pile angle slowly creeps from ${\theta }_c$ to zero in about 10 to 20 min. This two-regimes dynamic is observed as long as the initial tilt angle is larger than the critical angle ${\theta }_c$ (Fig. 1D). However, statolith piles are found to creep and relax even when the initial tilt is smaller than the critical angle (${\theta }_i<10^{°}$; Fig. 1D, Inset and Fig. S2 in Statolith Avalanches for a Small Initial Inclination). Hence, the final horizontal surface of the piles does not result from inertial effects induced by a large initial tilt, which is confirmed by the low value of the Reynolds number for this flow [$Re=\rho UL/\eta \sim 10^{-6}$, where $\rho \sim 10^3$ kg m⁻³ is the density of the cytoplasm, $U\sim 10$ $\mathrm{\mu }$m min⁻¹ the maximal statolith avalanche velocity, $L=20$ $\mathrm{\mu }$m the statolith pile size, and $\eta \sim$ 10 mPa s the cytoplasm viscosity (18)]. Our data thus show that statoliths move and respond to the weakest pile inclination. This liquid-like behavior is in striking contrast with the behavior of granular materials made of macroscopic grains like sand, for which no flow is possible below a critical angle (10). We emphasize that although the long-time behavior of statoliths resembles that of a liquid because the free surface relaxes to horizontal, the flowing properties of statoliths (rheology) are not that of a standard liquid. A viscous liquid would become flat with an exponential relaxation, while statoliths reach horizontal by a slow logarithm relaxation (creeping behavior).

Individual Statoliths Exhibit Random Motion.

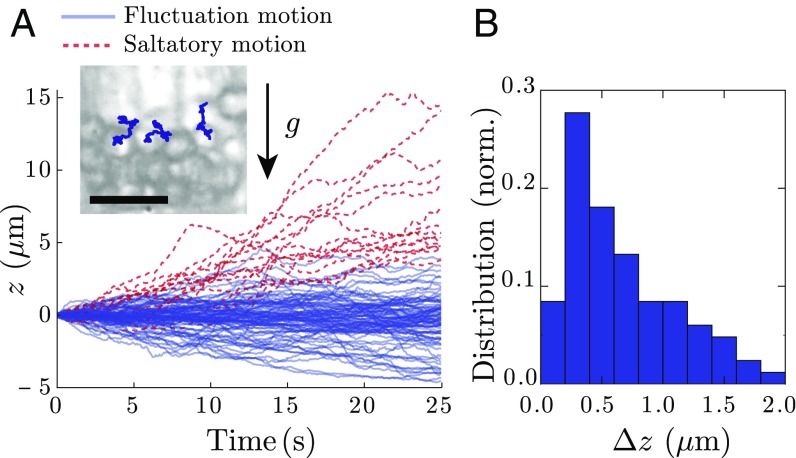
To understand the origin of the long-time liquid behavior of statoliths, we next focus on the particle level. Close-up videos of statolith piles during avalanche (Movie S3) or at rest (Movie S4) show that individual statoliths do not behave like passive grains but are strongly agitated as observed in other plant species and organs (6, 13, 15, 17, 18, 20). We have quantified this agitation by tracking the vertical motion of statoliths on top of piles at rest (Fig. 2A and Materials and Methods). Most statoliths are found to vibrate around their equilibrium position (called fluctuation motion in Fig. 2A), while some show high vertical drift against gravity [often called saltatory motion in the literature (6, 13, 17)]. Importantly, the SD $\mathrm{\Delta }z$ of the vertical fluctuations always represents a significant fraction of the statolith diameter $d$, even without considering the saltating particles (Fig. 2B). The statolith pile is thus analogous to a granular heap shaken from the outside (21). This agitation likely helps statoliths to unjam and move with respect to their neighbors, thus fluidizing the medium.

Fig. 2.

Statolith agitation. (A) Vertical trajectories of $n$ statoliths at the surface of a sedimented pile ($n=98$). Blue, fluctuating motion defined by $\mathrm{\Delta }{z}_{\text{max}}<d$ within the observation time window ($t=25$ s). Red, saltatory motion defined by $\mathrm{\Delta }{z}_{\text{max}}>d$. (Inset) Picture of statoliths at the top of a sedimented pile with individual 2D trajectories drawn. (Scale bar, 10 $\mathrm{\mu }$m.) (B) Measured distribution of $\mathrm{\Delta }z$ (SD of vertical trajectory) for the fluctuation motion ($n=83$).

Designing Biomimetic Gravisensing Cells.

These results suggest that statolith agitation is critical to explain the liquid-like behavior of statolith piles. Two main hypotheses can be advanced for this agitation. The first one is purely physical and comes from the Brownian motion undergone by any small objects immersed in a liquid due to thermal fluctuations. The second one is the cell activity and more precisely the dynamics of the actin cytoskeleton (22). This last hypothesis is supported by studies using actin inhibitors or actin mutants showing a decrease of saltation motion in Arabidopsis thaliana stems (14, 17). However, disrupting actin also decreases the cytoplasm viscosity and speeds up the diffusion of statoliths in other systems (roots) (18, 23), making the interpretation of these mutant or drug-based experiments difficult.

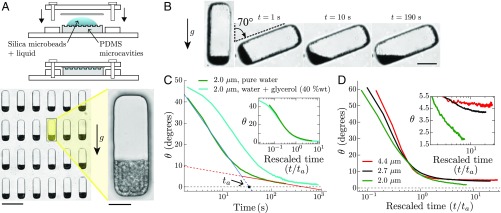
To decipher which agitation mechanism is the primary cause of the fluidity of statolith piles, we adopt a different strategy and use a biomimetic approach. We design an artificial system made of water-filled microfluidic cavities molded in a PDMS matrix that mimic the geometry of actual statocytes ($100\hspace{0.17em}\mathrm{\mu }\text{m}\times 30\hspace{0.17em}\mathrm{\mu }\text{m}\times 50\hspace{0.17em}\mathrm{\mu }\text{m}$). The cells are filled with microsize silica particles that mimic statoliths and form weakly Brownian piles at the bottom of the cells (Fig. 3A and Materials and Methods). In this system, Brownian motion is the only source of particle agitation. The strength of this agitation is given by the inverse of the dimensionless gravitational Péclet number:

$$P{e}^{-1}=\frac{k_{\mathrm{B}}T}{mgd},$$ [1]

which quantifies the ratio between the Brownian thermal forces that push particles in random directions and the weight of particles that pulls particles downward (24) [$d$ is the particles diameter, $m=\left(\pi d^3/6\right)\times \mathrm{\Delta }\rho$ is the particle mass corrected by the buoyancy where $\mathrm{\Delta }\rho$ is the difference of density between the particles and the surrounding fluid, $g=9.81\hspace{0.17em}\text{m}\hspace{0.17em}{\text{s}}^{-2}$ is the intensity of the gravity, $T=298\hspace{0.17em}\text{K}$ is the absolute temperature, and $k_{\mathrm{B}}=1.38\times 10^{-23}\hspace{0.17em}\text{J}\hspace{0.17em}{\text{K}}^{-1}$ is the Boltzmann constant]. Importantly, the inverse Péclet number strongly varies with the particle diameter as $d^{-4}$, since mass is proportional to $d^3$. We can thus easily tune the relative amplitude of thermal agitation compared with gravitational force by changing the particle diameter without changing the temperature. For statoliths in wheat coleoptiles, $d=4.5\pm 0.5$ $\mathrm{\mu }$m and $\mathrm{\Delta }\rho \sim 400\hspace{0.17em}\text{kg}\hspace{0.17em}{\text{m}}^{-3}$ (25, 26), giving inverse Péclet numbers between 3 $\times$ 10⁻³ and 8 $\times$ 10⁻³. In the biomimetic system, the diameter of the silica particles is chosen between 2 and 4.4 $\mathrm{\mu }$m, yielding $P{e}^{-1}$ between 2.5 $\times$ 10⁻³ and 6 $\times$ 10⁻².

Fig. 3.

“Statolike” avalanches in biomimetic cells made of PDMS microcavities filled with a suspension of heavy silica microparticles. (A, Top) Sketches of the biomimetic device, open and closed. (Bottom Left) Picture showing PDMS microcavities filled with 4.4 $\mathrm{\mu }$m silica particles that settled under gravity. (Scale bar, 100 $\mathrm{\mu }$m.) (Bottom Right) Close-up on a single biomimetic cell. (Scale bar, 20 $\mathrm{\mu }$m.) (B) Time-lapse pictures of an avalanche for 2.0 $\mathrm{\mu }$m silica particles in water ($P{e}^{-1}\approx 0.06$). (Scale bar, 25 $\mathrm{\mu }$m.) (C) Pile angle vs. time for 2.0 $\mathrm{\mu }$m silica particles initially inclined at $50^{°}$ in pure water (green curve, viscosity $\eta \approx 0.85\hspace{0.17em}\text{mPa}\hspace{0.17em}\text{s}$, averaged over $n=40$ biomimetic cells) or in water$/$glycerol 40% (wt) mixture (cyan curve, viscosity $\eta \approx 2.9\hspace{0.17em}\text{mPa}\hspace{0.17em}\text{s}$, $n=24$). The two regimes (fast avalanche and slow creep) are visible in both curves, and typical characteristic time $t_a$ can be defined as for statoliths. (Inset) Same data when the time axis is rescaled by the characteristic time $t_a$ for each viscosity. The ratio of $t_a$ found from the curves corresponds rather well to the ratio of fluid viscosity (2.9 vs. 3.4). (D) Pile angles vs. rescaled time for different sizes of silica particles corresponding to a different inverse Péclet number: $P{e}^{-1}\approx 0.06$ ($d=$ 2.0 $\mathrm{\mu }$m, $n=40$), $P{e}^{-1}\approx 0.017$ ($d=$ 2.7 $\mathrm{\mu }$m, $n=38$), and $P{e}^{-1}\approx 0.0025$ ($d=$ 4.4 $\mathrm{\mu }$m, $n=39$). (Inset) Close-up on the creep regime.

The Péclet Number Controls the Transition Between Granular to Liquid-Like Avalanches in Biomimetic Cells.

Fig. 3B and Movie S5 show typical avalanche dynamics with the biomimetic system in the case of the smallest particle size investigated—that is, the highest thermal agitation relative to particle weight ($P{e}^{-1}\approx 0.06$). Contrary to macroscopic granular media, the free surface of the Brownian pile relaxes to horizontal, revealing a liquid-like behavior similar to the one observed with statoliths. The time evolution of the pile angle also reproduces the two-time dynamics observed in statolith avalanches, with a fast avalanche regime of characteristic time $t_a$ followed by a slow creep regime (Fig. 3C; see Silica Particles Avalanches for a Small Initial Inclination and Fig. S3 for data at small initial inclinations). Interestingly, changing the viscosity of the liquid surrounding the particles only changes the time scale of the dynamics but not its characteristic shape. When time $t$ is rescaled by $t_a$ for two different viscosities, the whole dynamic collapses on the same curve, showing that viscosity has no influence on the creeping behavior of the pile as expected from dimensional analysis (Fig. 3C, Inset; see Dimensional Analysis for the dimensional analysis of the problem). By contrast, increasing the diameter of the particles, and thus decreasing the thermal agitation relative to their weight, strongly affects the creep regime (Fig. 3D). As $P{e}^{-1}$ decreases, a transition is observed from a liquid-like behavior where the pile rapidly relaxes to horizontal (small particles, large agitation; Movie S6) to a granular-like behavior where the creeping time dramatically increases and the pile angle seems to saturate to a finite value (large particles, low agitation; Fig. 3D, Inset and Movie S7).

Active (Non-Brownian) Fluctuations Are Responsible for Statoliths’ Liquid-Like Behavior.

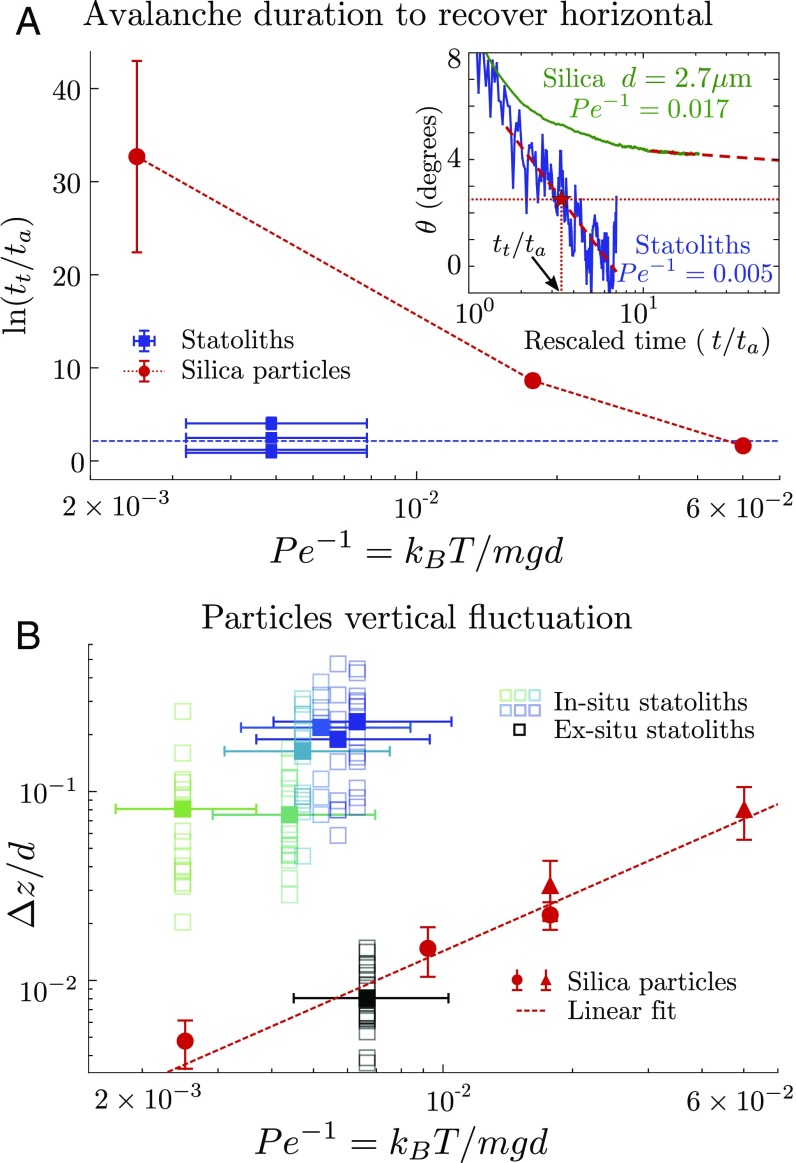
Our finding that the creeping behavior of Brownian avalanches is solely controlled by the Péclet number, and not by viscosity, enables us to test whether or not thermal agitation is responsible for the high fluidity of statoliths in plant cells. To this end, we normalize the total duration needed for the pile to reach an arbitrary small angle, $t_t$, by the characteristic time $t_a$ that contains the contribution of the viscosity (Fig. 4A, Inset; see Methodology to Define and Fit the “Avalanche” and “Creep” Regimes for the procedure to measure $t_t$). We can then compare the rescaled duration $t_t/t_a$ of the biomimetic and biological systems, even though the liquid viscosity might not be the same in both cases. Fig. 4A gives $\ln \left(t_t/t_a\right)$ as a function of the inverse Péclet number $k_{\mathrm{B}}T/mgd$ for both the biomimetic and biological systems. For purely Brownian particles (red dots), the avalanche duration strongly increases when $k_{\mathrm{B}}T/mgd$ decreases, as evidenced by the logarithm scale. However, statoliths (blue squares) clearly deviate from the Brownian case. They flow about 10,000 times faster than purely Brownian particles of the same inverse Péclet number ($k_{\mathrm{B}}T/mgd\approx 0.005$). Fig. 4A shows that statoliths actually behave as Brownian particles having an inverse Péclet number one order of magnitude larger than theirs ($k_{\mathrm{B}}T/mgd\approx 0.06$). Everything thus happens as if statoliths were agitated by an apparent temperature 10 times larger than the actual temperature.

Fig. 4.

Comparison between the biological and biomimetic (Brownian) systems. (A) Logarithm of the rescaled duration for the pile to reach an arbitrary small threshold angle of $2.5^{°}$, $\ln \left(t_t/t_a\right)$, vs. $P{e}^{-1}$. Horizontal error bars for statoliths come from the dispersion in statolith diameter. Vertical error bars for silica particles represent the dispersion of results obtained by changing the length of data used to extrapolate the avalanche to the threshold angle. (Inset) Pile angle vs. rescaled time $t/t_a$ for statoliths and purely Brownian silica particles of diameter $d=2.7$ $\mathrm{\mu }$m. (B) Rescaled vertical fluctuations $\mathrm{\Delta }z/d$ of statoliths (green and blue squares, in situ measurements; black squares, ex situ measurements) and purely Brownian silica particles (circles and triangles) vs. $P{e}^{-1}$. Empty squares correspond to individual particle trajectories and filled squares to the average over trajectories from one sample.

We confirmed this result by directly comparing the vertical amplitude of agitation $\mathrm{\Delta }z$ of silica particles and individual statoliths at the top of the pile at rest in the biomimetic and biological systems (Fig. 4B and Materials and Methods). The normalized vertical fluctuation $\mathrm{\Delta }z/d$ for silica particles (red symbols) linearly increases with the inverse Péclet number, as predicted from the balance between the gravitational and thermal energy: $mg\mathrm{\Delta }z\sim k_{B}T$—that is, $\mathrm{\Delta }z/d\sim P{e}^{-1}$ (24). By contrast, the agitation of statoliths in the gravisensing cells (green and blue symbols) is about 10 times larger than that of purely Brownian particles with the same $P{e}^{-1}$. Finally, when statoliths are extracted from the cells and immersed in pure liquids, they precisely recover the Brownian agitation predicted by their density and size (black squares in Fig. 4B; see also Materials and Methods). Therefore, the agitation of statoliths in the cells is not Brownian and must come from biological—that is, active—processes inside the cell.

Discussion

The sensor of gravity in plants was recently shown to be a highly sensitive clinometer rather than a force or acceleration sensor (4). In this paper, we have addressed the physical basis of this sensitivity at the cellular level, by focusing on the flow behavior of the statoliths—the intracellular granular piles at the origin of gravity perception in plants.

Our results show that, despite their granular nature, statolith piles move and respond to the weakest angle, as a liquid would do. We showed that such liquid-like behavior can be recovered in a biomimetic system made of heavy Brownian particles, if the amplitude of the thermal agitation of the particles relative to their weight, quantified by the inverse Péclet number $k_{\mathrm{B}}T/mgd$, is large enough. However, comparison between the biological and biomimetic system revealed that statoliths are much more agitated and mobile than purely Brownian particles of the same temperature and weight. Statoliths thus behave like an active granular material, in which particle agitation results from cell activity rather than Brownian motion.

The cytoskeleton activity, and more precisely the actin–myosin network dynamics, is a good candidate for this agitation. Statoliths are embedded in the cytoskeleton and were shown to strongly interact with actin filaments (AFs) through the SGR9 ligase in the statocytes of the inflorescence stem of A. thaliana (17). Experiments using actin inhibitors and mutants inducing a fragmentation of AFs also reported a reduction of the saltatory motion of statoliths (17), suggesting a key role of actin in statolith agitation. However, actin inhibitors also decrease the cytoskeleton viscosity, making statoliths more mobile (18, 23). Our study shows that it is possible to disentangle both effects. Viscosity only affects the time scale $t_a$ of the flow of statoliths in response to inclination. However, the rescaled avalanche dynamics $t/t_a$ and the normalized vertical agitation of statoliths under gravity $\mathrm{\Delta }z/d$ are both independent of viscosity; they only depend on the relative agitation compared with particle weight. Fig. 4 thus provides a benchmark to quantify the role of the actin–cytoskeleton network on statolith dynamics for future studies using actin mutants or drugs.

Our finding gives a physical ground to the high sensitivity of plants to small inclination. Statolith fluctuations driven by cell activity play the role of an external agitation that unlocks statoliths and help them to respond to any inclination. The rheology of such an active granular material is still an open issue, but recent numerical simulations suggest that grain activity could indeed erase the avalanche angle and the flow threshold in active dry granular media (27). Our biomimetic system where fluctuations are thermally activated provides a first step for better understanding the flow of such active granular matter. It also offers a route for designing clinometers at small scale based on dense Brownian suspensions, which are not hindered by surface tension effects like classical bubble levels or liquid-based clinometers.

Overall, our study supports the growing consensus that the sensor of gravity in plants is a position sensor, related to the averaged position of the statoliths inside the cell (4, 20, 28) [the position-sensor hypothesis (2)]. When statocytes are inclined, statolith piles flow to recover a horizontal free surface like a liquid. Therefore, more statoliths are found on one side of the cell than on the other, whose proportion varies with the sine of the cell inclination (2). According to the position-sensor hypothesis, the gravitropic stimulus should thus also be proportional to the sine of the tilt angle. It is remarkable that such a “sine law” is recovered at the macroscopic level for the gravitropic response of plant shoots to inclination (3, 4, 29). The activated liquid-like rheology of statoliths, together with the position-sensor hypothesis, could thus provide a robust explanation for the sine law based on simple geometrical arguments. To further investigate this picture, it would be interesting to link the distribution of statoliths within the cell to the distribution of key molecular signals of graviperception (1). Finally, our study suggests that sensitivity and robustness in plant graviperception arise from interplay between local active noise and global integration of statolith position within the cell. Such strategy brings the gravisensor of plants closer to other biological sensors like hair cells (30) or tactile whiskers (31).

Materials and Methods

Plant Material.

Wheat coleoptiles used in the experiments are grown from wild-type wheat seeds (Triticum aestivum cv Demeter; see ref. 4 for the detailed growing conditions). Experiments are carried out when the coleoptiles are between 1.5 and 2.5 cm tall (about 4 d after germination) before the leaves emerge. The coleoptiles are manually cut close to the apex with razor blades in the longitudinal direction. A slice (few millimeters in length) is then put between a polydimethylsiloxane (PDMS) container and a glass coverslip with a few droplets of 0.2 mol ${\text{L}}^{-1}$ sorbitol solution. The PDMS container is a $1.5\hspace{0.17em}\text{cm}\times 1.2\hspace{0.17em}\text{cm}$ rectangle with 100 $\mathrm{\mu }$m depth. It has small pillars to prevent the motion of the coleoptile cut when the container is rotated under the inclined microscope. The PDMS chamber is clamped on a custom-build Plexiglas vise to avoid any slip during observation. All visualizations are done under low illumination and within a few hours after cutting to maintain the cell activity.

Biomimetic Samples.

The biomimetic cells were made in PDMS using standard microfluidic fabrication techniques (32): A negative mold with the desired pattern (a matrix of about 25,000 pillars with $30\hspace{0.17em}\mathrm{\mu }\text{m}\times 100\hspace{0.17em}\mathrm{\mu }\text{m}$ size and $50\hspace{0.17em}\mathrm{\mu }\text{m}$ height) was made in SU-8 photoresist, and then the mold was used to create a positive replica with the Sylgard$Ⓡ$ 184 Silicone Elastomer Kit (10% wt cross-linker, cured one night at $6{0\hspace{0.17em}}^{°}\text{C}$ in an oven). The final PDMS container is a matrix of cells (each one is a cavity $30\hspace{0.17em}\mathrm{\mu }\text{m}\times 100\hspace{0.17em}\mathrm{\mu }\text{m}$ size and $50\hspace{0.17em}\mathrm{\mu }\text{m}$ depth). The inert particles are commercial silica particles from Microparticles GmbH, with diameter size $2.06\pm 0.05$, $2.68\pm 0.05$, $3.18\pm 0.13$, and $4.40\pm 0.24$ $\mathrm{\mu }$m, and density $1850\hspace{0.17em}\text{kg}\hspace{0.17em}{\text{m}}^{-3}$, available in aqueous solutions (5% wt of particles).

Microscopic Observations.

All observations were made using a microscope (Leica DM 2500P) flipped horizontally so that the plane of observation is vertical and contain the gravity vector. Samples are held on a rotational stage (M-660 PILine$Ⓡ$) with a maximal velocity of $72{0\hspace{0.17em}}^{°}{\text{s}}^{-1}$ and controlled by a C-867 PILine$Ⓡ$Controller. Small magnifications (10$\times$, 20$\times$) are used to visualize piles of particles with a good contrast; bigger magnifications (40$\times$, 100$\times$) are used to resolve single trajectories of particles. Images ($3696\times 2448$ pixels, with an acquisition rate up to 1 fps) and movies ($1920\times 1080$ pixels at 24 fps) are taken with a Nikon D7000.

Image and Data Processing.

All image analyses were done with custom-developed Python scripts, based on usual scientific libraries (Numpy 1.11.1 and Matplotlib 1.5.1) and image processing tools from Scikit-image (version 0.12.3) and OpenCV (version 2.4.11).

Pile Angle.

Statolith pile angles were measured using the following method. First, potential image drifts are corrected over the whole movie using image correlation on a reference pattern. Then, the edges of the statocyte cells are manually delineated for each cell where a pile is visible on the first frame of the movie (yellow line in Fig. 1B). The image is cropped along the cell edges and a local minimum filter is applied to enhance the contrast of the pile, whose contour is extracted using a contour finding algorithm (blue line in Fig. 1B). Finally, the pile angle is defined by linking the two points where the pile ceases to be in contact with the edges of the cell (purple line in Fig. 1B and Movie S2).

Particle Tracking.

The trajectories of statoliths and silica particles on top of piles at rest were determined using a two-step tracking method and image correlation. In a first step, approximate trajectories are obtained using a reference circle for image correlation and an adaptive threshold that enhances the edge of the particle. These approximate trajectories are used to reconstitute, for each particle, an averaged particle image. In a second step, this reference image is used to obtain a more precise trajectory.

Vertical Fluctuations $\mathrm{\Delta }z/d$.

For silica particles in water, $\mathrm{\Delta }z$ was estimated by computing the SD on independent 10-s times windows taken on longer trajectories. To avoid any enhancement of the SD due to external drifts, all trajectories were corrected beforehand by a low-pass filtered trajectory of a stuck particle of the same sample. For statoliths, the SD was computed on independent 30 s-long trajectories, because the dynamics are slower due to the higher viscosity. Note that for the smallest silica particle studied ($2.06\hspace{0.17em}\mathrm{\mu }\text{m}$), it was not possible to track single particles on top of piles even at the highest magnification. The amplitude of the vertical fluctuations $\mathrm{\Delta }z$ was then estimated by taking the temporal fluctuations of the free surface of the pile. Using the 2.68-$\mathrm{\mu }\text{m}$ particles, we checked that both methods (particle tracking and free surface fluctuations) give the same result (see red circles and triangles in Fig. 4B).

Statolith Extraction.

Statoliths were extracted from cells by cutting coleoptiles in the longitudinal direction with a razor blade in a 0.8 mol ${\text{L}}^{-1}$ sorbitol solution, which prevents the osmotic bursting of the statoliths (33). The cut coleoptiles were then placed in the PDMS container described in Plant Material. Statoliths leaking out of the cut cells were let to sediment 2 h under gravity in the clear sorbitol solution. Measurement of vertical fluctuations was performed on individual statoliths that had fallen to the bottom of the container (black squares in Fig. 4B).

Data are available on the open-source database Zenodo, https://zenodo.org/record/1186833.