Partitioning ground reaction forces for multi-segment foot joint kinetics

Abstract

Background

Kinematic multi-segment foot models have been increasingly used to study foot function. The addition of kinetics to these models may enhance their utility; however, this been hindered by limitations in measuring ground reaction forces (GRFs) under individual foot segments.

Purpose

To determine the accuracy of partitioning segment GRFs from a single force platform on foot joint kinetics.

Methods

Two potential partitioning methods were applied to a previously published three-segment kinetic foot model. The first method calculated joint kinetics only when the center of pressure crossed anterior to a joint (CPcross). The second method utilized a virtual pressure mat and a proportionality assumption to partition GRFs from the force platform (PRESS). Accuracy was assessed by comparing joint moments and powers obtained from each partitioning method to those obtained from a dual force plate approach that isolated forces under two segments at a time (2Plate). Thirteen healthy pediatric subjects walked in a controlled manner so as to isolate the kinetics acting at the metatarsophalangeal (MTP) joint and, subsequently, the midtarsal joint.

Results

The PRESS method was generally more accurate than the CPcross method, and both methods were more accurate at the midtarsal joint than at the MTP joint. At the MTP joint, sagittal plane moment peaks, power peaks, and work done were slightly overestimated, more so by CPcross than PRESS. At the midtarsal joint, sagittal plane moments were captured well by PRESS, while CPcross missed the early portion of the moment, but both methods captured power profiles fairly accurately.

Significance

Analysis of kinetics in multi-segment foot models may provide insight into foot function, pathologies, and interventions. Partitioning accuracy and generalizability is promising for analysis of the midtarsal joints but has limitations at the MTP joint.

1. INTRODUCTION

In clinical gait analysis and human movement research, traditional single segment foot models are increasingly being replaced by models that subdivide the foot into several segments (e.g. [1–4]). To date, these multi-segment foot (MSF) models have primarily been confined to the analysis of joint angles. Expanding these kinematic-only models to also allow for kinetics analysis may provide additional insights into foot function [5–9], but requires several additional parameters. In addition to segment orientations, inverse dynamics based kinetics calculations also rely on identification of joint centers of rotation, estimation of segment inertial properties, and measurements of ground reaction forces (GRFs) under each segment. Of these, measuring segment GRFs is perhaps the most difficult hurdle from a technological standpoint, as commercial devices capable of measuring both segment vertical and shear forces are not yet commonplace [10], and the use of multiple adjacent force plates [5, 11, 12] requires targeted walking which may not be clinically feasible.

A method that can accurately partition the GRFs from a single force plate is attractive because it would allow MSF joint kinetics to be calculated from commonly employed equipment already found in gait and movement analysis clinics and laboratories. Two potential methods of GRF partitioning have been developed previously. The first method quantifies joint kinetics from a single force plate only when the location of the center-of-pressure (CoP) passes anterior to the joint, i.e. the entire GRF is applied to adjacent segments sequentially. This technique has only been used to examine kinetics of the metatarsophalangeal joints [e.g. 13–15], but could theoretically also be applied to other joints in the foot, such as the midtarsal joint. The second method employs an additional pressure mat secured to the top of the force plate. The segment vertical forces from the pressure mat are then used to help partition the shear forces from the force plate using an assumption of proportionality [7, 16]. The accuracy of this latter method on segment GRFs alone has been evaluated [9, 17, 18], but neither method has been validated in terms of application to inverse dynamics based MSF joint kinetics.

The purpose of the present study was to assess the accuracy of potential GRF partitioning methods on the calculation of MSF joint kinetics (i.e. moments, powers, and work), using a previously published kinetic multi-segment foot model [5, 19]. This was accomplished by comparing estimates obtained from the partitioning methods to those from a multiple force plate approach that isolated forces under two segments at a time. By studying the potential errors inherent in these methods, we hope to better understand their validity and applicability. The ability to calculate foot joint kinetics from a single force platform would provide researchers and clinicians with a new tool with which to study foot muscle function, better understand foot pathologies, and evaluate potential treatment interventions.

2. METHODS

2.1 Participants

We re-analyzed data that were previously collected [5, 17, 19], consisting of 13 healthy pediatric participants(9M/4F; age 13.1 ± 3.1; height 156 ± 18 cm, weight 51 ± 18 kg). Four of the original 17 subjects were excluded due to concerns over foot placement accuracy. All participants were volunteers and signed consent forms approved by the local Institutional Review Board.

2.2 Protocol

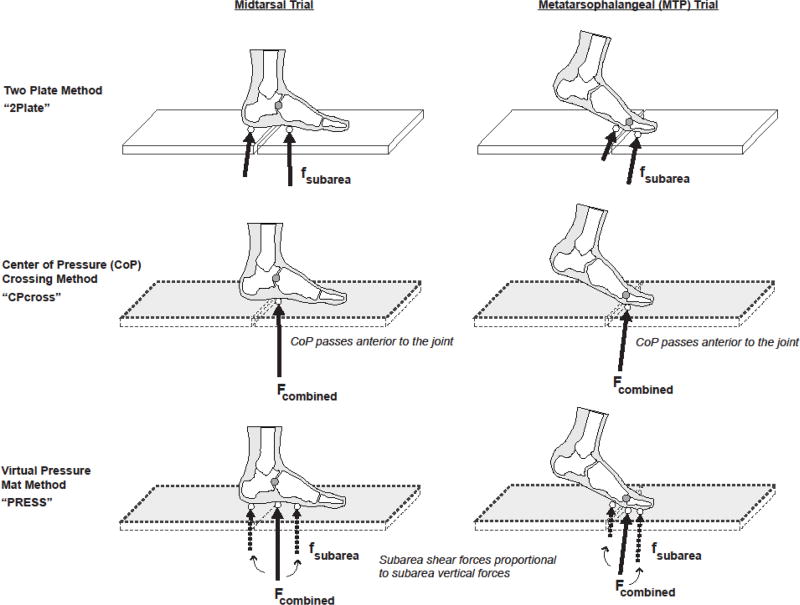
The employed marker set, associated multi-segment foot model, and collection protocol have all been previously documented [5, 19]. Details that are particularly relevant to this study are described briefly here. Nineteen total reflective markers were first placed on the right leg and foot of each participant. The associated three segment foot model consists of hindfoot, mid/forefoot (hereafter referred to as simply the ‘forefoot’ segment), and hallux segments separated by midtarsal and metatarsophalangeal (MTP) joints. The midtarsal joint center was defined as the midpoint between markers placed on the navicular and cuboid bones, while the MTP joint was estimated at the center of the first metatarsal head by projecting a dorsal marker vertically downward. Each participant next walked at a self-selected speed across a floor containing two force plates (AMTI inc., Watertown MA USA, model OR6-7-1000) that were positioned directly adjacent to each other (separated by a 2mm gap). Two sets of trials (Figure 1) were collected using a controlled three-step approach. In the MTP trials, the third step was intended to position the entire hallux segment so that it contacted the anterior force plate, while the rest of the foot contacted the posterior force plate. These trials were used to analyze the kinetics of the MTP joint. In the midtarsal trials, the hallux and forefoot segments contacted the anterior force plate, while the hindfoot was isolated on the posterior plate. These trials were used to analyze the kinetics of the midtarsal joint. Participants were instructed to walk as normally as possible, while the investigators adjusted the starting positions to ensure appropriate foot contact. Obtaining three successful trials typically required 15–30 trials, and proper foot contacts were verified visually by two video cameras located on either sides of the force plates.

FIGURE 1.

Trial types and partitioning methods. Two sets of trials were collected: Midtarsal trials (left column) isolated the hindfoot and forefoot segments on separate force plates, while MTP trials (right column) isolated the forefoot and hallux segments on separate force plates. Inverse dynamics computations were performed three times: (1) using the two adjacent plates (2Plate method, top row), (2) using the summed force plates, assigning the force to each segment sequentially based on anterior-posterior center-of-pressure location (CPcross, 2^nd row), and (3) using the summed force plates, the vertical forces from the two individual plates, and an assumption of proportionality (PRESS, 3^rd row). Accuracy of the CPcross and PRESS methods were assessed by comparing estimates of midtarsal and MTP joint kinetics (moment and power) to those obtained from the 2Plate method.

2.3 Data Analysis

Marker trajectories were collected at 120 Hz (Vicon 612 system, Oxford England UK) and filtered at 6 Hz, while GRF data was collected at 1560 Hz, filtered at 50 Hz, and threshold cutoff at 1N. MTP and midtarsal joint moments and powers were calculated in Visual 3D software (C-Motion, inc., Germantown MD USA) by assigning the separate GRFs from the adjacent force plates to their corresponding segments; i.e. to the forefoot and hallux in the MTP trials, and to the hindfoot and forefoot in the midtarsal trials. The results were considered the gold standard and referred to as “2Plate” in comparisons. The inverse dynamics computations were then performed two additional times for each trial, representing GRF segment partitioning methods (Figure 1). Only the GRF input changed among methods.

In the first partitioning method (called “CPcross”), the two GRF vectors from the individual force plates were mathematically summed to simulate a single GRF vector from a single force plate, and the summed GRF was applied to a segment based on the anterior-posterior location of the CoP (in laboratory coordinates). For instance, in the MTP joint trials, the GRF was applied to the forefoot from initial contact until the CoP passed anterior to the MTP joint, at which point it was applied entirely to the hallux segment [14]. Similarly, in the midtarsal trials, the GRF was applied first to the hindfoot, followed by the forefoot once the CoP passed the midtarsal joint.

In the second method (called “PRESS”), the data from the two force plates were synthesized to simulate signals that would be obtained from a single force plate in conjunction with a pressure mat. First, the vertical forces and CoPs for the two segments of interest were taken from the individual force plates, mimicking the same data outputs from a pressure mat. The GRF vectors from the two plates were summed to simulate a single plate, and the segment shear forces and free moments were then estimated from the summed GRF by assuming they were distributed in the same proportions as the vertical forces [7, 16]:

$${\mathrm{f}}_{\text{APi}}=\left(\frac{{\mathrm{f}}_{\text{Vi}}}{{\mathrm{F}}_{\mathrm{V}}}\right){\mathrm{F}}_{\text{AP}}$$

$${\mathrm{f}}_{\text{MLi}}=\left(\frac{{\mathrm{f}}_{\text{Vi}}}{{\mathrm{F}}_{\mathrm{V}}}\right){\mathrm{F}}_{\text{ML}}$$

$${\mathrm{m}}_{\mathrm{i}}=\left(\frac{{\mathrm{f}}_{\text{Vi}}}{{\mathrm{F}}_{\mathrm{V}}}\right)\mathrm{M}$$

Where f_i represents the segment force and F represents the total (summed) force, whether vertical (V) anteroposterior (AP) or mediolateral (ML). For example, f_vi represents the vertical force under segment i (extracted from an individual force plate), and F_v represents the summed force from both plates. Similarly, m_i represents the segment free moment and M the summed free moment.

Midtarsal and MTP joint moments and powers for the PRESS and CPcross methods were compared to the 2Plate method to assess accuracy. Joint moment vectors were expressed as internal moments in the proximal segment’s coordinate system. Sagittal and transverse plane moments were analyzed for the MTP joint, while all three planes of midtarsal moments were included. Joint power was calculated as the scalar dot product of the joint moment and joint angular velocity. Moments and powers were both normalized by body mass. Comparisons were primarily made descriptively, using mean time series waveforms. These were created by first time-normalizing a representative trial from each subject to 100% of stance, then taking the mean across subjects at each time point. Following initial waveform inspection, a few selected metrics were chosen to provide numerical context. These included peak sagittal plane MTP moments and peak MTP powers, sagittal plane MTP and midtarsal angular impulse (integral of moment), and MTP and midtarsal total negative and positive mechanical work (integral of power). In addition, the timing of various relevant events was recorded. These included the times when the CoP crossed anterior to the midtarsal and MTP joints, as well as the onset times when GRF was first and last recorded under each segment (from the 2Plate data). These were expressed as percentages of stance phase (see Table 1). All metrics are presented as means ± standard deviations across subjects.

TABLE 1.

Ground reaction force (GRF) onset and unloading times under each segment, along with the times when the GRF crossed each joint center (i.e. the proximal end of each segment). All values are expressed as a percentage of stance phase (mean ± standard deviation).

	GRF onset	GRF unload	GRF cross proximal end
Hindfoot	0%	60 ± 10%	0%
Forefoot	7 ± 3%	97 ± 1%	33 ± 8%
Hallux	18 ± 11%	100%	71 ± 6%

3. RESULTS

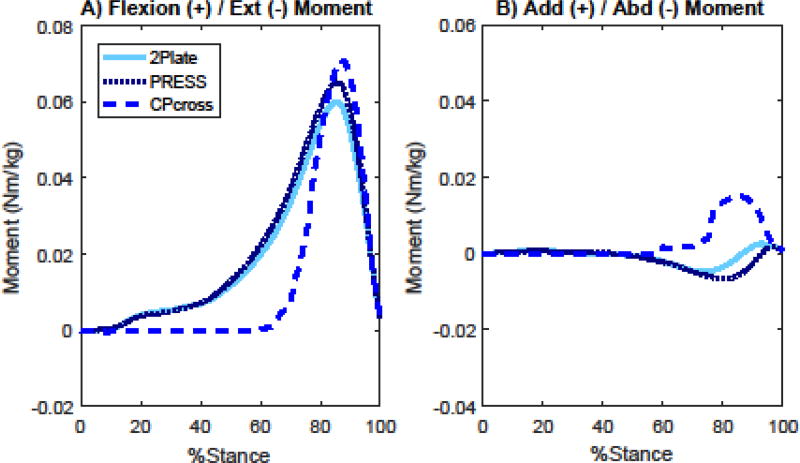
3.1 MTP joint moments (Figure 2)

Figure 2.

Mean MTP Joint moment waveforms for the sagittal (A) and transverse planes (B), normalized to 100% of stance phase. The two GRF partitioning algorithms, CPcross and PRESS, are shown along with the gold standard 2Plate.

In the sagittal plane, the CPcross method resulted in a substantial delay in the onset of the MTP extension moment, thereby missing a large portion of the early signal. The onset of GRF under the hallux segment varied substantially among subjects, occurring on average at 18% of stance (Table 1). The CoP, on the other hand, did not pass the MTP joint until 71% of stance. At this point, the extension moment increased rapidly, then overshot the 2Plate peak by 17% (CPcross: 0.145 ± 0.032 Nm/kg; 2Plate: 0.124 ± 0.021 Nm/kg). Total angular impulse was still underestimated by 31% (CPcross: 0.022 ± 0.005 Nm/kg∙s; 2Plate: 0.033 ± 0.008 for 2Plate Nm/kg∙s). The PRESS method performed better, tracking the 2Plate method closely until it peaked, and then overestimating the peak extension moment by 10% (0.136 ± 0.021 Nm/kg). Angular impulse was therefore slightly overestimated by 9% (0.035 ± 0.008 Nm/kg∙s).

In the transverse plane, 2Plate showed a relatively sizeable abduction moment through most of late stance, followed by a smaller adduction moment at the very end of stance. The CPcross method registered an erroneous adduction moment throughout this period. The PRESS method, on the other hand, followed the pattern of the abduction moment, but slightly overestimated its magnitudes, then slightly underestimated the ending adduction moment. The MTP waveforms in both planes never fully converged, as the forefoot was loaded until 97% of stance (Table 1).

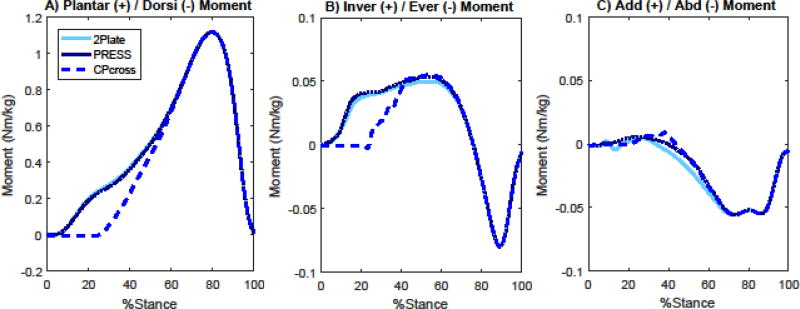
3.2 Midtarsal joint moments (Figure 3)

Figure 3.

Mean midtarsal joint moment waveforms for all three planes (A. Sagittal, B. Frontal, C. Transverse), normalized to 100% of stance phase. The two GRF partitioning algorithms, CPcross and PRESS, are shown along with the gold standard 2Plate.

At the midtarsal joint, in the sagittal plane, the CPcross method again missed the first portion of the midtarsal plantarflexion moment, while the PRESS method tracked the 2Plate method almost exactly. The delay between midtarsal loading and CPcross computation was not as dramatic as in the MTP joint, but was still substantial. The onset of GRF under the forefoot occurred shortly after initial contact, at 7% of stance, while the CoP crossed anterior to the midtarsal joint at 33% (Table 1). Peak sagittal plane moments were captured accurately by both methods, as the hindfoot was fully unloaded by this point (about 75 % of stance). Hindfoot unloading occurred at 60% of stance, although the GRF on the hindfoot was sufficiently small before that, so that curves for all subjects converged by around 55% of stance. Total angular impulse was underestimated by 16% in CPcross (CPcross: 0.347 ± 0.066 Nm/kg∙s; 2Plate: 0.409 ± 0.056 for 2Plate Nm/kg∙s), but only 1% in PRESS (0.405 ± 0.057 Nm/kg∙s).

Frontal plane moments followed similar error patterns as the sagittal plane, with the PRESS method tracking the 2Plate method closely, while the CPcross method missed the early portion of the inversion moment. Both methods slightly overestimated the peak inversion moment. Transverse plane moments were small, with an abduction moment beginning around 30% of stance. This was captured equally well by both methods, with a small underestimation of the initial moment.

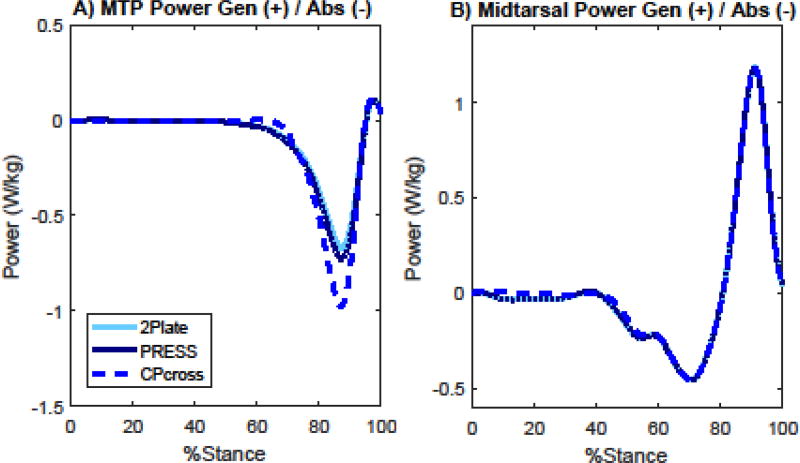
3.3 Midtarsal and MTP Joint Powers (Figure 4)

Figure 4.

Mean MTP (A) and midtarsal (B) scalar joint power profiles, normalized to 100% of stance phase. The two GRF partitioning algorithms, CPcross and PRESS, are shown along with the gold standard 2Plate.

Midtarsal and MTP joint power profiles computed from both partitioning methods were much more accurate than the joint moments. While the CPcross method could not capture early moment production at either joint, joint angular velocities, and thus powers, were low during these periods. No MTP joint power was visible until about 60% of stance, while midtarsal power was small until around 40% of stance. At the MTP joint, a small amount of power absorption was missed by the CPcross method, after which the method substantially overshot the peak power absorption by 41% (CPcross: −0.96 ± 0.30 W/kg; 2Plate: −0.67 ± 0.17 W/kg). PRESS tracked very closely with 2Plate, but also slightly overestimated the peak by 9% (−0.73 ± 0.18 W/kg). Total negative work at the MTP joint was therefore overestimated in both methods, by 21% for CPcross (CPcross: −0.073 ± 0.023J/kg; 2Plate: −0.061 ± 0.011 J/kg) and 10% for PRESS (−0.067 ± 0.011 J/kg). A transition to power generation occurred in the MTP joint at the very end of stance, but this was extremely small and captured fairly well by both methods. At the midtarsal joint, both methods tracked 2Plate closely, with CPcross just missing the very small power absorption wave in early stance. Total negative work at the midtarsal joint was slightly underestimated by 11% in CPcross (CPcross: −0.058 ± 0.016 J/kg; 2Plate: −0.065 ± 0.017in J/kg), while PRESS was nearly identical. Total positive work occurred entirely after the hindfoot was unloaded and was therefore captured accurately by both methods.

4. DISCUSSION

The purpose of this study was to evaluate the accuracy of two different single-plate GRF partitioning methods on MSF joint kinetics. Overall, the results show that the PRESS method was generally more accurate than the CPcross method, and both methods were more accurate at the midtarsal joint than at the MTP joint. Each method may have potential utility when applied to specific joints, planes, and conditions, provided the potential errors are well understood. Discussion below focuses on understanding the source of the errors as well as projecting how they might influence other applications. Due to the small mass of the foot, joint moments during walking can be considered to be almost entirely a product of the GRF and its moment arm, as opposed to inertial effects [20]. The reader is therefore referred to a prior paper on multi-segment foot GRFs [17] as an additional aid in interpreting moment errors.

Substantial hurdles exist in applying both methods at the MTP joint due primarily to the shared loading that occurs between the forefoot and hallux segments during propulsion. The PRESS method generally preserved the shape of the moment waveforms, but overestimated the peaks. In the sagittal plane this was primarily due to overestimation of the propulsive (A/P) shear forces under the forefoot, which resulted in a more anteriorly directed GRF and thus a longer moment arm [17]. Part of this can be attributed to the presence of opposing anterior/posterior (A/P) shear forces under the forefoot (a propulsive force) and hallux (braking force) that are not captured by a single force plate [17]. In the transverse plane, PRESS’s overestimation was mainly due to overestimation of the free moment under the hallux. The CPcross method introduced additional errors. In late stance, the forefoot was loaded until just before toe off, and applying the entire GRF to the hallux segment therefore substantially overestimated the force applied to the hallux and thus the sagittal plane moment. In the transverse plane, the large adduction moment was due mostly to errors in the medial/lateral CoP location, as the forefoot CoP was lateral to the hallux CoP and pulled the summed plate CoP laterally, changing the GRF moment arm. Overall, generalizability of both methods, and in particular CPcross, is somewhat difficult to predict. Because of the shared loading between the segments, substantial variability in errors is possible. Other movements, pathologies, and footwear could increase the uncertainty of the measurements.

Errors at the midtarsal joint were much smaller than at the MTP joint in both methods due to a smoother GRF transition between segments, lack of opposing A/P shear forces, and because most of the salient features occurred after the hindfoot was unloaded. Sagittal plane moments were therefore captured well by both methods, with CPcross just missing the first portion of the moment. In the frontal plane, slight overestimation of peak inversion moments was similar in both methods, but for differing reasons: underestimation of medial shear force in PRESS and overestimation of vertical force in CPcross. Transverse plane underestimation of early abduction moments in both methods was due to slight underestimation of medial shear forces. Additional hurdles could be introduced by pathologies or movements that affect the GRF transition, such as pes planus, steppage styles of gait, or cutting movements. On the other hand, a number of foot related pathologies result in early heel rise, such as triceps surae contracture, which would likely further minimize errors in midtarsal kinetics.

Joint power predictions show more promise than moments at both joints. Scalar power calculations were dominated by sagittal plane moments and motion. At the MTP joint, this resulted primarily in overestimation of peak power absorption, more so in CPcross than PRESS. Although CPcross missed a substantial portion of the early sagittal plane moments at both joints, there was a delay between the onsets of the joint moments and the onsets of the joint powers, reducing power errors compared to moment errors. In fact, at the midtarsal joint, very little power absorption occurred prior to the hindfoot becoming fully unloaded, so that errors in total negative work done were relatively small using CPcross. For many applications, it appears that midtarsal power can be calculated with a high degree of accuracy using a single force plate whether in conjunction with a pressure mat or without. Ironically, the CPcross method has only been applied to the MTP joint previously [13–15], yet it appears to be much better suited to the midtarsal joint.

The methodology employed in this study contained a few limitations. The controlled foot placement approach used in this study may have slightly affected the natural walking patterns of the subjects. However, since the current study compares methods within a trial type, these do not affect the comparisons, only their generalizability (see also [5, 17]). Additionally, only pediatric subjects were tested; however, gait is generally considered mature by ages 7–8 [21].

Overall, both methods show some promise and generalizability at the midtarsal joint. The PRESS method accurately characterized all midtarsal joint moment planes and power, while CPcross accurately captured peak sagittal plane moments and power curves. Additional care should be taken when analyzing MTP joint kinetics, particularly with CPcross. The PRESS method should certainly be considered preferable to CPcross from an accuracy standpoint when a pressure mat and a force plate are both available (along with the means to synchronize and process the data). With only a single force plate, CPcross may still have utility, provided its limitations are understood. Ultimately, we hope that the methods and inferences provided in this paper will increase the use of multi-segment foot kinetics, which we believe could aid our understanding of foot function and pathologies and eventually help guide treatment interventions.

Highlights.

• Multi-segment foot model kinetics are possible using a single force platform.

• The two partitioning methods may both be applicable at the midtarsal joint.

• Both partitioning methods have some limitations at the metatarsophalangeal joint.