Visualizing angle-independent principal strains in the longitudinal view of the carotid artery: phantom and in vivo evaluation

Abstract

Non-invasive vascular elastography can evaluate the stiffness of the carotid artery by visualizing the vascular strain distribution. Axial strain estimates of the longitudinal cross-section of the carotid artery are sensitive to the angle between the artery and the transducer. Anatomical variations in branching and arching of the carotid artery can impact the assessment of arterial stiffness. In this study, we hypothesized that principal strain elastograms computed using compounded plane wave (CPW) imaging can reliably visualize the strain distribution in the carotid artery, independent of the transducer angle.

We corroborated this hypothesis by conducting phantom and in vivo studies using a commercial ultrasound scanner (Sonix RP, Ultrasonix Medical Corp., Richmond, BC, Canada). The phantom studies were conducted using a homogeneous cryogel vessel phantom. The goal of the phantom study was to assess the feasibility of visualizing the radial deformation in the longitudinal plane of the vessel phantom, independent of the transducer angle (±30°, ±20°, ±10°, and 0°). The in vivo studies were conducted on 20 healthy human volunteers, in the age group of 50–60 years. All echo imaging was performed at a transmit frequency of 5 MHz, and sampling frequency of 40 MHz.

The elastograms obtained from the phantom study demonstrated that for straight vessels, which had their lumen parallel to the transducer, principal strains were similar to axial strains. At non-parallel configurations (angles ±30°, ±20°, and ±10°), the magnitude of the mean principal strains were within 2.5% of the parallel configuration (0° angle) estimates, and thus were observed to be relatively unaffected to change in angle. However, in comparison, the magnitude of the axial strain decreased with increase in angle, due to coordinate dependency. Further, the pilot in vivo study demonstrated that the principal and axial strain elastograms were similar for subjects with relatively straight arteries. However, for arteries with arched geometry, axial strains were significantly lower (p<0.01) than the corresponding principal vascular strains, which was consistent with the results obtained from the phantom study.

In conclusion, the results of the phantom and in vivo studies demonstrated that principal strain elastograms computed using CPW imaging could reliably visualize angle-independent vascular strains in the longitudinal plane of the carotid artery.

Introduction

Atherosclerotic stiffening of the carotid artery is the leading cause of cerebrovascular diseases (Benjamin et al., 2017). Advanced stages of carotid atherosclerosis can lead to stroke and transient ischemic attacks (Redgrave et al., 2008). Noninvasive vascular elastography can evaluate the stiffness of the carotid artery by visualizing the vascular strain distribution (Catalano et al., 2011; Kawasaki et al., 2009; Korshunov et al., 2017; De Korte et al., 2016; Hansen et al., 2016a; de Korte et al., 2000; Bjällmark et al., 2010; Maurice et al., 2004; Hansen et al., 2016b); clinicians can use this information to assess the atherosclerotic burden, and identify patients at high risk for life threatening cerebrovascular events (Weber and Noels, 2011).

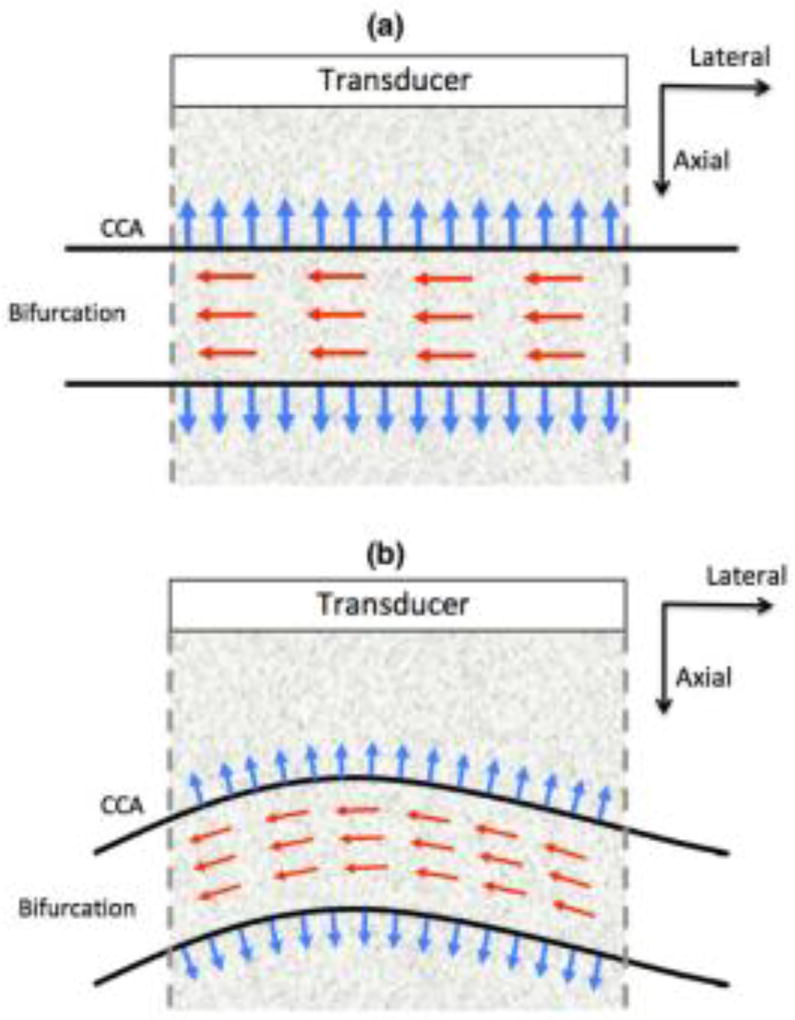
Strain elastograms visualized across the longitudinal plane of the carotid artery are typically measured in Cartesian coordinates. Specifically, the radial and longitudinal strains in the carotid artery are visualized by computing the axial and lateral strains, respectively, assuming that the corresponding axes are aligned (Fig. 1(a)). However, if the beam propagation direction is not aligned with the radial motion (e.g. Fig. 1(b)), axial strain may not accurately represent the radial deformation in the vessel (Mercure et al., 2008, 2011, 2014; Maurice and Dahdah, 2012). Accordingly, vascular strains visualized in Cartesian coordinates are subject to anatomical variations in branching and arching of the carotid artery (Fig. 1(b)), which can limit the scope of vascular elastography. Mercure et al. (Mercure et al., 2014) proposed an angle compensation framework to correct the bias in axial strain estimates. However, the approach assumes that the arterial tissue is incompressible and vascular shear stains are nonexistent, which may not be clinically valid (Holzapfel et al., 2004; Chai et al., 2015; Zhou and Fung, 1997; Nayak et al., 2017a).

Fig. 1.

Illustrations showing examples of the orientation of the carotid artery relative to the ultrasound transducer. The red and blue arrows indicate the direction of blood flow and the radial deformation in the vessel wall, respectively. The figures correspond to the instances when the radial deformation in the vessel wall is (a) aligned and (b) not aligned with the direction of beam propagation (axial).

To estimate the vascular strain in the vessel reliably, it is important that the measured mechanical parameters are independent of vessel and transducer coordinate systems. The goal of this study is to evaluate the feasibility of using principal strain imaging to visualize coordinate-independent vascular strain in the longitudinal plane of the carotid artery. Principal strain elastograms visualize the maximum tensile and compressive strain at any spatial location, and are inherently coordinate-independent (Dieter and Bacon, 1986).

Several researchers have used principal strain imaging to improve the accuracy and robustness of elastographic assessment of tissue stiffness (Zervantonakis et al., 2007; Nayak et al., 2017a; Lee et al., 2008; Jia et al., 2009; Fung-Kee-Fung et al., 2005). Fung et al. and Zervantonakis et al. demonstrated that principal strain imaging could visualize angle- and centroid-independent strain in myocardial elastographic imaging (Zervantonakis et al., 2007; Fung-Kee-Fung et al., 2005). They also highlighted the shortcomings of using Cartesian (axial and lateral) strain estimates for assessing the stiffness of the myocardium, because of its inherent dependence on the orientation of the transducer relative to the myocardium motion. However, all of these studies reported a common limitation associated with visualizing principal strains – the subpar quality of the lateral displacements obtained using conventional ultrasound imaging. In a recent study (Nayak et al., 2017a), we addressed this limitation by using compounded plane wave (CPW) imaging, and demonstrated that high quality principal strain elastograms could be produced by beam-steering and compounding plane waves over ±14°, in increments of 2°. It was also demonstrated that coordinate-independent principal strain elastograms could visualize the polar strains in the transverse cross-section of the carotid artery when precise estimates of the vessel center are not known, which is common in stenosed vessels (Kumar and Balakrishnan, 2005; McPherson et al., 1992).

In this paper, we hypothesized that principal strains estimated using CPW imaging can reliably estimate the radial deformation in the carotid artery due to the arterial blood pressure, independent of the transducer angle (Fig. 1(b)). We tested this hypothesis by conducting phantom and in vivo studies using a commercial ultrasound scanner implemented with CPW imaging. The phantom experiments were conducted to evaluate the impact of variation in the transducer angle on the axial and principal strain elastograms, in a controlled environment. Subsequently, the proposed technique was validated under more realistic physiological conditions, by conducting an in vivo pilot study on 20 healthy volunteers, in the age group of 50–60 yrs. All experiments were conducted using a transmit frequency of 5 MHz and sampling frequency of 40 MHz.

Methods

The proceeding subsections describe the methods used in both the phantom and in the in vivo studies. These include phantom fabrication, image acquisition and beam-forming, displacement and strain estimation, and data analysis.

Phantom Study

The goal of the phantom study was to test the efficacy of using principal strains to visualize the radial deformation in the sagittal plane of the vessel, independent of the transducer’s scanning angle. Specifically, the elastographic experiments were conducted by scanning a homogenous vessel phantom suspended horizontally in a water bath, at different transducer angles (±30°, ±20°, ±10°, and 0°). The following sub-sections describe the methods used in the phantom and in vivo studies.

Phantom Fabrication

We fabricated a homogeneous vessel phantom of length 100 mm and outer and inner diameters of 12 and 3 mm, respectively. The phantom was fabricated from a 10% by weight suspension of polyvinyl alcohol (PVA, Evanol 71-30, Dupont, Wilmington, Delaware, USA), and 2% by weight carborundum (320 Grit, Fisher Scientific, Fair Lawn, New Jersey, USA) using a highly controlled and repeatable process, as described in (Korukonda and Doyley, 2012; Korukonda et al., 2013; Huntzicker et al., 2014). The process involved freeze-thaw cycling the liquid solution in a sealed cylindrical mold (20 mm diameter by 100 mm long) for five times, from 20°C to +20°C, over a 120-h (24 h per cycle) period. After the thermal cycling, the phantom was removed from the mold and stored at room temperature, dissolved in water.

We used a Landmark Servo-hydraulic Test System (MTS Systems Corp., Eden Prairie, MN, USA) and a 5-lb load cell to measure the mechanical properties of representative samples of the vessel wall phantom (Korukonda and Doyley, 2011b). These measurements were performed on five cylindrically-shaped homogeneous samples (of size 20 mm diameter by 10 mm height) at room temperature (20°C). The Young’s modulus of the vessel wall was 41.6 ± 0.3 kPa.

Elastographic Data Acquisition

The plane wave radio-frequency (RF) echo data was acquired using a commercial Sonix RP ultrasound scanner (Ultrasonix Medical Corp., Richmond, BC, Canada). This scanner was equipped with a 128 element linear transducer array (L14–5/38 probe), and a multichannel data acquisition system (Sonix DAQ, Ultrasonix Medical Corp.). The scanner was programmed to operate at a transmission frequency of 5 MHz — the maximum frequency that could be used with this array for CPW imaging. All echo imaging was performed at 5 MHz with a 128 element linear transducer array (L14–5/38 probe). We used a multichannel data acquisition system (Sonix DAQ, Analogic, Peabody, MA, USA) to acquire plane wave RF echo data. We programmed the ultrasound scanner using a software development kit (TEXO SDK, v5.6.6, Ultrasonix Medical Corp.) to acquire CPW data for transmission angles of −14° to 14° in increments of two degrees (Korukonda et al., 2013; Huntzicker et al., 2014; Nayak et al., 2017a,b).

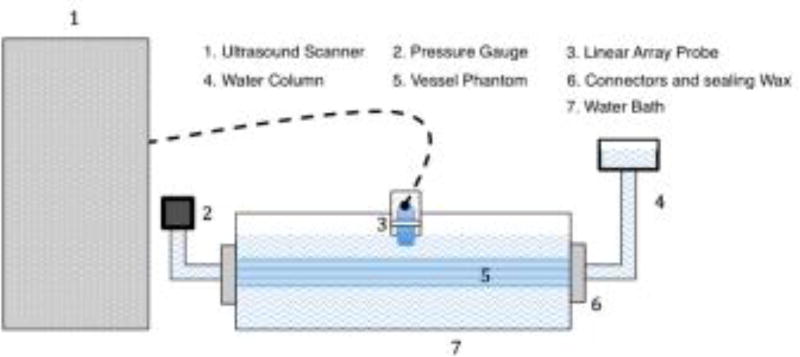
The elastographic experiments were performed in a water tank measuring 10 (width) × 15 (length) × 10 (height) cm, which was filled with degassed water. For elastographic imaging, a simple water column and a pressure gauge (DPG1000ADA, Omega Engineering Inc., Stamford, CT, USA) was used to regulate the pressure in the vessel lumen (Nayak et al., 2017b) (Fig. 2). A static water column system was used to vary the pressure within the vessel from 5 to 15 mm Hg (666.61 to 1999.83 Pa), in increments of 5 mmHg (666.61 Pa). The phantom elastographic experiments were conducted by rotating the transducer on a rotation stage, up to an angle of ±30°, with respect to the horizontal. The ultrasound RF data for all CPW imaging angles were acquired within a total acquisition and download time of less than 1 minute, and with a maximum pressure level variation of less than ± 0.1 mmHg during the acquisition. This protocol was repeated for all the transducer scanning angles used in this study. The received echo signal was sampled to 12 bits, at sampling frequency of 40 MHz. The received echo signal was reconstructed using delay-and-sum beamforming (Appendix. A).

Fig. 2.

Schematic diagram illustrating the setup used for phantom experiments.

Patient Study

The goal of this patient study was to evaluate strain elastograms (principal and axial) acquired with a clinical prototype system of CPW vascular elastography. With the approval of the University of Rochester Institutional Review Board (IRB), we imaged carotid arteries of twenty volunteers in the age group 50–60 years, with no history of cardiovascular disease. All volunteers provided written informed consent for the study. The volunteers recruited for this study were screened to ensure that there were 10 participants for each category, i.e. (i) artery parallel and (ii) non-parallel to the aperture plane of the transducer.

An experienced sonographer collected data from the right common carotid artery (CCA) of the human volunteers, using the same scanner that was used in the phantom experimental studies, described in section c. Radio-frequency echo data was acquired at a frame rate of 1000 fps; an ECG device (Model 7600, Ivy Biomedical, CT, USA) triggered the start of all acquisition at the beginning of systole. We sampled the received echo signal to 16 bits at 40, which was stored on a workstation for off-line analysis using the MATLAB (MathWorks Inc., Natick, MA, USA) programming language. We measured the pressure in the brachial artery of all volunteers in the supine position one hour before elastographic imaging. The in vivo strain estimates obtained from each subject were normalized by their corresponding arterial pulse pressure, which was estimated by computing the difference between the systolic and diastolic blood pressure measurements (Nayak et al., 2017a). Also, the tests for statistically significant differences (p<0.01) between the in vivo strain estimates, paired-sample t-tests were performed using the ttest.m function in MATLAB. It conducts a hypothesis-based test to check if the paired sample data belongs to a normal distribution with mean equal to zero and unknown variance, and also reports the probability p-value to determine the significance of the results.

Estimating Displacement and Strain

To compute axial and lateral displacements, we applied a 2D cross-correlation echo tracking algorithm to the reconstructed RF echo data. All echo tracking was performed with 2D kernels (0.8 mm × 0.8 mm), which overlapped by 75% in both directions. A 2D spline interpolator provided sub-pixel displacement estimates, and we used a median filter (0.2 mm × 0.2 mm) to remove spurious axial and lateral displacement estimates. The displacement estimates obtained from consecutive RF images at incremental pressures were averaged. The least square strain estimator (Kallel and Ophir, 1997) was used to compute the normal (ε_zz, ε_xx) and shear (γ_xz, γ_zx) components of the 2D strain tensor (ε), from the averaged displacement maps. The strain estimation was performed using a 1D kernel size of size 0.5 mm.

Estimating Principal Strain

Solving the Eigenvalue equation for the 2D case: |ε_ij − ε^(k) δ_ij| = 0, where k = 1,2 provided the magnitude (λ₁, λ₂) and direction (θ_p+, θ_p−) of the principal strain; and δ_ij is the Kronecker delta. We computed the two Eigenvalues representing the major (λ₁) and minor (λ₂) principal strains as follows:

$${\lambda }_{1,2}=\frac{1}{2}[({\epsilon }_{11}+{\epsilon }_{22})\pm \sqrt{{({\epsilon }_{11}-{\epsilon }_{22})}^2+{({\epsilon }_{12}+{\epsilon }_{21})}^2}].$$ (1)

The principal strain directions (i.e., the Eigenvectors) were computed as follows:

$${\theta }_{p+}={\text{tan}}^{-1}(\frac{{\epsilon }_{11}-{\epsilon }_{22}}{{\epsilon }_{11}+{\epsilon }_{22}})/2$$

$${\theta }_{p-}={\theta }_{p+}+\frac{\pi }{2},$$ (2)

where ε_{i, j} denotes any pair of strain components, separated by θ = π/2 (i.e., axial, lateral or radial, circumferential, etc.).

Results

Phantom study

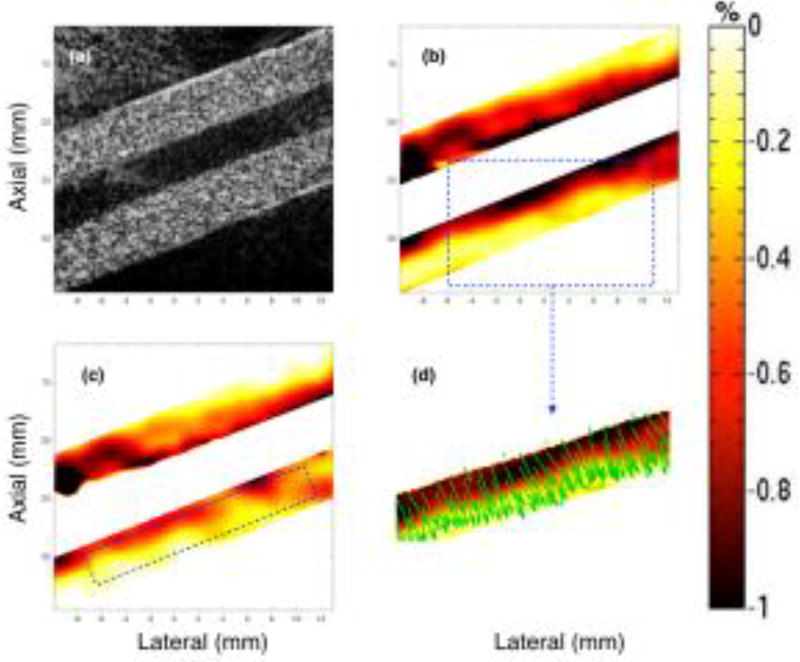
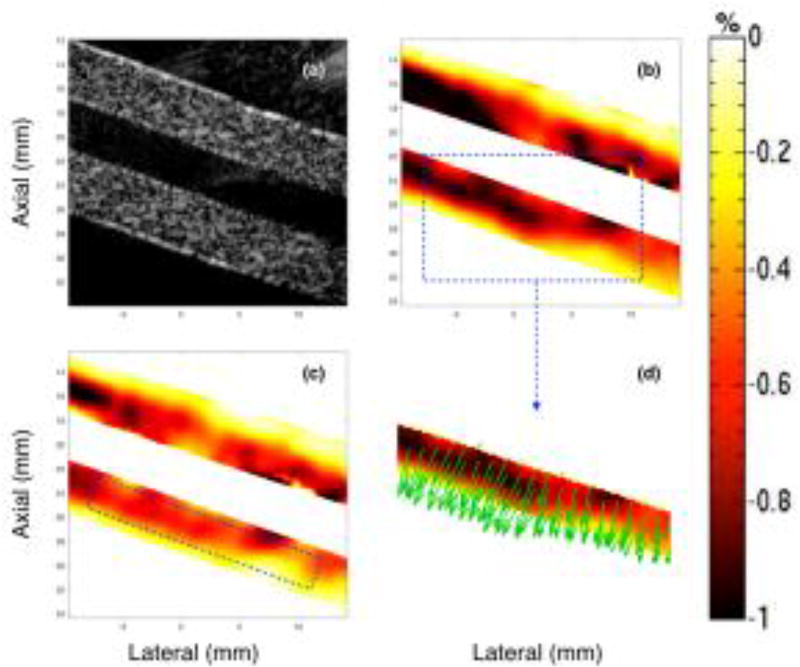
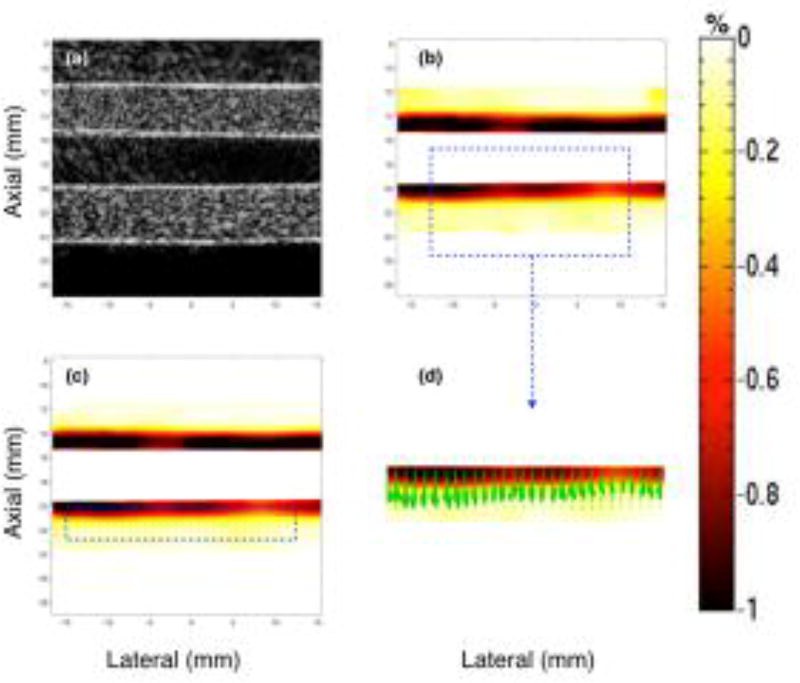
Figs. 3–5 show representative sonograms and corresponding strain elastograms obtained from a homogenous vessel phantom using CPW imaging, at transducer angles +20°, 0° and −20°, respectively. The radial deformation in the vessel wall was maximum near the lumen, and decayed with increase in distance, as reported by previous studies (Korukonda and Doyley, 2012; Korukonda et al., 2013; Huntzicker et al., 2014). For the non-parallel transducer configurations (Figs. 3 and 5), the strain magnitude in the principal strain elastograms was considerably higher than that observed in the axial strain elastograms. However, at 0° transducer angle, no visible differences were observed between the principal and axial strains elastograms, as shown in Fig. 4. Further, Figs. 3–5 (d) display that independent of the angle of the transducer, the principal strain direction vectors were consistently oriented perpendicular to the lumen, along the direction of radial motion of the vessel wall. These studies were conducted using the cryogel vessel phantom and the The Youngs modulus of the vessel wall was estimated to be 41.6 ± 0.3 kPa, which were measured using a Landmark Servo-hydraulic Test System (MTS Systems Corp., MN, USA).

Fig. 3.

Montage of ultrasound sonogram (a), principal (b) and axial (c) strain elastograms, and the direction vectors map (d) associated with the major component of the principal strain displayed in (b). These images are obtained from a homogenous vessel phantom at a transducer angle of 20°, using CPW imaging.

Fig. 5.

Montage of ultrasound sonogram (a), principal (b) and axial (c) strain elastograms, and the direction vectors map (d) associated with the major component of the principal strain displayed in (b). These images are obtained from a homogenous vessel phantom, at a transducer angle of −20°, using CPW imaging.

Fig. 4.

Montage of ultrasound sonogram (a), principal (b) and axial (c) strain elastograms, and the direction vectors map (d) associated with the major component of the principal strain displayed in (b). These images are obtained from a homogenous vessel phantom at a transducer angle of 0°, using CPW imaging.

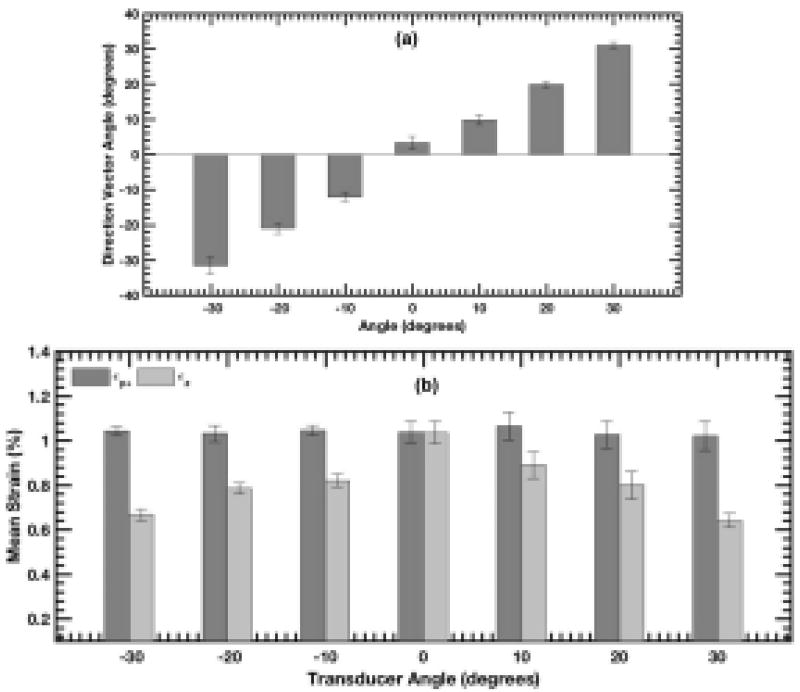
The bar plot in Fig. 6 (a) quantifies the angle of the principal strain direction vectors displayed in Figs. 3–5 (d), as a function of transducer angle. The results show that regardless of the transducer orientation, the principal strain vectors estimated using CPW imaging were consistently aligned along the radial direction. The bar plot corroborated the visual assessment of direction vectors obtained from the principal strain elastograms.

Fig. 6.

The bar plot displays the mean of (a) principal strain direction vectors and (b) strain in principal and axial strain elastograms, as a function of transducer angle. The mean in bar plots (a) and (b) is computed over the rectangular region of interests (ROIs) shown in Fig. 3 (c), and the error bars correspond to ±1 std. dev.

Fig. 6 (b) displays a bar plot of mean strain associated with the principal and axial strain elastograms, computed over the ROI indicated in Figs. 3–5 (c), as a function of transducer angles. The magnitude of axial and principal strain were similar, when the axial and radial axes were aligned. However, at non-parallel angles, the magnitude of axial strain estimates gradually decreased with increase in transducer angle (in either positive or negative direction). In comparison, the principal strains had little variation with change in transducer angle, and measured within 2.5% of the ±0° angle estimate. These results were consistent with the visual assessment of the strain elastograms displayed in Figs. 3–5.

Patient Study

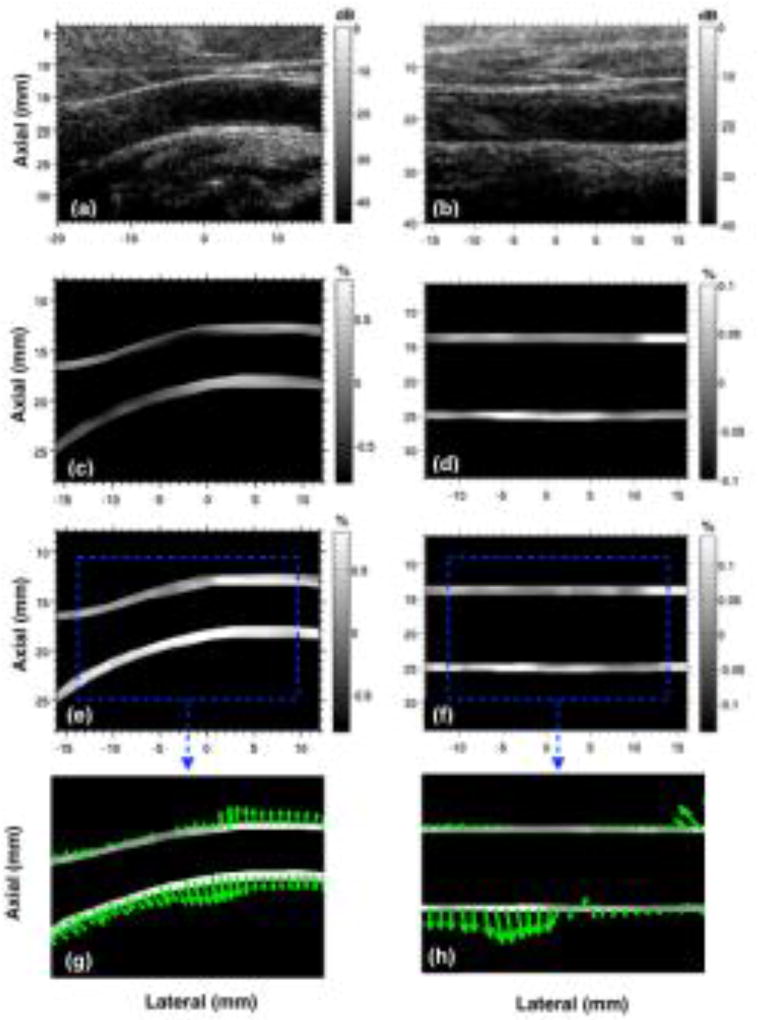
Fig. 7 shows representative sonograms and strain elastograms of the common carotid artery obtained from two healthy volunteers. The results show that when the carotid artery is parallel to the transducer, principal and axial strain elastograms were comparable, however, in non-parallel instances, principal strain elastograms displayed higher strains compared those in the axial direction. These observations were in agreement with the results obtained from the phantom study.

Fig. 7.

Montage displays representative images of carotid artery sonogram (a,b) and their corresponding axial (c,d) and principal (e,f) strain elastograms associated with two healthy male subjects. Subplots (g,h) corresponds to the principal strain direction vectors associated with (e,f). The two columns correspond to images from two healthy volunteers with their common carotid artery non-parallel (a,c,e) and parallel (b,d,f) to the transducer.

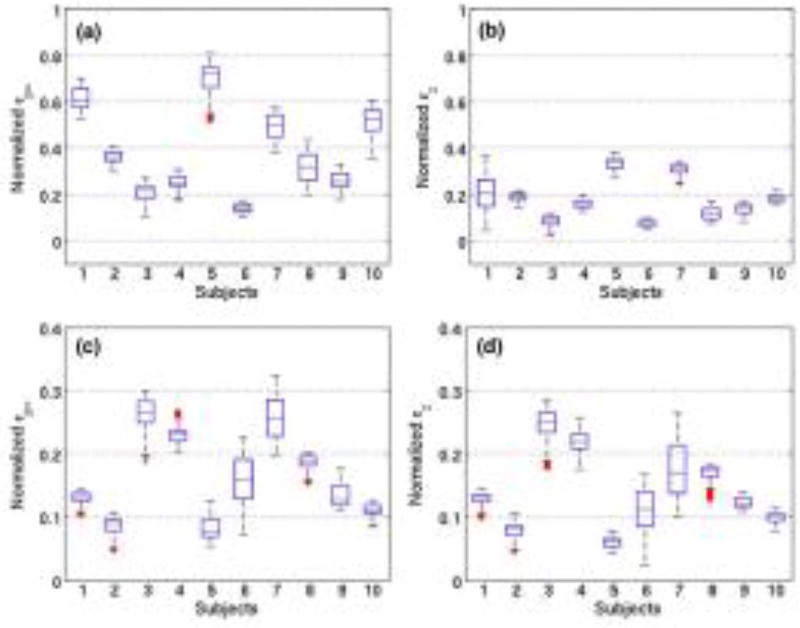
Fig. 8 shows boxplots of normalized strains (principal and axial) measured across the sagittal cross-section of the carotid arteries of 20 healthy volunteers. The estimated carotid strains were normalized using the arterial pulse pressure of the corresponding subject. We observed that for straight vessels, when radial and axial axes were aligned, no significant difference was observed. However, for bent vessels with non-parallel configurations, principal strains were significantly higher than axial strains (p<0.01).

Fig. 8.

The box and whisker plots of principal (a,c) and axial strain (b,d) elastograms of 20 healthy volunteers in the age group 50–60 years. Plots (a,b) and (c,d) correspond to strains associated with volunteers with carotid artery non-parallel and parallel to the transducer, respectively. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. A representative sonogram and elastogram for each configuration is displayed in Fig. 7.

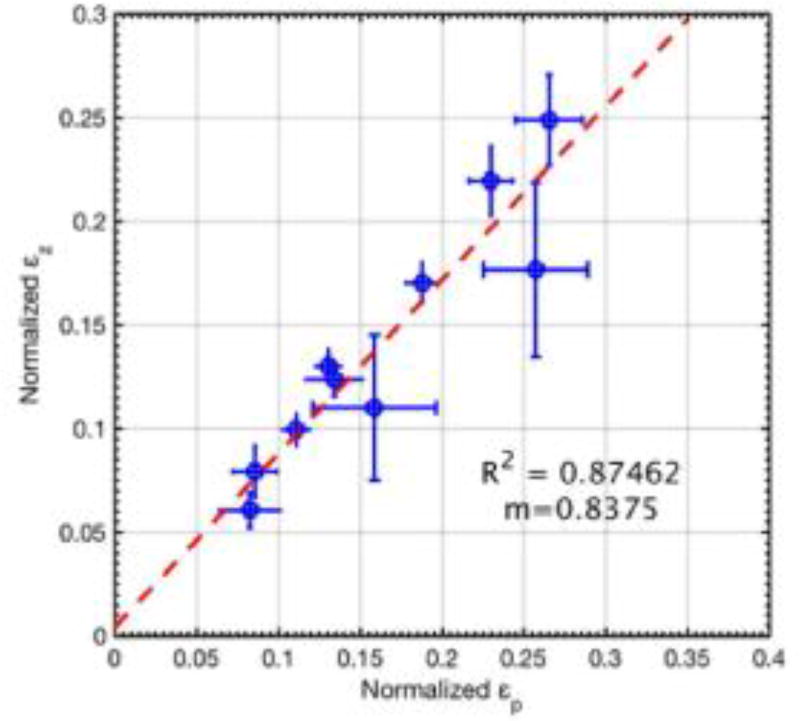
Fig. 9 displays a scatter plot of the normalized axial and principal strains estimates displayed in Fig. 8 (c, d), for straight vessels and the corresponding line of least square fit. The slope of the line of least square fit was 0.83, and the corresponding goodness of fit (R²) was 0.87.

Fig. 9.

Scatter plots of axial and principal strains estimates displayed in Fig. 8. The scatter plot displays mean strain associated with subjects with straight vessels, with error-bars denoting ± 1 standard deviation. The line of least-square fit is displayed in red, and its corresponding coefficient of linear regression and slope is reported as R² and m, respectively.

Discussion

Axial strain measurements of the carotid artery are sensitive to the angle between the artery and the transducer, which can vary across subjects (Maurice and Dahdah, 2012; Mercure et al., 2008; Rodda, 1986; Phan et al., 2012). This limitation could hamper reliable assessment of the stiffness of the artery, and limit the scope of vascular elastography in the clinic. In this paper, we investigated the feasibility of using principal strain elastography to overcome this issue, and compared its performance with conventionally used axial strain elastograms. The results demonstrate that the principal strain elastograms computed using CPW imaging could reliably estimate the vascular strain in the radial direction, independent of the transducer angle (Figs. 3–5). Specifically, the phantom results demonstrated that when the axes of the transducer and the vessel were aligned, both principal and axial strains were similar (Fig. 4). This was because radial strains, which constituted the maximum compressive strain in the vessel, were aligned along the axial direction. Therefore, both principal strain and axial strain elastograms visualized the radial components of strain in the vessel. These results were also consistent with the results reported by Larsson et al. (Larsson et al., 2015) who used a straight vessel tube to demonstrate that the axial and radial strain estimated in the sagittal and transverse planes were similar, and further validated their claim using sonomicrometry. At non-parallel transducer angles, the magnitude of the axial strain decreased with increase in angle. This was expected since axial strains are coordinate-dependent, computed in the frame of reference of the transducer. At non-zero angles, axial strains can visualize only the component of the actual radial strain in the direction of the beam-propagation (Maurice and Dahdah, 2012; Mercure et al., 2008, 2011, 2014). However, in comparison, the magnitude of the principal strains demonstrated less variation (< 2.5% with respect to 0° angle estimate), with change in transducer angle (Fig. 6 (b)). This was because principal strain, which is obtained from the Eigen decomposition of the 2D strain tensor, is intrinsically coordinate independent, and visualizes the maximum strain (i.e the radial strain) at any spatial location, irrespective of the transducer orientation (Figs. (3–5)) (d). The pilot study conducted on the healthy volunteers confirmed the results obtained from the phantom experiments (Fig. 7). For subjects with vessel lumen parallel to the transducer, principal and polar strain elastograms were observed to be similar, with no statistically significant difference (p>0.01) (Fig. 8 (b)). This was also corroborated through the scatter plot (Fig. 9), which reported a slope of 0.83 for the least-square line fit, with an R² value of 0.87. However, at non-parallel vessel configurations, principal strains visualized in the vessel wall were significantly higher than the corresponding axial strains (p<0.01) (Fig. 8 (a)).

Several researchers have used axial strain elastograms to visualize the periodic radial deformation in the carotid artery (Maurice et al., 2005; Schmitt et al., 2007; Kanai et al., 2003). The key advantage of visualizing axial strain is that ultrasound can reliably estimate tissue deformation in the direction of beam propagation. However, sensitivity of axial strain estimates to geometrical factors can lead to sub-optimal assessment of the tissue stiffness and its pathological condition (Maurice and Dahdah, 2012; Mercure et al., 2008, 2011, 2014; Zervantonakis et al., 2007; Lee et al., 2008). Further, it can also compromise the accuracy of the modulus and stress recovery process (Richards et al., 2015). Mercure et al. (Mercure et al., 2011, 2014) reported the bias incurred in axial strain estimates obtained from the longitudinal cross-section of the carotid artery at different transducer angles. They addressed this issue using a projection based technique to compensate the bias in axial strain estimates. However, the overall framework of the proposed approach was based on the assumptions that (i) the arterial tissue is incompressible, and (ii) shear strains were nonexistent, which may not be valid in the clinic since vascular tissues are associated with transversely anisotropic mechanical behavior (Holzapfel et al., 2004; Chai et al., 2015; Zhou and Fung, 1997; Nayak et al., 2017a).

Coordinate-independent mechanical parameters, such as arterial pulse-wave velocity (Vappou et al., 2010) and shear wave elasticity imaging (Widman et al., 2015) have also been used to characterize tissue stiffness (De Korte et al., 2016). Furthermore, several other studies have employed model-based elastography techniques to obtained coordinate-independent parameters for assessment of tissue mechanical properties (Richards et al., 2015; Floc’h et al., 2010; Hansen et al., 2013; Huntzicker et al., 2014). Each of these techniques estimates a different aspect of vascular stiffness, and have their own advantages and limitations. However, most of these techniques are at a preliminary stage of development and evaluation, and patient validation studies are yet to be performed to assess their diagnostic potential (De Korte et al., 2016). Researchers have also estimated carotid artery distensibility (Reneman et al., 2005) to assess arterial stiffness, and have evaluated its diagnostic potential through numerous in vivo studies, correlating distensibility with age and other cardiovascular risk factors.

In the principal strain imaging technique, the deformation in the vascular tissue is calculated using the Eigenvalue decomposition approach, which is coordinate independent, and therefore insensitive the transducer’s orientation (Dieter and Bacon, 1986). With advanced synthetic aperture beam-forming and beam-steering techniques (sparse array and compounded plane wave imaging) (Korukonda and Doyley, 2011a; Oddershede and Jensen, 2007; Gammelmark and Jensen, 2003; Karaman et al., 1995; Korukonda and Doyley, 2012; Nayak et al., 2013; Hansen et al., 2010, 2009, 2016a), the full 2D strain tensor can be reliably estimated to produce useful principal strain elastograms (Poree et al., 2015; Hansen et al., 2016b; Nayak et al., 2017a). More specifically, this approach can also be used to assess angle-independent longitudinal strain in the vessel wall, which was not investigated in this study (Au et al., 2016; Cinthio et al., 2006). Although, it might be possible in certain cases to estimate the vascular strain in a small section of the carotid artery by aligning the transducer beam perpendicular to the arterial wall. Nonetheless, the current approach can improve the flexibility and robustness of non-invasive vascular elastography in the clinic. Further, principal strain imaging will be crucial in visualizing the strain distribution across the internal carotid artery – an important indicator of cardiovascular health (Dijk et al., 2004; Inzitari et al., 2000) – which typically incurs a huge angle away from the surface (Mercure et al., 2011, 2014; Tsiskaridze et al., 2001).

The current elastographic study was conducted at a transmit center frequency of 5 MHz, which is lower than the typical range of frequencies used in the clinic (7–12 MHz). This was done to minimize grating lobe artifacts associated with compounded plane wave imaging (Korukonda et al., 2013; Nayak et al., 2017a,b; Verma and Doyley, 2017), such that the wavelength of the transmit beam was less than the pitch of the L38/5-14 transducer (Szabo, 2013). Further, we did not perform experiments with conventional linear array imaging, primarily because of its relatively low imaging frame rate (35–50 frames-per-second), which makes for vascular elastography studies challenging (De Korte et al., 2016; Poree et al., 2015). Although conventional plane wave imaging (without compounding) typically has very high frame-rates, however, it has been demonstrated unsuitable for principal strain imaging due to lack of transmit focusing, which makes it difficult for estimating lateral motion (Korukonda et al., 2013; Nayak et al., 2017a,b; Verma and Doyley, 2017; Poree et al., 2015; Hansen et al., 2009). Compounded plane wave imaging was specifically used in the present study, to improve lateral beam properties (Korukonda et al., 2013; Montaldo et al., 2009), which is pivotal for reliably estimating the 2D strain tensor (Nayak et al., 2017a,b).

This study had some limitations. The geometry and thickness of the vessel phantom used in this study were much larger than those observed anatomically, and were chosen because of the limitations associated with our current cryogel phantom fabrication process. In future studies, we plan to use more advanced phantom fabrication techniques to produce more realistic vessel models (Nikitichev et al., 2016). The phantom study experiments were conducted at pressure values lower than physiological values obtained in vivo. This was primarily due to limitations with our current elastographic experimental setup. We will address this in future studies by using a system similar to that reported in (Poree et al., 2015). The phantom study was primarily used as a guide for the in vivo experiments that were conducted on 20 volunteers. Given the limitation of the phantom experiments, the validity of the phantom results may not be directly extendable to the physiological scenario. Further, the strain elastograms reported in this manuscript were computed by directly averaging the displacement estimates, without transforming them to the pre-deformed vessel coordinates. This could have lead to small registration errors at regions of large displacements such as at the boundary of the inner vessel wall. A limitation of the study’s patient protocol was that the systolic and diastolic blood pressure readings were measured an hour before the ultrasound scans were performed. This could have led to deviation from actual pulse pressure at the time of the ultrasound scan. Further, brachial blood pressure was used in this study, rather than carotid arterial pressure, to normalize the estimated strain values (Catalano et al., 2011). This could lead to patient-dependent over-estimation of the actual carotid artery pressure at the site of scanning, which may have influenced the normalization of the strain estimates across different subjects. Although this study demonstrated the advantages of using principal strain imaging, future studies will be needed to test whether principal strain imaging can improve the diagnostic performance of vascular elastography.

Conclusion

In this study, we demonstrated that principal strain elastograms computed using compounded plane wave imaging could reliably estimate arterial strains, regardless of the transducer angle. The results of the in vitro and in vitro experiments demonstrated that when the axes of the transducer and the vessel were aligned, principal strains had no additional advantage over the axial strains. However, at non-parallel configurations, principal strain was unbiased to variation in angular orientation of the transducer. Further, the results of phantom and in vivo studies were consistent.

Appendix A

Image Reconstruction

We used the delay-and-sum beam-forming method to reconstruct RF echo frames (Korukonda and Doyley, 2012) on a 40mm × 40mm grid with lateral and axial sampling frequency of 52 lines/mm and 40 MHz. The delay-and-sum beam-forming method is a commonly used beamforming technique, and since there are several good references that describe its principle (Van Trees, 2002), in this subsection we will provide only a brief description of the approach. We compute the backscatter intensity (S) at a given point (x₀, z₀) in the beam-formed image as follows:

$$S(x_0,z_0)=\sum _{i=1}^{N_{\mathit{\text{tx}}}}\sum _{j=1}^{N_{\mathit{\text{rx}}}}{w}_{\mathit{\text{ij}}}{\mathit{\text{RF}}}_{\mathit{\text{ij}}}(t-\tau (x_0,z_0)),$$ (3)

where N_tx and N_rx represent the total number of active transmission and reception elements, respectively; RF_ij(t) represents the RF echo obtained when the i^th element transmits and j^th element receives; t represents the time of flight of the echo; τ(x₀, z₀) represents the time of flight of the acoustic wave traveling from the transmit element to point (x₀, z₀) and back to the receive element; and w_ij represents the apodization weight. We computed the time required to transmit a plane wave (τ_tx) at an arbitrary angle (θ) from a point (x₀, z₀) as follows:

$${\tau }_{\mathit{\text{tx}}}=(x_o\text{ sin}(\theta )+z_o\text{ cos}(\theta )+\frac{W}{2}\text{sin}(|\theta |))/c,$$ (4)

where c and W represent the speed of sound, 1540 m s⁻¹, and the width of the transducer array, respectively. We computed the receive time (τ_tx) as follows

$${\tau }_{\mathit{\text{rx}}}=(\sqrt{{(x_j-x_0)}^2+z_0^2})/c,$$ (5)

where x_j represents the location of the receiving element. The total round-trip time, τ, to and from the point (x₀, y₀) was

$$\tau (x_0,z_0)={\tau }_{\mathit{\text{tx}}}+{\tau }_{\mathit{\text{rx}}}.$$ (6)

The delay-and-sum beam-forming was performed with boxcar apodization on both transmit and receive. Further, the f-number of the compounded plane wave imaging (Denarie et al., 2013) was $\frac{1}{28}$.