Measuring pulmonary arterial compliance: mission impossible? Insights from a novel in vivo continuous-flow based experimental model

Abstract

Arterial compliance (C) is related to the elasticity, size, and geometrical distribution of arteries. Compliance is a determinant of the load that impedes ventricular ejection. Measuring compliance is difficult, particularly in the pulmonary circulation in which resistive and compliant vessels overlap. Comparing different methods for quantification of compliance to a method that involves a continuous flow might help to identify the optimal method. Pulmonary arterial compliance was computed in six pigs based on the stroke volume to pulse pressure ratio, diastolic decay exponential fitting, area method, and the pulse pressure method (PPM). Compliance measurements were compared to those obtained under continuous flow conditions through a right ventricular bypass (Heartware Inc., Miami Lakes, FL, USA). Compliance was computed for various flows using diastolic decay exponential fitting after an abrupt interruption of the pump. Under the continuous flow conditions, resistance (R) was a decreasing function of the flow, and the fitting to P = e^-t/RC yielded a pulmonary time constant (RC) of 2.06 s ( ± 0.48). Compliance was an increasing function of flow. Steady flow inter-method comparisons of compliance under pulsatile flow conditions showed large discrepancies and values (7.23 ± 4.47 mL/mmHg) which were lower than those obtained under continuous flow conditions (10.19 ± 1 0.31 mL/mmHg). Best agreement with steady flow measurements is obtained with the diastolic decay method. Resistance and compliance are both flow-dependent and are inversely related in the pulmonary circulation. The dynamic nature of the pulsatile flow may induce a non-uniformly distributed compliance, with an influence on the methods of measurement.

Introduction

The pulmonary circulation is a low-resistance high-compliance system that exhibits certain remarkable functional properties distinguishing it from the systemic circulation. For instance, it has been reported that the product of pulmonary vascular resistance (R) and total pulmonary artery (PA) compliance (C), RC, is constant,¹ which might explain the observation that the systolic pulmonary artery pressure (SPAP) relates linearly to the mean pulmonary pressure (mPAP).² This behavior has been ascribed to the anatomical and physiological organization of the pulmonary arterial vasculature, with the extension of compliant vessels to the capillary level, overlapping the resistive vessels.³

However, clinical and experimental studies have shown discrepancies in the RC product, questioning its constancy.⁴ The methodological nature of these studies, however, may contribute to this uncertainty. While resistance is calculated in a well-defined and undisputed manner as (mPAP–left atrial pressure)/mean flow), there are several ways to calculate pulmonary arterial compliance, which may explain the disparities observed among several studies. All methods used to estimate volume compliance are implicitly or explicitly based on Windkessel models, which are a relatively crude approximation of a more complex physiological reality. These models do not account for wave travel; however, the estimates are based on pressure and flow measurements which are affected by waves and wave reflections, and thereby influence the accuracy of the compliance measurement.⁵

The primary goal of this study was to design an in vivo experimental model to quantify the pulmonary vascular response to steady flow. A continuous flow pump was used to bypass the right ventricle thereby creating a non-pulsatile steady state in the pulmonary vasculature that is unaffected by waves. We hypothesized that a net interruption of the flow would induce a mono-exponential pressure decay as described by Franck, which would allow for the extraction of a time constant (RC).⁶ This methodology should allow for the verification of the constancy of RC and the identification of the more appropriate method for calculating compliance compared with other methods. A reliable measurement of compliance in the pulmonary circulation is clinically relevant and can eventually allow for a better outlining of the prognosis of patients with pulmonary arterial hypertension (PAH), the determination of the operability of patients with certain forms of pulmonary hypertension,⁷ and the refinement of the management of PAH patients who are in need of left and/or right ventricular assist devices.⁸

Materials and methods

The study protocol was performed according to the standards of The Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health (publication 85-23, revised 1996) and approved by the Ethical Committee for Animal Research of the Ghent University Hospital (ECD 15/46).

Experimental preparation

Six landrace pigs (all animals were female pigs aged six months; the average weight was 68.3 ± 10.4 kg) were included in the study. Following a pre-treatment of intramuscular tiletamine and zolazepam in a combined solution with xylazine 2% (0.2 mL/kg), anesthesia was induced with intravenous propofol (3 mg/kg), sufentanil (0.005 mg/kg), and rocuronium bromide (1 mg/kg). After the endotracheal intubation, the animals were mechanically ventilated with 40% FiO2 and a tidal volume of 0.1–0.15 L/kg. The anesthesia was maintained with a continuous sevoflurane ET (2.5%) administration via the AnaConda® System (Sedana Medical, Sundbyberg, Sweden) and eventually with additional boluses of sufentanil (0.005 mg/kg). Basic monitoring included an electrocardiogram, body temperature measurement, and ventilatory CO₂ emission measurements via capnography. Arterial blood gas sampling was used to control the oxygenation.

A central venous line was inserted via the external jugular vein for a saline infusion at a constant rate of 3–5 mL/kg/h. The left carotid artery was punctured and a single lumen fluid-filled catheter was used to continuously monitor the systemic pressures.

Pulsatile flow conditions (normal physiology)

The heart was exposed through a midline sternotomy and longitudinal opening of the pericardium. A pressure transducer-tipped catheter (Millar SPR-524; Millar Instruments, Houston, TX, USA) was inserted into the PA with the tip at the level of the main pulmonary trunk.

A 16-mm perivascular flow probe (Transonic Systems, Ithaca, NY, USA) was placed around the PA for continuous measurement of PA flow. A second pressure transducer-tipped catheter (Millar SPR-524; Millar Instruments, Houston, TX, USA) was inserted into the left atrial appendage to monitor left atrial pressure (LAP), and a 7-F dual-field pressure-volume catheter (Millar SPC-570-2 , Millar Instruments, Houston, TX, USA) was inserted via direct puncture into the right ventricle to monitor intraventricular pressures. The pressure and flow in the PA and the left atrial and right ventricular pressure were recorded at baseline and during dobutamine continuous infusion (15 µgr.kg⁻¹.min⁻¹) to increase cardiac output and pulmonary pressures (Fig. 1).

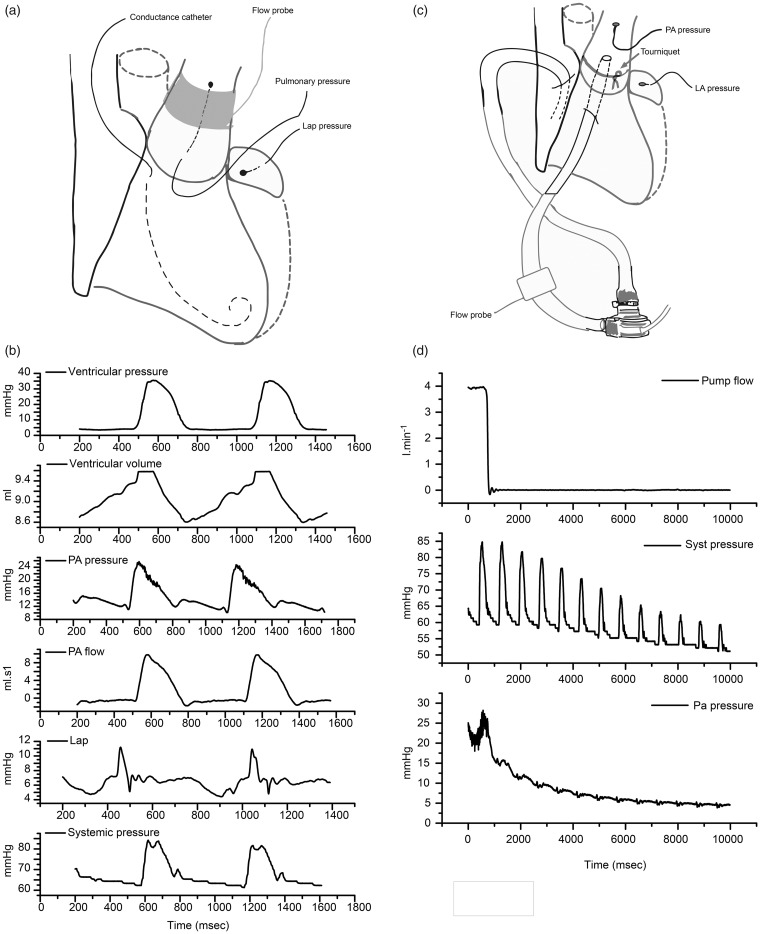
Fig. 1.

Experimental setting. (a) Pulsatile flow setting. (b) Recordings from top to bottom are as follows: right ventricular pressure, right ventricular volume, pulmonary pressure, pulmonary flow, left auricular pressure and systemic pressure. (c) Continuous flow setting. (d) One occlusion episode is shown from top to bottom: pump flow, systemic pressure, and pulmonary pressure.

Steady flow conditions (novel experimental protocol)

During a second phase, the PA perivascular flow probe was removed and the PA was encircled using umbilical tape with a tourniquet to constrict the PA. A 29-Fr multi-perforated cannula (Stöckert Instruments, München, Germany) was inserted into the right atrium, and a straight 22-Fr cannula (Medtronic Inc., Minneapolis, MN, USA) was inserted into the PA through the right ventricular outflow tract and secured with a 5/0 prolene purse-string suture. The cannulas were connected to a continuous centrifugal flow pump (Heartware Inc., Miami Lakes, FL, USA) via two silicon tubes, a 31-Fr tube at the inflow side and a 27-Fr tube at the outflow side (Fig. 1). The pump was started at 2000 rotations/min and the tourniquet was tied around the PA cannula to ensure that all pulmonary flow was exclusively delivered via the continuous flow pump. The exact pump flow rate was recorded via a flow probe (MA-16 PAU, Transonic Systems, Ithaca, NY, USA) that was adapted around the arterial tubing. The pump flow was progressively increased with increments of 100 rotations/min until the flow doubled. Per increment increase, the flow was abruptly interrupted with a clamp to measure the pressure decrease in the PA.

Data acquisition and processing

All pressures, flows, and intraventricular volume were recorded and digitized at 1000 Hz using a data acquisition system (Powerlab 16/9, Ad Instrument, Dunedin, New Zealand) and software (Labchart 7, Ad Instrument, Dunedin, New Zealand). The recordings were done with the animal disconnected at least 5 s from the ventilator to achieve airway pressure equal to the atmospheric pressure. The data analysis was performed using embedded or custom-made functions programmed in a MATLAB environment (MATLAB, Mathworks, Natick, MA, USA).

Assessing total pulmonary arterial compliance under pulsatile flow conditions

Pulmonary arterial compliance was computed according to the following four methods:

1. The ratio of stroke volume (in mL) and pulse pressure (in mmHg). The stroke volume was measured using the integral of the positive values of the PA flow meter; negative values were discarded.

2. Diastolic pressure decay time method. During diastole, the pressure drops mono-exponentially in a Windkessel system according to the following equation:

   $$P=P_{\text{diast}}{\text{e}}^{-\text{t}/\text{RC}}$$ (1)

   Fitting the diastolic pressure curve to an exponential curve yields RC, where R is resistance calculated as (mPAP–P_LAP)/mean flow. Because the first portion of diastole is perturbed by waves, we started the fitting after the peak value of diastolic pressure.
3. The area method initially described by Liu.⁹ The area method divides the cardiac cycle into two areas, systole and diastole, based on the incisura of the dicrotic notch. We defined the onset of the diastolic period and area as the period during which no flow entered the vascular circuit, and thus, a ventricular volume reduction was not observed via the impedance catheter. This instant defines the pressure at the beginning of the diastole ($P_{\text{diast}}^{*}$), splitting the systolic (A_s) and diastolic (A_d) areas (Fig. 2). Compliance is calculated as

   $$C=\frac{\text{Strokevolume}}{K(P_{\text{diast}}*-P_{\text{enddiast}})}\text{ with }K=\frac{(A_{\text{s}}+A_{\text{d}})}{A_{\text{d}}}$$ (2)

   with P_{end diast} defined as the pressure at the end of the diastole in mmHg.

4. The pulse pressure method.^10,11 According to Stergiopulos et al., this method iteratively adapts the value of C in a two-element Windkessel model until the measured and predicted pulse pressures are identical, considering a calculated value of R.

Fig. 2.

Modified area method to compute compliance. (a) The beginning of the diastolic phase is usually defined at the first dicrotic peak (black arrow) and the corresponding area is shaded in (b). We used the conductance catheter to identify the moment when there is no outflow from the ventricle (large gray arrow) and started the diastole at the corresponding pressure recording, which enlarged the diastolic area shaded in (c).

Assessing total pulmonary arterial compliance under continuous flow conditions

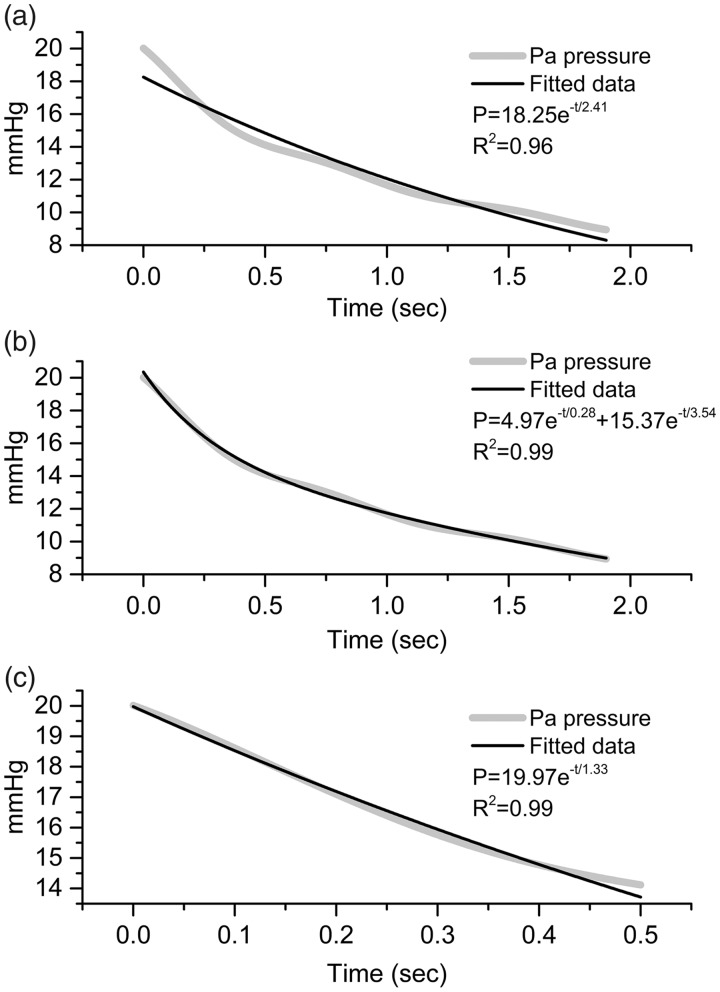
Compliance computation under continuous flow conditions is based on the PA pressure decay once the flow is abruptly ceased. The pressure decrease was best fitted by a bi-exponential decay function rather than a mono-exponential function; however, when only considering the first 500 ms of the pressure curve, a mono-exponential fit is reasonable (R² = 0.99) (Fig. 3) and compliance is computed by the same equation as that used under the pulsatile flow conditions as follows: P = P_diast e^-t/RC.

Fig. 3.

Mono-exponential fitting of the pressure decay curve over the whole decay (a) is less satisfactory than a bi-exponential decay (b). However, considering the first 500 ms (c), the mono-exponential fitting yielded satisfactory results.

Assessing pulmonary arterial resistance and RC

The resistance was calculated as (mPAP–P_LAP)/mean flow. The RC is either the product of the resistance and compliance when they are individually derived (using the area method, SV/PP method, and pulse pressure method) or the value obtained from the fitting of the exponential curve using the decay method (in pulsatile and continuous flow conditions).

Statistics

The comparison between the pulsatile and continuous flow conditions was performed using the Wilcoxon-signed rank test. The comparisons in-between animals were performed using a Kruskal–Wallis analysis. Correlations were established using Spearman's correlation. Comparisons between the different types of compliance measurements were performed using the Bland–Altman method of agreement.¹² The test results were considered statistically significant at P < 0.05.

Results

Relationship between mPAP and SPAP

The arterial pressures (mPAP and SPAP) that were recorded under pulsatile flow conditions were averaged over 10 beats in end-expiratory conditions. Every animal had five recordings distributed during the experiment under pulsatile conditions. The recordings yielded 30 pairs of values (SPAP and mPAP) for the six animals. The analysis of the pooled data demonstrated that mPAP and SPAP were linearly related according to the following equation: mPAP = 0.59 SPAP + 2.48 mmHg (r² = 0.913) (Fig. 4).

Fig. 4.

The linear relationship between the mPAP and the SPAP.

Pulmonary arterial compliance under pulsatile flow conditions

The values of compliance under pulsatile flow conditions using the four different methods at baseline and following dobutamine infusion are presented in Table 1. In all animals except for one, dobutamine infusion sufficiently increased the flow, allowing for the calculation of compliance at two significantly different flow levels. In each animal, the increase in flow was accompanied by a moderate increase of PA pressure and significant decrease of resistance. None of the four methods used to estimate compliance under pulsatile flow conditions provided consistent trends during dobutamine administration (Table 1). In animal 3, for example, compliance decreased with dobutamine using the pulse pressure method and SV/PP method, while higher values were found using the two other methods. We highlighted in gray the pairs of values where a decrease in resistance supposed an increase of compliance and instead a decrease was observed. This “paradoxical” evolution occurred once with the decay method, twice with the area method, four times with the PPM method, and five times with the SV method.

Table 1.

Compliance measurement in pulsatile flow.

		Flow	P mean	Lap	R	Period	SV	C (SV/PP)	C (decay)	C (area)	C (ppm)
Pig 1	BL	39.45	20.96	8.65	0.312	0.74	33.71	2.77 (0.02)	2.97 (0.04)	1.93 (0.02)	1.66
Pig 1	DOBU	41.02	20.55	7.90	0.308	0.72	34 .01	2.66(0.03)	2.94 (0.03)	1.99(0.02)	1.70
Pig 2	BL	35.91	21.88	2.95	0.527	0.67	23.10	1.32 (0.03)	1.41 (0.02)	1.72 (0.05)	0.73
Pig 2	DOBU	66.96	29.12	5.37	0.355	0.39	25.77	0.74 (0.03)	0.73 (0.03)	0.74 (0.08)	0.35
Pig 3	BL	17.47	17.95	7.05	0.623	0.89	27.08	2.23 (0.06)	1.99 (0.07)	1.41 (0.04)	1.51
Pig 3	DOBU	44.33	20.22	8.47	0.265	0.72	39.13	1.91 (0.09)	2.55 (0.26)	1.51 (0.06)	1.39
Pig 4	BL	27.32	10.38	3.56	0.249	0.62	16.95	1.88 (0.02)	1.19 (0.03)	1.88 (0.10)	0.38
Pig 4	DOBU	48.54	12.43	3.17	0.191	0.61	29.87	1.57 (0.03)	1.95 (0.03)	2.83 (0.15)	0.59
Pig 5	BL	47.14	13.53	4.49	0.192	0.66	41.24	4.38 (0.13)	2.79 (0.20)	3.47 (0.22)	2.97
Pig 5	DOBU	59.84	14.43	4.92	0.159	0.62	44.54	3.94 (0.06)	3.28 (0.18)	5.60 (0.36)	1.97
Pig 6	BL	24.68	13.78	6.23	0.306	0.71	23.26	2.22 (0.05)	3.04 (0.09)	1.58 (0.09)	1.18
Pig 6	DOBU	32.93	15.36	7.01	0.253	0.60	23.61	1.68 (0.02)	3.50 (0.15)	1.32 (0.09)	1.09

Flow is expressed in mL/s.

Pairs of compliance values where a decrease are observed instead of the expected increase are highlighted in gray.

P mean, mean pressure in mmHg; Lap, left atrial pressure in mmHg; R, resistance in mmHg.ml⁻¹.s; Period, heart cycle duration in seconds; SV, stroke volume in mL; C, compliance in mL.mmHg⁻¹.

Assessing the pressure-flow relationship and total pulmonary arterial compliance under continuous flow conditions

Fig. 5a shows the pump rate to pressure relationship. In five of the six animals, PAP remained constant (the 95% confidence interval of a linear fit crosses 0 for the angular coefficient [pigs 5 and 6]) or slightly increased with the pump rate increase (pigs 1, 2, and 3: maximum angular coefficient < 0.002). One animal showed an obvious decrease of PAP as the pump rate increased (pig 4: angular coefficient of –0.004). Fig. 5b shows the relationship between the flow and resistance and indicates that there is a decrease of resistance with increasing flow. Fig. 5c shows the relationship between the flow and compliance. In all animals, there is an increase of compliance with increasing flow. Combining R and C in Fig. 5d, it was observed that RC was fairly constant in each animal with increasing flow, except for pig 3, which showed an RC decrease.

Fig. 5.

(a) Pressure vs. pump flow rate; (b) resistance vs. flow; (c) compliance vs. flow; (d) RC vs. flow.

In the individual animals, the average RC over all flow levels varied from 1.13 ± 0.36 s (pig 1) to 2.91 s ± 0.20 (pig 2), resulting in statistically significant difference between animals (P < 0.01). When the RC product was normalized for the weight, it varied from 0.023 ± 0.04 s (pig 1) to 0.039 ± 0.001 s (pig 2) and the difference remained statistically different.

Comparing the pulsatile and continuous regimes

The flow at which compliance was measured in the pulsatile regime (Table 1) was used as the reference. The different flows in the continuous regime were screened and the flow closest to the reference value was chosen. The concomitant compliance value was then compared with that obtained under the pulsatile flow conditions. The flows selected (two for each animal except for pig 1 for which only one value was available) are presented in Table 2. Some of the flow levels in the pulsatile regime were low and were not reproduced by the continuous flow. Compliance values were significantly higher under continuous flow conditions than under pulsatile flow conditions regardless of the used measurement method with a very poor correlation. With compliance measured in the continuous flow regime as reference, Bland–Altman analysis showed a Pearson correlation coefficient of 0.021 for the decay method, 0.027 for the SV method, 0.101 for the PPM method, and 0.317 for the area method.

Table 2.

Compliance measurement in continuous flow.

	Flow	P mean	Lap	R	C
Pig 1	39.31	14.81	5.94	0.225	4.43
Pig 2	36.66	15.62	2.75	0.369	8.27
Pig 2	65.66	16.36	4.34	0.183	15.04
Pig 3	17.47	NA	NA	NA	NA
Pig 3	44.50	18.90	5.62	0.305	6.55
Pig 4	27.32	NA	NA	NA	NA
Pig 4	35.51	14.93	3.26	0.329	4.92
Pig 4	48.23	13.08	5.03	0.168	10.68
Pig 5	47.50	15.07	4.93	0.213	10.91
Pig 5	59.66	15.12	6.79	0.140	16.34
Pig 6	24.68	NA	NA	NA	NA
Pig 6	34.27	22.51	6.33	0.469	3.53

Flow is expressed in mL/s.

P mean, mean pressure in mmHg, Lap, left atrial pressure in mmHg; R, resistance in mmHg.mL⁻¹.s; C, compliance in mL.mmHg⁻¹; NA, not applicable.

In the pulsatile regime, when plotting C as a function of R, no evident relationship emerges whatever the method considered, whereas in the continuous flow regime, there is an inverse relationship according to the following equation:

$$\text{Resistance}=2.52*\text{complianc}{\text{e}}^{-0.88}({\text{R}}^2=0.84)(\text{Fig}.6).$$

Discussion

In this study, we designed an experimental setting and methodology that provides a reliable method for compliance measurements by eliminating wave perturbations in the pressure curves in the pulmonary circulation. Compared to this measurement, all conventionally used methods appear to underestimate compliance and lead to large discrepancies between other compliance estimations.

The use of a continuous flow pump allowed for the creation of steady conditions in the pulmonary circulation, thereby eliminating the dynamics caused by the transmitted and reflected waves from pressure and flow recordings. Consequently, the pressure/flow relationship at equilibrium, without elastic variations, only corresponds to the vascular resistance, dismissing effects of inertance and compliance (which both contribute to the complex input and characteristic impedance). The abrupt interruption of the flow after an equilibrium state has been reached allows for an approximation that is close to a two-element Windkessel configuration, which is confirmed by the monotonically decaying pressure, consistent with the discharge of a loaded capacitance. We therefore believe that an exponential fitting to the pressure decrease yields a reference value for pulmonary compliance.

The purpose of our study was not to validate this method for clinical use in humans but to identify the best invasive method of compliance estimation among the few usable methods available in the human clinic, which could then be used as a standard for comparisons with less invasive methods, such as MRI.¹³ Interestingly, the values obtained for the resistance and compliance under continuous flow conditions were significantly lower and higher, respectively, than those under the pulsatile flow conditions. Moreover, this observation seemed to be independent of the used method of compliance estimation.

Regarding the resistance, we observed a decrease as the pump flow increased, which we ascribe to the progressive recruitment of under-perfused vessels and/or vessel dilatation with increasing pump flow rates.¹⁴ The flow-resistance curves can be approximated by an exponential fitting or a second power fitting. More important is the observation that a 5% increase of the flow entailed a 10–25% decrease of the resistance. Despite that a constant value is not applicable to the pulmonary resistance,¹⁵ most clinical studies use resistance as a single value without normalization for the variability in body surface or flow.¹⁶ Further studies are needed to identify the type of flow normalization that should be applied to adjust for the resistance.

Whether the observed decrease in resistance is due to a passive mechanical effect or mediated by a decreased vasomotor tone is a relevant question that cannot be answered in our study since vasomotor tone was not blocked. Although it is a very important topic in the pulmonary circulation witnessed by positive clinical results on pulmonary vasodilators¹⁷ and by the physiological relevance of hypoxic vasoconstriction,¹⁸ the exact role and pathways of pulmonary vasomotor tone in normal lungs at rest and at exercise is still under investigation with some argument in favor of passive control¹⁹ and some for active control.²⁰ Transition from pulsatile shear stress to constant shear stress should have an impact on vasoactive mediators; however, the phenomenon is complex and deserves attention that extends the primary goal of our experiment.

The compliance/Windkessel effect leads to the monotonically decaying pressure upon cessation of flow. Interestingly, the abrupt flow interruption induces a bi-exponential decay of pressure rather than a mono-exponential decay (Fig. 3). This bi-exponential decay has previously been described and has been explained by a compartmental design of the pulmonary vasculature: there could be a sequential voiding from the arterial compartment into the capillary bed and from there in the venous compartment.²¹ The capillary bed led to particular interest since the capillary pressure could be a determinant of the alveolar transmural pressure. Quantification of the pressure through the bi-exponential decay to help diagnosis and therapy of lung disorders such as pulmonary edema or ARDS has been extensively investigated but with poor positive results.²² Resistance partitioning to predict operability of CTEPH was also explored with the bi-exponential method with limited applications.²³

The design of the continuous flow model adopted in this experiment uniformize the flow and the pulmonary vasculature can be more properly viewed as a continuously distributed resistance-compliance system. All the aforementioned arterial, capillary, and venous compartments are abolished, and still bi-exponential decay is observed. The sequential voiding of compartments can hardly be defended in our continuous flow setting to account for a bi-exponential pressure decrease.

The non-linearity of the vascular resistance is sufficient to justify a bi-exponential decay (or, more generally, a multi-exponential decay), hereby questioning the use of the capillary pressure as a measure of resistance partitioning in the clinical setting.

Since a bi-exponential decrease cannot be used to extract a value for compliance, we had to consider fitting only a part of the pressure decay in compliance computations under continuous flow conditions We chose a time interval larger than a half period of the average heart rate based on the assumption that a large time interval would reflect the diastole and yield acceptable values for our derived measures; this time interval was suitable for a mono-exponential decrease analysis.

The value of compliance obtained with this methodology are significantly higher than the values obtained in the pulsatile flow regime.

Getting rid of waves and wave reflections was the premises of the use of the continuous flow pump, the objective being to be as close as possible to a two-element Windkessel; however, it resulted in a uniformization of the different compartment of the vascular tree, the compliance measured being the addition of the arterial, capillary, and venous sector hence the observed compliance is high. The continuous flow setting cannot be used as a gold standard to determine the compliance of the arterial compartment that is the most valuable for the clinician. Nevertheless, the setting can still be used to assess the relation of the resistance and compliance.

The RC time constant of the pulmonary arterial bed

Otto Franck was the first to formalize the Windkessel function of the arterial system by considering the diastolic pressure a mono-exponential decay in the formula P = P_diast e -^t/RC under zero inflow conditions. Franck noticed that the ratio of the time derivative of pressure to the pressure should then be constant, i.e. RC.⁶ However, his deduction did not consider the impact of waves disturbing the pressure analysis. In the normal pulmonary circulation, the diastolic part of the pressure curve is severely distorted from a mono-exponential; fitting is typically restricted to approximately the last one-third of diastole. However, under continuous flow conditions, the wave perturbations are abolished and a mono-exponential curve fits well to the pressure decay during the first 500 ms following flow cessation. This allows for measurements of the RC time constant over a wide range of flow variations.

RC has been reported to be a constant with a mean value of 0.5 s in every patient regardless of the pathology.²⁴ The constancy of RC is a surrogate for another remarkable property of the pulmonary hemodynamic, i.e. the linear relationship between the mean and the systolic pressure. This relationship has been demonstrated in healthy^25,26 and diseased states²⁷ and under different physiological conditions.²⁸ This pressure relationship has been shown to be related to the constancy of the RC product.¹

In our study, we showed that mPAP and SPAP are linearly related as mPAP = 0.59 SPAP + 2.48, which is remarkably close to what has been observed in humans (mPAP = 0.6 SPAP + 2).²⁹ While the linear relationship between SPAP and mPAP is widely supported in literature (with some notable modulation in chronic thrombo-embolic patients),^30,31 its putative cause, the constancy of RC, is not unequivocally accepted and is associated with wide variations (from 0.25 s³² to 0.75 s³³) around the mean value of 0.5 s. One of the possible causes of this variability might be related to the methodology of the RC measurement, which is often computed as the product of the resistance and compliance (defined as SV/PP), hereby being subject to mathematical coupling.³⁴

Due to the design of this experiment, we could reliably assess the RC. In five of the six animals, the RC was effectively constant with only a slight variation around the mean value (Fig. 5).

While the RC product was constant within most animals, values were significantly different among the animals. Two different approaches of the time constant should be considered. One approach is the time for the pressure to decrease to one-third of its protodiastolic value. This definition can cope with a uniform time constant through health and disease, the time constant being the result of an equilibrium between the dynamics the ventricle and the properties of the pulmonary circulation. When the system is started, volume accumulates in the pulmonary reservoir decreasing resistance and compliance until their inverse relationship is reached, this in turn will determine the pressure.

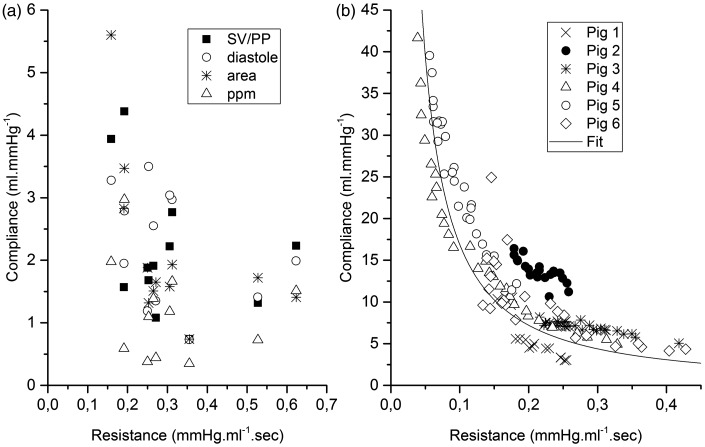
The other approach is based on a two-element Windkessel where the time constant is computed as the product of the resistance and compliance. Based upon the complex expression of resistance and the complex expression of compliance, their product can hardly be a uniform constant. The simplest expression of resistance is the Poiseuillean expression, with a dependence to the fourth power of the radius while a simple expression of compliance is function of the third power of the radius.³⁵ Given the complexity of the relation (adding the visco-elastic properties of the arteries and the possibility of recruiting vessels), it is remarkable that the compliance showed a clear relationship to the resistance when considering the pooled group of animals (Fig. 6b) with some form of inverse relationship.

Fig. 6.

Relationship between resistance and compliance in the pulsatile regime (a) and the continuous flow regime (b) using different methods of compliance assessment.

The differences that we observed in the product are small (RC is in the range of 1.13–2.91 s) but significant and persisted when normalized for weight. Based on our observations, it would be more accurate to question the invariability of the resistance/compliance relationship through health and disease than to question the constancy of the product, which due to the complexity of the system could hardly be met.

The constancy of RC is not only relevant from a physiological viewpoint but also has important clinical implications. If RC is effectively constant and/or the coefficient of the mPAP/SPAP is constant regardless of the nature or importance of the pulmonary artery disease, the estimation of the pulmonary arterial compliance should have no value in the diagnosis nor the prognosis of an illness because it is then a surrogate of resistance. This situation has been described previously.^26,36 However, if RC is variable, it could help to discriminate the nature of PAH according to studies that have shown discrepancies between the coefficient of the mPAP/SPAP slope or the values of the RC product.³¹ Since achieving a continuous flow, which is a prerequisite for a correct estimation of RC, cannot be easily obtained in a clinical setting, a reliable independent estimate of compliance must be identified to answer the question of RC constancy.

From a methodological point of view, we wish to add that there is a concern related to the asymptotic value of the decay curve included in P = (P_diast−P_asympt)e^-t/RC + P_asympt.²⁴ The asymptotic value is the offset pressure that is reached after an infinite amount of time. Usually, the chosen value of the asymptotic pressure is the wedge pressure, which is considered constant. In this experimental setting, the outflow pressure is the left atrial pressure. Filling (and pressure) of the LA depends on the outflow from the right side, which was discontinued along with the pump interruption, causing the pressure to decrease; P_asympt is therefore not constant. Subtracting instantaneous LAP pressure from the PAP yielded a function that is not an exponential or a reflection of the physiological situation in which the outflow is constant. We therefore assumed that P_asympt, = 0, thereby simplifying the model while introducing a small error that affects the pressure decay fitting in such a way that it underestimates compliance, which only reinforces our observations.

Pulmonary arterial compliance (and what estimation method to use in vivo)

Compliance is defined as the volume change due to the pressure change of an enclosed system and is determined by the volume of the system and its elasticity/distensibility. Clinically, an impairment of vessel compliance has been related to a worse outcome.³⁷ Therefore, the correct estimation of compliance is important. However, despite its conceptual simplicity, the practical estimation of compliance is difficult due to the dynamic nature of the pressure/flow relationship and the existence of waves. In our novel experimental model, the pressure curve after the cessation of flow—and rid of wave interferences—was well fitted by a mono-exponential decay function during the first 500 ms. It was observed that compliance was inversely related to resistance, which is likely to be explained by the structural properties of the pulmonary vasculature, including the overlap of resistive and compliant vessels. The latter implies that resistance vessels, upon “inflation” with higher imposed flows, contribute less to resistance, but start to contribute to the total compliance in the pulmonary arterial system.

One of our main goals was to define the best in vivo method for the measurement of compliance, postulating the measure under continuous flow conditions as gold standard for the same level of (mean) flow. For every method used, compliance under pulsatile flow conditions was substantially lower than that under continuous flow conditions. Our results also showed large discrepancies between methods, which has been observed by others.⁹ Segers et al. found that the SV/PP method overestimates compliance by 80% compared to the PPM method.¹¹ However, our results showed a more striking observation in the relationship between the method of compliance assessment and the vascular resistance. Using our observation in continuous flow conditions as guidance, one anticipates an increase in compliance when the resistance decreases. A paradoxical decrease in compliance shown in Table 1 is highlighted in gray. When the method of compliance computation was based on the systolic part, such as in the SV/PP method or the PPM method, four of the five measures showed a paradoxical decrease in compliance. It occurred in two animals using the area method and in only one animal using the diastolic decay method. Overall, quantitative comparison showed a very poor correlation between continuous and pulsatile condition. Since the inverse relation between resistance and compliance is unequivocal in respect to the continuous flow regime, we consider the semi-quantitative observations relating compliance and resistance as valid and the decay time method as the method showing the closest agreement with the expected changes, and hence as the method of choice.

The different values of compliance according to the method of measurement question the appropriateness of each method and the major differences in compliance when comparing the pulsatile and continuous flow conditions question the nature itself of a unique value for a global compliance of the whole lung. A unique value for compliance would imply a linear relation between pressure and volume which is not true since arteries have visco-elastic properties showing a curvilinear pressure volume relation and moreover a three-dimensional elastic container with increasing volume will have an increasing compliance due to Laplace's law.

Just as for resistance, we could argue that a mean value would be appropriate to draw clinical conclusions. When computing resistance, the use of mean pressure and mean flow over the whole cardiac cycle reflect mean resistance. When computing compliance, the different methods are more prone to explore compliance during systole such as for the PPM method or during diastole such as for the diastolic decay method. Compliance during one phase of the cardiac cycle can barely be used as a mean value reflecting elastic and geometrical properties of the system. Our experiment pointed out that the distribution of the flow could have an influence, uniformly distributed volume induces a high compliance. In pulsatile flow conditions, due to inertia, the volume is not instantaneously distributed, and the most proximal arterial segments are first pressurized and recruited. Measurement of compliance during systole, such as SV/PP and the pulse pressure method, will yield lower values, reflecting the compliance at higher pressure of a proximal compartment. The methods that explore a later phase of the cycle may measure the compliance of a more uniformly distributed vascular system, thereby indicating higher values.

Conclusions

In this experiment, we were able to design a model of two-element Windkessel in the pulmonary circulation using a continuous pulmonary flow pump. Based on the inverse relation of resistance and compliance, in pulsatile flow conditions, the decay time method of compliance assessment yields results in closest agreement with the reference method. Absolute value of compliance in pulsatile flow conditions were significantly lower than in the continuous flow conditions whatever the method considered. We speculate that in vivo, in pulsatile flow conditions, inertial effects lead to non-uniform distribution of the flow with compartmental recruitment of compliance. The four different methods of compliance assessment used in our experiment do not allow to estimate compliance in the entire compartment. True arterial compliance in the pulmonary circulation remains difficult to assess. The different methods available are entailed with error and should be used with circumspection in the clinical setting.

Conflict of interest

The author(s) declare that there is no conflict of interest.

Funding

This work was supported by a grant from “Le fond pour la chirurgie cardiaque.”