Determination of an effective scoring function for RNA–RNA interactions with a physics-based double-iterative method

Abstract

RNA–RNA interactions play fundamental roles in gene and cell regulation. Therefore, accurate prediction of RNA–RNA interactions is critical to determine their complex structures and understand the molecular mechanism of the interactions. Here, we have developed a physics-based double-iterative strategy to determine the effective potentials for RNA–RNA interactions based on a training set of 97 diverse RNA–RNA complexes. The double-iterative strategy circumvented the reference state problem in knowledge-based scoring functions by updating the potentials through iteration and also overcame the decoy-dependent limitation in previous iterative methods by constructing the decoys iteratively. The derived scoring function, which is referred to as DITScoreRR, was evaluated on an RNA–RNA docking benchmark of 60 test cases and compared with three other scoring functions. It was shown that for bound docking, our scoring function DITScoreRR obtained the excellent success rates of 90% and 98.3% in binding mode predictions when the top 1 and 10 predictions were considered, compared to 63.3% and 71.7% for van der Waals interactions, 45.0% and 65.0% for ITScorePP, and 11.7% and 26.7% for ZDOCK 2.1, respectively. For unbound docking, DITScoreRR achieved the good success rates of 53.3% and 71.7% in binding mode predictions when the top 1 and 10 predictions were considered, compared to 13.3% and 28.3% for van der Waals interactions, 11.7% and 26.7% for our ITScorePP, and 3.3% and 6.7% for ZDOCK 2.1, respectively. DITScoreRR also performed significantly better in ranking decoys and obtained significantly higher score-RMSD correlations than the other three scoring functions. DITScoreRR will be of great value for the prediction and design of RNA structures and RNA–RNA complexes.

INTRODUCTION

RNA–RNA interactions play important roles in the regulation of gene expression and cell development (1–3). Therefore, determination of their complex structures is valuable to understand the molecular mechanism of related biological processes and thus develop therapeutic interventions or drugs targeting RNA–RNA interactions (4–9). However, due to the high cost and technical difficulties, the number of experimentally determined RNA–RNA complex structures is very limited, compared to thousands of identified RNA–RNA interactions by various methods (10). Therefore, computational methods like molecular docking (11) provide a necessarily complementary way to experimental methods for the determination of RNA–RNA complex structures. Given two individual RNA three-dimensional (3D) structures, molecular docking first samples putative binding poses of one structure relative to the other around a binding site if the binding site is available or around the whole RNA structure. Meanwhile, an energy scoring function is used to evaluate all the sampled binding poses and rank them according to their binding energy scores (11). Therefore, the scoring function is a key component of molecular docking, which directly determines the accuracy of a docking algorithm (11–14).

For years, a number of scoring functions have been developed for molecular docking, which can be broadly grouped into three categories: force field-based, empirical, and knowledge-based scoring functions (13). Force field-based scoring functions use force field parameters to measure the binding energy between molecules. Despite their lucid physical meaning, rigorous force field-based scoring functions are normally computationally expensive and sometimes involve empirical weighting coefficients that are difficult to generalize. Empirical scoring functions are based on a set of weighted energy terms whose coefficients are derived by reproducing the binding affinities of a training set with known 3D structures. Although the empirical scoring function is computationally efficient, its general applicability is training set-dependent. The knowledge-based scoring function is directly converted from the occurrence frequencies of atom pairs in a database of known structures (15). Because of its good balance between the accuracy/general applicability and the computational speed, the knowledge-based scoring function has been widely used in protein docking and structure predictions and achieved considerable successes (14,16).

Despite the significant progresses in the scoring functions for protein–protein recognition (17–33), protein–RNA interactions (34–45), and RNA structure prediction (46–53), little effort has been made in the scoring functions for RNA–RNA interactions (6,54). One of the reasons is the limited number of experimental RNA individual and RNA–RNA complex structures in the protein data bank (PDB) (55). Given the important role of free energy in stabilizing RNA–RNA complexes, computational tools like molecular docking is playing an increasing role in the determination of RNA–RNA complex structures. Therefore, as a key component, a fast and accurate scoring function is pressingly needed for the development of RNA–RNA docking algorithms. The rapidly increasing number of experimentally determined structures of RNA–RNA complexes also make the development of a knowledge-based scoring function for RNA–RNA interactions feasible.

However, there is one hurdle in the development of knowledge-based scoring functions. That is the calculation of the ‘reference state’ in which the interactions between atoms are zero (56–59). As pointed out in previous studies (56), such an ideal reference state is not accessible for the systems of biological molecules. Therefore, various methods have been tried to obtain a ‘reasonable’ reference state, though the reference state problem is still an issue in the knowledge-based scoring functions (13). Recently, based on an iterative approach, we have circumvented the reference state and significantly improve the accuracy of knowledge-based scoring functions (19,41,60–62). However, the iterative method depends on the pre-generated decoys that are used to update the potentials because it is impossible for the decoys to completely cover the whole binding space. The decoy-dependent limitation may significantly affect the general applicability of the iterative method and may result in an arbitrary influence on the derived scoring function. Therefore, a strategy to address the limitation is necessary. To this end, we have developed a physics-based double-iterative algorithm to derive the effective interaction potentials from experimentally observed complex structures. Through the double-iterative strategy, our method not only circumvented the reference state problem by improving the potentials through iteration in the inner loop, but also removed the decoy-dependent limitation by updating the binding decoys iteratively through molecular docking in the outer loop. As a test example, we have applied our double-iterative method to derive an effective scoring function for RNA–RNA interactions. Our scoring function was evaluated and compared with three other scoring methods on a benchmark of 60 diverse RNA–RNA complexes, demonstrating the significantly better performance of our scoring function than the other three scoring functions in both identifying near-native structures and ranking decoys.

MATERIALS AND METHODS

Double-iterative algorithm

We have developed a statistical mechanics-based double-iterative method to derive the effective potentials for RNA–RNA interactions from experimentally determined RNA–RNA complex structures. Our method can circumvent the challenging ‘reference state’ problem in knowledge-based scoring functions. The basic idea behind the method is to improve the inter-atomic pair potentials step by step through iterations by comparing the predicted pair distribution functions and the experimentally observed pair distribution functions of the native structures in a training set of RNA–RNA complexes. Our method can also overcome the decoy-dependent limitation by updating the binding decoys iteratively. A flowchart of our double-iterative method is illustrated in Figure 1.

Figure 1.

A flowchart of our double-iterative algorithm to derive the effective interaction potentials for RNA–RNA interactions, where the input/output, outer loop, and inner loop are colored in blue, green, and orange, respectively.

The initial potentials

Starting from a training set of experimentally determined RNA–RNA complex structures, we can calculate the observed pair distribution function 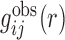of atom pair ij at distance r as follows:

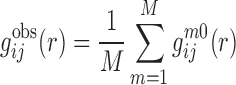(1)

where M is the number of the complexes in the training database. is the pair distribution function of the mth native complex structure and can be calculated as

(2)

where

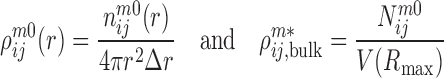(3)

are the densities of the ij atom pairs in a spherical shell of radius from r − Δr/2 to r + Δr/2 and in a reference sphere of radius R_max, respectively. 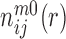is the number of ij pairs in the spherical shell at distance r and 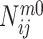is the total number of ij pairs in the reference sphere for the mth native structure.

With the calculated 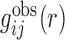from native structures, the initial potential 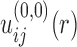was obtained as follows:

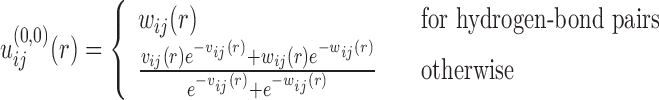(4)

where _ij(r) is the 6–12 van der Waals (VDW) potential and 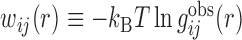is the potential of mean force (19). Here, the VDW parameters were taken from the corresponding values given in the AMBER force field (63). It should be noted that the basic purpose to include VDW potentials in Eq. (4) is to add a reasonable repulsion part to the PMF potentials, as the atom pairs don’t have enough occurrence frequencies to give accurate PMF potentials at short distance because of the strong repulsive VDW interactions. In principle, one should use a weighted form of PMF and VDW potentials as the initial potentials for all the atom pairs. However, one also needs to ensure that the inclusion of VDW potentials should not significantly change the statistically derived PMF potentials at the equilibrium distance. Therefore, a compromise should be reached to consider these two factors. Given the very different feature of hydrogen-bonding interactions from that of VDW potentials, we have used the PMF potentials alone as the initial potentials for hydrogen-bond pairs because the inclusion of VDW potentials would significantly change the well depth and equilibrium position of such hydrogen-bonding PMF potentials. However, for the atom pairs other than hydrogen bonds, we have adopted the weighted values of PMF and VDW interactions as the initial potentials, as their PMF potentials and VDW interactions are relatively consistent and thus the inclusion of VDW potentials can add an effective repulsion part without significantly changing the PMF potentials.

The outer loop

With a set of initial potentials, the method goes into the double-iterative cycle, which consists of an outer loop and an inner loop. The role of the outer loop is to remove the decoy-dependence of the iterative method by updating the binding decoys iteratively through our global docking program HDOCK with the current potentials 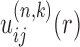, where n and k stand for the iterative steps of the outer and inner loops, respectively. HDOCK uses a fast Fourier transform (FFT)-based docking algorithm to systematically sample all possible binding modes of one molecule relative to the other and calculate their binding scores through the given potentials (18,64). The top 1000 binding modes were kept according to their binding energy scores, resulting in a total of 1001 binding structures (i.e. one native complex structure plus the top 1000 binding modes) for each case. The outer loop conducts one iteration cycle when the inner loop is completed once. The outer iteration repeats until the iterative step reaches a set number. As the outer loop updates the binding decoys on-the-fly through a systematically global docking with the current potentials, the decoys will not depend on pre-set potentials or local docking algorithm. Thus the decoy-dependence issue of the method can be eliminated.

The inner loop

With the constructed binding decoys from the outer loop, the protocol enters the inner loop. The function of the inner loop is to circumvent the ‘reference state’ problem by iteratively improving the potentials based on the constructed decoys. Specifically, the inner iterative method can be represented by the following formula:

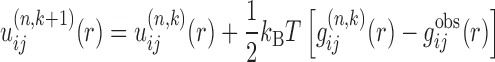(5)

where k stands for the iterative step of the inner loop, i and j represent the types of a pair of atoms from the two RNA structures of a complex. 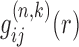is the predicted pair distribution functions by the current potentials at the k-th inner iteration cycle. It can be calculated by using a statistical mechanical principle as follows. We regard each binding decoy (l) as a microstate, and consider the native structure (l = 0) and the pre-generated decoys (l = 1, 2, 3, ⋅⋅⋅, L) for the m-th complex of the training set as the mth subsystem. Thus, the partition function for the m-th complex (or subsystem) can be calculated as

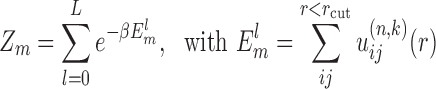(6)

where β = 1/k_BT, k_B is the Boltzmann constant, and T is the absolute temperature. 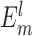is the binding energy score of the lth binding decoy/microstate for the m-th complex, and the summation is over all possible atom pairs from two interacting RNAs within a distance cutoff r_cut. Thus, the probability for the mth complex to occupy the lth microstate is

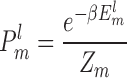(7)

Then, we can calculate the Boltzmann-average pair distribution function of atom pair ij for the whole system of M RNA–RNA complexes (i.e. over all the binding decoys for each complex) as

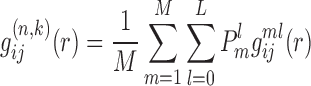(8)

where is the pair distribution function for atom pair ij for the l-th decoy of the m-th complex and can be calculated the way similar to Eq. (2). Apparently, .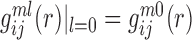

With the initial potentials of 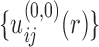, the first iteration will lead to an improved set of pair potentials 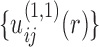via Eq. (5), followed by 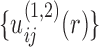, , 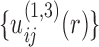and so on. The inner iteration continues until all the native complex structures were discriminated from decoys by the current potentials or a maximum iteration step was reached. Then, the iteration returns to the outer loop for constructing a new set of binding decoys.

The final output potentials

After the double iteration ends, we can obtain a final set of effective pair potentials that distinguish near-native structures from decoys. The potentials were further treated with the following smoothing algorithm to account for statistical fluctuations in the experimentally determined structures. Namely, the potential at the i-th bin was set to the weighted average of 1:2:4:2:1 of the potentials from bins (i − 2) to (i + 2). The effective potentials form our double-iterative scoring function for RNA–RNA interactions (DITScoreRR).

Iteration parameters

In this study, only heavy atoms were considered and the effects of hydrogens were implicitly incorporated in the potentials. The categorization for the RNA atom types is the same as that in our previous study (41), which gave a total of 12 atom types (Table 1). The van der Waals radii and well depths for the calculation of the initial potentials were taken from our previous study (60). The radius of the reference sphere used for pair distribution function calculations was set to 12 Å. The bin size Δr for the distance was set to 0.2 Å. The cutoff distance r_cut of the potentials for binding score calculations was set to 10 Å, as the potentials approach zero at this distance. The maximum penalty for the potentials at short distances was set to 10 kcal/mol unless otherwise specified.

Table 1. List of 12 RNA atom types used in DITScoreRR.

No.	Symbol	Atom name
1	C2X	C_C2, G_C6, U_C2, U_C4
2	Car	C_C4, C_C5, C_C6, G_C2, U_C5, U_C6, A_C2, A_C4, A_C5, A_C6, A_C8, G_C4, G_C5, G_C8
3	C3X	A_C1′, A_C2′, A_C3′, A_C4′, A_C5′, C_C1′, C_C2′, C_C3′, C_C4′, C_C5′, G_C1′, G_C2′, G_C3′, G_C4′, G_C5′, U_C1′, U_C2′, U_C3′, U_C4′, U_C5′
4	N2N	C_N1, G_N1, U_N1, U_N3
5	N2X	A_N6, C_N4, G_N2
6	Nar	C_N3, G_N3, A_N1, A_N3, A_N7, G_N7
7	N21	A_N9, G_N9
8	O2	C_O2, G_O6, U_O2, U_O4
9	O31	A_O2′, C_O2′, G_O2′, U_O2′
10	O32	A_O3′, A_O4′, A_O5′, C_O3′, C_O4′, C_O5′, G_O3′, G_O4′, G_O5′, U_O3′, U_O4′, U_O5′
11	O2-	A_OP1, A_OP2, C_OP1, C_OP2, G_OP1, G_OP2, U_OP1, U_OP2
12	P	A_P, C_P, G_P, U_P

Dataset preparation

To derive the effective potentials through our double-iterative algorithm, we have constructed a diverse dataset of experimentally determined RNA–RNA complex structures. Specifically, we have queried all the X-ray crystal structures with resolution better than 4.0 Å and NMR structures to identify those PDB entries that contain at least two RNA chains without protein and DNA chains. As of 12 March 2017, the search yielded a total of 1158 entries. These PDB entries were manually examined and only reasonable RNA–RNA complexes were kept. Here, a reasonable RNA–RNA complex was defined as a structure that meets all following criteria. First, both the interacting RNA chains should belong to the same biological unit. Second, the complexes that contain only backbone atoms in the RNAs should be excluded. Third, there exist direct interactions with at least one base pair between the interacting RNA chains. A total of 440 structures of such RNA–RNA complexes met the three criteria. Among these 440 complex structures, 356 structures are A-form helices at the interaction site, one structure is in the Z-form, and the rest 83 structures can not be classified, where the helix form was calculated using the program DSSR of the 3DNA suite (65,66). If any of the base pairs at the interaction site is in the A-form, the complex structure will be classified as the A-form one. We have manually inspected the 83 unclassified structures and found that most of them do not form a well-defined helix at the interaction site and their RNAs interact with each other in either a side-by-side or a head-to-head style.

Then, the structures of these 440 complexes were downloaded from the PDB. The receptor and ligand RNAs were extracted for each complex and subject to manual inspection. To obtain a nonredundant dataset, all the receptor and ligand structures were converted into sequences, and clustered according to their sequence similarities to remove the redundancy. Here, the program Align of the FASTA package was used to perform all-against-all pairwise sequence alignment for the RNA structures of 440 complexes (67). The sequence identity cutoff was set to 60% during clustering of the RNA sequences (68). According to the criterion, the 440 complexes were then grouped into 160 clusters. For each cluster, one RNA–RNA complex with the best solution or the NMR structure was selected as the representative. This yielded a nonredundant set of 160 RNA–RNA complex structures.

The 160 nonredundant RNA–RNA complexes were then divided into two groups: the training and test sets. Specifically, 97 complex structures were selected to form the training set for deriving the effective potentials (Supplementary Table S1). During the selection, preference was given to those complexes that are not present in our RNA–RNA docking benchmark (69), so that the derived potential will not introduce a bias in validating our scoring function on the benchmark.

Evaluation of the derived potentials

Our scoring function of the effective potentials was extensively evaluated on the 60 test cases from our RNA–RNA docking benchmark. Of the 60 complexes, 38 cases are well-defined A-form duplex helices and the rest 22 cases are formed by non-helical interactions (Supplementary Table S1). Specifically, our RNA docking program HDOCK was used to sample possible binding modes. The effective potentials were integrated into the docking program to evaluate and rank the generated binding modes according to their binding energy scores. The performance was measured by the average number of hits per complex and the success rate in binding mode predictions with top predictions. Here, a binding mode was defined as a successful prediction or a hit if the interface RMSD between the predicted binding mode and the native complex structure is <5.0 Å after optimal superimposition of interfaces (69). The interface was defined as those residues of the bound structures consisting of at least one atom within 10 Å from the other partner. The superimposition was based on one backbone atom for each nucleotide, that is C4′ atom for RNAs (41,70). The success rate was defined as the number of cases with at least one correct prediction divided by the total number of cases in the benchmark when a certain number of top predictions were considered.

For comparison, we have evaluated the performances of three other scoring functions, ITScorePP (19), ZDOCK2.1 (71) and VDW interactions, on the same test set of 60 RNA–RNA cases. To ensure the comparative evaluation is fair, all the tested scoring functions were evaluated using their native docking packages. Namely, the results of the ZDOCK scoring function were directly obtained from the docking calculations by ZDOCK. ITScorPP and VDW interactions were also evaluated as an integrated part of the docking algorithm. During the docking calculations, conformational changes were not explicitly included, as we focused on the scoring part in this study. However, all the scoring functions were able to implicitly consider some flexibility by allowing a certain degree of penetration between two RNAs during docking (11,29).

RESULTS AND DISCUSSION

Derived pair potentials

Based on the training set of 97 diverse RNA–RNA complexes, we have extracted the effective interaction potentials for RNA–RNA interactions through our statistical mechanics-based double-iterative method. With the 12 atom types of RNA (Table 1), we had a total of 144 possible atom pairs. The occurrence frequencies for an atom pair depend on specific RNA atom types, which range from 177 178 occurrences for Car–Car to 2471 occurrences for N2X-P. All types of atom pairs have a high frequency of more than 2000, guaranteeing the sufficient statistics for generating reliable pair potentials during iteration. The iteration was efficient and converged fast, which is normally within 20 cycles. It is known that two base pairs in RNAs, A-U (adenine-uracil) and G–C (guanine–cytosine) are formed through the hydrogen bonds, which correspond to the interactions of atom pairs N21–O2 and Nar–Nar. As shown in Figure 2, the interaction potentials do show a minimum for hydrogen bonding. The more favorable (negative) potential for N21–O2 than Nar–Nar is due to the attractive electrostatic interaction in addition to the hydrogen-bonding interactions for N21–O2.

Figure 2.

The derived interaction potentials for two typical atom pairs: N21–O2 and Nar–Nar in DITScoreRR. The dashed line of y = 0 is for a reference.

Test on bound cases

We first tested our scoring function DITScoreRR on the bound structures of 60 RNA–RNA complexes (Supplementary Table S1). Docking with bound structures (i.e. bound docking) serves as a preliminary test for a developed scoring function, as the docking process does not need to consider the conformational changes in RNA structures. Being able to distinguish native structures from decoys for bound docking is the most basic capability for a scoring function.

Figure 3 shows the success rates and average number of hits per complex as a function of the number of top RNA binding modes for bound docking by DITScoreRR. The ranking and interface RMSD of the first hit for each complex is listed in Supplementary Table S2. For validation purpose, the results of three other scoring methods, VDW interactions, ITScorePP (19), and ZDOCK 2.1 (71), are also listed in the figure and table. ITScorePP is an iterative scoring function for protein–protein interactions. ZDOCK 2.1, which was originally developed for protein–protein docking, is approximated as a shape complementary-based scoring function. It can be seen from Figure 3 that DITScoreRR showed a significantly better performance in binding mode predictions and was able to predict correct binding modes for almost all the test cases, while the other three scoring methods still had some failed predictions until the top 1000 predictions were considered. Specifically, DITScoreRR yielded a success rate of 90.0% on the benchmark of 60 complexes if only the top ranked orientation was considered, compared to 63.3% for VDW, 45.0% for ITScorePP, and 11.7% for ZDOCK 2.1 (Figure 3A and Supplementary Table S2). If the top 10 ranked orientations were considered, DITScoreRR achieved a success rate of 98.3%, compared to 71.7% for VDW, 65.0% for ITScorePP, and 26.7% for ZDOCK 2.1 (Figure 3A and Supplementary Table S2). Similar trends in the average number of hits per complex can also be observed in the performances of four scoring methods. For example, DITScoreRR yielded an average of 45.43 hits per complex in the top 100 predictions, compared to 7.10 hits for VDW interactions, 8.03 hits for ITScorePP, and 2.38 hits for ZDOCK 2.1 (Figure 3B). The higher success rate and average number of hits of DITScoreRR than the other scoring methods within top predictions suggests the accuracy and robustness of DITScoreRR in binding mode prediction for bound docking.

Figure 3.

The success rates (A) and average number of hits per complex (B) in binding mode predictions for bound docking by DITScoreRR, VDW interactions, ITScorePP and ZDOCK 2.1, on the test set of of 60 RNA–RNA cases.

Basically, a satisfactory scoring function should be able to identify the native structure from decoys for an RNA–RNA complex. However, in many cases native structures are unknown. Therefore, an ideal scoring function should also be able to provide a quantitative ranking of decoys with better scores for those closer to the native structure than for those that are farther from the native structure. As such, the scoring function can always identify the binding mode with a better accuracy, or be used to guide efficient sampling of near-native binding modes. To quantify the ability of DITScoreRR in ranking binding modes, we have calculated the score-RMSD correlation coefficient with the binding decoys for each RNA–RNA case. The correlation coefficients range from –1.0 to 1.0, and a higher correlation coefficient means a better performance in ranking decoys. Figure 4 shows a comparison of the score-RMSD correlations between DITScoreRR and the other three scoring functions: VDW interactions, ITScorePP and ZDOCK 2.1. The detailed correlation coefficients are listed in Supplementary Table S3. It can be seen from Figure 4 and Supplementary Table S3 that DITScoreRR obtained a significantly better performance and had a higher correlation for most of the test cases than the other three scoring methods. Specifically, among the 60 test cases, DITScoreRR is better than VDW for 58 cases, better than ITScorePP for 55 cases, and better than ZDOCK 2.1 for 59 cases in the score-RMSD correlation (Figure 4). On average, DITScoreRR yielded a correlation coefficient of 0.752, compared to 0.135 for VDW, 0.368 for ITScorePP, and –0.108 for ZDOCK 2.1 (Supplementary Table S3), suggesting the ability of DITScoreRR in ranking decoys for bound docking.

Figure 4.

Comparison of DITScoreRR against VDW interactions, ITScorePP, and ZDOCK 2.1 using the score-RMSD correlations for bound docking on the test set of 60 RNA–RNA cases. The diagonal line stands for equal correlations, above which DITScoreRR is better and below which DITScoreRR is worse than its compared scoring function.

Test on unbound cases

In real applications, the bound structures are often not known. Individual structures will experience conformational changes when forming a complex structure upon binding. It is challenging to predict the conformational changes during docking calculations. Therefore, docking with unbound structures (i.e. unbound docking) is considered to be a more realistic assessment for a scoring function, because of the involvement of conformational changes and uncertainties in the structures. Therefore, we have also tested our scoring function DITScoreRR on the unbound structures of 60 RNA–RNA complexes in the benchmark (Supplementary Table S1). Here, the unbound structure of a bound RNA was obtained by searching its sequence against the PDB using the FASTA program (72). If an RNA structure had >90% sequence identity to the bound structure and the alignment covered at least 90% of the sequence of the bound structure, the RNA structure was considered as a candidate of the unbound structure. If there were multiple unbound structure candidates for a bound structure, the unbound structure was selected according to the following priorities: highest sequence identity, structure in free form, highest resolution crystal structure unless only NMR structures were available. For the case with an ensemble of NMR structures, the first model was selected as a representative of the unbound structure.

Figure 5A and D shows the success rates and average number of hits per complex as a function of the number of top RNA binding modes for unbound docking by DITScoreRR. The ranking and interface RMSD of the first hit for each complex is listed in Supplementary Table S2. For validation purpose, the results of three other scoring methods, VDW interactions, ITScorePP, and ZDOCK 2.1, are also listed in the figure and table. It can be seen from Figure 5 that DITScoreRR showed a significantly better performance in binding mode prediction. Specifically, DITScoreRR yielded a success rate of 53.3% on the benchmark of 60 complexes if only the top ranked orientation was considered, compared to 13.3% for VDW, 11.7% for ITScorePP and 3.3% for ZDOCK 2.1 (Figure 5A). If the top 10 ranked predictions were considered, DITScoreRR achieved a success rate of 71.7%, compared to 28.3% for VDW, 26.7% for ITScorePP and 6.7% for ZDOCK 2.1. (Figure 5A). Similar trends in the average number of hits can also be observed in the performances of four scoring methods. For example, DITScoreRR yielded an average of 26.72 hits per complex in the top 100 predictions, which is significantly higher than 3.22 hits for VDW interactions, 4.03 hits for ITScorePP, and 1.08 hits for ZDOCK 2.1 (Figure 5D). The higher success rate and average number of hits of DITScoreRR than the other three scoring methods within top predictions suggests the robustness and accuracy of DITScoreRR in binding mode prediction for unbound docking.

Figure 5.

The success rates (upper row) and average number of hits per complex (lower row) in binding mode predictions by DITScoreRR, VDW interactions, ITScorePP, and ZDOCK 2.1 for unbound docking on the test set of of 60 RNA–RNA cases. The left (A and D), middle (B and E) and right (C and F) columns are for all, A-form, and non-helical cases of the test set, respectively.

It is known that most of RNA–RNA complexes are in the A-form, which are often well-defined duplex helices. Of our test set of 60 complexes, 38 cases belong to A-form helices and 22 cases are formed with non-helical interactions (Supplementary Table S1). On the one hand, a satisfactory scoring function should be able to correctly predict the structures of A-form complexes due to their well-fined base-pairing interactions. On the other hand, it is more important for a scoring function to recognize non-helical RNA–RNA structures because such non-helical interactions are more challenging to predict and would be the bottleneck in real applications. Therefore, we have also calculated the success rates and average number of hits per complex for the A-form duplex helices and non-helical cases. The results are shown in the middle and right columns of Figure 5 and Supplementary Table S2. It can be seen from the figure that DITScoreRR obtained a significantly better performance than the other three scoring functions on both the A-form subset (Figure 5B and E) and non-helical cases (Figure 5C and F). In addition, DITScoreRR performed significantly better on the A-form complexes than on the non-helical cases, as expected, because A-form helices are mainly formed through well-defined base-pairing interactions. Interestingly, ITScorePP and ZDOCK2.1 performed worse on the A-form cases than on the non-helical structures (Figure 5B and C and Supplementary Table S2). This suggests that scoring functions trained for other types of interactions are not efficient for characterizing the base-pairing interactions in RNAs. A scoring function like DITScoreRR that is specially derived for RNA–RNA complexes is necessary for the description of RNA–RNA interactions.

Figure 6 shows a comparison of the predicted binding modes and experimentally observed native complex for four example cases. It can be seen from the figure that DITScoreRR obtained correct binding modes with a few top predictions for all the four cases, while the other three scoring functions either has a poor ranking or even failed to give any hits (Supplementary Table S2). For example, DITScoreRR obtained a correct prediction with I_rmsd = 2.18 Å at ranking #2 for target 1KIS, while the VDW interaction and ITScorePP gave the rankings of 36 and 365 for their first hits on the same target. ZDOCK 2.1 even failed to yield any hits on this target. Similar trends in the performances of four scoring functions can also be observed for the other three test cases: 2P7E, 5FJ1 and 2RN1 (Figure 6 and Supplementary Table S2).

Figure 6.

Comparison between the predicted binding modes and experimentally determined native structure of four selected unbound cases, in which the experimental structures are colored in red/cyan and the predicted complex structures are colored in blue/yellow: (A) 1KIS (ranking #2, I_rmsd = 2.179 Å), (B) 2P7E (ranking #1, I_rmsd = 0.509 Å), (C) 5FJ1 (ranking #8, I_rmsd = 1.639 Å) and (D) 2RN1 (ranking #1, I_rmsd = 2.971 Å).

To quantify the ability of DITScoreRR in ranking realistic binding modes, we have further calculated the score-RMSD correlation coefficient for the binding decoys with unbound structures. Figure 7 shows the comparison of the score-RMSD correlations between DITScoreRR and the other three scoring functions: VDW interactions, ITScorePP, and ZDOCK 2.1. The detailed correlation coefficients were also listed in Supplementary Table S3. It can be seen from Figure 7 and Supplementary Table S3 that DITScoreRR obtained a significantly better performance and had a higher correlation for most of the test cases than the other three scoring methods. Specifically, DITScoreRR is better than VDW for 55 cases, better than ITScorePP for 49 cases, and better than ZDOCK 2.1 for 55 cases in the score-RMSD correlations (Figure 7). On average, DITScoreRR yielded a correlation coefficient of 0.661, compared to 0.134 for VDW, 0.404 for ITScorePP and –0.042 for ZDOCK 2.1 (Supplementary Table S3), suggesting the ability of DITScoreRR in ranking realistic decoys for unbound docking.

Figure 7.

Comparison of DITScoreRR against VDW interactions, ITScorePP and ZDOCK 2.1 using the score-RMSD correlations for unbound docking on the test set of 60 RNA–RNA cases. The diagonal line stands for equal correlations, above which DITScoreRR is better and below which DITScoreRR is worse than its compared scoring function.

Comparison of bound and unbound docking

Several features can be observed by closely examining the results of bound and unbound docking, which can provide insights into the future development of scoring functions for RNA–RNA interactions. First, ITScorePP obtained a lower success rate than VDW interactions for both bound and unbound docking when the top 10 predictions were considered (Figures 3 and 5). This suggested that the interaction potentials for proteins can not be directly used for RNAs even though we have used the same atom typing scheme in the derivation of knowledge-based potentials. The fair success rate of VDW interactions suggested that the shape complementarity plays an important role in RNA–RNA recognition. However, this will not change the advantage of the knowledge-based scoring functions. As shown in Figures 3 and 5, although ITScorePP has a lower success rate than VDW, but yields a significantly higher average correlation than VDW, giving an overall better performance for the knowledge-based scoring function ITScorePP (Figures 4 and 7). Second, ZDOCK 2.1 performs significantly worse than VDW in both success rates and average number of hits, even though they both belong to the category of shape-based scoring functions (Figures 3 and 5). The different performances can be understood because ZDOCK 2.1 is a grid-based shape-based scoring function (71), while VDW interaction is an atom-based scoring function. Unlike proteins, RNAs have more minor grooves on their surface which are challenging for grids to represent. Therefore, an atom-based scoring method is necessary to accurately describe the interactions between RNAs.

CONCLUSION

To circumvent the reference state problem and overcome the decoy-dependent limitation, we have developed a statistical mechanics-based double-iterative algorithm for deriving knowledge-based scoring functions. Based on a training set of 97 RNA–RNA complex structures, we have derived an atomic distance-dependent scoring function of effective pair potentials for RNA–RNA interactions, which is referred to DITScoreRR, using our double-iterative method. Testing on a benchmark of 60 test cases showed that DITScoreRR performed significantly better than the other three scoring methods (VDW interactions, ITScorePP, and ZDOCK 2.1) in binding mode predictions for both bound and unbound docking. On average, DITScoreRR obtained a success rate of 98.3% and an average of 7.58 hits for bound docking, and a success rate of 71.3% and an average of 4.40 hits for unbound docking when the top 10 predictions were considered. DITScoreRR also had a significantly better capability than the other three scoring functions in ranking binding decoys. The results also showed that special training for base-pairing interactions and atom-based representation of RNAs are necessary for the development of an accurate scoring function for RNA–RNA interactions. The present double-iterative algorithm will have a general application in the development of scoring functions for other biological systems.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Natural Science Foundation of China [31670724]; National Key Research and Development Program of China [2016YFC1305800 and 2016YFC1305805]; Huazhong University of Science and Technology [3004012104]. Funding for open access charge: NSFC [31670724].

Conflict of interest statement. None declared.