Adding a new analytical procedure with clinical interpretation in the tool box of survival analysis

In a long-term comparative oncology trial, progression-free survival or overall survival time is often the study endpoint. The hazard ratio (HR) has been routinely utilized to quantify the between-group difference in survival analysis for the past five decades [1]. The validity of HR estimation procedure depends on a strong assumption of proportional hazards (PH), i.e. the ratio of the two hazard functions is constant over the entire study period. When the PH assumption is not met, the resulting estimate is not a simple average of HRs over time and is difficult to interpret clinically [2–6]. As indicated by Fei et al. [7], a standard goodness-of-fit test for the adequacy of the PH assumption generally is not informative. First, it has insufficient statistical power to detect model misspecification when the number of events of interest in the trial is small. Second, when the number of events is large, the same test may identify even a negligible misspecification. For most immunotherapy studies discussed in the article [7], the PH assumption appeared to be violated upon visual inspection. Moreover, even when the PH assumption is plausible, it is not clear that a statistically significant HR of, for example, 0.80 (immunotherapy versus control), could be translated to inform effective clinical decision making. When the underlying hazard for the control arm is low, a reduction of 20% may not represent a clinically meaningful treatment effect. The treatment decision process in practice should not be based on a single contrast such as HR without a benchmark value from the control arm. These issues and concerns have been discussed extensively [2–6]. One may argue that the HR or the log-rank test is a valid procedure to reject a null hypothesis of no treatment effect even without the PH assumption. However, it is known that such a test may lack the power to detect a treatment effect when PH assumption is not valid. Coupled with HR, median survival time or the survival rate at a specific time point is often used to summarize the ‘local aspect’ of the survival profile for each group. The median survival time may not capture the long-term survival profile or may not be estimable due to limited follow-up time in the study. Good alternatives to HR are highly desirable.

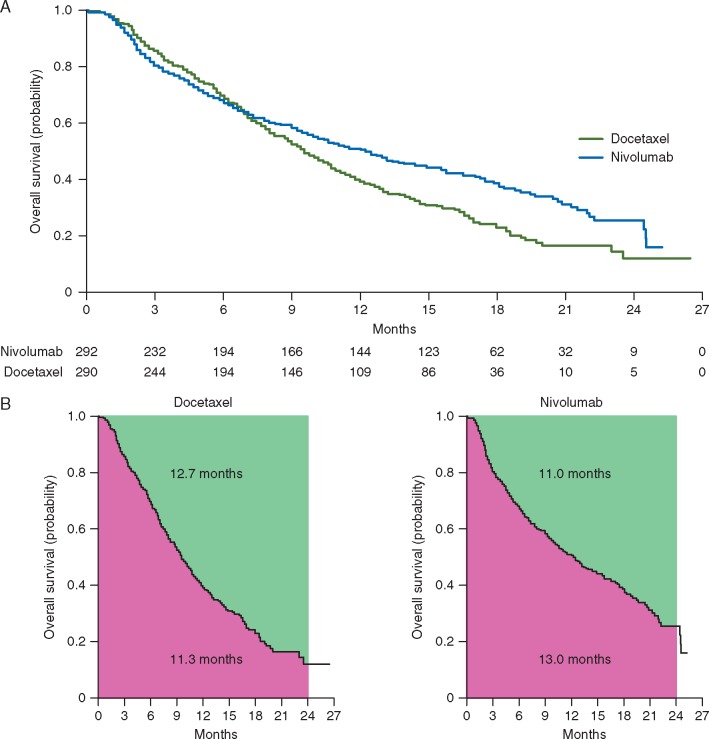
Fei et al. [7] considered an alternative to HR to quantify the group difference based on the ratio of two restricted mean survival times (RMST) or restricted mean time lost (RMTL) [2–5, 8, 9]. As an illustration of the RMST, in Figure 1A, we present the Kaplan–Meier curves for the immunotherapy group and control group based on the reconstructed individual patient overall survival data from Borghaei et al. [10, 11], which is one of the studies utilized by Fei et al. [7]. Figure 1B depicts the RMST (or t-year mean survival time) and RMTL for each arm. The RMST, the area under the Kaplan–Meier curve, through 24 months is 13.0 for nivolumab versus 11.3 months for docetaxel. That is, on average, patients treated by nivolumab would survive 13.0 months out of 24-month follow-up. The corresponding RMTLs, the area above Kaplan–Meier curve, are 11.0 and 12.7 months, respectively. The ratio of RMSTs (nivolumab versus docetaxel) is 1.15 [95% confidence interval (CI) 1.03–1.29], and corresponding ratio of RMTLs is 0.87 (95% CI 0.77–0.97). The validity of these estimates and CI’s requires no model assumptions. Moreover, there are absolute values from the control group with which to better interpret these ratios clinically.

Figure 1.

Estimated survival curves, restricted mean survival times (RMST) and restricted mean time lost (RMTL) based on reconstructed overall survival data for lung cancer study. (A) Kaplan–Meier curves for nivolumab (blue) and docetaxel (green). (B) RMST through 24 months (the area under the Kaplan–Meier curve) and RMTL through 24 months (the area above the Kaplan–Meier curve) for docetaxel (left) and nivolumab (right).

Fei et al. [7] compared the ratio of RMSTs or RMTLs with the HR. However, these two ratios are not comparable summaries for the treatment effect since they estimate different population quantities. When the survival rates are low, the ratio of RMTLs is often numerically similar to HR since the survival time for each group can be approximated by an exponential distribution. On the other hand, the relative merit of these two ratios may be assessed via the statistical power for detecting the positive treatment effect. Empirically, the authors found that these two ratios as test statistics tend to have coherent results with respect to the statistical significance using type-I error rate of 0.05. This, coupled with other recent publications [12], ease concerns that the RMST-based tests might not be as powerful as the HR-based test when the PH assumption is plausible.

Regarding the time-window from zero to a time point t to define the RMST or RMTL, Fei et al. [7] commented that this choice of ‘t’ should be based on a clinical consideration at the design stage. As suggested by the authors, after the data were collected, various time-windows may be chosen empirically. For example, one may identify the last observed or censored survival time as the upper bound of the time-window for each group, then choose the minimum of these two values as time ‘t’ for the RMSTs or RMTLs. For example, in the above example, we may choose 25.5 months instead of 24 months. The resulting ratios are identical to those with t being 24 months. Note that the HR estimate may utilize less data than RMSTs. In the above example, the information that contributes to the HR estimation ends at t = 23.5 months, which is the minimum of the last observed event time in each of the two groups (Figure 1A). This phenomenon is not widely known in practice. Moreover, since the HR estimation procedure is event driven, the above ‘t’ cannot be completely determined at the design stage.

It is important to make statistics more translational so that clinicians and patients can use them for decision making under the risk-cost-benefit consideration. The HR is not a readily translatable summary measure of the between-group difference. Alternative approaches that provide a robust and interpretable quantitative summary, such as difference or ratio of RMSTs or RMTLs, may be considered. We thank Fei et al. [7] for providing us with useful information regarding the relative merits between procedures using HR and RMST, and the editors for inviting comments on RMST as a new analytical procedure in the tool box of survival analysis.

Funding

The work was partially supported by NIH/NHLBI (R01 HL089778), NIH/AHRQ (R00 HS022193), NIH/NIA (R21 AG049385) and NIH/NIA (K08 AG0511587).

Disclosure

HF in an employee of Eli Lilly. BH is an employee of Pfizer. All remaining authors have declared no conflicts of interest.